Journal of Modern Physics, 2013, 4, 481-485
http://dx.doi.org/10.4236/jmp.2013.44068 Published Online April 2013 (http://www.scirp.org/journal/jmp)
Method of Forming Stable States of Dense
High-Temperature Plasma
Stanislav I. Fisenko, Igor S. Fisenko
Rusthermosynthesis, Moscow, Russia
Received January 26, 2013; revised February 25, 2013; accepted March 7, 2013
Copyright © 2013 Stanislav I. Fisenko, Igor S. Fisenko. This is an open access article distributed under the Creative Commons At-
tribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is prop-
erly cited.
ABSTRACT
The concept of gravitational radiation as a radiation of one level with the electromagnetic radiation is based on theo-
retically proved and experimentally confirmed fact of existence of electron’s stationary states in own gravitational field,
characterized by gravitational constant K = 1042 G (G-Newtonian gravitational constant) and by irremovable space-time
curvature. The received results strictly correspond to principles of the relativistic theory of gravitation and the quantum
mechanics. The given work contributes into further elaboration of the findings considering their application to dense
high-temperature plasma of multiple-charge ions. This is due to quantitative character of electron gravitational radiation
spectrum such that amplification of gravitational radiation may take place only in multiple-charge ion high-temperature
plasma. In elaboration of the authors’ works [1-4], an essential instantiation of the concept of fusion plasma’s steady
states formation (as the last paragraph outlines) and boundary conditions refinement in the electron’s stationary-
states-in-proper-gravitational-field problem are appended to this article.
Keywords: Gravity; Electron; Spectrum; Discharge; Fusion
1. Gravitational Radiation as a Radiation of
the Same Level as Electromagnetic
For a mathematical model of interest, which describes a
banded spectrum of stationary states of electrons in the
proper gravitational field, two aspects are of importance.
First, in Einstein’s field equations
 is a constant which
relates the space-time geometrical properties with the
distribution of physical matter, so that the origin of the
equations is not connected with the numerical limitation
of the
 value. Only the requirement of conformity with
the Newtonian Classical Theory of Gravity leads to the
small value 4
8πGc  
2
4πGc   
, where G, c are, respectively,
the Newtonian gravitational constant and the velocity of
light. Such requirement follows from the primary con-
cept of the Einstein General Theory of Relativity (GR) as
a relativistic generalization of the Newtonian Theory of
Gravity. Second, the most general form of relativistic
gravitation equations are equations with the  term. The
limiting transition to weak fields leads to the equation
,
where  is the field scalar potential,
 is the source den-
sity. This circumstance, eventually, is crucial for ne-
glecting the  term, because only in this case the GR is a
generalization of the Classical Theory of Gravity. There-
fore, the numerical values of 4
8πGc  0 and


in the GR equations are not associated with the origin of
the equations, but follow only from the conformity of the
GR with the classical theory.
From the 70’s onwards, it became obvious [5] that in
the quantum region the numerical value of G was not com-
patible with the principles of quantum mechanics. The
essence of the problem of the generalization of relativis-
tic equations on the quantum level was thus outlined:
such generalization must match the numerical values of
the gravity constants in the quantum and classical re-
gions.
In the development of these results, as a micro-level
approximation of Einstein’s field equations, a model is
proposed, based on the following assumption [1,2]:
“The gravitational field within the region of localiza-
tion of an elementary particle having a mass m0 is char-
acterized by the values of the gravity constant K and of
the constant
 that lead to the stationary states of the
particle in its proper gravitational field, and the particle
stationary states as such are the sources of the gravita-
tional field with the Newtonian gravity constant G.”
The most general approach in the Gravity Theory is
C
opyright © 2013 SciRes. JMP

S. I. Fisenko, I. S. Fisenko 482
the one which takes torsion into account and treats the
gravitational field as a gauge field, acting on equal terms
with other fundamental fields [6].
Complexity of solving this problem compels us to em-
ploy a simpler approximation, namely: energy spectrum
calculations in a relativistic fine-structure approximation.
In this approximation the problem of the stationary states
of an elementary source in the proper gravitational field
will be reduced to solving the following equations:

22
0
2ee
2n
ff
K
r



 


 
 




2
10 ll
Kf
r

 


(1)
 
22
222
02
11
e
1
21ee n
r rr
ll
lf KKr














 



2
e
f
 









(2)
 
22
22 2
02
11
e
21 e
n
r rr
ll
lfKKr













2
1e
f





 








(3)



1
1e 0
n
rr



 


2
2
11
24rr

 



 





(4)

10f


0
n
fr
(5)

(6)



000  
22
0
d1
n
(7)
r
f
rr
 (8)
Equations (1)-(3) follow from Equations (9) and (10)
2
00ggK
 


 





xx x



 


(9)

1
2
RgR Tg

 
 , (10)
after the substitution of in the form of 
 
i
,exp
El
Et
fr 


 



22 222222
ded dsindedSc trr

  
lm
Y into them and specific
computations in the central-symmetry field metric with
the interval defined by the expression [7]
(11)
The following notation is used above:
E
l
f
is the ra-
dial wave function that describes the states with a defi-
nite energy E and the orbital moment l (hereafter the
subscripts El are omitted),


,
lm
Y


—are spherical func-
tions, nn
K
Ec

, 00 Kcm

,



4πm  0
Condition (4) defines rn, whereas Equations (10)
through (7) are the boundary conditions and the normali-
zation condition for the function f, respectively. Condi-
tion (4) in the general case has the form
.


,r
n
RK



,RGr
n. Neglecting the proper gravitational field with
the constant G, we shall write down this condition as


,0RKr
n, to which equality (4) actually corresponds.

The right-hand sides of Equations (2) and (3) are cal-
culated basing on the general expression for the energy-
momentum tensor of the complex scalar field:

,2
,, ,,,0
TK

 
 

  
 
(12)
The appropriate components T

are obtained by
summation over the index т with application of charac-
teristic identities for spherical functions [8] after the sub-
stitution of i ,exp
lm
Et
frY 


 

 into (12).
In its simplest approximation (from the point of view
of the original mathematical estimates) the problem on
steady states in proper gravitational field (with constants
K and

) is solved by [1]. The solution of this problem
provides the following conclusions.
1) With the numeric values K  5.1  1031 N·m2·kg–2
and  = 4.4  1029 m
–2, there is a spectrum of steady
states of the electron in proper gravitational field (0.511
MeV - 0.681 MeV). The basic state is the observed elec-
tron rest energy 0.511 MeV.
2) These steady states are the sources of the gravita-
tional field with the G constant.
3) The transitions to stationary states of the electron in
proper gravitational field cause gravitational emission,
which is characterized by constant K, i.e. gravitational
emission is an emission of the same level as electromag-
netic (electric charge e, gravitational charge mK). In
this respect there is no point in saying that gravitational
effects in the quantum area are characterized by the G
constant, as this constant belongs only to the macro-
scopic area and cannot be transferred to the quantum
level (which is also evident from the negative results of
registration of gravitational waves with the G constant,
they do not exist).
Existence of such numerical value  denotes a phe-
nomenon having a deep physical sense: introduction into
density of the Lagrange function of a constant member
independent on a state of the field. This means that the
time-space has an inherent curving which is connected
with neither the matter nor the gravitational waves. The
distance at which the gravitational field with the constant
К is localized is less than the Compton wavelength, and
for the electron, for example, this value is of the order of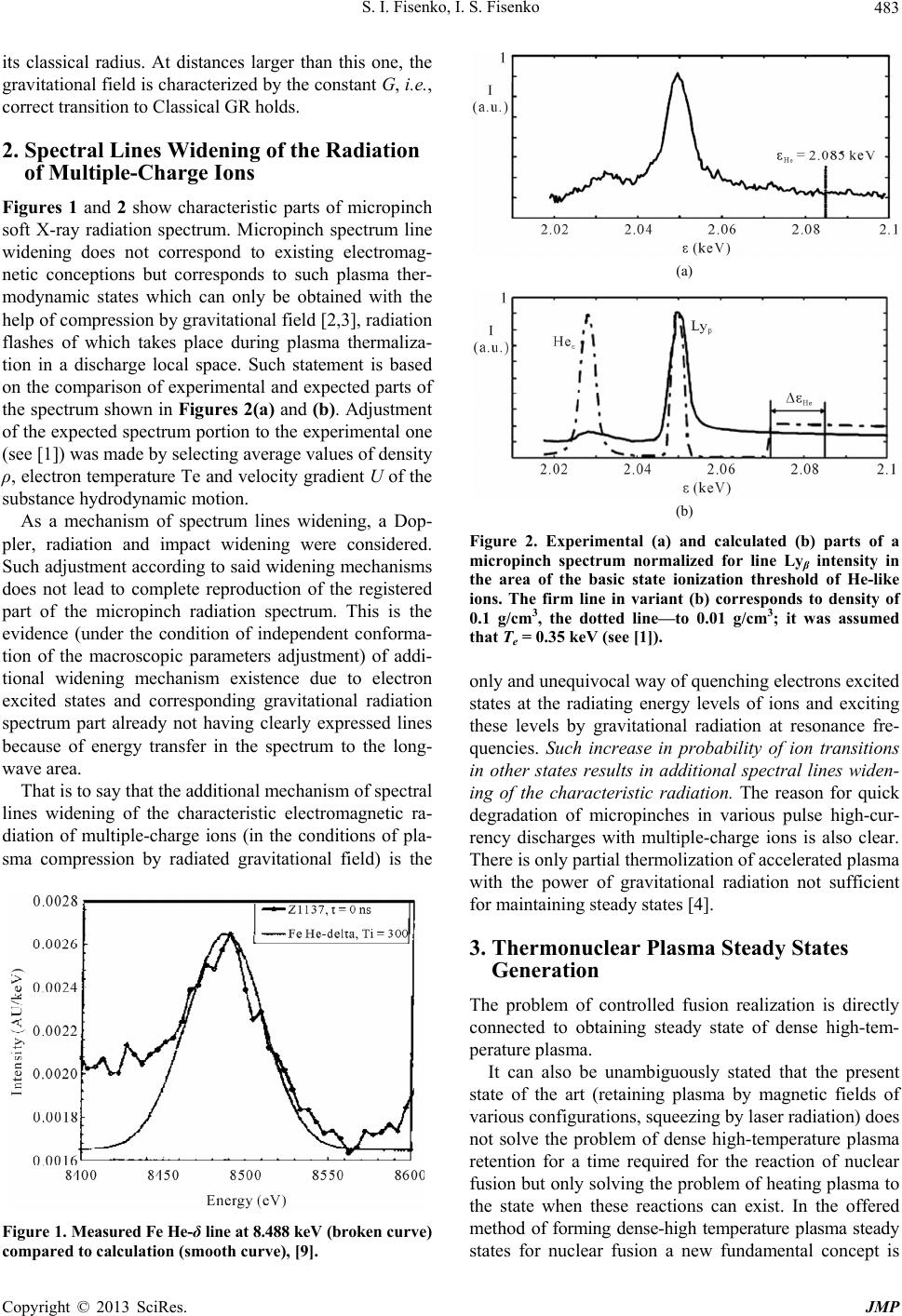

S. I. Fisenko, I. S. Fisenko 483
its classical radius. At distances larger than this one, the
gravitational field is characterized by the constant G, i.e.,
correct transition to Classical GR holds.
2. Spectral Lines Widening of the Radiation
of Multiple-Charge Ions
Figures 1 and 2 show characteristic parts of micropinch
soft X-ray radiation spectrum. Micropinch spectrum line
widening does not correspond to existing electromag-
netic conceptions but corresponds to such plasma ther-
modynamic states which can only be obtained with the
help of compression by gravitational field [2,3], radiation
flashes of which takes place during plasma thermaliza-
tion in a discharge local space. Such statement is based
on the comparison of experimental and expected parts of
the spectrum shown in Figures 2(a) and (b). Adjustment
of the expected spectrum portion to the experimental one
(see [1]) was made by selecting average values of density
ρ, electron temperature Te and velocity gradient U of the
substance hydrodynamic motion.
As a mechanism of spectrum lines widening, a Dop-
pler, radiation and impact widening were considered.
Such adjustment according to said widening mechanisms
does not lead to complete reproduction of the registered
part of the micropinch radiation spectrum. This is the
evidence (under the condition of independent conforma-
tion of the macroscopic parameters adjustment) of addi-
tional widening mechanism existence due to electron
excited states and corresponding gravitational radiation
spectrum part already not having clearly expressed lines
because of energy transfer in the spectrum to the long-
wave area.
That is to say that the additional mechanism of spectral
lines widening of the characteristic electromagnetic ra-
diation of multiple-charge ions (in the conditions of pla-
sma compression by radiated gravitational field) is the
Figure 1. Measured Fe He-δ line at 8.488 keV (broke n cur v e)
compared to calculation (smooth curve), [9].
(a)
(b)
Figure 2. Experimental (a) and calculated (b) parts of a
micropinch spectrum normalized for line Lyβ intensity in
the area of the basic state ionization threshold of He-like
ions. The firm line in variant (b) corresponds to density of
0.1 g/cm3, the dotted line—to 0.01 g/cm3; it was assumed
that Te = 0.35 keV (see [1]).
only and unequivocal way of quenching electrons excited
states at the radiating energy levels of ions and exciting
these levels by gravitational radiation at resonance fre-
quencies. Such increase in probability of ion transitions
in other states results in additional spectral lines widen-
ing of the characteristic radiation. The reason for quick
degradation of micropinches in various pulse high-cur-
rency discharges with multiple-charge ions is also clear.
There is only partial thermolization of accelerated plasma
with the power of gravitational radiation not sufficient
for maintaining steady states [4].
3. Thermonuclear Plasma Steady States
Generation
The problem of controlled fusion realization is directly
connected to obtaining steady state of dense high-tem-
perature plasma.
It can also be unambiguously stated that the present
state of the art (retaining plasma by magnetic fields of
various configurations, squeezing by laser radiation) does
not solve the problem of dense high-temperature plasma
retention for a time required for the reaction of nuclear
fusion but only solving the problem of heating plasma to
the state when these reactions can exist. In the offered
method of forming dense-high temperature plasma steady
states for nuclear fusion a new fundamental concept is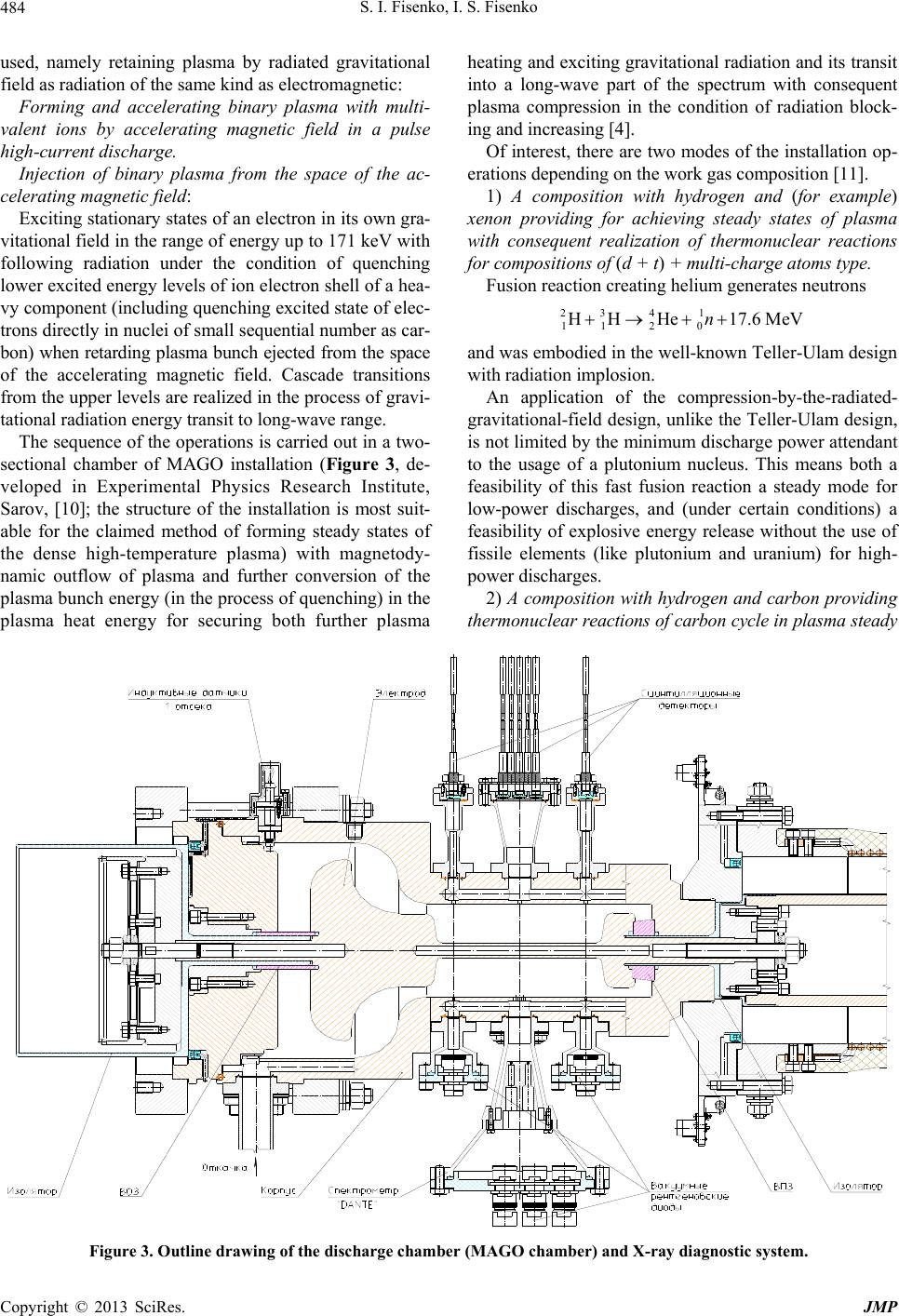

S. I. Fisenko, I. S. Fisenko
JMP
484
used, namely retaining plasma by radiated gravitational
field as radiation of the same kind as electromagnetic:
heating and exciting gravitational radiation and its transit
into a long-wave part of the spectrum with consequent
plasma compression in the condition of radiation block-
ing and increasing [4].
Forming and accelerating binary plasma with multi-
valent ions by accelerating magnetic field in a pulse
high-current discharge. Of interest, there are two modes of the installation op-
erations depending on the work gas composition [11].
Injection of binary plasma from the space of the ac-
celerating magnetic field: 1) A composition with hydrogen and (for example)
xenon providing for achieving steady states of plasma
with consequent realization of thermonuclear reactions
for compositions of (d + t) + multi-charge atoms type.
Exciting stationary states of an electron in its own gra-
vitational field in the range of energy up to 171 keV with
following radiation under the condition of quenching
lower excited energy levels of ion electron shell of a hea-
vy component (including quenching excited state of elec-
trons directly in nuclei of small sequential number as car-
bon) when retarding plasma bunch ejected from the space
of the accelerating magnetic field. Cascade transitions
from the upper levels are realized in the process of gravi-
tational radiation energy transit to long-wave range.
Fusion reaction creating helium generates neutrons
23 4 1
112 0
HH He17.6MeVn 
and was embodied in the well-known Teller-Ulam design
with radiation implosion.
An application of the compression-by-the-radiated-
gravitational-field design, unlike the Teller-Ulam design,
is not limited by the minimum discharge power attendant
to the usage of a plutonium nucleus. This means both a
feasibility of this fast fusion reaction a steady mode for
low-power discharges, and (under certain conditions) a
feasibility of explosive energy release without the use of
fissile elements (like plutonium and uranium) for high-
power discharges.
The sequence of the operations is carried out in a two-
sectional chamber of MAGO installation (Figure 3, de-
veloped in Experimental Physics Research Institute,
Sarov, [10]; the structure of the installation is most suit-
able for the claimed method of forming steady states of
the dense high-temperature plasma) with magnetody-
namic outflow of plasma and further conversion of the
plasma bunch energy (in the process of quenching) in the
plasma heat energy for securing both further plasma
2) A composition with hydrogen and carbon providing
thermonuclear reactions of carbon cycle in plasma steady
Figure 3. Outline drawing of the discharge chamber (MAGO chamber) and X-ray diagnostic system.

S. I. Fisenko, I. S. Fisenko 485
state mode, including energy pick-up in the form of elec-
tromagnetic radiation energy
CNO cycle is a set of fusion reactions resulting in con-
version of hydrogen into helium using carbon as a cata-
lyst.
In a compact notation, this cycle would be written as




12 1313
15 1512
Cp, NeCp
OeNp, C
 
14
, Np,






The

15 12
N
p, C  reaction rounds the cycle out. The
net result is that four protons turn into an

-particle—
4He nucleus with no neutrons among end products of the
cycle. Producing one helium nucleus releases 25 MeV,
the produced neutrinos carry away about 5% more of that
energy. A peculiarity of such fusion reaction cycle is that
it occurs in natural conditions of astrophysical objects. At
the same time, e.g. the design features of MAGO facility
allow achieving such a volt-ampere characteristics (VAC)
mode that boosts the speed of carbon cycle reactions. An
implementation of carbon cycle in the gravitational com-
pression design may possibly become a basic design to
form steady states of the thermonuclear plasma, bearing
in mind low abundance of hydrogen and lithium isotopes
that react with no neutrons being produced either.
REFERENCES
[1] S. I. Fisenko and I. S. Fisenko, “Gravitational Interaction
on Quantum Level and Consequences Thereof,” The Old
and New Concepts of Physics, Vol. 6, No. 4, 2009, pp.
495-521.
[2] S. I. Fisenko and I. S. Fisenko, “The Discrete Energy
Spectrum of the Gravitational Radiation in the Relativis-
tic Theory of Gravitation,” International Journal of Theo-
retical and Applied Physics (IJTAP), Vol. 2, No. 2, 2012,
pp. 32-39.
[3] S. I. Fisenko and I. S. Fisenko, “Concept of a Thermonu-
clear Reactor on the Principle of Gravitatational Confine-
ment of High-Temperature Plasma,” Applied Physics Re-
search, Vol. 2, No. 2, 2010, pp. 71-77.
[4] S. I. Fisenko and I. S. Fisenko, “Gravitational Radiation
of the Relativistic Theory of Gravitation,” British Journal
of Science, Vol. 2, No. 1, 2011, pp. 1-20.
[5] C. Siravam and K. Sinha, “The Concept of ‘Strong’ Grav-
ity,” Physics Reports, Vol. 51, No. 3, 1979, pp. 112-123.
[6] D. D. Ivanenko, et al., “Gauge Theory of Gravity,” MGU
Publishing House, Moscow, 1985, pp. 71-73.
[7] L. D. Landau and E. M. Lifshitz, “Field Theory,” Pub-
lishing House “Nauka”, Moscow, 1976, pp. 451-457.
[8] D. A. Warshalovich, et al., “Quantum Theory of Angular
Momentum,” Publishing House “Nauka”, Leningrad,
1975, pp. 282-285.
[9] M. G. Haines, et al., “Viscous Heating at Stagnation in Z-
Pinches,” Physical Review Letters, Vol. 96, No. 7, 2006,
pp. 075003-075008.
[10] O. M. Burenkov, Y. N. Dolin, P. V. Duday, V. I. Dudin,
V. A. Ivanov, A. V. Ivanovsky, G. V. Karpov, et al., “New
Сonfiguration of Experiments for MAGO Program,” XIV
International Conference on Megagauss Magnetic Field
Generation and Related Topics, Maui, 14-19 October
2012, pp. 95-99.
[11] S. Fissenko and I. Fissenko, “Method of Forming Stable
States of Dense High-Temperature Plasma,” PCT Gazette,
No. 46, 2005, p. 553.