 Journal of Modern Physics, 2013, 4, 474-480 http://dx.doi.org/10.4236/jmp.2013.44067 Published Online April 2013 (http://www.scirp.org/journal/jmp) Generalized BCS Equations and the Iron-Pnictide Superconductors Gulshan P. Malik1,2, Israel Chávez3, Manuel de Llano3 1Theory Group, School of Environmental Sciences, Jawaharlal Nehru University, New Delhi, India 2B-208 Sushant Lok I, Haryana, India 3Instituto de Investigaciones en Materiales, Universidad Nacional Autónoma de México, México DF, México Email: gulshanpmalik@yahoo.com, israelito@ciencias.unam.mx, dellano@unam.mx Received January 6, 2013; revised February 10, 2013; accepted February 20, 2013 Copyright © 2013 Gulshan P. Malik et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT A detailed quantitative study of the pnictide composite superconductor (CS) Ba0.6K0.4Fe2As2 is presented in the frame- work of the recently derived set of generalized BCS equations. Invoking multiple Debye temperatures to take into account anisotropy of the CS, we address the current experimental data on its Tc and the (not so clear-cut) gap-values via different theoretical scenarios that attempt to identify the ion species responsible for pairing in it. This is done with the aid of the Bogoliubov’s restriction on the BCS dimensionless electron-phonon coupling constant. Significantly, our study sheds light on the gaps which have recently been observed in different iron-pnictide CSs as nodes or line-nodes on the Fermi surface and have evinced considerable interest. Keywords: Generalized BCS Equation; Iron-Pnictide Superconductors; Multiple Gaps 1. Introduction Iron-pnictide superconductors (SCs) [1-4] constitute a promising new family because its members have rather high critical temperatures (Tcs); additionally, they readily allow a variety of chemical substitutions to be made. These attributes of the family suggest the possibility in the foreseeable future of fabricating SCs that might meet specific technological needs. It is therefore imperative to develop a theoretical understanding of these materials. To this end, we present in this paper the results of a de- tailed study, based on the new framework of the general- ized BCS equations (GBCSEs) [5], concerned with a pro- minent member of the family, namely Ba0.6K0.4Fe2As2 (Ba-As henceforth). We believe that our findings will help in the current flurry in the field. This paper is organized as follows. In §2 we summa- rize the main experimental features of Ba-As. §3 recalls the salient features of GBCSEs, which are then applied to this SC in §4 by taking into account different scenarios allowed by the current experimental situation. §5 sums up our findings. 2. Salient Experimental Features of Ba-As The features of Ba-As that concern us here are its Tc and the values of its multiple gaps. The experimental situa- tion with regard to the first of these is easily summarized because the values quoted for it in the literature are more or less consistent: Tc = 36.5 K [3,6]; 38 K [4,6] and 37 K [7]. The situation with regard to the gap-values, however, is not so clear cut. A broad statement about the T = 0 gap-values in ques- tion was made by [3] on the basis of angle-resolved pho- toemission spectroscopy (ARPES) measurements re- ported by [8]. The values so quoted are: 6 and 12 MeV. While reporting a gap at about 6 MeV and the absence of a gap at about 12 MeV, it was remarked in [6] that this discrepancy (the absence of the larger gap) may be in- duced by the difference in the methods adopted for de- termining the gap/s—a remark borne out by what follows. Gaps of single Ba-As crystals were determined both via scanning tunneling microscopy (STM) and spectroscopy in [7] and via penetration-depth measurements in [9]. While the latter of these approaches led to the values of 2.5 and 9.0 MeV, the values yielded by the former method are 3.3 and 7.6 MeV. The situation is further compounded because: 1) based on specific-heat data, three gap-values have been reported [10] at 3.6, 8.5 and 9.2 MeV, whereas 2) the recent ARPES experiment [11] has led to three gaps at 4, 7, and 12 MeV on hole-like C opyright © 2013 SciRes. JMP  G. P. MALIK ET AL. 475 Fermi surfaces with an additional gap at 9.5 MeV on the electron-like Fermi surface. For the application of GBCSEs to Ba-As, one requires, first of all, its Debye temperature. Then, in the two-gap scenario, given any two parameters from the set S = {∆1(0), ∆2(0), Tc}, one is enabled to calculate the re- maining parameter. In the scenario in which Ba-As is characterized by two gaps, guided by [7], we adopt for it the set S = {3.05 MeV, 8.3 MeV, Tc = 38 K} as our start- ing point. Also included in this study is an account of our findings in the scenario in which Ba-As may be charac- terized by three gaps different values for which have been quoted above. In concluding this summary of the experimental fea- tures of Ba-As we note that its Debye temperature is an essential input in this study. This is a parameter rarely quoted for the class of SCs addressed here. The value 274 K adopted by us is the one quoted in [6]. This will be further discussed below. 3. Salient Features of GBCSEs 1) They are based on the premise that superconductiv- ity arises from the formation of Cooper pairs (CPs). CPs in composite superconductors (CSs), however, are re- garded as bound via not only one-phonon exchanges, but also via exchanges of two or more species of phonons: these lead to GBCSEs [5]. This implies that CPs in a binary SC, for example, may be bound via two kinds of “glues” or “springs”—leading to two binding energies for the CPs and hence to two gaps. 2) They bypass the issue of the underlying mechanism that brings about pairing. This is so because a two-gap SC requires the specification of two dimensionless inter- action parameters 1 c and 2 c which occur in three GBCSEs: two for the gaps and one for the Tc. It is this feature of GBCSEs that enables one to calculate any one of the parameters of the set S = {∆1(0), ∆2(0), Tc}, given the other two. 3) They take into account the anisotropy of CSs by characterizing them via multiple Debye temperatures (MDTs). These were first introduced by Born and von Karman in connection with a refinement of the Debye theory of specific heat by observing that elastic waves in an anisotropic solid travel with different velocities in different directions. For a review of this and other similar work, we refer to the textbook [12]. In the context of superconductivity, MDTs were resurrected in [13], and subsequently applied [14,15] to a variety of CSs. 4. GBCSEs Applied to Ba-As 4.1. Two-Gap Scenario The steps [14] to be followed are: 1) Identify the ion species responsible for pairing in the CS. For Ba-As we assume that these are the Ba and the Fe or/and the Ba and As ions. 2) Fix the Debye temperatures of the ions identified in 1) via the following equations meant to take into account the anisotropy of the CS: 22 1 cc xx (1) 12 21 2 1 221 2 1 1 c c mmm mmm (2) These are to be applied to both the Ba0.6K0.4 and the Fe2As2 layers. In (1) is Debye temperature of the CS; in (2) m1, m2 are the atomic masses of A, B if the layer is designated as AxBx−1. A derivation of (2) is given in [5] where it is assumed that the modes of vibration of the two ions in any layer of the SC are simulated by the modes of vibration of the two bobs of a double pendulum. Note that the ratio of the Debye temperatures in (2) de- pends on the relative positions of A and B in the double pendulum. In principle, therefore, each ion species may be characterized by two values of the Debye temperature. The values of c i (i = Ba, Fe, As) thus obtained appear in Table 1, where they are marked from (1) to (6). 3) To determine the values of 1 c and 2 c , employ the following GBCSEs [5] in which W1(0) and W2(0) are to be identified with 1(0) and 2(0) [14,15], respectively 1 1 1 2 1ln1 0 c D c W (3) 12 22 12 00 tanh tanh 1d d cc cc TT cc xx x xx (4) 1 1 2 2 2 2 2 1ln1 0 2 ln 1, 0 c D c c D c DB W k W c (5) where kB is the Boltzmann constant. The λs can be de- termined with the input of: a) 1(0) and 2(0) into (3) and (5); b) 1(0) and Tc into (3) and (4); c) Tc and 2(0) into (4) and (5). One is then enabled to calculate Tc via (4), or 2(0) via (5), or 1(0) via (3). 4) Regardless of how 1,2 are determined, impose on them the Bogoliubov upper bound on [16] that each dimensionless coupling constant be positive definite and satisfy 1,2 0.5 c (6) As will be seen, this criterion is an invaluable guide in this study. 5) If one follows either approach a) or b) of paragraph Copyright © 2013 SciRes. JMP 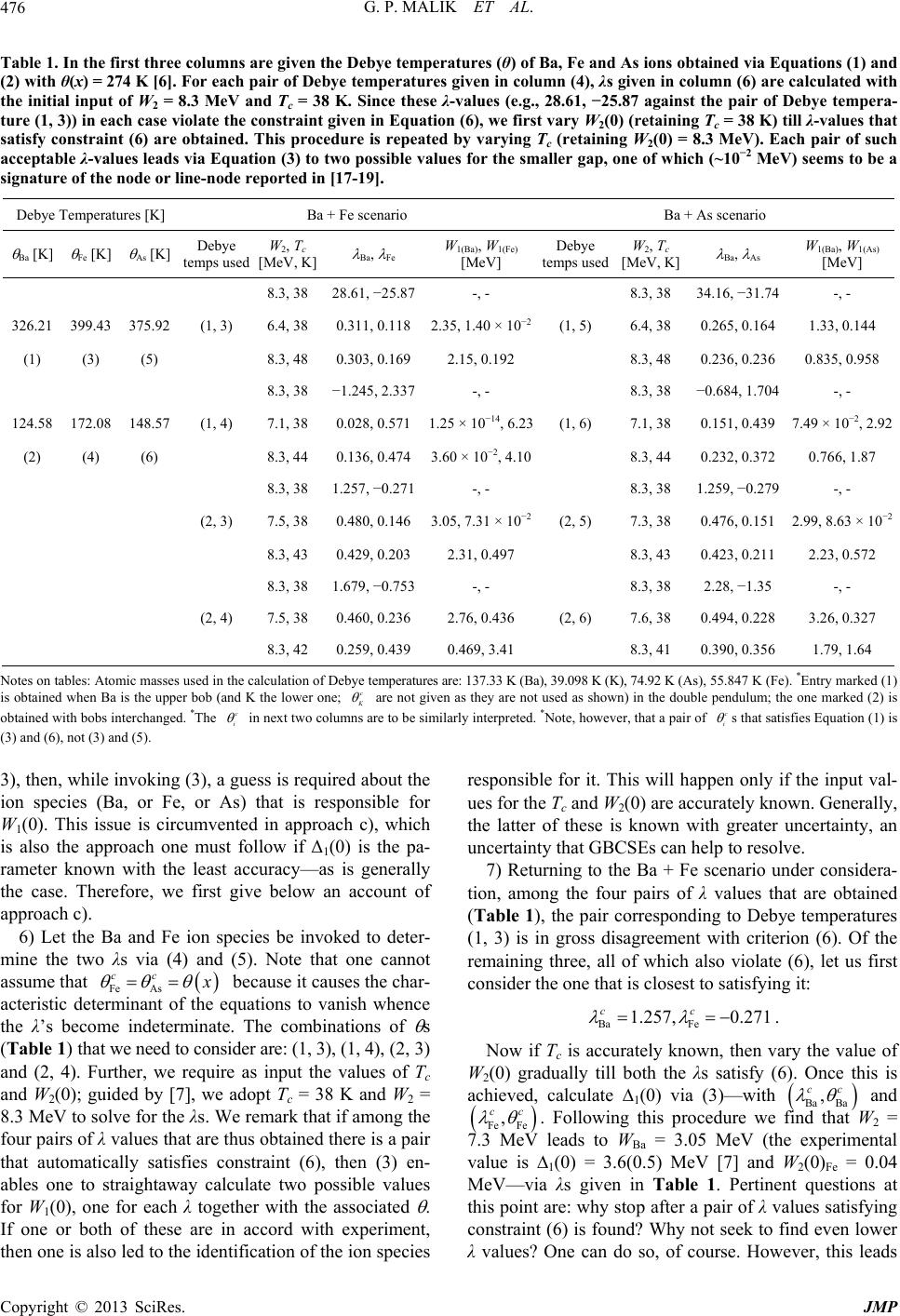 G. P. MALIK ET AL. Copyright © 2013 SciRes. JMP 476 Table 1. In the first three columns are given the Debye temperatures (θ) of Ba, Fe and As ions obtained via Equations (1) and (2) with θ(x) = 274 K [6]. For each pair of Debye temperatures given in column (4), λs given in column (6) are calculated with the initial input of W2 = 8.3 MeV and Tc = 38 K. Since these λ-values (e.g., 28.61, −25.87 against the pair of Debye tempera- ture (1, 3)) in each case violate the constraint given in Equation (6), we first vary W2(0) (retaining Tc = 38 K) till λ-values that satisfy constraint (6) are obtained. This procedure is repeated by varying Tc (retaining W2(0) = 8.3 MeV). Each pair of such acceptable λ-values leads via Equation (3) to two possible values for the smaller gap, one of which (~10−2 MeV) seems to be a signature of the node or line-node reported in [17-19]. Debye Temperatures [K] Ba + Fe scenario Ba + As scenario Ba [K] Fe [K] As [K] Debye temps used W2, Tc [MeV, K] Ba, Fe W1(Ba), W1(Fe) [MeV] Debye temps used W2, Tc [MeV, K] Ba, As W1(Ba), W1(As) [MeV] 8.3, 38 28.61, −25.87-, - 8.3, 38 34.16, −31.74 -, - 326.21 399.43 375.92 (1, 3) 6.4, 38 0.311, 0.118 2.35, 1.40 × 10−2(1, 5) 6.4, 38 0.265, 0.164 1.33, 0.144 (1) (3) (5) 8.3, 48 0.303, 0.169 2.15, 0.192 8.3, 48 0.236, 0.236 0.835, 0.958 8.3, 38 −1.245, 2.337-, - 8.3, 38 −0.684, 1.704 -, - 124.58 172.08 148.57 (1, 4) 7.1, 38 0.028, 0.571 1.25 × 10−14, 6.23(1, 6) 7.1, 38 0.151, 0.439 7.49 × 10−2, 2.92 (2) (4) (6) 8.3, 44 0.136, 0.474 3.60 × 10−2, 4.10 8.3, 44 0.232, 0.372 0.766, 1.87 8.3, 38 1.257, −0.271-, - 8.3, 38 1.259, −0.279 -, - (2, 3) 7.5, 38 0.480, 0.146 3.05, 7.31 × 10−2(2, 5) 7.3, 38 0.476, 0.151 2.99, 8.63 × 10−2 8.3, 43 0.429, 0.203 2.31, 0.497 8.3, 43 0.423, 0.211 2.23, 0.572 8.3, 38 1.679, −0.753-, - 8.3, 38 2.28, −1.35 -, - (2, 4) 7.5, 38 0.460, 0.236 2.76, 0.436 (2, 6) 7.6, 38 0.494, 0.228 3.26, 0.327 8.3, 42 0.259, 0.439 0.469, 3.41 8.3, 41 0.390, 0.356 1.79, 1.64 Notes on tables: Atomic masses used in the calculation of Debye temperatures are: 137.33 K (Ba), 39.098 K (K), 74.92 K (As), 55.847 K (Fe). *Entry marked (1) is obtained when Ba is the upper bob (and K the lower one; c K are not given as they are not used as shown) in the double pendulum; the one marked (2) is obtained with bobs interchanged. *The c i in next two columns are to be similarly interpreted. *Note, however, that a pair of c i s that satisfies Equation (1) is (3) and (6), not (3) and (5). 3), then, while invoking (3), a guess is required about the ion species (Ba, or Fe, or As) that is responsible for W1(0). This issue is circumvented in approach c), which is also the approach one must follow if Δ1(0) is the pa- rameter known with the least accuracy—as is generally the case. Therefore, we first give below an account of approach c). 6) Let the Ba and Fe ion species be invoked to deter- mine the two λs via (4) and (5). Note that one cannot assume that Fe As cc then one is also led to the identification of the ion species considera- tio Ba Fe Now if Tc is accurately known, then vy the value of W Ba Ba because it causes the char- acteristic determinant of the equations to vanish whence the λ’s become indeterminate. The combinations of s (Table 1) that we need to consider are: (1, 3), (1, 4), (2, 3) and (2, 4). Further, we require as input the values of Tc and W2(0); guided by [7], we adopt Tc = 38 K and W2 = 8.3 MeV to solve for the λs. We remark that if among the four pairs of λ values that are thus obtained there is a pair that automatically satisfies constraint (6), then (3) en- ables one to straightaway calculate two possible values for W1(0), one for each λ together with the associated . If one or both of these are in accord with experiment, responsible for it. This will happen only if the input val- ues for the Tc and W2(0) are accurately known. Generally, the latter of these is known with greater uncertainty, an uncertainty that GBCSEs can help to resolve. 7) Returning to the Ba + Fe scenario under n, among the four pairs of λ values that are obtained (Table 1), the pair corresponding to Debye temperatures (1, 3) is in gross disagreement with criterion (6). Of the remaining three, all of which also violate (6), let us first consider the one that is closest to satisfying it: 1.257, 0.271 cc . ar 2(0) gradually till both the λs satisfy (6). Once this is achieved, calculate 1(0) via (3)—with , cc and Fe Fe , cc . Following this procedure we findW2 = leads to WBa = 3.05 MeV (the experimental value is 1(0) = 3.6(0.5) MeV [7] and W2(0)Fe = 0.04 MeV—via λs given in Table 1. Pertinent questions at this point are: why stop after a pair of λ values satisfying constraint (6) is found? Why not seek to find even lower that 7.3 MeV λ values? One can do so, of course. However, this leads  G. P. MALIK ET AL. 477 one farther away from the starting point of W2(0) = 8.3 MeV. If W2(0) is believed to be accurately known, then apply the same procedure by varying Tc. In this case Tc has to be increased in order to obtain the λs that satisfy constraint (6). Thus, Tc = 43 K yields Ba 0.4 29 c , Fe 0.203 c , which lead to 1(0)Ba = 2.31 MeV, 1(0)Fe = 0.5 MeV. Also given in Table 1 are the results of a sim- for all the other pairs of λ values not only in the Ba + Fe scenario, but also in the Ba + As scenario. We are thus led to the results: a) In the Ba + Fe scenario, the only combination of Debye temperatures that can account for the experimental features of BaAs is (2, 3) since this leads to set {3.05 MeV, 7.3 MeV, 38 K}, the experimental range of the values of the gaps being: 1(0) = 3.6(0.5) MeV and 2(0) = 8.3(0.9) MeV; b) Similarly, in the Ba + As scenario the only acceptable combination of Debye temperatures is (2, 6) which leads to the set {3.27 MeV, 7.6 MeV, 38 K}; c) In both cases the smaller gap is due to Ba and the theory has led to it per se; d) It seems interesting to note that if both the Ba + Fe and the Ba + As scenarios are invoked for the formation of CPs then, in principle, one can account for the four gaps that have recently been reported from an ARPES experiment [11]. 8) We now deal with approach a), paragraph c). As- sumin i lar exercise g that (0) = 3.6 MeV and 3 MeV [7], w 1 e seek to calculate the Tc of the CS via (4) “after the λs are determined via (3) and (5) by invoking both the (Ba, Fe) and the (Ba, As) pairs. The combinations of Debye temperatures that we now have to deal with, together with the results that they lead to, have been given in Ta- ble 2. This table also provides a guide, should it be 2(0) = 8. needed, about employing approach b), paragraph c). The results in this table are not conclusive because of the un- certainties in both—the input values of Δ1(0) and 2(0). Nevertheless, it seems significant that the lowest best result for Tc, i.e. 40.7 K, should have been led to by the (2, 6) combination of Debye temperatures as was the case above. 4.2. Three-Gap Scenario The equality between |W| (which is defined via the rela- tion 2EF + W for the total energy of a CP where EF is the Fermi energy) and Δ [5] implies that there must be three |W|s if there are three gaps. We now take into account CPs bound via three-phonon exchanges in addition to those that are bound via one- and two-phonon exchanges. Equations (3) and (5) are therefore supplemented [14,15] by 12 12 33 3 3 3 22 1ln1 ln1 00 2 ln10 cc DD cc c D c WW W (7) Further, (4) now goes over to 12 3 22 12 00 2 3 0 tanh tanh 1d d tanh d cc cc cc TT cc T c xx x xx xx x fferent pairs of Debye temperatures given in Table 1, and the c-values that they lead to via ith the exception of two of these which are only marginally greater than 0.5 (e.g., (8) Table 2. Values of λs calculated via Equations (3) and (5) for di TEquation (4). W 0.515 in both the Ba + Fe and the Ba + As scenarios), all the λs satisfy constraint (6). Ba + Fe scenario Ba + As scenario Debye temps Tc Debye temps Tc λBa, λFe λBa, λAs (1, 3) 0.355 47.0.355 0.124 47.0.121 9 (1, 5) 8 (1, 4) 0.355 0.177 46 (1, 6) 0.355 0.192 45.5 (2, 3) 0.515 0.153 42.2 (2, 5) 0.515 0.157 42.2 (2, 4) 0.515 0.224 41.1 (2, 6) 0.515 0.242 40.7 (3, 1) 0.333 0.125 48.4 (5, 1) 0.339 0.127 48.2 (3, 2) 0.333 0.201 45.6 (5, 2) 0.339 0.204 45.4 (4, 1) 0.449 0.154 44.1 (6, 1) 0.477 0.159 43.2 (4, 2) 0.449 0.242 42 (6, 2) 0.477 0.256 41.2 Notes os: Atomic mased in the caln of Debye tematures are: 137.a), 39.098 K4.92 K (As), 5 K (Fe). *Entryd (1) is obtaen Ba is theob (and K r one; c K n table ined wh sses u upper b culatio the lowe per33 K (B (K), 75.847 marke at given as thet used as sh the double; the one (2) is re noy are noown) in pendulummarked obtained with bobs interchanged. *The c i in next two columns are to be similarly interpreted. *Note, however, that a pair of c i s that satisfies Equation (1) is (3) and (6), not (3) and (5). Copyright © 2013 SciRes. JMP  G. P. MALIK ET AL. 478 Scenario 1 Ba + Fe Scenario 2 Ba + As Scenario 3 Ba + Fe + A s Ba 0.6 K 0.4 Fe 2 As 2 Debye remperature θ = 274 K W 1 (0) = 3.05 meV W 2 (0) = 7.3 meV T c = 38 K W 1 (0) = 2.99 meV W 2 (0) = 7.3 meV T c = 38 K W 1 (0) = 3.3 meV W 2 (0) = 7.7 meV W 2 (0) = 8.4 meV T c = 38 K Figure 1. Schematic diagram giving the best-case values for the Tc and the gap-values led to by GBCSEs for Ba0.6K0.4Fe2As2 based on its characterization via 2- and 3-gap scenarios. Thus we have four Equations (3), (5), (7) and (8), in- olving the three interaction constants c v1 ,c 2 and 3 c nad which can be determined with the input of any three quantities from the set {1(0), 2(0), 3(0), Tc}. Since the greatest uncertainty among these pertains to 30, we first seek to calculate it by determining the three λs via (3), (5) and (8). Guided by the findings of Secto 4.1, we invoke Debye temperature (2), see Table 1, for pairs bound via one-phonon exchanges, the combination of Debye temperatures (2, 6) for pairs bound via two-pho- non exchanges, and the combination (2, 6, 3) in the equa- tion for Tc. As our starting point for the inputs, we use the set: {∆1(0) = 3.6 MeV, ∆2(0) = 8.3 MeV, 38 K}. This leads to va i n lues of the three λs as {0.515, 0.243, −0.02}. Since these values are in conflict with constraint (6), we first vary 1(0): lowering its value to 3.3 MeV reduces the first two values to 0.496 and 0.26, but the third value (0.02) remains unchanged. Keeping ∆1(0) = 3.3 MeV, we now reduce the value of 2(0) whence, at 7.6 MeV, we find 20.227 c and 5 32.871 10 c while 1 c remains unchanged at 0.496. This set of λs leads to |3(0)| = 7.6 MeV via (7), which is not surprising because 3 c is negligible. In a heuristic spirit, if we keep 1(0) and 2(0) fixed at 3.3 and 7.3 MeV respectively, and in- crease Tc from 38 to 42 K, |3(0)| attains a value of 8.5 MeV. As further illustrations of how the GBCSEs may be can determine the three λs by using these as input into (3), (5) and (7), and then calculate Tc via (8). Using the (2, 6, 3) used, we draw attention to the gap values determined via the specific heat data [10]: 3.6, 8.5, and 9.2 MeV. One combination of temperatures, the values of λs so found are: 0.515, 0.232 and 0.021. Since the first of these vio- lates constraint (6), we need to vary 1(0); changing its value from 3.6 to 3.3 MeV without changing the values of 2(0) and 3(0), we find the λ-values to be: 0.496, 0.27 and 0.02. Equation (8) now yields Tc = 44.5 K. We note that the input of 3.3, 7.7, and 8.4 MeV for the gap values leads to 0.496, 0.232, and 0.021 for the three λs, which lead to Tc = 41.4 K. We finally note that, of course, one can also seek to determine 1(0) or 2(0) with the input of {2(0) or 1(0), 3(0), Tc}. These lead to results simi- lar to those already quoted. The best scenarios are illus- trated in Figure 1. As just shown, two gaps and the Tc of the iron-pnictide CS dealt with here are calculated by determining the sets { 1, 1} and { 2, 2}. The use of both of these in (5) yields the larger gap, 2, while use of one of these in (3) yields the smaller gap, 1. Hence the question: what about the gap yielded by the other set via (3)? Not only in the present instance (see Table 1) but quite generally, the value of this gap is much smaller than 1 and often approaches zero [14,15]. Such gaps show up as nodes or lines of nodes on the Fermi surface and while for Ba-As they were reported by, among others [8], and have of late Copyright © 2013 SciRes. JMP  G. P. MALIK ET AL. 479 been studied with avid interest as evidenced by [17-19]. Note also that we found above a value of 2.871 × 10−5 for λ3 in the three-gap scenario, which leads to a vanishing value for gap. Based on [14,15] and the present work, we conjecture that the almost-vanishing gaps, such as that for λ3, should be a feature of most (if not all) CSs. We note that this feature, as also reported in [17-19], appears to support the scenario in which CPs are formed via more than one phonon exchanges. 5. Conclusions 1) We first note that if the drop in the property (e.g., resistivity) of a CS is sharp, then there is no ambiguity in defining its Tc. If not, the mid-point of the temperature- range over which the drop takes place is some e present study and also earlier in applying GBCSEs, Tc should be ta have been quoted in the literature. Th ni ch NCES 0, No. 11, 2008, pp. 3296-3297. doi:10.1021/ja800073m times work quoted as the Tc. Th [14,15] suggests that ken as the temperature which marks the onset of the said drop. 2) It was noted that the Debye temperature of the CS to which GBCSEs are applied is an important parameter. The value of this parameter used by us is the one quoted in [6] which need not necessarily be the value character- izing different samples of Ba-As for which the Tc and the gap valuese sig- ficance of the detailed quantitative results presented here needs to be assessed in light of this limitation. 3) Given the current experimental situation, we have shown that the GBCSEs can achieve for the iron pnictide SC Ba-As, which is a CS, what the usual BCS equations do for simple SCs. Hence they may be of value in the ongoing work concerned with the other iron-pnictide SCs. Extension of our approach to deal with CSs that may be aracterized by four gaps is straightforward. A tangible treatment for such an SC will, however, require precise experimental values of its Tc and at least some of its gaps. 6. Acknowledgements IC acknowledges support from CONACyT (Mexico) grant 103847, and MdeLl from UNAM-DGAPA-PAPIIT (Mexico) grant IN102011. REFERE [1] Y. Kamihara, T. Watanbe, M. Hirano and H. Hosono, “Iron-Based Layered Superconductor La[O1−xFex]FeAs (x = 0.05 - 0.12) with Tc = 26 K,” Journal of the American Chemical Society, Vol. 13 [2] H. Takahashi,mihara, M. Hirano K. Igawa, K. Arii, Y. Ka and H. Hosono, “Superconductivity at 43 K in an Iron- Based Layered Compound LaO1−xFxFeAs,” Nature, Vol. 453, No. 7193, 2008, pp. 376-378. doi:10.10/nature06972 [3] K. Ishida, Y. Nakai and H. J. Hosono, “To What Extent Iron-Pnictide New Superconductors Have Been Clarified: A Progress Report,” Journal of the Physical Society of Japan, Vol. 78, 2009, Article ID: 062001. doi:10.1143/JPSJ.78.062001 [4] P. M. Aswathy, J. B. Anooja, P. M. Sarun and U. Syama- prasad, “An Overview on Iron Based Superconductors,” Superconductor Science and Technology, Vol. 23, No. 7, 2010, Article ID: 073001. doi:10.1088/0953-2048/23/7/073001 [5] G. P. Malik, “On the Equivalence of Bindin Cooper Pair and the BCS Energ g Energy of a y Gap: A Framework for Dealing with Composite Superconductors,” International Journal of Modern Physics B, Vol. 24, No. 9, 2010, p. 1159. doi:10.1142/S0217979210055408 [6] G. Mu, H. Luo, Z. Wang, L “Low Temperature Specific Heat o . Shan, C. Ren and W. Wen, f the Hole-Doped Ba0.6K0.4Fe2As2 Single Crystals,” Physical Review B, Vol. 79, No. 17, 2009, Article ID: 174501. doi:10.1103/PhysRevB.79.174501 [7] L. Shan, Y. Wang, B. Shen, B. Zeng, Y. Huang, A. Li, et al., “Observation of Ordered Vortices with Andreev Bound States in Ba0.6K0.4Fe2As2,” Nature Physics, Vol. 7, 2011, pp. 325-331. doi:10.1038/nphys1908 [8] H. Ding, P. Richard, K. Nakayama, K. Sugawara, T. Arakane, Y. Sekiba, et al., “Observati faceDependent Nodeless Supercond on of Fermi-Sur- ucting Gaps in Ba0.6K0.4Fe2As2,” Europhysics Letters, Vol. 83, No. 4, 2008, Article ID: 47001. doi:10.1209/0295-5075/83/47001 [9] C. Ren, Z. Wang, H. Luo, H. Yang, L. Shan and W. Hai- Hu, “Evidence for Two Energy Gaps in Superconducting Ba0.6K0.4Fe2As2 Single Crystals and the Breakdown of the Uemura Plot,” Physical Review Letters, Vol. 101, No. 25, 2008, Article ID: 257006. doi:10.1103/PhysRevLett.101.257006 [10] P. Popovich, A. V. Boris, O. V. Dolgov, A. A. Golubov, 5.027003 D. L. Sun, C. T. Lin, et al., “Specific Heat Measurements of Ba0.6K0.4Fe2As2 Single Crystals: Evidence for a Multi- band Strong-Coupling Superconducting State,” Physical Review Letters, Vol. 105, No. 2, 2010, Article ID: 027003. doi:10.1103/PhysRevLett.10 u, X. F. Wang, X. [11] Y. Zhang, L. X. Yang, F. Chen, B. Zho H. Chen, X. H., et al., “Out-of-Plane Momentum and Sym- metry-Dependent Energy Gap of the Pnictide Ba0.6K0.4Fe2As2 Superconductor Revealed by Angle-Re- solved Photoemission Spectroscopy,” Physical Review Letters, Vol. 105, No. 11, 2010, Article ID: 117003. doi:10.1103/PhysRevLett.105.027003 [12] F. Seitz, “The Modern Theory of Solids,” McGraw Hill, New York, 1940. [13] G. P. Malik and U. Malik, “On the Calculationc Superconducting Binary Alloys Based on Two-Phonon Exchange Mechanism,” Physica B, Vol. 348, No. 1-4, 2004, pp. 341-346. of T’s of doi:10.1016/j.physb.2003.12.009 [14] G. P. Malik, “Generalized BCS Equations: Applications,” doi:10.1142/S0217979210055858 Internantional Journal of Modern Physics B, Vol. 24, No. 19, 2010, p. 3701. [15] G. P. Malik and U. Malik, “A Study of the Thallium- and Bismuth-Based High-Temperature Superconductors in the Copyright © 2013 SciRes. JMP  G. P. MALIK ET AL. Copyright © 2013 SciRes. JMP 480 No. Framework of the Generalized BCS Equations,” Journal of Superconductivity and Novel Magnetism, Vol. 24, 1-2, 2011, pp. 255-260. doi:10.1007/s10948-010-1009-0 [16] J. M. Blatt, “Theory of Superconductivity,” Academic Press, New York, 1964, p. 206. [17] D. Lee, “Iron-Based Superconductors: Nodal Rings,” Na- ture Physics, Vol. 8, 2012, pp. 364-365. doi:10.1038/nphys2301 [18] Y. Zhang, Z. R. Ye, Q. Q. Ge, F. Chen, J. Jiang, M. Xu, B. P. Xie, et al., “Nodal Superconducting-Gap Structure in Ferropnictide Superconductor BaFe2(As0. Physics, Vol. 8, 2012, pp 7P0.3)2,” Nature . 371-375. doi:10.1038/nphys2248 [19] M. P. Allan, A. W. Rost, A. P. Mackenzie, Y. Xie, J. C. Davis, K. Klhou, et al., “Anisotropic Energy Gaps of Iron-Based Superconductivity from In cle Interference in LiFeA traband Quasiparti- s,” Science, Vol. 336, No. 6081, 2012, pp. 563-567. doi:10.1126/science.1218726
|