Received 13 March 2016; accepted 10 April 2016; published 14 June 2016

ABSTRACT

In this paper, we introduce the notion of intuitionistic fuzzy α-generalized closed sets in intuitionistic fuzzy minimal structure spaces and investigate some of their properties. Further, we introduce and study the concept of intuitionistic fuzzy α-generalized minimal continuous functions.

Keywords:

Intuitionistic Fuzzy Topology, Intuitionistic Fuzzy α-Generalized Closed Set, Intuitionistic Fuzzy α-Generalized Continuous Function, Intuitionistic Fuzzy α-Generalized Continuous Mappings

1. Introduction

The concept of fuzzy sets was introduced by Zadeh [1] and later Atanassov [2] generalized this idea to intuitionistic fuzzy sets. Coker [3] introduced the notion of intuitionistic fuzzy topological space and other related concepts. The concept of minimal open set has been introduced by Nakaoka and Oda [4] in 2001. The concept of intuitionistic fuzzy generalized minimal open set has been introduced by Bhattacharya et al. [5] in 2008. Intuitionistic fuzzy α-generalized closed sets and its properties in intuitionistic fuzzy topology was introduced and studied in [6] [7] . Recently, some results on intuitionistic fuzzy generalized minimal closed sets were introduced by Bhattacharya [8] in 2010. In this paper, we introduce the notion of intuitionistic fuzzy α-generalized closed sets and intuitionistic fuzzy α-generalized* closed sets in intuitionistic fuzzy topological spaces and investigate some of their properties. Further, we introduce and study the concept of intuitionistic fuzzy α-generalized minimal continuous functions.

2. Preliminaries

Throughout this paper, by (X, τ) or simply by X we will denote the Coker’s intuitionistic fuzzy topological space (briefly, IFTS). For a subset A of a space (X, τ), cl(A), int(A) and 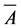denote the closure of A, the interior of A and the compliment of A respectively. Each intuitionistic fuzzy set (briefly, IFS) which belongs to (X, τ) is called an intuitionitic fuzzy minimal open set (briefly, IFMOS) in X. The complement A of an IFMOS 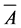in X is called an intuitionistic fuzzy minimal closed set (briefly, IFMCS) in X.

We introduce some basic notions and results that are used in the sequel.

Definition 2.1. [3] A subset A of a family τ of IF sets on X is called an IF minimal open set in X if an IF open set which is contained in A is either 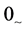or A.

Definition 2.2. [3] An IF set is said to be an IF Maximal open set of IFTS (X, τ) if and only if it is not contained in any other open set of τ.

Definition 2.3. [9] Let X be a nonempty fixed set and I be the closed interval [0, 1]. An intuitionistic fuzzy set (IFS) A is an object of the following form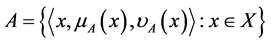, where the mappings 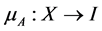and denote the degree of membership (namely) and the degree of non-membership (namely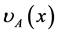) for each element 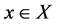to the set A, respectively, and 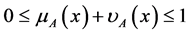for each.

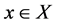Obviously, every fuzzy set A on a nonempty set X is an IFS of the following form

.

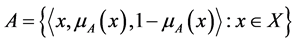Definition 2.4. [9] Let A and B are IFSs of the form 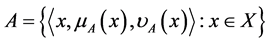and . Then

1) 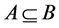if and only if and;

2);

3);

4).

Definition 2.5. [10] An IF topology on a nonempty set X is a family of IF Sets in X containing and closed under arbitrary infimum and finite supremum. In this case the pair (X, τ) is called an IFTS and each IFS in τ is known as an IF open set. The compliment of an IF open set in an IFTS (X, τ) is called an IF closed set in X.

Definition 2.6. [10] Let (X, τ) is an IF Topological Space and A an IF Set in X. Then closure of A is defined by and the fuzzy interior of A is defined by.

Definition 2.7. [10] Let f be a map from set X to set Y. Let be an IF open set in X and be an IF open set in Y. Then is an IF open set in X defined by and is an IFOS in Y defined by

Definition 2.8. [10] A map is said to be an IF continuous function from IFTS (X, τ) to IFTS (Y, s) iff is an IF open set in X for every open set V of Y.

Definition 2.9. [11] Let (X, τ) is a topological space. A family τ of IFSs on X is called an IF supra-topological space on X if and τ is closed under arbitrary supremum. Each member of τ is called an IF supra-open set and complement of an IF supra-open set is an IF supra-closed set.

Definition 2.10. [12] A fuzzy subset A of X is a fuzzy generalized closed set if whenever, H being a fuzzy open subset of X.

Definition 2.11. [12] A fuzzy subset A of X is a fuzzy dense set if.

Definition 2.12. [13] An IF set is said to be an IF α-open set of IFTS (X, τ) iff.

Definition 2.13. [14] Let an IF -structure on X. An IF open set is said to be an open if

3. On Intuitionistic Fuzzy α-Generalized Minimal Closed Sets

In this section the concept of IF α-generalized minimal open set is introduced and some of its properties are discussed. Lastly the IF topological structure obtained by the collection of this set is studied.

Definition 3.1. An IF set A is said to be an IF α-generalized minimal closed set, if there exist at least one IF Minimal Open Set U containing A such that.

Example 3.2. Let and be two IF subsets of X. Let the corresponding topological space be. Here is an IF Minimal Open Set of τ. Consider a set, then and. Hence C is an IF α-generalized minimal closed set.

Theorem 3.3.

1) Let, where U is an IF minimal open set. If B is an IF α-generalized minimal closed set, then A is also so.

2) If and B is an IF α-generalized minimal closed set then A is also so.

Proof. a) Let, where U is an IF minimal open set i.e.. From definition as B is an IF α-generalized minimal closed set implies. i.e. A is also an IF α-generalized minimal closed set.

b) Since B is an IF α-generalized minimal closed set i.e. where U is an IF minimal open set and from definition as B is an IF α-generalized minimal closed set implies i.e. A is also an IF α-generalized minimal closed set.

Theorem 3.4. An IF set A is IF α-generalized minimal closed and IF α-minimal open set then A is an IF closed set. Conversely if A be an IF α-closed set and an IF minimal open set then A is an IF α-generalized minimal closed set.

Proof. Let if possible A be an IF α-generalized minimal closed set i.e. there exist an IF minimal open set U containing A such that. Since A itself is IF α-minimal open set. But we know that. Hence. i.e. A is an IF α- closed set.

Conversely, Let A be an IF α- closed set and an IF minimal open set then from definition it is an IF α-generalized minimal closed set.

Theorem 3.5. Every IF α-generalized minimal closed set is either IF rare set or an IF minimal open set i.e. A is an IF rare set or the IF minimal open set containing A is an IF closed set i.e. A is an IF closed set.

Proof. Let if possible A be an IF α-generalized minimal closed set then there exist an IF minimal open set U containing A such that αcl(A) is contained in U. From Theorem 3.3., Let, where U is an IF minimal open set. If B is an IF α-generalized minimal closed set, then A is also so. We know that, Since A is IF α-generalized minimal closed set int(A) is also so, but int(A) is an IF open set and no non-null IF open set can be a proper subset of an IF minimal open set. So or. i.e. A is either an IF rare set or an IF minimal open set. Now if,. But we know that. i.e. U is an IF minimal closed set.

Converse of the above theorem need not be true which follows from the following example.

Example 3.6. Let, , and the IF topological space is. Here is the IF minimal open set but not the IF α-generalized minimal closed set. Let be another IF set. C is an IF rare set but not IF α-generalized minimal closed set. But if the IF minimal open set containing A is an If closed set then obviously A is an IF α-generalized minimal closed set.

Theorem 3.7. Every IF α-generalized minimal closed set is an IF α-generalized closed set.

Proof. Let A be an IF α-generalized minimal closed set then there exist an IF minimal open set U such that implies. Since U is an IF minimal open set where O is an IF open set. Hence. i.e. A is an IF α-generalized closed set.

Converse of the above theorem need not be true which follows from the following example.

Example 3.8. Let, , and the IF topological space is. Here is the IF minimal open set. Let be another IF set. C is not IF α-generalized minimal closed set but IF α-generalized closed set.

Theorem 3.9. Let A be any IF α-generalized minimal closed set then, for any IF minimal open set U and hence either is not an IF open set or.

Proof. Let A be an IF α-generalized minimal closed set then implies for any IF minimal open set U. Therefore, since U is an IF minimal open set. Hence. i.e. infimum of all IF open set containing A is less than the IF minimal open set but it is possible if and only if either is not an open set or, Since cannot be null IF set and any IF open set cannot be less than the IF minimal open set. Also we know that arbitrary infimum of IF open set need not be IF open set. So may not be an IF open set if X is an arbitrary set. But if X is a collection of IF finite set then.

Theorem 3.10. Let A be any IF generalized minimal closed set then if the set X is finite.

Proof. Since A is an If α-generalized minimal closed set, where U is an IF minimal open set then. Therefore, since is the infimum of all IF open set containing A and the set X being finite is an IF open set.

Theorem 3.11.

(i) is an IF α-generalized minimal closed set but is not an IF α-generalized minimal closed set.

(ii) Arbitrary union of IF α-generalized minimal closed set is an IF α-generalized minimal closed set.

(iii) Arbitrary intersection of IF α-generalized minimal closed set is an IF α-generalized minimal closed set.

Proof. (i) is obvious.

To prove (ii) Let be an arbitrary collection of IF α-generalized minimal closed set. Since in an IF topological space there exist a unique IF minimal open set. Let U be the corresponding IF minimal open set. i.e., where U is an IF minimal closed set, implies. Therefore, implies. But we know that. Thus arbitrary union of IF α-generalized minimal closed set is an IF α-generalized minimal closed set.

To Prove (iii) Let be an arbitrary collection of IF α-generalized minimal closed set. Since in an IF topological space there exist a unique IF minimal open set. Let U be the corresponding IF minimal open set. i.e., where U is an IF minimal closed set, implies. Obviously, and thus. Therefore arbitrary intersection of IF α-generalized minimal closed set is an IF α-generalized minimal closed set.

Definition 3.12. Let be a mapping such that inverse image of IF closed set in s is an IF α-generalized minimal closed set in τ. Then this mapping is called an IF α-generalized minimal continuous mapping.

Theorem 3.13. Let be an IF α-generalized minimal continuous function then it is an IF α-generalized continuous function.

Proof. It is obvious from Theorem 3.7.

Remark 3.14. Converse of the above theorem need not be true which follows from the following example:

Let, and the IF topological space is . Here is the IF minimal open set. Let be another IF set. C is not IF α-generalized minimal closed set but IF α-generalized closed set. Let us consider a mapping such that for all x in s. Here f is IF α-generalized continuous but not IF α-generalized minimal continuous function.

Theorem 3.15. Let be an IF α-generalized minimal continuous function and be an IF continuous function then is an IF α-generalized minimal continuous function.

Proof. Here. Now g is IF continuous function then is an IF closed set whenever z is an IF closed set in Z and hence is an IF α-generalized minimal closed, since f is an IF α-generalized minimal continuous function. Hence inverse image of a IF closed set in Z is an IF α-generalized minimal closed set in X. Thus is an IF α-generalized minimal continuous function.

4. On Intuitionistic Fuzzy α-Generalized* Minimal Closed Sets

In this section the concept of IF α-generalized* minimal open set is introduced and some theorems related to this newly constructed set are studied and also related properties are discussed.

Definition 4.1. An IF set B is said to be an IF α-generalized* minimal closed set, if there exist at least one IF Minimal Open Set A containing B such that.

Example 4.2. Let and be two IF subsets of X Let the corresponding topological space be. Here is an IF Minimal Open Set of τ. Consider a set, then and. Hence C is an IF α-generalized* minimal closed set.

Theorem 4.3.

(i) Let, where U is an IF minimal open set. If A is an IF α-generalized* minimal closed set, then B is also so.

(ii) If and B is an IF α-generalized* minimal closed set then A is also so.

Proof. (i) Let, where U is an IF minimal open set i.e.. From definition as A is an IF α-generalized* minimal closed set implies. i.e. B is also an IF α-generalized* minimal closed set.

(ii) Since B is an IF α-generalized* minimal closed set i.e. where U is an IF minimal open set and from definition as B is an IF α-generalized* minimal closed set implies. i.e. A is also an IF α-generalized* minimal closed set.

Remark 4.4. There does not exist any IF Minimal Open Set between A and B such that and A is an IF α-generalized* minimal open set.

Theorem 4.5 If A is an IF α-generalized* minimal open set then,. i.e. A is an IF rare set or an IF minimal open set.

Proof. As is an IF Open Set and (for some IF Minimal Open Set), or A as IF Minimal Open Set does not contain any IF Open Set other than itself or.

Remark 4.6. The converse of the above theorem may not be true and it can be shown with the help of an example:

Let be an IF of X and the corresponding topological space be. Here A is an IF Minimal Open Set of τ. Consider a set, , but C is not an IF α-generalized* minimal open set.

Theorem 4.7. Every IF Minimal Open Set is an IF α-generalized* minimal open set in itself.

Proof. Let A is an IF Minimal Open Set. We know that. Since A is a minimal open set, so from definition A is an IF α-generalized* minimal open set.

Remark 4.8. The converse of the above theorem need not be true, as IF Set C in example 4.2 is IF α-generalized* minimal open set but it is not an IF Minimal Open Set. According to the theorem 4.5 the converse is true if the set is not a rare set. i.e. for a set which is not rare, IF minimal open set and IF α-generalized* minimal open set are similar concepts.

Theorem 4.9. If is an IF Open Set then B will be IF α-generalized*minimal open set iff B is an IF Minimal Open Set.

Proof. Let B is an IF Open Set which is IF α-generalized* minimal open set. From definition there exist a IF minimal open set A containing B such that. But an IF Minimal Open Set does not contain any other IF Open Set except itself i.e. B = A implies B is an IF Minimal Open Set.

Conversely, let B is an IF Minimal Open Set, then as proved in theorem 4.7, B is an IF α-generalized* minimal open set.

Theorem 4.10. Every IF-dense set is an IF α-generalized* minimal open set if it is a subset of some IF Minimal Open Set but the converse is not true.

Proof. Let A is an IFτ dense set. If (B is an IF α-generalized* minimal open set), then. This implies A is an IF α-generalized* minimal open set.

The converse is not true as shown in example 4.6. C is an IF α-generalized* minimal open set, but C is not an IFτ dense set as.

Theorem 4.11. An IF α-generalized* minimal open set A is IF α-generalized closed set if and only if , where B is an IF Minimal Open Set.

Proof. Since A is an IF α-generalized* minimal open set, where B is an IF minimal open set and

(1)

But A is IF α-generalized closed set which implies

(2)

So from (1) and (2).

Conversely let and A is an IF α-generalized* minimal open set, from definition implies, but i.e. implies A is IF α-generalized closed set.

Theorem 4.12. If the IF minimal open set containing a α-generalized* minimal closed set is IF closed set then the α-generalized* minimal closed set is a IF Pre-open set.

Proof. Let U be a IF minimal open set containing A. Since A is a α-generalized* minimal closed set . Since,. Since U is an IF closed set. Therefore . Hence A is an IF Pre-open Set.

Theorem 4.13. Let A be an closed set and an IF α-generalized* minimal closed set then A is the minimal open set.

Proof. Let U be a IF minimal open set containing A. Since A is an IF α-generalized* minimal closed set, i.e. i.e. A = U. Hence A is an If minimal open set.

Theorem 4.14. Arbitrary union of IF α-generalized* minimal open set is an IF α-generalized* minimal open set if it is contained in an If minimal open set.

Proof. Let (where A is an IF Minimal Open Set and).) {B_i is an IF α-generalized* minimal open set} is also an IF α-generalized* minimal open set.

Remark 4.15. The collection of all IF α-generalized* minimal open set forms an IF supra topological space if and are included in the collection. This supra topological space may be denoted as and is named as IF α-generalized* minimal supra topological space.

Theorem 4.16. An IF set A of X is both IF α-generalized minimal closed set and IF α-generalized* minimal closed set iff.

Theorem 4.17. The union of an IF α-generalized minimal closed set and an IF α-generalized* minimal closed set is an IF α-generalized* minimal closed set.

Proof. Let A be an IF α-generalized minimal closed set and B be an IF α-generalized* minimal closed set in the same IF topological space. Let. Here. Therefore and. Hence P is an IF α-generalized* minimal closed set.

Cite this paper

Mani Parimala,Sivaraman Murali, (2016) Intuitionistic Fuzzy α-Generalized Closed Sets in Terms of Minimal Structure Spaces. Circuits and Systems,07,1486-1491. doi: 10.4236/cs.2016.78130

References