Paper Menu >>
Journal Menu >>
 I. J. Communications, Network and System Sciences. 2008; 1: 1-103 Published Online February 2008 in SciRes (http://www.SRPublishing.org/journal/ijcns/). Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 A Discrete Newton’s Method for Gain Based Predistorter Xiaochen LIN1, Minglu JIN2, Aifei LIU School of Electronic and Information Engineering Dalian University of Technology, Dalian, P.R.China E-mail:1 linxc0103@163.com,2 mljin@dlut.edu.cn Abstract Gain based predistorter (PD) is a highly effective and simple digital baseband predistorter which compensates for the nonlinear distortion of PAs. Lookup table (LUT) is the core of the gain based PD. This paper presents a discrete Newton’s method based adaptive technique to modify LUT. We simplify and convert the hardship of adaptive updating LUT to the roots finding problem for a system of two element real equations on mathematics. And we deduce discrete Newton’s method based adaptive iterative formula used for updating LUT. The iterative formula of the proposed method is in real number field, but secant method previously published is in complex number field. So the proposed method reduces the number of real multiplications and is implemented with ease by hardware. Furthermore, computer simulation results verify gain based PD using discrete Newton’s method could rectify nonlinear distortion and improve system performance. Also, the simulation results reveal the proposed method reaches to the stable statement in fewer iteration times and less runtime than secant method. Keywords: Predistortion, Discrete Newton’s Method, Power Amplifiers (PAs), Lookup Table (LUT) 1. Introduction Radio frequency (RF) power amplifiers (PAs) play an important role in wireless communication systems, but are inherently nonlinear. To compensate for nonlinear of PAs, linearization is an indispensable technique today. Furthermore, among various linearization techniques, digital baseband predistortion is more attractive than others by virtue of its simplicity and ease of implementation with digital signal processor (DSP) equivalently in baseband. In this paper, we take into account the gain based predistortion [1] which employs a lookup table (LUT) block using random access memory (RAM). PAs characteristics drift by reason of aging, temperature changing, channel switches, and source voltage variations, so a predistorter (PD) should have the ability of adaptation. And this paper focuses on adaptive techniques. The conventional adaptive algorithms including recursive least squares (RLS) and least mean squares (LMS) originate from adaptive filter theory. Based on above, [2] presents a broadcasting adaptive algorithm more efficient for updating PD. Moreover, [3] proposes a modified broadcasting adaptive algorithm, which does not require special form of training sequence. Meanwhile, in [1], J. K. Cavers generates an idea that the adaptation issue can be converted to the root finding problem on mathematics and presents secant method. In recent years, following J. K. Cavers, [4][5], and [6] present combining dichotomy with linear method, rapid secant method, and combing dichotomy with Newton’s method, respectively. Methods above meet the requirement of convergence rate and are able to reach to the stable statement, but the drawback of these methods is of high computational load. Therefore, in this paper, we propose discrete Newton’s method to adapt a PD which has the advantages of fast convergence and low computational load. This paper is organized as follows. Section 2 analyses and deduces new method and formula. Section 3 demonstrates the virtue of new method by computer simulation. Finally, we conclude the paper in Section 4. 2. Adaptive Gain Based Predistortion 2.1. Gain Based Predistortion Figure 1 shows the architecture of a communication system with gain based PD. PD, whose characteristic is opposite of PA’s, is used in baseband circuit. The symbol stream v is transferred to a PD via a P/S converter to get predistorted signal w. Then w is converted to analog waveforms via a digital-to-analog (D/A) converter. Finally, the analog signals are quadrature modulated,  A DISCRETE NEWTON’S METHOD FOR GAIN BASED PREDISTORTER 17 Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 upconverted, amplified, and transmitted to the air in sequence. ||⋅ ≈ ≈ ≈ ≈ Figure 1. Block diagram for communication system with gain based PD In Figure 2, we find the block diagram of a gain based PD [8]. The complex gains of PD are saved in a LUT whose entries are indexed. Supposed indexing function () Q⋅maps each input signal amplitude to LUT entry index. Also, efficient () Q⋅ can improve PD performance. LUT entries are either uniform of amplitude or power, or nonuniform diversely due to () Q⋅. With mapping input signal to a certain LUT entry, adaptive algorithm begins to update the gain value memorized in LUT to get the optimum gain. () Q ⋅ ⋅ ⊗ i v i r y () F y d v o v f v Figure 2. Block diagram of gain based PD 2.2. Discrete Newton’s Method As illustrated from Figure 2 d vand o vrepresent input complex signals and output complex signals of PA, respectively. Then PA is characterized by ( ) 2 od d vvGv= (1) where () G⋅denotes the complex characteristic function of PA, and2 ⋅is defined as squared amplitude of signals. Describing input complex signals of PD asi v , we can express PD characteristic function as () 2 di i vvFv= (2) where () F ⋅ denotes the complex characteristic function of PD. By substituting (2) into (1), we can obtain the whole linear characteristic function of PD and PA in series ( )() ( ) 2 22 ii iii vFvG vFvkv= (3) where the whole linear gain k is a positive constant, and usually less than PA’s midrange gain. Simplifying (3), we have ( )() ( ) 2 222 0 iii FvGvFvk−= (4) Hence, how to get the optimum gain F of LUT is transferred to the root finding problem for a nonlinear complex equation. As follows, we decompose the complex equation (4) into two real equations separately representing amplitude and phase characteristic. |()| ⋅ and ()∠⋅ label amplitude and phase of a complex number, respectively. Then, amplitude and phase characteristic functions of PA are given as follows () 2 adad vvGv= (5) and ( ) 2 apd d vGvv ∠ =+∠ (6) where ( ) a G ⋅ and ( ) p G ⋅ denote amplitude-modulated amplitude-distortion(AM/AM) and amplitude-modulated phase-distortion (AM/PM) of PA, respectively. Similarly ( ) a F ⋅ and ( ) p F⋅represent AM/AM and AM/PM of PD, respectively. We obtain amplitude and phase characteristic functions of PD () 2 diai vvFv= (7) and ( ) 2 dpi i vFv v ∠ =+∠ (8) Inserting (7) into (5), we get ( ) () () 2 22 aiaiai ai vvFv GvFv= (9) Similarly, combing (8) to (6), hence, ( ) ( ) () 2 22 2 apiaipi i vGvFvFv v ∠ =++∠ (10)  18 X.C. LIN ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 The whole gain of PD and PA in series is k, in other words, the whole amplitude gain is k, and the whole phase doesn’t change at all. Therefore, we can obtain () () () 22 2 aiaiai aii vvFv GvFvkv== (11) () () () 2 22 2 apiaipii i vGvFvFvv v∠=+ +∠=∠ (12) Simplifying and composing (11) and (12), we write equations as follows () ( ) () () () () 2 222 2 22 2 0 0 ai aiai piai pi Fv GvFvk GvFvFv −= += ⎧ ⎪ ⎨ ⎪ ⎩ (13) In the above system of equations, ( ) a F⋅and ( ) p F ⋅ are separately amplitude and phase gain memorized in LUT, as a result, the issue of updating LUT is converted to the roots finding problem for system of two element nonlinear equations. (13) is simply marked by H () ( ) () 1 2 ,0 , ,0 ap ap ap hFF HFF hFF ⎧= ⎪ =⎨= ⎪ ⎩ (14) We can apply Newton’s method for system of equations (9) to (14) 1 1 kk aa pb FFJH FF + − ⎛⎞ ⎛⎞ =− ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ (15) where J is Jocabian matrix, defined as 11 22 ap ap hh FF Jhh FF ∂∂ ⎛⎞ ⎜⎟ ∂∂ ⎜⎟ =⎜⎟ ∂∂ ⎜⎟ ⎜⎟ ∂∂ ⎝⎠ (16) However, in fact, since the derivatives of () 1 h⋅and ( ) 2 h⋅ are not available, we can not apply Newton method. Instead, we make use of discrete Newton’s method which substitutes differential entropy for derivative. ( ) ( ) ( ) ( ) ()( )()( ) 11 11 11 11 11 11 11 11 ,,,, ,,,, kk kkkk kk ap apap ap kk kk aa aa kk kkkk kk ap apap ap kk kk pp pp hF FhFFhF FhF F FF FF J hF FhFFhF FhF F FF FF −− −− −− −− ⎛⎞ −− ⎜⎟ −− ⎜⎟ ′=⎜⎟ −− ⎜⎟ ⎜⎟ −− ⎝⎠ (17) Only if J is a nonsingular matrix, iterative formula of discrete Newton’s method is () 1 1 kk aa pb FFJH FF + − ⎛⎞ ⎛⎞ ′ =− ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ (18) Moreover, we know of a simple way to get the inverse matrix of 2-D square matrix, it is that to say, supposed a 2-D square matrix11 12 21 22 aa A aa =⎛⎞ ⎜⎟ ⎝⎠ , hence, we obtain 22 12 1 21 11 11 221221 1aa Aaa aa aa −− =− − ⎛⎞ ⎜⎟ ⎝⎠ (19) Compared discrete Newton’s method for system of equations with secant method for an equation, they have the same order of convergence, super-linear convergence. However, the computational load of discrete Newton’s method is lower than that of secant method, due to secant method finding a root of a complex equation, concretely, each iteration requiring 4 complex multiplications, 2 complex additions, and 2 complex by real divisions, in total, 20 real multiplications and 14 real additions. On the contrary, system of equations using discrete Newton’s method are always in real number field, and each iteration only needs 6 real multiplications, 12 real additions and 4 real divisions. Obviously, real multiplications of the latter are fewer than those of former, so the computational load of discrete Newton’s method is much lower than that of secant under large numbers of symbols. From Figure 3, we can see the block diagram of a gain based PD with discrete Newton’s method. The drawback of the method is one more R/P. ( ) Q ⋅ ⋅ ⊗ i v i r y () Fy o v f v ⊕ d v Figure 3. Block diagram of gain based PD with discrete Newton’s method 3. Simulation Results The baseband simulation model block diagram of adaptive PD is shown in Figure 4. In our simulation, we used 16QAM signal and square root raised cosine filter (SRRCF). The channel is assumed to be an additive white Gaussian noise (AWGN) channel. Input backoff (IBO) is 4dB. In this paper, the simulation is restricted to the memoryless distortion. Because PA widely used for  A DISCRETE NEWTON’S METHOD FOR GAIN BASED PREDISTORTER 19 Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 satellite transmission is Traveling Wave Tube Amplifier (TWTA), we apply TWTA to our model as well and simulate the Saleh’s model [10]. In our simulation, input signal amplitude is normalized to vary from 0 to 1. We take for uniform amplitude distribution function as () Q ⋅ . ≈ ≈ ( ) T Hf ( ) R Hf Figure 4. Block diagram of baseband simulation It is apparent from Figure 5 that the iterative number of discrete Newton’s method for one input signal is less by about 10 times than that of secant method. In addition, when signal source generates 14 2 bits, runtime of secant is 74.8600s, while that of discrete Newton is 49.6410s; when there are16 2 bits, runtime of secant is 1536.40s, while that of discrete Newton is 858.7190s, about a half of secant’s. And all the above time is on average. Thus we can conclude the proposed method could reduce runtime of adaptation. And with input data increasing, the superiority of discrete Newton’s method is more outstanding. Figure 5. Compare for MSE curve Figure 6 shows constellation for 16QAM modulation signals. Figure 7 shows constellation for signals distorted by PA. Further more, Figure 8 and Figure 9 illustrates constellation of receiver signals predistorted by the gain based PD with secant and discrete Newton’s method, respectively. These simulation results prove the gain based PD with both the two adaptive method compensate nonlinear distortion, and their distorting effects are equally. Figure 6. 16QAM modulation signals constellation Figure 7. 16QAM signals constellation with PA Figure 8. 16QAM receiver signals constellation with secant 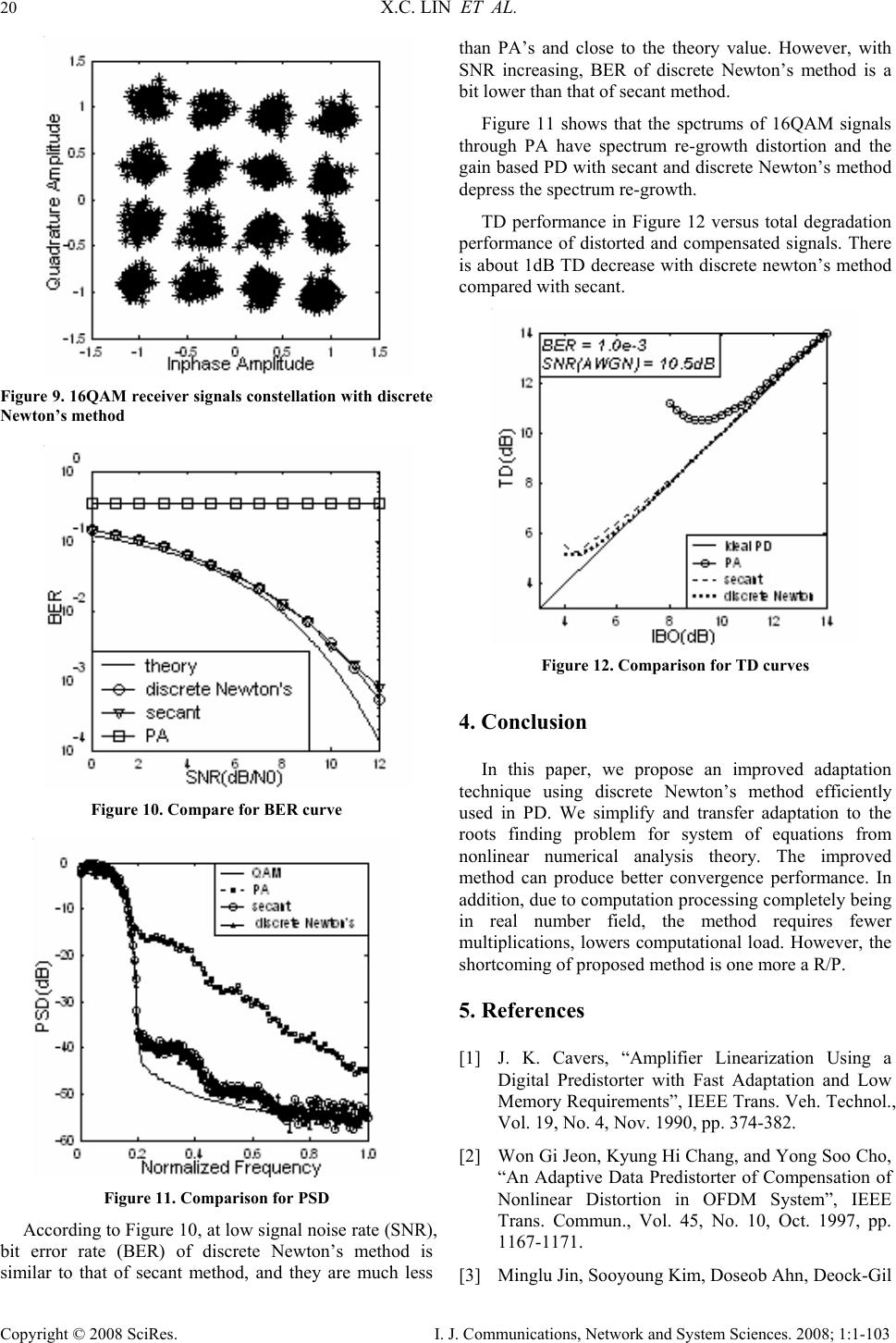 20 X.C. LIN ET AL. Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 Figure 9. 16QAM receiver signals constellation with discrete Newton’s method Figure 10. Compare for BER curve Figure 11. Comparison for PSD According to Figure 10, at low signal noise rate (SNR), bit error rate (BER) of discrete Newton’s method is similar to that of secant method, and they are much less than PA’s and close to the theory value. However, with SNR increasing, BER of discrete Newton’s method is a bit lower than that of secant method. Figure 11 shows that the spctrums of 16QAM signals through PA have spectrum re-growth distortion and the gain based PD with secant and discrete Newton’s method depress the spectrum re-growth. TD performance in Figure 12 versus total degradation performance of distorted and compensated signals. There is about 1dB TD decrease with discrete newton’s method compared with secant. Figure 12. Comparison for TD curves 4. Conclusion In this paper, we propose an improved adaptation technique using discrete Newton’s method efficiently used in PD. We simplify and transfer adaptation to the roots finding problem for system of equations from nonlinear numerical analysis theory. The improved method can produce better convergence performance. In addition, due to computation processing completely being in real number field, the method requires fewer multiplications, lowers computational load. However, the shortcoming of proposed method is one more a R/P. 5. References [1] J. K. Cavers, “Amplifier Linearization Using a Digital Predistorter with Fast Adaptation and Low Memory Requirements”, IEEE Trans. Veh. Technol., Vol. 19, No. 4, Nov. 1990, pp. 374-382. [2] Won Gi Jeon, Kyung Hi Chang, and Yong Soo Cho, “An Adaptive Data Predistorter of Compensation of Nonlinear Distortion in OFDM System”, IEEE Trans. Commun., Vol. 45, No. 10, Oct. 1997, pp. 1167-1171. [3] Minglu Jin, Sooyoung Kim, Doseob Ahn, Deock-Gil  A DISCRETE NEWTON’S METHOD FOR GAIN BASED PREDISTORTER 21 Copyright © 2008 SciRes. I. J. Communications, Network and System Sciences. 2008; 1:1-103 Oh, and Jae Moung Kim, “A Fast LUT Predistorter for Power Amplifier in OFDM Systems”, The 14th IEEE Intemational Sysmposium on personal Indoor and Mobile Radio Communication Proceedings , Beijing, China, Sep. 2003, pp. 1894-1897. [4] Hongxin Zhao, Yiyuan Chen, and Wei Hong, “A Baseband Predistortin Linearizer for RF power amplifier Prototype Simulation and Experimentation”, Journal of China Insttiute of Communications, Vol. 21, No. 5, May. 2000, pp. 41-47. [5] Shuyue Wu, Xinguang Tian, and Ping Bao, “A Fast Algorithm of the Linearizing Technology of the Adaptive Power Amplifiers”, Signal Processnig, Vol. 18, No.3, Jun.2002, pp. 254-256. [6] Shuyue Wu, Wenming Guo, Xin Song, and Xinguang Tian, “A New Algorithm of the Linearizing Technology of the Digital Baseband Predistortion”, J. Xiangtan Min. Inst., Vol. 19, No. 1, Mar. 2004, pp. 63-65. [7] Kathleen J. Muhonen, and Mohsen Kavehrad, “Look-Up Table Techniques for Adaptive Digital Predistortion: A Development and Comparison”, IEEE Trans. Veh. Technol., Vol. 49, No. 5, Sep.2000, pp.1995-2000. [8] Chih-Hung Lin, Hsin-Hung Chen, Yung-Yi Wang, and Jiunn-Tsair Chen, “Dynamically Optimum Lookup-Table Spacing for Power Amplifier Predistortion Linearization”, IEEE Trans. Micro. Theory Tech., Vol. 54, No. 5, May.2006, pp. 2118 - 2127. [9] Rubiao Xie, and Peiqing Jiang, Nonlinear Numerical Analysis, Press of Shanghai Jiaotong University, Shanghai, China, 1984. [10] A. A. M. Saleh, “Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers”, IEEE Trans. Commun., Vol. COM-29, Nov. 1981, pp. 1715-1720. |

