Journal of Electromagnetic Analysis and Applications
Vol.07 No.04(2015), Article ID:55929,5 pages
10.4236/jemaa.2015.74015
Performance Analysis on a Dual External Cavity Tunable Laser ECTL Source
Ahmed Fawzy1, Osama M. El-Ghandour2, Hesham F. A. Hamed1
1Department of Electrical Engineering, Minia University, Minia, Egypt
2Department of Electronics, Communications and Computer Engineering, Helwan University, Cairo, Egypt
Email: ah_fawzy86@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2015; accepted 21 April 2015; published 24 April 2015
ABSTRACT
This paper presents the diffraction effects on the performance of a dual external cavity tunable laser source, whose external cavities are constructed by micro electro mechanical systems (ME- MS). One of the main problems in these structures is the optical diffraction as the emitting surface of the laser diode is usually quite limited in the transverse directions. The emitted beam diffracts rapidly in the air and only a small amount of light is coupled back to the source that usually limits the tuning range of the source. Device characteristics such as tuning range, wavelength shift and sensitivity are evaluated. New expression is used and multiple reflections inside external cavities are considered. The simulation results have shown that single external cavity has limited tuning range. It is shown that multiple reflections have significant effect in our model. To get a better engineering for the dual ECTL dimensions, diffraction effects must be taken into account.
Keywords:
External Cavity Laser, Tunable Laser, MEMS, Optical Diffraction

1. Introduction
Tunable lasers have wide applications in communication, especially in wave length division multiplexing (WDM), sensing application and measurements [1] -[3] . There are three specifications that must be achieved in tunable laser to be applicable in modern applications. The specifications are the high tuning speed, miniaturized device dimensions and the wide tuning range [3] -[8] . These three specifications can be achieved using the Micro Electro Mechanical System (MEMS) technology [2] [3] .
There are many features that make MEMS technology preferred in fabrication of micromechanical structures such as high accuracy, self aligned, high speed response in moving and enhanced mechanical stability [3] [9] [10] . The MEMS technology can add a lot of features like the small size, low weight, high accuracy as well as fast speed in tuning. For this purpose, MEMS based tunable laser structures have been proposed and tested in the literature using different structures [2] [3] . These structures are mainly based on one external cavity semiconductor laser in which the external cavity is formed by a moving MEMS mirror but suffer from lower tuning range. To increase the tuning range, grating must be used in the structures such as Littrow or Littman but also these structures suffer from large size [2] -[4] . So in this paper dual external cavities are used to enhance tuning range rather than single external cavity and also to miniaturize size than Littrow and Littman [11] [12] . The configuration consists of two cavities: one reflective movable mirror element was placed close to the original cavity to form the first cavity; and the second mirror is a transparent mirror, it was placed far from original cavity to form the second cavity. One way to fabricate this moving mirror as well as its actuator is to use the Deep Reactive Ion Etching (DRIE) technology on SOI wafer [2] [9] [10] . The objective of this paper is to study the diffraction in the MEMS based on a dual external cavity tunable laser source and to prove that the tuning range is increased in case of the dual external cavity. Simulation of the optical field propagation in the structure is verified by accurate theoretical model [13] . In the model each external cavity can be represented by using effective reflection coefficient. The model is based on the plane wave expansion method. The calculation of tuning range through an effective phase perturbation technique is done by using effective reflection coefficient. In this technique phase oscillation condition for the laser oscillator is changed due to perturbation that come from external cavity phase. Based on that, the new resonance frequency (emission wavelength) is then calculated.
2. System Model
A MEMS dual external cavity tunable laser is shown in Figure 1 with two external mirrors assumed to have finite dimensions limited by the technological capabilities of the DRIE technology. In our model, we assume that 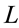 is the primary cavity’s length (containing the active medium), Lext1 is the length of the first external cavity, Lext2 is the length of the second external cavity,
is the primary cavity’s length (containing the active medium), Lext1 is the length of the first external cavity, Lext2 is the length of the second external cavity, 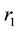 and
and 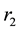 are the reflectivities of the facets forming the original cavity,
are the reflectivities of the facets forming the original cavity, 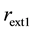 is the reflectivity of the first external mirror and
is the reflectivity of the first external mirror and 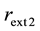 is the reflectivity of the second external mirror. The external reflector can be combined with the facet of the primary cavity yielding an effective reflectivity
is the reflectivity of the second external mirror. The external reflector can be combined with the facet of the primary cavity yielding an effective reflectivity 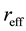 [12] [14] that can be expressed as:
[12] [14] that can be expressed as:
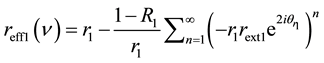 (1)
(1)
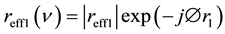 (2)
(2)
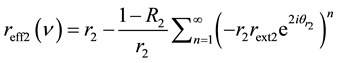 (3)
(3)
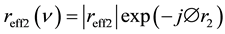 (4)
(4)
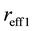 ,
, 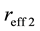 ,
, 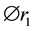 ,
, 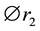 represent the amplitude and phase of effective reflectivity of the first external cavity and the second external cavity respectively,
represent the amplitude and phase of effective reflectivity of the first external cavity and the second external cavity respectively, 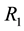 and
and 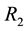 are the power reflectivities of the two facets of the primary cavity and
are the power reflectivities of the two facets of the primary cavity and 

Figure 1. Schematic diagram of the studied dual ECTL source.
paper we make classification for the coupled feedback based on the first external mirror only. In case of weak feedback, 



where 





This expression for the frequency shift is valid for both weak and strong feedback reflections. It can thus be used to study the effect of the diffraction on the frequency shift and hence on the resonance frequency of the laser. To calculate this frequency shift, it is required to evaluate both the amplitude and phase of the reflected beam after travelling in the external cavity. The suggested technique, the Plane Wave Expansion Method is based on the expansion of the optical field of finite spot size emitted from active cavity in terms of the proper propagation modes in the free space, the plane waves. The optical beam is thus decomposed into plane waves using the fast Fourier transform FFT algorithm. Propagation in the external cavity is represented for each plane wave component as a multiplication by a free space transfer function [16] . The total field composed of all the plan waves is then constructed again at the surface of the external reflector using the inverse Fourier transform IFFT to return to spatial domain. When the external mirror has finite dimensions, part of beam is reflected by mirror reflectivity and another part doesn’t reflect due to finite mirror size and thus we have a truncated beam. Outside the mirror surface reflection coefficient is considered as zero. The part that reflected from mirror is modulated by the shape of mirror. The reflected beam is then transformed again to the spectral domain and propagated in the free space as before. When arriving back to the laser diode surface, the beam is returned back to the spatial domain using the IFFT and its coupling to the cavity is calculated using the overlap integral with the cavity mode [6] .
For the infinite mirror, the tuning range of dual external cavity tunable laser is higher than single external cavity tunable laser as shown in Figure 2. In our model we assume that the laser output from primary cavity is an elliptical Gaussian beam with a spot size of about 1 μm in the 


where 




3. Results
For an external mirror with high reflection coefficient, the coupled power that come back to active cavity from external mirrors is affected by number of round trips through external cavities. For weak feedback with 

4. Conclusion
In this work we studied the diffraction effects on the single and dual external cavity tunable lasers and calculated the tuning range in both cases by using accurate developed model. The model shows that the dual external cavity has higher tuning range than single external cavity tunable laser. The model also accounts multiple reflection in the dual external cavity tunable laser. The model shows that multiple reflection has significant effect on the tun-
Figure 2. Tuning range of two different configurations as a function of the external mirror position.
Figure 3. Wavelength shift of an dual external cavity tunable laser as a function of the external mirror position for moderate reflection coefficient first external mirror (0.32).
Figure 4. Comparison of wavelength variation predicted by the dual external cavity model in case of one round trip and multiple round trips.
ing range as well as the tuning sensitivity of the laser. By taking multiple reflections in our calculations, we simulate practical external cavity laser, so we can engineer accurate dimensions for a required tuning range.
References
- Coldren, L.A., Fish, G.A., Akulova, Y., Barton, J.S., Johansson, L. and Coldren, C.W. (2004) Tunable Semiconductor Lasers: A Tutorial. Journal of Lightwave Technology, 22, 193-202. http://dx.doi.org/10.1109/JLT.2003.822207
- Liu, A.Q. (2004) Photonic MEMS Devices: Design, Fabrication and Control. CRC Press, Boca Raton.
- Liu, A.Q. and Zhang, X.M. (2004) A Review of MEMS External-Cavity Tunable Lasers. Journal of Micromechanics and Microengineering, 17, R1-R13.
- Liu, A.Q., Zhang, X.M., Tang, D.Y. and Lu, C. (2004) Tunable Laser Using Micro Machined Grating with Continuous Wavelength Tuning. Applied Physics Letters, 85, 3684-3686.
- Zhang, X.M., Liu, A.Q., Tang, D.Y. and Lu, C. (2004) Discrete Wavelength Tunable Laser Using Microelectromechanical Systems Technology. Applied Physics Letters, 84, 329-331
- Solgaard, O. (2009) Photonic Microsystems: Micro and Nanotechnology Applied to Optical Devices and Systems. Springer, New York.
- Liu, A.Q., Zhang, X.M., Murukeshan, V.M. and Lam, Y.L. (2001) A Novel Integrated Micromachined Tunable Laser Using Polysilicon 3-D Mirror. IEEE Photonics Technology Letters, 13, 427-429. http://dx.doi.org/10.1109/68.920739
- Zhu, W.M., Zhang, W., Cai, H., Tamil, J., Liu, B., Bourouina, T. and Liu, A.Q. (2009) A MEMS Digital Mirror for Tunable Laser Wavelength Selection. International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS 2009), Denver, 21-25 June 2009, 2206-2209.
- Sabry, Y.M., Khalil, D., Saadany, B. and Bourouina, T. (2013) Multi-Step Etching of Three-Dimensional Sub-Millimetre Curved Silicon Microstructures with In-Plane Principal Axis. Journal of Microelectronic Engineering, 114, 78-84.
- Sabry, Y.M., Saadany, B., Khalil, D. and Bourouina, T. (2013) Silicon Micromirrors with Three-Dimensional Curvature Enabling Lensless Efficient Coupling of Free-Space Light. Light: Science & Applications, 2, e94.
- Zhu, X. and Cassidy, D.T. (1996) Liquid Detection with InGaAsP Semiconductor Lasers Having Multiple Short External Cavities. Applied Optics, 35, 4689-4693. http://dx.doi.org/10.1364/AO.35.004689
- Abu-El-Magd, A.M. (2005) Double Tuning of A Dual External Cavity Semi Conductor Laser For Broad Wavelength Tuning With High Side Mode Suppression. Master Thesis, McMaster University, Hamilton.
- Fawzy, A., El-Sabban, S., Ismail, I. and Khalil, D. (2013) On the Modeling of an External Cavity Tunable Laser ECTL Source with Finite Mirror Dimensions. Progress in Electromagnetics Research Symposium Proceedings, Stockholm, 12-15 August 2013, 691-694.
- Voumard, C., Salathé, R. and Weber, H. (1977) Resonance Amplifier Model Describing Diode Lasers Coupled to Short External Resonators. Applied Physics, 12, 369-378.
- Petermann, K. (1988) Laser Diode Modulation and Noise. Kluwer, London. http://dx.doi.org/10.1007/978-94-009-2907-4
- Saleh, B.E.A. and Teich, M.C. (2007) Fundamentals of Photonics. Wiley, Hoboken.
- Bandres, M.A. and Gutiérrez-Vega, J.C. (2008) Elliptical Beams. Optics Express, 16, 21087-21092.
- Marincic, A. (2002) Huygens-Kirchhoff’s Theory in Calculation of Elliptical Gaussian Beam Propagation through a Lens. Mikrotalasna revija.
- Heikkinen, V., Aikio, J.K., Alojoki, T., Hiltunen, J., Mattila, A.-J., Ollila, J. and Karioja, P. (2004) Single-Mode Tuning of a 1540-nm Diode Laser Using a Fabry-Pe/Spl Acute/Rot Interferometer. IEEE Photonics Technology Letters, 16, 1164- 1166. http://dx.doi.org/10.1109/LPT.2004.824619





