Received 5 February 2015; accepted 23 February 2015; published 26 February 2015

ABSTRACT

We present a numerical investigation of the propagation and the switching of ultra-short pulses (100 fs) in a two-core nonlinear coupler of photonic crystal fibers constructed with periodically modulated the non-linearity fiber (PMNL-PFC). Our simulations are taking into account different amplitude and frequency modulations of the PMNL-PFC. A coupler for coupling whose length is L_c = 1.8 cm, the transmission characteristics, the compression factor, the crosstalk (Xtalk) and extinction ratio (Xratio) levels of the first order solitons were studied for low to high pump energies considering 2L_c. By an analysis on the reference channel (channel 2), it is observed that at low modulation frequencies an increase occurs in the switching power increasing transmission efficiency. For high modulation frequencies, the transmitted energy efficiency loses. The switching pulses are stronger for low frequency and high amplitude modulation. The Xtalk is a function of the measurement made on the secondary channel (channel 1). It was observed that this unwanted high-frequency energy increases to lessen the measure of the amplitude modulation. In summary, we have demonstrated that introduction of a non-linearity profile takes the periodically modulated PMNL-PFC to strong variations at transmission efficiency, Xtalk, Xratio a function of frequency and modulation amplitude and the input power.

Keywords:

Coupler of Photonic Crystal Fibers, Periodically Modulated the Non-Linearity, Two-Core Nonlinear, Crosstalk Level, Extinction Ratio Level

1. Introduction

Unlike conventional optical fibers, which are made from ultra-pure silicon oxide using doping to change their characteristics, photonic crystal fibers (PCF―Photonic Crystal Fiber) have characteristics defined by microstructures built inside. By allowing the optimization of the optical properties in an unreachable level for the technologies of conventional optical fibers, PCFs promise to revolutionize areas such as telecommunications, optical tomography, spectroscopy, medicine, metrology and sensor development. Photonic crystal fiber (PCF) is a fiber where light confinement is achieved by a regular array of air holes running along the fiber. Because of their many unusual characteristics, PCFs have found many important applications, such as dispersion control, endless single-mode operation, supercontinuum generation, and ultra-broadband soliton transmission, just to name a few [1] -[3] . Numerous designs of PCFs have been reported, which vary with the arrangement of air holes across the fiber cross-section. Optical fiber couplers have been studied for their potential applications to ultrafast all optical switching processing, like optical switch [4] -[7] . The structure of a two-core PCF shows in Figure 1, where d is the air-hole diameter, Λ is the hole-hole distance, and C is the core separation [3] [8] -[10] . In a nonlinear coupler constructed from a Kerr type medium, the dependence of the nonlinear refractive index n on the laser intensity is given by the expression n = n₀ + n₂I [11] , where n₀ is the refractive index at low intensity and n₂ is the Kerr nonlinear coefficient [4] . In particular, the analysis of soliton propagation in nonlinear inhomogeneous waveguides is an important topic with big possibilities of applications [9] [10] . The study of the propagation of fundamental solitons in a waveguide with a periodically modulated nonlinearity coefficient is a current topic of interest for optical communication systems [5] . In the following, we will examine the propagation and the switching of fundamental solitons in a two-core nonlinear fiber coupler in photonic crystal fiber constructed with periodically modulated nonlinearity (PMNL-PFC). Previous studies of soliton switching in dual core optical fibers, without loss, have shown excellent switching characteristics, with efficiencies around 96% for a wide range of input energies. In trying to control the switching efficiency, there is a great interest in the study of the crosstalk level (Xtalk) in directional couplers. For a given switch state or interconnection pattern and output, the crosstalk is the ratio of the output power at the unwanted waveguide by input to the power in all fiber. Usually, the Xtalk of a switch is defined as the worst-case crosstalk over all outputs and interconnection patterns. The Xtalk level has always been the focus of many investigations because of its importance in device applications and the difficulty of achieving a good level [8] [9] .

In addition to the Xtalk level, the other important parameter used to characterize the suitability of a switch for optical networking applications is the extinction ratio (Xratio). The Xratio of an on-off switch is the ratio of the output power in the on-state to the output power in the off-state. This ratio should be as large as possible and is particularly important in modulators.

This is a work of numerical simulation in which we present the dynamic propagation of ultra short pulses (100 fs) through a coupler dual core photonic crystal fibers constructed with periodically modulated the non- linearity fiber (PMNL-PFC). Our simulations are taking into account different amplitude and frequency modulations of the PMNL-PFC. The transmission characteristics, the compression factor, the crosstalk (Xtalk) and extinctionratio (Xratio) are based on the switching pulses. Although analysis of non-linearity as a function of frequency and amplitude modulation parameter was also performed.

2. Coupler-Mode Equations

The structure of a two-core PCF is shown in Figure 1, where d is the air-hole diameter, Λ is the hole-to-hole distance, and C is the core separation. Optical power transfer between the two cores of a two-core PCF (assumed lossless) can be described approximately by a pair of nonlinear coupled-mode equations that do not differentiate the two orthogonal polarization modes of the fiber [12] -[14] :

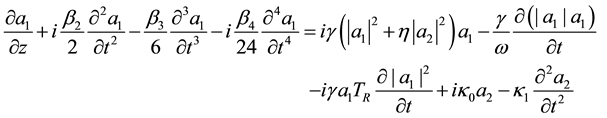(2.1)

(2.2)

In the above equations, z is the distance along the fiber; t is the time coordinate with reference to the transit time of the pulses; a₁ and a₂ are the amplitude envelopes of the pulses carried by the two cores, respectively; β₂, β₃, and β₄ are the group-velocity dispersion (GVD), third-order dispersion, and fourth-order dispersion, respectively; γ is the nonlinear parameter that accounts for self-phase modulation (SPM); η is a small ratio that measures the relative importance of cross-phase modulation (XPM) with regard to SPM; the time-varying term next to the SPM and XPM terms represents self-steepening (where ω is the angular optical frequency); T_R is the Raman scattering coefficient; κ₀ is the coupling coefficient; and κ₁ is the coupling coefficient dispersion given by (evaluated at the pulse carrier frequency). The coupling coefficient dispersion κ₁ is a measure of the wavelength dependence of the coupling coefficient; it is equivalent to the intermodal dispersion of the composite two-mode fiber structure [14] [15] . The concept of intermodal dispersion can in fact provide an intuitive explanation of the pulse breakup effect [15] . In the present study, in Equations (2.1) and (2.2) we ignore the fourth-order dispersion and the XPM. The parameter γ of non-linearity is written in the form of a periodic type modulation cosine given by:

(2.3)

where A and ω are the amplitude and frequency modulation respectively. In this paper, we will study different amplitude (A) and frequency modulations (ω) in a two-core nonlinear coupler of photonic crystal fibers (PMNL-PFC). We analyze the two-core PCF considered in [12] , which has an air-hole diameter d = 2.0 µm, a hole-to-hole distance Λ = d/0.9, a core separation C = 2Λ, and a coupling length L_c = 1.8 cm. The corresponding parameters for Equations (2.1) and (2.2) are β₂ = −47 ps²/km, β₃ = 0.1 ps³/km, (for an effective area A_eff = 41 µm²). The carrier wavelength is λ = 1.55 µm.

3. Numerical Procedure

The dynamics of pulse ultra-short (100 fs) propagation and switching along a two coupling length (2L_c) was analyzed numerically on PMNL-PFC two-core (Equations (2.1) and (2.2)) whit modulation given by Equation (2.3). The initial pulse at the input core is given by

(3.1)

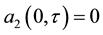(3.2)

where a₀ is a real constant giver by (P_o = 100 W is the peak power of the pulse).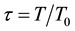, T = 8000 fs

is the temporal window of evolution of the signal and 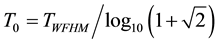is the reference time related to

the width temporal pulse. The evolution of the pulse occurs solving Equations (2.1) and (2.2) numerically. We use the 4th-order Runge-Kutta with 1024 temporal grid points taking in account the initial conditions given by Equations (3.1) and (3.2) for simulations [16] -[20] .

The study was based on analysis of the transmission, Xratio, factor of compression, always looking for channel 2 output devices. The level of crosstalk being a measure of unwanted energy, this analysis is done on the secondary channel (channel 1). We can define the transmission T_i as a function of the pulse energies,

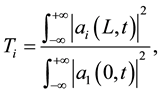(3.3)

with i = 1, 2 and an PMNL-PFC with length L = 2L_c.

The extinction ratio of an on-off switch is the ratio of the output power in the on state to the output power in the off state. This ratio should be as high as possible. For our PMNL-PFC it is expressed by

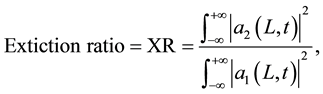(3.4)

where the extinction ratio in dB units is

(3.5)

The crosstalk level of the device was studied considering that the input pulse 1 (Equations (3.1) and (3.2)), will propagate in the coupler and will be switched to the second fiber then switch to channel 1 since we are considering L = 2L_c, for low pump energy. For high pump energy, the light is not switching to channel 2 and the light is switching out through channel 1. In this situation the Xtalk level should be low in channel 1. However, the conversion is not perfect. This will result in the presence of a crosstalk signal at channel 1 associated to the other mode:

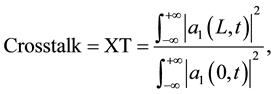(3.6)

where the extinction ratio in dB units is

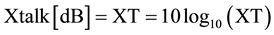(3.7)

We also define the final compression factor FC [21] [22] , achieved after propagation of the optical input pulse in the PMNL-PFC. It is defined as the ratio of the optical pulse FWHM at the output (transmitted) of the

PMNL-PFC two-core τ₂ (FWHM of the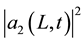, transmitted pulse) to that at the input of the PMNL-PFC two-core, τ₀ (FWHM of the, input pulse):

(3.8)

4. Results and Discussion

Figure 2 shows the transmission curve as a function of modulation frequency for various modulation amplitudes A (see Equation (2.3)). The coupled Equations (2.1) and (2.2) that describe the dynamics of the device were solved numerically using a hyperbolic secant pulse temporal width 100 fs for five different modulation amplitudes. One conclusion is that with increasing modulation amplitude for high frequency transmission efficiency is reduced. However, for low frequencies of modulation (ω < 125) the transmission efficiency depends strongly on amplitude modulation. For ω = 25 the transmitted energy change 0.06 to 0.68 when the modulation amplitude changes from 0.1 to 0.9 respectively. Based on the dynamics of the device non-linearity acts directly on the form of some effects, such as SPM (self-phasemodulation), self-steepeningand Raman espalhmentoyet. Due to the nonlinear dependence of PMNL-PFC response of transmission has a behavior that is a function of modulation described by Equation (2.3). This behavior can be expected to show non-linearity modulated with amplitudes above 0.8 with maximum transmission peaks. In Figure 3 we have the ratio of extinction curves, where it is observed that for ω < 125 frequencies Xratio depends nonlinearly amplitude modulation, so for ω = 25 to Xratio changes from −1.55 dB to 3.13 dB when the amplitude modulation changes of 0.1 to 0.9 respectively. The level of crosstalk measured the rate of unwanted energy transmitted to the channel 1 (since we consider the channel 2 reference measures for switching). The Xtalk should be least so that we have a maximum transmission power in the reference channel. Figure 4 shows that for low frequencies the modulation Xtalk tends to decrease for the various amplitudes A. When ω = 29.6 and A = 0.9, the Xtalk presents a lower value, around −4.93 dB. For high frequencies the Xtalk tends to increase significantly so that for ω > 125 Xtalk basically does not depend on the amplitude modulation, saturating at around −0.11 dB. In Figure 5 one has the compression factor FC (see Equation (3.8)) as a function of the frequency modulation. The profile of the pulse mater extended in all cases amplitude modulation. The compression factor changes and 3.94 to 2.4 when amplitudes modulation change 0.9 respectively, the pulse shows less extended to higher amplitude modulation. An interesting result can be seen in Figure 6, shows the behavior the non-linearity as a function of frequency modulation parameter considering various amplitudes. The non-linearity varies periodically as a function of modulation frequency. When ω = 43.7 and ω = 131 is the parameter of nonlinearity is the same for all cases considered amplitudes. This optimizes the component since we can use a value independent linearity of amplitude modulation and this is observed at low and high frequencies. As noted PMNL PFC has a non-linear dependence as a function of modulation frequency

for various values of amplitudes. Specific values of frequency modulation also exhibit particular behaviors as a function of increasing amplitude modulation. In this paper this study begins observing Figure 7, where we observe that grows as the transmission is increased when the amplitude modulation. The nonlinear behavior resembles, however, differs when we observe different values of frequency modulation. As we reduce the frequency of modulation switching occurs for smaller values of amplitude. The maximum transmission reaches 72% when the amplitude reaches 1.78 at ω = 10. Figure 8 shows the curves of extinction rate, amplitude is zero when the extinction rate goes around 13 dB thus increases as modulation amplitude increases. For ω = 10 the extinction rate this around 3.25 dB for A = 0.25. For the same amplitude is observed that XR = −1.75 dB that ω = 50. Accordingly, we conclude that for the same amplitude extinction rate depends on the values of frequency modulation, for higher frequencies the rate of extinction has values minors. Figure 9 shows the level of crosstalk due to some values amplitude modulation of frequencies observed in channel 1. Was observed that the level of crosstalk improved when increasing amplitude. Particularly crosstalk presents best values around A = 0.81 reaching close to −4.86 dB for ω = 10 and −2.88 dB at ω = 50. With the increasing frequency of modulation to amplitude values of the nonlinearity tends to decrease, then the transmission power in the channel 2 decreases in intensity causing unwanted energy in the channel 1 increases. Thus, for fixed values of amplitude modulation crosstalk increases as the modulation frequency increases to lower amplitudes than 0.8. However, amplitude variation with this observation can be made through a right shift by seen in Figure 9.

5. Conclusions

We present a numerical investigation of the propagation and switching of ultra-short pulses in a nonlinear coupler dual-core photonic crystal (PMNL-PFC) fibers constructed with non-linearity periodically modulated fibers. Our simulations take into account different frequencies and amplitudes of modulation of PMNL-PFC. The characteristics of transmission, compression factor and levels of extinction rate (Xratio) and crosstalk (Xtalk) went to a power of 100 W. It was observed that for modulation frequencies above 75, there is a low efficiency transmission independent of the amplitude modulation. For lower frequencies, the transmission efficiency decreases to lower amplitudes, such that ω = 30 to the valley transmission when A = 0.68 and 0.06 to 0.9, A = 0.1. The

pulse switches faster for high amplitudes at low frequencies. Levels of extinction rate grow at high amplitudes for low frequencies. At ω = 30, the rate of extinction is XR = 3.3 dB when A = 0.9 dB and XR = −11.8 dB for A = 0.1. Levels of crosstalk improve for modulation frequencies ω < 75. At ω = 30, XT = −4.9 dB when A = 0.9 and XT = −0.27 dB when A = 0.1. It can be concluded that the level of crosstalk improves low frequencies and high amplitude modulation.

In summary, we showed that the nonlinear coupling of dual-core photonic crystal (PMNL-PFC) fibers constructed with unmodulated linearity fibers. Periodically it presented strong variations in transmission efficiency and levels of crosstalk and extinction rate as a function of frequency and amplitude modulation.

The study of the switching ultra-short pulses in PMNL-PFC couplers offers the possibility of achieving high efficiency in the transmission of signals especially in ultrafast optical switching applications in the form of transistors.

References

NOTES

^*Corresponding author.