Received 7 March 2014; revised 5 April 2014; accepted 1 May 2014

ABSTRACT

Sensors for monitoring the salinity of water are useful tools in both environmental sciences and chemical engineering. Sensors based on a large variety of principles have been developed. Here we describe the design and testing of two different, noninvasive measurement methods for monitoring the salt concentration of water. The first method is based measurements of the refractive index using a folded-path optical refractometer, while the second utilizes an electromagnetic resonator, consisting of a magnetic coil and a capacitor, which is brought to resonance by an external magnetic field source. It is demonstrated that the folded-path optical refractometer allows one to monitor changes in salt concentration down to 1 mM in the range between 0 and 0.7 M, whereas the electromagnetic resonator has the capability of monitoring concentration changes as small as 0.3 mM over the more limited range between 0 and 5 mM.

Keywords:

Salinity, Electromagnetic Sensing, Optical Sensing

1. Introduction

Modern commercial sensors for measuring sea water salinity are often based on conductivity measurements. The relationship between conductivity and salinity depends strongly on temperature and pressure. Therefore both a temperature and a pressure sensor are required to make an accurate measurement of the salinity. Moreover, the conductivity sensors are invasive, which means that one needs to insert a probe into the sample itself. This is a challenge in many situation, and has triggered investigations of other sensor principles which do not require direct contact with the sample.

Optical laser refractometry for determining the salinity has been investigated by several research groups. Typically, these refractometers utilize the Pulfrich configuration [1] [2] or variations thereof [3] . In this configuration, the fluid under study is placed inside a container containing at least one optically transparent, refracting window. A collimated laser beam is passed through this window, and is refracted according to Snell’s law. The larger the difference in refractive index between the fluid and the solid window, the larger the angle of refraction. The position of the refracted beam is recorded using a high precision Position Sensitive Detector (PSD).

Other optical methods for monitoring sea water include optical spectroscopy and surface plasmon sensors. While reported studies on ultraviolet spectroscopy of water do not provide as high resolution as conductivity sensors, this method may allow one to unambiguously resolve the chemical composition of the salt water [4] [5] . Also infrared spectroscopy is a potential tool for monitoring sea water salinity [6] . Optical fiber sensors based on surface plasmon resonance do have the potential for very high salinity resolution, and have been tested in the laboratory as well as in-situ [7] -[9] . It should be emphasized that most of the optical methods reported above are critically dependent on a clear liquid and clear optical windows, such that the light is not scattered before entering the detector. However, in most practical systems windows collect dirt which scatters light, and it is likely that an autonomous system cannot depend entirely on optical principles.

In addition to optical refractometry, several other techniques have been developed for studying salinity. Lorentz flow meters are based on the Lorentz force acting on a body as the conducting liquid passes it, while electromagnetic resonators utilize the dependence of the resonance frequency of a resonating cavity or circuit on the permittivitty and conductivity of the liquid. Recent work on Lorentz flow meters and resonating magnetic coil sensors has revealed their great potential for applications in fluid and solid monitoring [10] -[13] . The Lorentz flow meters rely on the motion of charged species and are therefore very useful for monitoring flow at higher salinities [10] [14] , while the magnetic resonance systems have mostly been used in static settings to detect salinity based on accurate monitoring of the frequency and loss near resonance in the MHz region.

Here we report two different electromagnetic methods for measurement of concentration of salt water. The first method is based measurements of the refractive index using a folded-path optical refractometer. A laser beam is passed through a liquid, and a change in the refractive index is recorded as displacement of the laser beam on a position sensitive detector. The second method is based on an electromagnetic resonator, consisting of a magnetic coil and a capacitor, which is brought to resonance by an external magnetic field source, and the corresponding resonance frequency and decay time are determined using Fourier analysis combined with nonlinear curve-fitting. With increasing salt water concentration inside the resonator, the resonance frequency and decay time are altered, thus allowing one to monitor these parameters as a function of salt concentration. The experimental details and the testing of these two systems are presented. The sensors reported here were designed and tested as individual student research projects. However, they may also be suitable as experimental projects in upper-level bachelor courses.

2. Optical Salinity Measurements

Standard refractometers reported in the literature for salt concentration measurements have been of the Pulfrich configuration [1] -[3] , where the beam is refracted and depends on the direct transmission through the medium. In order to increase the path length, and therefore also the position deviation upon changes in refractive index, we report here a novel folded-path design. The idea is to increase the path length by using mirrors in contact with the liquid, and at the same time use two prisms instead of one to refract the laser beam. A sketch of the instruments physical construction and electrical connection is shown in Figure 1, and pictures of the actual setup in Figure 1(a) and Figure 1(b). The choice of optical path is a result of optimization through simulations conducted in the simple dynamic geometric sketching tool called CarMetal [15] . This program enables simulations of the beam displacement on the photo detector surface with changing refractive index of the sample medium. The system is divided into two compartments, separated by a watertight wall in the middle to protect the laser and Position Sensitive Diode (PSD). The laser is a Coherent VHK circular beam diode laser operating at 635 nm with an output power of 0.95 mW and beam diameter 1 mm. Approximately 0.1 mW is incident on the PSD.

The PSD is a Hamamatsu S3932 Position sensitive detector with responsivity about 0.4 A/W at 635 nm and equipped with a Hamamatsu C3683-01 signal processing circuit. According to the specifications, the minimum

detectable displacement of a focused laser beam on the PSD is 0.3 μm. The walls of the container consist of a Poly (Methyl-MethAcrylate), PMMA, as well as the prisms used in the optical path. The first prism is made of Zinc-Selenide (ZnSe) with a refractive index of 2.58 at 635 nm. The second prism is made of borosilicate crown glass (BK-7) with a refractive index of 1.51 at 635 nm. Both prisms also act as optical windows allowing one to make the sample chamber water proof. By introducing two prisms we increased the sensitivity of the setup without introducing further optical windows. In the upper corners of the liquid sample compartment mirrors are positioned to reflect the beam towards the PSD. This makes it possible to achieve a long path length for the laser, which is imperative for proper sensitivity, while the size of the instrument is kept small. The entire system has a size of 0.33 liter, with the liquid sample compartment covering 81 mL. Thus, for every run it is necessary to inject > 80 mL salt water solution to perform a measurement.

The temperature of the liquid sample is measured in situ using an NTC thermistor connected to a voltage divider, as shown in Figure 1. The data from the voltage divider as well as the PSD signal processing circuit are collected by a NI-USB 9239 data acquisition device. The resolution of its analog to digital converter is 24 bit. Its minimum sample frequency is 1.613 kHz, thus allowing monitoring of fast changes in refractive index.

2.1. Measurement Procedure

In total four measurements were performed on NaCl solution sample sets. The process of conducting an experiment involved some preparation. All parts of the instrument were given time (about 20 minutes) to warm up and reach a state of thermal equilibrium before the measurements. Then a pure water sample was pumped into the measurement chamber and the instrument prepared by slightly adjusting the laser angle to achieve a rightmost possible reading from the PSD. Deionized water was obtained from a Millipore Direct-Q 3 UV Water purifier, and the salt water solutions were made by adding a known amount of sodium chloride while stirring. The instrument was now ready to measure the remaining samples. A LabView program was used to control the data acquisition. The number of measurements per water sample was chosen to be 1000. When the measurement was done, the sample was pumped out and the next sample pumped into the chamber. This process was repeated until all the samples had been measured. Two of these experiments were conducted during a single day with the same ambient conditions to measure the instruments ability to produce repeatable results. The instrument was also partly disassembled and put together again, followed by two consecutive measurement series. The purpose of this was to measure the instruments ability to reproduce the results under slightly different conditions. The post processing of the data was done by finding the mean position displacement of the 1000 measured values along with its standard deviation, corresponding to a given salt concentration.

2.2. Results

The displacement of the laser beam on the PSD is shown as a function of the salt concentration in Figure 2. As seen in Figure 2, the laser beam was displaced by 6.3 mm over the entire salinity range. It is also seen that the

position is well described by the linear relationship x(c) = −ac + b, where a = 9.3 ± 0.1 mm/M and b = 2.4 ± 0.01 mm. According to the specifications from the vendor, the smallest change in laser beam position the PSD can resolve is Δx_min= 0.3 μm, thus corresponding to a change in concentration given by Δc ≈ Δx_min/a ≈ 0.03 mM. This figure does not account for the noise in the entire system (only the PSD itself), and we found that the actual smallest resolvable change in position was of the order of 10 μm after accounting for all noise sources, which means that the smallest measurable change in concentration one can monitor with this sensor is about 1 mM. The deviations from a straight line seen in Figure 2 are largest for large (>0.6 M) or small (<0.2 M) salt concentrations, which can be related to the nonlinearities that occur when the laser beam is incident on the prisms near the critical angle. In these regions we also found that the variations were larger between different trials. However, it should also be mentioned that some of the trials were undertaken after disassembling and subsequently reassembling the sensor. This could have shifted the laser beam such that the incidence angle on the prisms changed as well, thus resulting in a shift in the linearity range.

In the work reported here we were mainly interested in the relationship between the measured parameter (i.e. position on the PSD) and the salt concentration of the water. However, since many refractometer setups set out to measure refractive index as well, it may be useful to comment on this relationship.

Repeated applications of Snell’s law for the geometry of Figure 1 gives a complex expression for refractive index n as a function of the position x, in centimeter, on the PSD as n(x) = 1.34260 − 0.01150x + 0.00096x² + 0.00013x³. The function is almost linear in the described range, and the slight nonlinearity is caused by the fact that the transmitted angle from the first prism-water interface is very close to the critical angle.

Due to the fact that the smallest resolvable change in position was of the order of 10 μm, we found that the smallest change in refractive index the system could measure was 10⁻⁵. This is larger than that predicted using a simple Pulfrich configuration [2] . However, in our current system the limited performance is related to the noise, which again is related to the laser fluctuations, detector noise, amplifier noise as well as mechanical and hydrodynamic fluctuations during an experiments. It was found that laser-induced heating played a prominent role. When the laser beam passed through the water sample, some of the light was absorbed by the water molecules, resulting in an increase in temperature and corresponding change in refractive index. Moreover, the heated water rose due to convection, causing influx of cold water and corresponding fluctuations in refractive index. The laser beam also experienced scattering from the water and salt molecules as well as the local heating-induced fluctuations in refractive index. The scattered light caused spatial (speckle formation) as well as temporal noise, thus altering the ability to measure the position accurately. Next generations of optical refractometers must therefore strive to reduce these noise sources or invent methods which can overcome them.

3. Magnetic Resonator for Salinity Measurements

The magnetic resonator is based on an entirely different operating principle than that presented in the previous section. The same experimental setup as in Ref. [13] was used, with three coils located on a PMMA pipe with inner diameter 80 mm and outer diameter 90 mm. The resonator coil is made of one layer of 40 μm thick and 7 mm wide copper band. The coil has eight windings and is connected to a capacitor. Two coils, one for excitation and one for detection, each of one single winding, are placed on each side of the resonator coil. These two coils are made of 12 mm copper band connected to a short coaxial cable and a BNC-connector. All coils are glued to a paper sheet, making movement of the coils along the pipe axis possible. The coil system is shown in Figure 3.

Using an Agilent A4294A Impedance Analyzer, the resonance frequency of the resonator coil was measured to be 27.555 ± 0.006 MHz, whereas the self-inductance was found to be L₁ = 5.0 ± 0.1 μH and the coil resistance $R_1 = 226 ± 1 mΩ. In order to create an efficient resonator, an external capacitor C₁ = 151 ± 1 pF is connected in parallel with the coil, thus giving the resonance frequency 5.846 ± 0.001 MHz with a Q-factor Q = 275 ± 2. The resonance frequencies of the excitation and detection coils are about 30 MHz, such that resonant energy transfer is avoided.The resonator coil is excited through the lower coil, and the signal from the detection coil is fed through an amplifier (Stanford Research Systems SR445A) for 5X amplification into one channel on a PicoScope 5204. In the experiments, a positive voltage pulse of 10 V was sent with a frequency of 10 kHz into the excitation coil using a TTi TG2000 signal generator. The duty cycle, i.e. the ratio of the time interval for high voltage to the signal period, was set to 20%. This means that the pulse had duration of 20 μs out of the total period of 100 μs. Rise and fall times were nominally less than 22 ns.

All the experiments reported below were performed with a 1 mm thick aluminum screen of radius around 27

cm and length 55 cm placed around the measurement setup. The reason for using the screen was to avoid interference from surrounding electromagnetic waves. During the measurement series, the screen was grounded through the signal generator. It was found that both the resonance frequency and Q factor of the resonator system depended on the positioning of the coaxial cables and presence of the screen. In order to avoid that such effects influenced the the experiments, we made sure that the system remained in the same configuration during an experiment.

3.1. Measurement Procedure

Before the measurements, the PMMA-pipe (see Figure 3) was filled with approximately 2 liter salt water of various salt concentrations. Deionized water was obtained from a Millipore Direct-Q 3 UV Water purifier, and the weakly conducting salt water solutions were made by adding a known amount of sodium chloride while stirring. For concentrations above 0.02 M it was more feasible to use tap water, which due to its low conductivity (0.02 S/m) did not influence the experimental results at NaCl concentrations above 0.02 M. For each measurement series, temperature measurements were taken using a HANNA HI2210 meter, and found to be about 297 ± 1 K. For each measurement performed, 32 waveforms were stored to individual csv-files (comma separated values) for further analysis in Matlab. An interval of 40 μs from each of the 32 waveforms was collected. Fourier analysis of the signal has been found to allow efficient evaluation of the resonators. The basic idea is illustrated in Refs. [13] [16] , and utilizes that the detection coil records underdamped voltage oscillations given by

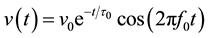, (1)

where f₀ is the resonance frequency and τ₀ is the decay time. Here the excitation and detection circuits are far from resonance in order not to disturb the resonator, and are assumed to not change the resonance frequency and decay time of the resonator significantly. The Fast Fourier Transform (FFT) of each data series was calculated using the fft function in MatLab, and the resulting frequency spectrum fitted to a lorentzian curve on the form

, (2)

where 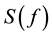is the spectral density, S_A is a constant, f is the frequency and τ the decaytime in presence of the sample. Fitting of equation Equation (2) to the experimental data was performed using the nlinfit function in Matlab (nonlinear least-squares fitting using the Levenberg-Marquardt algorithm [17] . As an example of the end-product of this procedure, Figure 4 shows the normalized spectral densities for deionized water (open circles) and 0.86M NaCl (filled circles).The corresponding whole and dashed lines are theoretical fits of Equation (2) to the experimental data.

It is seen that the resonance frequency and the decay time decrease as the salt concentration increases. Although the method above allows one to extract the decay time as well, its dependency on salt concentration was not monotonous. This phenomenon is possibly due to electrostatic interactions with the metallic screen and the metal wiring which otherwise would not be expected to influence the resonance frequency in any particular manner, and prompted us to leave out the decay time in the further study and instead concentrate on the behavior of the resonance frequency.

3.2. Results

In order to study systematically how the salt concentration of water inside the pipe altered the resonance frequency and time constant of the resonator, the pipe was first filled with deionized water of conductivity 5 × 10⁻⁶ S/m. Next, salt (NaCl) of known mass was gradually added followed by stirring and a period of at least 10 min where the system was allowed to equilibrate. The resonance frequency was recorded as a function of salt concentration, and is displayed in Figure 5. It is seen that the resonance frequency first decreased rapidly before it reached saturation at concentrations larger than 15 mM. Changes in concentration as small as 0.3 mM (within the uncertainty) could be monitored as long as the total concentration remained below 5 mM. Although we measured the resonance frequency for concentrations up to 850 mM, no changes were observed above 15 mM, to within the accuracy of the measurements, and these data are therefore not displayed in Figure 5.

The fact that the resonance frequency decreases and finally reaches saturation can be explained by noting that when the salt concentration increases, the amount of electric energy stored inside the resonator increases at the expense of the magnetic energy, which decreases with due to damping caused by eddy currents in the water column. When the ratio of electric to electromagnetic (electric plus magnetic energy) reaches saturation (i.e. the

ratio becomes close to one), there can be no further changes in resonance frequency. This can be put in more quantitative terms if Bethe-Schwinger perturbation theory is used to obtain the following expression for the resonance frequency [16] [18]

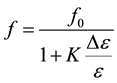, (3)

where

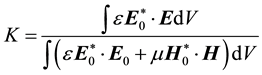. (4)

Here E₀ and H₀ are the fields before the sample is introduce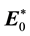d (and 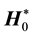are the complexconjugates), whereas E and H are the fields in presence of the sample. It is assumedthat the sample has permittivity ε and permeability μ. The change in permeability isfurthermore assumed to be zero upon introducing the sample into the sensor. The changesin the permittivity (Δε) relate to the sample, which is occupying parts of the volume of integration. The integration is taken over the entire space. It should be emphasized that since the changes in resonance frequency observed in this study are small (typically less than 15%), Equation (3) is a reasonable first approach for most samples. Furthermore, Equation (2) (the lorentzian spectral density) remains on the same functional form but now with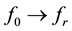, where f_r is the resonance frequency in presence of a sample. If the conductivity of the medium inside the resonator fulfills the condition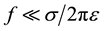, and the resonator is first excited and left alone, the magnetic field in the axial direction inside the medium decays exponentially according to, where σ is the conductivity of the sample itself (assumed to be small) and e_z is a unit vector along the pipe on which the coils are wound. Neglecting the field outside the medium (and coil) we find that a pipe of radius R_a has

(5)

It is seen from Equation (5) that one may expect a larger linear range, i.e. before the resonance frequency saturates with salt concentration, of applicability upon reducing the radius of pipe. However, such a move would also reduce the resolution of the system, and was found not to be ideal for the applications considered here. It should be noted that the conductivity depends nearly linearly on the salt concentration c as s = ec, where e ≈ 10 Sm⁻¹∙M⁻¹, such that Equation (5) can be expressed as

(6)

Here A and are not known, due to the complexity of the sensors geometry and the surrounding screen, and we therefore used these two as fitting parameters. The solid line of Figure 5 represents a fit of Equation (3) with Equation (6) to the experimental data using A = 1.5 × 10⁵ M⁻² and = 4.7 × 10⁻³. The good agreement between the experimental data and the fitted curve suggests that the theory used here is reasonable, although it would be of interest to obtain more precise theoretical information about the fitting constants used here. However, this is outside the scope of the current report.

4. Conclusions

The results reported here suggest that the electromagnetic resonator can be used to monitor a rather narrow range of salt concentrations between 0 and 15 mM. Above 15 mM the resonance frequency could not be used as a tool to monitor the salinity due to saturation issues. On the other hand, this method provides a very high resolution and concentration changes as small as 0.3 mM can be detected as long as the salt concentration remains below 5 mM. This should be contrasted to the folded-path optical refractometer, which allows one to monitor changes in NaCl concentration of 1 mM over a range between 0 and 0.7 M.

The smallest resolvable change in salt concentration was in both cases determined by noise. For the electromagnetic resonator, the noise in the underdamped sinusoidal signal was caused by electronic noise as well as the ability of the coil system to pick up radio signals in the vicinity. Although a metal screen was implemented to remove these noise sources, they were still present and did not allow us to determine the resonance frequency with a smaller uncertainty than 100 Hz under the best circumstances. Improvements in the resolution would need further shielding, although it remains uncertain how this should be done in a salinity sensor deployed e.g. at sea. On the other hand, the main noise source in the folded path refractometer was the laser induced heating and corresponding convection. Reduction of uncertainty in this instrument would require using pulsed laser sources combined with a more temperature-stabilized chamber. Such efforts would probably allow one to reduce the uncertainty by an order of two magnitudes, thus improving the resolution such that it is better than that of the electromagnetic resonator.

References