Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 8 (2011) , Article ID: 6561 , 7 pages DOI:10.4236/jemaa.2011.38050
A Broadband Complex Permittivity Probe Using Stepped Coaxial Line
![]()
Faculty of Engineering, Department of Electrical Engineering, King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand.
Email: somporn_nb@rmutsb.ac.th, prayoot@kmutnb.ac.th
Received June 13th, 2011; revised July 11th, 2011; accepted July 20th, 2011.
Keywords: Complex Permittivity, Reflection Coefficient, Stepped Coaxial Probe
ABSTRACT
This paper proposes the stepped coaxial line sensor using the reflection coefficient in microwave range for complex permittivity measuring. The proposed probe is adapted from the conventional SMA connector which is cheap and easy to fabricate. The analysis model of the probe has been done by using FDTD method with the reference material such as the distilled water. The stepped SMA probe presents the accurate result compared with the convention one. The permittivity values of the concentrated alcohols of 10%, 15% and 20% as DUTs at 24˚C in a frequency range of 0.1 GHz to 6 GHz have been measured using the proposed probe. Also, the measurement of salted butter permittivity has been performed. The measured results are more accurate compared with the commercial probe.
1. Introduction
In determination of properties of materials, many papers characterized the complex permittivity values in a broad frequency band. The dielectric properties of ordinary materials describe how those materials interact with electromagnetic radiation [1]. The dielectric constant of material is associated with the energy storage capability in the electric field in the material and the loss factor is associated with the energy dissipation, conversion of electric energy to heat energy in the material [2,3]. The dielectric properties of usual interest are the dielectric constant and the dielectric loss factor to form the real and imaginary parts of the relative complex permittivity, 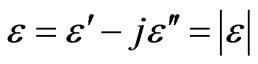 e–jd, where d is the loss angle of the dielectric. Often, the loss tangent,
e–jd, where d is the loss angle of the dielectric. Often, the loss tangent, 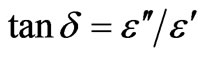 , will be the important specified parameter of the materials.
, will be the important specified parameter of the materials.
In any material, the water Volume is a primary content. Changes in moisture content and the composition of various components alter the dielectric properties of most materials, especially agricultural products. Therefore, a thorough dielectric study of various common solvents is essential for agricultural product researches [4,5].
In food research, the dielectric properties of butter have been studied in order to control the quality of food with butter content as a major part. Dielectric properties of butter in the microwave frequency range could be affected by salt and temperature. It was found that at a frequency band between 500 MHz and 3000 MHz, the salt significantly affected to the dielectric property of butter. Also, a gradual change in dielectric parameters was observed for unsalted butter as temperature increased, whereas an increasing trend was noticed for salted butter. A decrease in moisture content significantly affected dielectric spectra of unsalted butter [6]. Alcoholic beverage properties were also very interested [7]. For dielectric characterization of alcoholic beverages and solutions, researchers have developed a model of the ethyl alcohol content in the solution using the Debye model. This technique was very fast and low cost. The permittivity of various alcoholic solutions as a function of concentrations at 1 GHz and 7 GHz measured by a commercial probe were linear responses, except for some drinks containing sugar and some types of beer [8].
For a broad frequency band, the reflection method is a common microwave measurement procedure to determine the complex permittivity of materials using nonresonant technique. By employing this method, coaxial transmission line probes have been proposed, resulting in accurate complex permittivity values. The electromagnetic waves applied to a sample under study and the properties of the material sample are deduced from the reflection coefficient at a defined reference plane [9].
The advantages of these proposed probes are non-destructive and non-invasive testing. In general basic, principle of the measurement is to measure the reflection coefficient of the material under test and displayed in complex permittivity parameters.
In previous researches, the N-type and SMA coaxial connectors have been applied to be open-ended coaxial probes. The probe structure is very simple and convenient for complex permittivity measurement. However, the limitation of frequency ranges up to 1 GHz for N-type and 3 GHz for SMA has been found. It can be seen that the error of measurement of distilled water is about 5.7% at 1 GHz for N-type connector and 20% at 2450 MHz for SMA connector [10]. In many applications, the complex permittivity values of materials at higher frequencies are required. Therefore, we propose a new probe using a modified SMA connector with a stepped structure for measuring complex permittivity in a wide range. Nevertheless, the proposed probe is based on a commercial SMA connector, resulting in low cost and ease for utilizing. To analyze a stepped coaxial probe, FDTD method will be used to calculate the important parameters of the probe model. In order to verify the accuracy, the distilled water and its Debye model at various temperatures have been used to determine the parameters in the probe model. The proposed probe will be then employed to measure the complex permittivity of butters. Also, ethyl alcohols diluted with various amount of water will be used as material under test for complex permittivity measurement. The results will be compared with the permittivity values from the commercial dielectric probe (Agilent 85070E).
2. Probe Structure and Analysis
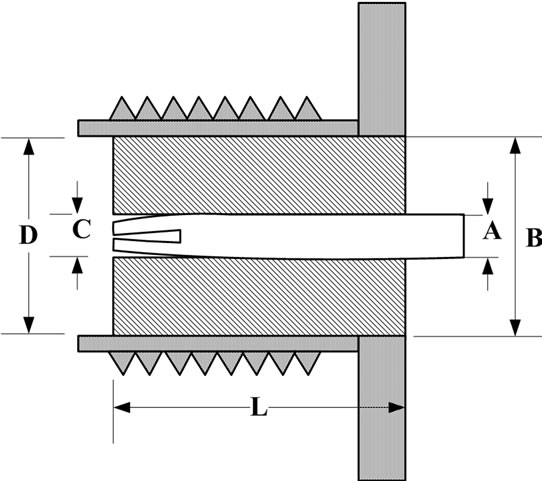
An SMA connector for a printed circuit board and an SMA coaxial cable connector for small diameter cable are chosen as permittivity probes. Those SMA probes with cross-section structures shown in Figure 1 will be analyzed in this research. Figure 1(a) shows the conventional SMA probe and Figure 1(b) shows the SMA coaxial cable connector modified to be a stepped SMA probe by cutting off the excess part. The probes have their parameters including substrate length of L, inner pin diameter of C, and inner connector diameter of D.
As described in [10] the error of measurement is produced from measured area, therefore how to reduce this problem should be considered. To reduce the contact area suitable for accurate permittivity measurement, we use the SMA coaxial cable connector to be the proposed probe as shown in Figure 1(b). The parameters A and B are a diameter of inner pin and outer diameter of the stepped section, the semi-rigid cable part. The cutting plane in Figure 1(b) is the interconnection of the conductor of the semi-rigid cable and the SMA connector. All dimensions of the probes are presented in Table 1, which are based on the size of the commercial microwave cable and connectors. Figure 2 shows the photographs of probes. The probes will be analyzed by FDTD method.
The equivalent circuit of the probe including the coaxial line section and its discontinuity effects has been presented by a parallel capacitance model [11-13]. The capacitances of the conventional and stepped SMA probes characterized by using FDTD method are shown in Figure 3. It is obvious that the capacitance of the proposed probe is higher due to the effect of stepped impedance.
 (a)
(a)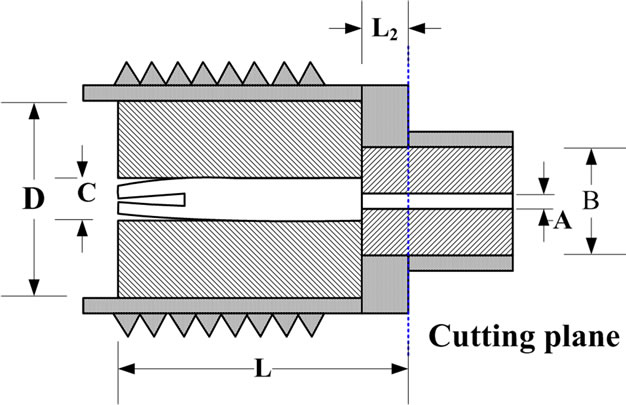 (b)
(b)
Figure 1. Cross-sections (a) the conventional and (b) the proposed probes. (a) SMA connector; (b) SMA coaxial cable connector.
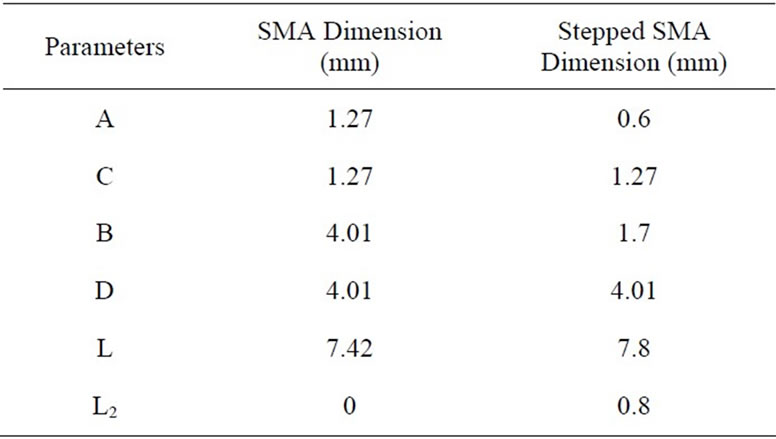
Table 1. Dimension of the connectors.
 (a)
(a) (b)
(b)
Figure 2. Photographs of the probes. (a) SMA probe; (b) Stepped SMA probe.
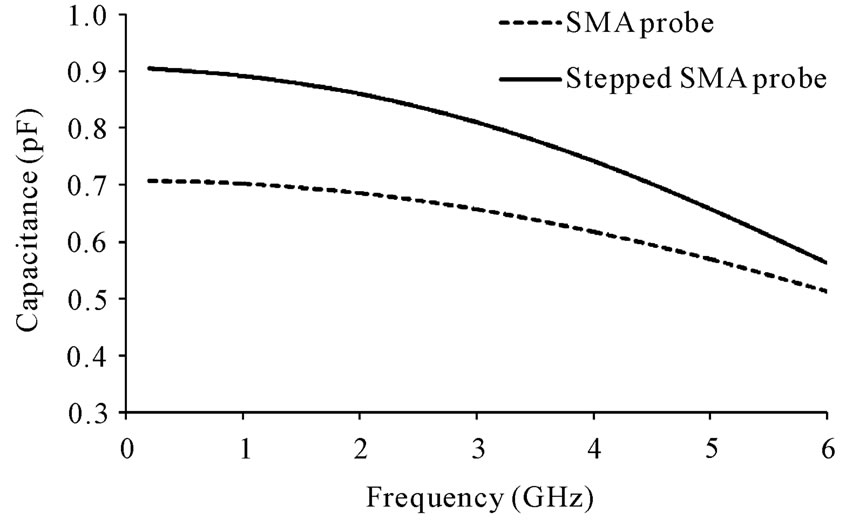
Figure 3. Capacitances of the SMA and the stepped SMA probes by using FDTD method.
When the dielectric under test (εDUT) is connected to the aperture of the probe, the equivalent circuit can be modified as shown Figure 4. The circuit model consists of a parallel conductance G0 and a capacitive susceptance C0. The amount of G0 is a coefficient accounting for the radiation loss and C0 consists of two parts which are the inside of the probe capacitance and the fringing field as a consequence of the test material [14]. For the components calculation, a radiation model has been presented by Radim [15].
The input admittance of the coaxial transmission line is then
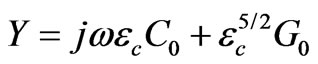 (1)
(1)

Figure 4. An equivalent circuit of the probe.
where Y is the measured admittance of the probe, C0 and G0 are constants. The admittance value of Y is related to the measurement reflection coefficient S11. The characteristic impedance Z0 of the probe is related to the Y as
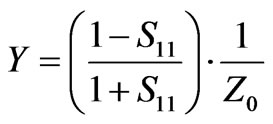 (2)
(2)
In calculation, the complex admittance parameters are computed for a measured reflection coefficient which an aperture plane is connected to the reference material. The distilled water is usually employed as a reference material. The complex permittivity of distilled water, ec, is corrected by the Debye model [16]. Their real and imaginary parts are individual of each temperature, so that the complex admittance value, C0 and G0 are calculated by using (1) and (2). Table 2 shows an example of their results calculated at 931 MHz for temperatures of 15˚C, 25˚C, and 29˚C, respectively.
For a frequency range between 100 MHz to 2 GHz, the values of C0 and G0 can be determined, as results shown in Figure 5. From Figure 5(a) shown the capacitances, C0, it is found that the conventional SMA probe has the capacitance value of about 0.048 pF and its values are increased around 30% at 1.0 GHz. For the stepped SMA probe, the capacitance values are about 0.035 pF and increased approximately 30% at 1.15 GHz. It is also found that the capacitance of the stepped SMA probe has a smaller change than the conventional SMA probe.
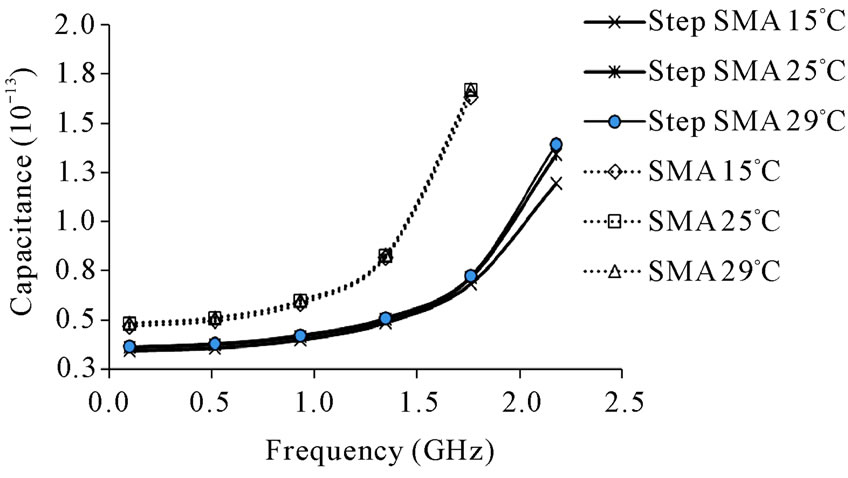
In the same way, Figure 5(b) shows the conductances, G0. It is found that the conductance values of the conventional SMA and stepped SMA probes are changed to 0.003 × 10–6 mho at 0.7 GHz and 0.85 GHz, respectively. It also can be seen that the conductance of stepped SMA probe has a smaller change than the conventional SMA probe.
The rapid changes of C0 and G0 are main problems, resulting in errors in permittivity measurement as shown in Figure 6. It can be conclude that the stepped SMA probe provides higher accurate result compared with the SMA probe due to the values of C0 and G0 are more constant for higher frequency range than the conventional SMA probe.
3. Experiment and Results
As it is described above, the measurement process is im-
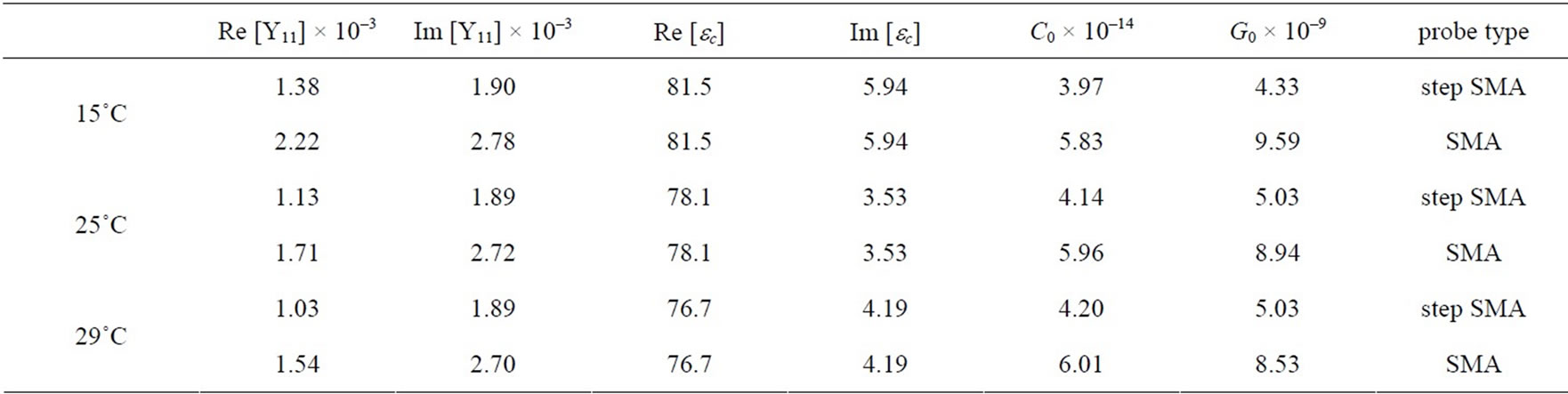
Table 2. Calculation of the probe parameters at 931 MHz and three values of temperature.
 (a)
(a)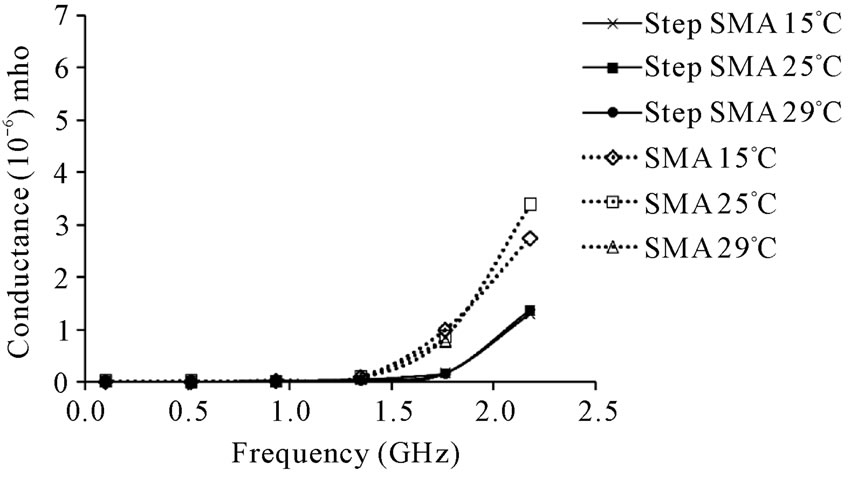 (b)
(b)
Figure 5. The capacitance and conductance responses of the probes in distilled water. (a) Capacitance responses of the probes; (b) Conductance responses of the probes.
portantly needed to prepare. It is classified into two parts, one is a probe calibration with the calibration standard kit 85052D setup and another is using a standard material. The calibration standard setup supported for SMA connector is shown in Figure 7. Distilled water is usually used to be the material standard because of its known complex permittivity, ec. Then the reflection coefficient is measured in complex form after that the characteristic of the distilled water is calculated by using (2). Equation (1) is then used to compute for the values of C0 and G0. Figure 6 shows the validated distilled water permittivity measurement. It is noticed that the results of the proposed
 (a)
(a) (b)
(b)
Figure 6. Measurement of ec by using distilled water at 25˚C. (a) Real part; (b) Imaginary part.
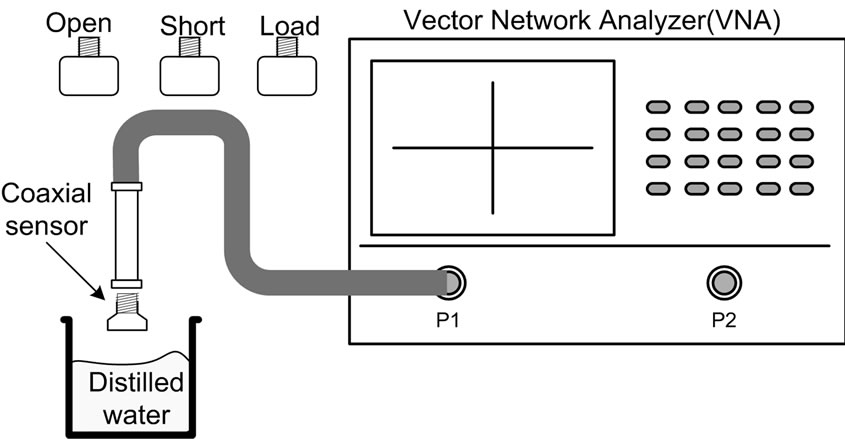
Figure 7. Measurement setup for analysis of probe parameters.
stepped SMA probe is agreed very well when compared with the Debye model in range of 100 MHz to 2.25 GHz.
Besides, our complex permittivity will be uncorrected due to the changes of C0 and G0 values.
In order to extract the complex permittivity of dielectric-under-test (DUT), we need to de-embed the effect of the unknown network between the measurement plane and the aperture plane. From Figure 8, the reflection coefficient should be measured at the DUT plane. If the reference plane has previously been defined at the entrance of the probe, GVNA, then we should find the phase difference between two planes. Figure 9 displays phase responses of two planes.
It is noted that, the phase of GVNA is not rapidly varied. In the contrast way, the phase of GDUT as shown in Figure 9 is hasty changed because of probe effect. Therefore, the phase of GDUT must be compensated using GDUT(air) by conjugated computation. Figure 10 shows the results of distilled water at 15˚C by measuring the proposed stepped SMA probe and comparing with the conventional SMA probe and Debye theory. It is noticed that the result of the proposed stepped SMA probe is closed to theory comparing with the result of the conventional SMA probe. Figure 11 shows the photograph of stepped SMA probe in measuring setup. Its dimension is 15 cm including a copper tube connected to the HP85053 VNA (Vector Network Analyzer).
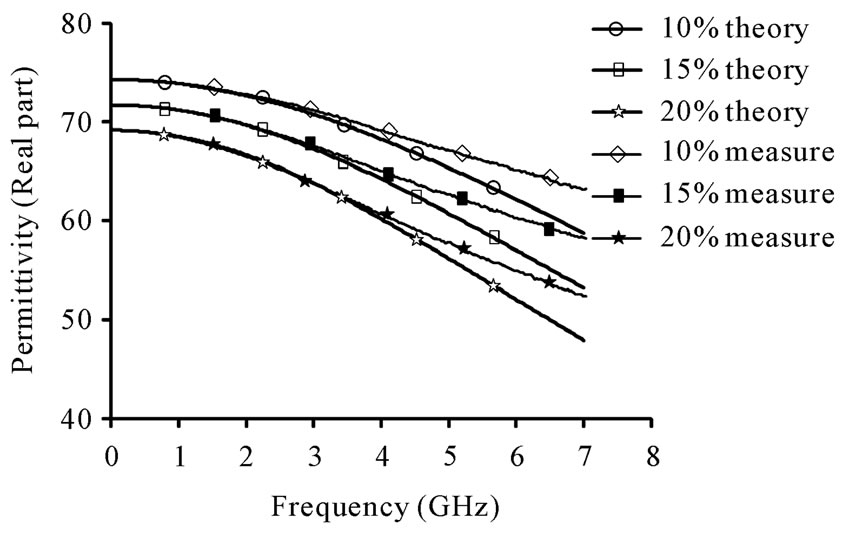
After calibration method, using open-end, short-end, and 50 ohm load, we then have measured the concentrated alcohols of 10%, 15% and 20% as DUTs at 24˚C in frequency range of 0.1 to 6 GHz. However, the phase of GDUT must be compensated using GDUT(air) and Debye model of alcohols must be employed to determine the values of C0 and G0 of the probe. Figure 12 shows the complex permittivity values of concentration alcohols compared with the theory. It is found that their measured results are agreed very well with theory. Although, some relative errors are produced, especially imaginary values at low frequency as shown in Figure 13.
Additionally, we have tested the proposed probe with the salted butter as a DUT. The butter product is made in Thailand farm, which its content consists of butter oil of 80%, salt of 2%, and powder milk of 2%. When measuring, the butter temperature at each probe position must be the same in order to obtain the corrected results. Figure 14 shows the comparison of permittivity of salted butter at 23˚C measured by the stepped SMA probe and the commercial probe (Agilent 85070E Dielectric Probe Kit), which the results are agreed very well.
4. Conclusions
The stepped coaxial line probe has been developed and compared with the conventional SMA connector probe.

Figure 8. Reflection coefficient measurement planes.
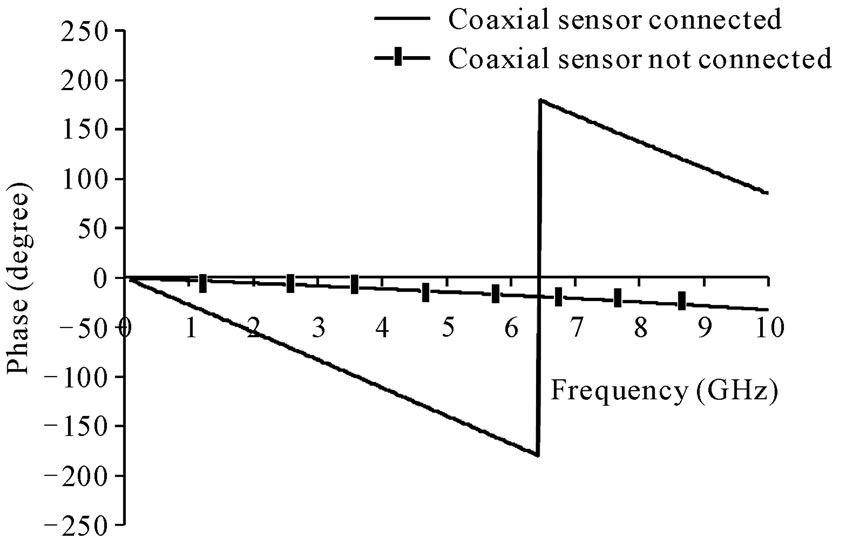
Figure 9. Phase responses of reflection coefficients.
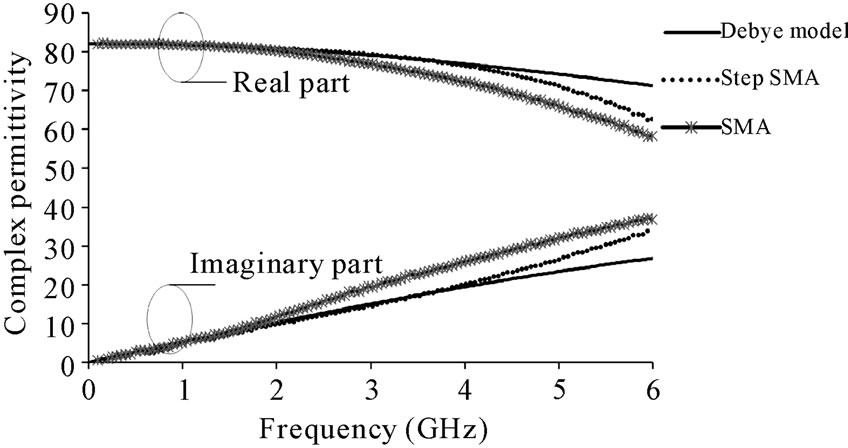
Figure 10. Real and Imaginary parts of distilled water at 15˚C after phase compensation.



Figure 11. Measurement of concentration alcohols using the stepped SMA probe.
 (a)
(a)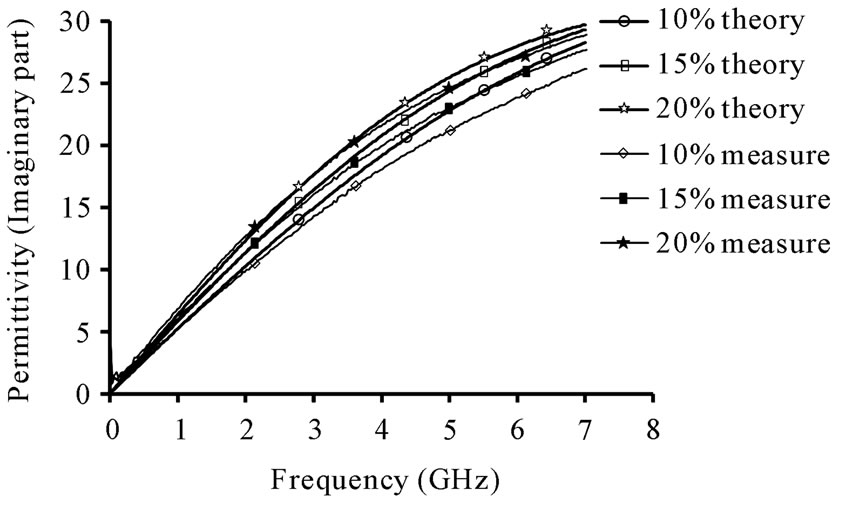 (b)
(b)
Figure 12. Dielectric permittivities of concentration alcohols of 10%, 15% and 20% corresponding with the Debye model (a) real part and (b) imaginary part.
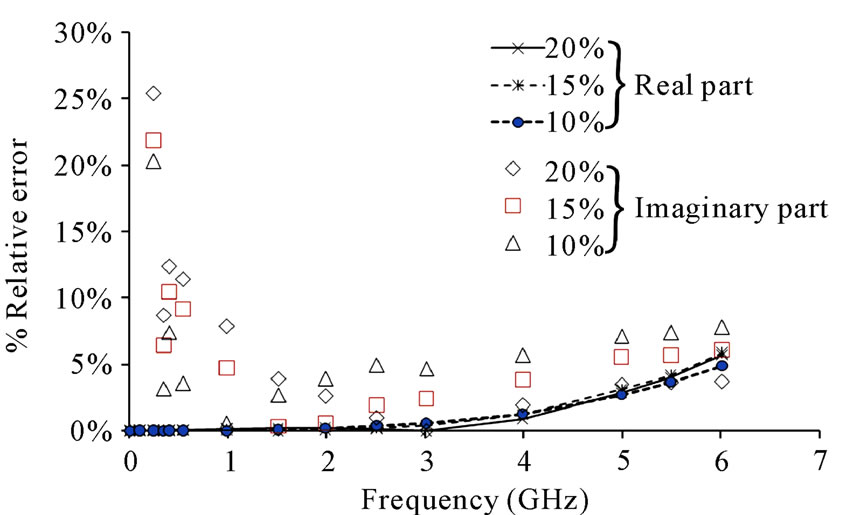
Figure 13. Relative errors of real and imaginary parts of solutions of 10%, 15%, 20% ethyl alcohols in water.
The total capacitance and conductance of the probes are analyzed. Changing the probe model parameters of G0 and C0 will affect to complex permittivity. It has been found that the changes in G0 and C0 of the proposed stepped SMA probe are lower than the conventional SMA probe, resulting in higher accurate results. The proposed probe has been tested by measuring the complex permittivity values of concentrated alcohols of 10%,
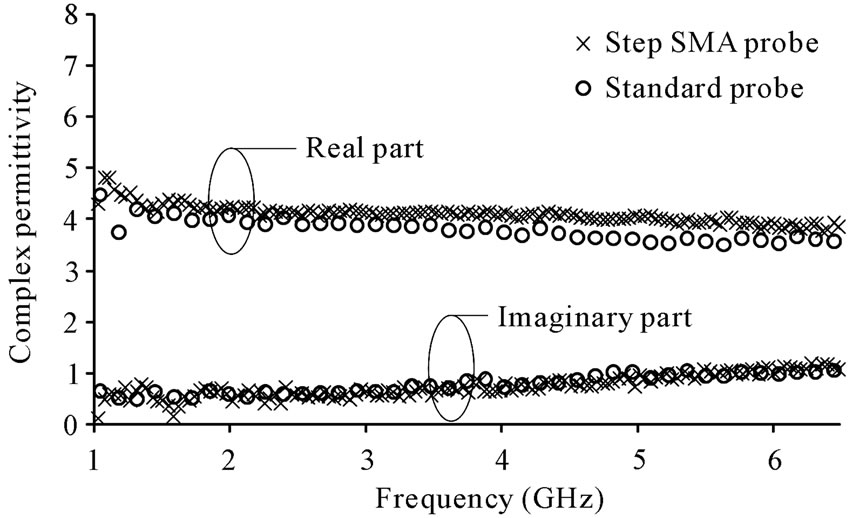
Figure 14. Complex permittivity of salted butter at 23˚C.
15% and 20% and the salted butter. It has been confirmed that the proposed probe can be operated well in a frequency range of 100 MHz to 6 GHz. The measured permittivity results using the proposed probe are agreed well with the commercial probe.
5. Acknowledgements
Authors would like to thank Dr. Denchai Worasawate at the NTC Telecommunications Research Laboratory, Department of Electrical Engineering, Kasetsart University for supporting the dielectric probe kit.
REFERENCES
- H. P. Schwan and K. R. Foster, “RF-Field Interactions with Biological System: Electrical Properties and Biophysical Mechanisms,” Proceedings of the IEEE, Vol. 68, No. 1, 1980, pp.104-113. doi:10.1109/PROC.1980.11589
- A. C. Metaxas and R. J. Meredith. “Industrial Microwave Heating,” Peter Peregrinus, London, 1988.
- C. Amatore, M. Berthou and S. Hebert. “Fundamental Principles of Electrochemical Ohmic Heating of Solutions,” Journal of Electroanalytical Chemistry, Vol. 457, No. 1-2, 1998, pp. 191-203. doi:10.1016/S0022-0728(98)00306-4
- S. O. Nelson, “Agricultural Applications of Dielectric Measurements,” IEEE Transaction on Dielectrics and Electrical Insulation, Vol. 13, No. 4, 2006, pp. 688-702. doi:10.1109/TDEI.2006.1667726
- S. O. Nelson, “Dielectric Properties of Agricultural Products and Some Applications,” Research in Agricultural Engineering, Vol. 54, 2008, pp. 104-112.
- A. Jasim, S. R. Hosahalli and G. S. R. Vijaya, “Dielectric Properties of Butter in the MW Frequency Range as Affected by Salt and Temperature,” Journal of Food Engineering, Vol. 82, No. 3, 2007, pp. 351-358. doi:10.1016/j.jfoodeng.2007.02.049
- S. Seiichi and S. Naoki, “Dielectric Relaxation Time and Relaxation Time Distribution of Alcohol-Water Mixtures,” The Journal of Physical Chemistry A, Vol. 106, No. 3, 2002, pp. 458-464.
- X. Bohigas and J. Tejada, “Dielectric Characterization of Alcoholic Beverages and Solutions of Ethanol in Water under Microwave Radiation in the 1 - 20 GHz Range,” Food Research International, Vol. 43, No. 6, 2010, pp. 1607-1613. doi:10.1016/j.foodres.2010.04.021
- T. W. Athey and M. A. Stuchly, “Measurement of Radio Frequency Permittivity of Biological Tissues with an Open-Ended Coaxial Line,” (Part 1 and 2) IEEE Transactions on Microwave Theory and Techniques, Vol. MTT- 30, January 1982, pp. 82-92. doi:10.1109/TMTT.1982.1131021
- R. Zajíček, L. Oppl and J. Vrba, “Broadband Measurement of Complex Permittivity Using Reflection Method and Coaxial Probes,” Radio Engineering, Vol. 17, No. 1, April 2008, pp. 14-19.
- P. L. Somlo, “The Computation of Coaxial Line Step Capacitance,” IEEE Transactions on Mircrowave Theory and Techniques, Vol. MTT-15, No. 1, January 1967, pp. 48-53. doi:10.1109/TMTT.1967.1126368
- A. Jurkus, “Computation of Step Discontinuities in Coaxial Line,” IEEE Transactions on Mircrowave Theory and Techniques, Vol. 20, No. 10, October 1972, pp. 708- 709. doi:10.1109/TMTT.1972.1127852
- W. K. Gwarek, “Computer-Aided Analysis of Arbitrarily Shaped Coaxial Discontinuities,” IEEE Transactions on Mircrowave Theory and Techniques, Vol. 36, No. 2, 1988, pp. 337-342. doi:10.1109/22.3523
- G. B. Gajda and S. S. Stuchly, “Numerical Analysis of Open-Ended Coaxial Lines,” IEEE Transactions on Microwave Theory and Techniques, Vol. MTT-31, No. 5, May 1983, pp. 380-384. doi:10.1109/TMTT.1983.1131507
- L. S. Anderson, G. B. Gajda and S. S. Stuchly, “Dielectric Measurements Using a Rational Functional Model,” IEEE Transactions on Microwave Theory and Technique, Vol. 42, No. 2, 1994, pp. 199-204. doi:10.1109/22.275247
- U. Kaatze, “Complex Permittivity of Water as a Function of Frequency and Temperature,” Journal of Chemical & Engineering Data, Vol. 34, No. 4, 1989, pp. 371-374. doi:10.1021/je00058a001

