Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 7 (2011) , Article ID: 5907 , 4 pages DOI:10.4236/jemaa.2011.37043
On the Effects of Complex Conjugate Medium on TM Scattering by a Strip
![]()
1National Center for Physics (NCP), Quaid-i-Azam University, Islamabad, Pakistan; 2Department of Physics, Allama Iqbal Open University, Islamabad, Pakistan.
Email: amjadqau@hotmail.com, ahsanilahi@gmail.com
Received April 24th, 2011; revised May 27th, 2011; accepted June 10th, 2011.
Keywords: Complex Conjugate Medium, Kobayashi Potential Method, Scattering from Strip, Mixed Boundary Value Problem etc.
ABSTRACT
In this paper, Method of Kobayashi Potential is used to determine the scattering behavior of a strip which is placed at the air-complex conjugate medium interface. And discussion is presented that how the complex conjugate medium modifies the scattering properties of the strip. A comparison is also given with that if we replace the conjugate medium with standard dielectric medium. E-polarized electromagnetic plane wave is supposed to be obliquely incident upon the geometry. Scattered fields in both the half spaces are supposed in terms of unknown weighting functions. Discontinuous properties of Weber-Schafheitlin integral and orthogonal properties of Jacobi’s polynomials are used to determine these unknown weighting functions. Far scattered fields have been calculated using Saddle Point Method and computed for different parameters of interest.
1. Introduction
The complex value of the constitutive parameters (i.e. permittivity and permeability) of a medium cause the medium to be lossy as the refractive index 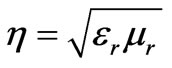 or the propagation constant of the medium also become complex (where
or the propagation constant of the medium also become complex (where  and
and  is the relative permittivity and relative permeability of the medium). But such medium may also be lossless if
is the relative permittivity and relative permeability of the medium). But such medium may also be lossless if 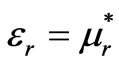 (that is they are complex conjugate of each other) because in this case refractive index/propagation constant will become real and this real value of
(that is they are complex conjugate of each other) because in this case refractive index/propagation constant will become real and this real value of  will ensure the unattanuated wave propagation through the medium. Such medium is named as complex conjugate medium by Dregoman in his recently published paper [1]. In this paper, he has discussed the reflection and transmission properties of this medium. He also has proposed a scheme to realize such materials. These materials have many potential applications in optoelectronics, miniaturized amplifiers and lasers.
will ensure the unattanuated wave propagation through the medium. Such medium is named as complex conjugate medium by Dregoman in his recently published paper [1]. In this paper, he has discussed the reflection and transmission properties of this medium. He also has proposed a scheme to realize such materials. These materials have many potential applications in optoelectronics, miniaturized amplifiers and lasers.
In the present work, analysis has been presented which investigates the effects of complex valued constitutive parameters of the complex conjugate medium on the scattering properties of a conducting strip. Illustrative computations are given for far field patterns as the function of imaginary part of permittivity/permeability whose value is zero for standard dielectric medium. Present analysis is based on the Kobayashi Potential (KP) Method. This method has successfully been applied to various problems in electromagnetic and acoustics [2-6]. The method exploits the discontinuous properties of Weber-Schafheitlin’s integrals and orthogonal properties of Jacobi’s polynomials to construct the solution. In this method the problem at its final stage reduce to matrix equations. The elements of matrix equations are usually infinite integrals which has branch points as well as poles depending upon the nature of the problem. Analytic solutions of these integrals are not possible for most of the cases. Therefore algorithms are developed to numerically solve these integrals and hence the matrix equations.
2. Formulation and Solution of the Problem
The geometry of the problem and coordinate system are shown in figure 1. A thin conducting strip of width 2 is located at the interface between air and complex conjugate medium.
is located at the interface between air and complex conjugate medium.  are supposed to be the constitutive parameters of upper half space
are supposed to be the constitutive parameters of upper half space  medium, while the lower half space
medium, while the lower half space  , which is occupied by the complex conjugate medium, has the constitutive
, which is occupied by the complex conjugate medium, has the constitutive
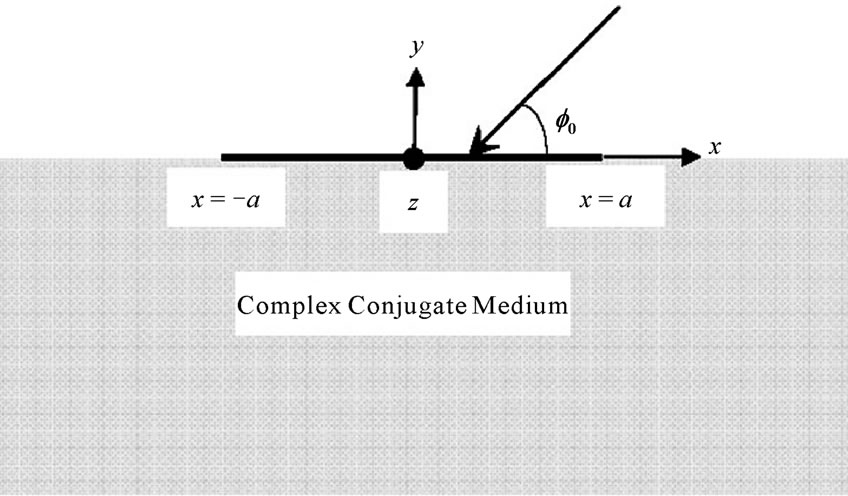
Figure 1. Geometry of the problem.
parameters . For the sake of simplicity, we suppose that an E-polarized field,
. For the sake of simplicity, we suppose that an E-polarized field, 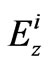 , is obliquely incident upon the geometry, therefore
, is obliquely incident upon the geometry, therefore
 (1a)
(1a)
where 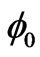 is the angle of incidence with x-axis and
is the angle of incidence with x-axis and 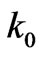 be the wave number for
be the wave number for 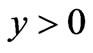 half space. In each region, scattered field may be assumed in terms of unknown weighting functions. Therefore, expressions for scattered field,
half space. In each region, scattered field may be assumed in terms of unknown weighting functions. Therefore, expressions for scattered field, 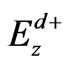 in upper half space and in lower half space, can be assumed in the form
in upper half space and in lower half space, can be assumed in the form
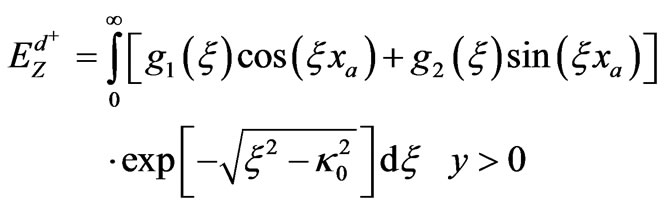 (1b)
(1b)
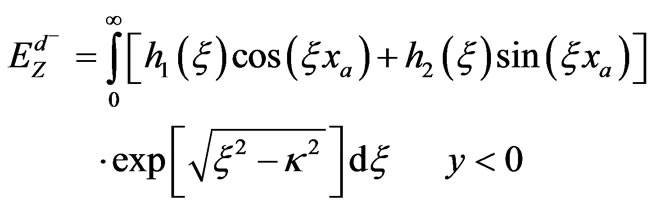 (1c)
(1c)
where  is the propagation constant of complex conjugate medium and
is the propagation constant of complex conjugate medium and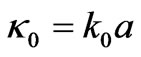 ,
,  ,
, 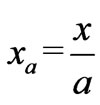 ,
,
 and the functions
and the functions 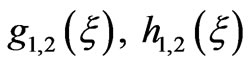 are the weighting functions to be determined from the boundary conditions.
are the weighting functions to be determined from the boundary conditions.
Geometry supports the following boundary conditions
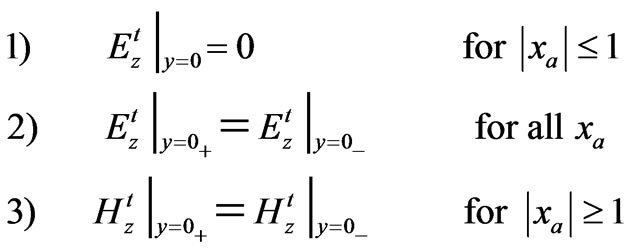 (2)
(2)
where superscript stands for total. Applying boundary condition 2) we have
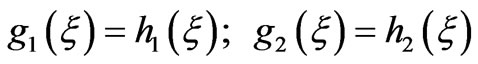
Imposing the boundary conditions 1) and 3) give
 (3a)
(3a)
 (3b)
(3b)
where R is the reflection coefficient of the complex conjugate half space without strip and

where 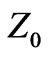 and
and  are intrinsic impedances of free space and complex conjugate medium respectively and
are intrinsic impedances of free space and complex conjugate medium respectively and 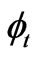 is the angle of refraction which is related to angle of incidence through second relation of last expression.
is the angle of refraction which is related to angle of incidence through second relation of last expression.
Dependency of  and
and 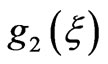 may be decided by comparing (3a) with Weber-Schafheitlin’s integral and exploiting the properties of Gamma function at negative integer values, we have
may be decided by comparing (3a) with Weber-Schafheitlin’s integral and exploiting the properties of Gamma function at negative integer values, we have
 (4a)
(4a)
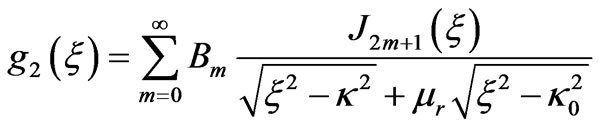 (4b)
(4b)
where  and
and  are expansion coefficients and
are expansion coefficients and 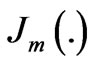 be the Bessel’s function of order m. Separating even and odd functions of the expression (3b) and putting the values of weighting functions as given in (4), we get
be the Bessel’s function of order m. Separating even and odd functions of the expression (3b) and putting the values of weighting functions as given in (4), we get
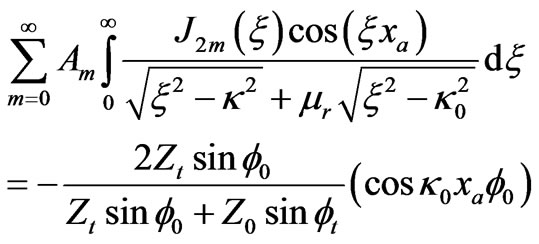 (5a)
(5a)
 (5b)
(5b)
Expanding the trigonometric functions in above expressions in terms of Jacobi’s polynomials  [7]we get the following matrix equations
[7]we get the following matrix equations
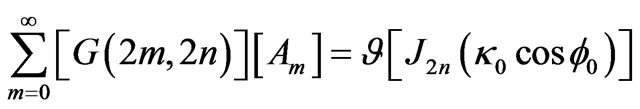 (6a)
(6a)
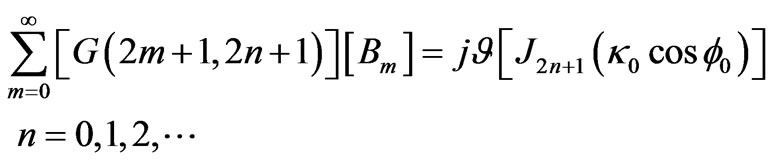 (6b)
(6b)
where notations used in above expressions are defined as
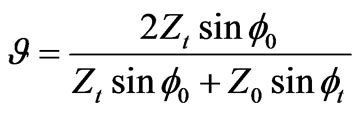 (6c)
(6c)
 (6d)
(6d)
In obtaining (6a) and (6b) we have made use of following relations

and orthogonal properties of Jacobi’s polynomials 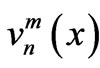 .
.
Far Scattered Field
Far scattered fields can be calculated by using Saddle Point Method. Therefore, substituting the values of  and
and 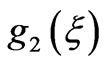 and then applying the said method, (1b) finally reduces to
and then applying the said method, (1b) finally reduces to
 (7)
(7)
where  ,
,  is the angle of observation and
is the angle of observation and 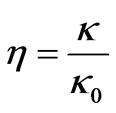 is the refractive index of lower half space. Expansion coefficients
is the refractive index of lower half space. Expansion coefficients  and
and 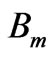 can be computed using matrix equations (6a) and (6b).
can be computed using matrix equations (6a) and (6b).
3. Results and Discussion
Since both 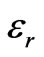 and
and  are complex quantities, so we can consider
are complex quantities, so we can consider 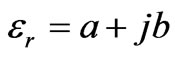 or in general
or in general  such that
such that 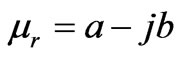 and refractive index of complex conjugate medium
and refractive index of complex conjugate medium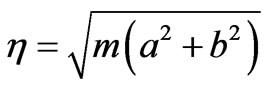 . Equation (6a) and
. Equation (6a) and
(6b) are the matrix equations which can be used to determine the values of unknown expansion coefficients  and
and .
. 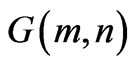 are the matrices, the elements of which are in terms of infinite integrals as indicated by (6d). Algorithms were developed to numerically evaluate these integrals. The matrix size was taken as
are the matrices, the elements of which are in terms of infinite integrals as indicated by (6d). Algorithms were developed to numerically evaluate these integrals. The matrix size was taken as
 . The values of expansion coefficients
. The values of expansion coefficients  and
and 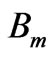 , as determined from (6a) and (6b), were then used in equation (7) to determine the far scattered fields in upper half space. Since the most important parameter in our discussion is the imaginary part of permittivity/permeability that is designated by b. Therefore, Figure 2 represents the dependence of real part of scattered field on b. This figure also gives the comparison if we replace complex conjugate medium in lower half space with standard dielectric medium. For the standard dielectric case we have taken
, as determined from (6a) and (6b), were then used in equation (7) to determine the far scattered fields in upper half space. Since the most important parameter in our discussion is the imaginary part of permittivity/permeability that is designated by b. Therefore, Figure 2 represents the dependence of real part of scattered field on b. This figure also gives the comparison if we replace complex conjugate medium in lower half space with standard dielectric medium. For the standard dielectric case we have taken 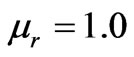 and
and
 . Figure 3 gives imaginary part of the scattered field from complex conjugate medium and standard dielectric medium. These figures show that the real and imaginary parts of scattered field follow the similar trend for the case of dielectric medium. They only differ quantitatively. But for the case of complex conjugate medium, the situation is different. The behaviors of these parts of the scattered field with respect to b are distinct. This situation may be exploited to differentiate complex conjugate materials from standard dielectric materials of same refractive index [8,9]. Figure 4 gives the variations in the far scattered field as a function of mfor
. Figure 3 gives imaginary part of the scattered field from complex conjugate medium and standard dielectric medium. These figures show that the real and imaginary parts of scattered field follow the similar trend for the case of dielectric medium. They only differ quantitatively. But for the case of complex conjugate medium, the situation is different. The behaviors of these parts of the scattered field with respect to b are distinct. This situation may be exploited to differentiate complex conjugate materials from standard dielectric materials of same refractive index [8,9]. Figure 4 gives the variations in the far scattered field as a function of mfor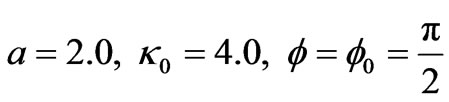 . This figure shows that as we increase the values of m, the strength of the fields decrease. Figure 5 shows the influence of b on field distribution in whole upper half space.
. This figure shows that as we increase the values of m, the strength of the fields decrease. Figure 5 shows the influence of b on field distribution in whole upper half space.
4. Conclusions
Complex conjugate and ordinary dielectric materials are
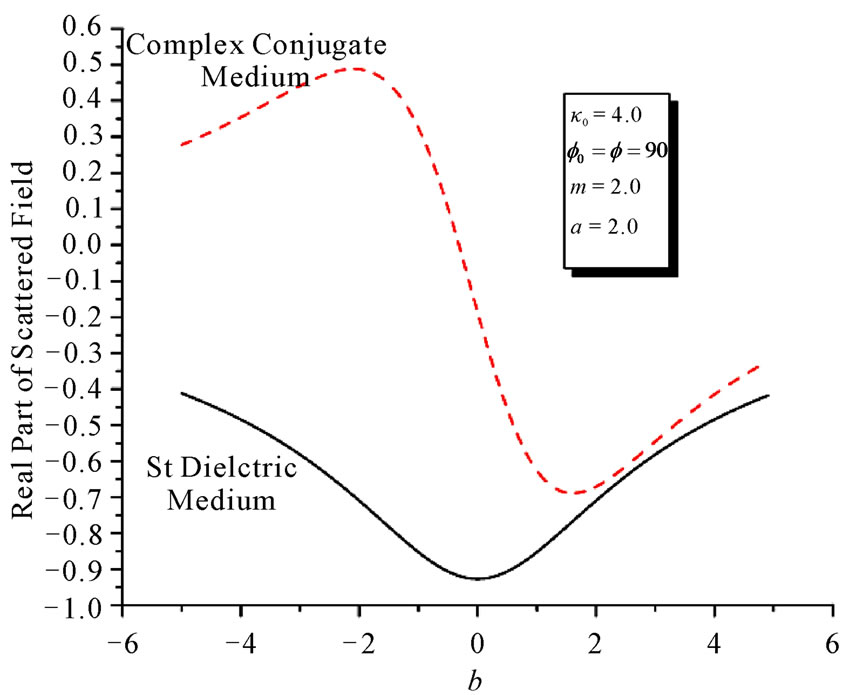
Figure 2. Dependence of real part of scattered field on b.

Figure 3. Dependence of imagnary part of scattered field on b.
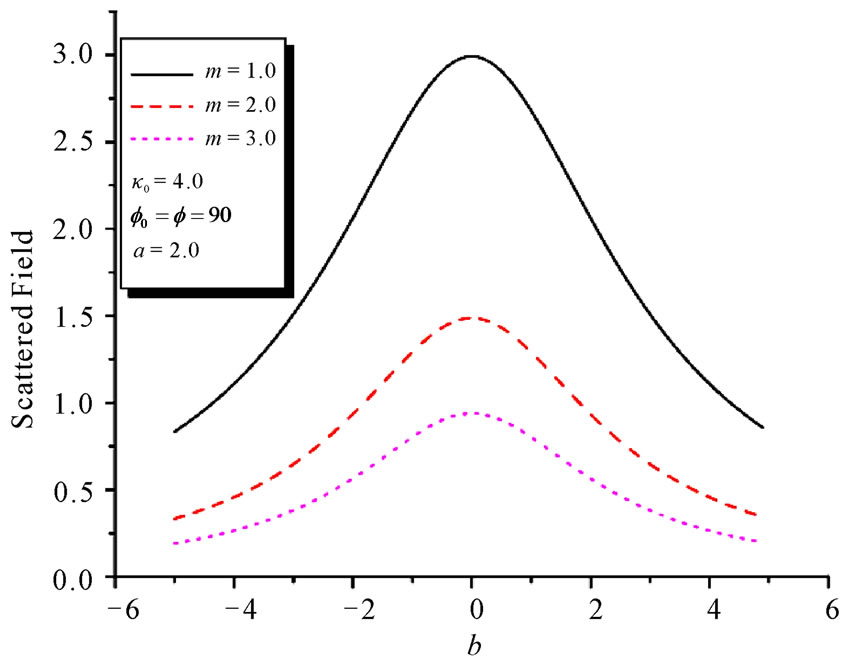
Figure 4. Effects of m on scattered field from complex conjugate medium.

Figure 5. scattered field in upper half plane.
both lossless but distinction between then is that the constitutive parameters of complex conjugate materials are complex valued and that of ordinary materials are real valued of same sign. In the present study, the effects of these newly conceived complex conjugate materials on the scattering properties of a strip are analyzed. For this purpose, the Method of Kobayashi Potential is used which is well known in dealing with mixed boundary problems. A comparison with ordinary dielectric material with same refractive index is also presented. It is concluded that behavior of real and imaginary parts of the scattered field for both the cases differ qualitatively and quantitatively. Although both are lossless media but still they are distinguishable.
REFERENCES
- D. Dragoman, “Complex Conjugate Media: Alternative Configurations for Miniaturized Lasers,” Optics Communication, Vol. 284, No. 8, 2011, pp. 2095-2098. doi:10.1016/j.optcom.2010.12.069
- I. Kobayashi, “Collected Papers of I. Kobayashi,” Memorial Publication Committee, Faculty of Engineering, Nihon University, Tokyo, 1970.
- K. Hongo, “Diffraction of Electromagnetic Plane Wave by the Slit,” Transactions of the Institute of Electronics and Communication Engineers of Japan, Vol. 55-B, No. 6, 1972, pp. 328-330.
- K. Hongo, “Diffraction of Electromagnetic Plane Wave by an Infinite Slit Embedded in an Anisotropic Plasma,” Journal of Applied Physics, Vol. 43, No. 12, 1972, pp. 4996-5001. doi:10.1063/1.1661059
- K. Hongo, “Diffraction by a Flanged Parallel Plate Waveguide,” Radio Science, Vol. 7, No. 10, 1972, pp. 955-963. doi:10.1029/RS007i010p00955
- K. Hongo and H. Serizawa, “Diffraction of an Acoustic plane Wave by a Rectangular Plate,” Journal of Applied Physics, Vol. 82, No. 6, 1997, pp. 2719-2729.
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions,” Dover Publishing Inc., New York, 1968.
- H. Fujiwara, “Spectroscopic Ellipsometry: Principles and Applications,” Wiley, Hoboken, 2007.
- H. G. Tompkins and W. A. McGahan, “Spectroscopic Ellipsometry and Reflectometry: A User’s Guide,” Wiley Interscience, 1999. doi:10.1063/1.366266

