Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 4 (2011) , Article ID: 4621 , 4 pages DOI:10.4236/jemaa.2011.34019
Computation of Protection Zone of a Lightning Rod Using Method of Moments and Monte Carlo Integration Technique
![]()
Department of Electronics and Communication Engineering, Birla Institute of Technology, Mesra, India.
Email: {abhaysrivastava2313, mrinal.mishra}@gmail.com
Received October 28th, 2010; revised November 22nd, 2010; accepted March 17th, 2011.
Keywords: Lightning Rod, Quasi Monte Carlo Integration, Method of Moments, Protection Zone
ABSTRACT
An accurate determination of lightning protection zone is an important issue in the analysis and design of an appropriate lightning protection system. This paper presents a fast and accurate protection zone determination methodology for metallic lightning rod. The methodology is based on Quasi Monte Carlo Integration technique applied to Method of Moments (MoM) solution of Integral Equations. As an example, solution of the integral equation for unknown charge distribution on lightning rod is obtained. The electric field in the region surrounding the rod is then computed and the protection zone plotted accordingly. The effect of the thickness of the rod on the protection zone is also studied.
1. Introduction
Lightning and thunder strike has been a subject of interest and research since years but the progress has been slow owing to the random nature of the lightning strikes and long time needed to gather data for the same. Recent developments in the field of computational techniques have resulted in more accurate and fast modeling of this phenomenon. Various types of lightning protection systems which consist of lightning attachment points and down-conductors for allowing lightning current to flow to the earth safely are employed. There have been many attempts to examine the effectiveness of the lightning rod used in the lightning protection systems. The effectiveness of a lightning rod as a strike receptor has been studies recently [1], particularly in relation to the influence of the tip radius of curvature.
In 1752, B. Franklin invented lightning rod for safely discharge of cloud on a structure. In 2000, Moore had given a guideline to installation of lightning rod with the relationship in height and diameter [2,3]. In the present work, the protection zone of the lightning rod is computed for several dimensions of the rod and the effect of varying the thickness of the rod is examined on the protection zone. It is in fact well known that numerical methods like Method of Moments (MoM) [4] can give accurate and efficient solutions to a large variety of such problems. The solution of the problem involves the computation of singular integral equation appearing in the MoM analysis of the problem. Point matching technique commonly employed in MoM solution usually makes the diagonal terms singular. However, if two separate quasi random sequences spread over the domain are chosen for the source and the field points, then they are not equal to each other, and thus the integration will not be singular. The QMCI technique [5-7] using Halton sequence is employed here for this purpose for the solution of singular integral equation, which uses prime numbers as bases to generate uniformly distributed quasi random points in the domain of integration for function evaluation. This is because of the fact that sample points in a quasi -random sequence are, in a precise sense, “maximally avoiding” of each other.
2. Problem Formulation
In electrostatic field problems, in the homogeneous medium, the potential 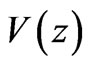 due to a charge distribution characterized by density
due to a charge distribution characterized by density 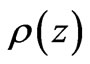 over the rod of length L is given by:
over the rod of length L is given by:
 (1)
(1)
If this equation is applied to the lightning rod where the potential 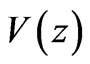 is known, then this becomes an integral equation for the unknown charge density
is known, then this becomes an integral equation for the unknown charge density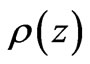 .
.
For MoM solution of the integral equation, taking some known basis function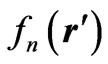 , the unknown charge on the conducting surface is expanded as
, the unknown charge on the conducting surface is expanded as 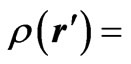
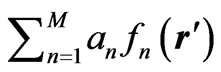 with unknown coefficient
with unknown coefficient 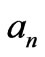 to be determined. Then on the surface we have
to be determined. Then on the surface we have
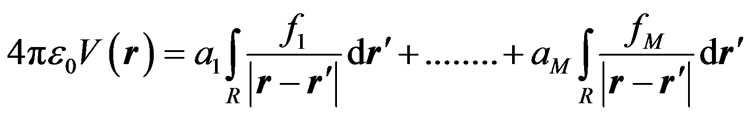 (2)
(2)
Applying the point matching approach, in which the voltage at the observation points as given (2) is applied at M observation points, we get a matrix equation from which the unknown coefficients can be obtained to get the charge density distribution over the entire metal surface. These equations can be written in the matrix form as
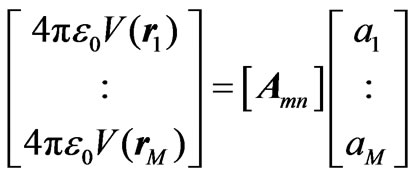 (3)
(3)
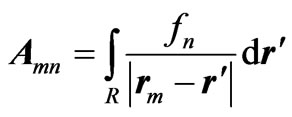 (4)
(4)
The unknown vector 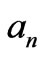 can be obtained by matrix inversion and an approximate solution can be obtained for the entire surface.
can be obtained by matrix inversion and an approximate solution can be obtained for the entire surface.
It is evident from (4) that a typical element of the moment matrix is singular at the point . The integration of singular function cannot be evaluated exactly or by ordinary numerical quadrature methods. However, the specialized Gauss Quadrature rules are developed for integrating singular functions. One specific rule is the LinLog rule for integrating singular functions with known Log type singularity. However, it is suited for point singularity problem. Thus it is necessary to adopt means that is universal for any type of singularity inside the integral and provides a good approximation of the actual result. The technique adopted here is the QMCI technique [5] that overcomes the problem of the singularity, making integration much simpler and justified specially, in case of two dimensional and three dimensional problems. The Halton sequences are generated for
. The integration of singular function cannot be evaluated exactly or by ordinary numerical quadrature methods. However, the specialized Gauss Quadrature rules are developed for integrating singular functions. One specific rule is the LinLog rule for integrating singular functions with known Log type singularity. However, it is suited for point singularity problem. Thus it is necessary to adopt means that is universal for any type of singularity inside the integral and provides a good approximation of the actual result. The technique adopted here is the QMCI technique [5] that overcomes the problem of the singularity, making integration much simpler and justified specially, in case of two dimensional and three dimensional problems. The Halton sequences are generated for 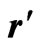 uniformly in the domain of integration. Thus the QMCI technique does not require any analytical processing before going for the numerical integration.
uniformly in the domain of integration. Thus the QMCI technique does not require any analytical processing before going for the numerical integration.
3. Protection Zone of a Lightning Rod
A lightning rod as a 1 dimensional structure of length L is considered as shown in Figure 1 and the charge distribution developed as a result of a sea of charges formed due to friction in the clouds at a height h is evaluated as shown in Figure 2. This has been found using the equation
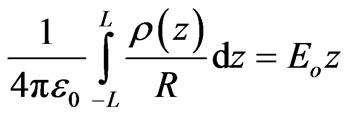 (5)
(5)
where 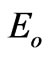 is taken as 1.5e5 V/m.
is taken as 1.5e5 V/m.
The charge being known the potential in the Y-Z plane is calculated, the gradient of which is used for evaluating the electric field in the surrounding space.
On the basis of this charge distribution electric field variation is calculated. The protection zone of the lightning rod is computed for several test cases. In all the cases, the rod is placed at Y = 30.5 m, X = 30.5 m and the length of the rod is considered as 20 m. Figure 3 shows the protection zone plotted in the Y-Z plane as the side view of the electric field and in Figure 4 and Figure 5, the protection zones are plotted in a plane parallel to the X-Y plane at Z = 5 m and Z = 15 m respectively as the top view of the electric field with on different height of rod.
Charge distribution on lightning rod structure, as in Figure 1, shown in Figure 2.
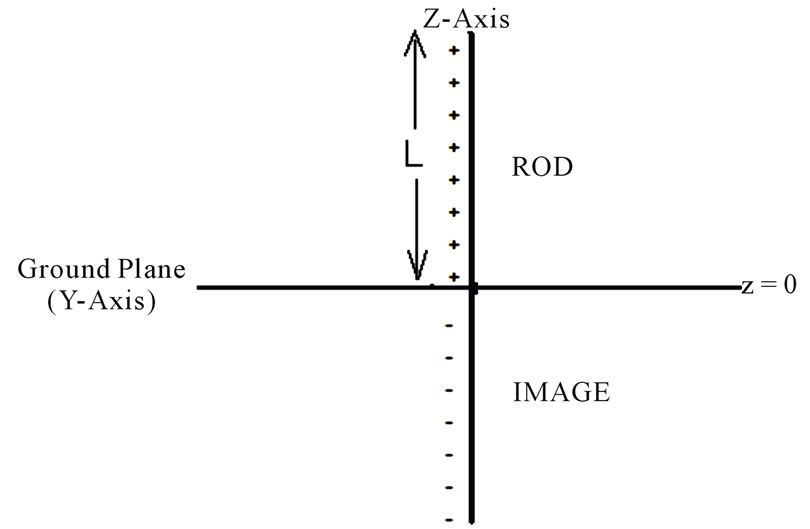
Figure 1. Lightning rod modeled as a 1-dimensional structure.
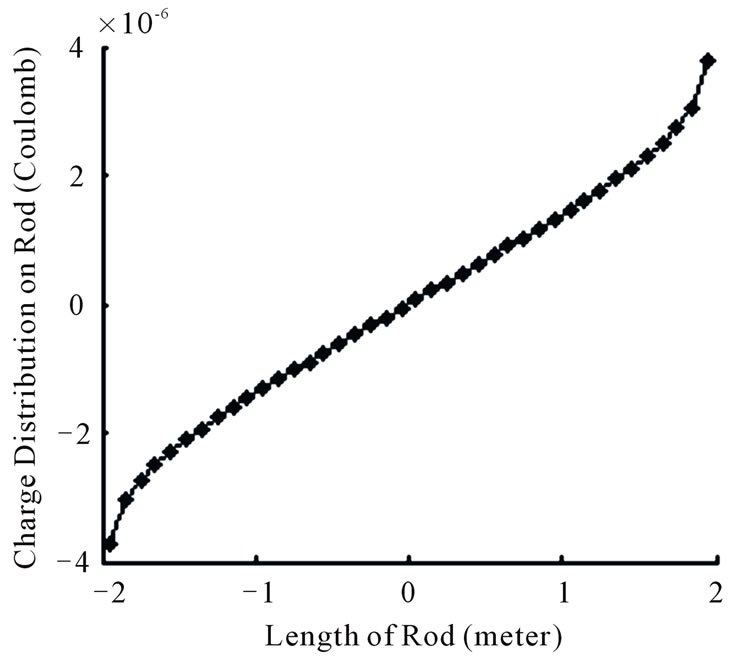
Figure 2. Charge distribution on the lightning rod, L = 4 m.
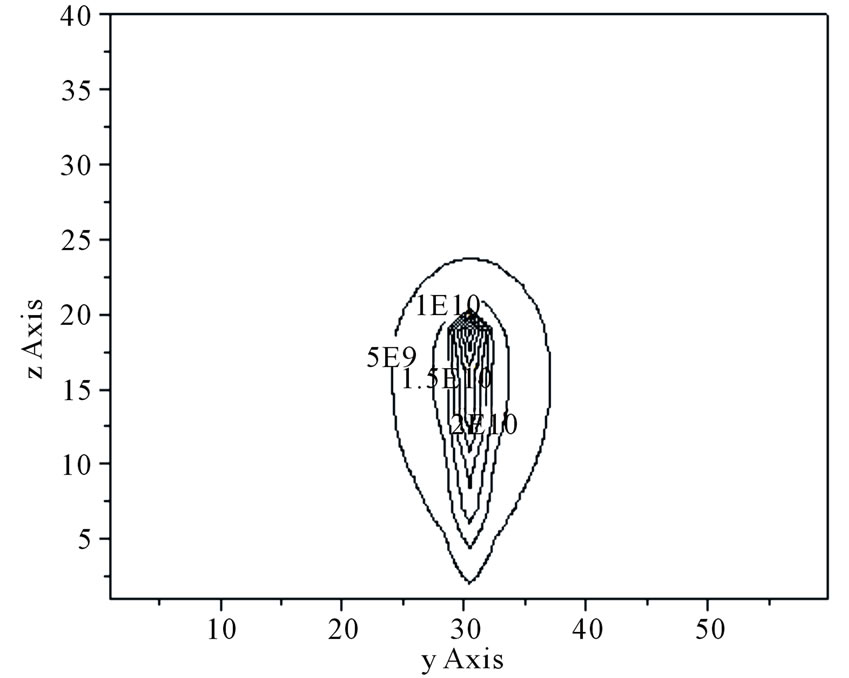
Figure 3. Protection zone of the lightning rod, L = 20 m.
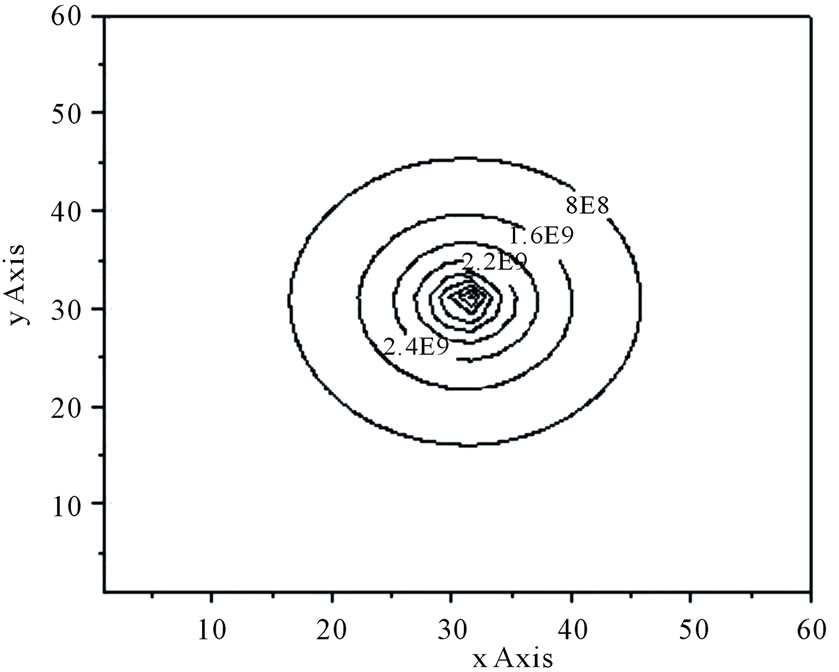
Figure 4. Protection zone of the lightning rod at Z = 5 m, L = 20 m.
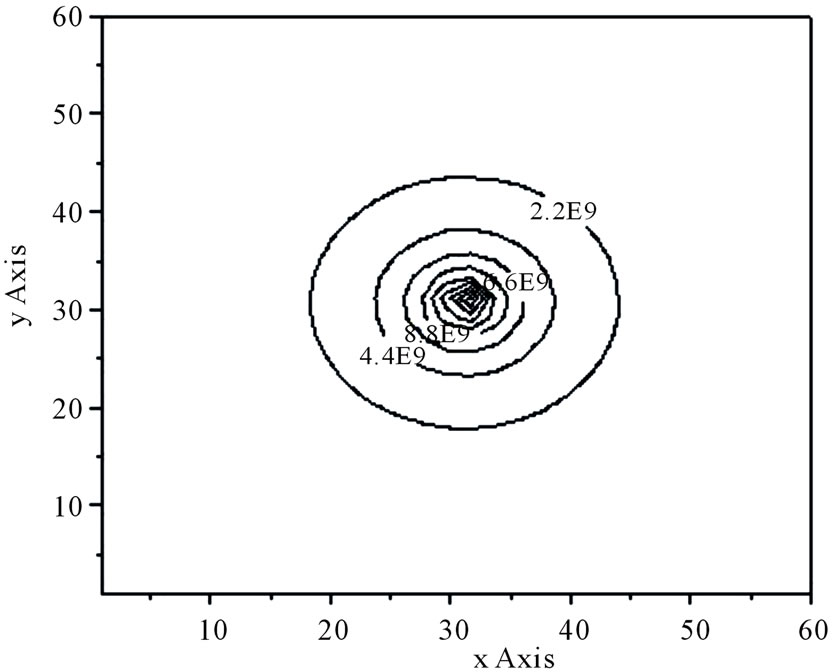
Figure 5. Protection zone of a lightning rod at Z = 15 m, L = 20 m.
4. Effect of Variation of Radius of Lightning Rod on the Protection Zone
The radius of the lightning rod is varied and the variation in the total charge on the surface of the lightning rod and on the protection zone is observed. First, the length of the rod is fixed at 4 meter and radius is varied from 0 millimeter to 10 millimeter. Figure 6 shows the variation of protection zone for the lightning rod when the length is kept constant. In the increment in radius of rod the charge is increases over the rod.
In Figures 7, 8 and 9, the protection zones plotted in X-Z planes are shown for a particular length of lightning rod equal to 40 m and radius equal to 0.005 m, 0.001 m and 0.015 m respectively. Table 1 shows the Electric field strength calculated at a particular distance x = 20 m for several values of the radius. As seen, an increasing
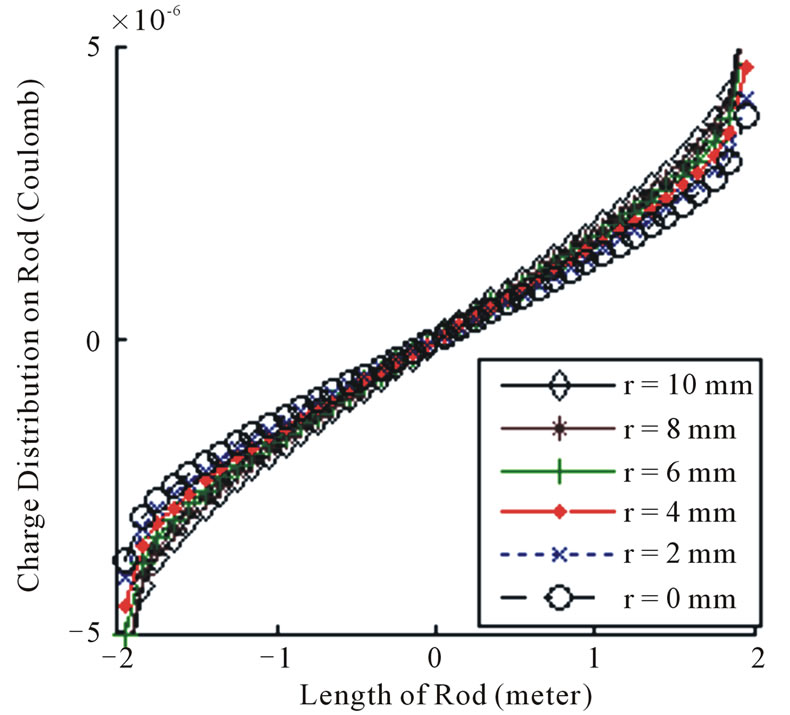
Figure 6. Charge Distribution on the lightning rod L = 4 meter.
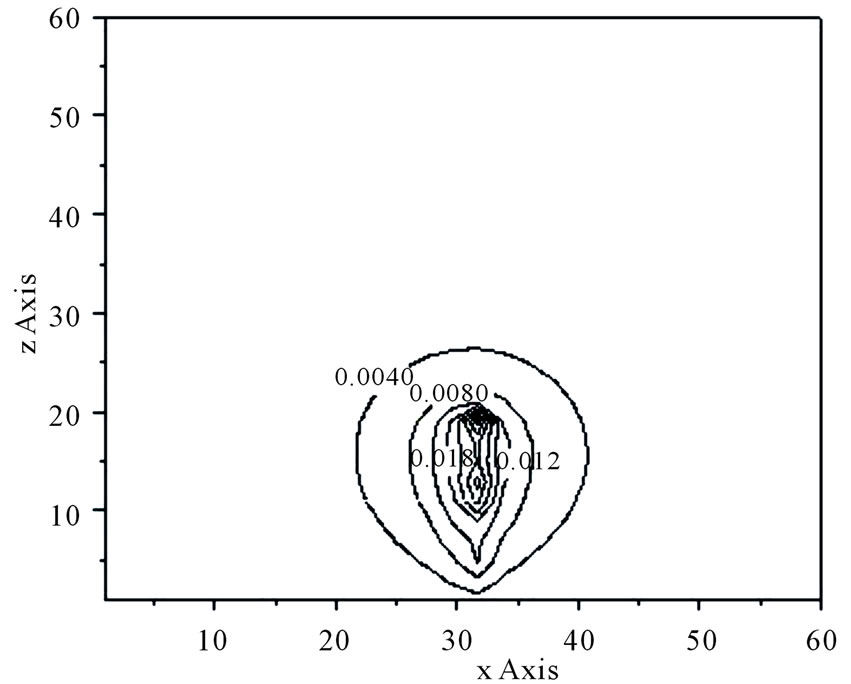
Figure 7. Protection zone, L = 40 m, r = 0.005 m.
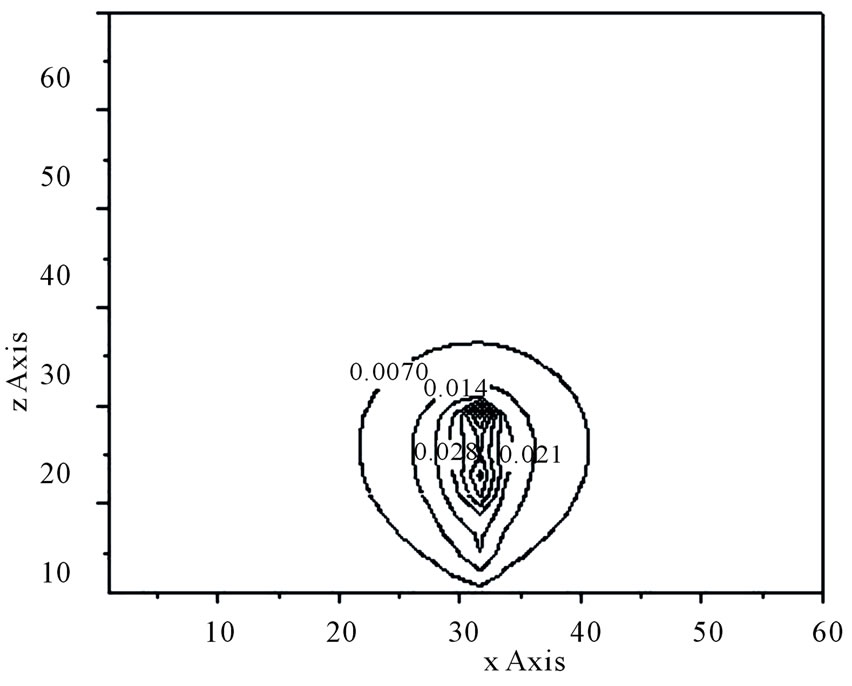
Figure 8. Protection zone, L = 40 m, r = 0.01 m.

Figure 9. Protection zone, L = 40 m, r = 0.015 m.
radius increases the electric field strength value. However, a particular radius of the lightning rod is selected keeping in mind all the practical aspects and examining the feasibility of the dimensions of the rod.
5. Conclusion
The fast and efficient method using QMCI technique employed in MoM solution of the problem is proposed for the determination of the protection zone of metallic lightning rod. Here the singularity treatment in MOM is reduced using QMCI. The protection zone is computed in two different planes and the results are obtained as a function of the rod length. Next the effect of varying the thickness of the rod on the protection zone is computed. It is seen that the Electric field strength increases with the increase in diameter of the rod. However, the optimum diameter of the rod for the lightening protection system is selected based on the practical feasible conditions.
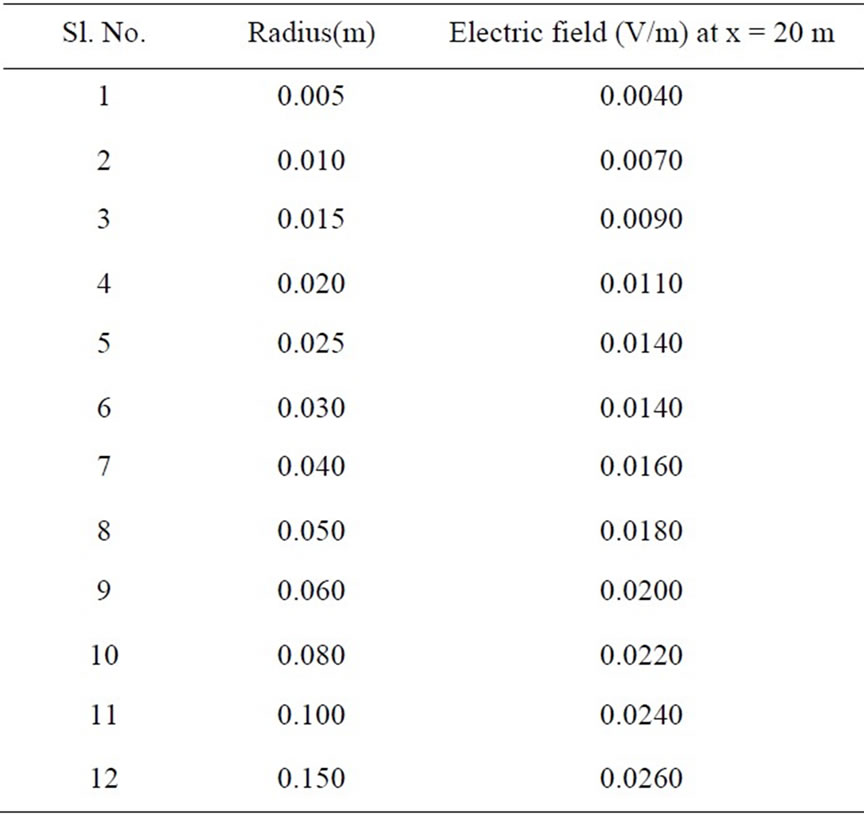
Table 1. variation in electric field with radius of rod.
6. Acknowledgment
This work is supported by Department of Science and Technology, Government of Jharkhand, India. Authors are thanking to them for their sponsorship to do this work.
REFERENCES
- F. D’Alessandro, “On the Optimum Rod Geometry for Practical Lightning Protection Systems,” Journal of Electrostatics, Vol. 65, No. 2, February 2007, pp. 113-121. doi:10.1016/j.elstat.2006.07.011
- C. B. Moore, W. Rison, J. Mathis and G. Aulich, “Lightning Rod Improvement Studies,” Journal of Applied Meteorology, Vol. 39, No. 5, May 2000, pp. 593-609.
- V. A. Rakov and M. A. Uman, “Lightning: Physics and Effects,” Cambridge University Press, Cambridge, 2003.
- R. F. Harrington, “Field Computation by Moment Methods,” Macmillan, New York, 1968.
- H. Niederreiter, “Random Number Generation and QuasiMonte Carlo Methods,” The Society for Industrial and Applied Mathematics (SIAM), Pennsylvania, 1992.
- J. H. Halton, “On the Efficiency of Certain Quasi-Random Sequences of Points in Evaluating Multi-Dimensional Integrals,” Numerische Mathematik, Vol. 2, No. 1, 1996, pp. 84-90. doi:10.1007/BF01386213
- M. Mishra, N. Gupta, A. Dubey and S. Shekhar, “Application of Quasi Monte Carlo Integration Technique in Efficient Capacitance Computation,” Progress in Electromagnetics Research, Vol. 90, 2009, pp. 309-322. doi:10.2528/PIER09011310

