Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 6 (2010) , Article ID: 2147 , 5 pages DOI:10.4236/jemaa.2010.26046
Optical Constants for MBE n-Type GaAs Films Doped by Si or Te between 1.50-4.75 eV
![]()
1Rzhanov Institute of Semiconductor Physics, Siberian Branch, Russian Academy of Sciences, Novosibirsk, Russia.
Email: Svitasheva@thermo. isp. nsc. ru
Received October 5, 2009; revised February 26, 2010; accepted April 16, 2010.
Keywords: GaAs, Heterostructure, Optical Properties, Thin Films, Spectroscopic Ellipsometry
ABSTRACT
The thickness and spectral dependence of the complex refractive index of upper layer in thin-film MBE-grown GaAs heterostructures were calculated basing on an classical oscillatory model of dielectric function from spectra measured by spectroscopic ellipsometry (nondestructive, contactless optical method) in the range of 1.5-4.75 eV.
1. Introduction
High-frequency (GHz) transistors and integrated circuits on the A3B5-type semiconductors are commonly used in mobile and satellite communication devices, and also in on-board radar stations owing to their small weight and high efficiency. At present, microwave transistors based on MBE-grown heterostructures have the best parameters.
Bakarov et al. [1] developed a technology for producing heteroepitaxial n+-GaAs/n-GaAs/GaAs structures for powerful MESFET microwave transistors with a specific output power of 0.8 W/mm and n+-GaAs/AlGaAs/nGaAs/GaAs structures for powerful HFET microwave transistors with a specific output power of 0.9 W/mm at 17.7 GHz.
The gate width of these transistors is usually 0.13-0.50 mm, whereas the length is about fractions of millimeter. The active layer thickness is 0.15-0.30 mm and the doping level is within (1-5) 1017 cm-3.
The requirements imposed on an epitaxial layer can easily be formulated according to functional properties of a device (although, it is extremely difficult to satisfy them) [2]:
1) the buffer layer must contain the minimal number of shallowand deep traps and ensure a spatially sharp barrier of a desired height for electrons in the channel;
2) homogeneity of thickness and doping level of the active layer must be ultimately high.
At optimizing of the modes of growth of separate layers, for monitoring their parameters are usually used the following techniques: low-temperature photoluminescence, Hall, and C-V measurements. However, working structures control requires nondestructive and contactless methods. We suggest to pay attention to application of spectroscopic ellipsometry between 1.50-4.75 eV for restoration of thicknesses and optical constants of layers included into heterostructure (Figure 1).
2. Substantiation
The energy of the GaAs edge self-absorption at a room temperature is 1.425 eV. Since this semiconductor is a direct gap semiconductor, the absorption drastically grows near edge self-absorption, and for the photon energy hv » 1.6 eV the absorption coefficient a = 4pk/l = 104 cm-1 which corresponds to the extinction coefficient k » 0.1. Casey et al. [3] showed that the doping level between

Figure 1. Scheme of structure: SL is a superlattice, thicknesses of its layer are given in terms of monolayers (ML). The AGCP-10 substrate is a semi-insulating GaAs. All the structures were grown in the same setup
5.9 1017 ¸ 3.0 1018 cm-3 appreciably changes the absorption coefficient a for the n-type GaAs for photon energies between 1.3-1.6 eV, however, the increment of a may change the sign even in this narrow range (Figure 2).
It is also known that the greatest changes in the optical properties can be registered in the region of critical points, i.e., at energies of interband transitions. In the region of spectrum between 1-7 eV, there are several optical transitions, as shown in Table 1 that contains parameters of a GaAs band structure [4].
However, the present-day representation of the GaAs dielectric function e by the sum of oscillators (1) between 1.5 and 5.5 eV leads to the different values of transition energies [5] (Table 2):
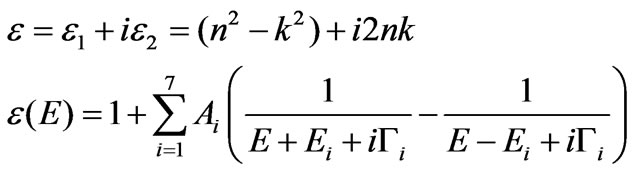 (1)
(1)
where Ei is energy and Gi is the damping factor of i-the oscillator, respectively.
In above mentioned tables there are marked oscillators (borrowed from [4,5]) whose energies are beyond the range of our measurements. Therefore, the most interesting regions for our investigation are between 3.0-3.5 eV and in the vicinity of 4.5 eV.
In the region of weak absorption between 1.5 and 2.4 eV, we should expect appearance of an interference effect in the spectra because thickness of the GaAs layer (0.3 m) is less than thickness which in 10 times attenu-
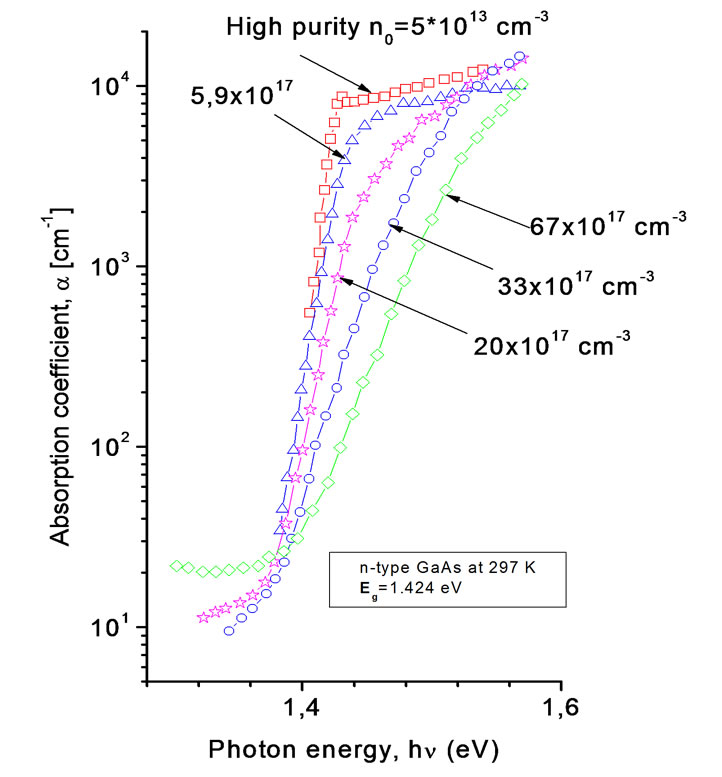
Figure 2. Spectral dependences of the coefficient a from the doping level of the n-type GaAs in the range of 1.3-1.6 eV (they was extracted from reflectivity spectra using the Kramers-Kronig relationship [3]

Table 1. Parameters of energy-band structure of c-GaAs [4, p.86]

Table 2. Energies of oscillators for harmonic oscillator approximation of c-GaAs dielectric functiom [5]
ates intensity of the reflected light, according the Bugger-Lambert law, and the last is changing from 2.57 to 0.4 m .
3. The Goal of Paper
The goal of paper is to determine for MBE-grown n-type GaAs films the spectral dependence of the complex refractive index N = n + ik =e1/2 and, therefore, complex dielectric function (1). In addition, goal is to calculate thicknesses of two upper layers of the structures and is to show reproducibility of the technological process and on the other hand, is to demonstrate impact of doping level on energy position of critical points too.
4. Experiment
The structures were grown by molecular beam epitaxy in a Riber-32P setup. The substrates were semi-insulating gallium arsenide wafers 40 mm in diameter. The monitoring of growth rate with an accuracy of ±1% was based on registration of intensity oscillations of a zero reflex of the RHEED picture.
Optical measurements were carried out on a Jobin Yvon spectroscopic ellipsometer in the range of photon energies between 1.50-4.75 eV.
The measured spectra of ellipsometric angles Y(E) and D(E) are related with the relative reflection coefficient r(E) by the identity:
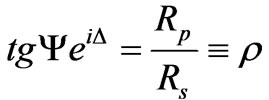 (E).(2)
(E).(2)
These spectra were corrected using the Drude, Archer, and Saxena [6] relationship (3) by the taking into account of the formed oxide. Herein, Rp and Rs are the Fresnel coefficients for pand s-polarized light; Y, D and `Y, `D are the ellipsometric angles for structures with a thin (d «l) oxide and without it, respectively; CD and CY are the constants depending on the structure parameters:
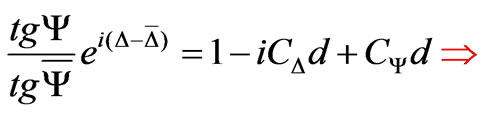
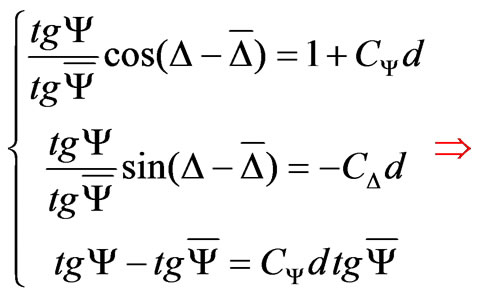
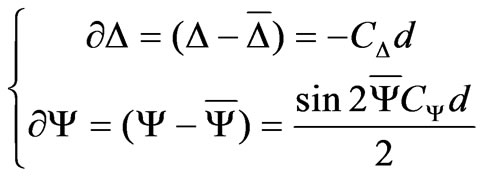 (3)
(3)
The oxide thicknesses were determined by basing on the known oxidation time and using the logarithmic oxidation law [7]: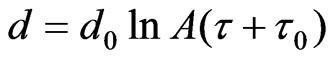 . This time corresponds to formation of an oxide »13 Å for the investigated structures.
. This time corresponds to formation of an oxide »13 Å for the investigated structures.
5. Solving the Inverse Problem Ellipsometry
In this paper, we do not consider some aspects of solving the inverse ellipsometric problem (IEP): choosing a calculation technique, the reason of choosing a functional or an error function, etc. A lot of attention earlier has been given to these aspects in works [8-12].
The algorithm of solving the IEP in this paper consists in the division of problem into two parts to determine the parameters of two layers that differ by the doping level:
1 Part. In the region of weak absorption, a restoration of six parameters simultaneously: the thicknesses of upper layers d1 and d2 (see Figure 1) and four parameters of one oscillator describing the dielectric function of the upper layer:
 (4)
(4)
where e¥ and es are the high-frequency and static dielectric constants, respectively; G0 is the damping factor (G0 > 0); wT is the oscillator energy in electron volts, wÎ 1.5-2.6 eV. For minimizing the error function of c2 (which is defined by the difference between the measured value and the value calculated according to proposed model (4)), we used the Marquardt-Levenberg method:
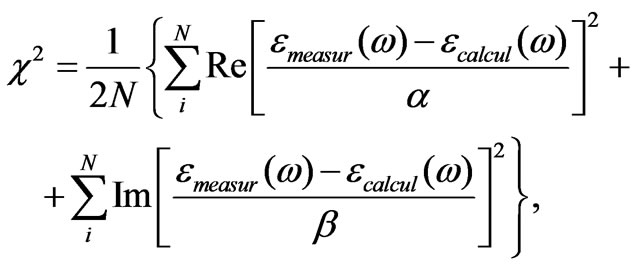 (5)
(5)
where a and b are the weight factors.
2 Part. In the region of energies higher than 2.6 eV, where the light penetration depth is much smaller than the film thickness, it is possible to determine the spectral dependence of the dielectric function only for the top layer according to (2) and (6) with regard to the angle of light incidence j0:
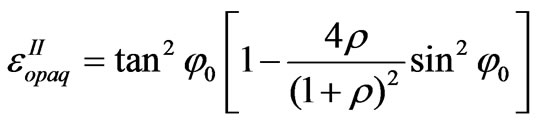 (6)
(6)
As it has been expected in Substantiation, interference oscillations in spectra of the measured angles and for structures 1, 2, 3 (Figure 3) in the region of weak absorption between 1.5 and 2.6 eV were registered, and their amplitude decreased in according to the increase of photon energy (or of the absorption of MBE GaAs films). Although all the structures were grown in the same setup and in the same regime, the oscillations differ in amplitude and in energy position of its extremums; this fact evidently shows that the properties of at least two upper layers differ; because the contribution of the light reflected by deeper layers is negligiblely small. Fragments in Figure 3 show that the Y amplitude, which characterizes the module of the relative reflection coefficient r, varies between 10-17°, whereas the phase of D of the complex r, or the difference phases of Rp and Rs: dp - ds = D, changes from 160 to 182°. At the same time, the positions of the first maximum in Y are 1.65, 1.70, and 1.50 eV for the first, second, and third samples, whereas
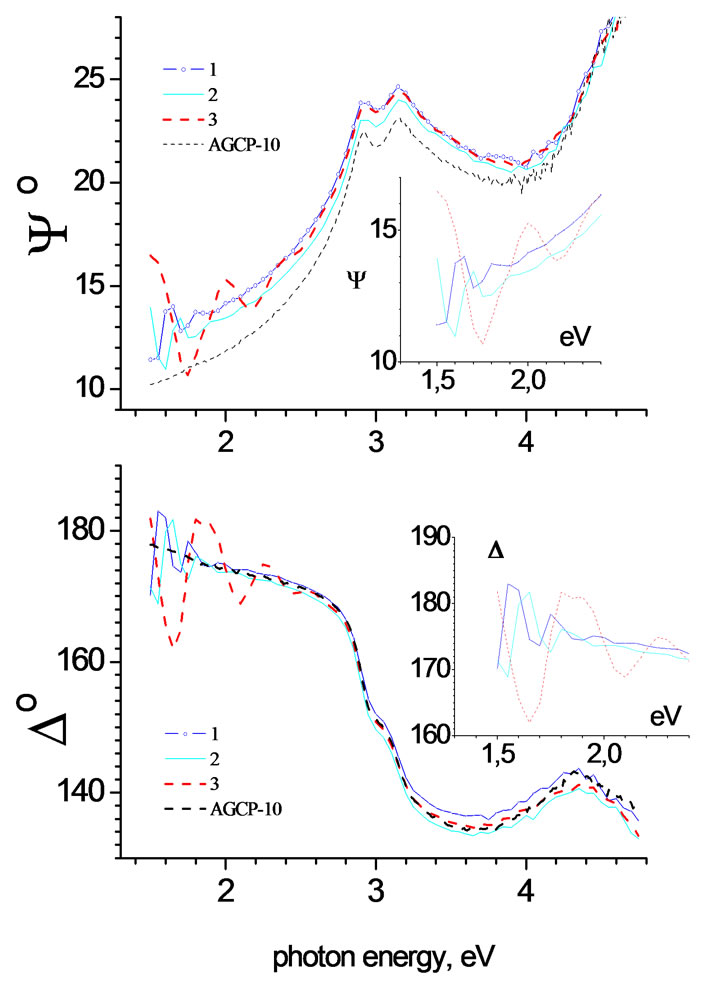
Figure 3. Experimental spectral dependences of Y and D for three structures with correction of oxidation effect (d » 13Å). Oscillation of Y and D in the region of weak absorption are fragmented. A semiinsulating GaAs spectra are shown for comparison [5]
the positions of the first minimum in D are 1.67, 1.75, and 1.65 eV, respectively. Thus, even without calculating, it is clear fact that spectroscopic ellipsometry possessing high phase sensitivity makes it possible to detect the difference in the properties of the structures under investigation.
6. Results and Discussion
In order to find values of these dissimilarities, it is necessary to solve IEP by calculation of Fresnel coefficients for all layers shown in Figure 1.
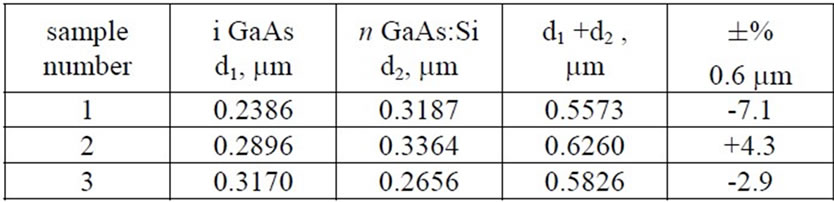
The thicknesses and spectral dependences of dielectric functions of all layers except for two upper layers are assumed to be known. For describing the unknown function e(E) we used oscillator model (4) that involves four unknown parameters. Results of minimizing procedure (5), namely, the thickness, are listed in Table 3.
In Figure 4 the spectral dependences of optical constants n(E) and k(E) (for the region of energies 1.5-2.6 eV) are represented and they show that compared with the bulk semi-insulating GaAs, the real part increases approximately by 5-9%, whereas the imaginary part, that characterizes the absorption, increases by 15% and more, remaining equal to ~0.1 (for a photon energy of 1.54 eV).
The curves of the absorption coefficient are noticeably shifted toward lower energies. The deviations of the to

Figure 4. Optical properties of MBE-grown n-type GaAs films doped by silicon (concentration of 3.0-3.5)-1017 cm-3, which were found from the ellipsometric spectra, for the upper structure layer (see Figure 1). Spectra of a bulk semi-insulating GaAs are shown for comparison
-tal thickness of two upper layers from the designed value for these samples vary from -7 to +4%, and this fact should be taken into account in a manufacturing of transistors.
The complex refractive index for energies higher than 2.6 eV, which was calculated from (2) and (6), is also depicted in Figure 4. In the vicinity of the first oscillator (see Table 2), the greatest increase of n is not more than 3-9% and the maximum absorption grows by 15-20% compared with the semi-insulated gallium arsenide. Probably, additional levels responsible for increasing number of transitions from valence band to conductance band are formed in the band gap. Generally, influence of an dopant on optical constants of GaAs depends not only on its concentration, but also from type of an doping element, as shown in a Figure 5. It seems that in the region of energies greater than 3.5 eV, curves of n(E) intersect.
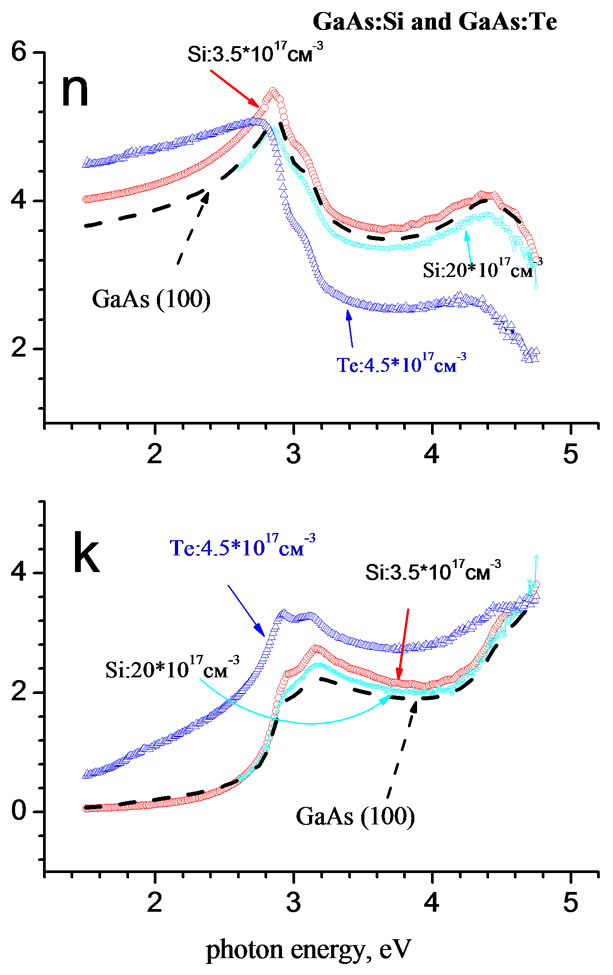
Figure 5. Impact of the doping elements (Si or Te) on dispersion of GaAs optical constants in vicinity of critical point energies. Spectra of GaAs (100) constants are inserted for comparison from [5]. Approximately the same doping level of different elements (Si or Te) influences on GaAs optical constants by other way
In fact, there are no intersections. This clearly can be seen in the 3D space of the parameters E, n, and ik in Figure 6. The 3D graph shows movement of the vector of the complex refractive index via function of photon energy. Besides, the level of doping of upper layer causes slight impact on n + ik in the range of great photon energies.
7. Conclusions
We have shown the possibility of determining the spectral dependence of the complex refractive index and the thicknesses of n-type GaAs layers with different levels of doping. It is remarkable that in the region of weak absorption (from 1.5 to 2.5 eV) everybody can without calculating evaluate the difference or identity of operating layers, i.e. to evaluate repeatability of structures; this is of particular importance for manufacturing GHz transistors.
8. Acknowledgments
The author is grateful to A. I. Toropov and V. V. Preobrazhenskii for the samples and fruitful discussion.
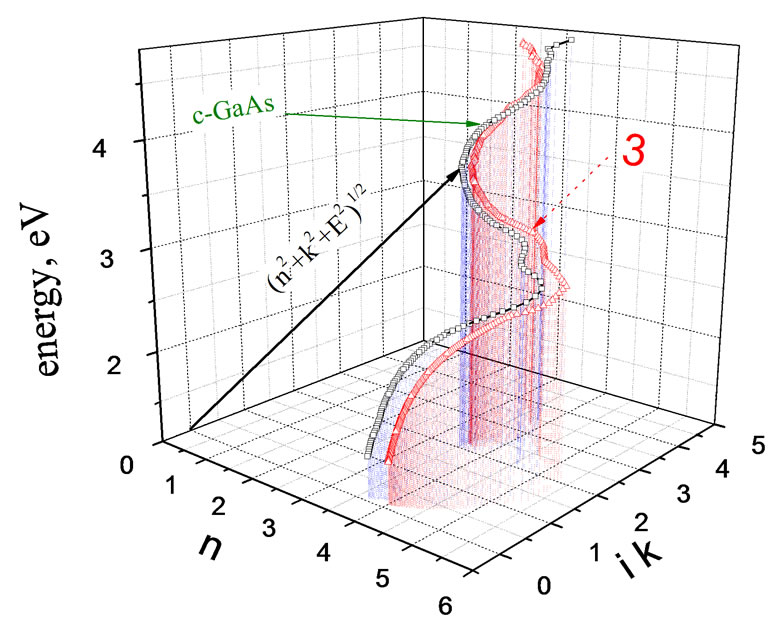
Figure 6. Spectral dependences of the complex refractive index for the bulk single-crystal GaAs and sample 3 in the 3D space with the vector coordinates E, n, and ik, whose two projections are shown in Figure 4.
REFERENCES
- A. K. Bakarov, K. S. Zhuravlev. A. I. Toropov, T. S. Shamirzaev, Y. B. Myakishev and Y. N. Rakov, “HighPower Microwave FETs on Epitaxial AlGaAs GaAs Structures,” Mikroelektronika, Vol. 31, No. 3, 2002, pp. 163-169.
- J. V. D. Lorenzo and D. D. Khandelwal, “GaAs FET Principles and Technology,” Artech House, Dedham, 1982.
- H. C. Jr. Casey, D. D. Sell and R. W. Wecht, “Concentration Dependence of the Absorption Coefficient for nand p-Type GaAs between 1.3 and l.6 eV,” Journal of Applied Physics, Vol. 46, No. 1, 1975, pp. 250-257.
- V. I. Gavrilenko, A. M. Grekhov, D. V. Korbutyak and V. G. Litovchenko, “Optical Properties of Semiconductors,” in Russian, Nauk. Dumka, Kiev, 1987, pp. 85-93.
- M. Erman, J. B. Theeten, P. Chambon, S. M. Kelso, D. E. Aspnes, “Optical Properties and Analysis of GaAs Single Crystal Partly Amorphized by Ion Implantation,” Journal of Applied Physics, Vol. 56, No. 10, 1984, pp. 2664-2671.
- N. Saxena, “Changes in Phase and Amplitude of Polarized Light Reflected from a Film-Covered Surface and Their Relations with Thickness,” Journal of the Optical Society of America, Vol. 55, No. 9, 1965, pp. 1061-1067.
- Y. G. Galitsyn, Y. P. Petrenko and S. N. Svitasheva, “Investigation of Kinetics of Formation and Oxide Composition on a Cleaved Surface of GaAs(l10),” Ser Fizika Khimiya Mekhanika, Poverkhnost, No. 11, 1987, pp. 51-58.
- R. M. A. Azzam and N. M. Bashara, “Ellipsometiy and Polarized Light,” North-Holland, Amsterdam, 1977.
- S. N. Svitasheva, “Exact Solution to the Inverse Eliipsometric Problem for Absorbing Films,” DAN SSSR, Vol. 318, No. 5, 1991, p. 1154.
- Y. E. Voskoboinikov, E. V. Petukhova and S. N. Svitasheva, “An Efficient Algorithm for Solving the Inverse Eliipsometric Problem for Stronglv Absorbing Films,” Avtometriva, No. 4, 1996, p. 110; Optoelectronics Instrumentation Data Process, No. 4, 1996, p. 99.
- S. N. Svitasheva, “Some Aspects of Solving the Inverse Eliipsometric Problem for Strongly Absorbing Films,” Avtometriva, No. 4, 1996, p. 119; Optoelectronics Instrumentation Data Process, No. 4, 1996, p. 108.
- V. G. Polovinkin and S. N. Svitasheva, “Determination of the Number of Inverse Eliipsometric Problem Solutions in the Given Domain of Parameters,” Avtometriva, No. 4, 1999, p. 94; Optoelectronics Instrumentation Data Process, No. 4, 1999, p. 79.