Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 1 (2010) , Article ID: 1223 , 7 pages DOI:10.4236/jemaa.2010.21003
A Probabilistic Analysis on the Harmonic Cancellation Characteristics of the Scott Transformer
![]()
Department of Electrical and Computer Engineering, University of Alberta, Edmonton, Canada.
Email: herfania@ece.ualberta.ca, jggallan@ualberta.ca
Received August 14th, 2009; revised September 22nd, 2009; accepted September 28th, 2009.
Keywords: Terms-Harmonics, Harmonic Cancellation, Scott Transformer, Probabilistic, Power Quality
ABSTRACT
The Scott transformer is widely used in electric railway systems when there are two unbalanced single-phase loads as this transformer can reduce unbalance currents. This paper investigates whether or not the Scott transformer can also reduce harmonic current. Our study shows that it can reduce the harmonic current when single-phase loads have identical harmonic characteristics. This harmonic reduction occurs through the cancellation of harmonic currents of single-phase loads in the transformer windings. Our studies also show that there is some degree of cancelation even when the loads do not have identical harmonic characteristics. The cancellation depends on load balance factor and harmonic order.
1. Introduction
Supplying electrical traction loads presents some power quality challenges to power system. Electric trains are fed by a single-phase AC catenary line (Figure 1), presenting an unbalanced load to the three-phase power system. In an electric train, the single-phase AC power is rectified into DC power. This leads to the generation of harmonic currents. As a result, an electric railway load is a large unbalanced and harmonic-generating load.
Dividing the catenary line to the in-coming and outgoing sides makes it possible to present each side as a separate single-phase load. The Scott transformer is a widely used transformer that converts the three-phase supply into two single-phase power supplies. Scott transformers have been used in many electric railway systems, (for instance in the Tokaido-Shinkansen electric railway [1]), to reduce the aforementioned unbalance problem. If two loads are equal, the Scott transformer presents them as one balanced three-phase load to the three-phase supply system. This solves the imbalance problem. In reality, however, these two single-phase loads are rarely equal and the transformer still draws unbalanced power from the system. In this case, the degree of unbalance is, at least, reduced in comparison with the case in which loads are directly connected the system. References [2–4] investigated the degree of load unbalance seen from the three-phase system when two single-phase loads have different sizes.
A recent study by the author [5] showed that Scott transformer can also reduce the harmonic current when single-phase loads have identical harmonic characteristics. The results showed that the Scott transformer reduces the injected harmonic currents into the system by cancelling out the harmonic currents generated by single-phase harmonic loads.
Intuitively, this leads to the question of whether the Scott transformer is also able to reduce the generated harmonics by two single-phase loads when loads are not identical. The purpose of this paper is to study the amount of this harmonic cancellation when single-phase loads do not have identical harmonic characteristics.
This paper is organized as follows. Section 2 presents the problem definition and study model. Section 3 inves-
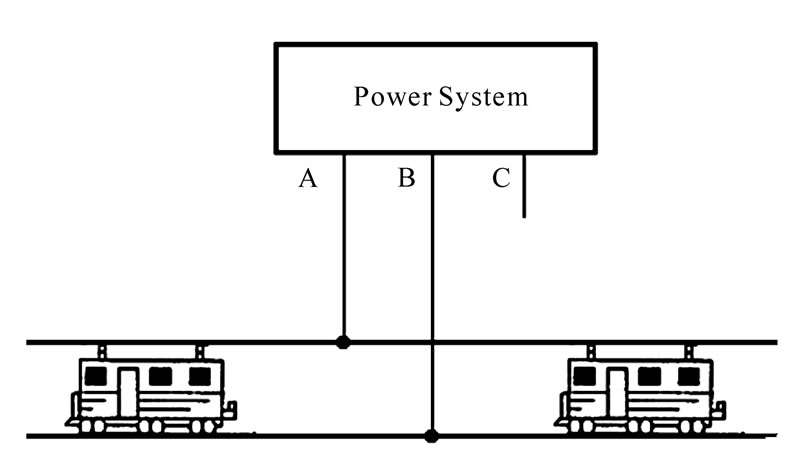
Figure 1. Single-phase AC catenary line supplies the electric train
tigates the harmonic reduction when single-phase loads have the same size. Section 4 presents the results when the single-phase loads do not have the same size, and Section 5 summarizes the findings.
2. Problem Description and Study Model
The model under investigation is illustrated by (Figure 2) and can be described as follows: Two single-phase nonlinear loads are supplied using a Scott transformer. The non-linear loads inject harmonic currents into the secondary side of the transformer. The aim is to find out the amount of these injected harmonic currents observed form the primary side of the transformer. These values are compared with the injected harmonic currents when two single-phase loads are directly connected to the utility side. In the direct connection case, the two non-linear loads are connected between phase A and B of the utility side.
Our study investigates the impact of Scott transformers on the reduction of harmonic currents observed from the utility side. To study this characteristic, we need to develop a study model for the non-linear loads, Scott transformer and power system. In our study, the power system is simply modeled by ideal sinusoidal voltage sources. Also, for this work, the power system impedance and voltage background harmonics in the power system are neglected.
2.1 Traction Load Model
The harmonic current source model is the most commonly used model to represent power-electronic based loads [4]. In this paper, this model is utilized to model traction loads. A traction load is modeled by a harmonic current source in each harmonic order (Figure 2). Since this paper is investigating the harmonic cancellation effects of Scott transformers, not the performance of the traction load, this model is sufficient. In this study, accurate inclusion of the phase angle information (θha and θhb) is essential to estimate harmonic cancellation effects. To study the cases where single-phase loads have identical harmonic characteristics, these phase angles are calculated as shown in Equations (1) and (2). For the Scott transformer case,
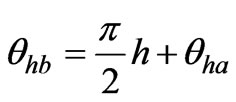 (1)
(1)
where h is the harmonic order. For direct connection case,
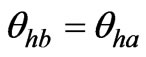 (2).
(2).
In both cases, θha is assumed as the reference angle and set to zero. To study cases where single-phase loads do not have identical harmonic characteristics, a random variable with uniform distribution is added to the phase angles [6]. Phase angles are then calculated as shown in Equations (3) and (4). For the Scott transformer case,
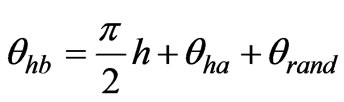 (3)
(3)
For the direct connection case,
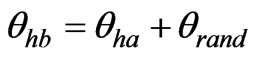 (4)
(4)
where θrand is a random variable.
2.2 Transformer Modeling
A diagram illustrating the connection of windings for the Scott transformer is shown in Figure 3. A Scott transformer consists of one two-winding transformer (T1) and one three-winding transformer (T2). Neglecting the magnetization current, we get the following equation from the MMF Equations

Figure 2. Supplying two single-phase harmonic-generating loads by Scott transformer
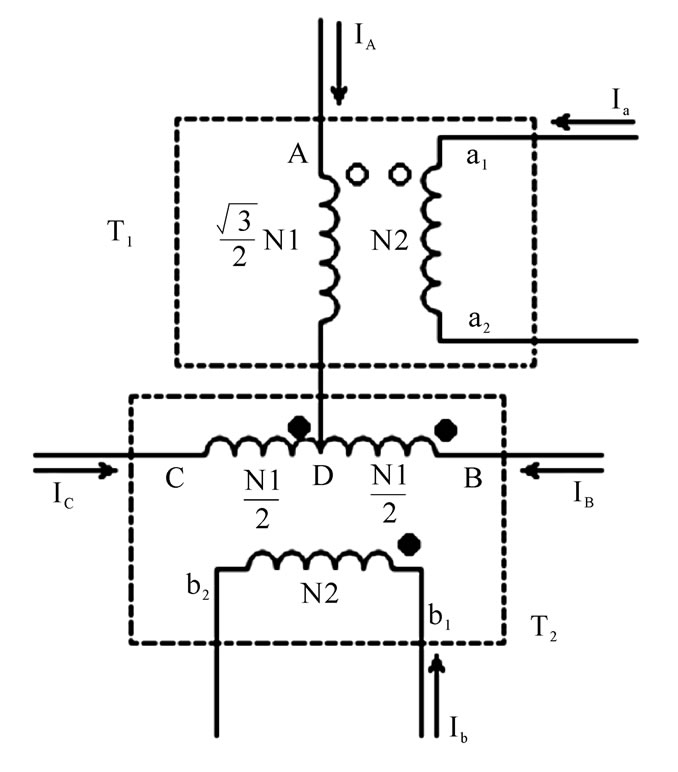
Figure 3. A diagram showing the connection of windings for the Scott transformer
 (5)
(5)
From Kirchhoff’s current law, we know that,
 (6)
(6)
Finally using Equations (5) and (6), the following equation is derived that relates the secondary-side currents to the primary-side currents.
 (7)
(7)
Similarly for the direct connection of the load to the system (See Figure 4), we get
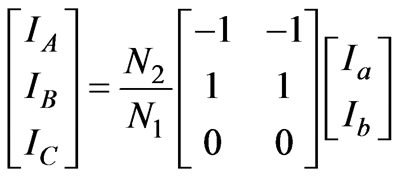 (8)
(8)
In our study, we set 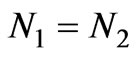
3. Study Case 1: Equal Single-Phase Loads
In this case, both  and
and 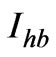 have the same magnitude. Two scenarios are studied; 1) when single-phase loads have identical harmonic characteristics, and 2) when single-phase loads do not have identical harmonic characteristics.
have the same magnitude. Two scenarios are studied; 1) when single-phase loads have identical harmonic characteristics, and 2) when single-phase loads do not have identical harmonic characteristics.
3.1 Identical Harmonic Characteristic
When two single-phase loads are identical, the Scott transformer presents these loads as a balanced threephase load to the power system. In this study case, we investigate the impact of the Scott transformer on the
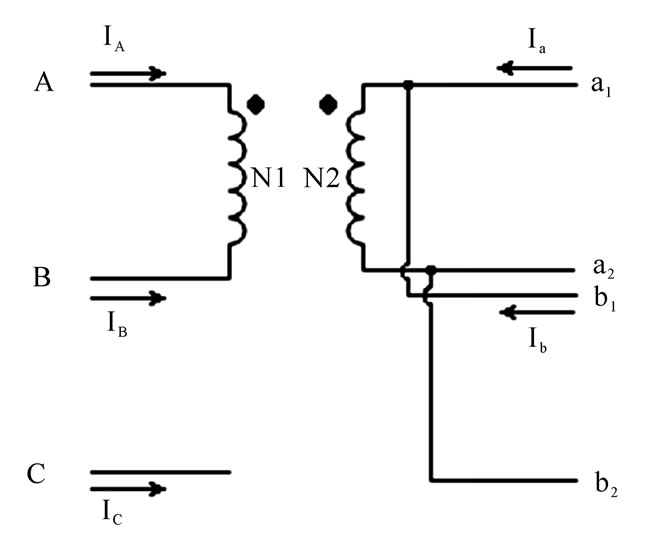
Figure 4. Connection diagram of windings for the direct connection case
harmonic current measured in the power system. For each harmonic order, we set |Iha|=|Ihb|=0.5pu. The harmonic currents observed in the primary side are calculated using Equations (5) and (6) and are shown in Table 1.
When loads are directly connected to the power system, there is no current in phase C and the harmonic current is uniformly distributed between Phase A and B. The Scott transformer distributes generated harmonics among three phases resulting in less harmonic currents in each phase. In this regard, the maximum magnitude current through the Scott transformer is reduced by 42.4% in comparison to the direct connection case.
Another analysis to be performed is the symmetrical component analysis of the results. Although the magnitude of harmonic currents in each phases with the Scott transformer connection are equal, triple-order harmonics are not necessarily zero sequence. Similarly, non-tripleorder harmonics are not necessarily negative and positive sequences.
The analysis of the symmetrical components of harmonic currents permits the study of harmonic cancellation from another perspective. The three-phase primary-side harmonic currents are decomposed into symmetrical components, 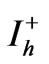 ,
,  and
and  as shown in Table 2.
as shown in Table 2.

Table 1. The magnitude of harmonic currents (per-unit) in phases measured in the primary side for direct and scott connections
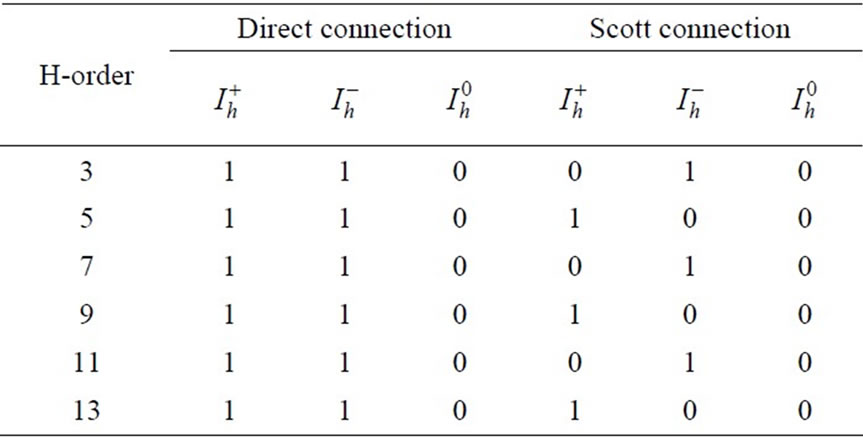
Table 2. The symmetrical components of harmonic currents (per-unit) measured from the primary side for direct and Scott connections
Both the direct connection and Scott transformer do not generate zero sequence harmonic current. The results also reveal that the Scott transformer cancels out the positive-sequence component of (4k-1) order harmonics completely (i.e. 3, 7, and 11), while it does not affect the negative-sequence component of these harmonic orders at all. The reverse phenomenon happens for the (4k+1) order harmonics (i.e. 5, 9, and 13). These results can be verified through Equation (1). For (4k-1) order harmonics, we have that, 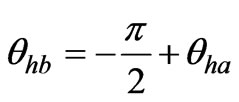 , and for (4k+1) order harmonics we have that,
, and for (4k+1) order harmonics we have that,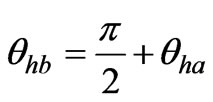 .
.
3.2 Non-Identical Harmonic Characteristic
In this case, we set |Iha|=|Ihb|=0.5pu. θha is assumed to be the reference angle and set to zero. θhb is calculated by using Equations (3) and (4). Since θhb is a function of a random variable, IhA, IhB, and IhC are not deterministic. In this regard, the cumulative density function (CDF) of the maximum harmonic current observed from the primary side can be evaluated as follows:

where  is the distribution function of the random variable.
is the distribution function of the random variable.
Figure 5 shows CDF of the maximum harmonic current observed at the primary side for odd harmonic orders, when θrand has uniform distribution over [-10º,10º]. In this case, the amount of harmonic cancellation by the Scott transformer is reduced in comparison to the case where loads are not identical (see Table 1). However, the Scott transformer still has better performance when compared with the direct connection approach. Interestingly, this predominance is not continual, and increasing the range of the random variable (θrand) decreases this predominance. For example, Figure 6 shows the CDFs when θrand is uniformly distributed over [-90º,90º]. In the most severe case when the range is [-180º,180º] the cancellation performance is reduced dramatically (see Figure 7).
4. Study Case 2: Unequal Single-Phase Loads
In this study case, we study the harmonic reduction characteristics of the Scott transformer when singlephase loads do not have the same magnitude. To express the load balance of this distribution, we define the load balance factor as follows:
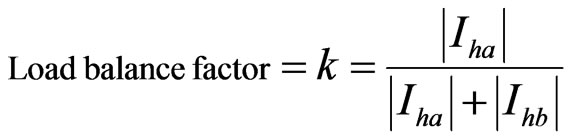 ,
,

Figure 5. CDFs of maximum harmonic currents where θrand is uniformly distributed over [-10º,10º]
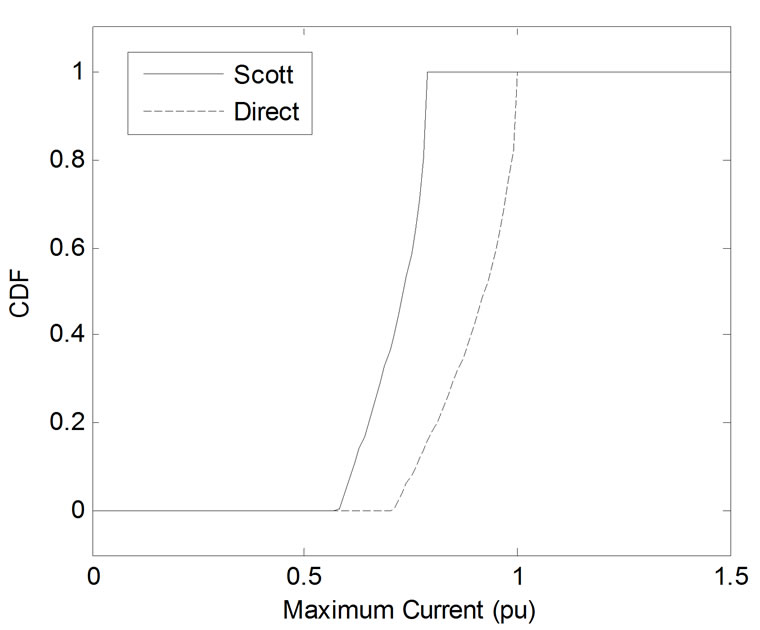
Figure 6. CDFs of maximum harmonic currents where θrand is uniformly distributed over [-90º,90º]
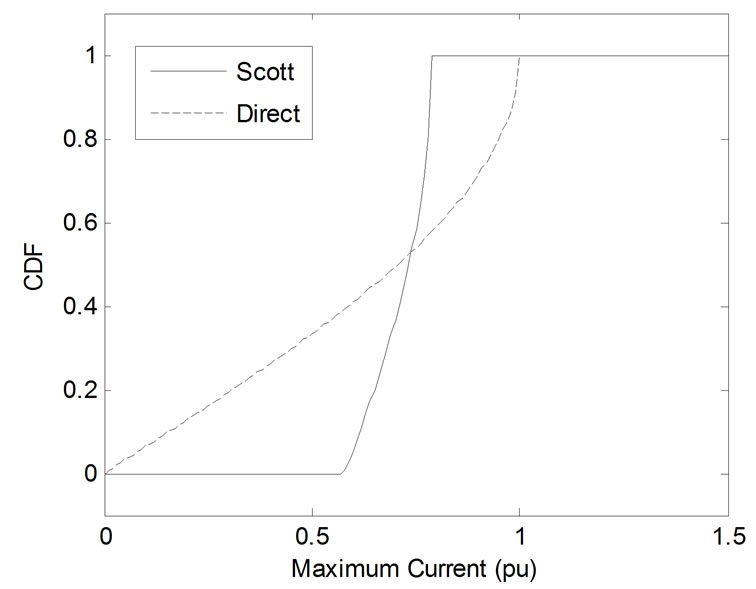
Figure 7. CDFs of maximum harmonic currents where θrand is uniformly distributed over [-180º,180º]
where k varies from 0 to 1. The summation of |Iha| and |Ihb| is to be 1 per-unit, so we have
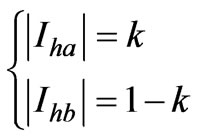
4.1 Identical Harmonic Characteristic
In this case, although loads do not necessarily have the same size, they have the same harmonic characteristics (i.e. identical locomotives). For instance when seven loads (trains) are fed by side a and three loads (trains) are fed by side b, the load balance factor is 0.7. In direct connection, both side a and b are supplied from the same place, so the variation of load balance factor does not affect the primary side harmonic currents. Magnitude of the third-order harmonic current in the primary-side of the Scott transformer versus load balance factor is shown in Figure 8.
When load balance equals zero (all loads are fed by side b), the magnitude of IhA is zero and the magnitude of IhB and IhC are maximum. Increasing the load balance factor results in increase of harmonic currents in Phase A and decrease of harmonic currents in other phases. When
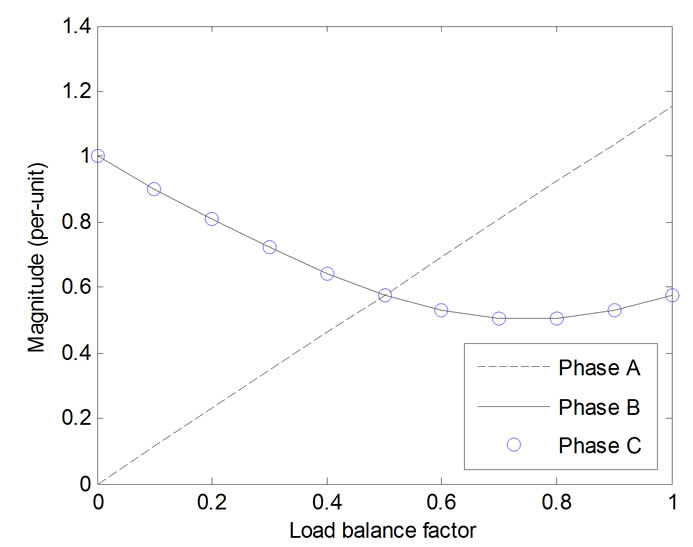
Figure 8. Magnitude of the third order harmonic current seen from the primary-side of the Scott transformer

Figure 9. Angle of the third order harmonic current seen from the primary-side of the Scott transformer versus load balance factor
load balance factor equals 0.5, the harmonic currents in all phases become equal.
An examination of the effect of harmonic current angle is also relevant to this study. This is apparent when considering the angle of the third order harmonic current measured from the primary-side of the Scott transformer versus load balance factor as shown in Figure 9. Variation of the load balance factor does not affect the phase angle of the harmonic current in phase A and it is always 180 degrees. Conversely, the phase angles in phases B and C are sensitive to the variation of the load balance factor.
4.1.1 Maximum-Magnitude Index
Maximum magnitude among the utility side injected harmonic currents, |IhA|, |IhB|, and |IhC|, is defined as the maximum-magnitude index. Our study shows that maximum-magnitude indices of the Scott transformer obey the same pattern for all of the studied harmonic orders (odd harmonic orders). The maximum-magnitude index for the Scott and direct connections versus load balance factor are shown in Figure 10.
While the direct connection’s maximum-magnitude index does not depend on the load balance factor, the Scott transformer connection’s index does. For load balance factors less than 0.82, the Scott transformer cancels out the injected harmonic currents resulting in less harmonic currents in the primary side. The maximum cancellation occurs when |Iha| and |Ihb| are equal, yielding a reduction of 42.3%. For highly unbalanced single-phase loads (when the load balance factor is greater than 0.82) the Scott transformer amplifies the injected harmonic. The maximum amplification (roughly 15%) occurs when |Iha| is supplying the entire load.
4.1.2 Symmetrical Components of the Harmonic
In this part, the impact of the Scott transformer on the reduction of symmetrical components of harmonic currents is investigated. The Scott transformer cancels the negative sequence of the (4k+1) order harmonics depending on the load balance factor as seen in Figure 11. Maximum cancellation occurs when the load balance factor is equal to 0.5. The Scott transformer does not affect the negative sequence of these harmonic orders. The reverse situation happens for the (4k-1) harmonic orders as shown in Figure 12.
4.2 Non-Identical Harmonic Characteristic
The harmonic cancellation performance of the Scott transformer when loads are not identical is studied in this section. In this case, a similar study to that which was performed in Subsection 3.2 can also be performed for each load balance factor. Figure 13 shows the contour plot for CDF of the maximum harmonic current observed at the primary side of the Scott transformer versus each load balance factor when θrand is a random variable uniformly
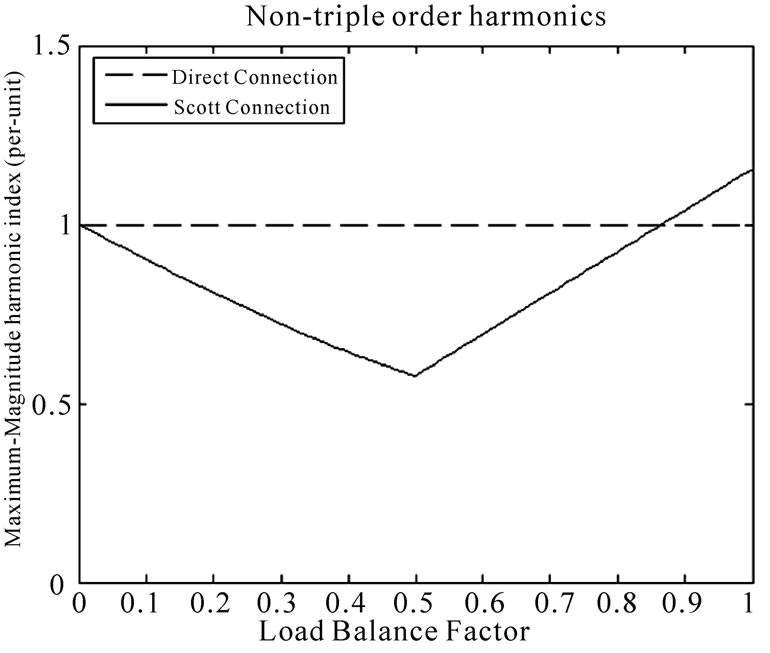
Figure 10. The maximum-magnitude harmonic index for the Scott and Direct connections versus load balance factor

Figure 11. The symmetrical components of the (4k+1) order harmonic currents as seen from the primary side of the Scott transformer

Figure 12. The symmetrical components of the (4k-1) order harmonic currents as seen from the primary side of the Scott transformer

Figure 13. Contour plot for CDF of the maximum harmonic current for Scott transformer where θrand is uniformly distributed over [-10º,10º]
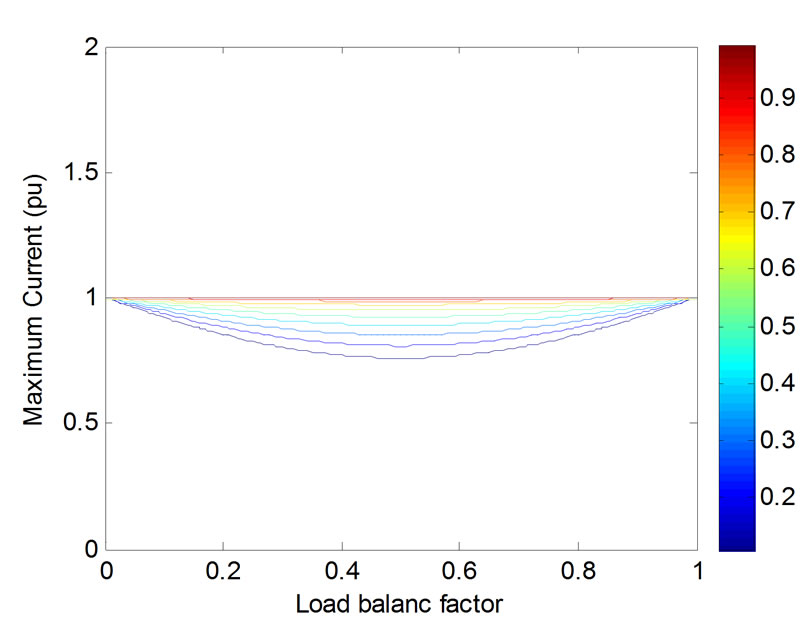
Figure 14. Contour plot for CDF of the maximum harmonic current for direct connection where θrand is uniformly distributed over [-90º,90º]
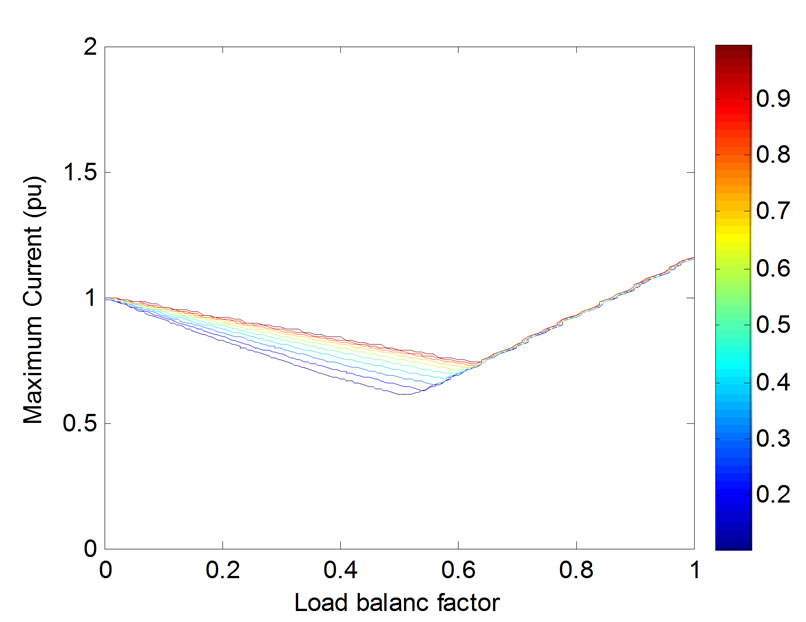
Figure 15. Contour plot for CDF of the maximum harmonic current for Scott transformer where θrand is uniformly distributed over [-90º,90º]
distributed over [-10º,10º]. Compared with Figure 6, the harmonic cancellation performance is very similar to the case where the load has identical harmonic characteristics. It should be noted however, that changing the range of variation of θrand causes more change in this performance. Figure 15 shows the contour plot for CDF of the maximum harmonic current for the Scott transformer when θrand is [-90º,90º]. Observing the contour plot for the direct connection case (Figure 14), one can see that the predominance of the Scott transformer in harmonic cancellation is highly reduced in this range.
5. Conclusions
The paper has investigated the harmonic cancellation characteristics of the Scott transformer. The main findings are summarized as follows:
1) When single-phase loads have identical harmonic characteristics the Scott transformer reduces the maximum harmonic current observed at the primary side for load balance factors less than 0.82.
2) The Scott transformer completely cancels out the positive sequence components of the (4k-1) harmonic orders. The same happens to the negative sequence components of the (4k+1) harmonic orders.
3) When single-phase loads do not have identical harmonic characteristics, there is still some degree of cancellation. The level of cancellation varies from 42.3% to 0% depending on the degree of harmonic characteristics difference.
REFERENCES
- Y. Mochinaga, Y. Akatsuka, K. Arai, and M. Ono, “ Development of three-winding transformer for shinkansen
- auto-transformer feeding system receiving extra high voltage,” The Institute of Electrical Engineers of Japan, Vol. 111-d, No. 3, pp. 237–244, 1991.
- B. K. Chen and B. S. Guo, “Three phase models of specially connected transformers,” IEEE Transactions on Power Delivery, Vol. 11, No. 1, pp 323–330, January 1996.
- T. H. Chen and H. Y. Kuo, “Network modeling of traction substation transformers for studying unbalance effects,” IEE Proceedings Generation, Transmission and Distribution, Vol. 142, No. 2, pp. 103–108, March 1995.
- S. Chen, R. Li, and P. His, “Traction system unbalance problem - Analysis methodologies,” IEEE Transactions on Power Delivery, Vol. 19, No. 4, pp. 1877–1883, October 2004.
- H. Erfanian and W. Xu, “An investigation on the effectiveness of Scott transformer on harmonic reduction, power and energy society general meeting - Conversion and delivery of electrical energy in the 21st century,” 2008 IEEE, pp. 1–4, 20–24, July 2008.
- A. Cavallini and G. C. Montanari, “A deterministic/ stochastic framework for power system harmonics modeling,” IEEE Transactions on Power Systems, Vol. 12, No. 1, pp. 407–415, February 1997.

