ABSTRACT

An important issue in society is the attempt to balance communities working co- operatively and cohesively with one another while allowing members the ability to retain individuality and fostering an environment of cultural diversity. We seek to study the cohesive properties of a culturally diverse dynamic social network. By considering a multi-agent dynamic network, we seek to model a social structure and find conditions under which cohesion and coexistence are maintained. We present a specific illustration that serves to establish the framework in which explicit sufficient conditions in terms of system parameters are found for which the network is cohesive. By utilizing Lyapunov’s Second Method and comparison equations, we are able to find such conditions for the given illustration. Further, for the illustration, we decompose the cultural state domain into invariant sets and consider the behavior of members within each set. Moreover, we analyze the relative cultural affinity between individual members relative to the center of the social network. We also demonstrate how conservative the estimates are using Euler type numerical approximation schemes based on the given illustration. We are then able to consider how changes in the various parameters affect the dynamics of the illustrated network. By gaining such insight into the behavior of the illustrated network, we are able to better understand the impact of both attractive and repulsive influences on the network. This leads to establishing a schema for helping when creating policies and practices catered to promoting both diversity and cohesion within a cultural network.

Keywords:

Multi-Agent Network, Cohesiveness, Lyapunov Second Method, Invariant Sets, Social Network

1. Introduction

The goal of this work is to explore the cohesive properties and behavior of individual members of a dynamic social network. Dynamic network systems are often used to model the behavior patterns of animals, autonomous vehicles, the spread of a contagion, traffic flow, and many other types of situations. In this work, we are interested in modeling the behavior of members within a social network. In particular, we are interested in the cultural shifts of members within culturally diverse groups. We seek to better understand the internal and environmental factors that may foster a sense of cooperation between members of the network while allowing individuality and diversity to be maintained and enhanced.

One of the concepts studied using network dynamics is that of consensus [1] [2] [3] [4] . In such models, the conditions under which a group collectively comes to an agreement are studied. Another question of interest for such a network is when the group might subdivide into smaller subgroups each converging to a consensus but never reaching a consensus as an overall group. Such dynamic network models are useful in many areas beyond just social networks. For example, work in both biological networks and control theory considers such large-scale dynamic models in the context of connectivity, stability and convergence [5] [6] [7] . Using these ideas, much of the work done in these areas look to develop consensus seeking algorithms and consider long term co-existence, cohesion, and stability of the network under consideration [8] [9] [10] [11] .

Cohesion within a social network is a current topic of great interest and many authors have done research within this area [12] [13] . The concepts of cohesion and cooperation within a group are often multi-faceted, dynamic, and complex but are important concepts when trying to better understand how nations or human groups interact and function [14] . As Knoke and Yang note [15] , it is social cohesion that enables information to spread and allows a group to act as a unit rather than individuals.

We often seek to create situations for which people of different backgrounds and beliefs are able to coexists and create a thriving sense of community. We seek to better understand the group dynamics of such a society in order to create policies and practices that encourage a sense of community among individuals from a variety of cultural backgrounds. We use the term multicultural social network to describe a social network in which the agents have a diverse cultural and/or ethical background and are actively seeking to enhance and to maintain diversity with harmony and prosperity. In such a network, the goal of agents is not in approaching a consensus but rather the ability to live and work cooperatively with one another for a common good and goal. For example, consider a population in an area for which there exists a sub-populace of immigrants. In such a situation, the subgroups or sub-communities of immigrants desire to be an integral part of the community and seek to be respectable productive members of the community and the society in general while retaining their cultural diversity. In exploring the dynamics of a multi-cultural network, we are looking to better understand the delicate balance between a culturally diverse cohesive social structure and a social structure for which cohesion does not exists. For when cohesion is lacking in the social network, cooperation may not be as prevalent and we begin to see features such as segregation, violence, economic destabilization and crime within the network.

We seek to model such a situation and better understand the social dynamics of a group seeking to find such a balance. In particular, we are looking to model a dynamic social network for which there is a balance between consensus and cohesion. We wish to model a network that is cohesive but for which there is not a consensus of culture, that is to say the network does not develop a singular cultural identity. In doing so, we are interested in better understanding the cohesive properties of a multicultural social network. We present a prototype of a dynamic model for which we explore the features of such a network. The presented example is used to exhibit the quantitative and qualitative properties of the network. Further, the techniques used are computationally attractive, easy to verify and algebraically simple. In addition, the presented results are in terms of network parameters that characterize the attributes of the network. The byproduct of this provides tools for planning and making policies regarding a dynamic network.

In Section 2, we present an example of such a network, as well as assumptions and notations used throughout this work. In Section 3, using Lyapunov’s Second Method and the comparison method [16] , we consider the dynamics of individual members within the network. In Section 4, long and short term behaviors of group members and invariant cultural state sets are investigated. In Section 5, we consider numerical simulations of the network to better understand the extent that conservative estimates in Sections 4 and 5 are in a given example. Finally, in Section 5, we consider parametric variations within the model affecting the dynamics of the network. Further, we will consider how the model relates to a multicultural network.

2. Problem Formulation

We wish to model a multi-cultural social network and therefore desire to capture the behavior of individual agents who are seeking to belong to the group but also wanting to retain individuality and diversity from other agents. In order to do so, we therefore consider dynamic equations subjected to both attractive and repulsive forces. In [17] , one such function considered when modeling biological dynamic networks is given by

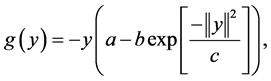(1)

where a, b and c are positive constants and. The function g has long-range attraction and short-range repulsion.

In the following, we formulate a modified version of a network dynamic model in which individuals seek to retain a balance between individual member identity and a group/community membership. We consider a network whose dynamics are described by incorporating a long-range attraction and short-range repulsion similar to that in Equation (1).

Let us consider a network of m members. For each member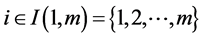, is a cultural position at time t > 0. The vector 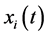can be representative of many various aspects of culture such as beliefs, behaviors, ways of life, etc. depending on the network being considered. Further, let us define a relative cultural state of ith member with a kth member of the community as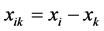, and a center of cultural state of the network

(2)

Consider the network whose dynamic is given by

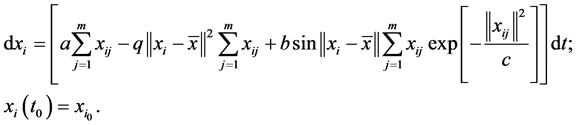(3)

The constant coefficient parameters, a, b, c and 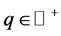represent the weight of the social moderation attractiveness (q), the repulsive forces (a), the rate of decay of the long range attractiveness (c), and the long-range attractiveness (b) between individual members and social groups. We say that the network is cohesive if there exist constants T and M such that 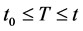and that is to say that the members of the network after some point in time remain within a certain distance of the network center. Further, we say that the network reaches a consensus if 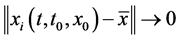as for all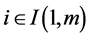. In this case each member of the network draws closer to each other and the network center. Moreover, we define the term relative cultural affinity to be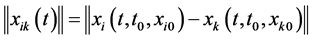, the distance between the cultural vector states of members 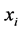and.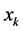

3. Characteristics of the Network

In this section, we wish to explore the dynamics of the agents with the network dynamic described by Equation (3). We will be considering the cohesion, qualitative and quantitative properties such as the overall stability of the network center, and various types of invariant sets. While exploring these ideas, we will also consider what happens as the size of the network increases and what roles the parameters a, b and c play within the model. Moreover, the presented example is utilized to exhibit the quantitative and qualitative properties of the network. In order to accomplish such a task, we utilize Lyapunov’s Second Method [16] . This method is algebraically simple, easy to verify and computationally attractive. Furthermore, the results depend on the system parameters a, b, c and q.

Let us first consider the dynamic of the network center, 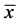as defined in Equation (2). We note that, and

(4)

and is a stationary center of the network. We define the transformation of the network by, noting that

(5)

Therefore, the dynamics of the transformed network are given by

(6)

Dynamic Equation (6) can be useful in modeling a variety of multicultural social networks. In Equation (6), the magnitude of the repulsive force is represented by and the magnitude of the long range attractive force is described by

. Furthermore, is the sine-cyclical influence due to the

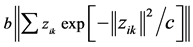
magnitude of the deviation of the ith agent’s cultural state from the center of the network. Attractive influences can be thought of as attributes that bring people to active membership within the group. Social acceptance, gaining social status, economic opportunity, career growth, common purpose and membership, personal development, and a sense of mutual respect, trust and understanding are examples of attractive influences within a social cultural network. Repulsive forces are attributes that create some desire for individuals to leave or be less involved in the group or to preserve some personal identity from one other with their individual magnitude of inner repulsive force. A desire to retain a sense of individuality, economic or emotional cost, interpersonal conflict within the group, or disagreement with parts of the overall philosophies of the group are forces that may be considered as repulsive forces. In short, economic, educational, and social inequalities coupled with the race, gender, ethical and religious bias are sources of repulsive forces. A balance between the total attraction and repulsive forces attributes to a general sense of individual agents maintaining a “live and let live” philosophy for the greater benefit of the community and the common good of society.

In order to better understand the dynamics of Equation (6), we will use Lyapunov’s Second Method in conjunction with the comparison method [16] . These methods will provide a computationally attractive means to better understand the movement of members within the network. To that end, let us consider a candidate for energy function defined by

(7)

Then the differential of V along the vector field generated by Equation (7) is given by

(8)

where

(9)

In Subsections 3.1 and 3.2, we will find upper and lower estimates for respectively. Using Lyapunov’s Second Method and the comparison method [16] , we will then use these estimates to consider the behavior of the agents over time t. For instance, we consider the stability of the network, and establish invariant sets for the network.

3.1. Upper Estimate of

In this subsection, we seek constraints on a, b, c, and q such that for outside of a given ball, we can establish an upper estimate of. We will then use these assumptions in conjunction with the Lyapunov method and comparison theorem [16] to establish the case for which

(10)

where is the maximal solution of a comparison differential equation through.

By considering the derivative of the function,

(11)

We note that

(12)

has a global maximum when with a maximum value of

(13)

From Equation (12), Equation (13), and the fact that, for, Equation (9) reduces to:

(14)

Assumption H_1: Suppose. Let us define

(15)

and let. Further, let us denote the compliment of the by. For any, Equation (14) yields the following inequality:

(16)

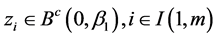
Using Equation (16) along with the comparison theorems [16] , we establish the following result.

Lemma 1. Let V be the energy function defined in Equation (7), be a solution of the initial value problem defined in Equation (6). For each satisfying the differential inequality Equation (16), it follows that the network is cohesive and

(17)

where is the maximal solution of the initial value problem

(18)

provided that; that is,

(19)

Proof: Under the assumptions of the lemma and using the standard argument [16] combined with the above discussion, the proof of the lemma follows from Equation (16). The cohesiveness of the network follows by definition as the solution to Equation (18) is bounded. □

Remark 1: We remark that the assumption H₁ is an alternative sufficient condition as: From Equation (14), we have

(20)

where, and

, (21)

for any.

3.2. Lower Estimate of

Next, we look to establish a lower estimate of such that

(22)

where is the minimal solution to a comparison equation through.

Imitating the argument used to arrive at Equation (14) and noting that, for if and only if, for, Equation (9) reduces to the inequality

(23)

Assumption H₂: Let us define

(24)

and, with its complement being. For , Equation (23) reduces to the following differential inequality:

(25)

Using Equation (25) along with the comparison theorems [16] , we establish the following result.

Lemma 2. Let V be the energy function defined in Equation (7) and z_i a solution of the initial value problem defined in Equation (6). For each satisfying the differential inequality Equation (25), it follows that

(26)

where is the minimal solution of the initial value problem

(27)

Provided; that is,

(28)

Proof: Under the assumptions of the lemma and using the standard argument [16] combined with the above discussion, the proof of the lemma follows from Equation (25). □

Remark 2: A remark similar to remark 1 is as follows: From Equation (23), we have

(29)

where, where

(30)

For any.

4. Long and Short Term Behavior of Members and Invariant Sets

After First let us note from, the minimal solution to the initial value problem in Equation (23) in Lemma 2, we find

(31)

Similarly, from the solution of the comparison differential Equation (17) and Lemma 1, we note that

(32)

Therefore, by Lemmas 1 and 2, when, it follows that

(33)

From Equations (31), (32) and (33), we consider one case and the associated invariant sets. First, let us consider the case for which. That is, let us suppose that

(34)

Let us further suppose that it is the case that

(35)

For and, let us define the following sets (Figure 1):

(36)

In the following, we state and prove a few qualitative properties of the solution process of the center of the multi-agent determinist dynamic network described by Equation (3). The following result exhibits the major influence of long range attractive forces.

Theorem 1. For, if for all, a neighborhood of the center, then Equation (9) reduces to the inequality

(37)

Further, if, there exists such that for when, for all.

Proof. Let and for all. Then,

(38)

Considering the non-homogeneous comparison equation,

(39)

it follows that

(40)

where is the minimal solution of Equation (39) when. Let be the solution of the homogeneous differential equation

(41)

Then, by using the method of variation of parameters, the solution to the non-ho- mogenous differential equation given in Equation (39) is given by

(42)

where

(43)

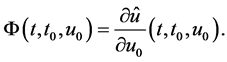
Using separation of variables, the solution of the homogeneous differential equation is given by

(44)

and

(45)

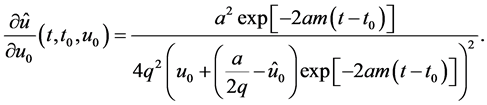
Therefore, from Equation (42),

(46)

where

(47)

Let be the function defined as

(48)

We note that is continuous on and

(49)

As the limit as of is finite, for any given there exists a such that

(50)

and so has an upper bound on say. Further, as is continuous on, has an upper bound on this interval, say. Let. As, it must be the case that and hence Equation (42) reduces to

(51)

Suppose that it is the case that and so the solution is monotonically increasing as. Choosing, such that and, it follows that Equations (51) has the lower bound

(52)

Thus, for all when for all. □

Theorem 2. Let the hypotheses of Lemmas 1 and 2 be satisfied. Then

1) the set is conditionally invariant relative to;

2) the set is either self-invariant or is conditionally invariant relative to;

3) set C is either self-invariant or 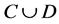is conditionally invariant relative to C;

4) the set is self-invariant;

5) the set is conditionally invariant relative to.

Proof. For, the hypotheses of Lemmas 1 and 2 are satisfied. Thus by the application of these Lemmas, we have

(53)

for, , where; and are the minimal and maximal solutions of the comparison differential equations given in Equations (27) and (18) respectively. Moreover, for, with and, the solutions and

are both monotonically decreasing and approaching to and respectively. This yields

(54)

for. From Equation (54), and the definitions of self-invariant and conditionally invariant [18] , it follows that statement 1) is valid. The proofs of 2), 3) and 4) follow by imitating the argument used in the proof of 1). For, we note that is monotonically decreasing and is monotonically increasing to and as respectively. This together with Equation (54) establishes that proving statement 2). For, is decreasing and the proof of 3) and 4) follows from 1) and 2). Similarly, the proof for statement 5) also follows by imitating the argument used in 1). For, the solutions to the comparison equation given by Equation (27), is monotonically increasing to as. Therefore, by Equation (54), proving statement 5). □

Let us expand upon the results of Theorems 1 and 2. First, let us note that these two theorems provide the qualitative and quantitative requirements on the cultural state parameters to insure that the model is cohesive (Theorem 2) and simultaneously does not reach a cultural consensus (Theorem 1). We introduce the definition of cultural bound to describe the boundary between two cultural sets, dividing the degree of individual versus community level interaction domains of the cultural state. Suppose. It can be shown that there exists a neighborhood, of the center such that for, the individual member cultural state is pushed out/re- pulsed from the cultural state center at some time depending on. Therefore, if the cultural state of the ith member of the network is such that the relative cultural affinity between and the center, of the network is sufficiently close to zero, then the agent’s cultural state is repulsed from the center. That is to say, the membership of the social network will obtain and then maintain a relative cultural affinity between members and the center that is bounded below by a value strictly greater than zero. Once the state of the ith member has moved away from the center, it may be the case that remains in or the case that the state moves to the cultural set, at which time the agent’s cultural state behavior will follow that of another category of membership described by the cultural state set discussed below.

Suppose the initial value, that is the function of the magnitude of the cultural state, of the comparison equation is such that. Then the solution to the lower comparison equation grows as t grows and approaches asymptotically to the threshold limit from below resulting in stronger ties with the community center state,. If the initial value of the lower comparison equation is such that, then the solution decays and asymptotically approaches to the threshold limit from above. Therefore, if is a member of the transformed social network such that, then by Theorem 2, over time, moves to the cultural bound of the set. It may also cross the cultural bound or it may be the case that approaches asymptotically to the cultural bound of. Similarly, if, may stay in, approaching the cultural bounds of sets and/or or it may be the case that crosses the cultural bound of at which point the member will behave as other members of. However, if, even though it may approach the cultural bound of, it will never cross the bound. In terms of a given social network, this implies that members with a distinct enough cultural state from the weighted average of cultural states will retain that distinctiveness of culture. Thus, if the relative cultural affinity between a member and the center of the network is at least initially, then the relative cultural affinity will always be at least that value.

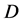
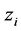
Turning to the upper comparison equation, we can consider the behavior of the transformed network members whose initial positions are in the sets and. Let be the initial position of the solution to the upper comparison equation given in Lemma 1. If, then the solution grows and approaches asymptotically to the value from below. If, the solution decays and approaches asymptotically to the limit from above. Therefore, if, may approach and cross the cultural boundary of (but will remain in) or may approach but not cross the cultural boundary of. For, may either cross the cultural boundary of or the member’s cultural state will approach asymp- totically to the cultural boundary of. Thus, for agents within the network whose initial relative cultural affinity with respect to the center is sufficiently large, as, the relative cultural affinity will remain large and the although the agent is attracted back towards the center of the network, the relative affinity is bounded below by.

Further, from Lemmas 1 and 2, if all parameters other than the size of the network are held constant, then as the size of the network increases, so also the difference between the upper and lower bounds on the relative cultural affinity between agents and the center of the network increases. Naturally, increasing the size of the network leads to the concept of the crowding effect. Competition over ideology or cultural traits creates a stronger desire for agents to retain more of their individuality within the society or group. Cultural subgroups that have a high degree of separation in terms of their relative cultural affinities are an emergent characteristic of such large scale multi- cultural networks. In the modeling for members whose cultural state is in (so one aspect of culture/interest being considered), we see the network dividing into two subgroups with agents converging to states that are symmetric with respect to the time axis. One can think of situations like a large urban environment in which there exist communities each with a strong cultural identity. In such a case, agents within the community seek to retain their cultural diversity. Thus, it is expected that a large relative cultural affinity between agents of different communities, but a small relative cultural affinity between agents within the same community, is expected to exist.

5. Numerical Simulation

In this section, using Euler’s type numerical to approximation scheme applied to Equation (6), we consider the numerical simulations for the network dynamics governed by Equation (6). The goal is to compare the long term behavior of the simulated solution with the theoretical long term behavior given in Section 4. We consider a network consisting of 50 members with parameters a = 0.5, q = 0.04, b = 0.41, and c = 2. Further, we note that in this case, and

(55)

In this example, the conditions for the invariant sets given in Theorems 1 and 2 in Section (4) are satisfied. Hence, for such that, it is the case that after some time,; that is, the member does not move towards the center of the network. Further, for such that, after some time,. Figure 2 is a plot of the approximate solutions for the full membership of the network. In order to make the dynamics of the network clearer, Figure 3 is a plot of the approximate solution of Equation (6) for six of the members of the network.

Next, we consider the network with the same initial values with the parameters a = 0.25, b = 0.14 and q = 0.04. In this case and

(56)

For such that, the member does not move towards the center of the network and for such that, after some time,. Similar to above, we have plotted the approximate solution for the full network in Figure 4 and the approximate solution for the same six members as Figure 3 in Figure 5.

The last case we considered is the network with the same initial positions with the parameters a = 0.5, b = 0.18 and q = 0.2. Thus, with the given parameters, , and

(57)

For such that, the member does not move towards the center of the network and for such that, after some time,. Similar to above we have plotted the approximate solution for the full network in Figure 6 and the approximate solution for the same six members in Figure 7.

6. Conclusions

We have considered requirements on network parameters for long term qualitative properties of the network. We develop a model and establish conditions on the parameters that ensure a balance between cohesion and consensus. Further, we have considered how the initial cultural state of a network member affects the behavior of that member over time. The presented conditions of the system are algebraically simple, easily verifiable and computationally attractive. The developed results provide a tool for planning, decision making, and performance. Furthermore, the presented sufficient conditions are conservative but robust, verifiable, and reliable. From the above conditions, we are able to consider certain dynamic properties of the social networks governed by Equation (3).

In this paper, we explored the features of a multi-cultural network with dynamics described by a specific differential equation and the long term stability and behaviors of individual members within such a network. We are interested in further exploring social networks in the context of better understanding the relative cultural affinity between agents and not just the cultural affinity between an agent and the center of the network. Our hopes are to better understand what factors may lead to preserving a lower bound on the relative cultural affinity that is strictly greater than zero as. In modeling such a network, we are looking to better understand how diversity between all members may be maintained over the long term within a culturally diverse network. Further, we are exploring the effect of noise on the network by considering similar dynamics and stochastic differential equations. The goal for both such questions is to better understand the impact of perturbations/impulses, both internal and external, on the behavior and diversity of multi-cultural networks.

Acknowledgements

The authors would like to acknowledge the research support by the Mathematical Sciences Division, US Army Research Office, Grants No. W911NF-12-1-0090 and W911NF-15-1- 0182.

Cite this paper

Hilton, K.B. and Ladde, G.S. (2016) Deterministic Multicultural Dynamic Networks: Seeking a Balance between Attractive and Repulsive Forces. Int. J. Communications, Network and System Sciences, 9, 582-602. http://dx.doi.org/10.4236/ijcns.2016.912045

References