International Journal of Communications, Network and System Sciences
Vol.09 No.01(2016), Article ID:63070,9 pages
10.4236/ijcns.2016.91003
Consensus Control for a Kind of Dynamical Agents in Network
Hongwang Yu
School of Science, Nanjing Audit and University, Nanjing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 November 2015; accepted 24 January 2016; published 27 January 2016
ABSTRACT
This paper discusses consensus control for a kind of dynamical agents in network. It is assumed that the agents distributed on a plane and their location coordinates are measured by remote sensor and transmitted to its neighbors. By designing the linear distributed control protocol, it is shown that the group of agents will achieves consensus. The simulations are given to show the effectiveness of our theoretical result.
Keywords:
Distributed Control, Graph Laplacian, Dynamical Agents

1. Introduction
Distributed coordination of network of dynamic agents has attracted a great attention in recent years. Modeling and exploring these coordinated dynamic agents have become an important issue in physics, biophysics, systems biology, applied mathematics, mechanics, computer science and control theory [1] -[11] . How and when coordinated dynamic agents achieve aggregation is one of the interesting topics in the research area. Such problem may also be described as a consensus control problem.
To describe the collective behavior of agents in a large scale network, the agent in the network usually is modeled by a very simple mathematical model, which is an approximation of real objects. Saber and Murray [3] [4] proposed a systematical framework of consensus problems in networks of dynamic agents. In their work the dynamics of the agent is modelled by a simple scalar continuous-time integrator , the convergence analysis is provided in different types of the network topologies. Following the work of [3] [4] , Guangming Xie [10] study the case where the agent is a point-mass distributed in a line, and its dynamics is described by the Newton’s law
, the convergence analysis is provided in different types of the network topologies. Following the work of [3] [4] , Guangming Xie [10] study the case where the agent is a point-mass distributed in a line, and its dynamics is described by the Newton’s law . In their work the dynamic agents connected by a network, which is characterized by a graph and each agent is Lyapunov stable. They show that by means of a simple linear control protocol based on the structure of the graph, the dynamical agents will eventually achieve aggregation, i.e. all agents will gradually move into a fixed position, meanwhile their velocities converge to zero.
. In their work the dynamic agents connected by a network, which is characterized by a graph and each agent is Lyapunov stable. They show that by means of a simple linear control protocol based on the structure of the graph, the dynamical agents will eventually achieve aggregation, i.e. all agents will gradually move into a fixed position, meanwhile their velocities converge to zero.
In our work a similar problem is studied under the condition that the agents move in a plane. The agents may represent the vehicles or mobile robots spread over a wild area and they communicate by means of some remote sensors with certain error. When the agents are moving in a plane, the collective behavior conditions will depend on the communicated error and the algebraic characterization of the communicated network topology, as well as the dynamical behavior of agents.
This paper is organized as follows. In Section 2, we recall some properties on graph theory and give the problem formulation. In Section 3 the main results of this paper are given and some simulation results are presented in Section 4. Final section is a conclusion.
2. Preliminaries
Consider a network of dynamical agents defined by a graph . The node set
. The node set 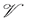 consists of dynamical agents
consists of dynamical agents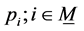 . The dynamics of
. The dynamics of  for
for 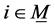 is described as follows.
is described as follows.
Let 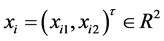 be the coordinate of dynamical agent
be the coordinate of dynamical agent  in
in , then the dynamical equation of agent
, then the dynamical equation of agent 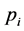 is
is
 (1)
(1)
where 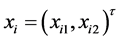 indicates the location of agent
indicates the location of agent 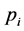 in the plane,
in the plane, 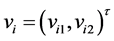 represents the velocity of the i-th agent and
represents the velocity of the i-th agent and 

servation matrix of the agent by some remote sensor.
In what follows we simply assume that 



neighbors through the network. The matrix C is assumed to be an orthogonal matrix in the form
The parameter 
For the dynamic agent (1) in network we have following assumption.
Assumption 2.1 The dynamics (1) is Lyapunov stable when it disconnected with its neighbors, meaning that the dynamical agent as an autonomous will gradually stop by moving a finite distance for any non-zero initial velocity
The collective behavior of dynamical agents in network can be described by




In this work, we discuss the collective behavior of the dynamical agents under a decentralized control law in the form that

where indexes
We claim that a group of dynamical agents associated with 





In our work, let (2) be

where 

Remark 1: If we choose 

for

3. Collective Behaviors of Dynamical Agents
Consider a group of dynamical agents in network associated with a graph






Denote

where
Let

where

and L is the aforementioned Laplacian associated with the graph
The collective behavior problem of dynamical agents can be described in 






As dynamics (7) is a standard linear time-invariant dynamical system, its trajectory can be described by

The consensus asymptotical stability implies that the matrix 

Lemma 3.1 The matrix 



and
Proof: It is well known that the graph 




Thus, 




The following Lemma is key to our work.
Lemma 3.2 If the control gain k in dynamical agent (1) satisfies Assumption 2.1, and 

with

where





Proof: Denote the eigenvalues of L by


One can verify the following formulae.
The dynamical behavior of the network (7) is characterized by the eigenvalues of 

First we discuss the block with





For




Consider the characteristic polynomial of
where

Construct the Routh array of
with 
criterion, for stability it is necessary that

By (14) one has

and

The inequalities (15) can be rewritten as the following form by using the conditions of Lemma 3.2 and the Equations (16)-(17).

We can further show that the second inequality in above implies the first one. Obviously, it is true when

where 
Thus, one can consider the following inequalities
The last inequality obviously holds. Therefore, the solution of (18) leads
If



computing process. It shows that 
Therefore, 
By 


where 








Let



correspondingly.
As
and
Let 

Due to the fact that



Theorem 3.1 Under conditions of Lemma 3.2 the control protocol (4) globally and asymptotically achieves the collective behavior of the dynamic agents.
Proof: As 

Therefore,

and it is obvious that

This implies the protocol (5) globally asymptotically achieve aggregation.
Corollary 3.1 If the control gain k satisfies 

Under Assumption 2.1 one has



Corollary 3.2 The dynamical agents achieve collective behavior if 

4. Simulations
We study some examples to show that our results are effective. The network of dynamic agents is described in Figure 1.
We can obtain the Laplacian matrix L of the graph 




We consider that the dynamic agent (1) in the network has 



Figure 1. A undirected graph 




When a control protocol (4) is applied into the agents in network, the collective behavior of dynamic agents takes place according to our result.
Figure 2 gives simulation results of the collective behavior of the agents with initial conditions





















It is found that when the agents approach to
5. Conclusion
We discuss the consensus control of dynamical agents in network which associated with a graph
Figure 2. State and velocity trajectories of the agents in
agents are moving in a plane, the aggregation of the dynamical agents are depended on not only the communicated error, but also the algebraic characterization of the communicated network graph and the dynamical properties of agents.
Acknowledgements
This work was supported by the Natural Science Foundation of Jiangsu Higher Education Institutions of China (Grant no. 13KJB110015).
Cite this paper
HongwangYu, (2016) Consensus Control for a Kind of Dynamical Agents in Network. International Journal of Communications, Network and System Sciences,09,29-37. doi: 10.4236/ijcns.2016.91003
References
- 1. Fax, A. and Murray, R.M. (2004) Information Flow and Cooperative Control of Vehicle Formations. IEEE Transactions on Automatic Control, 49, 1465-1476.
http://dx.doi.org/10.1109/TAC.2004.834433 - 2. Toner J. and Tu, Y. (1998) Flochs, Herds, and Schools: A Quantitative Theory of Flocking. Physical Review E, 58, 4828-4858.
http://dx.doi.org/10.1103/PhysRevE.58.4828 - 3. Saber, R.O. and Murray, R.M. (2003) Consensus Protocols for Networks of Dynamic Agents. Proceedings of the American Control Conference, 2, 951-956.
http://dx.doi.org/10.1109/acc.2003.1239709 - 4. Saber, R.O. and Murray, R.M. (2004) Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Transactions on Automatic Control, 49, 1520-1533.
http://dx.doi.org/10.1109/TAC.2004.834113 - 5. Liu, Y. and Passino, K.M. (2003) Stability Analysis of One-Dimensional Asynchronous Swarms. IEEE Transactions on Automatic Control, 48, 1848-1854.
http://dx.doi.org/10.1109/TAC.2003.817942 - 6. Liu, Y. and Passino, K.M. (2003) Stability Analysis of M-Dimensional Asynchronous Swarms with a Fixed Communication Topology. IEEE Transactions on Automatic Control, 48, 76-95.
http://dx.doi.org/10.1109/TAC.2002.806657 - 7. Gazi, V. and Passion, K.M. (2004) Stability Analysis of Social Foraging Swarms. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 34, 539-557.
- 8. Liu, Y. and Passino, K.M. (2004) Stable Social Foraging Swarms in a Noisy Environment. IEEE Transactions on Automatic Control, 49, 30-44.
http://dx.doi.org/10.1109/TAC.2003.821416 - 9. Savkin, A.V. (2004) Coordinate Collective Motion of Groups of Autonomous Mobile Robots: Analysis of Vicsek’s Model. IEEE Transactions on Automatic Control, 49, 981-983.
http://dx.doi.org/10.1109/TAC.2004.829621 - 10. Xie, G.M. and Wang, L. (2006) Consensus Control for a Class of Networks of Dynamic Agents. International Journal of Robust and Nonlinear Control, 17, 941-959.
- 11. Algebraic, B.N. (1994) Graph Theory. Cambridge University Press, Cambridge, UK.
- 12. Horn, R.A. and Johnson, C.R. (1987) Matrix Analysis. Cambridge University Press, Cambridge, UK.























