Int'l J. of Communications, Network and System Sciences
Vol.7 No.3(2014), Article ID:43727,10 pages DOI:10.4236/ijcns.2014.73011
The Impact of User and Traffic Models on the Design of the Communications Network in the Smart Grid
A. T. Burrell1, Fernando Mancilla-David2, P. Papantoni-Kazakos2
1Computer Science Department, Oklahoma State University, Stillwater, USA
2Electrical Engineering Department, University of Colorado Denver, Denver, USA
Email: titsa.papantoni@ucdenver.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 January 2014; revised 27 February 2014; accepted 6 March 2014
ABSTRACT
A critical component of the smart grid (SG) infrastructure is the embedded communications network, where an important objective of the latter is the expansion of its throughput, in conjunction with the satisfaction of specified latency and accuracy requirements. For the effective design of the communications network, the user and traffic profiles, such as known-user vs. unknown-user populations and bursty vs. non-bursty data traffics, must be carefully considered and subsequently modeled. This paper relates user and traffic models to the deployment of effective multiple access transmission algorithms in the communications network of the SG.
Keywords:Smart Grid Communications; User Models; Traffic Models; Matching Multiple Access Communications Algorithms

1. Introduction
With the recent emphasis on a smart grid (SG) deployment within the United States and the passing of EISA (Energy Independent and Security Act of 2007) into law [1] , the race for the SG design has begun. This paper addresses the role and impact of user and traffic models on the design of the SG’s communications network. Factors such as bursty vs. non-bursty data traffics as well as knownvs. unknown-user population models must be factored in the design of the latter.
A communications network is a key component of the SG infrastructure [2] . SG communication technologies must allow for timely access of the utility’s control center by data resulting from the sampling of meters at the rate of several times per second [3] . As detailed in [4] , communications networks for energy management must possess distinct performance attributes including: high reliability and availability, automatic redundancy, coverage of large distances, support of a large number of nodes, low delays (latency), security (able to meet NERC cyber security standards) and ease of deployment and maintenance. The various functions of the distribution network (DN) impose different requirements on the communications network. For example, meter reading may be scheduled at specific time and does not require permanent real-time communications. On the other hand, event or fault data must be communicated reliably in real time with maximum allowed delay of 300 milliseconds [2] . Defining network requirements is the first and most important step in designing a communications network that meets current and future demands. The communications network of the SG is a data network whose design is affected by the following performance criteria: 1) Bandwidth or data rate: Various parts of the SG have different bandwidth requirement [5] . A communications throughput of 2 - 5 Mb/s was estimated as a guideline for SG links [6] . 2) Latency: It is a measure of time delay experienced in a communications network. Communication involving a request for reactive power has the second most rigid latency requirement [2] . For both rural islanding and urban meshed distribution scenarios, the maximum tolerated latency in this case is six cycles or 100 ms [6] . 3) Security: Network security is extremely important to ensure all customers’ data remaining private and no unauthorized access to the network. Since wireless network uses broadcast medium, it must be resistant to tampering of confidential information and prevents unauthorized access [7] . 4) Scalability: It is the ability of a system or network to handle expansion without the need for replacing major segments of the network. 5) Resilience: It is the ability of a network to function properly during interference either random or intentional. 6) Reliability: It is the ability of a network to perform within its normal operating parameters to provide a specific level of service. 7) Interoperability: It means that devices and services from multiple vendors are compatible with each other and can be integrated into a network. Interoperability is very important considering in network deployment. 8) Distance Reach: Each wireline and wireless communication technology has its unique signal reach distances. Terrain characteristics affect wireless signal reach and must be considered during technology evaluation stage. 9) Existing Geographic Coverage: The electric distribution network covers vast geographic areas with varying terrain characteristics. Selecting technologies that already cover areas where Smart Grid will be deployed will reduce the deployment cost. However, a single technology may not provide coverage in all areas. 10) Cost of Ownership: Capital expenditure (CAPEX) and operation expenditure (OPEX) are practical considerations when designing a communications network.
Regarding the communications medium, both wireline and wireless communication technologies are viable options for the SG. Some of the popular communication technologies are Power Line Communications (PLC), Cellular, licensed and unlicensed radio, existing internet connection, Wi-Fi and WiMAX [8] . In certain situations, wireless technology has advantages over wired technologies, such as low cost and ease of connection but suffers from interference and signal attenuation [9] . On the other hand, wireline communication technologies are more reliable, less prone to interference, but are very expensive to deploy as a new infrastructure. However, the smart grid, as a complex system, requires heterogeneous communication technologies to meet its diverse needs [10] .
While common communications network design criteria apply to realize the SG, the user and traffic models will have a significant impact on the technology selection. The proliferation of Electric Vehicles and Distributed Generation (DG) will introduce additional significant challenges for Grid operators due to the then induced variability in time and space. As a result, the communications network supporting the Smart Grid must be versatile to handle large shifts in user populations and data traffic variations and must be able to accommodate multiple users on common channels. In this paper, we focus on user and traffic modeling for the communications network of the SG, in conjunction with imposed latency as well as resources conservation requirements, and present matching multi-user transmission techniques. We point out that a pertinent research focus may be recognized in [11] , where the authors distinguished among five different traffic classes in terms of bandwidth and latency requirements.
The paper is organized as follows: In Section II, we present user and traffic models, as well as transmission models. In Section III, we present deterministic multi-user transmission techniques. In Section IV, we discuss random access transmission policies. In Section V, we discuss hybrid techniques, for the accommodation of mixed user traffics. In Section VI, we present discussion and conclusions.
2. User, Traffic and Channel Models
As stated in the introduction of this paper, the communications network of the SG is a data network. In data networks, the deployable transmission multiple-access algorithms which satisfy the required performance criteria are dictated by the active user population model, where two major such model distinctions are pertinent: 1) Known User Population Model, where the identities of all users are distinct and known to the system; this class implies finite, and practically limited, membership. 2) Unknown User Population Model, where the identities of the users are unknown to the system, usually due to time-varying user characteristics and/or mobility; the membership of this class may be either finite or infinite.
In the SG Distribution Network, the known user population model arises when the residential units and businesses in a relatively limited area are considered, since their identities (IDs) (user IDs in record, as well as location) are then limited in number and known to the system. On the other hand, the unknown user population model arises when either the Electric Vehicles (EV) and portable Distributed Generation (DG) systems are considered; since they may change location and consequently interconnect with the SG at various time-changing points, or dense areas containing a large number of residential units and businesses.
Regarding data traffics generated within the communications network of the SG, data files are “packetized”, where all packets have identical lengths in bits. The transmission of packets through a given channel in the communications network is considered synchronous: a universal clock determines the beginnings of channel “slots”, where a single slot corresponds to the time required for the transmission of a single packet and where each packet starts transmission at the beginning of some slot; the actual time length of a channel slot in milliseconds is determined by the speed of the channel in bits per second. Within the local area network scenario, propagation delays in packet transmissions are fractions of a slot length; in retransmission events, the system may be then modeled as one which does not induce propagation delays. In addition, we may initially model the noise environment, in conjunction with the deployed error correcting code, as such that a single packet transmission per slot results in successful transmission, while multiple packet simultaneous transmissions per slot result in collision and subsequent total destruction of all packets involved; retransmission of the collided packets is then required. Finally, we will adopt the well-accepted binary feedback model, where the observable (via channel sensing or broadcasting) by the users outcome per channel slot is either Non-Collision (NC); when no packet or a single packet has been transmitted, or Collision (C); when at least two packets have been simultaneously transmitted.
A considerable percentage of the packet stream traffic generated in the SG is bursty; corresponding to packets occurring with low probability per channel slot, while, in addition, some fraction of the packet traffic may require strict delay limitations; such is the case of the SG control data, for example. A worst case scenario of bursty traffic is represented by the Limit Poisson User Population Model comprised of infinitely many identical Bernoulli users, whose aggregate packet generating process is Poisson, where each packet represents a separate user. The Limit Poisson user population model is a special case of the unknown user population model and induces lower bounds on the throughput and delay performance for a large class of multiple access transmission algorithms [12] .
Due to limitations in transmission resources, such as bandwidth, the channels of the communications network in the SG are generally shared by several packet generating users for transmission, as implemented by deployed multiple-access transmission techniques. As we will elaborate upon in the sequel, the appropriate such techniques are dictated by the user model, in conjunction with the burstiness of the packet traffic [13] and the possible rigid latency constraints for some of the traffic [14] . In this paper, we focus on multiple-access transmission techniques, as induced by the user and traffic models. In our presentation, we distinguish between deterministic and random access such techniques, while we explain their evolution and interrelationship.
To summarize the discussion included in the following sections, when the known user population model is present and the number of users is relatively limited, the class of deterministic multiple-access algorithms is appropriate for deployment. When the unknown user population model is present, instead, the only deployable class of multiple access algorithms is the random access class. The operations of the algorithms in the latter class are relatively insensitive to changes in the user population, but, as compared to the deterministic multiple-access class, they induce variable delays. At the same time, unknown user populations normally generate bursty traffics, while the traffics generated by known user populations may be either bursty or non-bursy; in the presence of the known user population with relatively limited cardinality and bursty traffics, the deployment of deterministic multiple access transmission algorithms with tree-search characteristics is delay-efficient.
In the communications network of the SG, we will integrate diverse data traffics; where a well-defined part of the user population, consisting of a relatively limited number of known users, may generate possibly high-priority data (network control data included); and where an ill-defined, time varying, possibly mobile and frequently large population of users (unknown user population) generate data which may tolerate variable delays. We may assume the existence of a strict upper bound on the maximum per high-priority packet delay, and we will impose a stability requirement for the whole system; that is, we will not allow data losses. For the above system, we will present transmission algorithms some of which may be hybrid, accommodating both high and low priority data. The algorithms may attain low delays and relatively high throughputs for all data traffics, while simultaneously maintaining a strict upper bound on the maximum per high-priority packet delay. For clarity in our following presentation, we conclude this section by providing precise definitions of throughput and delays, as induced by any multiple access algorithm.
Throughput: The maximum aggregate packet traffic rate l*, in expected packets per slot, for which the user/algorithm system is stable; maintaining all traffic with finite delays. Then, (0, l*) is named the stability region of the system.
Per Packet Delay: The distance, in slot units, between the arrival instant of a packet arrival and the instant when its transmission has been completed.
3. Deterministic Multi-User Transmission Techniques
We consider the case where a number of packet generating users access a single channel independently for transmission, where the channel model is as in Section II: it is slotted; a single packet transmission per slot is successful, while multiple packet transmissions per slot result in destruction of all involved packets; the outcome per slot “visible” to the users is C versus NC. Deterministic multi-user techniques are then represented by collision resolution algorithms whose steps are all deterministic; that is, no steps involve random numbers. Such algorithms generally correspond to tree searches and may have built-in dynamic features which allow them to adapt to various levels of traffic burstiness. As tree searches, such algorithms are only applicable to known user population models, where the user IDs are then known to the system. By close inspection of the deterministic tree search operations, we will conclude that, as the number of users in this population increases to large values, these algorithms are more effectively implemented by their random access counterparts. Thus, deterministic multiple access algorithms are appropriate for the known user population whose membership is relatively limited.
We now consider deterministic multi-user transmission algorithms which use a binary tree search for collision resolution. That is, when a packet collision occurs, it is resolved via a binary tree search during which all the initially collided packets are successfully transmitted, while those that did not withhold. We will discuss two separate collision resolution algorithms utilizing a binary tree search. We will first explain the common to both algorithms virtual placement of the users on the binary tree, as exhibited in Figure 1.
Without lack in generality, we assume that the number of packet generating users is 2N. Let the 2N users be indexed from1 to 2N, and let this indexing be known to them all. Let the 2N users form 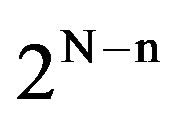 disjoint groups, where 0 ≤ n ≤ N and where the kth group contains the users with indexes from
disjoint groups, where 0 ≤ n ≤ N and where the kth group contains the users with indexes from 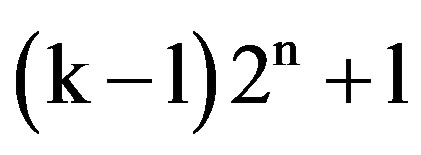 to k2n, 1 ≤ k ≤
to k2n, 1 ≤ k ≤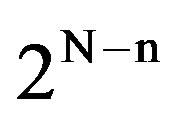 . This grouping is referred to as the initialization part of the algorithm. Let n and the grouping be known to the 2N users. Then, initially collided packets are retransmitted by “examining” the
. This grouping is referred to as the initialization part of the algorithm. Let n and the grouping be known to the 2N users. Then, initially collided packets are retransmitted by “examining” the 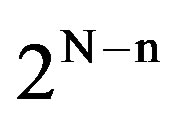 groups sequentially, from group 1 to group
groups sequentially, from group 1 to group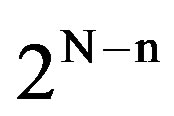 ; that is, all possible packets in group k are transmitted after those in groups 1 to (k − 1) have completed successful transmission. The transmissions within each group are accommodated via the rules of the specific collision resolution algorithm deployed and the transmissions from group k start immediately after the last successful transmission from group (k − 1). We point out that the selected number
; that is, all possible packets in group k are transmitted after those in groups 1 to (k − 1) have completed successful transmission. The transmissions within each group are accommodated via the rules of the specific collision resolution algorithm deployed and the transmissions from group k start immediately after the last successful transmission from group (k − 1). We point out that the selected number 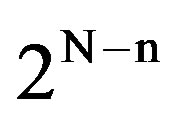 of groups is dictated by the traffic rate: As this rate increases, the number of groups increases, as well, where, in the limit, the number of groups equals the number of users and the sequential examination of the groups for retransmission becomes then the Time Division Multiple Access (TDMA) algorithm.
of groups is dictated by the traffic rate: As this rate increases, the number of groups increases, as well, where, in the limit, the number of groups equals the number of users and the sequential examination of the groups for retransmission becomes then the Time Division Multiple Access (TDMA) algorithm.
3.1. Collision Resolution Process—Algorithm 1
We consider the collision resolution process within one of the 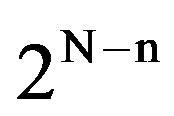 groups in the binary tree of Figure 1. In this section, we state the operations of the algorithm first presented in [15] . Consider the binary sub-tree with 2n leaves which represents the group. The 2n users in the group are perceived as being placed on the latter leaves. The resolution of the tree starts with a root transmission; that is, all users who may have a packet to transmit, first attempt transmission; it said that the root of the sub-tree is then “visited”. The number of slots needed for
groups in the binary tree of Figure 1. In this section, we state the operations of the algorithm first presented in [15] . Consider the binary sub-tree with 2n leaves which represents the group. The 2n users in the group are perceived as being placed on the latter leaves. The resolution of the tree starts with a root transmission; that is, all users who may have a packet to transmit, first attempt transmission; it said that the root of the sub-tree is then “visited”. The number of slots needed for
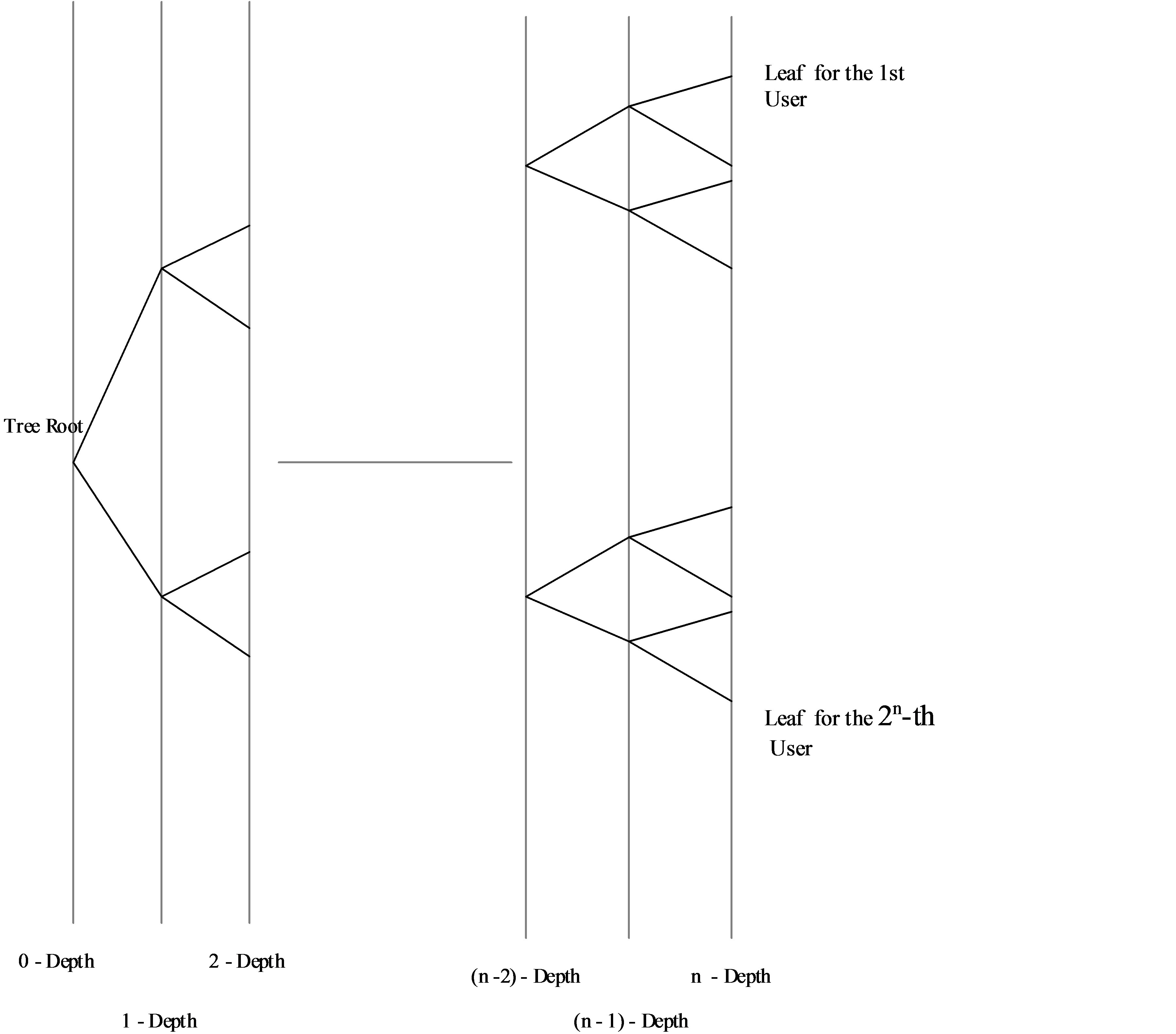
Figure 1. User virtual binary tree placement.
the tree resolution (for the successful transmission of all the packets on its leaves) is called the collision resolution interval (CRI). If the feedback from the root transmission is NC, the CRI lasts one slot. If, instead, the feedback from the root transmission is C, then a collision resolution process starts with the next slot. The process involves sequential binary subdivisions of the tree described below, where we will denote by xt the C or NC outcome of slot t and where slot t occupies the time interval (t − 1, t].
Let the root of the 2n—leaves sub-tree be denoted R. Let the tree nodes at the 1st level of the sub-tree be assigned the codeword IDs 0 and 1. Let the codeword IDs of the nodes at level k + 1 be determined by adding one 0 or 1 bit at the codeword ID of each one of the nodes at level k; 0 for branching off upwards and 1 for branching off downwards. The binary codeword IDs of the sub-tree leaves coincide with the user IDs. Let 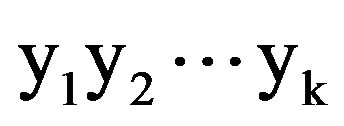 denote the binary codeword ID of some node at level k of the sub-tree. The collision resolution process is then described by the following transitions, where when a node of the sub-tree is “visited”, all users whose IDs branch off this node transmit, while all other users withhold.
denote the binary codeword ID of some node at level k of the sub-tree. The collision resolution process is then described by the following transitions, where when a node of the sub-tree is “visited”, all users whose IDs branch off this node transmit, while all other users withhold.
1) If R is visited at slot t and xt = C, then, the sub-tree node with ID 0 is visited at slot t + 1.
2) If the sub-tree node with ID 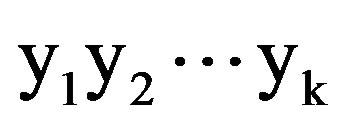 is visited at slot t and xt = C, then, the sub-tree node with ID
is visited at slot t and xt = C, then, the sub-tree node with ID 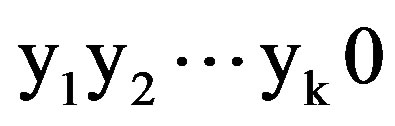 is visited at slot t + 1.
is visited at slot t + 1.
3) If the sub-tree node with ID 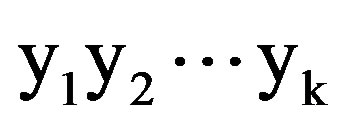 is visited at slot t and xt = NC, then, the codeword ID of sub-tree node visited at slot t + 1 isa)
is visited at slot t and xt = NC, then, the codeword ID of sub-tree node visited at slot t + 1 isa)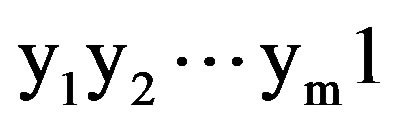 ; if there exists m + 1 ≤ k such that ym + 1 = 0 and yl = 1, for all l ≥ m + 1.
; if there exists m + 1 ≤ k such that ym + 1 = 0 and yl = 1, for all l ≥ m + 1.
b) otherwise, the collision resolution process has ended.
The longest CRI induced by this algorithm is when all users are present, in which case each one of the subtree nodes are visited; the length of the CRI is then 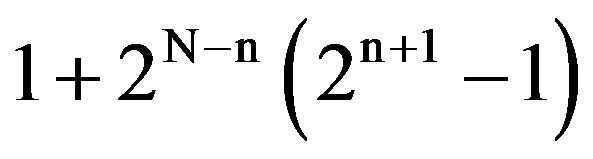 slots and the throughput of the algorithm is
slots and the throughput of the algorithm is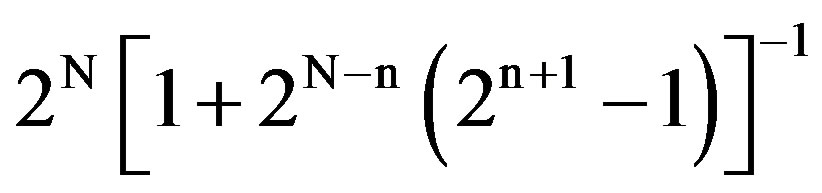 . The algorithm induces CRIs whose endings are not distinguishable. That is, there are no distinct unique C vs. NC feedback patterns which identify the ends of CRIs. As a result, unless synchronized with the algorithmic system from the beginning of its operations, a user has no other indication as to when it may attempt transmissions and participate in CRIs.
. The algorithm induces CRIs whose endings are not distinguishable. That is, there are no distinct unique C vs. NC feedback patterns which identify the ends of CRIs. As a result, unless synchronized with the algorithmic system from the beginning of its operations, a user has no other indication as to when it may attempt transmissions and participate in CRIs.
3.2. Collision Resolution Process—Algorithm 2
The collision resolution process of this algorithm defers from that of Algorithm 1 only in step (c) of the latter. Instead, in the event of NC occurrence during a CRI, Algorithm 2 visits the root of the sub-tree next. The advantage of this algorithm, which was first presented in [14] , in contrast to Algorithm 1, the endings of induced CRIs are distinguishable. Indeed, a CRI which starts with a collision ends with the first occurrence of two successive NC slots. This permits a user to synchronize with the collision resolution process (after some delay) without the need of synchronization from the beginning of the algorithmic operations; we name this property of Algorithm 2, real-time synchronization. On the other hand, the longest CRI induced by Algorithm 2, when all users are present, equals 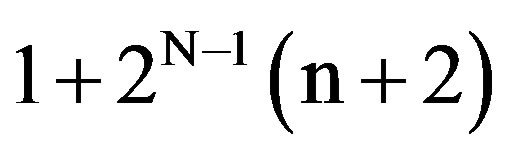 slots, [14] , which is of order n times longer than the longest CRI induced by Algorithm 1, and its throughput is
slots, [14] , which is of order n times longer than the longest CRI induced by Algorithm 1, and its throughput is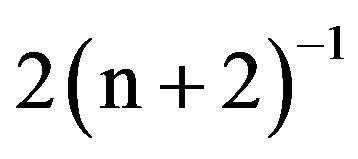 . As compared to Algorithm 1, this disadvantage is eliminated in the limit (increasing number of users), however, via appropriate user sub-grouping, when the throughputs of both algorithms become identical, while the advantage of real-time synchronization remains. We will discuss this further in Sections IV and V, where we will also explain the specifics of real-time synchronization implementation.
. As compared to Algorithm 1, this disadvantage is eliminated in the limit (increasing number of users), however, via appropriate user sub-grouping, when the throughputs of both algorithms become identical, while the advantage of real-time synchronization remains. We will discuss this further in Sections IV and V, where we will also explain the specifics of real-time synchronization implementation.
3.3. Asymptotic Algorithmic Behavior
As it is clear from the above, the implementation of the collision resolution process, for both Algorithms 1 and 2, involves the bit-by-bit search of the binary codeword IDs of the users. As the number of users increases, the lengths of these code words increase as well making the implementation of the deterministic search impractical, and after a point, infeasible. When the number of users thus increases to large numbers, it is more practical to use an equivalent probabilistic search, instead. Indeed, the subdividing of a binary tree becomes equivalent to selecting each one of its leaves with probability 0.5, when the dimensionality of the tree increases to large values. Therefore, the deterministic multi-user transmission algorithms transform to random access algorithms, when the user IDs are known, but their population is large. In Section IV below, we will present the random access evolution of Algorithms 1 and 2 presented in this section.
4. Random Access Transmission Techniques
As we stated in Section III.C, random access algorithms evolve from deterministic algorithms, when the user population increases to large numbers, when it is unreasonable to use user IDs. As a result, random access algorithms do not use user IDs and are appropriate for the unknown user population, as well. In this section, we will present and discuss the random access evolution of the Algorithms 1 and 2 discussed in Section III. These random access evolutions will be named Binary Split Random Access Algorithm and 2-Cell Random Access Algorithm, respectively. In their random access versions and in the presence of the limit Poisson user model (when each packet is a separate user), the initialization part of the algorithms evolves from user grouping to a window of size Δ on the packet arrival axis.
4.1. The Binary Split Random Access Algorithm
As with its deterministic counterpart, this algorithm requires system synchronization by all users from the beginning of the system’s operation; it thus not truly implementable, since such requirement is normally nonfeasible, [13] . Each CRI transmits arrivals within a window of size Δ, selected on the first come-first serve basis; the window size Δ is selected for throughput maximization in the presence of the limit Poisson user model worst case scenario and its value is given below together with the attained then algorithmic throughput.
The algorithmic operations during a CRI may be implemented independently by the packets/users, via the use of a counter whose values may be any one of the positive integers. Let then ct denote the counter value of some packet at slot t, where 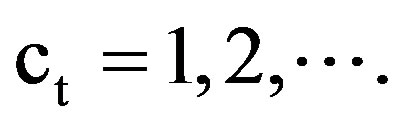 The packet is transmitted in slot t if and only if ct = 1. The algorithmic operations during a CRI for any involved packet are then described by transitions of its counter values, as follows:
The packet is transmitted in slot t if and only if ct = 1. The algorithmic operations during a CRI for any involved packet are then described by transitions of its counter values, as follows:
1) If xt = NC and ct = 1, then the packet is successfully transmitted within slot t.
2) If xt = NC and ct ³ 2, then ct + 1 = ct – 1.
3) If xt = C and ct ³ 2, then ct + 1 = ct + 1.
4) If xt = C and ct = 1, then, ct + 1 = 1; with probability 0.5 or ct + 1 = 2; with probability 0.5.
In the presence of the limit Poisson user model, the throughput of the algorithm; in expected number of packets per slot and the window size that attains it; in slot units are:
λ* = 0.4295 ≈ 0.43; D* = 2.677; Stability region: λ ε (0, 0.43).
4.2. The 2-Cell Random Access Algorithm
As with its deterministic counterpart, CRI endings are distinguishable; thus users may synchronize with the algorithmic operations in real-time and the algorithm is implementable, [13] . As with the Binary Split Random Access Algorithm, the initialization part of the algorithm, in the presence of the limit Poisson user model, involves the selection of a window of size Δ on the packet arrival axis, for throughput maximization, where the arrivals in the window are selected asynchronously on the last come-first serve basis, as will be explained below. To implement the algorithm, each packet arrival is required to sense the channel feedback sequence continuously, from the slot of its arrival, to slot within which it is successfully transmitted.
In the presence of the limit Poisson user population, where each packet is an independent user, a packet that arrives at time instant τ1 located within slot t1, follows the initialization process described below before entering a CRI, where the window of size Δ is utilized.
1) Starting with the slot t1 of its arrival, the packet observes slot feedbacks passively, until the first occurrence of 2 successive NC slots ending with slot t2. At the end of slot t2, the packet is synchronized with the algorithmic collision resolution process, being in the position to recognize all CRI endings after t2 (including those of the trivial one –slot-length CRIs).
2) At the end of slot t2, the packet checks its arrival instant τ1 against the arrival interval (t2 – 1 – Δ, t2 – 1):
a) If τ1 ε (t2 – 1 – Δ, t2 – 1), the packet participates in the CRI that begins with slot t2 + 1 and is successfully transmitted during its process.
b) If, instead, τ1 < t2 – 1 – Δ, the packet updates its arrival instant to τ2 = τ1 + Δ and continues observing slot feedbacks sequentially and passively, until the end slot t3 of the next CRI, when it repeats step 2), for t2 substituted by t3.
3) In general, if tk is the ending slot of the (k − 1)th CRI after the packet’s arrival and the packet has not yet participated in a CRI, the packet’s arrival instant update at tk equals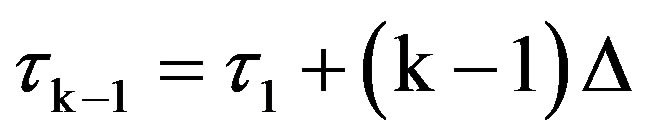 . The packet checks then
. The packet checks then 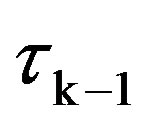 against the arrival interval (
against the arrival interval (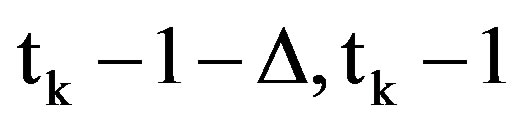 ) and:
) and:
a) If 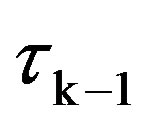 is contained in (
is contained in (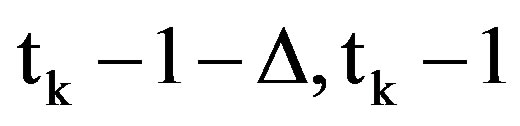 ), the packet participates in the CRI that begins with slot tk + 1 and is successfully transmitted during its process.
), the packet participates in the CRI that begins with slot tk + 1 and is successfully transmitted during its process.
b) If, instead, 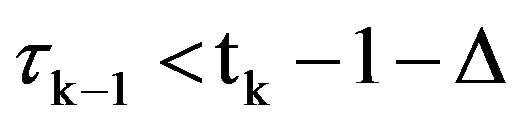 , the packet updates its arrival instant update to
, the packet updates its arrival instant update to 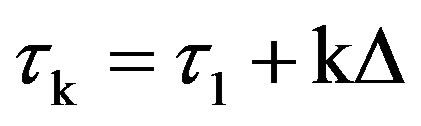 and continues observing slot feedbacks sequentially until the next CRI end.
and continues observing slot feedbacks sequentially until the next CRI end.
The last come-first serve window initialization behavior of the algorithm is exhibited in Figure 2.
The operations during a CRI are carried independently by each involved packet/user via the use of a counter. Let ct denote the counter value of a packet at slot t. This value may be one of the positive integer numbers 1 to K, where the packet is transmitted within slot t iff ct = 1. The transition of the counter values during a CRI are as follows:
1) If xt = NC and ct = 1, then the packet is successfully transmitted within slot t.
2) If xt = NC and ct = 2, then ct + 1 = ct – 1.
3) If xt = C and ct = 2, then ct + 1 = ct.
4) If xt = C and ct = 1, then, ct + 1 = i; i = 1, 2, with probability 0.5.
As concluded from the above collision resolution operations, after a collision within which it is involved, a packet places itself in either one of the transmission vs. withholding states with equal probability, while after a collision within which the packet is not involved, it maintains its existing state.
In the presence of the limit Poisson user population, the throughput of the algorithm; in expected number of
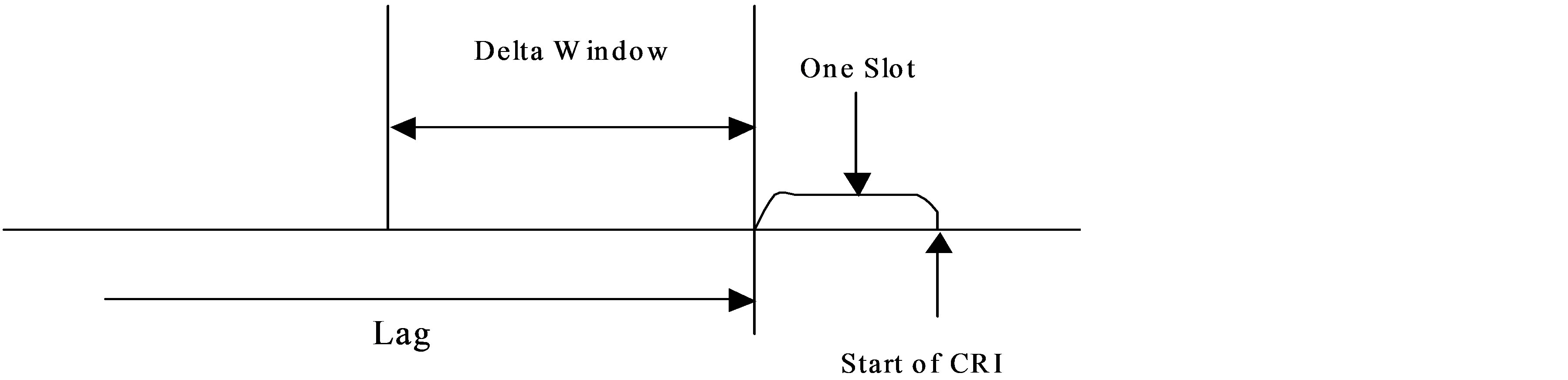
Figure 2. The initialization of the 2-cell algorithm.
packets per slot and the window size that attains it; in slot units are:
λ* = 0.4295 ≈ 0.43; D* = 2.33; Stability region: λ ε (0, 0.43).
4.3. Comparative Discussion
The algorithms presented in this section are the random access evolutions of the deterministic algorithms in Section III. While the throughput of the deterministic Algorithm 2 is considerably lower than that of deterministic Algorithm 1, for the same user grouping, grouping adaptation may resolve this deficiency.
This is clearly exhibited by the random access versions of the two algorithms, where, in the worst case scenario of the limit Poisson user population, they attain the same throughput, for different optimal window sizes, while the induced by the 2-Cell Random Access Algorithm delays are higher than those of the Binary Split Random Access Algorithm, due to the last come-first serve characteristics of the former (see Figure 3). At the same time, the 2-Cell Random Access Algorithm induces real-time implementation, while the Binary Split Random Access Algorithm does not. Thus, weighing favorably real-time implementability against somewhat increased delay performance, the 2-Cell Random Access Algorithm has superior qualities, as compared to the Binary Split Random Access Algorithm. In addition, the 2-Cell Random Access Algorithm is robust in the presence of feedback errors [13] .
5. Hybrid Transmission Techniques
Hybrid transmission techniques multiplex known user populations with unknown user populations for transmission through a common channel. Such techniques incorporate both deterministic and random access algorithmic components, to satisfy the constraints imposed by both population classes.
In this section, we will assume that the known user population consists of 2N packet users generating highpriority data. In particular, we assume that each such user requires a strict upper bound B on the delay experienced by each generated packet, where B is such that 2N + 1 < B. Regarding the packet arrival process generated by the 2N users, it is assumed that, in a period of 2N − 1 (n + 2) slots; for some n in [0, [2−N B – 2]], each of the 2N users generates a single packet with probability p, and generates no packet with probability 1 – p.
Regarding the unknown user population, the limit Poisson user population will be considered, generating an aggregate Poisson packet stream with rate λ, and imposing no strict delay constraints.
A hybrid transmission policy which is stable for both user populations, while it also satisfies the delay upper bound imposed by the high-priority users, may be represented by a combination of the deterministic Algorithm 2; in Section III. B and the 2-Cell Random Access Algorithm; in Section IV. B, [14] . The hybrid transmission policy is described as follows:
For some n in [0, [2−N B – 2]], the 2N high-priority users are divided into 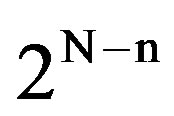 groups. Subsequently, the channel time is subdivided into “frames”, each of length
groups. Subsequently, the channel time is subdivided into “frames”, each of length 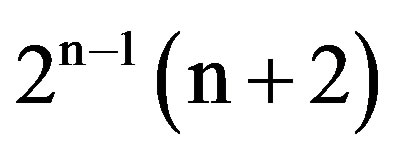 slots, and
slots, and 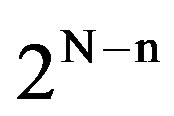 consecutive frames comprise a “superframe” (see Figure 4). The boundaries of the frames and superframes are assumed known to all users. Each of the
consecutive frames comprise a “superframe” (see Figure 4). The boundaries of the frames and superframes are assumed known to all users. Each of the 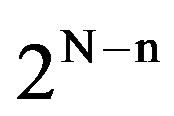 high-priority user groups transmits its packets within the corresponding frame of a superframe, via the deterministic Algorithm 2. In view of the high-priority packet generating process considered above, in conjunction with the properties of the deterministic Algorithm 2, all high priority packets generated within a superframe are successfully transmitted within the superframe following it, simultaneously satisfying the required delay upper bound B.
high-priority user groups transmits its packets within the corresponding frame of a superframe, via the deterministic Algorithm 2. In view of the high-priority packet generating process considered above, in conjunction with the properties of the deterministic Algorithm 2, all high priority packets generated within a superframe are successfully transmitted within the superframe following it, simultaneously satisfying the required delay upper bound B.
Since the probability p of a packet arrival per high-priority user and per frame is less than 1, a portion of each
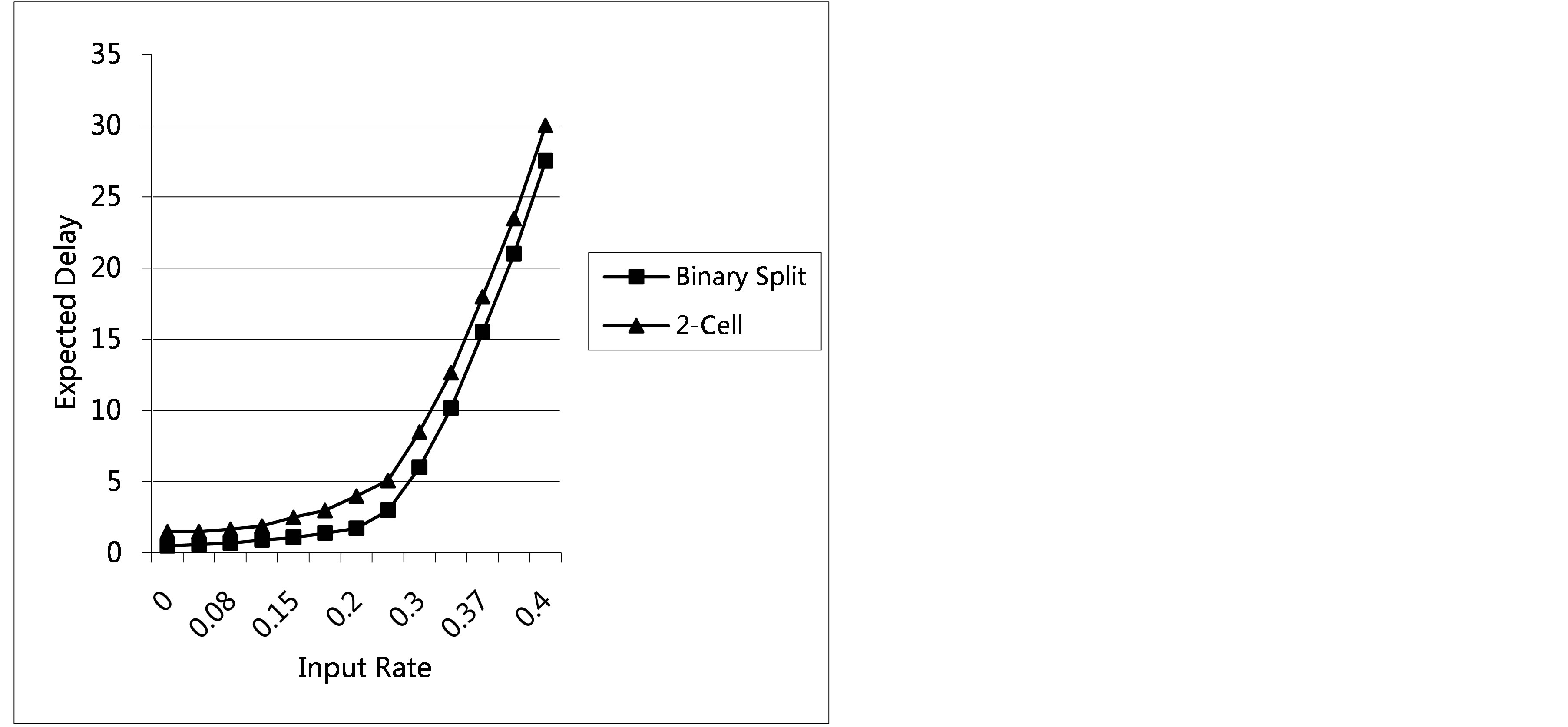
Figure 3. Expected delays in slot units for the 2-cell and binary split random access algorithms.
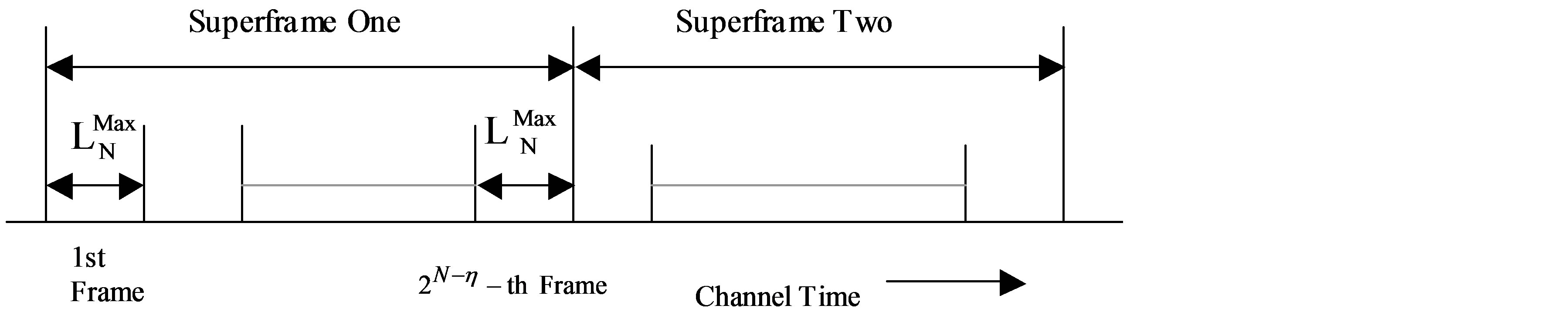
Figure 4. Frames and superframes.
frame is generally not utilized by high-priority transmissions. Such portions are then utilized for transmissions by the unknown limit Poisson user population, (see Figure 5). Thus, the collision resolution process for the unknown limit Poisson user population operates in an interruptive mode; on frame portions that are unused by the high-priority traffic, where the beginnings of such portions are recognizable by the users due to the identifiable unique endings of the CRIs induced by both the deterministic Algorithm 2 and the 2-Cell Random Access Algorithm: two successive NC slots.
From the description of the hybrid algorithm, it is clear that, as the probability p of a packet arrival per highpriority and per frame increases, the frame portion dedicated to transmissions by the unknown user population decreases, where the actual length of this portion is also determined by the frame length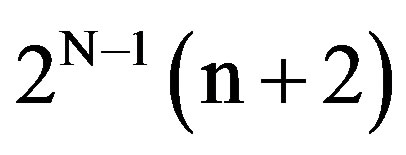 , which is in-turn specified by the value of n. Thus, as p increases, the throughput of the 2-Cell Random Access Algorithm used by the unknown user population decreases, while, as n increases, the same throughput increases. Specific values of this throughput, for varying values of p and n, can be found in [14] , Table II. The hybrid algorithm is real-time implementable, accommodating effectively the high-priority packets, at the expense of increased delays for the packets generated by the unknown user population, as induced by the interruptive transmission mode they experience.
, which is in-turn specified by the value of n. Thus, as p increases, the throughput of the 2-Cell Random Access Algorithm used by the unknown user population decreases, while, as n increases, the same throughput increases. Specific values of this throughput, for varying values of p and n, can be found in [14] , Table II. The hybrid algorithm is real-time implementable, accommodating effectively the high-priority packets, at the expense of increased delays for the packets generated by the unknown user population, as induced by the interruptive transmission mode they experience.
6. Discussion and Conclusions
A major component of the SG is its embedded communications network. The effective design of this network requires systematic modeling of the environment the network operates in, for the subsequent development of communication techniques which respond efficiently to the imposed constraints and performance demands.
In this paper, we focused on the effect of user and traffic environments on the design of the communications network for the SG. In that spirit, we presented distinct models of user populations present in the SG and subsequent, matching to each model, stable multiple access transmission techniques, which also satisfy specific delay
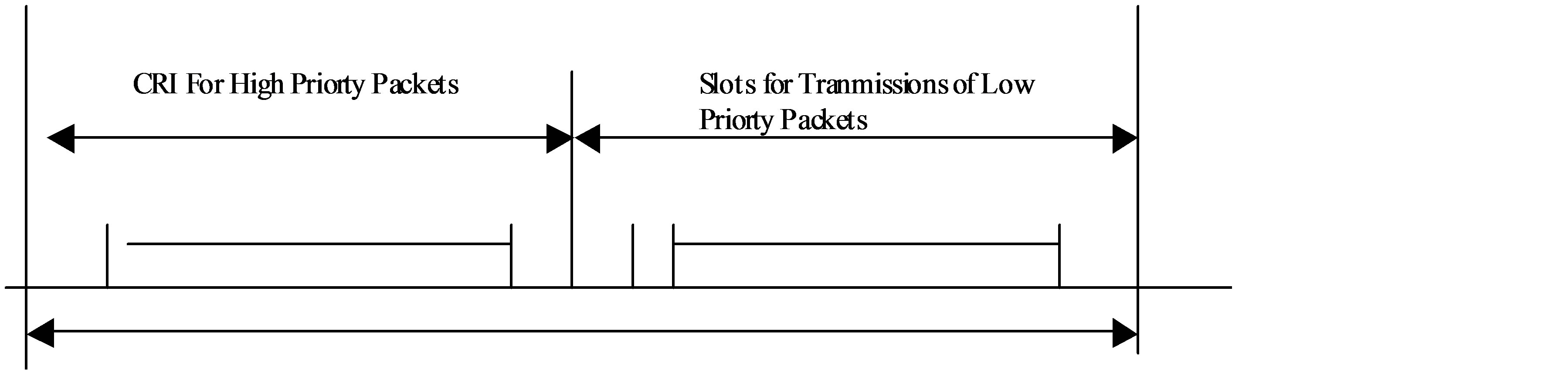
Figure 5. Transmissions per frame.
constraints. We also presented a hybrid technique which allows the sharing of a common channel by both highpriority and regular data, for bandwidth conservation, while it simultaneously satisfies the strict delay constraints demanded by the high-priority data traffic.
References
- Congress of the United States of America (2007) Energy Independence and Security Act of 2007.
- Otani, T. (2010) A Primary Evaluation for Applicability of IEC62056 to a Next-Generation Power Grid. 1st IEEE International Conference on Smart Grid Communications, Tokyo, 4-6 October 2010, 67-72. http://dx.doi.org/10.1109/SMARTGRID.2010.5622019
- Srinivasa Prasanna, G.N., Lakshmi, A., Sumanth, S., Simha, V., Bapat, J. and Koomullil, G. (2009) Data Communication over Smart Grid. Proceedings of IEEE International Symposium on Power Line Communications and Its Applications, ISPLC, April 2009, 273-279.
- Sauter, T. and Lobashov, M. (2011) End-to-End Communication Architecture for Smart Grids. IEEE Transactions on Industrial Electronics, 58, 1218-1228. http://dx.doi.org/10.1109/TIE.2010.2070771
- Yan, Y., Qian, Y., Sharif, H. and Tipper, D. (2012) A Survey on Cyber Security for Smart Grid Communications. IEEE Communications Surveys Tutorials, 99, 1-13.
- Sood, V.K., Fisher, D., Eklund, J.M. and Brown, T. (2009) Developing a Communication Infrastructure for Smart Grid. Proceedings of IEEE Electrical Power Energy Conference (EPEC), Montreal QC Canada, 22-23 October 2009, 1-7.
- Akyol, B., Kirkham, H., Clements, S. and Hadley, M. (2010) A Survey of Wireless Communications for the Electric Power System. US Department of Energy, PNNL-19084.
- Depuru, S.S.S., Wang, L., Devabhaktuni, V. and Gudi, N. (2011) Smart Meters for Power Grid—Challenges, Issues, Advantages and Status. Power Systems Conference and Exposition (PSCE), IEEE/PES, Phoenix, 20-23 March 2011, 1- 7.
- Gungor, V.C., Sahin, D., Kocak, T., Ergut, S., Buccella, C., Cecati, C. and Hancke, G.P. (2011) Smart Grid Technologies: Communication Technologies and Standards. IEEE Transactions on Industrial Informatics, 7, 529-539. http://dx.doi.org/10.1109/TII.2011.2166794
- Fan, Z., Kulkarni, P., Gormus, S., Kalogridis, G., Sooriyabandara, M., Zhu, Z., Lambotharan, S. and Chin, W. Smart Grid Communications: Overview of Research Challenges, Solutions and Standardization Activities. IEEE Communications Surveys & Tutorials, 15, 21-38.
- Hammoudeh, M.A., Mancilla-David, F., Selman, J.D. and Papantoni-Kazakos, P. (2013) Communication Architectures for Smart Grid Distribution Networks. 2013 IEEE 5th Annual Green Technologies Conference, Denver, 4-5 April 2013.
- Paterakis, M., Georgiadis, L. and Papantoni-Kazakos, P. (1987) On the Relation between the Finite and the Infinite Population Models for a Class of RAAs. IEEE Transactions on Communication, COM‑35, 1239‑1240.
- Burrell, A.T. and Papantoni-Kazakos, P. (2012) Random Access Algorithms in Packet Networks—A Review of Three Research Decades. International Journal of Communications Network and System Sciences (IJCNS), 5, 691-707. http://dx.doi.org/10.4236/ijcns.2012.510072
- Papantoni-Kazakos, P. (1992) Multiple Access Algorithms for a System with Mixed Traffic: High and Low Priority. IEEE Transactions on Communication, 40, 541‑555. http://dx.doi.org/10.1109/26.135724
- Capetanakis, J.I. (1979) Tree Algorithms for the Packet Broadcast Channel. IEEE Transactions on Information Theory, IT-25, 505-515. http://dx.doi.org/10.1109/TIT.1979.1056093

