Int'l J. of Communications, Network and System Sciences
Vol.6 No.7(2013), Article ID:34647,5 pages DOI:10.4236/ijcns.2013.67037
Computational Performances of OFDM Using Different FFT Algorithms
Department of Electrical and Electronic Engineering, East West University, Dhaka, Bangladesh
Email: azim@mail.ewubd.com
Copyright © 2013 Anwarul Azim. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 10, 2013; revised June 10, 2013; accepted July 10, 2013
Keywords: Orthogonal Frequency Division Multiplexing (OFDM); Discreate Fourier Transform (DFT); Fast Fourier Transform (FFT); Very Fast Fourier Transform (VFFT)
ABSTRACT
In this paper, an intuitive comparison of the computational performance of orthogonal frequency division multiplexing (OFDM) system has been made in terms of complex calculations required using different Fourier transform techniques. The different transform techniques are introduced such as discrete Fourier transform (DFT) and various types of fast Fourier transform (FFT) as 2-radix FFT, 4-radix FFT etc. and the very recent very fast Fourier transform (VFFT). With intuitive mathematical analysis, it has been shown that with the reduced complexity that VFFT can offer, OFDM performance can be greatly improved in terms of calculations needed.
1. Introduction
Orthogonal Frequency Divisional Multiplexing (OFD-M) is a modulation scheme that allows digital data to be efficiently and reliably transmitted over a radio channel, even in multi-path environments [1]. OFDM transmits data by using a large number of narrow bandwidth carriers. These carriers are regularly spaced in frequency, forming a block of spectrum. The frequency spacing and time synchronization of the carriers is chosen in such a way that the carriers are orthogonal, meaning that they do not cause interference to each other. In OFDM system, Discrete Fourier Transforms (DFT)/Fast Fourier Transforms (FFT) are used instead of modulators. The computational complexity of implementing DFT/FFT/Very Fast Fourier Transform (VFFT) has been calculated in an OFDM system and compared their performance. At the current state of wireless communication techniques facing ever increasing demand of high data rates, single carrier systems are offering limited solutions due to frequency selectivity of wideband channel resulting in severe complexities in equalizer design at the receiver end [2]. OFDM, as a multicarrier system, has become an effective modulation technique for next generation wireless communication methods. Using FFT algorithms provides speed enhancements for data processing for OFDM systems. This technique is being used for Digital Audio Broadcasting (DAB), Digital Video Broadcasting (DVB), Wireless Local Area Network (WLAN), Wireless Metropolitan Area Network (WMAN), Multi Band-OFDM Ultra Wide Band (MB-OFDM-UWB) etc. Also it is used in wired communication systems such as Asymmetric Digital Subscriber Line (ADSL) and Power Line Communication (PLC) [3]. In the next section, the basic OFDM system model using FFT has been described.
2. OFDM System Model
OFDM is a kind of frequency division multiplexing (FDM) technique in which we divide a data stream into a number of bit streams which are transmitted through sub-channels [4]. The characteristics of these sub-channels are that they are orthogonal to each other. As the data that are transmitted through a sub-channel at a particular time are only a portion of the data transmitted through a channel so bit rate in a sub-channel can be kept much low. After splitting the data in N parallel data streams each stream is then mapped to a tone at a unique frequency and combined together using the Inverse Fast Fourier Transform (IFFT) to yield the time domain waveform to be transmitted [5]. After IFFT is done, the time domain signals are then converted to serial data and cyclic extension is added to the signal. Then the signal is transmitted. At the receiving side we do the reverse process to get original data from the received one [5,6].
In case of deep fade, several symbols in single carrier is damaged seriously, but in parallel transmission each of N symbol is slightly affected. So even though the channel is frequency selective, the sub-channel is flat or slightly frequency selective. This is why OFDM provide good protection against fading [7].
In an OFDM system there are N number of sub-channels. If N is high then it will be very complex to design a system with N modulators and demodulators. Fortunately, it can be implemented alternatively using DFT/FFT to reduce the high complexity. A detailed system model for OFDM system is shown in Figure 1 [6,7].
3. Fourier Transform Algorithms
3.1. Discrete Fourier Transform (DFT) Algorithm
For a sequence of data x(n) of length N, the DFT may be expressed as [6]
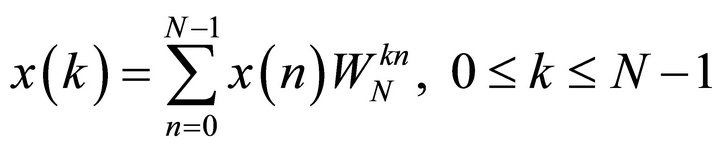 (1)
(1)
For each value of k direct computation of x(k) involves N complex multiplications and N − 1 complex additions. So, to compute N values of the DFT, 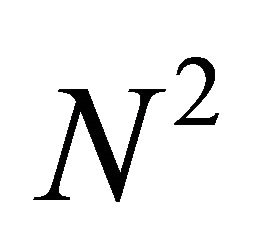 complex multiplications and N2 − N complex additions. Direct computation of DFT is inefficient because of inability to use symmetrical and periodical properties of phase factor WN for computation. These properties are symmetry property,
complex multiplications and N2 − N complex additions. Direct computation of DFT is inefficient because of inability to use symmetrical and periodical properties of phase factor WN for computation. These properties are symmetry property,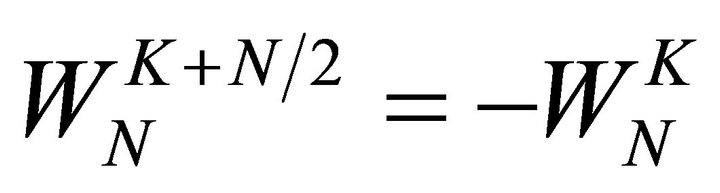 ; periodicity property:
; periodicity property: 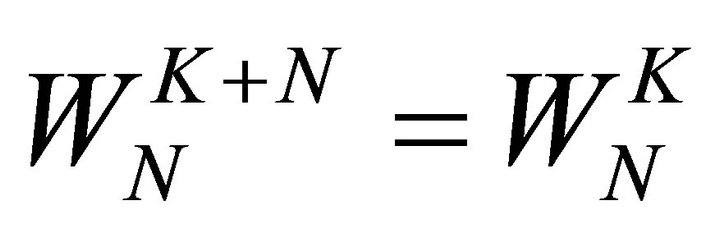 [6].
[6].
3.2. Radix-2 FFT Algorithm
For speed demanding applications which requires implementation of FFT algorithm, FFT algorithms are decimated in terms of time or frequency. If we consider N points of data points where it can be factored as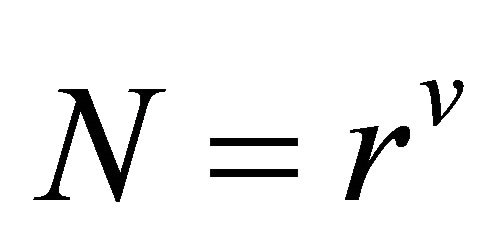 . In such case, DFTs are of r size and the number r is called radix of the FFT algorithm.
. In such case, DFTs are of r size and the number r is called radix of the FFT algorithm.
If N-point data sequence is decimated by a factor of 2, it is called radix-2 algorithm. Now from expression of N-point DFT, we can get
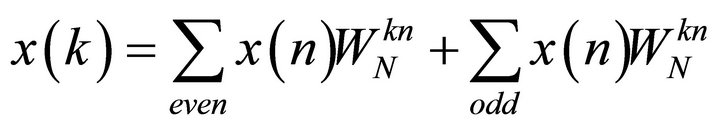 (2)
(2)
 (3)
(3)
But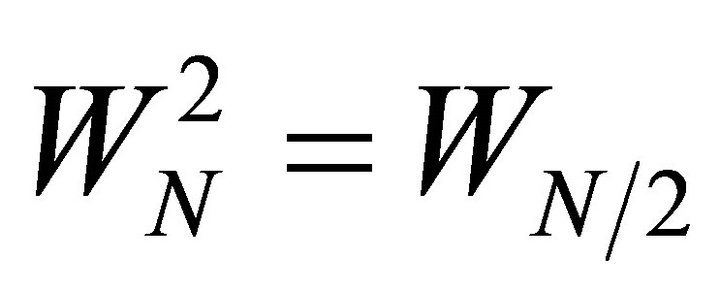 . So the expression can be written as,
. So the expression can be written as,
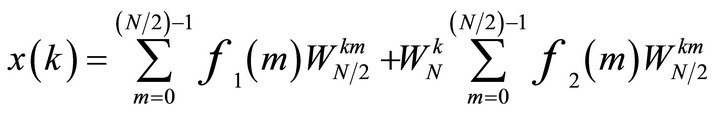 (4)
(4)
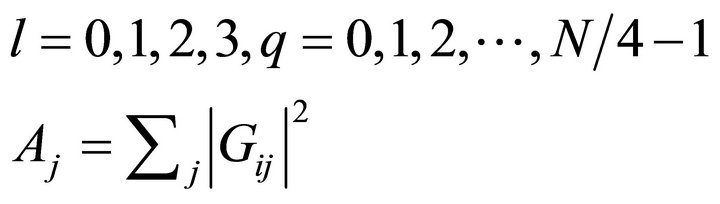 (5)
(5)
where F1(k) and F2(k) are the 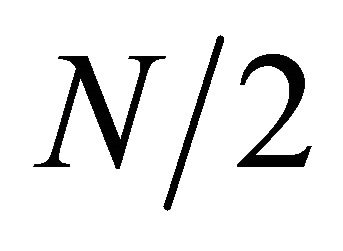 -point DFTs of the sequences f1(m) and f2(m) respectively. Since F1(k) and F2(k) are periodic, with period
-point DFTs of the sequences f1(m) and f2(m) respectively. Since F1(k) and F2(k) are periodic, with period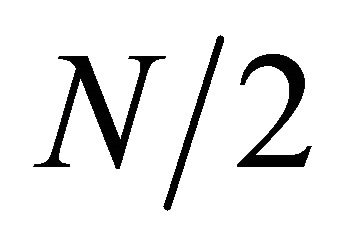 , we can evaluate:
, we can evaluate:
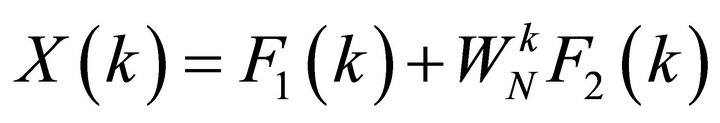 (6)
(6)
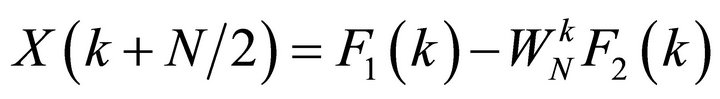 (7)
(7)
For Equations (5) and (6) 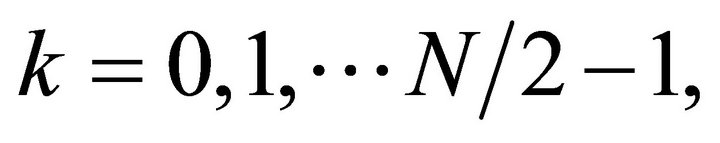 So there is a reduction of number of multiplications from
So there is a reduction of number of multiplications from 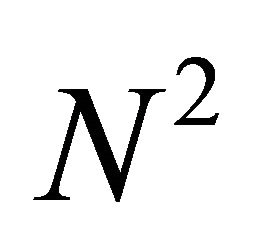 to
to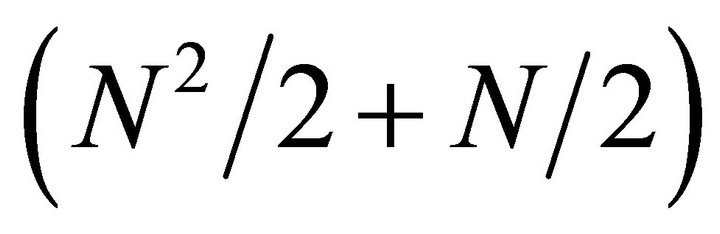 , which is about a factor of 2, showing the
, which is about a factor of 2, showing the
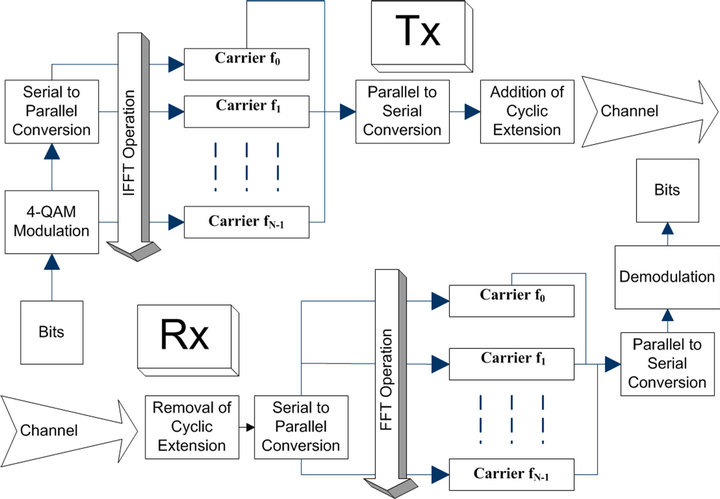
Figure 1. OFDM system model.
significance of radix-2 algorithm for efficient computation. So this algorithm can compute N-point FFT in 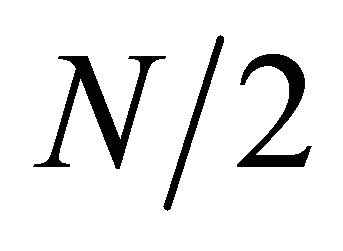 cycles.
cycles.
3.3. Radix-4 FFT Algorithm
In case of N-data points expressed as power of 4v, we can employ radix-4 algorithm instead of radix-2 algorithm for more efficient estimation. If we consider a column-wise mapping for x(n) as n = Ml + m and row-wise mapping as k = Mp + q and N be factored as N= LM, then we can write [6],
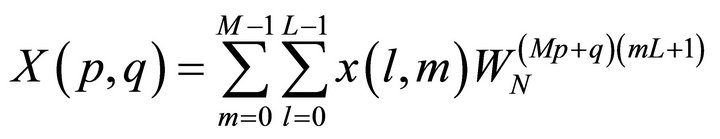 (8)
(8)
After simplification, we get
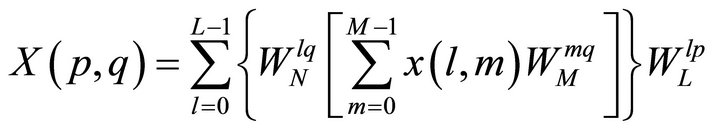 (9)
(9)
Let us consider L = 4, M = N/4, so it results in,
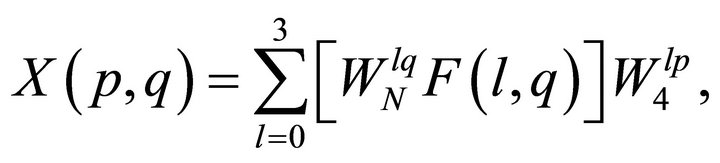 (10)
(10)
where, 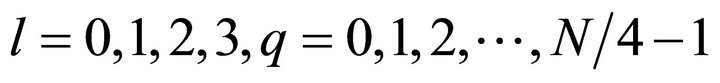 and p = 0,1,2,3 also,
and p = 0,1,2,3 also,
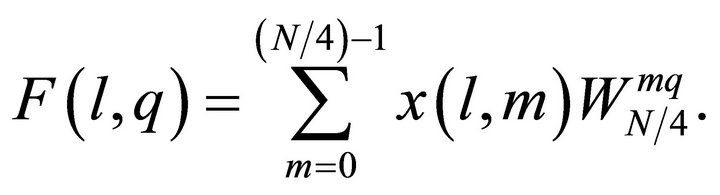 (11)
(11)
So, the four 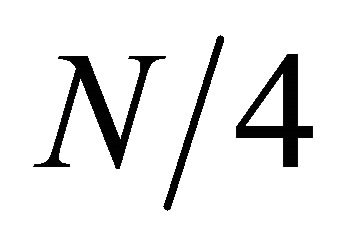 points DFTs obtained from the above expression, which are combined in previous expression to evaluate N-point DFT. So this algorithm results in
points DFTs obtained from the above expression, which are combined in previous expression to evaluate N-point DFT. So this algorithm results in 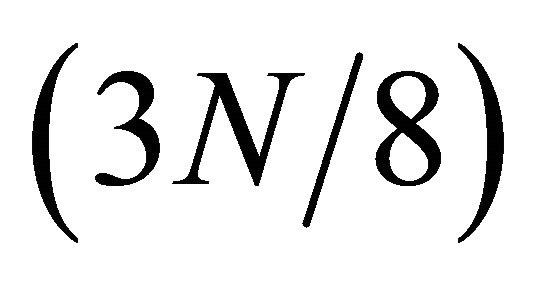 log2N complex multiplications and
log2N complex multiplications and 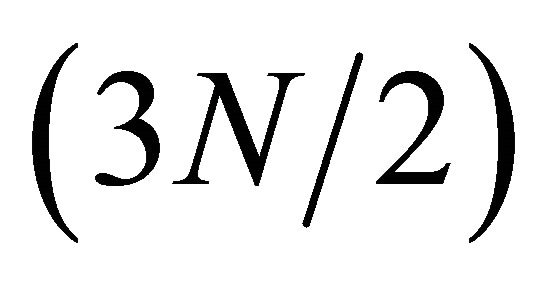 log2N complex additions. So the number of multiplications is reduced by 25%, but the number of addition is increased by 50%.
log2N complex additions. So the number of multiplications is reduced by 25%, but the number of addition is increased by 50%.
3.4. Very Fast Fourier Transforms (VFFT)
The VFFT is a new approach in the field of computing DFT and attributed to mainly Simon Shepherd [8]. It can be implemented either by various level of approximation or replacing the FFT exactly with floating point accuracy. G-Matrix is a suitable tool in this regard with different quantization level concept.
Fourier matrix FN is normalized by 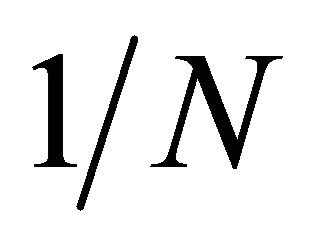 in the G-matrix. Important properties of G-matrix are outlined as follows [8,9]:
in the G-matrix. Important properties of G-matrix are outlined as follows [8,9]:
*Non-unitary matrix
 (12)
(12)
 (13)
(13)
where  defines conjugate transpose of
defines conjugate transpose of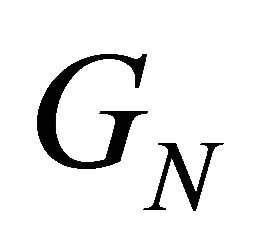 .
.
*Non-singular matrix
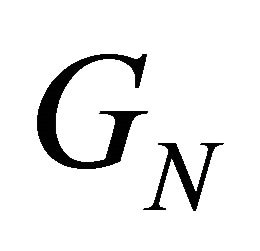 matrix is non-singular, i.e., its determinant is non-zero.
matrix is non-singular, i.e., its determinant is non-zero.
*Non-uniform row-gain matrix The row gain 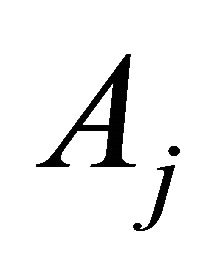 of the
of the 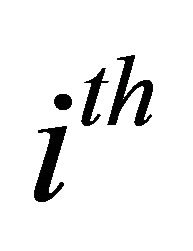 row of
row of 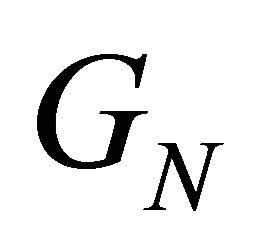 is defined as
is defined as
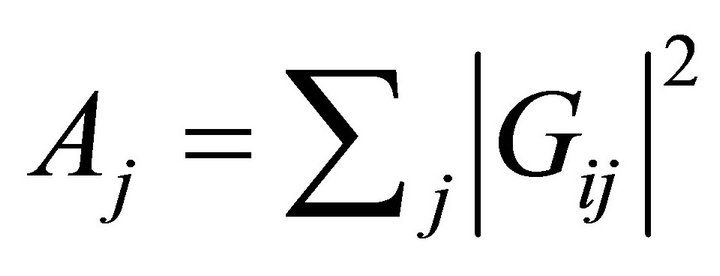 (14)
(14)
Row-gain is unity for the Fourier matrix, whereas 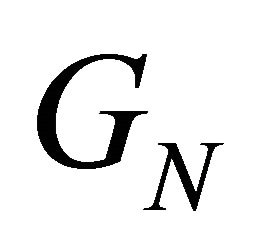 is not necessarily unity.
is not necessarily unity.
This causes non-uniform power spectral density in the transmitted signal and non-uniform noise power in the received demodulated signal. This is the main disadvantage in this G-matrix design. To recover this n-level quantization is applied, where n = 2x; x is integer.
4. Computational Performance Analyses
In order to compare the computational complexities among the different Fourier transforms on OFDM, the calculations based on the OFDM block sizes have been performed which are given in Table 1. In case of multiplication computation for VFFT, the speed improvement factor is as high as 204.8 for large block size 1024. That indicates the multiplication complexity is decreased by 99.5% and 20% from DFT to FFT to VFFT. This is due to the computational savings done by VFFT with complexity reduced to only of the order of N. This rate of complexity reduction in terms multiplication would be a huge factor for OFDM systems to meet the demand of multi-user high data traffic environment. It can also be seen that, the advantage of implementing VFFT only becomes significant as the size of OFDM block (N) is increased.
In Table 2, the comparison of the different FFT algorithms evolved has been shown. We can see that higher radix FFT algorithms reduces the number of both multiplications and additions and as such can give less complexity for OFDM calculations for larger FFT blocks [10,11]. For example, for OFDM block size of 64, multiplication complexity reduces by almost 23% and addition complexity reduces by almost 6%. This less complexity leads to more robust and effective multicarrier system design for OFDM. It also assures optimum performance in terms of high speed data processing for communication systems using OFDM technique.
Figure 2 summarizes the results shown in Tables 1 and 2 for DFT, FFT & VFFT algorithms. VFFT algorithm surely can save a lot of computational power but it has been often effected by a slight degradation of 1dB bit error rate (BER) performance [8,12]. But still it will provide the robust & reliable performance needed in terms of computation for OFDM systems with ever increasing demand multi user support using high data rate applications. Overall, FFT algorithms provide the different
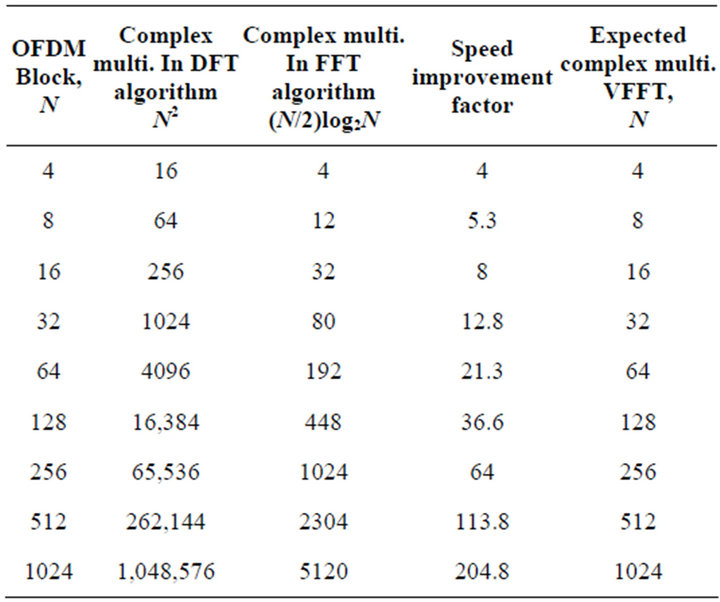
Table 1. Comparison of different fourier transforms.
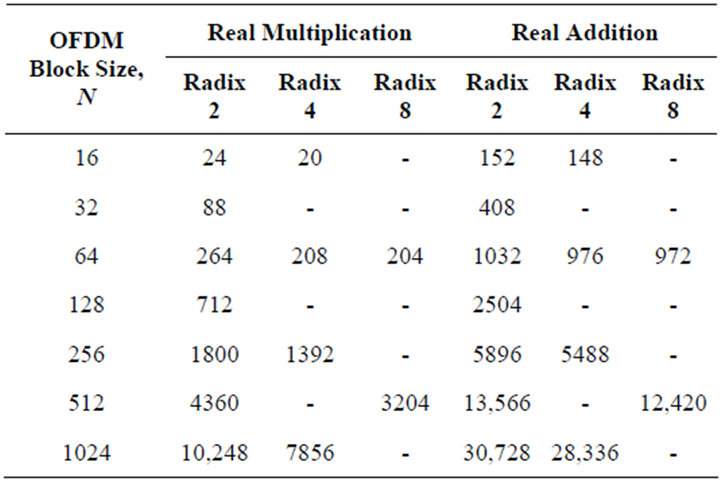
Table 2. Comparison of different FFT algorithms.

Figure 2. Comparison of different fourier transforms (multiplications only).
techniques to deliver wireless communication system designs with required Quality of Service (QoS) and network specifications.
5. Conclusion
The performance of an OFDM system depends on DFT/FFT as in an OFDM system DFT/FFT works as a modulator. If the complexity of DFT/FFT decreases, then the speed of OFDM system increases. VFFT will certainly increase the speed of OFDM system with the drawbacks of non-uniformity of Power Spectral Density (PSD) and non uniformity of Signal to Noise Ratio (SNR) among the sub-carriers. Even though VFFT’s implementation is in primary stages, but it is emerging as the compact solution for OFDM systems used in next generation communication networks.
6. Acknowledgements
Author would like to thank Mr. Nafiz Imtiaz and Dr. Rishad Ahmed Shafik for all their helpful advice and support.
REFERENCES
- B. E. E. P. Lawrey, “Adaptive Techniques for Multi-User OFDM,” Ph.D. Thesis, James Cook Univeristy, Townsville, 2001, pp. 33-34.
- M. N. Suma and B. Kanmani, “Developments in Orthogonal Frequency Division Multiplexing (OFDM) System—A Survey,” 2011 Second Asian Himalayas International Conference, Kathmandu, 4-6 November 2011, pp. 1-4. doi:10.1109/AHICI.2011.6113955
- A. Cortes, I. Velez, M. Turrillas and F. Sevilano, “Fast Fourier Transform Processors: Implementing FFT and IFFT Cores for OFDM Communication Systems,” 2013.
- S. Chen, “Fast Fourier Transform,” Lecture Note, Radio Communications Networks and Systems, 2005.
- “OFDM for Mobile Data Communications,” The International Engineering Consortium WEB ProForum Tutorial, 2006. http://www.iec.org
- A. Goldsmith, “Wireless Communications,” Cambridge University Press, Cambridge, 2005. doi:10.1017/CBO9780511841224
- J. G. Proakis and D. G. Manolakis, “Digital Signal Processing: Principles, Algorithms and Applications,” 3rd Edition, 2002, pp. 448-475.
- C. Langton, “Orthogonal Frequency Divisional Multiplex (OFDM) Tutorial,” 2006. http://www.complextoreal.com
- N. Wirastuti, J. M. Noras and S. M. R. Jones, “Evaluation of the Very Fast Fourier Transform Applied to OFDM,” 2nd IEE-EURASIP DSPEnabled Radio Conference, Southampton, 19-20 September 2005.
- M. Zalewski and S. Schuupp, “Polymorphic Algorithms, FFT-Implementation That Share,” Technical Report, RPI, New York, 2002.
- R. A. Shafik, “Personal Multimedia CommunicationSimulations and Analyses,” Technical Report, Univeristy of Southampton, Southampton.
- H. Harada and R. Prasad, “Simulation and Software Radio for Mobile Communication,” ArTech House, New York, 2002, pp. 165-169.

