Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 3 (2012) , Article ID: 17997 , 11 pages DOI:10.4236/ijcns.2012.53020
Cryptanalysis of a Substitution-Permutation Network Using Gene Assembly in Ciliates
Electrical Engineering Department, Iran University of Science and Technology, Tehran, Iran
Email: ar_karimi@elec.iust.ac.ir, *bhshsh@iust.ac.ir
Received November 26, 2011; revised January 12, 2012; accepted January 27, 2012
Keywords: Nature-Inspired Computation; Accepting Intramolecular Recombination (AIR) Systems; Cryptanalysis; Gene Assembly; Block Ciphers
ABSTRACT
In this paper we provide a novel approach for breaking a significant class of block ciphers, the so-called SPN ciphers, using the process of gene assembly in ciliates. Our proposed scheme utilizes, for the first time, the Turing-powerful potential of gene assembly procedure of ciliated protozoa into the real world computations and has a fewer number of steps than the other proposed schemes to break a cipher. We elaborate notions of formal language theory based on AIR systems, which can be thought of as a modified version of intramolecular scheme to model the ciliate bio-operations, for construction of building blocks necessary for breaking the cipher, and based on these nature-inspired constructions which are as powerful as Turing machines, we propose a theoretical approach for breaking SPN ciphers. Then, we simulate our proposed plan for breaking these ciphers on a sample block cipher based on this structure. Our results show that the proposed scheme has 51.5 percent improvement over the best previously proposed nature-inspired scheme for breaking a cipher.
1. Introduction
L. Adleman, during a laboratory experiment, for the first time discovered the potential of DNA molecules to solve computationally hard problems [1]. His revolutionary paper started the interdisciplinary area of DNA computing. Since then, a bulk of research has tried to concentrate on the theoretical ability of DNA strands to solve hard problems. Specifically, language theory has helped researchers find mathematical constructions to build computing machines based on ability of biomolecules represented in form of words. Natural computing which utilizes the potential of biomolecules in their living environments (i.e. cells) is of special interest. In this respect, Kari et al. in [2,3] considered the gene assembly process in ciliates and demonstrated that it has computational capability just like Turing machines. Their findings aroused a hot line of research in cellular computing.
Ciliates are single-celled eukaryotes that have special features which make them appealing and distinctive. They possess cilia which are used for their motion and also for making a current of water to sweep bacteria and other nutrients into their oral cavities. In addition, they have two different sorts of nuclei: A diploid micronucleus and a polyploid macronucleus. The former is germline nucleus which is activated only during the sexual process of conjugation and remains dormant in the vegetative cycle. And the latter is the somatic nucleus which is the housekeeping nucleus responsible for production of RNA transcripts which is a must for cell development during its life cycle. A species of ciliated protozoa Oxytricha trifallax is shown in Figure 1.
Ciliates do sorting, inversion and excision of their DNA sequences. We adopt the strategy of encoding all solution candidates into a micronuclear gene, then assembling the gene using intramolecular model [4] and ultimately filtering the results and checking through the cipher to find the right key.
In [5], Adleman et al. proposed a scheme to break the Data Encryption Standard using DNA molecules, by molecular biology tools.
In this paper we want to replace formal biological operations by ciliate bio-operations for cryptanalysis of SPN ciphers. For this reason, we use language-theoretic notions to describe the process of cryptanalysis and by utilizing an encoding scheme of the words of our constructed notion to the MIC genes of a hypothetical ciliated protozoa from the Stichotrichous family as shown in Figure 2, we design AIR systems which simulate different blocks necessary to do the cryptanalysis of a large class of block ciphers, called substitution-permutation
Figure 1. Ciliated protozoa Oxytrichia trifallax.
Figure 2. Ciliated protozoa Stichotricha.
networks and then using these Turing machine constructions, we simulate our theoretical attack on this structure defined by specific and predefined blocks.
The rest of this paper is organized as follows. In Section 2, the substitution-permutation networks are introduced which constitute a large class of block ciphers, in Section 3.1, the concept of splicing schemes that is necessary to understand AIR systems which is a variant of intramolecular operations for modeling ciliate bio-operations is briefly introduced. In Section 3.2, we define the accepting intramolecular recombination systems (or AIR systems) on which our proposed scheme to break the cipher is based. In Section 4, we propose and build the necessary blocks which we need for cryptanalysis of the cipher. In Section 5, based on our previously designed AIR systems, we devise a theoretical approach to attack the cipher. In Section 6, we evaluate the performance of our proposed scheme and derive the total bio-steps necessary to mount the attack. In Section 7, our simulations are discussed and the results are reported. Finally, in Section 8, we summarize our paper and conclusions are drawn, and the plans for the future research based on this work are presented.
2. Substitution-Permutation Networks
A variety of modern block ciphers are built using an iterative structure of Substitution-Permutation Networks or SPN for short. AES (Rijndael), Shark, Khazad and Anubis are good examples for SPN ciphers [6]. The selected example SPN is as shown in Figure 3 and we will focus our discussion on this network. As demonstrated in Figure 3, the block size of our cipher is 16-bits and each block of the plaintext is processed by repeating basic operations of a round which are substitution, permutation and key mixing. Indeed, our considered scheme is similar to what is found in many modern block ciphers including Rijndael from basic operations viewpoint and provides us with an insight into cryptanalysis of the real-world block ciphers using natural computing methods.
3. Preliminary Definitions
Our proposed scheme to break the cipher is based on Accepting intramolecular recombination systems (AIR systems) which is a variant of intramolecular models of gene assembly in ciliated protozoa. In this section we bring some basic notions and notations that are necessary to conceive the attack procedure.
3.1. Splicing Schemes
A splicing scheme [7] is defined as a pair  in which
in which  is an alphabet and ~ is a binary relation over
is an alphabet and ~ is a binary relation over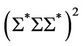 . Assuming that this relation exists between two triples of strings as follows
. Assuming that this relation exists between two triples of strings as follows  we say that given the abovementioned binary relation, strings
we say that given the abovementioned binary relation, strings 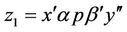 and
and  can be obtained by recombination from
can be obtained by recombination from 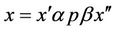 and
and 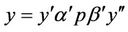 .
.
3.2. AIR Systems
An accepting intramolecular recombination system is defined as a quadruple 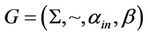 in which
in which  is the splicing scheme and
is the splicing scheme and 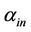 and
and  are input and the target words, respectively. Considering a splicing scheme,
are input and the target words, respectively. Considering a splicing scheme,  , we define the contextual intramolecular operations of translocation, trl, and deletion, del, which are generalizations of dlad and ld intramolecular operations, respectively, as follows [8].
, we define the contextual intramolecular operations of translocation, trl, and deletion, del, which are generalizations of dlad and ld intramolecular operations, respectively, as follows [8].
Assuming 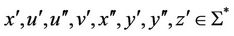 and
and ,
, 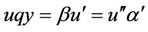 ,
, 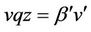 ,
,  ,
,  ,
,  The trl operation with respect to R is defined as
The trl operation with respect to R is defined as
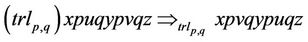 (1)
(1)
Therefore, in the  operation the strings of u and v which are flanked by pointers p and q are swapped. The del operation with respect to R is also defined as:
operation the strings of u and v which are flanked by pointers p and q are swapped. The del operation with respect to R is also defined as:
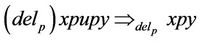 (2)
(2)
where 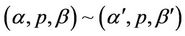 and for
and for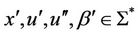 ,
, 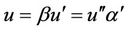
 ,
,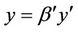 . Hence, intuitively,
. Hence, intuitively,
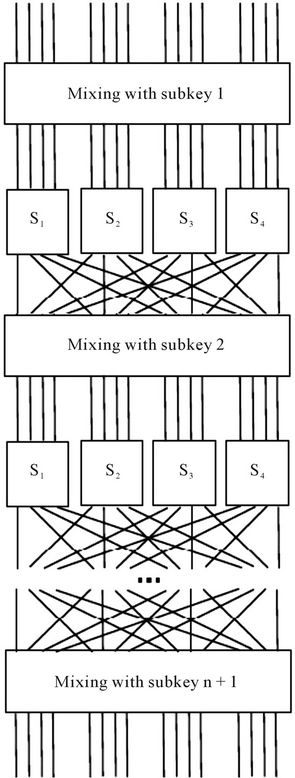
Figure 3. The basic substitution-permutation network.
if the contexts of occurrences p are in the relation ~, the  operation removes the string u that is flanked by two occurrences of p. We can now define the set
operation removes the string u that is flanked by two occurrences of p. We can now define the set  of all contextual intramolecular operations under guidance of ~ as:
of all contextual intramolecular operations under guidance of ~ as:
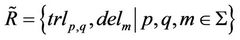 (3)
(3)
Accordingly, we can define the language that is accepted by the AIR system, G, as all the words  for which by consecutive application of any number of
for which by consecutive application of any number of 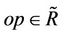 operations from
operations from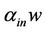 , we can get to the target word
, we can get to the target word .
.
4. Constructing Necessary Building Blocks for Attacking the Cipher
Our proposed scheme to break the SPN family of block ciphers considers the modified approach of intramolecular recombination for modeling gene assembly process in ciliates, and then applies this approach in constructing necessary building blocks for breaking the cipher. Our attack approach is brute force in which we assume that we possess a (plaintext, ciphertext) pair and by exhausttive search over all possible keys, we aim to find the correct key of the cipher. Therefore, in the first step, we should produce all genes of a hypothetical ciliate each of which codes for an individual key of the cipher and then using gene assembly process that naturally happens in ciliated protozoa, we construct Turing machines that imitate main operations that we need in the procedure of cryptanalysis such as the substitution, permutation and logical XOR, and ultimately, we can find the key that when mixed with the plaintext, gives the ciphertext if in each step of the computation the micronuclear (MIC) genes are assembled to the expected macronuclear (MAC) genes. In the next section we introduce the main operations needed for cryptanalysis and then, build Turing machines that imitate these operations.
4.1. Generation of All Possible Keys
In order for generation of all genes that code for all possible combinations of the key, we utilize the graph of Figure 4 in which all possible paths that start from 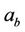 and terminate at
and terminate at  code for a different n-bit key. We use intramolecular model of gene assembly in ciliates. Therefore, beginning with a single MIC gene pattern for which there exist more than two occurrences of a pointer, we can assemble different MAC gene patterns that code for different keys of the cipher. Now, assuming that graph of Figure 4 is demonstrated with
code for a different n-bit key. We use intramolecular model of gene assembly in ciliates. Therefore, beginning with a single MIC gene pattern for which there exist more than two occurrences of a pointer, we can assemble different MAC gene patterns that code for different keys of the cipher. Now, assuming that graph of Figure 4 is demonstrated with  for which V and E denote sets of vertices and edges, respectively, we define an encoding of G in the MIC gene pattern in terms of MDS descriptors as follows: we associate a pointer p to each vertex of G and to each directed edge
for which V and E denote sets of vertices and edges, respectively, we define an encoding of G in the MIC gene pattern in terms of MDS descriptors as follows: we associate a pointer p to each vertex of G and to each directed edge 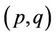 we associate MDS of
we associate MDS of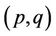 . Therefore, a path
. Therefore, a path 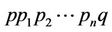 of G can be encoded by an intermediate MDS
of G can be encoded by an intermediate MDS  in which p and q are the incoming and outgoing pointers, respectively, and
in which p and q are the incoming and outgoing pointers, respectively, and ,
, 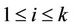 are those pointers for which MIC MDSs that correspond with edges
are those pointers for which MIC MDSs that correspond with edges 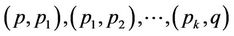 belonging to set of edges of G, have been spliced. Note that MIC MDSs are spliced on their common pointers. For our graph of representation of all possible keys (graph of Figure 4) we have
belonging to set of edges of G, have been spliced. Note that MIC MDSs are spliced on their common pointers. For our graph of representation of all possible keys (graph of Figure 4) we have
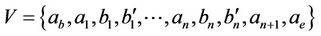
and

hence, for instance, we associate an MDS
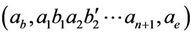 to a path
to a path  and with different strategies to the same MIC gene pattern, we can obtain different MAC genes which represent all
and with different strategies to the same MIC gene pattern, we can obtain different MAC genes which represent all

Figure 4. The graph for generation of all possible keys.
possible keys. According to the universality result of [9] for intramolecular operations, each path of G can be assembled using intramolecular ciliate operations ld, hi and dlad. Since we are looking for all those paths that start from 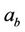 and end at
and end at , our desired assembled MAC gene would be of the form,
, our desired assembled MAC gene would be of the form, 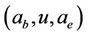 , in which u is any path that contains all
, in which u is any path that contains all ’s
’s  and all different
and all different ’s or
’s or ’s
’s . Therefore, if each edge of G is encoded as a MIC MDS then, we show that one can produce all possible keys of the cipher using ld operation only from a single string of MDS descriptors that demonstrate all edges of G as shown in Theorem 1. For this reason, we say that a descriptor
. Therefore, if each edge of G is encoded as a MIC MDS then, we show that one can produce all possible keys of the cipher using ld operation only from a single string of MDS descriptors that demonstrate all edges of G as shown in Theorem 1. For this reason, we say that a descriptor 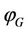 is associated to G if it is of the form
is associated to G if it is of the form 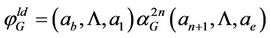 where
where
 is defined as a descriptor that encodes all edges of G.
is defined as a descriptor that encodes all edges of G.
Theorem 1. Any successfully assembled  for which all
for which all 
 ’s and a total number of n of either
’s and a total number of n of either ’s or
’s or ’s appear and
’s appear and 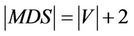 , produces any possible path that is representative for every one of possible keys of the cipher.
, produces any possible path that is representative for every one of possible keys of the cipher.
Implementation of logical XOR using ciliate bio operations is explained in Section 4.2.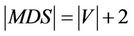 , produces any possible path that is representative for every one of possible keys of the cipher.
, produces any possible path that is representative for every one of possible keys of the cipher.
Implementation of logical XOR using ciliate bio operations is explained in Section 4.2.
4.2. An Intramolecular Model for Computing Logical XOR
We define logical XOR as satisfiability of a Boolean relationship that is depicted in Equation (4).
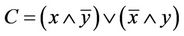 (4)
(4)
And here we provide a ciliate solution for Equation (4) using intramolecular model which computes the result of XOR in polynomial time. For this reason, we construct an AIR system  [9] that evaluates the output of Equation (4). The circuit that implements XOR is depicted in Figure 5.
[9] that evaluates the output of Equation (4). The circuit that implements XOR is depicted in Figure 5.
As can be seen in Figure 5, the circuit is composed of three layers and we show its output with the following notation demonstrated in Equation (5).
 (5)
(5)
In the above notation, each gate is shown with  in which i denotes number of layer of the circuit and j denotes number of that gate in the
in which i denotes number of layer of the circuit and j denotes number of that gate in the 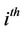 layer and
layer and  and
and  and
and  denote logical AND, OR and NOT gates, respectively. In this circuit we have
denote logical AND, OR and NOT gates, respectively. In this circuit we have 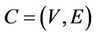 where
where 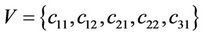 and
and 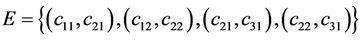 . Now we construct an AIR system for the Boolean circuit of Figure 5 as
. Now we construct an AIR system for the Boolean circuit of Figure 5 as  where
where
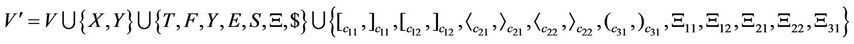
YES is the axiom and 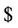 and
and  are not included in alphabet of the Turing machine. Furthermore,
are not included in alphabet of the Turing machine. Furthermore,  is the splicing scheme. Assuming that
is the splicing scheme. Assuming that 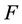 is used instead of logical zero and
is used instead of logical zero and 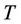 is used instead of logical one, x and y are encoded into inputs for
is used instead of logical one, x and y are encoded into inputs for  by utilizing the mapping
by utilizing the mapping 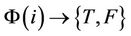 in which
in which  is the set of inputs of the circuit. Now, if we consider Equations (6) and (7):
is the set of inputs of the circuit. Now, if we consider Equations (6) and (7):
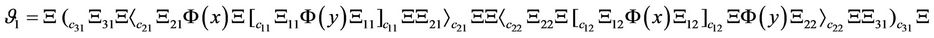 (6)
(6)
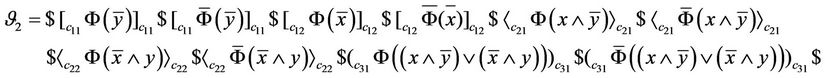 (7)
(7)
The input of our AIR system  is then
is then  and
and  accepts the input string if result of XOR is 1 and the axiom YES is produced. Therefore if result of XOR equals 1, Gc accepts input string in 4 steps. In the following we construct splicing schemes necessary for computation of XOR in the proposed AIR system.
accepts the input string if result of XOR is 1 and the axiom YES is produced. Therefore if result of XOR equals 1, Gc accepts input string in 4 steps. In the following we construct splicing schemes necessary for computation of XOR in the proposed AIR system.
 (8)
(8)
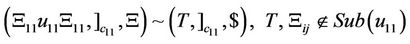 (9)
(9)
 (10)
(10)
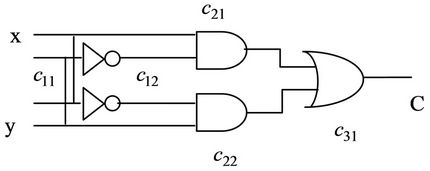
Figure 5. Operation of XOR.
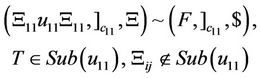 (11)
(11)
 (12)
(12)
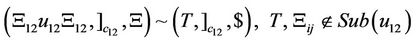 (13)
(13)
 (14)
(14)
 (15)
(15)
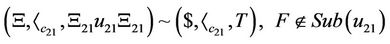 (16)
(16)
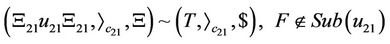 (17)
(17)
 (18)
(18)
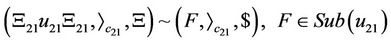 (19)
(19)
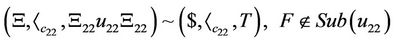 (20)
(20)
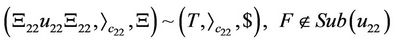 (21)
(21)
 (22)
(22)
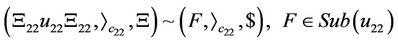 (23)
(23)
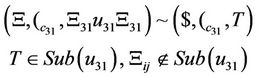 (24)
(24)
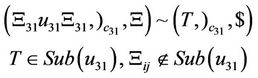 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
Furthermore, in Equations (8)-(28) 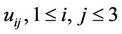 are defined as shown in Equation (29).
are defined as shown in Equation (29).
 (29)
(29)
and the computed words in each step of computation can be written as Equations (30)-(33):
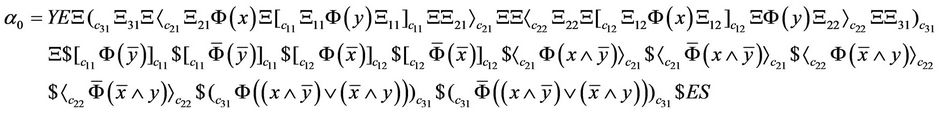 (30)
(30)
 (31)
(31)
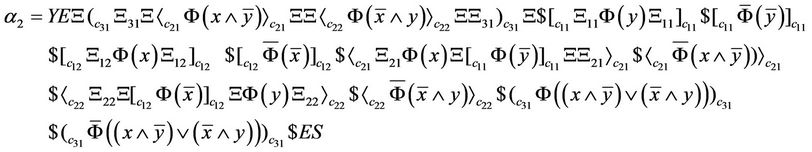 (32)
(32)
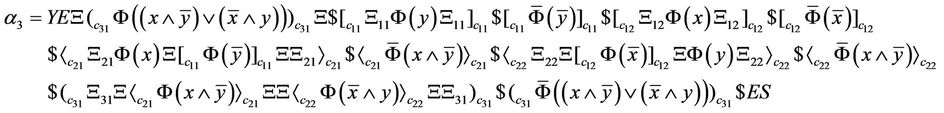 (33)
(33)
In the next step, by applying deletion operation to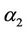 , if the result of the computation equals one, the axiom YES will be produced.
, if the result of the computation equals one, the axiom YES will be produced.
4.3. Simulation of S-Box with AIR Systems
We assume the word of Equation (34) as input to S-boxes of Figure 3
 (34)
(34)
The following splicing rules will be used to guide recombinations of our AIR system for simulating S-boxes.
 (35)
(35)
 (36)
(36)
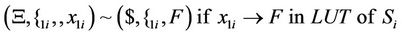 (37)
(37)
 (38)
(38)
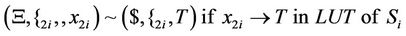 (39)
(39)
 (40)
(40)
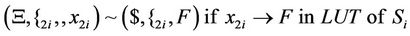 (41)
(41)
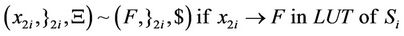 (42)
(42)
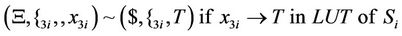 (43)
(43)
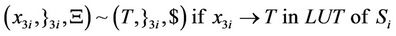 (44)
(44)
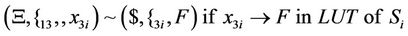 (45)
(45)
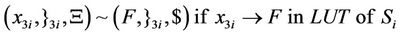 (46)
(46)
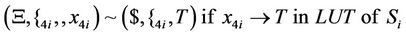 (47)
(47)
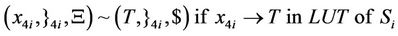 (48)
(48)
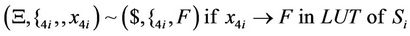 (49)
(49)
 (50)
(50)
As can be seen in splicing relations of S-boxes, trl operation is applied to the input word in a parallel fashion in accordance with the look-up table of the corresponding S-box and therefore, all input bits are assigned a True or a False value at the same time.
After applying the above splicing rules, the following word is obtained in which we assumed that the 4-bits of input in S-box i are all mapped to logical one or T. Other mappings can be defined as well according to the look-up table of each S-box.
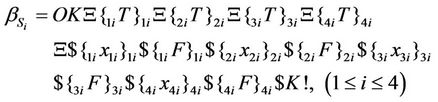 (51)
(51)
Then, the following splicing scheme is applied to the resultant word. Then, the following splicing scheme is applied to the resultant word.
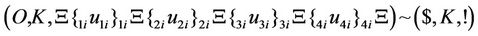 (52)
(52)
After applying the above rule, a deletion rule (which is based on ld operation) is applied as follows.
 (53)
(53)
Therefore, axiom OK! Is produced which implies that the S-box has been calculated.
The start sequence for calculation of the substituted words for computing S-box can be written as shown in Equation (54), in which p and  are assumed blank symbols.
are assumed blank symbols.
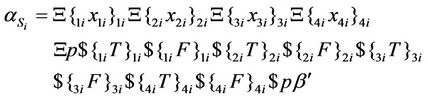 (54)
(54)
After applying the splicing rules of Equations (35)-(50) to 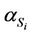 we can obtain
we can obtain 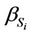 as written in Equation (55).
as written in Equation (55).
 (55)
(55)
Now, we can obtain the output of S-boxes by applying a deletion rule which is guided by the splicing scheme which is written in Equation (56).
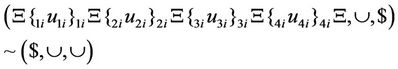 (56)
(56)
In Equation (56), 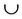 shows the blank symbol and
shows the blank symbol and 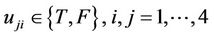 in which j is the number of output bit of S-boxes and i is number of S-boxes. Therefore, after applying the above rules, we can write the output of S-boxes as shown in Equation (57).
in which j is the number of output bit of S-boxes and i is number of S-boxes. Therefore, after applying the above rules, we can write the output of S-boxes as shown in Equation (57).
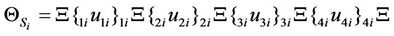 (57)
(57)
In Equation (57), 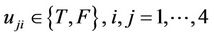 and
and 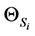 is the output of S-box number i.
is the output of S-box number i.
4.4. Simulation of P-Box with AIR Systems
In this section, we build a Turing machine based on AIR systems that simulates P-boxes of Figure 3. For this reason, we write the input word and splicing schemes for P-box as shown in Equation (58).
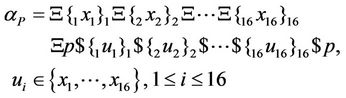 (58)
(58)
In the above equation which describes input to the P-boxes of “Figure 3”, we further assume that all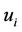 ,
,  are distinctive and p is the blank symbol. Therefore, we can write the splicing schemes as shown in Equation (59).
are distinctive and p is the blank symbol. Therefore, we can write the splicing schemes as shown in Equation (59).
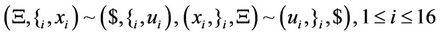 (59)
(59)
After applying trl rules in a parallel fashion, such that they are guided by splicing rules of Equation (59), we can get to the word that is shown in Equation (60).
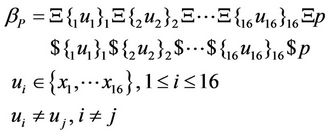 (60)
(60)
Then, a deletion rule as shown in Equation (61) which is guided by splicing rule of Equation (62) produces the output of P-boxes. The output word of P-boxes is demonstrated in Equation (63).
 (61)
(61)
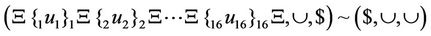 (62)
(62)
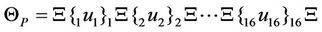 (63)
(63)
In Equation (63),  is the output of P-box.
is the output of P-box.
5. The Proposed Attack Plan
In order to demonstrate our algorithm, we use the attack graph of Figure 6 in each node of which a fraction of the attack takes place. In the following, we explain the operations that are accomplished in each node of the graph of Figure 6.
In node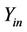 , all possible keys are generated the process of which was explained in Section 4.1. In node
, all possible keys are generated the process of which was explained in Section 4.1. In node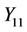 , all possible keys that were generated in
, all possible keys that were generated in 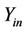 are bitwise XORed with the given plaintext using AIR system of Section 4.2 that is guided by splicing rules of Equations (8)-(28). Then, the generated strings are forwarded to S-boxes
are bitwise XORed with the given plaintext using AIR system of Section 4.2 that is guided by splicing rules of Equations (8)-(28). Then, the generated strings are forwarded to S-boxes 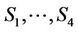 of Figure 3 and in node
of Figure 3 and in node , Sboxes are applied in parallel to the output of node
, Sboxes are applied in parallel to the output of node  in accordance with splicing relations of Section (4.3). In
in accordance with splicing relations of Section (4.3). In  the generated strings are permuted in a fashion dictated by the cipher instructions according to the splicing relations of Equations (59) and (62). The process of consecutive mixing with subkey and applying substitution and permutation operations go on in an iterated fashion in the next nodes such that in node
the generated strings are permuted in a fashion dictated by the cipher instructions according to the splicing relations of Equations (59) and (62). The process of consecutive mixing with subkey and applying substitution and permutation operations go on in an iterated fashion in the next nodes such that in node ,
,  and
and  mixing with the
mixing with the 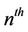 subkey, the
subkey, the 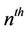 round substitution and the
round substitution and the 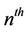 round permutation take place, respectively, and in
round permutation take place, respectively, and in 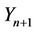 these gained strings are XORed with corresponding bits of the
these gained strings are XORed with corresponding bits of the 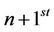 subkey and eventually, in node
subkey and eventually, in node 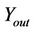 the generated bits are compared with the given ciphertext and we can find the key of the cipher if they are equal.
the generated bits are compared with the given ciphertext and we can find the key of the cipher if they are equal.
6. Performance Evaluation of the Proposed Scheme
Considering that the operations of each node take place concurrently for all strings that exist in that node, we can find the number of steps that takes to produce the key of the cipher. In node  by applying different combinations of consecutive ciliate bio-operations to a single initial word which is applied in parallel and takes one step, we can produce all possible key of the cipher. In node
by applying different combinations of consecutive ciliate bio-operations to a single initial word which is applied in parallel and takes one step, we can produce all possible key of the cipher. In node  the XOR operation is applied between the generated words of node and the plaintext and considering that each XOR operation has a depth of three, four steps are required to evaluate XOR of two bits that produces output of one. In node
the XOR operation is applied between the generated words of node and the plaintext and considering that each XOR operation has a depth of three, four steps are required to evaluate XOR of two bits that produces output of one. In node 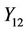 two steps are required to produce the resulting words. In node
two steps are required to produce the resulting words. In node  two steps should be accomplished to evaluate P-boxes. So, there will be the same steps for other nodes of
two steps should be accomplished to evaluate P-boxes. So, there will be the same steps for other nodes of 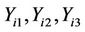 for
for . We further assume that there are n-rounds of substitutions and permutations. So, before the last node,
. We further assume that there are n-rounds of substitutions and permutations. So, before the last node,  , we need to do
, we need to do  operations. The operations of the last node can be carried out as follows: Those bits that have been generated in node
operations. The operations of the last node can be carried out as follows: Those bits that have been generated in node

Figure 6. The attack graph for breaking the cipher.
 are XORed with the corresponding given ciphertext bits which take 4-steps and then, the AND operation is applied to the results of XORs which takes one step. So, altogether
are XORed with the corresponding given ciphertext bits which take 4-steps and then, the AND operation is applied to the results of XORs which takes one step. So, altogether  steps are mandatory to accomplish our attack in which n is the number of SP rounds.
steps are mandatory to accomplish our attack in which n is the number of SP rounds.
Assuming that we use our proposed scheme to break 16-Round DES cipher (n = 16) which has a Feistel structure which can be assumed as a variant of SPN ciphers, using the analysis of Section 6, we need 138 steps of computation which gives it a superior performance over the proposed schemes of breaking DES using DNA computer [10] which requires 916 steps and membrane computing [11] which requires 278 steps of computations as well as breaking DES using network of evolutionary processors with parallel string rewriting rules (NEPPS) which requires 268 steps [12]. Furthermore, our proposed scheme, as opposed to [11] which needs exponential space, does not need exponential space and for a specific set of instructions of a given cipher, utilizes a constant number of splicing rules. The performance of our proposed scheme for cracking 16R-DES cipher in compareson with the previously proposed schemes has been depicted in Figure 7.
7. Simulation of the Proposed Attack
We conduct a computer simulation to test our proposed theoretical scheme to break a sample cipher based on the SPN of Figure 3 and in this section, first, we introduce the parameters of the sample cipher which we aim to cryptanalyze and then we explain the steps of our simulations and finally, we present the results of simulations.
7.1. Parameters of the Considered Cryptosystem
In what follows, we introduce the cryptosystem under consideration for simulation in this paper. As can be seen in Figure 3, the input block size of our cryptosystem equals to 16 bits and a certain operation takes place for n rounds. Each round consists of substitution block, permutation and mixture of bits. This structure looks like the one that is used in DES and other modern block ciphers such as Rijndael [13]. The utilized blocks of the cipher can be defined as follows.
7.1.1. Substitution Block
In the cipher of Figure 3, we break the 16-bit block of input into four 4-bit blocks. Each sub-block constitutes an input to each S-box (a 4-to-4-bit S-box) that can be realized with a look-up table containing sixteen 4-bit values that can be defined with the integer numbers that are shown in the input bits of Table 1. The considered S-box is non-linear and the output bits of each S-box cannot be written as a linear combination of the inputs bits. Furthermore, it is assumed that all substitution boxes of  are equivalent. Our considered substitution box for the cipher is shown in Table 1.
are equivalent. Our considered substitution box for the cipher is shown in Table 1.
7.1.2. Permutation Block
The considered permutation schedule for the cipher of Figure 3 is shown in Table 2. Numbers of this table show the position of the bits in the block such that 1 shows the leftmost bit and 16 is the rightmost bit of the input block.
7.1.3. Mixing with Subkey
We define the operation of mixture with the key to be simply equal to applying the XOR gate between round key bits and the input block to the round.
In what follows, we design different sub-systems necessary for implementation of our proposed theoretical attack to the cipher.
Considering the above parameters in the cipher of
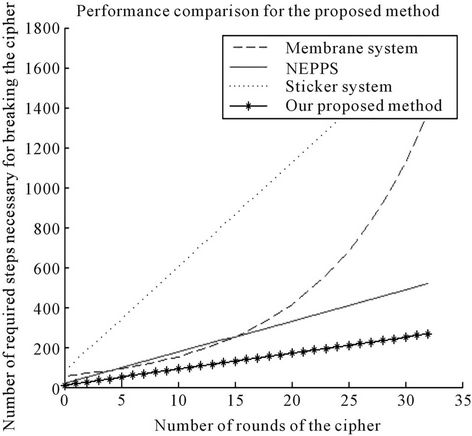
Figure 7. Graph of comparison for performance evaluation.

Table 1. Look-up table for the considered S-box.
Figure 3 and using splicing rules derived in Section 4, we simulate the proposed attack on the cipher.
We utilize Turing Machine Simulator software [14] to simulate our proposed attack on the cipher. For this reason, based on the splicing rules of Section 4, we write an initial program to simulate the main blocks of cryptanalysis according to the cipher parameters (such as generation of all keys, doing XOR, S-boxes and P-boxes). We write appropriate programs for each block to do computations on the words written on the tape of the Turing machine which simulate the AIR systems designed in Sections 4.1-4.4. Then we combine all the written programs based on the graph of Figure 4. In our simulation, we consider the following assumptions: we assume the number of rounds of the cipher equal to 1. Therefore we have one subkey string which is same as the main key and has a length of 16 bits. We further assume that the plaintext equals to “0000000000000000” and also the ciphertext is assumed to be “01011110011 00110”. Now, based on the our designed AIR system, we write the applied algorithm for cryptanalysis as follows.
Initially, by applying different splicing rules on an initial sequence, we can produce all possible combinations of the key on the tape and then we put these strings on different segments of the tape with a certain distance from each other. Then, according to the splicing rules of Equations (8)-(28) we apply bitwise XOR operation between key bits of each key and the corresponding plaintext bits and their output is placed in another place on the tape. Then, by using splicing rules of Equations (35)-(50) and (56), we apply the substitution boxes of Table 1 to the derived words in a parallel fashion and the resultant words are rewritten on the same words. Then, P-box of Table 2 is applied in to the derived words in a parallel manner which utilizes the splicing rules of Equations (59) and (62) and we rewrite them on the previously derived words. Then, we apply the logical XOR operation between bits of the resultant words of this stage and the key bits which had been mixed with the resultant sequence of the previous steps (which have known location on the tape) and therefore, we can get to the enciphered message. Now, in accordance with the proposed operations in the last node of the graph of Figure 4, in this node, the achieved strings must be compared with the predefined ciphertext and if all the corresponding bits were equal, the used key is known as the cipher key.
We wrote appropriate programs to accomplish the abovementioned instructions and ultimately, we successfully derived the secret key equal to “0001001000 110100” which was predicted.
It is noteworthy that breaking the cipher of “Figure 3” with more rounds can be done in the same way. But for the sake of demonstration of our algorithm and also the problem of taking a long time for execution of the program we tested it on the cipher with 1 round of operations.
The codes shown in Appendix 1 are our specifically written programs to simulate Turing machines related to different building blocks necessary for the cryptanalysis procedure as demonstrated in Section 4 which are appropriate for execution on the Turing Machine Simulator software [14].
Note that all the written programs halt and generate appropriate output strings in a finite number of iterations The results of execution of codes of Appendix 1 for the considered cipher, defined in Section 7.1, are shown in Tables 3-6.
8. Conclusion
In this paper, we proposed a language-theoretic notion to break SPN class of block ciphers which is based on the gene assembly process that naturally occurs in ciliated protozoa during the procedure of converting scrambled MIC gene to MAC gene. Our scheme utilizes the AIR system which includes two modified versions of intramolecular ciliate bio-operations  and
and 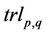 which renders it the computational flavor of Turing machine. Assuming that we use our proposed scheme to break 16-Round DES cipher (n = 16) which has a Feistel structure which can be assumed as a variant of SPN ciphers, using the analysis of Section 6, we need 138 steps of computation which gives it a superior performance over the proposed schemes of breaking DES using DNA computer [13] which requires 916 steps and membrane
which renders it the computational flavor of Turing machine. Assuming that we use our proposed scheme to break 16-Round DES cipher (n = 16) which has a Feistel structure which can be assumed as a variant of SPN ciphers, using the analysis of Section 6, we need 138 steps of computation which gives it a superior performance over the proposed schemes of breaking DES using DNA computer [13] which requires 916 steps and membrane

Table 3. Results of simulation of S-boxes.

Table 4. Results of simulation of P-boxes.

Table 5. Results of simulation of mixing with subkey.

Table 6. All operations of attack on the cipher.
computing [14] which requires 278 steps of computations as well as breaking DES using network of evolutionary processors with parallel string rewriting rules (NEPPS) which requires 268 steps [15]. Furthermore, our proposed scheme, as opposed to [14] which needs exponential space, does not need exponential space and for a specific set of instructions of a given cipher, utilizes a constant number of splicing rules. Finding nature-inspired computational models like L-systems or modified versions of P-systems or our utilized model, seem to be promising in developing efficient computational models which simulate universal Turing machines and for future works, other computational problems can be suggested to be solved using these models.
REFERENCES
- L. M. Adleman, “Molecular Computation of Solutions to Combinatorial Problems,” Science, Vol. 266, No. 5187, 1994, pp. 1021-1024. doi:10.1126/science.7973651
- L. Kari and L. F. Landweber, “Computational Power of Gene Rearrangement,” In: V. E. Winfree and D. K. Gifford, Eds., Proceedings of DNA Bases Computers, American Mathematical Society, 1999, pp. 207-216.
- L. F. Landweber and L. Kari, “The Evolution of Cellular Computing: Nature’s Solution to a Computational Problem,” Proceedings of the 4th DIMACS Meeting on DNA- Based Computers, Philadelphia, 15-19 June 1998, pp. 3- 15.
- R. Lipton, “Using DNA to Solve NP-Complete Problems,” Science, Vol. 268, 1995, pp. 542-545. doi:10.1126/science.7725098
- L. M. Adleman, P. W. K. Rothemund, S. Roweis and E. Winfree, “On Applying Molecular Computation to the Data Encryption Standard,” Proceedings of 2nd Annual Meeting on DNA Based Computers, DIMACS Workshop, Princeton University, Princeton, 10-12 June 1996, pp. 28-48.
- D. R. Stinson, “Cryptography: Theory and Practice,” CRC Press, Boca Raton, 2002.
- T. Head, “Formal Language Theory and DNA: An Analysis of the Generative Capacity of Specific Recombinant Behaviors,” Bulletin of Mathematical Biology, Vol. 49, No. 6, 1987, pp. 737-759.
- T.-O. Ishdorj and I. Petre, “Gene Assembly Models and Boolean Circuits,” International Journal of Foundations of Computer Science, Vol. 19, No. 5, 2008, pp. 1133- 1145. doi:10.1142/S0129054108006182
- T.-O. Ishdorj, I. Petre and V. Rogojin, “Computational Power of Intramolecular Gene Assembly,” International Journal of Foundations of Computer Science, Vol. 18, No. 5, 2007, pp. 1123-1136. doi:10.1142/S0129054107005169
- W. Stallings, “Cryptography and Network Security Principles and Practices,” 4th Edition, Prentice Hall, Upper Saddle River, 2005, pp. 134-173.
- http://www3.wittenberg.edu/bshelburne/Turing.htm
- J. Castellanos, C. Martin-Vide, V. Mitrana and J. Sempere, “Networks of Evolutionary Processors,” Acta Informatica, Vol. 39, No. 6-7, 2003, pp. 517-529.
- D. Boneh, C. Dunworth and R. Lipton, “Breaking DES Using a Molecular Computer,” In: R. J. Lipton and E. B. Baum, Eds., DNA Based Computers: Proceedings of a DIMACS Workshop, Princeton, 10-12 June 1996, pp. 37-66.
- S. N. Krishna and R. Rama, “Breaking DES Using P System,” Theoretical Computer Science, Vol. 299, No. 1-3, 2003, pp. 495-508. doi:10.1016/S0304-3975(02)00531-5
- A. Choudhary and K. Krithivasan, “Breaking DES Using Networks of Evolutionary Processors with Parallel String Rewriting Rules,” International Journal of Computer Mathematics, Vol. 86, No. 4, 2009, pp. 567-576. doi:10.1080/00207160701351168
Appendix 1: Program Codes for Simulation of the Proposed AIR Systems
In this section, the code lines written for simulation of the proposed AIR systems for each building block of the attack are shown. Note that the programs have been written to be suitable for the Turing simulator software that was used for our simulations. R and L in the written programs demonstrate directions of right and left, respectively, of head of the considered Turing machines on the tape.
Code Lines for Simulation of S-Boxes Using AIR Systems
(A0, 0, 1, B0, R) (B0, 0, 1, C0, R)
(C0, 0, 1, D0, R) (D0, 0, 0, E0, R)
(E0, , , E0, R) (E0, 0, 0, A1, R)
(A1, 0, 1, B1, R) (B1, 0, 0, C1, R)
(C1, 1, 0, D1, R) (D1, , , D1, R)
(D1, 0, 1, A2, R) (A2, 0, 1, B2, R)
(B2, 1, 0, C2, R) (C2, 0, 1, D2, R)
(D2, , , D2, R) (D2, 0, 0, A3, R)
(A3, 0, 0, B3, R) (B3, 1, 0, C3, R)
(C3, 1, 1, D3, R) (D3, , , D3, R)
(D3, 0, 0, A4, R) (A4, 1, 0, B4, R)
(B4, 0, 1, C4, R) (C4, 0, 0, D4, R)
(D4, , , D4, R) (D4, 0, 1, A5, R)
(A5, 1, 1, B5, R) (B5, 0, 1, C5, R)
(C5, 1, 1, D5, R) (D5, , , D5, R)
(D5, 0, 1, A6, R) (A6, 1, 0, B6, R)
(B6, 1, 1, C6, R) (C6, 0, 1, D6, R)
(D6, , , D6, R) (D6, 0, 1, A7, R)
(A7, 1, 0, B7, R) (B7, 1, 0, C7, R)
(C7, 1, 0, D7, R) (D7, , , D7, R)
(D7, 1, 0, A8, R) (A8, 0, 0, B8, R)
(B8, 0, 1, C8, R) (C8, 0, 1, D8, R)
(D8, , , D8, R) (D8, 1, 1, A9, R)
(A9, 0, 0, B9, R) (B9, 0, 1, C9, R)
(C9, 1, 0, D9, R) (D9, , , D9, R)
(D9, 1, 0, F0, R) (F0, 0, 1, G0, R)
(G0, 1, 1, H0, R) (H0, 0, 0, I0, R)
(I0, , , I0, R) (I0, 1, 1, F1, R)
(F1, 0, 1, G1, R) (G1, 1, 0, H1, R)
(H1, 1, 0, I1, R) (I1, , , I1, R)
(I1, 1, 0, F2, R) (F2, 1, 1, G2, R)
(G2, 0, 0, H2, R) (H2, 0, 1, I2, R)
(I2, , , I2, R) (I2, 1, 1, F3, R)
(F3, 1, 0, G3, R) (G3, 0, 0, H3, R)
(H3, 1, 1, I3, R) (I3, , , I3, R)
(I3, 1, 0, F4, R) (F4, 1, 0, G4, R)
(G4, 1, 0, H4, R) (H4, 0, 0, I4, R)
(I4, , , I4, R) (I4, 1, 0, F5, R)
(F5, 1, 1, G5, R) (G5, 1, 1, H5, R)
(H5, 1, 1, I5, R) (I5, , , I5, R)
(I5, , , Z, L)
Code Lines for Simulation of P-Boxes Using AIR Systems
(A0, a, a, B0, R) (B0, b, e, C0, R)
(C0, c, i, D0, R) (D0, d, m, E0, R)
(E0, e, b, A1, R) (A1, f, f, B1, R)
(B1, g, j, C1, R) (C1, h, n, D1, R)
(D1, i, c, A2, R) (A2, j, g, B2, R)
(B2, k, k, C2, R) (C2, l, o, D2, R)
(D2, m, d, A3, R) (A3, n, h, B3, R)
(B3, o, l, C3, R) (C3, p, p, D3, R)
(D3, , , D3, R) (D3, , , Z, L)
Code Lines for Simulation of XOR Using AIR Systems
(R2, 1, 1, R2, R) (R2, +, +, R2, R)
(R2, 0, 0, R2, R) (R2, 1, 1, R2, R)
(R2, 0, 0, R2, R) (R2, 1, 1, R2, R)
(R2, 0, 0, R2, R) (R2, , , L0, L)
(L0, 1, 0, L1, L) (L0, 0, 1, L0, L)
(L0, +, , R4, R) (R4, 1, , R4, R)
(R4, , , Z, R) (Z, , , Z, L)
(L1, +, +, L3, L) (L3, 1, 0, L3, L)
(L3, , 1, R2, R) (L3, 0, 1, R2, R).
NOTES
*Corresponding author.


