Int'l J. of Communications, Network and System Sciences
Vol.4 No.2(2011), Article ID:4023,10 pages DOI:10.4236/ijcns.2011.42011
Maximum Likelihood Detection for Detect-and-Forward Relay Channels
Department of Computer Science and Engineering, Nagoya Institute of Technology, Nagoya, Japan
E-mail: azlan@rose.elcom.nitech.ac.jp
Received November 30, 2010; revised December 17, 2010; accepted December 30, 2010
Keywords: Cooperative Relay, Detect-and-Forward, Maximum-Likelihood Criterion Detection
Abstract
This paper introduces a simple combining technique for cooperative relay scheme which is based on a Detect-and-Forward (DEF) relay protocol. Cooperative relay schemes have been introduced in earlier works but most of them ignore the quality of the source-relay (S-R) channel in the detection at the destination, although this channel can contribute heavily to the performance of cooperation schemes. For optimal detection, the destination has to account all possible error events at the relay as well. Here we present a Maximum Likelihood criterion (ML) at the destination which considers closed-form expressions for each symbol error rate (SER) to facilitate the detection. Computer simulations show that significant diversity gain and Packet Error Rate (PER) performance can be achieved by the proposed scheme with good tolerance to propagation errors from noisy relays. In fact, diversity gain is increased with additional relay nodes. We compare this scheme against the baseline Cooperative-Maximum Ratio Combining (C-MRC).
1. Introduction
Cooperative communication has been developed as a promising technique to realize spatial diversity through user cooperation [1]. Various relaying schemes have been proposed to explore the benefits of cooperative communication, mainly divided into three categories, including Decode-and-Forward (DF), Amplify-and-Forward (AF) [1-3] and Detect-and-Forward (DEF). In DF, the relay always decodes, re-encodes and re-transmits the decoded signal to the destination. That is, any errors at the relay can be corrected and thus, error propagation can eventually be avoided. On the other hand, AF simply amplifies the received signals and forwards them to the destination after power scaling. The disadvantage of AF strategy is that it will also forward noises which received at the relay. Another relaying protocol which is simple in complexity is DEF where the relay simply detects the signals (hard-decision detection), modulates before forwarding to the destination. With DEF, in [4] the author has shown that the diversity gain can also be achieved provided the destination knows the relay probability of error.
Recently, many works were devoted to improve the relay complexity and yet strive for better error rate performance. For example, our earlier works in coded cooperative schemes [5] adopted DEF at the relay node with further enhancements at the destination. The destination employs Maximum Likelihood criterion detection (ML) to combine the direct and relayed transmissions. However, this detection at the destination does not account sufficiently the error probability of making errors at the relays resulting in serious performance degradation. In coded relay schemes, the channel decoder is initialized with channel log-likelihood ratio (LLR); hence, requires high accuracy of LLR computation. The authors in [4] have developed a piece-wise linear receiver approximating the ML criterion detection that requires knowledge of the average signal-to-noise-ratio (SNR) of the first hop. However, this scheme cannot achieve full diversity for more than one relay. In [6], another combining technique namely Cooperative-Maximum Ratio Combining (C-MRC) is introduced that approximates the ML detector. Unfortunately, C-MRC results in serious propagation error under asymmetrical networks when SNR of R-D link is larger than that of S-D link (or S-R link). Another work in [7], has studied the performance of the hard-decision ML criterion detection-based combining technique under uncoded cooperative scheme. In [8,9], the authors have proposed a non-coherent combiner in uncoded cooperative relaying scheme using DEF protocol with limited Channel State Information (CSI). In [4-12], the authors have derived sub-optimal receivers but exploiting effectively perfect knowledge of all links is still an open problem, specifically the error probability at the relay. However, many of the previous works assumed that the destination only knows the average probability of symbol error at the relays. Since the detection rule in ML criterion detection at the destination has to consider every symbol error probability, this error model may substantially affect the attainable end-to-end performance. Thus, to guarantee an optimal ML criterion detection, the destination needs to know the error characteristics of the S-R link (perfect CSI) in the form of relay error probabilities.
In this paper, we aim at providing the destination with a more accurate CSI in its decision criterion. While the idea itself of having perfect CSI is not new [9,11,13], the CSI in the previous works is calculated based on the assumption of average error probability. For binary phase-shift keying (BPSK) case, the solution is straightforward, but for quarternary phase-shift keying (QPSK) and higher modulation constellation, the Euclidean distance between symbols become no longer the same; hence the symbol error probability can also differ. To circumvent this problem, here we develop a simple ML detection algorithm for the destination node for QPSK modulation. For simplicity, we analyze this ML performance with a simple DEF in uncoded cooperative relay networks and compare against the baseline C-MRC. Unlike in C-MRC, the instantaneous CSI in the proposed scheme involves Q-function expression for each symbol in the modulation which provides accurate knowledge of S-R link. Our scheme also outperforms C-MRC especially when SNR of R-D link is sufficiently high or low (asymmetrical network). We show through computer simulations that the performance of the proposed cooperative relay schemes can be improved significantly particularly in multiple relay nodes. We observe that there is remarkable potential to achieve increasing orders of diversity with better packet error rate (PER) performance than that of C-MRC.
The organization of this paper is as follows: Section 2 is System Description and the proposed scheme, Simulation Results and Discussions are given in Section 3, and finally in 4, the paper is summarized. The derivation of the individual SER for QPSK in Gray mapping is presented in the Appendix.
2. System Description
With reference to Figure 1, we first consider a classical relay model in which only one relay (R) assists the source
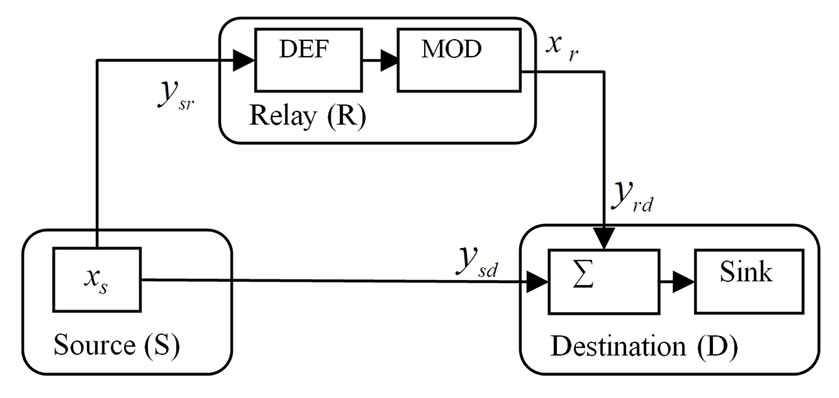
Figure 1. Block diagram of the cooperative relay system with a DEF protocol. MOD denotes the modulation of the received signal at the relay.
(S) to communicate with the destination (D). We assume each node has only one antenna and is not equipped with cyclic redundancy-check (CRC) codes. In this paper, we consider a time division multiple access (TDMA) mode where data transmission is split into two phases, that of the source node and that of the relay node. It is assumed that all the receiving nodes have perfect CSI. Furthermore, the destination also requires CSI of all three links for detection.
2.1. System Model
At timeslot 1, the source broadcasts its information, 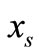 to the destination and the relay with the average power
to the destination and the relay with the average power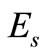 . Due to the broadcast nature of wireless channel, both the destination and the relay receive a noisy observation of
. Due to the broadcast nature of wireless channel, both the destination and the relay receive a noisy observation of 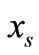 denoted by
denoted by  and
and 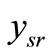 respectively in the following relation
respectively in the following relation
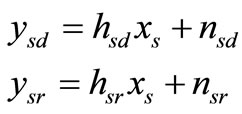 (1)
(1)
where the subscripts indicate the node relation such that 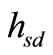 and
and 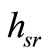 are independent complex-valued channel gains for the S-D and S-R links respectively. For simplicity, all channels are Quasi-static Rayleigh fading channels i.e.,
are independent complex-valued channel gains for the S-D and S-R links respectively. For simplicity, all channels are Quasi-static Rayleigh fading channels i.e.,  and
and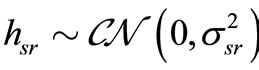 , where
, where 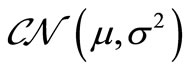 denotes a complex Gaussian random variable with mean
denotes a complex Gaussian random variable with mean 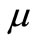 and variance
and variance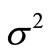 ;
; 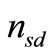 and
and 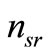 are modeled as independent additive white Gaussian noise with zero mean and equal variance
are modeled as independent additive white Gaussian noise with zero mean and equal variance 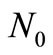 at the destination and relay respectively. We assume that the average SNR for all links are the same denoted as
at the destination and relay respectively. We assume that the average SNR for all links are the same denoted as 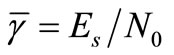 , while the instantaneous SNR is represented as
, while the instantaneous SNR is represented as 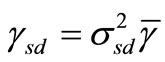 and
and 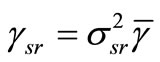 respectively. The relay performs a hard-decision detection (DEF) and re-modulates (MOD) the detected signals as
respectively. The relay performs a hard-decision detection (DEF) and re-modulates (MOD) the detected signals as 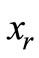 with the same average power
with the same average power 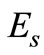 for re-transmissions in timeslot 2. The symbol received at the destination is given as
for re-transmissions in timeslot 2. The symbol received at the destination is given as
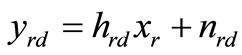 (2)
(2)
where and
and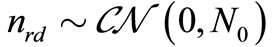 . The instantaneous SNR is
. The instantaneous SNR is .
.
At the destination, the signals from the source and the relay node are combined to recover the original source data.
2.2. Processing at the Destination
2.2.1. Baseline Scheme
Many cooperative relay schemes use MRC to exploit spatial diversity gain. It is one of the simplest and practical approaches when S-R link is reliable. However, this conventional MRC at the destination cannot guarantee full diversity in cooperative schemes. The destination node requires perfect (instantaneous) CSI of S-R link with effective combining.
In [6], the authors have proposed an improved version of MRC termed as C-MRC. The combined signal at the destination node is given by
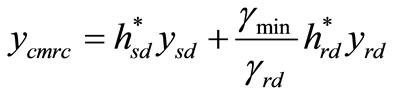 (3)
(3)
where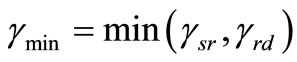 ,
, 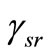 and
and 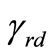 are instantaneous SNR of the S-R and R-D channels respectively. The usual intuitive meaning associated with (3) is that when
are instantaneous SNR of the S-R and R-D channels respectively. The usual intuitive meaning associated with (3) is that when 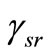 is high, the detector places full confidence to the arriving signals from the relay. In case of low
is high, the detector places full confidence to the arriving signals from the relay. In case of low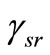 , the confidence is weighted according to the ratio of both hops, that is S-R-D link.
, the confidence is weighted according to the ratio of both hops, that is S-R-D link.
2.2.2. Proposed ML-Based Combining Strategy
In this section, we first derive the proposed ML combining technique in case of one relay. In the subsequent section, we generalize it to multiple relays. The main purpose of this algorithm is to optimally combine the noisy signals received at the destination node, 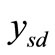 and
and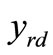 . It should be noted here that the maximum likelihood detector at the destination should also consider the effect of detection errors at the output of the relay. Such errors are mainly due to fading events in the S-R link. When this link is affected by a deep fade, the detection errors committed at the relay are propagated to the destination. To mitigate these errors which are originated from both source-relay and relay-destination links, an end-to-end ML-based detector should be employed. Thus, the basic assumption for this strategy is that the destination node makes a coherent detection for the signals from the source and the relay nodes requiring all three channels to be known at the destination node, i.e.,
. It should be noted here that the maximum likelihood detector at the destination should also consider the effect of detection errors at the output of the relay. Such errors are mainly due to fading events in the S-R link. When this link is affected by a deep fade, the detection errors committed at the relay are propagated to the destination. To mitigate these errors which are originated from both source-relay and relay-destination links, an end-to-end ML-based detector should be employed. Thus, the basic assumption for this strategy is that the destination node makes a coherent detection for the signals from the source and the relay nodes requiring all three channels to be known at the destination node, i.e., 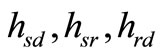 and the noise variances are available at the destination (only the received symbol
and the noise variances are available at the destination (only the received symbol 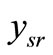 is not known). This is a standard assumption based on the fact that these parameters have been estimated as a priori. For a fair comparison, we maintain the same assumptions applicable for the baseline scheme C-MRC. The proposed ML decision rule at the destination is determined by taking all the possible symbol detection scenarios both at the destination and the relay. By applying Bayes’ rule, the decision criterion can be shown as
is not known). This is a standard assumption based on the fact that these parameters have been estimated as a priori. For a fair comparison, we maintain the same assumptions applicable for the baseline scheme C-MRC. The proposed ML decision rule at the destination is determined by taking all the possible symbol detection scenarios both at the destination and the relay. By applying Bayes’ rule, the decision criterion can be shown as
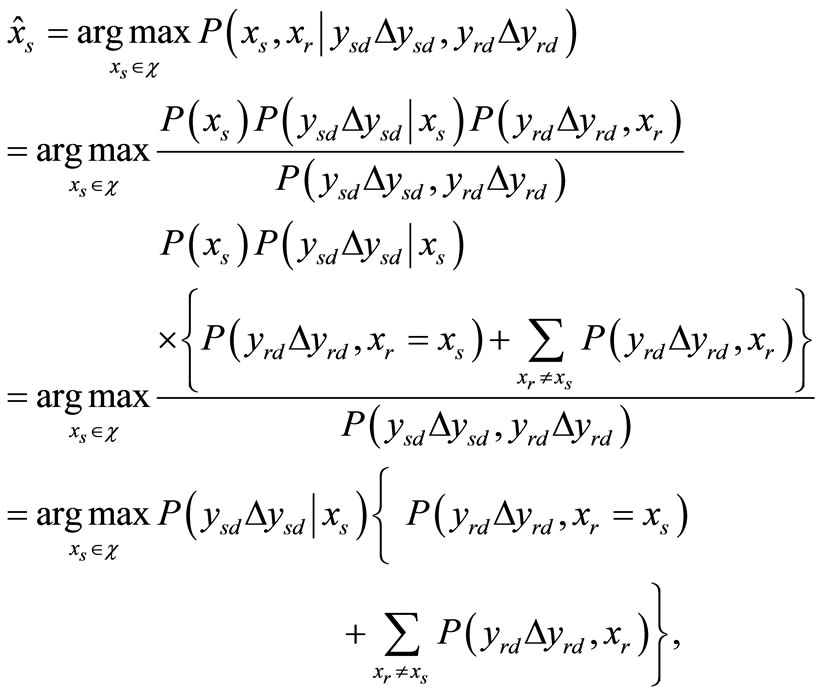 (4)
(4)
From (4), by considering the potential errors at the relay node, the decision criterion can be expanded as
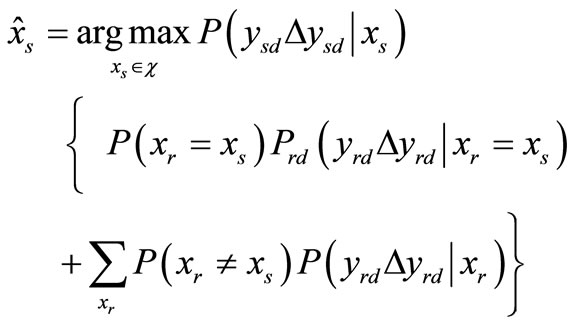 (5)
(5)
where we assume 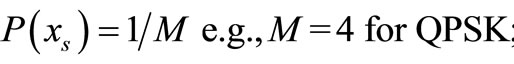 c denotes the finite set of the constellation and
c denotes the finite set of the constellation and  is the observation space for the respective received symbol. First, we assume that the transmit signals are modulated by QPSK and later, we consider a special case of BPSK. Throughout the sequel, we use capital P as the probability function. From (5), after some simplifications, the detector at the destination will find
is the observation space for the respective received symbol. First, we assume that the transmit signals are modulated by QPSK and later, we consider a special case of BPSK. Throughout the sequel, we use capital P as the probability function. From (5), after some simplifications, the detector at the destination will find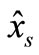 , an estimate of
, an estimate of 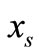 by using the following criterion
by using the following criterion
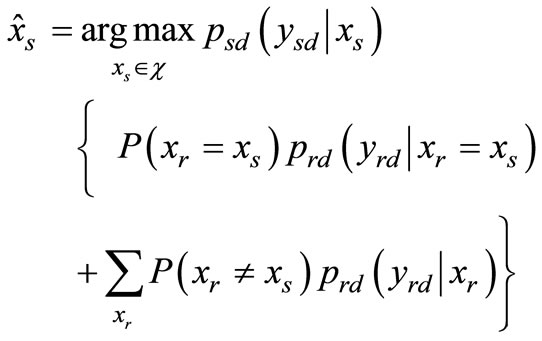 (6)
(6)
where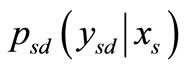 is the probability density function (PDF) of the source signal
is the probability density function (PDF) of the source signal 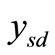 conditioned upon the transmitted data
conditioned upon the transmitted data 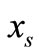 and
and 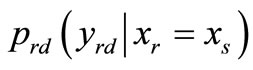 is the PDF of the relayed signal
is the PDF of the relayed signal 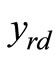 conditioned on the equality of both transmitted symbols
conditioned on the equality of both transmitted symbols .. However the bracketed terms in (6) has to consider the error probability of the received signals
.. However the bracketed terms in (6) has to consider the error probability of the received signals 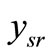 at the relay accounting the SER of each signal point.
at the relay accounting the SER of each signal point.
For QPSK case, the solution is not straightforward due to different Euclidean distance among symbols. In QPSKa symbol with two bits, 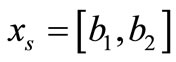 takes from the constellation set
takes from the constellation set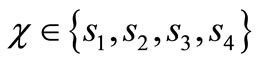 . Assuming the Gray mapping, we represent the complex symbols of
. Assuming the Gray mapping, we represent the complex symbols of  as
as . The detection at the destination is performed jointly by the ML criterion and we can expand (5) as
. The detection at the destination is performed jointly by the ML criterion and we can expand (5) as
 (7)
(7)
where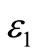 ,
,  and
and 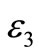 denote the symbol error probabilities from
denote the symbol error probabilities from ,
, 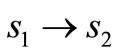 and
and 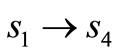 respectively;
respectively;  and
and 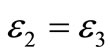 are analytically expressed as the Gaussian
are analytically expressed as the Gaussian 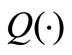 function where
function where 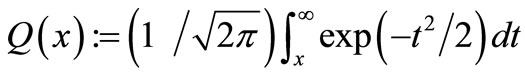 . In the 2nd term of(6), we include the multiplicative error term in exponential function,
. In the 2nd term of(6), we include the multiplicative error term in exponential function, 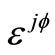 with the following equality
with the following equality where
where 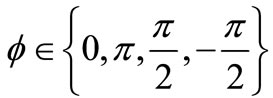 denoting the phase changes that depends on the symbols transmitted from the relay. This means that (7) takes into account that the relay does not operate error-free. In this paper, we derive closed– form expressions for the probability of error for each constellation symbol for QPSK as
denoting the phase changes that depends on the symbols transmitted from the relay. This means that (7) takes into account that the relay does not operate error-free. In this paper, we derive closed– form expressions for the probability of error for each constellation symbol for QPSK as
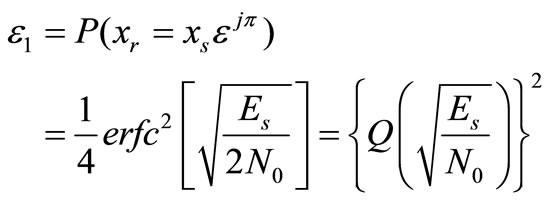 (8)
(8)
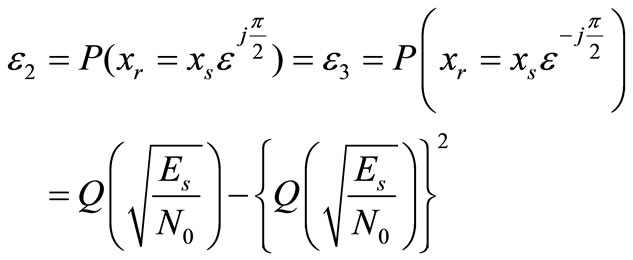 (9)
(9)
where erfc is the complementary error function. When 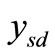 and
and 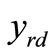 are received at the destination, by inserting
are received at the destination, by inserting  to
to 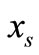 and examining how large the argument value from the augment (7), we can determine the transmit signal point
and examining how large the argument value from the augment (7), we can determine the transmit signal point 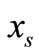 from the finite set
from the finite set 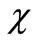 in QPSK constellation. The PDF for each term corresponding to the following expressions:
in QPSK constellation. The PDF for each term corresponding to the following expressions:
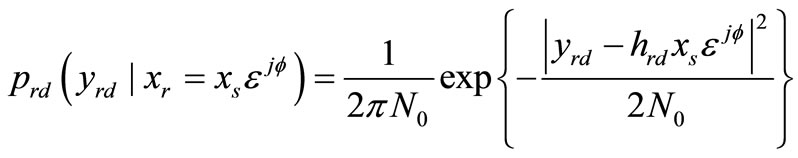 (10)
(10)
where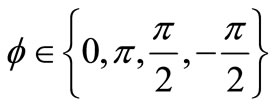 .Detail derivations of (8) and (9) are presented in the Appendix. It is clear from (8) and (9) that each QPSK symbol takes on a different symbol error probability. The analytical results presented thus far in previous works have been derived from studies which examined the SER problem assuming that the symbol error probability of each QPSK symbol is equally likely. Thus, these results cannot be treated as offering a complete ML solution. Note that another advantage in the proposed ML over C-MRC is its flexibility of combining different modulated signals from different nodes since each link can be treated independently (symbol-wise detection). In C-MRC, if the potential errors cannot be accurately modeled, maximizing the SNR would not result in the improvement of the scheme.
.Detail derivations of (8) and (9) are presented in the Appendix. It is clear from (8) and (9) that each QPSK symbol takes on a different symbol error probability. The analytical results presented thus far in previous works have been derived from studies which examined the SER problem assuming that the symbol error probability of each QPSK symbol is equally likely. Thus, these results cannot be treated as offering a complete ML solution. Note that another advantage in the proposed ML over C-MRC is its flexibility of combining different modulated signals from different nodes since each link can be treated independently (symbol-wise detection). In C-MRC, if the potential errors cannot be accurately modeled, maximizing the SNR would not result in the improvement of the scheme.
For completeness, we also examine the scheme in the absence of the CSI of S-R link at the destination node. The destination ignores the error possibility at the relays i.e., 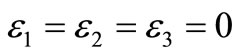 in (7). Hence, we obtain
in (7). Hence, we obtain
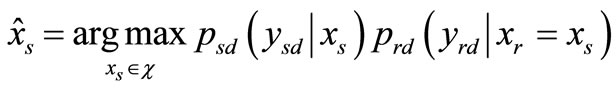 (11)
(11)
One can gain insight about (11) that it is identical with the conventional MRC. This means the combiner at the destination does not explicitly take into account the uncertainty of the relay decisions when S-R link is erroneous.
Next, we present a special case when BPSK is used, instead. For BPSK, the relay decision process can be simply modeled as a binary symmetric channel (BSC) with the probability of a binary decision error at the relay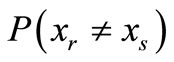 . This is because the S-R link is modeled as a Quasi-static Rayleigh fading channel and each channel is equivalent to a specific AWGN channel having a complex gain of
. This is because the S-R link is modeled as a Quasi-static Rayleigh fading channel and each channel is equivalent to a specific AWGN channel having a complex gain of . When the relay node R receives the signal from the source node, it does a hard decision
. When the relay node R receives the signal from the source node, it does a hard decision 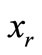 for
for 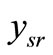 and forwards it to the destination node.
and forwards it to the destination node.
The relay decision process can be characterized by a random variable 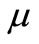 defined as
defined as
 (12)
(12)
with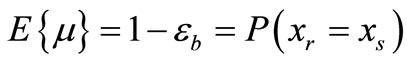 where
where 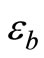 is the probability of bit error at the relay. Therefore,
is the probability of bit error at the relay. Therefore, 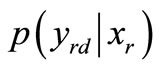 can be shown as
can be shown as
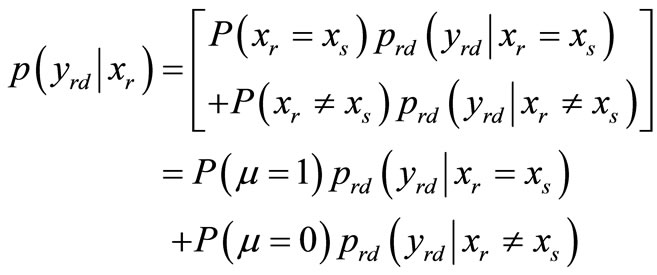 (13)
(13)
where the transition PDF of 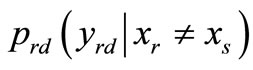 is represented by
is represented by
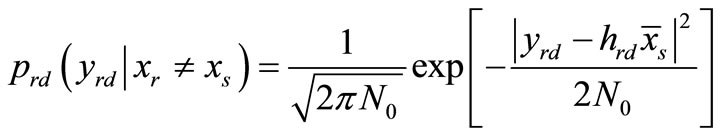 (14)
(14)
In (14), 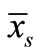 is the complement of
is the complement of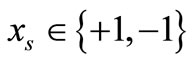 .
.
Inserting the conditional PDF into (13), the transition PDF of this relayed path for BPSK case can be shown as
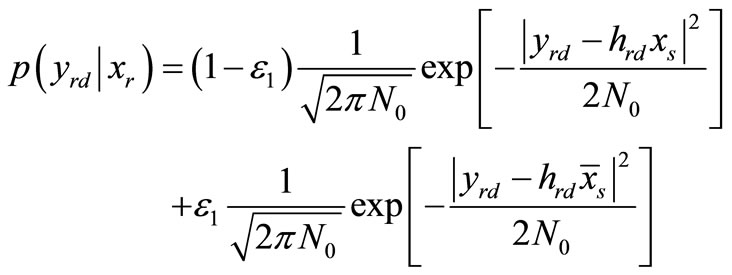 (15)
(15)
In brief, the proposed scheme features:
1) A simple detector which is capable of mitigating the potential errors at the noisy relays.
2) A new error model which serves as the side information for the detection at the destination by considering individual SER of the signal points in QPSK. Since (7) considers individual SER in its decision, our framework also suits well for other type of modulations Nonetheless, since having complete CSI for S-R link can be resource-exhaustive, we propose another scheme as in (26) for QPSK considering only average SER for each modulation.
2.3. Multiple-Relay Scheme (MRS)
In this section, we generalize (7) to multi relay schemes (MRS) with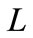 relay nodes denoted as
relay nodes denoted as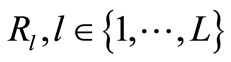 . The system model for MRS is shown in Figure 2 where in the 1st timeslot, the source broadcasts its information to the destination (dashed line) and the relay nodes. In the following
. The system model for MRS is shown in Figure 2 where in the 1st timeslot, the source broadcasts its information to the destination (dashed line) and the relay nodes. In the following 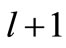 timeslot, relay
timeslot, relay 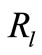 re-transmits the received signal to the destination in TDMA orthogonal channels where the corresponding received symbol at the destination is
re-transmits the received signal to the destination in TDMA orthogonal channels where the corresponding received symbol at the destination is . Note that the total timeslots are
. Note that the total timeslots are . The orthogonality is observed due to the constraints in the practical radio transceivers which cannot transmit and receive at the same time. Finally, at
. The orthogonality is observed due to the constraints in the practical radio transceivers which cannot transmit and receive at the same time. Finally, at
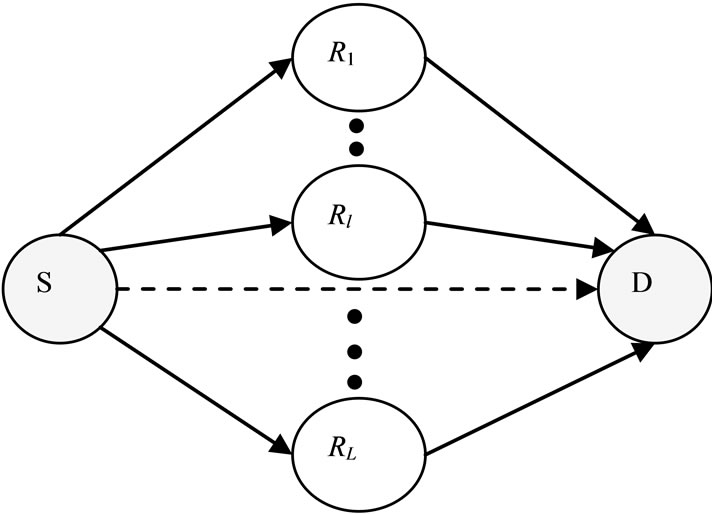
Figure 2. Multiple relay scheme in parallel channel setup.
the destination, all signals transmitted from the relays are combined by the proposed ML combining technique. All relays are considered to employ uniform relay function e.g. DEF.
From (5), we let the bracketed term denote the decision criterion for the received symbol from a relay 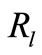 as
as
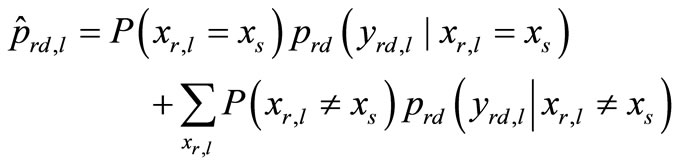 (16)
(16)
Therefore, for MRS, we can rewrite (5) compactly as
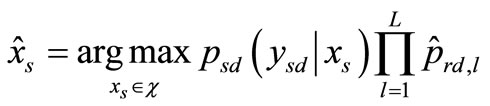 (17)
(17)
The destination will detect the symbols from all relays (plus the direct link) by using the proposed ML assuming that the perfect knowledge of every S-R link is available at the destination.
3. Simulation Results and Discussions
We analyze Packet Error Rate (PER) against average SNR in decibel (dB). We first assume the source and relay nodes transmit with the same average power 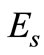 resulting in the average SNR,
resulting in the average SNR, 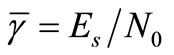 (symmetrical network). For C-MRC, we also consider the destination has a perfect knowledge of S-R links (i.e., instantaneous SNR) and perfect channel estimation is assumed. In this simulation, we only consider blind cooperative relaying schemes where relay nodes always re-transmit to the destination whether the signal is correctly detected or contains errors. No automatic repeat request (ARQ) protocol is used to avoid the error propagation from the relay nodes to the destination.
(symmetrical network). For C-MRC, we also consider the destination has a perfect knowledge of S-R links (i.e., instantaneous SNR) and perfect channel estimation is assumed. In this simulation, we only consider blind cooperative relaying schemes where relay nodes always re-transmit to the destination whether the signal is correctly detected or contains errors. No automatic repeat request (ARQ) protocol is used to avoid the error propagation from the relay nodes to the destination.
First, we check the PER performance of the proposed scheme as shown in (7) against the baseline for multiple relay nodes i.e.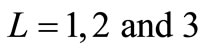 . In Figure 3, as expected, the proposed schemes outperform C-MRC (3) in all cases with around 0.2 dB, 0.5 dB and 1 dB gap at
. In Figure 3, as expected, the proposed schemes outperform C-MRC (3) in all cases with around 0.2 dB, 0.5 dB and 1 dB gap at 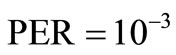

Figure 3. PER comparison between the proposed ML scheme and C-MRC (dashed lines) using DEF protocols for 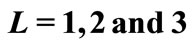 relays.
relays.
for 1, 2 and 3 relay cases respectively. In particular, we can also observe that all the cooperative schemes achieve full order diversity as observed from the slopes of the curves i.e., 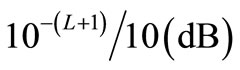 (diversity order of
(diversity order of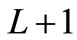 ) but a significant decrease in diversity gain for No CSI cases (11). This result demonstrates that the proposed algorithm has better accuracy of symbol detection due to the sufficient statistics of the received signals
) but a significant decrease in diversity gain for No CSI cases (11). This result demonstrates that the proposed algorithm has better accuracy of symbol detection due to the sufficient statistics of the received signals 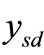 and
and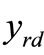 . For this reason, the conditional probability
. For this reason, the conditional probability
 can be computed using the observations
can be computed using the observations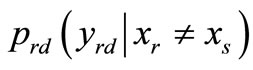 . As for the No CSI case, the diversity order of 1 is achieved for all cases. PER performance further degrades from
. As for the No CSI case, the diversity order of 1 is achieved for all cases. PER performance further degrades from 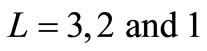 relay case. We note that when no CSI of S-R link is available at the destination, the decision by the destination are done using significantly erroneous assumptions that there are no detection errors at the relay nodes. As a result, they convey false reliability measures to the decoder and the performance is noticeably affected (more than 15 dB loss at
relay case. We note that when no CSI of S-R link is available at the destination, the decision by the destination are done using significantly erroneous assumptions that there are no detection errors at the relay nodes. As a result, they convey false reliability measures to the decoder and the performance is noticeably affected (more than 15 dB loss at 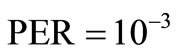 compared to the proposed ML schemes for all cases). In practice therefore, a cooperative scheme with DEF which does not account for the S-R CSI may not be very effective.
compared to the proposed ML schemes for all cases). In practice therefore, a cooperative scheme with DEF which does not account for the S-R CSI may not be very effective.
Second, we simulate the lower bounds corresponding to each case where a perfect relay is employed i.e., the same signal from the source is transmitted to the destination (complete MRC). As shown in Figure 4, for PER = 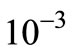 the gap between the lower bound and the proposed scheme is 2 dB for 1 relay case and 3 dB for 2 and 3 relay cases each. In perfect relay cases, the relays just replicate the same data as the source node; hence the performance can be regarded as the lower bound of the cooperative schemes. We can also notice that the gap to the lower bounds become almost constant if larger network is applied (multiple relays). This performance improvement is achieved by employing only a hard-decision protocol (DEF) at the relay nodes. Such a system design is practical for wireless networks which usually cannot compromise on the high energy consumption and longer time delay at the relays. We also plot no relay case using BPSK modulation for fair comparison. It is clear that the gain from the proposed ML scheme is significantly large due to cooperative gain.
the gap between the lower bound and the proposed scheme is 2 dB for 1 relay case and 3 dB for 2 and 3 relay cases each. In perfect relay cases, the relays just replicate the same data as the source node; hence the performance can be regarded as the lower bound of the cooperative schemes. We can also notice that the gap to the lower bounds become almost constant if larger network is applied (multiple relays). This performance improvement is achieved by employing only a hard-decision protocol (DEF) at the relay nodes. Such a system design is practical for wireless networks which usually cannot compromise on the high energy consumption and longer time delay at the relays. We also plot no relay case using BPSK modulation for fair comparison. It is clear that the gain from the proposed ML scheme is significantly large due to cooperative gain.
Third, we investigate the proposed ML schemes when the detector considers the average SER of QPSK in the decision criterion (26) as shown in Figure 5. Interestingly,
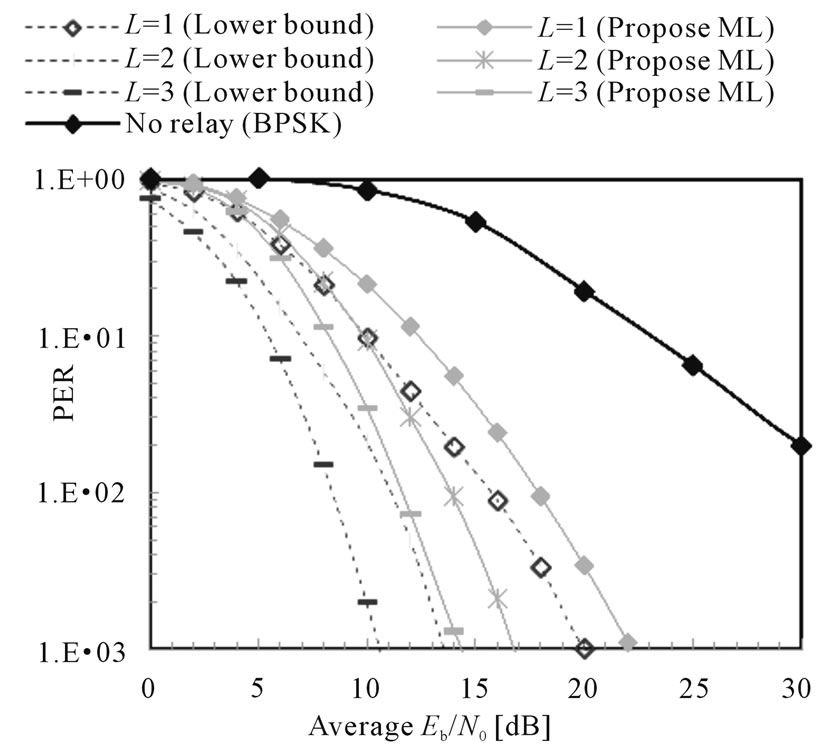
Figure 4. PER comparison between the lower bounds (dashed lines) and the proposed ML schemes (solid lines) in multiple relay schemes. The lower bounds are simulated with perfect relays.
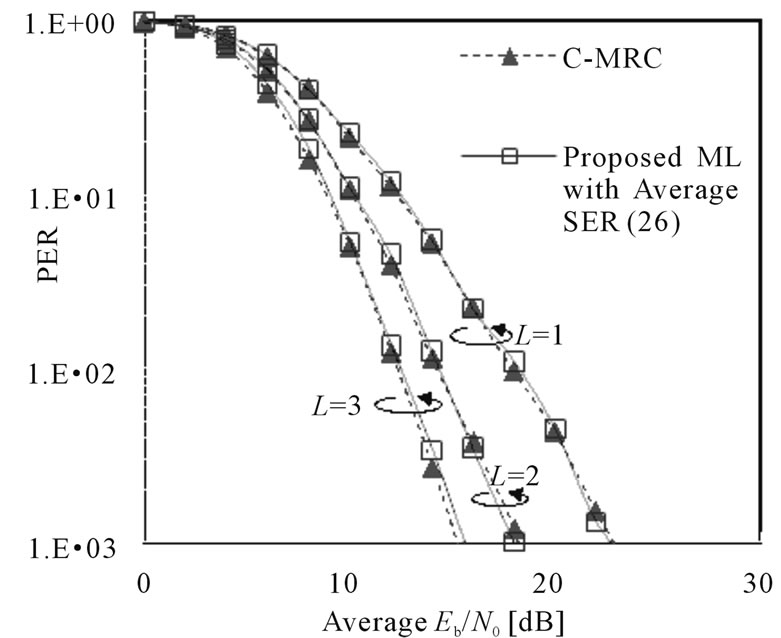
Figure 5. PER performance when the proposed ML scheme (solid lines) using only average SER, 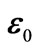 against the baseline C-MRC (dashed lines).
against the baseline C-MRC (dashed lines).
their performance is almost the same in all SNR regions as C-MRC. By using average SER in the algorithm, the observation in 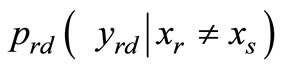 is equally weighted for all QPSK symbols. As a result, this has caused some degradation in PER performance compared to the proposed pure ML case (7) as shown in Figure 3. In fact, the convergence of the two schemes is also expected due to the approximation at high SNR of the baseline scheme [6]. Note that keeping perfect CSI of S-R link at the destination can be energy consuming and involve higher computations i.e.,
is equally weighted for all QPSK symbols. As a result, this has caused some degradation in PER performance compared to the proposed pure ML case (7) as shown in Figure 3. In fact, the convergence of the two schemes is also expected due to the approximation at high SNR of the baseline scheme [6]. Note that keeping perfect CSI of S-R link at the destination can be energy consuming and involve higher computations i.e., 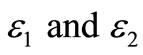 required for perfect CSI, but only
required for perfect CSI, but only 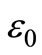 is required for the average case. Thus, this proposed ML strategy poses a practical solution which constitutes a good tradeoff between the perfect CSI requirement and error rate performance Finally, in Figure 6, we simulate the proposed scheme and C-MRC when only one relay node is used but we vary the average SNR for R-D link
is required for the average case. Thus, this proposed ML strategy poses a practical solution which constitutes a good tradeoff between the perfect CSI requirement and error rate performance Finally, in Figure 6, we simulate the proposed scheme and C-MRC when only one relay node is used but we vary the average SNR for R-D link 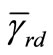 and we keep the average SNR for S-D link and S-R link the same,
and we keep the average SNR for S-D link and S-R link the same, . We simulate the schemes at three different scenarios of R-D link quality:
. We simulate the schemes at three different scenarios of R-D link quality:  + 15 dB (+15 dB),
+ 15 dB (+15 dB), 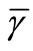 – 15 dB (–15 dB) and
– 15 dB (–15 dB) and 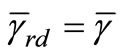 (equal). In view of this result, we infer that the proposed scheme can outperform C-MRC when R-D link has sufficiently high SNR quality (+15 dB) with 1dB gap at PER = 10-3 and 2.5 dB gap at PER = 10-2 for low SNR quality (–15 dB). When R-D link has higher SNR compared to S-D or S-R links, the combined signal at the destination is dominated by the erroneous signal from the relayed link. Thus, the PER performance is degraded further compared to the case of equal SNR. This significant performance demonstrated by the proposed ML scheme renders it more suitable when the relayed link has poor SNR quality. In
(equal). In view of this result, we infer that the proposed scheme can outperform C-MRC when R-D link has sufficiently high SNR quality (+15 dB) with 1dB gap at PER = 10-3 and 2.5 dB gap at PER = 10-2 for low SNR quality (–15 dB). When R-D link has higher SNR compared to S-D or S-R links, the combined signal at the destination is dominated by the erroneous signal from the relayed link. Thus, the PER performance is degraded further compared to the case of equal SNR. This significant performance demonstrated by the proposed ML scheme renders it more suitable when the relayed link has poor SNR quality. In
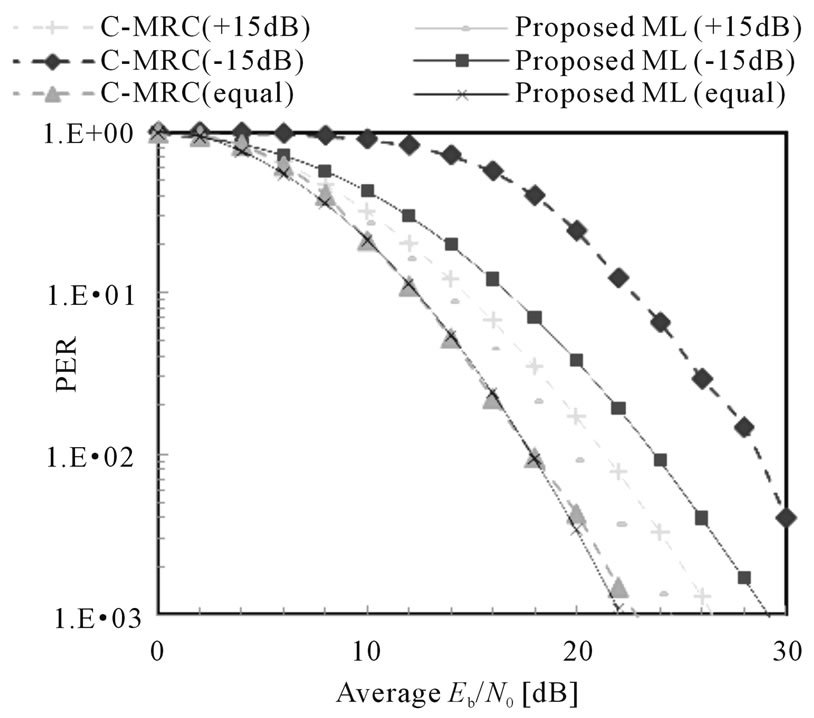
Figure 6. PER comparison between the proposed ML scheme (solid lines) and C-MRC (dashed lines) when the average SNR of R-D link, 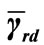 varies at
varies at  relay case.
relay case.
C-MRC, one can also check from (3) that the suboptimality of C-MRC becomes inherently evident when the weighted signal from the relayed link becomes larger than that of the direct link. C-MRC effectiveness is largely conditioned on the link quality of R-D link over S-D link (direct path). Surprisingly, it can be easily seen that the proposed ML scheme achieves the advantages of the cooperative gain by using only simple DEF protocol with increasing improvement in multiple relay schemes. In particular, re noisy and only DEF is used at the relays, the proposed scheme improves achievable PER performance. Furthermore, the proposed scheme also even provides better error rate performance at low and high SNR of R-D link which becomes an added advantage compared to C-MRC.
4. Conclusions
In this paper, we developed a new signal combining strategy based on ML criterion for cooperative relay scheme which accounts the potential errors at relays. The errors are expressed as the Gaussian Q-function for each SER in QPSK symbols. By applying these expressions in the detection at the destination, we can accurately model the transition probabilities for the erroneous transmission from noisy relays. The proposed ML scheme is superior to the conventional C-MRC in PER performance in all cases under the same CSI requirement. The proposed ML scheme has more flexibility in implementation compared to C-MRC depending on CSI at the destination. In fact, unlike C-MRC, the proposed scheme remains resilient to propagation errors even if R-D link has different SNR quality. In addition, with DEF protocol, this proposed ML scheme has shifted the processing complexity to the destination node whilst the relay nodes can conserve the energy and simple data processing. Thus, this makes this proposed strategy amenable to implementation especially for resource-constraint environment such as wireless sensor networks.
5. Acknowledgements
This study has been supported by the Scientific Research Grant-in-aid of Japan No. 21560396, the Telecommunication Advancement Foundation (TAF) and the A-STEP by JST (Japan Science and Technology Agency).
6. References
J. Laneman, D. Tse and G. Wornell, “Cooperative Diversity in Wireless Networks: Efficient Protocols and Outage Behaviour,” IEEE Transactions on Information Theory, Vol. 50, No. 12, December 2004, pp. 3062-3080. doi:10. 1109/TIT.2004.838089
A. Sendonaris, E. Erkip and B. Aazhang, “User Cooperation Diversity Part I and Part II,” IEEE Transactions on Communications, Vol. 51, No. 11, November 2003, pp. 1927-1948. doi:10.1109/TCOMM.2003.818096
A. Nosratinia and T. E. Hunter, “Diversity through Coded Cooperation,” IEEE Transactions on Wireless Communications, Vol. 5, No. 2, February 2006, pp. 283-289. doi:10. 1109/TWC.2006.1611050
D. Chen and J. N. Laneman, “Modulation and Demodulation for Cooperative Diversity in Wireless Systems,” IEEE Transactions on Wireless Communications, Vol. 5, No. 7, July 2006, pp. 1785-1794. doi:10.1109/TWC.2006. 1673090
A. A. Aziz, Y. Iwanami and E. Okamoto, “On the Improvement of Maximum Likelihood in Multiple Relay Systems,” Proceedings of IEEE Wireless Communications & Networking Conference, Sydney, 18-21 April 2010, pp. 1-6. doi:10.1109/WCNC.2010.5506662 T. Wang, A. Cano, G. Giannakis and N. Laneman, “High Performance Cooperative Demodulation with Decode-andForward Relays,” IEEE Transactions on Wireless Communications, Vol. 55, No. 7, July 2007, pp. 1427-1438.
B. Djeumou, S. Lasaulce and A. G. Klein “Combining Decoded and Forwarded Signals in Gaussian Cooperative Channels,” Proceedings of IEEE International Symposium on Signal Processing and Information Technology, Vancouver, 27-30 August 2006, pp. 622-627.
M. R. Souryal and H. You, “Diversity Performance of a Practical Non-Coherent Detect-and-Forward Receiver,” Proceedings of IEEE Global Telecommunications Conference, New Orleans, 30 November-4 December 2008, pp. 1-6.
M. Benjillali and L. Szczecinski, “A Simple Detect-andForward Scheme in Fading Channels,” IEEE Communications Letters, Vol. 13, No. 5, May 2009, pp. 309-311. doi: 10.1109/LCOMM.2009.090139
M. N. Khormuji and E. G. Larsson, “Receiver Design for Wireless Relay Channels with Regenerative Relays,” Proceedings of IEEE International Conference on Communications, Glasgow, 24-28 June 2007, pp. 4034-4039.
J. P. K. Chu, R. S. Adve and A. W. Eckford, “Using the Bhattacharyya Parameter for Design and Analysis of Cooperative Wireless Systems,” IEEE Transactions on Wireless Communications, Vol. 8, No. 3, March 2009, pp. 1384-1395. doi:10.1109/TWC.2008.080071
K. Lee and L. Hanzo, “MIMO-Assisted Hard versus Soft Decoding-and-Forwarding for Network Coding Aided Relaying Systems,” IEEE Transactions on Wireless Communications, Vol. 8, No. 1, January 2009, pp. 376-385. doi: 10.1109/T-WC.2009.080048
X. Hu, M. Benjillali and L. Szczecinski. “Bit Error Rate for Rectangular QAM with Arbitrary Constellation Mapping in Nakagami-m Channels,” Wiley Journal on Wireless Communications and Mobile Computing, Vol. 8, No. 1, 2008, pp. 93-99. doi:10.1002/wcm.437
M. S. Alouini and A. J. Goldsmith, “A Unified Approach for Calculating Error Rates of Linearly Modulated Signals over Generalized Fading Channels,” IEEE Transactions on Communications, Vol. 47, No. 9, September 1999, pp. 1324-1334. doi:10.1109/26.789668
Appendix: Derivation of Symbol Error Rate (SER) of QPSK Signals in Gray Mapping
Employing the two-dimensional (2-D) Gaussian Qfunction representation, we present closed-form expressions for the individual SER of each QPSK signal. Figure 7" target="_self"> Figure 7 illustrates the signal points for QPSK when Gray mapping is used. Let us denote 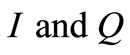 as the in-phase and quadrature components respectively. Since each complex symbol of QPSK corresponds to two binary bits, as presented in Figure 7" target="_self"> Figure 7 we assign the respective symbols
as the in-phase and quadrature components respectively. Since each complex symbol of QPSK corresponds to two binary bits, as presented in Figure 7" target="_self"> Figure 7 we assign the respective symbols 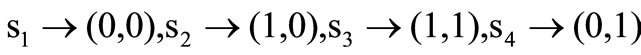 accordingly.
accordingly.
1. Derivation of ε1
In this sub-section, we derive the symbol error probability of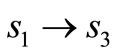 . Figure 7 depicts the difference of Euclidean distance between
. Figure 7 depicts the difference of Euclidean distance between 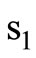 and other symbols. Here we assume
and other symbols. Here we assume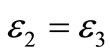 . First, it is convenient to define several assumptions used in the analysis.
. First, it is convenient to define several assumptions used in the analysis.
Consider the i-th received signal vector 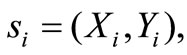
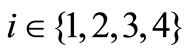 of QPSK transmitted over an AWGN channel with the channel gain
of QPSK transmitted over an AWGN channel with the channel gain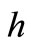 . Hence,
. Hence, 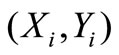 in
in 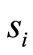 is given by the following in-phase and quadrature components
is given by the following in-phase and quadrature components
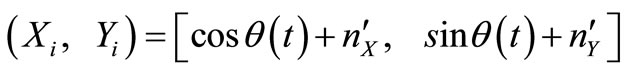 (18)
(18)
where 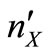 and
and 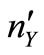 are jointly Gaussian with zero mean and equal variance
are jointly Gaussian with zero mean and equal variance 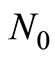 such that the expected value is
such that the expected value is
 (19)
(19)
The symbol error probability when 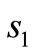 is sent and
is sent and 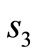 is detected can be shown by the 2-D Gaussian probability
is detected can be shown by the 2-D Gaussian probability
integral as follows
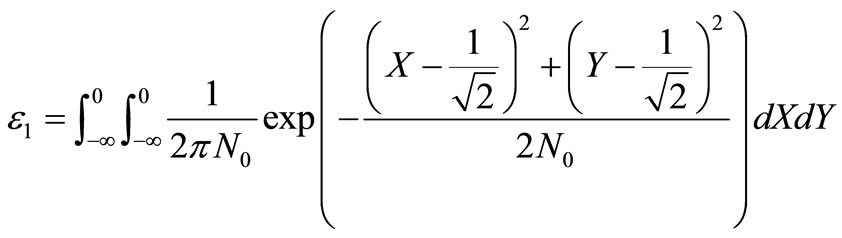 (20)
(20)
(20) can be analytically calculated and we can re-write it as
 (21)
(21)
where 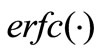 is the complementary error function.
is the complementary error function.
2. Derivation of ε2
In this sub-section, we derive the transition probability of a signal point that falls into an adjacent quadrant e.g.,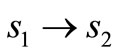 .
.
Similarly, from (20)
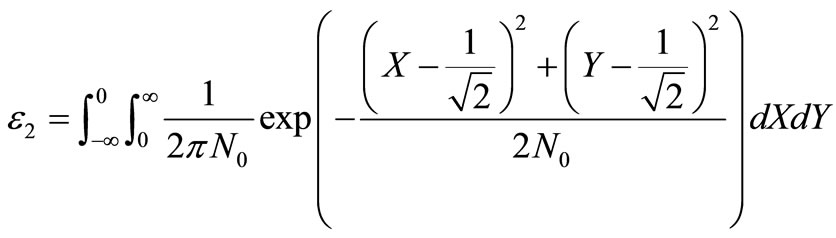 (22)
(22)
Then, (22) can be analytically calculated and we obtain
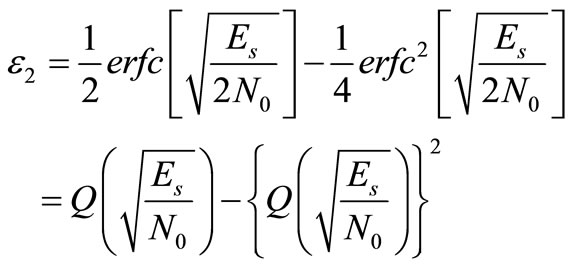 (23)
(23)
Proof: Derivation of 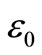 using
using 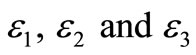 which is equivalent to the standard closed-form expression of the average probability of error for QPSK in AWGN channel [14].
which is equivalent to the standard closed-form expression of the average probability of error for QPSK in AWGN channel [14].
In this sub-section, we provide an alternative derivation for the average SER of QPSK,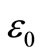 . We prove that the sum of all individual SER of QPSK symbols amounts to the average SER of QPSK. Since
. We prove that the sum of all individual SER of QPSK symbols amounts to the average SER of QPSK. Since ,
,
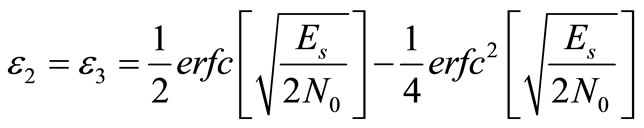 (24)
(24)
Therefore, the average SER for QPSK is simply
 (25)
(25)
For comparison, we also investigate the effect of having only average SER in the proposed ML algorithm. From (7), by setting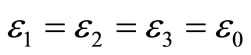 , we have the following criterion
, we have the following criterion
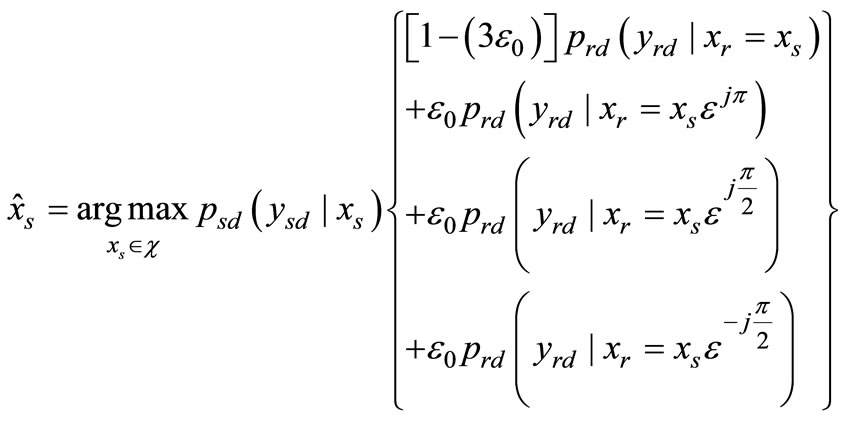 (26)
(26)
(26) can be viewed as suboptimal since it only considers average SER for all symbols in QPSK modulation.


