Int'l J. of Communications, Network and System Sciences
Vol.2 No.4(2009), Article ID:538,9 pages DOI:10.4236/ijcns.2009.24029
Investigations into the Effect of Spatial Correlation on Channel Estimation and Capacity of Multiple InputMultiple Output System
1Student Member IEEE, School of ITEE, The University of Queensland, Brisbane, Australia
2Fellow IEEE, School of ITEE, The University of Queensland, Brisbane, Australia
Email: {xialiu, meb, fwang}@itee.uq.edu.au
Received December 17, 2008; revised March 28, 2009; accepted May 25, 2009
Keywords: MIMO, Channel Estimation, Channel Capacity, Spatial Correlation, Channel Modelling
ABSTRACT
The paper reports on investigations into the effect of spatial correlation on channel estimation and capacity of a multiple input multiple output (MIMO) wireless communication system. Least square (LS), scaled least square (SLS) and minimum mean square error (MMSE) methods are considered for estimating channel properties of a MIMO system using training sequences. The undertaken mathematical analysis reveals that the accuracy of the scaled least square (SLS) and minimum mean square error (MMSE) channel estimation methods are determined by the sum of eigenvalues of the channel correlation matrix. It is shown that for a fixed transmitted power to noise ratio (TPNR) assumed in the training mode, a higher spatial correlation has a positive effect on the performance of SLS and MMSE estimation methods. The effect of accuracy of the estimated Channel State Information (CSI) on MIMO system capacity is illustrated by computer simulations for an uplink case in which only the mobile station (MS) transmitter is surrounded by scattering objects.
1. Introduction
In recent years, there has been a growing interest in multiple input multiple output (MIMO) techniques in relation to wireless communication systems as they can significantly increase data throughput (capacity) without the need for extra operational frequency bandwidth. In order to make use of the advantages of MIMO, precise channel state information (CSI) is required at the receiver. The reason is that without CSI decoding of the received signal is impossible [1–5]. In turn, an inaccurate CSI leads to an increased bit error rate (BER) that translates into a degraded capacity of the system [6–8].
Obtaining accurate CSI can be accomplished using suitable channel estimation methods. The methods based on the use of training sequences, known as the trainingbased channel estimation methods, are the most popular. In [9,10], several training-based methods including least square (LS) method, scaled least square (SLS) method and minimum mean square error (MMSE) method have been investigated. It has been shown that the accuracy of the investigated training-based estimation methods is influenced by the transmitted power to noise ratio (TPNR) in the training mode, and a number of antenna elements at the transmitter and receiver. In particular, it has been pointed out that when TPNR and a number of antenna elements are fixed, the SLS and MMSE methods offer better performance than the LS method. This is due to the fact that SLS and MMSE methods utilize the channel correlation in the estimator cost function while the LS estimator does not take the channel properties into account.
It is worthwhile to note that the channel properties are governed by a signal propagation environment and spatial correlation (SC) that is dependent on an antenna configuration and a distribution of scattering objects that are present in the path between the transmitter and receiver. The works in [9,10] have demonstrated superiority of SLS and MMSE estimation methods, which make use of channel correlation, over the LS method neglecting channel properties. However, no specific relationship between spatial correlation and channel estimation accuracy has been shown. The works presented in [11,12] have reported on the relationship between spatial correlation and estimation accuracy of MMSE method. However, only simulation results, giving trends without any further mathematical insight have been presented.
In this paper, we try to fill the existing void by presenting the mathematical analysis explaining the effects of channel properties on SLS and MMSE channel estimation methods. It is shown that for a fixed TPNR, the accuracy of SLS and MMSE methods is determined by the sum of eigenvalues of channel correlation matrix, which in turn characterizes the signal propagation conditions. In addition, we report on the effect of spatial correlation on both the channel estimation and capacity of MIMO system. In the work presented in [13–16], it has been shown that the existence of spatial correlation leads to the reduced MIMO channel capacity. However, these conclusions rely on the assumption of perfect CSI available to the receiver. In practical situations, obtaining perfect CSI can not be achieved. Therefore, in this paper we take imperfect knowledge of CSI into account while evaluating MIMO capacity.
The rest of the paper is organized as follows. In Section 2, a MIMO system model is introduced. In Section 3, LS, SLS and MMSE channel estimation methods are described and the channel estimation accuracy analysis is given. Section 4 shows derivations for the lower bound of MIMO channel capacity when the channel estimation errors are included. Section 5 describes computer simulation results. Section 6 concludes the paper.
2. System Description & Channel Model
We consider a flat block-fading narrow-band MIMO system with Mt antenna elements at the transmitter and Mr antenna elements at the receiver. The relationship between the received and transmitted signals is given by (1):
 (1)
(1)
where Ys is the Mr × N complex matrix representing the received signals; S is the Mt × N complex matrix representing transmitted signals; H is the Mr × Mt complex channel matrix and V is the Mr × N complex zero-mean white noise matrix. N is the length of transmitted signal. The channel matrix H describes the channel properties which depend on a signal propagation environment. Here, the signal propagation is modeled as a sum of the line of sight (LOS) and non-line of sight (NLOS) components. As a result, the channel matrix is represented by two terms and given as [17,18],
 (2)
(2)
where HLOS denotes the LOS part as and HNLOS denotes NLOS part. K is the Rician factor defined as the ratio of power in LOS and the mean power in NLOS signal component [17]. The elements of HLOS matrix can be written as [18]
 (3)
(3)
where Drt is the distance between t-th transmit antenna and r-th receive antenna. Assuming that the components of NLOS are jointly Gaussian, HNLOS can be written as [19,20],
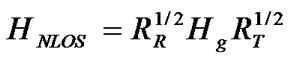 (4)
(4)
where Hg is a matrix with i.i.d Gaussian entries.
Here, the Jakes fading model [21,22] is used to describe the spatial correlation matrices RR at the receiver and RT at the transmitter. An uplink case between a base station (BS) and a mobile station (MS) is assumed, as shown in Figure 1.
The BS antennas are assumed to be located at a large height above the ground where the influence of scatterers close to the receiver is negligible. In turn, MS is assumed to be surrounded by many scatterers distributed within a “circle of influence”. For this case, the signal correlation coefficients at the receiver BS and transmitter MS, ρRBS and ρTMS, can be obtained from [22] and are given as:
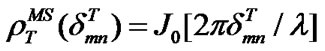 (5)
(5)

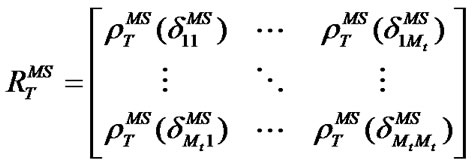
where, δmnT and δmnR are the antenna spacing distances between m-th and n-th antennas at transmitter and receiver, respectively; λ is the wavelength of the carrier; γmax is the maximum angular spread (AS); θ is the AoA of LOS and J0 is the Bessel function of 0-th order. Using ρRBS(δmnT) and ρTMS(δmnR), the correlation matrices RRBS and RTMS for BS and MS links can be generated as
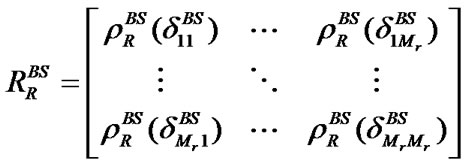 (7)
(7)
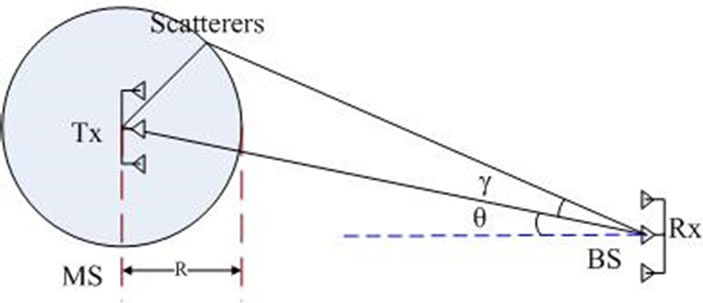
Figure 1. Jakes model for the considered MIMO channel.
 (8)
(8)
3. Training-Based Channel Estimation
For a training based channel estimation method, the relationship between the received signals and the training sequences is given by Equation (1) as
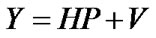 (9)
(9)
Here the transmitted signal S in (1) is replaced by P, which represents the Mt × L complex training matrix (sequence). L is the length of the training sequence. The goal is to estimate the complex channel matrix H from the knowledge of Y and P.
Here the transmitted signal S in (1) is replaced by P, which represents the Mt × L complex training matrix (sequence). L is the length of the training sequence. The goal is to estimate the complex channel matrix H from the knowledge of Y and P.
The transmitted power in the training mode is assumed to be constrained by 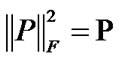 where P is a constant and ||.||F2 stands for the Frobenius norm. According to [9,10], the estimation using LS, SLS or MMSE method requires orthogonality of the training matrix P. In the undertaken analysis, the training matrix P is assumed to satisfy this condition.
where P is a constant and ||.||F2 stands for the Frobenius norm. According to [9,10], the estimation using LS, SLS or MMSE method requires orthogonality of the training matrix P. In the undertaken analysis, the training matrix P is assumed to satisfy this condition.
3.1. LS Method
In the LS method, the estimated channel can be written as [23],
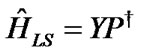 (10)
(10)
where {.}† stands for the pseudo-inverse operation.
The mean square error (MSE) of LS method is given as
 (11)
(11)
in which E{.} denotes a statistical expectation. According to [9,10], the minimum value of MSE for the LS method is given as
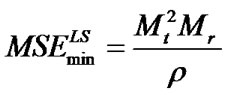 (12)
(12)
in which ρ stands for transmitted power to noise ratio (TPNR) in training mode. Equation (12) indicates that the optimal performance of the LS estimator is not influenced by channel matrix H.
3.2. SLS Method
The SLS method reduces the estimation error of the LS method. The improvement is given by the scaling factor γ which can be written as
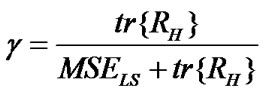 (13)
(13)
The estimated channel matrix is given as [9], [10]
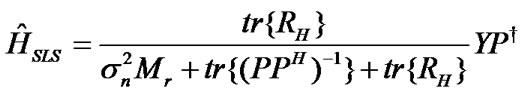 (14)
(14)
Here, σn2 is the noise power; RH is the channel correlation matrix defined as RH=E{HHH} and tr{.} implies the trace operation. The SLS estimation MSE is given as [9,10]
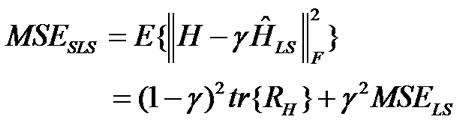 (15)
(15)
The minimized MSE of MMSE method can be written as [9,10]
 (16)
(16)
By taking into account expression (12), the minimized MSE of the SLS method (16) can rewritten as
 (17)
(17)
where n=min(Mr, Mt) and is λi the i-th eignvalue of the channel correlation RH.
If TPNR is fixed then the following equality can be derived
 (18)
(18)
As observed from (18), MSE decreases when the sum of eignvalues of RH decreases. This shows that in order to minimize MSE, the sum of eigenvalues of RH has to be reduced.
3.3. MMSE Method
In the MMSE method, the estimated channel matrix is given as (19) [9,10,23],
 (19)
(19)
The MSE of MMSE estimation is given as
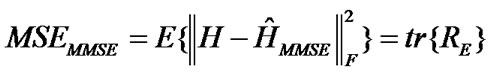 (20)
(20)
in which RE is an estimation error correlation written as
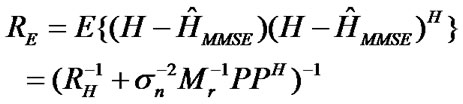 (21)
(21)
The minimized MSE is given as (22) [2,3,11]
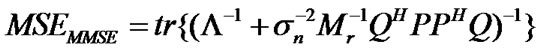 (22)
(22)
In (22), Q is the unitary eigenvector matrix of RH and Λ is the diagonal matrix with eigenvalues of RH. The minimized MSE for the MMSE method, given by Equation (22), can be rewritten using the orthogonality properties of the training sequence P and the unitary matrix Q, as shown by
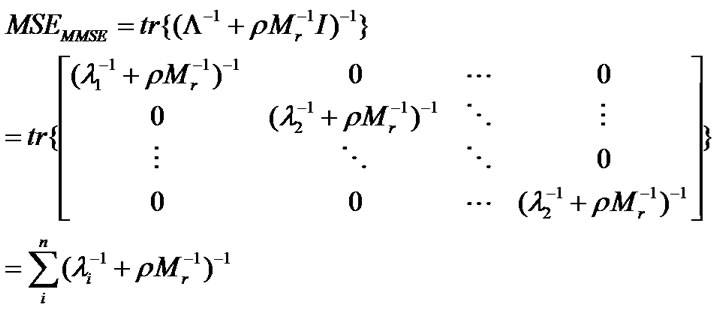
Assuming that TPNR in expression (13) is fixed, the bound for MSE is given by
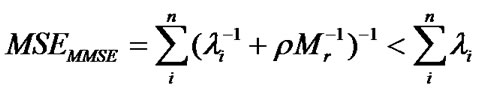 (24)
(24)
The expression (24) shows that, similarly as in the SLS method, a smaller sum of eigenvalues of the channel correlation RH leads to a smaller estimation error for the MMSE method. In other words, a smaller sum of eigenvalues of the channel correlation leads to the more accurate channel estimation.
From the above mathematical analysis it becomes apparent that when the value of TPNR is fixed the accuracy of a training-based MIMO channel estimation is governed by the sum of eigenvalues of the channel correlation matrix RH. In turn, the properties of RH and its eigenvalues are determined by the channel properties which are influenced by a signal propagation environment and an array antenna elements and configuration.
It is worthwhile to note that the spatial correlation (for example due to the presence of LOS component) is responsible for the channel rank reduction. In this case, the sum of eigenvalues of RH has a smaller value. Thus from the derived expressions, it is apparent that the spatial correlation (due to an increased LOS component) contributes in a positive manner to improving the training-based MIMO channel estimation accuracy.
4. MIMO Channel Capacity Taking into Account Channel Estimation Errors
The achievement of high channel capacity in a MIMO system depends on two factors. One is a rank of channel matrix or effectiveness of freedom (EDOF). The other one is the availability of CSI at the receiver. In [26,27,29] it has been shown that higher accuracy of CSI leads to higher channel capacity. However, the undertaken investigations have not considered the channel properties.
If CSI is perfectly known at the receiver (but unknown at the transmitter), the capacity of a MIMO system with Mr receive antennas and Mt transmit antennas can be expressed as [1,24,25],
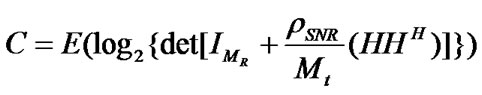 (25)
(25)
In Equation (25), ρSNR is a signal to noise ratio (SNR). The channel matrix H is assumed to be perfectly known at the receiver.
In practical cases, H has to be replaced by the estimated channel matrix, which carries an estimation error. By assuming that the channel estimation error is defined as e and the estimated channel matrix as 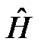
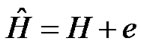 (26)
(26)
The received signal can accordingly be written as,
 (27)
(27)
Correlation of e is given as
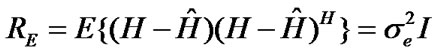 (28)
(28)
in which σe2 is the error variance. In [26,27], the definition of error variance is slightly different. Using Equation (20), we have
 (29)
(29)
The channel capacity of MIMO system with an imperfectly known H at the receiver is defined as the maximum mutual information between Y and S and is given as
 (30)
(30)
If the transmitter does not have any knowledge of the estimated channel, the mutual information in Equation (30) can be written as [26–29],
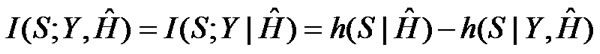 (31)
(31)
Because adding any dependent term on Y does not change the entropy [28], then
 (32)
(32)
in which u is the MMSE estimator given as
 (33)
(33)
Combining this with Equation (27), we have
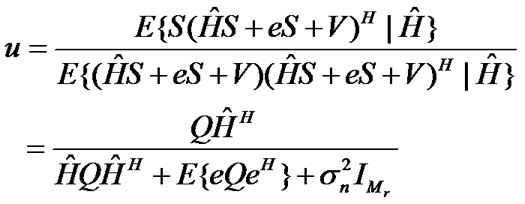
where Q=E{SSH} is a Mt by Mt correlation matrix of transmitted signal S defining the signal transmission scheme. The autocorrelation matrix holds the property that trace(Q) equal to the total transmitted signal power Ps (ρSNR=Ps/σn2). If we assume the special case of Mt equal to Mr and the transmitted signal power being equally allocated to transmitting antennas, (34) becomes
 (35)
(35)
in which p=Ps/Mt is the power allocated to the signal transmitted through each transmit antenna. Because conditioning decreases the entropy therefore
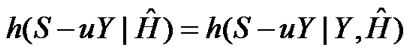 (36)
(36)
Then we have
 (37)
(37)
In this case,
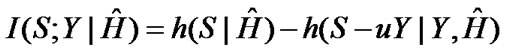 (38)
(38)
For the case of 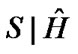 and
and 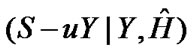 having a Gaussian distribution, (38) can be expressed as [26,27,29],
having a Gaussian distribution, (38) can be expressed as [26,27,29],
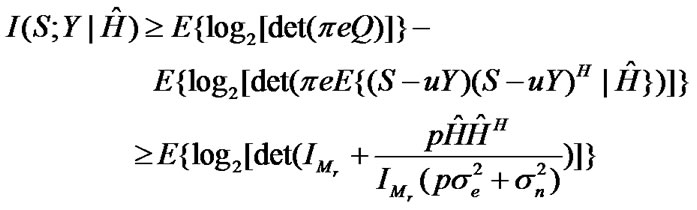
The lower bound of the ergodic channel capacity can be shown to be given as
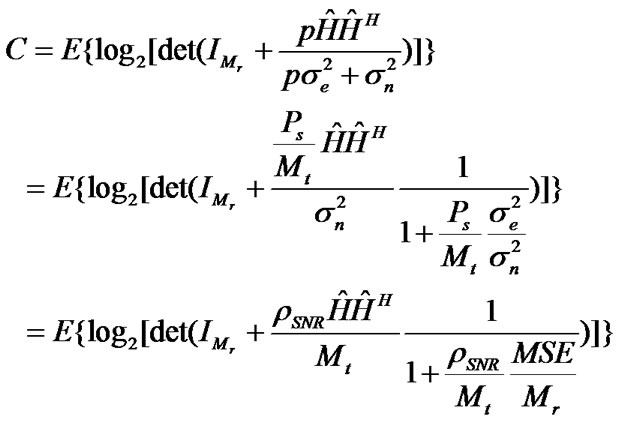
Equation (40) indicates that for a fixed value of SNR, the capacity is a function of the estimated channel matrix 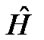 and the channel estimation error σe2. As a result, the channel properties and the quality of channel estimation influence the MIMO capacity.
and the channel estimation error σe2. As a result, the channel properties and the quality of channel estimation influence the MIMO capacity.
5. Simulation Results
Here we present computer simulation results which demonstrate the influence of channel properties on the training-based channel estimation. A 4×4 MIMO system including 4-element linear array antennas both at the transmitter and receiver is considered. The Jakes model presented in Section 2 is used to describe the propagation environment between BS and MS. The distance between transmitter and receiver is assumed to be 100λ. The Angle of Arrival (AoA) of LOS is set to 0°. The training sequence length L is assumed to be 4. The default antenna element spacing at both BS and MS is set to 0.5λ (wavelength).
Figure 2 shows a relationship between MSE and the sum of eigenvalues of the channel correlation matrix for both MMSE and SLS methods. The results include an effect of maximum angle spread (AS), antenna spacing and Rician factor K, which are related to the sum of eigenvalues of RH. The obtained results are given in four sub-figures A, B, C and D.
Sub-figure A supports the theory presented in Section 3 that for MMSE and SLS methods channel estimation errors are smaller for smaller sums of eigenvalues of RH. When the sum of eignvalues increases, the channel estimation accuracy becomes worse.
The relationship between the sum of eignvalues of RH and the maximum AS is shown in sub-figure B. The sum of eigenvalues increases when AS increases. Larger values of AS correspond to a lower level correlation while smaller values of AS correspond to a higher level correlation. Higher values of spatial correlation lead to a smaller sum of eigenvalues of RH. This condition helps to improve the accuracy of the training based MIMO channel estimation.
Sub-figure C presents the relationship between the sum of eigenvalues and the MS transmitter antenna spacing. One can see that the sum of eigenvalues becomes smaller when the spacing distance is less than 0.2λ.
Sub-figure D gives the relationship between the sum of eigenvalues and the Rician factor K. The sum of eigenvalues is smaller at higher values of K (when the LOS component is strongest). This means that a stronger LOS component reduces the sum of eigenvalues and thus improves the channel estimation accuracy.
Figure 3 is plotted in three dimensions (3D) to provide a further support for the results of Figure 2. In this figure, the relationship between MSE, TPNR ρ and K for MMSE method is presented at three different values of maximum AS (indicating three special correlation levels). One can see that when TPNR is increased to 30dB the estimation error decreases almost to zero. When the value of Rician factor K is increased, indicating a stronger LOS component in comparison with NLOS components, the MSE decreases. This is consistent with the trend observed in Figure 2 that a stronger LOS component results in better estimation accuracy.

Figure 2. Relationship between MSE vs Sum of eigenvalues of RH showing an impact of antenna spacing and the Rician factor K.
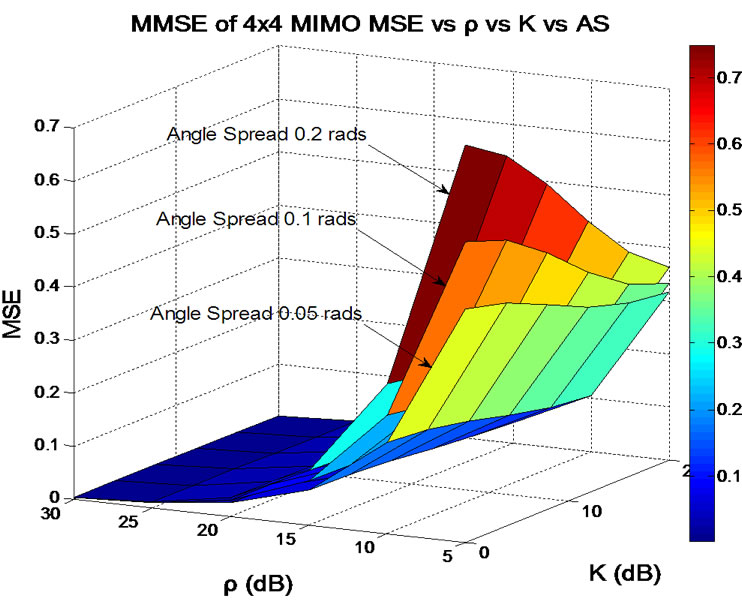
Figure 3. 3D plot of MSE vs TPNR and K for different values of AS for MMSE method.
The presented results also show that for MMSE method MSE is reduced for the smallest AS, which corresponds to the highest level of spatial correlation.
In the next step, we simulate the MIMO channel capacity under the condition of channel estimation error. Simulations are run for the cases of 2×2 MIMO and 4x4 MIMO systems. The simulation settings including the distance between the transmitter and receiver, training sequence length, AoA, AS and antenna element spacing are same as in the earlier undertaken simulations. The minimum mean square error (MMSE) channel estimation method is applied for the Jakes model representing the channel between the BS and MS. The channel capacity is determined using Equation (40). For simulation purposes, RH is obtained using the actual channel matrix H and TPNR is assumed to be equal to SNR. 100000 channel realizations are used to obtain the value of capacity. Figure 4 shows the results for the 2×2 MIMO system.
Simulation results are plotted in two-dimensions (2D) and include two sub-figures. Sub-figure A presents the relationship between MSE and angle spread (AS). There are three groups of lines drawn for three different values of SNR. In each group, the lines correspond to three different values of K factor. The relationship between channel capacity and the angle spread is given in subfigure B.
From Figure 4, one can see that the mean square error increases as the angle spread becomes larger. For all three groups, at K factor of 20dB, MSE shows the best performance while the worst accuracy occurs at the K factor of 0dB. In sub-figure B, the relationship trends are different from the ones observed in sub-figure A. As the angle spread increases, the channel capacity is enhanced. In all three groups of lines at three SNR values, the highest capacity occurs at K equal to 0dB while at 20dB the capacity is decreased. These two sub-figures indicate that the channel capacity is increased when the channel estimation accuracy is reduced. This finding is opposite to the one shown in [26,27,29]. This could be due to the fact that in [26,27,29] the influence of spatial correlation or K factor on the channel capacity was not considered. The presented simulation results strengthen the notion that the higher spatial correlation (due to a stronger LOS component) helps to improve the channel estimation accuracy. At the same time it decreases the rank and EDOF of the channel matrix.
Similar findings are obtained for the 4×4 MIMO system, as illustrated in Figure 5. The results are shown for SNR of 5, 10 and 15dB and the Rician factor K of 0 and 10dB.


Figure 4. MSE vs Angle Spread and Channel estimation vs Angle Spread of a 2×2 MIMO
under 3 different SNR and 3 different K factor.
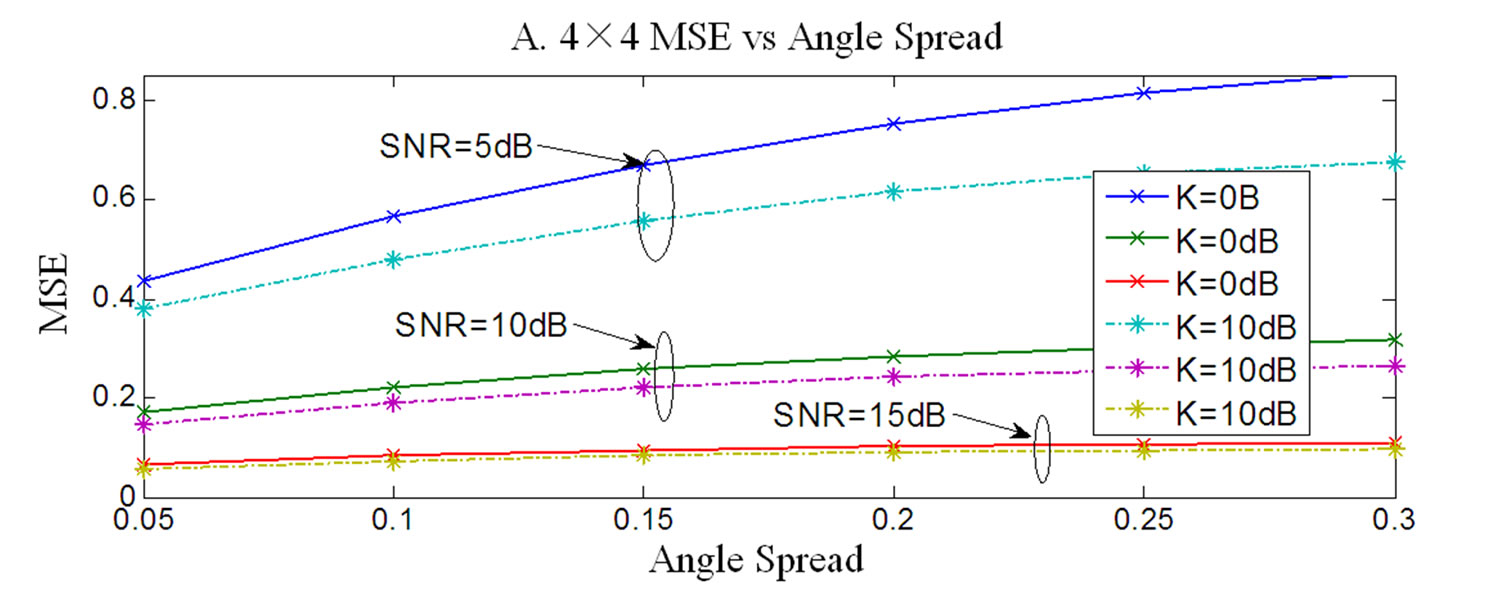

Figure 5. MSE vs Angle Spread and Channel estimation vs Angle Spread of a 4×4 MIMO under 3 different SNR and 3 different K factor.
At K factor of 10dB, MSE shows the best performance while the worst accuracy occurs at the K factor of 0dB. As the angle spread increases, the channel capacity increased. The highest capacity occurs at K equal to 0dB while at 10dB the capacity is decreased.
6. Conclusions
In this paper, the effect of spatial correlation on MIMO channel estimation accuracy and the resulting channel capacity has been investigated. The mathematical analysis and simulation results have shown that the accuracy of the training based MIMO channel estimation is governed by the sum of eigenvalues of the channel correlation matrix when the transmitted power to noise ratio (TPNR) in the training mode is fixed. Specifically, a smaller sum of eigenvalues leads to a more accurate channel estimation. A higher level of spatial correlation (that is due to a stronger LOS component and smaller angle spread) leads to a reduced value of the sum of channel correlation eigenvalues and hence has a positive influence on the channel estimation accuracy. However, this improvement in channel estimation does not necessarily lead to improving the channel capacity. This is because the channel matrix rank becomes reduced. The undertaken computer simulations undertaken for the uplink case, in which a mobile station (MS) transmitter is surrounded by scattering objects, have shown that higher spatial correlation levels due to a stronger LOS component decrease MIMO channel capacity despite the fact that channel estimation accuracy is improved.
7. References
[1] E. Telatar, “Capacity of multi-antenna Gaussian channels,” European Transactions on Telecommunications, Vol. 10, No. 6, pp. 585- 596, November 1999.
[2] T. L. Marzetta and B. M. Hochwald, “Capacity of a mobile multiple-antenna communication link in Rayleigh flat fading,” IEEE Transactions on Information Theory, Vol. 45, No. 1, pp. 139-157, January 1999.
[3] A. Narula, M. J. Lopez, M. D. Trott, and G. W. Wornell, “Efficient use of side information in multiple-antenna data transmission over fading channels,” IEEE Journal on Selected Areas in Communications, Vol. 16, No. 8, pp. 1423-1436, October 1998.
[4] C. Budianu and L. Tong, “Channel estimation for spacetime orthogonal block codes,” IEEE Transactions on Signal Processing, Vol. 50, pp. 2515-2528, October 2002.
[5] A. Grant, “Joint decoding and channel estimation for linear MIMO channels,” Proceedings of IEEE Wireless Communications Networking Conference, Vol. 3, pp. 1009-1012, Chicago, IL, September 2000.
[6] A. S. Kyung, R. W. Heath, and B. K. Heung, “Shannon capacity and symbol error rate of space-time block codes in MIMO Rayleigh channels with channel estimation error,” IEEE Transactions on Wireless Communication, Vol. 7, No. 1, pp. 324-333, January 2008.
[7] X. Zhang and B. Ottersten, “Performance analysis of VBLAST structure with channel estimation errors,” IEEE 4th Workshop on Signal Processing Advances in Wireless Communications SPAWC, pp. 487-491, June 2003.
[8] P. Layec, P. Piantanida, R. Visoz and A. O. Berthet, “Capacity bounds for MIMO multiple access channel with imperfect channel state information,” IEEE Information Theory Workshop ITW08, pp. 21-25, May 2008.
[9] M. Biguesh and A. B. Gershman, “MIMO channel estimation: Optimal training and tradeoffs between estimation techniques,” Proceedings of International Conference on Communications, ICC’04, Paris, France, Vol. 5, pp. 2658-2662, June 2004.
[10] M. Biguesh and A. B. Gershman, “Training-based MIMO channel estimation: A study of estimator tradeoffs and optimal training signals,” IEEE Transactions on Signal Processing, Vol. 54, No. 3, pp. 884-893, March 2006.
[11] X. Liu, S. Lu, M. E. Bialkowski and H. T. Hui, “MMSE Channel estimation for MIMO system with receiver equipped with a circular array antenna,” Proceedings of IEEE Microwave Conference APMC2007, pp. 1-4, December 2007.
[12] X. Liu, M. E. Bialkowski, and S. Lu, “Investigation into training-based MIMO channel estimation for spatial correlation channels,” Proceedings of IEEE International Antennas Propagation Symposium (APS-2007), pp. 51-55, August 2007.
[13] P. B. Rapajic and D. Popescu, “Information capacity of a random signature multiple-input multiple-output channel,” IEEE Transactions on Communications, Vol. 48, pp. 1245-1248, August 2000.
[14] P. J. Smith and M. Shafi, “On a Gaussian approximation to the capacity of wireless MIMO systems,” Proceedings of International Conference on Communications, ICC’02, pp. 406-410, 2002.
[15] P. F. Driessen and G. J. Foschini, “On the capacity formula for multiple-input multiple-output wireless channels: A geometric interpretation,” IEEE Transactions on Communications, Vol. 47, pp. 173-176, February 1999.
[16] D. Shiu, G. J. Foschini, M. J. Gans, and J. M. Kahn, “Fading correlation and its effect on the capacity of multielement antenna systems,” IEEE Transactions on Communications, Vol. 48, No. 3, pp. 502-513, March 2000.
[17] V. Erceg, “Indoor MIMO WLAN channel models,” IEEE 802.11-03/161r2, September 2003.
[18] P. Uthansakul, M. E. Bialkowski, S. Durrani, K. Bialkowski, and A. Postula, “Effect of line of sight propagation on capacity of an indoor MIMO system,” Proceedings of IEEE International Antennas Propagation Symposium (APS-2005), Washington, DC, pp. 707-710, 2005.
[19] E. G. Larsson and P. Stoica, “Space-time block coding for wireless communication,” Cambridge University Press, 2003.
[20] C. N. Chuah, D. N. C. Tse, and J. M. Kahn, “Capacity scaling in MIMO wireless systems under correlated fading,” IEEE Transactions on Information Theory, Vol. 48, pp. 637-650, March 2002.
[21] W. C. Jakes, “Microwave mobile communications,” New York: John Wiley & Sons, 1974.
[22] T. L. Fulghum, K. J. Molnar and A. Duel-Hallen, “The Jakes fading model for antenna arrays incorporating azimuth spread,” IEEE Transactions on Vehicular Technology, Vol. 51, No. 5, pp. 968-977, September 2002.
[23] S. M. Kay, “Fundamentals of statistic signal processing: Estimation theory”, Prentice-Hall, Inc., 1993.
[24] G. J. Foschini and M. J. Gans, “On the limits of wireless communications in fading environment when using multiple antennas,” Wireless Personal Communications, Vol. 6, pp. 311-335, 1998.
[25] B. M. Hochwald and T. L. Marzetta, “Capacity of a mobile multiple antenna communication link in Rayleigh flat fading,” IEEE Transactions on Information Theory, Vol. 45, No. 1, pp. 139-157, January 1999.
[26] T. Yoo and A. Goldsmith, “Capacity and power allocation for fading MIMO channels with channel estimation error,” IEEE Transactions on Information Theory, Vol. 52, No. 5, pp. 2203-2214, May 2006.
[27] T. Yoo and A. Goldsmith, “Capacity of fading MIMO channels with channel estimation error,” IEEE International Conference on Communications, Vol. 2, pp. 808- 813, June 2004.
[28] M. Medard, “The effect upon channel capacity in wireless communications of perfect and imperfect knowledge of the channel,” IEEE Transactions on Information Theory, Vol. 46, pp. 933-946, May 2000.
[29] M. Torabi, M. R. Soleymani, and S. Aissa, “On the performance of MIMO-OFDM systems with imperfect channel information,” International Conference on Wireless Networks, Communications and Mobile Computing, Vol. 1, pp. 600-605, June 2005.

