Journal of Intelligent Learning Systems and Applications
Vol.06 No.04(2014), Article ID:50485,9 pages
10.4236/jilsa.2014.64014
A Reinforcement Learning System to Dynamic Movement and Multi-Layer Environments
Uthai Phommasak1, Daisuke Kitakoshi2, Hiroyuki Shioya1, Junji Maeda1
1Division of Information and Electronic Engineering, Muroran Institute of Technology, Muroran, Japan
2Department of Information Engineering,
Email: 12092001@mmm.muroran-it.ac.jp, kitakosi@tokyo-ct.ac.jp, shioya@csse.muroran-it.ac.jp, junji@csse.muroran-it.ac.jp
Academic Editor: Dr. Steve S. H. Ling, University of Technology Sydney, Australia
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 August 2014; revised 26 September 2014; accepted 8 October 2014
ABSTRACT
There are many proposed policy-improving systems of Reinforcement Learning (RL) agents which are effective in quickly adapting to environmental change by using many statistical methods, such as mixture model of Bayesian Networks, Mixture Probability and Clustering Distribution, etc. However such methods give rise to the increase of the computational complexity. For another method, the adaptation performance to more complex environments such as multi-layer environments is required. In this study, we used profit-sharing method for the agent to learn its policy, and added a mixture probability into the RL system to recognize changes in the environment and appropriately improve the agent’s policy to adjust to the changing environment. We also introduced a clustering that enables a smaller, suitable selection in order to reduce the computational complexity and simultaneously maintain the system’s performance. The results of experiments presented that the agent successfully learned the policy and efficiently adjusted to the changing in multi-layer environment. Finally, the computational complexity and the decline in effectiveness of the policy improvement were controlled by using our proposed system.
Keywords:
Reinforcement Learning, Profit-Sharing Method, Mixture Probability, Clustering

1. Introduction
Along with the increasing need for rescue robots in disasters such as earthquakes and tsunami, there is an urgent need to develop robotics software for learning and adapting to any environment. Reinforcement Learning (RL) is often used in developing robotic software. RL is an area of machine learning within the computer science domain, and many RL methods have recently been proposed and applied to a variety of problems [1] -[4] , where agents learn the policies to maximize the total number of rewards decided according to specific rules. In the process whereby agents obtain rewards; data consisting of state-action pairs are generated. The agents’ policies are effectively improved by a supervised learning mechanism using the sequential expression of the stored data series and rewards.
Normally, RL agents need to initialize the policies when they are placed in a new environment and the learning process starts afresh each time. Effective adjustment to an unknown environment becomes possible by using statistical methods, such as a Bayesian network model [5] [6] , mixture probability and clustering distribution [7] [8] , etc., which consist of observational data on multiple environments that the agents have learned in the past [9] [10] . However, the use of a mixture model of Bayesian networks increases the system’s calculation time. Also, when there are limited processing resources, it becomes necessary to control the computational complexity. On the other hand, by using mixture probability and clustering distribution, even though the computational complexity was controlled and the system’s performance was simultaneously maintained, the experiments were only conducted on fixed obstacle 2D-environments. Therefore, examination of the computational complexity load and the adaptation performance in dynamic 3D-environments is required.
In this paper, we describe modifications of profit-sharing method with new parameters that make it possible to work on dynamic movement of multi-layer environments. We then describe a mixture probability consisting of the integration of observational data on environments that agent learned in the past within framework of RL, which provides initial knowledge to the agent and enables efficient adjustment to a changing environment. We also describe a novel clustering that makes it possible to select fewer elements for a significant reduction in the computational complexity while retaining system’s performance.
The paper is organized as follows. Section 2 briefly explains the profit-sharing method, the mixture probability, the clustering distribution, and the flow system. The experimental setup and procedure as well as the presentation of results are described in Section 3. Finally, Section 4 summarizes the key points and mentions our future work.
2. Preparation
2.1. Profit-Sharing
Profit-sharing is an RL method that is used as a policy learning mechanism in our proposed system. RL agents learn their own policies through “rewards” received from an environment.
2.1.1. 2D-Environments
The policy is given by the following function:
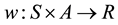 (1)
(1)
where 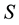 and
and 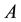 denote a set of state and action, respectively. Pair
denote a set of state and action, respectively. Pair 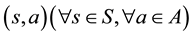 is referred to as a rule.
is referred to as a rule. 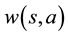 is used as the weight of the rule (
is used as the weight of the rule (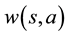 is positive in this paper). When state
is positive in this paper). When state 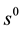 is observed, a rule is selected in proportion to the weight of rule
is observed, a rule is selected in proportion to the weight of rule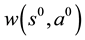 . The agent selects a single rule corresponding to given state
. The agent selects a single rule corresponding to given state 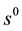 using the following probability:
using the following probability:
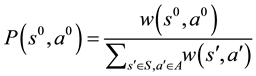 (2)
(2)
The agent stores the sequence of all rules that were selected until the agent reaches the target as an episode.
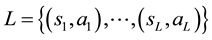 (3)
(3)
where 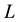 is the length of the episode. When the agent selects rule
is the length of the episode. When the agent selects rule 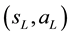 and requires reward
and requires reward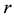 , the weight of each rule in the episode is reinforced by
, the weight of each rule in the episode is reinforced by
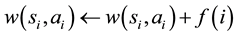 (4)
(4)
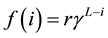 (5)
(5)
where 

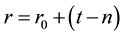
where 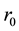

2.1.2. 3D-Environments
The weight 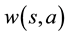

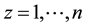

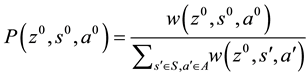
and the new episode is given in the following function:
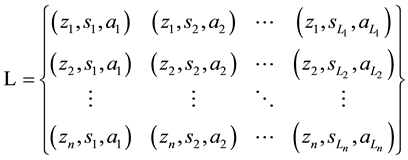
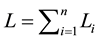
By the movement on
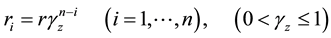
and update the weights according to the following function by using function (10):
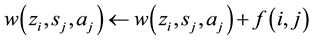
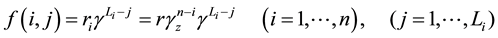
2.1.3. Ineffective Rule Suppression
As Figure 1, agent selects rule 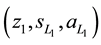
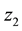
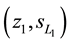

The ineffective rule has more negative effect such as the rules continue being selected repeatedly on the movement of 
In this paper, we use this following method to suppress the ineffective rule:
Here, we use 
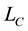
When
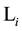
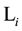
nal rule in 
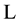
2.2. Mixture Probability
Mixture probability is a mechanism for recognizing changes in the environment and consequently improving the agent’s policy to adjust to those changes.
The joint distribution [14] 
Figure 1. Example of ineffective rule.
probabilistic knowledge about the environment. Furthermore, the policy acquired by the agent is improved by using the mixture probability of 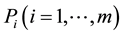
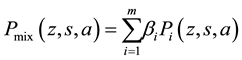
where 
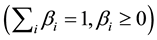
adjusting the environment subject to this mixing parameter, we expect appropriate improvement of the policy on the unknown dynamic environment.
In this paper, we use the following Hellinger distance [15] function to fix the mixing parameter:
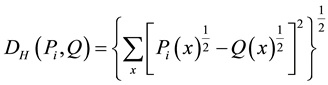
where 
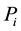
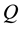

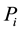

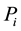
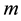
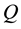
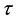
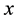
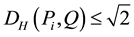

However, when
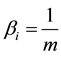
2.3. Clustering Distributions
We expect that the computational complexity of the system can be controlled and it will be possible to maintain the effectiveness of policy learning by selecting only the suitable joint distributions as the mixture probability elements based on this clustering method.
In this study, we used the group average method as opposed to the clustering method. The distance between the clusters can be determined by the following function:
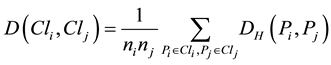
where 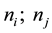
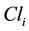
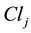


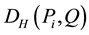
2.4. Flow System
The system framework is shown in Figure 2. A case involving the application of mixture probability and clustering distributions to improve the agent’s policy is explained in the following procedure:
Figure 2. System framework.
Step 1 Learn the policy in 
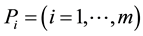
Step 2 Cluster distributions into 
Step 3 Calculate the Hellinger distance 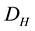
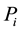

Step 4 Select the element having the minimum 
Step 5 Calculate the mixing parameter
Step 6 Mix probability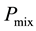
Step 7 Update the weight of all rules by using the following function:

and then continue learning the updated weight by using the profit-sharing method.
3. Experiments
We performed an experiment to demonstrate the agent navigation problem and to illustrate the applied improvement in the RL agent’s policy through the modification of parameters of the profit-sharing method and using the mixture probability scheme. The purpose of this experiment was to evaluate the adjustment performance in the unknown dynamic 3D-environment by applying the policy improvement, and to evaluate its effectiveness by using mixture probability.
3.1. Experimental Setup
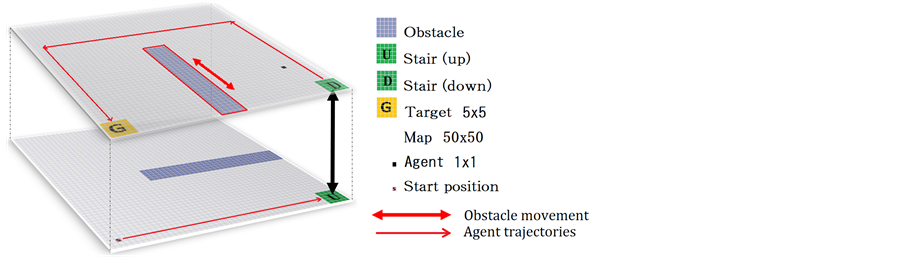
The aim in the agent navigation problem is to arrive at the target from the default position of the environment where the agent is placed. In the experiment, the reward is obtained when the agent reaches the target by avoiding the obstacle in the environment, as shown in Figure 3.
The types of state and action are shown in Table 1 and Table 2, respectively. Table 1 shows the output actions of an agent in 8 directions and Table 2 shows 256 types of the total input states coming from the combination of existing obstacles in 8 directions. The 8 directions are the top left, top, top right, left, right, bottom left, bottom, and bottom right. The agent has 2048 (8 actions × 512 states) rules in total that result from a combination of input states and output actions in a layer. The size of agent, target, and environment are 1 × 1, 5 × 5, and 50 × 50, respectively.
3.2. Experimental Procedure
The agent learns the policy by using the profit-sharing method. A trial is considered to be successful if an agent
Figure 3. Environment of agent navigation problem.
Table 1. Types of action.
Table 2. Some types of state.
reaches the target at least once out of 200 action attempts. The action is selected by randomization and that action continues until the state is changed.
The purpose of the experiment is to learn the policy in unknown dynamic environments 
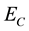
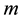
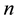
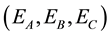
3.3. Discussion
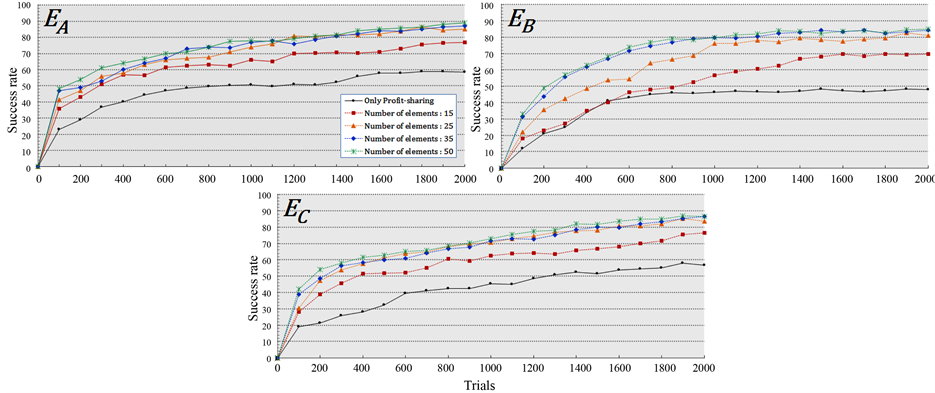
The success rate of policy improvement in 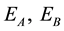
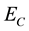
Figure 6 shows that the immediate success rate obtained by policy improvement is higher than that obtained by only the profit-sharing method in all environments. This means the speed of adaptation in unknown environment is higher and the higher success rate continues until the experiments end. This results shows the success rate by policy improvement is higher than using only the profit-sharing more than 20% in 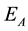
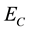
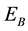
Even the success rate by using only 15 elements is also higher than that using only the profit-sharing method, but is still lower compared to the results using 25 and 35 elements. Hence, we can say by reducing the number of elements too much, the influence on policy improvement is apparent in all environments. However, although
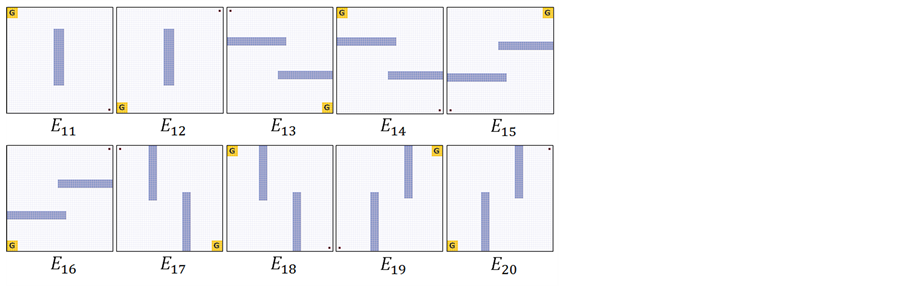
Figure 4. Some of known environments.
Figure 5. Unknown environments.
Figure 6. Transition of success rate.
Table 3. Experimental parameters.
Table 4. Processing time.
the success rate using all 50 elements was the highest, but that obtained using 25 elements was almost the same as that using all the elements in this result. So, the decline in effectiveness can still be controlled even if the number of mixture probability elements is reduced to half.
Furthermore, from the results in Table 4, we can see that by reducing the number of elements, the processing time was reduced considerably. Hence, we can say by using 25 elements, we can reduce the processing time without declining in policy improvement performance.
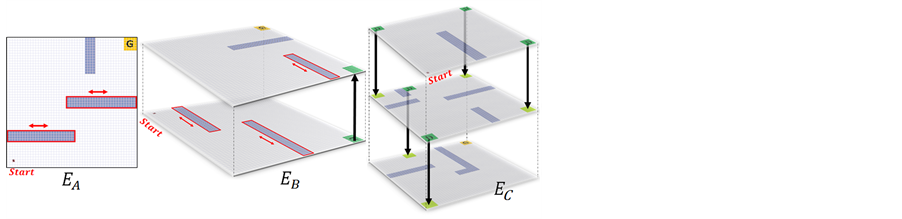
Figure 7 shows the typical trajectories of agent following the policy acquired while selecting data in environment 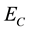
In these results, we can see in the first 500 trials, agent reached to all sub-targets in top layer. But due to the agent which started from sub-target 1 was the most difficult for reaching next sub-target, the number of time that agent reached to sub-target 1 became fewer in 501 - 1000 trials and finally almost reached to sub-target 2 and 3 in 1001 - 2000 trials. Also in middle layer, agent reached to all sub-targets in first 500 trials. But due to the agent which started from sub-target 5 was more easily for reaching to the final goal, the more number of trials there are, the more frequency of agent’s trajectories from sub-target 5 to the final goal increased clearly.
From the results of typical agent’, we can say by using the pseudo-reward, the agent can choose more suitable rules to reach the target in each layers even agent might be sometimes more difficult to reach in some layer, but more easily to reach to the final goal.
3.4. Supplemental Experiments
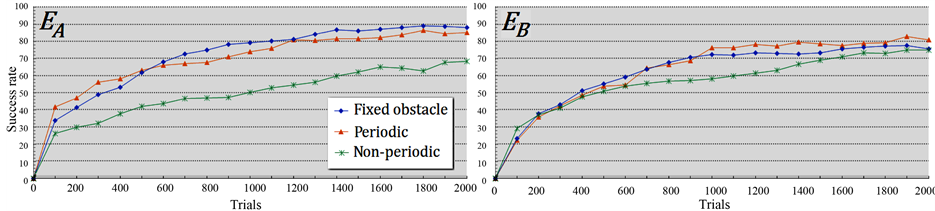
These experiments were conducted to compare the performance of the policy improvement in cases of fixed obstacle, periodic dynamic movement and nonperiodic dynamic movement on 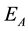

4. Discussion
The results of policy improvement by using 25 elements of mixture probabilities in three cases are shown in Figure 8, and the results of five sets of experiments in periodic and nonperiodic dynamic movement are shown in Figure 9, respectively.
Figure 8 shows that the success rate in the case of periodic dynamic movement was almost no difference in the early period compared with the fixed obstacle case in both 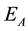
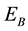
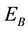
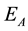
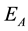
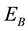
From these results, we can deduce that agent successfully learns the policy in the periodic dynamic movement environment and can more easily reach the target when the obstacle moves out from the trajectory as in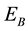
5. Conclusions
In this research, we used the joint distributions 
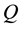
Figure 7. Typical agent trajectories in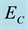
Figure 8. Transition of success rate (3 cases).
Figure 9. Five sets of experiments.
find the degree of similarity between the unknown and each known environment. We then used this as the basis to update the initial knowledge as being very useful for the agent to learn the policy in a changing environment. Even if obtaining the sample distribution is time-consuming, it is still worthwhile if the agent can efficiently learn the policy in an unknown dynamic environment.
Also, by using the clustering method to collect similar elements and then selecting just one suitable joint distribution as the mixture probability elements from each cluster, we can avoid using similar elements to maintain a variety of elements when we reduce their number.
From the results of the computer experiment as an example application in the agent navigation problem, we can confirm that the policy improvement in dynamic movement environments is effective by using the mixture probabilities. Furthermore, agent is possible to select suitable rules to reach to the target in multi-layer by using the pseudo-reward. And the decline in effectiveness of the policy improvement can be controlled by using the clustering method. We conclude that the improvement of stability and speed in policy learning, and the control of computational complexity are effective by using our proposed system.
Improvement of the RL policy is also required by using mixture probability with a positive and negative weight value for making the system adaptable to unknown environments that are not similar to any known environments. Finally, a new reward process is needed as well as a new mixing parameter for the agent to adjust to a changing environment more efficiently and to be able to work well in any complicate environments in future work.
Acknowledgements
This research paper is made possible through the help and support by Honjo International Scholarship Foundation.
References
- Sutton, R.S. and Barto, A.G. (1998) Reinforcement Learning: An Introduction. MIR Press, Cambridge.
- Croonenborghs, T., Ramon, J., Blockeel, H. and Bruynooghe, M. (2006) Model-Assisted Approaches for Relational Reinforcement Learning: Some Challenges for the SRL Community. Proceedings of the ICML-2006 Workshop on Open Problems in Statistical Relational Learning, Pittsburgh.
- Fernandez, F. and Veloso, M. (2006) Probabilistic Policy Reuse in a Reinforcement Learning Agent. Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multi-Agent Systems, New York, May 2006, 720- 727. http://dx.doi.org/10.1145/1160633.1160762
- Kober, J., Bagnell, J.A. and Peters, J. (2013) Reinforcement Learning in Robotics: A Survey. International Journal of Robotics Research, 32, 1238-1274. http://dx.doi.org/10.1177/0278364913495721
- Kitakoshi, D., Shioya, H. and Nakano, R. (2004) Adaptation of the Online Policy-Improving System by Using a Mixture Model of Bayesian Networks to Dynamic Environments. Electronics, Information and Communication Engineers, 104, 15-20.
- Kitakoshi, D., Shioya, H. and Nakano, R. (2010) Empirical Analysis of an On-Line Adaptive System Using a Mixture of Bayesian Networks. Information Science, 180, 2856-2874. http://dx.doi.org/10.1016/j.ins.2010.04.001
- Phommasak, U., Kitakoshi, D. and Shioya, H. (2012) An Adaptation System in Unknown Environments Using a Mixture Probability Model and Clustering Distributions. Journal of Advanced Computational Intelligence and Intelligent Informatics, 16, 733-740.
- Phommasak, U., Kitakoshi, D., Mao, J. and Shioya, H. (2014) A Policy-Improving System for Adaptability to Dynamic Environments Using Mixture Probability and Clustering Distribution. Journal of Computer and Communications, 2, 210-219. http://dx.doi.org/10.4236/jcc.2014.24028
- Tanaka, F. and Yamamura, M. (1997) An Approach to Lifelong Reinforcement Learning through Multiple Environments. Proceedings of the Sixth European Workshop on Learning Robots, Brighton, 1-2 August 1997, 93-99.
- Minato, T. and Asada, M. (1998) Environmental Change Adaptation for Mobile Robot Navigation. 1998 IEEE/RSJ International Conference on Intelligent Robots and Systems, 3, 1859-1864.
- Ghavamzadeh, M. and Mahadevan, S. (2007) Hierarchical Average Reward Reinforcement Learning. The Journal of Machine Learning Research, 8, 2629-2669.
- Kato, S. and Matsuo, H. (2000) A Theory of Profit Sharing in Dynamic Environment. Proceedings of the 6th Pacific Rim International Conference on Artificial Intelligence, Melbourne, 28 August-1 September 2000, 115-124.
- Nakano, H., Takada, S., Arai, S. and Miyauchi, A. (2005) An Efficient Reinforcement Learning Method for Dynamic Environments Using Short Term Adjustment. International Symposium on Nonlinear Theory and Its Applications, Bruges, 18-21 October 2005, 250-253.
- Hellinger, E. (1909) Neue Begrü ndung der Theorie quadratischer Formen von unendlichvielen Verä nderlichen. Journal für die Reine und Angewandte Mathematik, 136, 210-271.
- Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann Pub. Inc., San Francisco.