Journal of Intelligent Learning Systems and Applications
Vol.4 No.3(2012), Article ID:22027,14 pages DOI:10.4236/jilsa.2012.43018
A Competitive Markov Approach to the Optimal Combat Strategies of On-Line Action Role-Playing Game Using Evolutionary Algorithms
![]()
Graduate School of Advanced Integration Science, Chiba University, Chiba, Japan.
Email: *chenhaoyang@graduate.chiba-u.jp
Received March 1st, 2012; revised June 25th, 2012; accepted July 3rd, 2012
Keywords: Game Design; Game Balance; Competitive Markov Decision Process; Cooperative Coevolutionary Algorithm; Competitive Coevolution
ABSTRACT
In the case of on-line action role-playing game, the combat strategies can be divided into three distinct classes, Strategy of Motion(SM), Strategy of Attacking Occasion (SAO) and Strategy of Using Skill (SUS). In this paper, we analyze such strategies of a basic game model in which the combat is modeled by the discrete competitive Markov decision process. By introducing the chase model and the combat assistant technology, we identify the optimal SM and the optimal SAO, successfully. Also, we propose an evolutionary framework, including integration with competitive coevolution and cooperative coevolution, to search the optimal SUS pair which is regarded as the Nash equilibrium point of the strategy space. Moreover, some experiments are made to demonstrate that the proposed framework has the ability to find the optimal SUS pair. Furthermore, from the results, it is shown that using cooperative coevolutionary algorithm is much more efficient than using simple evolutionary algorithm.
1. Introduction
In recent years, on-line Action Role-Playing Games (ARPGs) become more and more popular all over the world. An on-line ARPG is a virtual world that consists of several distinct races. Player first creates a character of any race, then plays the game by both exploring the virtual world and fighting with others. During gaming, player has direct control over the created character. Usually, the on-line ARPG is regarded as an extension of the off-line one by the reason that it allows players to fight with each other besides AI opponent. Such new feature results in more complexity of the game balance.
What is the game balance? In the off-line ARPG, game balance means the difficulty control of the game and can be reached simply by adjusting the power of AI opponent. On the other hand, however, in the on-line ARPG, game balance mainly refers to power balancing among the races. Currently, on-line ARPGs are balanced by hand tuning, but this approach presents several problems. Human players are expensive in both time and resources, and even human players can not explore all strategies to find out whether a dominate one exists [1]. Moreover, since strengthening one race will definitely weaken the others, the result of tuning operations may, somehow, become worse. It is hard to control. Hence, a more theoretical and efficient design method is needed.
Chen, et al. [2,3] have proposed an evolutionary design method for both turn-based and action-based on-line role-playing games. In such approaches, they, successfully, constructed an automated testing framework to verify whether the game world is well-balanced. However, they just investigated the case in which each race has only one skill. The situation of having multi-skills was ignored because they failed to retrieve the optimal Strategy of Using Skill (SUS), which plays a crucial role in the automated testing framework.
In this paper, we propose an evolutionary framework, including integration with competitive coevolution and cooperative coevolution, to search the optimal SUS pair of a basic action-based game model, where the combat is modeled by the Discrete Competitive Markov Decision Process (DCMDP) [4]. Also, by introducing the Chase Model and the Combat Assistant Technology (CAT), we analyze the optimal Strategy of Motion (SM) and the optimal Strategy of Attacking Occasion (SAO) of the game model.
The paper is organized as follows. In Section 2, a brief description of DCMDP and a theorem are given. The details of Cooperative Coevolutionary Algorithm (CCEA) technology are explained in Section 3. Section 4 presents a basic action-based game model and its optimal SM as well as SAO. Section 5 describes the proposed competetive framework. Experimental results are reported in Section 6. The conclusions and possible future research directions are given in Section 7.
2. Discrete Competitive Markov Decision Process
A DCMDP is a multi-player dynamic system that evolves along discrete time points. At each time point t, the state of the system, denoted by St, is a random variable that can take on values from the finite set S = 1, 2, ···, N. At these discrete time points, called stages, both players have the possibility to influence the course of the system. In this paper, we only consider the case of two players, and we associate two finite action sets A1(s) = {1, 2, ···, m1(s)} for player 1 and A2(s) = {1, 2, ···, m2(s)} for player 2, then at any stage, the system is one of the states and both players are allowed to choose an action out of their respective action sets independently of one another. If in a state s, at some decision moment, player 1 chooses  and player 2 chooses
and player 2 chooses , then two things happen:
, then two things happen:
1) Player 1 earns the immediate reward r1(s, a1, a2) and player 2 earns r2(s, a1, a2).
2) The dynamic of the system is influenced. The state at the next decision moment is determined in a stochastic sense by a transition vector which is denoted as:

a simple example of the DCMDP is shown in Figure 1.
2.1. Classes of Strategy
Strategies for players are rules that tell them what action to choose in any situation. The choice at a certain decision moment may depend upon the history of the play up to that moment. Furthermore, as is usual in game theory,
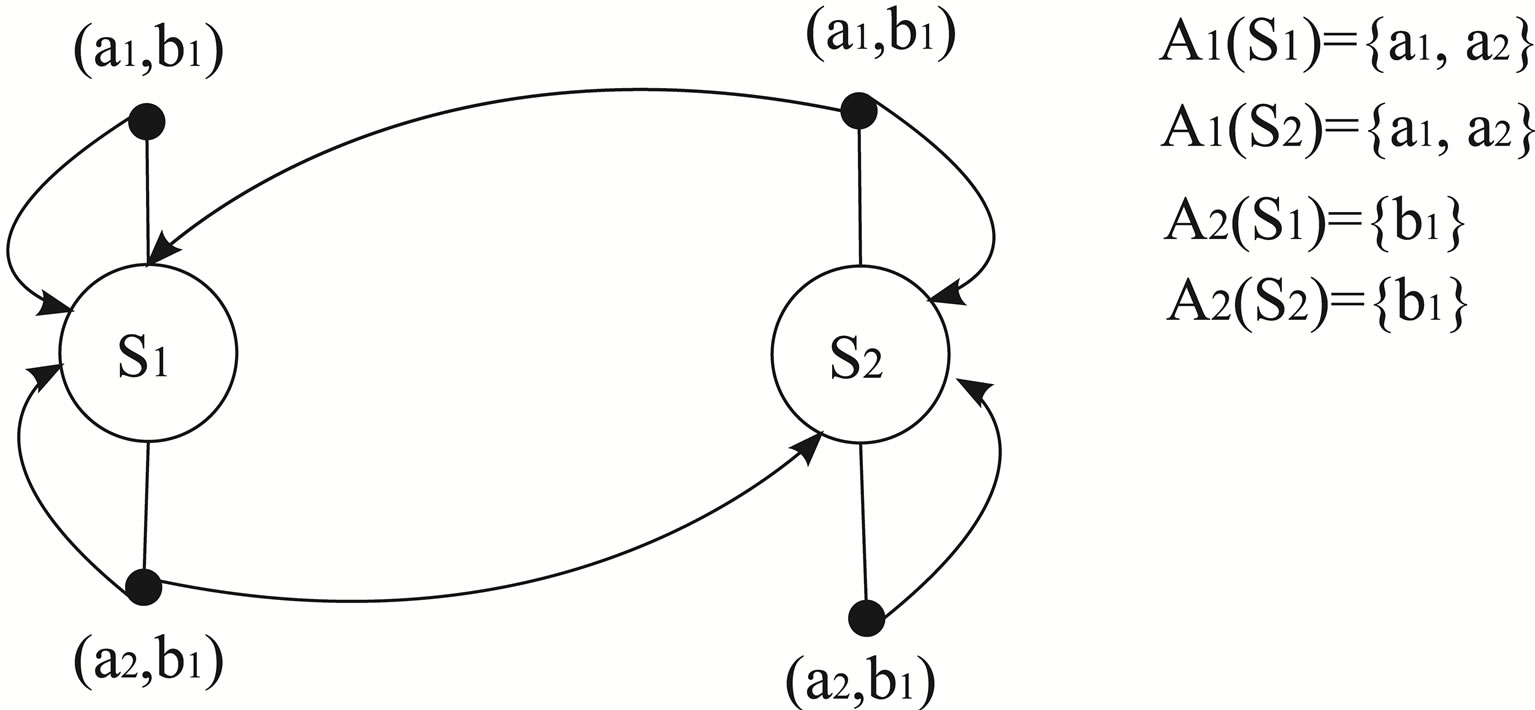
Figure 1. A discrete competitive markov decision process with two states.
the choice of an action may occur in randomized way, that is, the players can specify a probability vector over their action spaces and next the action is the result of a chance experiment according to this probability vector.
There are three classes of strategy exist, namely, the behavior strategy, the Markov strategy, and the stationary strategy.
Behavior strategy, denoted by FB, being the most general type of strategy, can be represented by a sequence π = (f(0), f(1), f(2), ···), where, for each t = 0, 1, 2, ···, the decision rule ft = (ft(1), ft(2), ···, ft(N)) specifies for each state s a probability vector ft(s) on A(s) as a function of history of the game up to decision moment t.
A Markov strategy, denoted by FM, is a behavior strategy where, for every t = 0, 1, 2, ···, the decision rule ft is completely determined by the decision moment t and the current state st at moment t.
A stationary strategy is a Markov strategy where, for every t = 0, 1, 2, ···, the decision rule ft is completely determined by the current state st at moment t. Thus, a stationary strategy can be represented by a sequence π = (f, f, f, ···), where f = (f(1), f(2), ···, f(N)) specifies for each state s 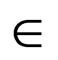 S a probability vector f(s) on A(s). We will denote such stationary strategy by FS. If the players use
S a probability vector f(s) on A(s). We will denote such stationary strategy by FS. If the players use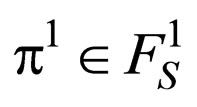 ,
, 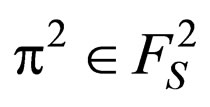 as their strategy respectively, there exist stationary transition probabilities:
as their strategy respectively, there exist stationary transition probabilities:
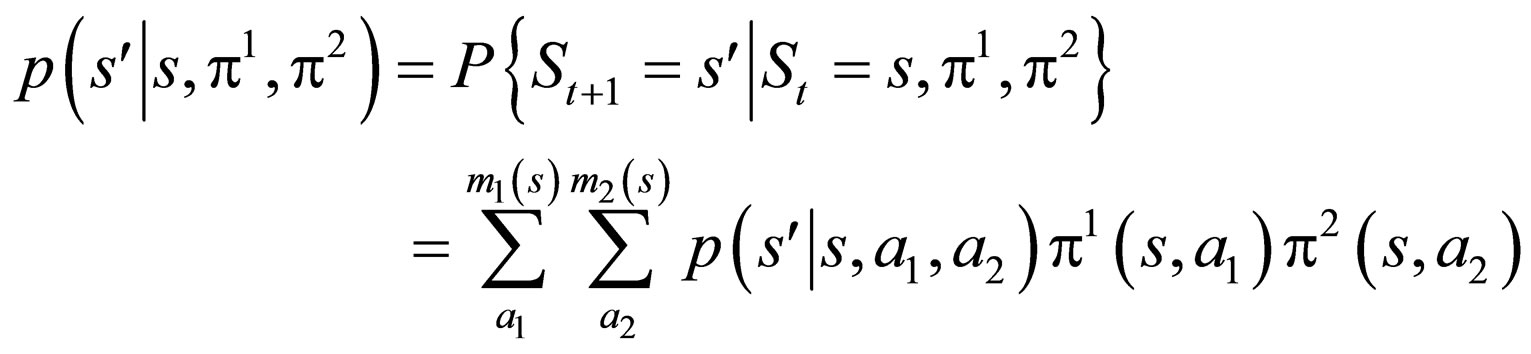 (1)
(1)
for all t = 0, 1, 2, ···, and Formula 1 is called Stationary Markov Transition Property.
2.2. β-Discounted Competitive Markov Decision Model
The infinite stream of rewards that results during a particular implementation of a strategy pair 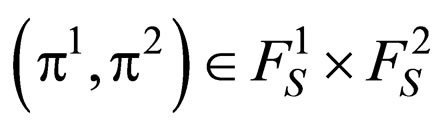 need to be evaluated in some manner. So, the β-Discounted Competitive Markov Decision Model, denoted by Γβ, is introduced.
need to be evaluated in some manner. So, the β-Discounted Competitive Markov Decision Model, denoted by Γβ, is introduced.
We have  denoting the reward at time t to player k, as well as
denoting the reward at time t to player k, as well as

denoting the immediate excepted reward vector to player k corresponding to a strategy pair (π1, π2) mentioned above, where k = 1, 2, and rk(s, π1, π2), for each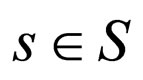 , can be calculated by the following formula:
, can be calculated by the following formula:
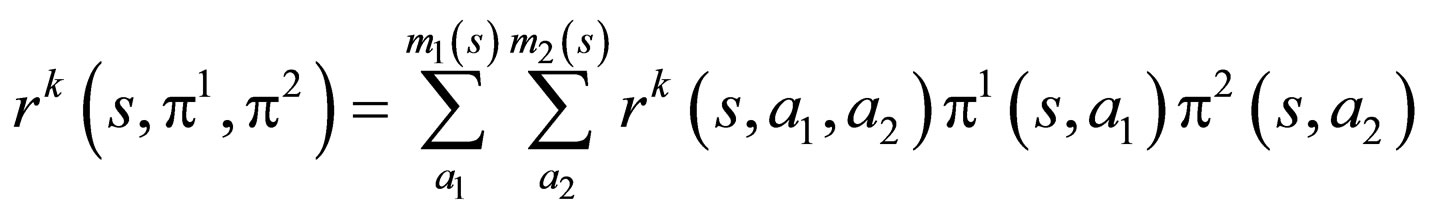
The expected reward at stage t to player k resulting from (π1, π2) and an initial state s is denoted by:

where [u]s denotes the sth entry of a vector u, Pt(π1, π2) is the t-step Transition Probability Matrix (TPM). Consequently, the sth entry of the overall discounted value vector of a strategy pair (π1, π2) to player k will be given by:
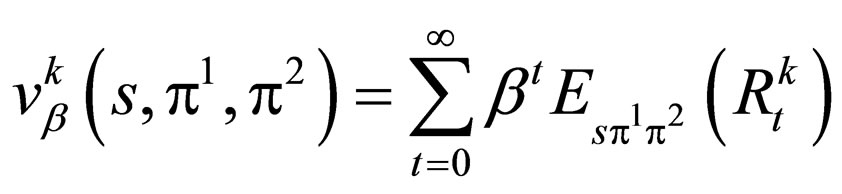 (2)
(2)
where .
.
Theorem 1
Let  be a optimal strategy pair of Γβ, then (π1*, π2*) is optimal in the entire class of behavior strategies. That is:
be a optimal strategy pair of Γβ, then (π1*, π2*) is optimal in the entire class of behavior strategies. That is:
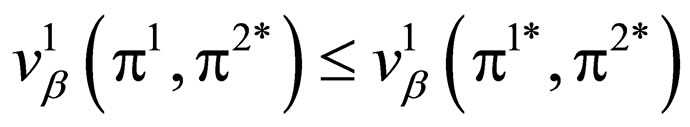
and

for all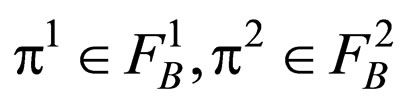 .
.
Proof:
Let either π1* or π2* be fixed, then the Γβ will reduce to the discounted Markov decision model which has only one player. Further, for the discounted Markov decision model, it is well-known that the optimal stationary strategy is optimal in the entire class of behavior strategies [4]. This completes the proof.
In the game theory, we also call that 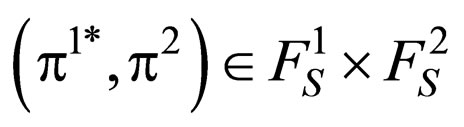 is a Nash Equilibrium Point (EP) of the space
is a Nash Equilibrium Point (EP) of the space . This theorem is vary important because it suggests that we can retrieve the EP of
. This theorem is vary important because it suggests that we can retrieve the EP of 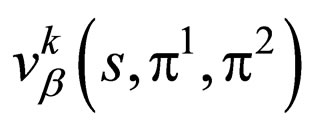 with
with 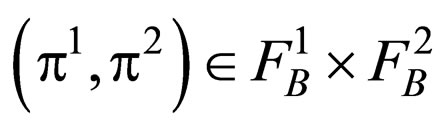 by just searching the space of
by just searching the space of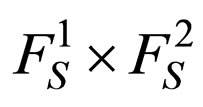 .
.
2.3. Zero-Sum Γβ
A Γβ will be called sum-zero if
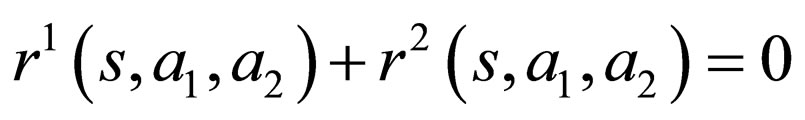 (3)
(3)
for all ,
,  ,
, . Thus we may drop the superscript k by defining:
. Thus we may drop the superscript k by defining:
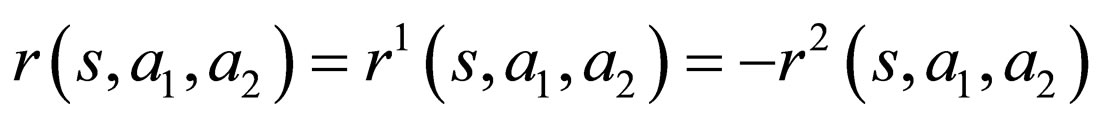
so, a extension of this definition lead to the following:
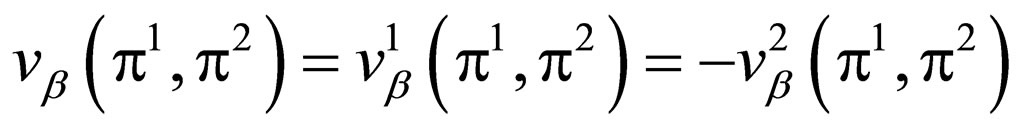
for all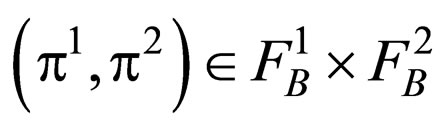 .
.
Hence, in the case of zero-sum Γβ, the two sets of inequalities defining an EP reduce to the single set of saddle-point inequality as follow:
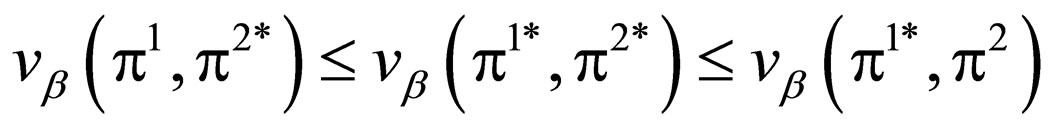 (4)
(4)
Formula 4 leads to an important property, that is, if 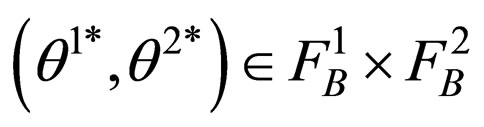 is another pair of optimal strategies, then we have the following equation:
is another pair of optimal strategies, then we have the following equation:
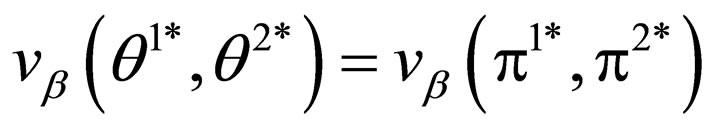 (5)
(5)
this simply means that in the case of zero-sum Γβ, the overall discounted value vectors of all optimal strategy pair coincide and can be denoted by:
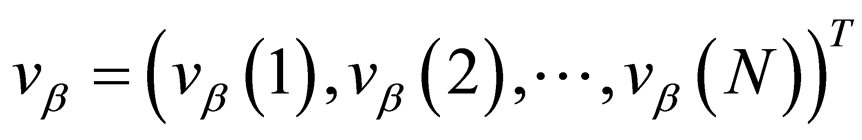
Thus, we can retrieve vβ by searching the space  instead of
instead of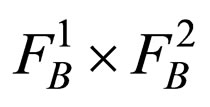 , and the result follows from Theorem 1 and Formula 5.
, and the result follows from Theorem 1 and Formula 5.
3. Cooperative Coevolutionary Algorithm
CCEAs [5,6] have been applied to solve large and complex problems, such as multiagent systems [7-9], rule learning [10,11], fuzzy modeling [12], and neural network training [13]. It models an ecosystem which consists of two or more species. Mating restrictions are enforced simply by evolving the species in separate populations which interact with one another within a shared domain model and have a cooperative relationship. The original architecture of the CCEA for optimization can be summarized as follows:
1) Problem Decomposition: Decompose the target problem into smaller subcomponents and assign each of the subcomponents to a population;
2) Subcomponents Interaction: Combine the individual of a particular population with representatives selected from others to form a complete solution, then evaluate the solution and attribute the score to the individual for fitness;
3) Subcomponent Optimization: Evolve each population separately by using a different evolutionary algorithm, in turn.
The empirical analyses have shown that the power of CCEAs depends on the decomposition work as well as separate evolving of these populations resulting in significant speedups over Simple Evolutionary Algorithm (SEA) [14-16]. Here, we give the theoretical evidence of such results with the following two assumptions.
1) The elitists of CCEA populations are chosen as the representatives;
2) There are no variational operators in both the SEA and CCEA.
Let’s begin with some definitions.
Definition 1. Given schemata: H1, H2, ···, Hn where Hi denotes a schema of the ith CCEA population, the n-expanded schema, denoted by H1, is the sequential concatenation of the n schemata. For example, let H1 = [1*0*], H1 = [*1*1], then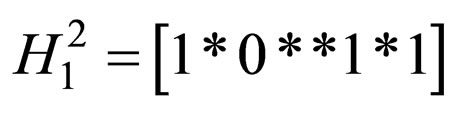 .
.
Definition 2. Let there be n populations in the CCEA. A complete genotype is the sequential concatenation of n individuals selected from n different populations. If all the individuals are representatives, then the complete genotype is the best one.
Definition 3. Given an individual I of the ith CCEA population, the expanded genotype of I is the best complete genotype in which the ith representative is replaced by I.
Definition 4. Given a target problem J, the two algorithms, SEA and CCEA, are comparable if the population of the SEA consists of all the expanded genotypes in the CCEA.
Theorem 2
Let a target problem f be decomposed into n subcomponents, ri be the increasing rate of the individuals matching Hi in the ith CCEA population, rccEA be the increasing rate of the complete genotypes matching  in the CCEA, and rSEA be the increasing rate of the individuals matching
in the CCEA, and rSEA be the increasing rate of the individuals matching 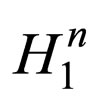 in the SEA. If the two algorithms are comparable, then1)
in the SEA. If the two algorithms are comparable, then1) 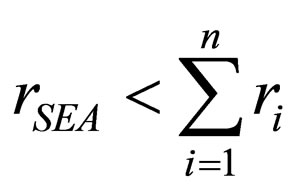
2) 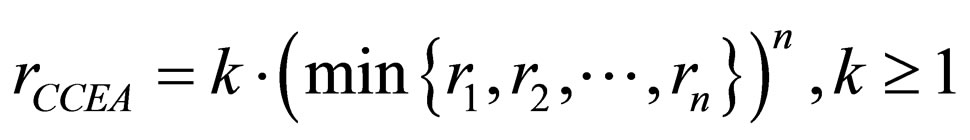
Proof:
Since the two algorithms are comparable, in the SEA, the number of individuals matching 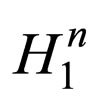 at generation t can be calculated by:
at generation t can be calculated by:
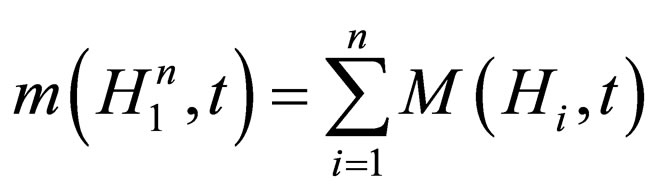
where M(Hi, t) denotes the number of individuals matching Hi at generation t, in the ith CCEA population. Then according to the schema theorem (refer to Thm. 1), we have,

where in the ith CCEA population, 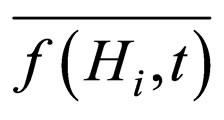 and
and 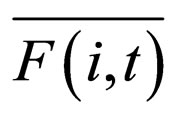 denote the mean fitness of individuals matching Hi and the mean fitness of all individuals, at generation t, respectively.
denote the mean fitness of individuals matching Hi and the mean fitness of all individuals, at generation t, respectively.
In the case of CCEA, because 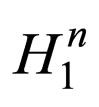 is the conjunction of Hi, the number of the complete genotypes matching
is the conjunction of Hi, the number of the complete genotypes matching  at generation t is given by:
at generation t is given by:
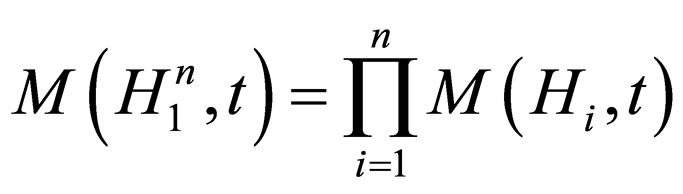
Again, according to the schema theorem, we obtain the following equation:

Then,

where .
.
Hence, obviously, with the increasing of the min {r1, ···, rn}, 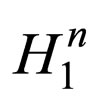 will receive a much higher increasing rate in the CCEA.
will receive a much higher increasing rate in the CCEA.
However, Theorem 2 does not mean that CCEAs are superior to SEAs, which depends on the target problems. Actually, since the representatives are necessary in calculating the fitness of the individual of an arbitrary population, the relationships between populations impose a great influence on the efficiency of CCEAs [17,18]. It has been proved that even with prefect information, infinite population size and no variational operators, CCEAs can be expected to converge to suboptimal solution [18], while SEAs do not suffer from such affliction [19-21]. However, Liviu [22] has emphasized that CCEAs will settle in the globally optimal solution with arbitrarily high probability, when properly set and if given enough resources.
4. Game Model
In this section, we construct a two-dimensional ARPG model in which three distinct races (A, B and C) are designed with maximum level of L. Each race has seven properties, which are Health (H), Dodge Rate (DR), Skill Damage (SD), Skill Critical Hit Rate (SCHR), Skill Cool Down Time (SCDT), Skill Range (SR) and Velocity (V), as well as two skills. Except H and SD which are monotone increasing functions of l = {1, 2, ···, L – 1, L} he other properties are designed to be constant. SCHR denotes the probability that player outputs the double damage. SCDT, belonging to the time feature, means that how much time should the character rest after an attack, and SR, a kind of space feature, denotes the range in which the skill can be used. Specially, in the game world, Velocity is measured in pixels per frame instead of miles per second.
In order to evaluate the power of the race, a standard square map with width w is introduced, and all battles will be held in it. In this case, we only concern the “1 versus 1” fighting type which contains two players (the defender and the attacker), because it is the core of the combat system of on-line ARPG, and we design the low-velocity race to play the role of defender, because if a high-velocity defender chose the strategy of keeping escaping, the battle will become meaningless and uninteresting. As a principle, after being attacked, the defender should be able to launch at least one attack. And there is no constrain on battle time, that is, players are allowed to fight as long as they like. The basic design contents are as follows:
1) The width of the standard map: w = 400;
2) Health: HA(l) > HB(l) > HC(l);
3) Skill Damage:
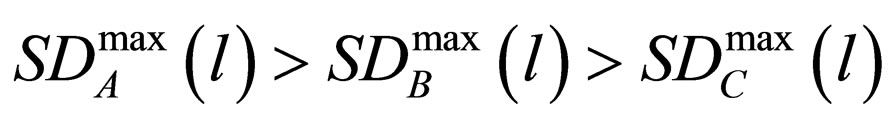 ;
;
4) Dodge Rate: DRC > DRB > DRA;
5) SCDT: SCDTC > SCDTB > SCDTA;
6) Skill Range: SRC > SRB > SRA;
7) Velocity: VC > VB > VA.
where  denotes the maximum damage among two skills of race k with level l.
denotes the maximum damage among two skills of race k with level l.
Based on these ideas, we model the motion of the players by using the Chase Model (refer to Figure 2), and by the theory of vector differential, we acquire the following formula:

Figure 2. The chase model.
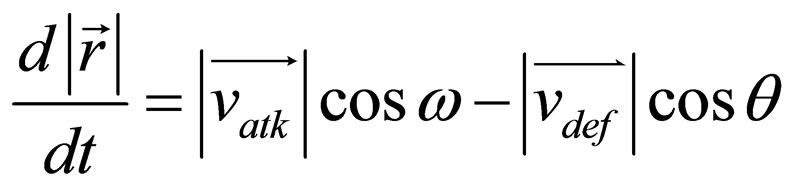 (6)
(6)
where 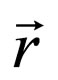 is the distance vector of the two players,
is the distance vector of the two players,  and
and 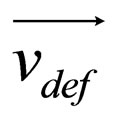 denote the velocity of attacker and defender.
denote the velocity of attacker and defender.
According to Formula 6, the attacker should maximize 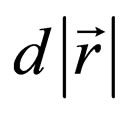 by maximizing cosω and the defender should minimize
by maximizing cosω and the defender should minimize 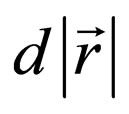 by maximizing cosθ. These can be recognized as the optimal SM.
by maximizing cosθ. These can be recognized as the optimal SM.
Before analyzing the optimal SAO, we introduce the Combat Assistant Technology (CAT) which has been applied to most of on-line ARPGs (such as JXOnline, World of Warcraft, etc.). It helps players to run towards the opponent automatically and attack if possible. The optimal SAO will be analyzed based on it.
Figure 3 demonstrates a freeze-frame of the attacking process in which each combatant uses the CAT to attack. For the defender, after the attacker launched an attack at point f, the defender will strikes back at a point within (a, b], which enables he(she) to output the maximum damage because . So using the CAT to attack is the optimal SAO of the defender. On the other hand, in fact, the attacker may launch the attack in the range (c, d] or (d, e] or (e, g] with the probability of P1, P2 and P3 respectively. We define (P1, P2, P3) as the Action Probability Vector (APV), which represents the action feature and can be obtained through statistical analyze. Therefore, the CAT with the APV of the expert-level players is the optimal SAO of the attacker.
. So using the CAT to attack is the optimal SAO of the defender. On the other hand, in fact, the attacker may launch the attack in the range (c, d] or (d, e] or (e, g] with the probability of P1, P2 and P3 respectively. We define (P1, P2, P3) as the Action Probability Vector (APV), which represents the action feature and can be obtained through statistical analyze. Therefore, the CAT with the APV of the expert-level players is the optimal SAO of the attacker.
Unlike the SM and SAO, an optimal SUS completely depends on the competent’s SUS, which means that the optimal SUS pair is an EP. Also, each combat group has a limit state space which is defined as follows:
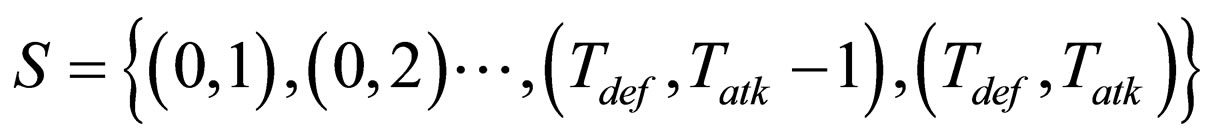
 (7)
(7)
where the (0, 0) state does not exist, Tdef and Tatk are the maximum lifetime of defender and attacker, Hk(l) denotes the health value of k with level l, and 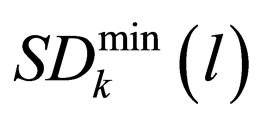 is defined as the minimum damage among two skills of k with level l.
is defined as the minimum damage among two skills of k with level l.
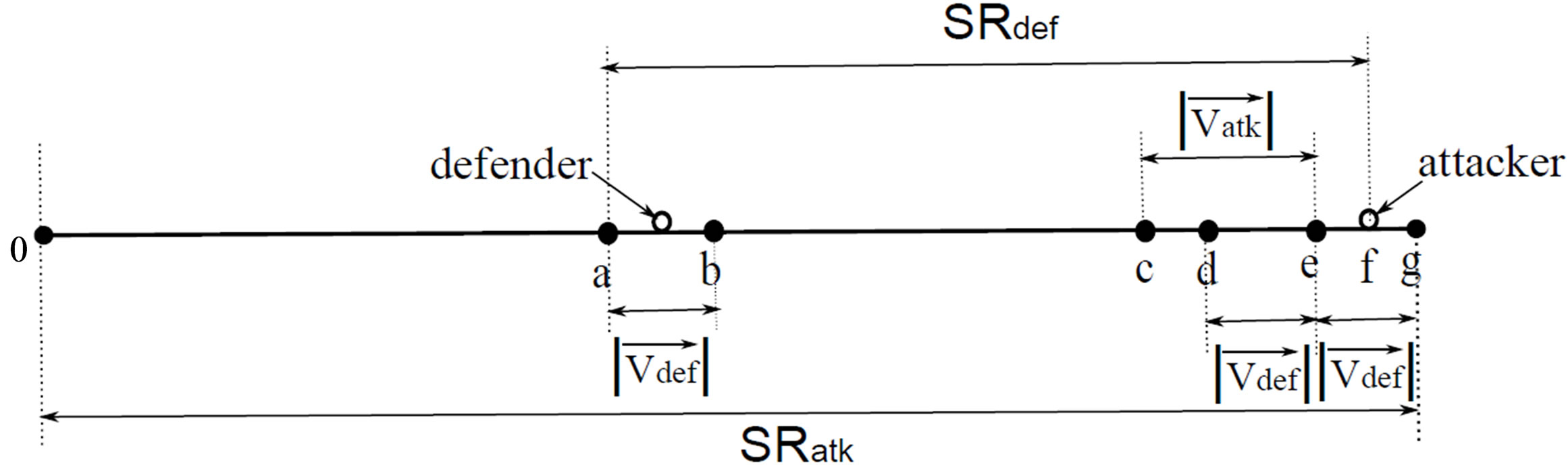
Figure 3. A freeze-frame of the attacking process with the combat assistant technology.
5. Competitive Coevolutionary Framework
In this section, firstly, we model the combat process by using the zero-sum Γβ process, in this step, the fitness function will be constructed. Next, we will introduce the competitive framework as well as demonstrate how to use it to find the optimal SUS pair.
As the preceding section stated, there is no time constrain during fighting, that is, the combat can be regarded as an infinite process, where players keep changing their state from one to another by their actions. And this infinite process can be evaluated by Γβ.
It is natural for any player that he(she) wants to maximize his(her) win probability during battles. Thus, we use the increment of win probability from stage t to t + 1, as the expectation of immediate reward of the decision rule pair (ft, gt). Let p1(t), p2(t) be the win probabilities of player 1 and player 2 at stage t respectively, then, by the fact that the larger t becomes, the higher probability of game over will be, we obtain the follows:
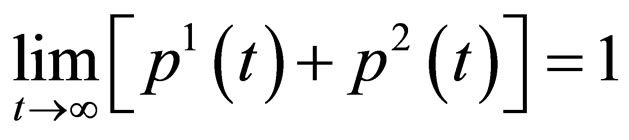
from such formula, it can be inferred that an increment of p1(t) will bring a potential decrement to p2(t).
With these results, in this case, combat can be regarded as the zero-sum game, and can be modeled by zerosum Γβ process. The immediate reward vector and the overall discounted value vector are defined as follows:
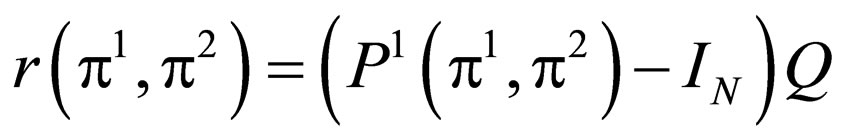
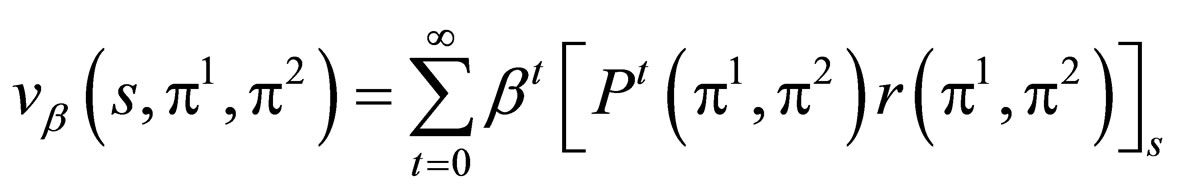 (8)
(8)
where

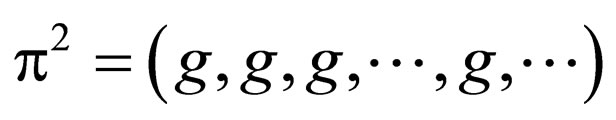
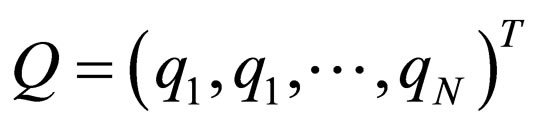
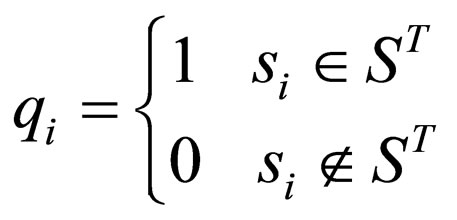 (9)
(9)
Here, π1, π2 are the SUS of the defender and the attacker, N is the size of the state space, IN is the identity matrix of size N, ST denotes the absorbing state set in which the lifetime of attacker is 0. Particularly, in this case, the vβ(s, π1, π2) will always converge into a certain value, even the discount factor, β, is set to 1.
Since the combat always starts from the state (Tdef, Tatk), denoted by sN, it is natural that we shall use v1(sN, π1, π2), denoting the win probability of defender, as the fitness function of our evolutionary algorithm.
The competitive framework consists of two symmetrical blocks (refer to Figure 4), the left block denotes the evolutionary process of π1 while the right block represents π2. Both blocks use CCEA to search the solution space, that is, each decision rule, f or g, is divided into N groups which will be evaluated in turn. Such group, for example, group i, denotes the probability vector on actions of state i, that is, f(i) or g(i). Through the elite pair of current generation, (f*, g*), the two blocks of framework interact in a competitive way, and this enables the framework to lead such elite pair to converging in the decision rule pair of an EP.
The pseudo-code of the algorithm is shown as follows:
1) Create species 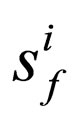 for f(i) and
for f(i) and 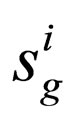 for g(i), where i = {1, 2, ···, N};
for g(i), where i = {1, 2, ···, N};
2) Initialize population for every species by using the uniform distribution, where each bit of chromosome has the same probability to be a 1;
3) Select a individual from each f(i) and g(i), randomly, to form the initial elite decision rule pair (f*, g*);
4) Set generation t = 0;
5) Set i = 1;
6) Evaluate the individuals of species 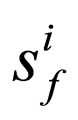 with g* as well as f*(j), where
with g* as well as f*(j), where  (maximize vβ);
(maximize vβ);
7) Replace the f*(i) by the current elite, if necessary;
8) Select the outstanding individuals, and construct the new probability distribution from them. Then new generation can be obtained by sampling this distribution and mutation;

Figure 4. The competitive coevolutionary framework.
9) While (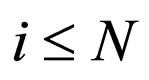 ) set i = i + 1, goto 6;
) set i = i + 1, goto 6;
10) Set i = 1;
11) Evaluate the individuals of species 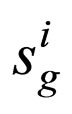 with f* as well as g*(j), where
with f* as well as g*(j), where 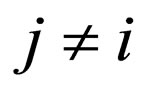 (minimize vβ);
(minimize vβ);
12) Replace the g*(j) by the current elite, if necessary;
13) Select the outstanding individuals, and construct the new probability distribution from them. Then new generation can be obtained by sampling this distribution and mutation;
14) While ( ) set i = i + 1, goto 11;
) set i = i + 1, goto 11;
15) If the termination criteria are not met, set t = t + 1, goto 5.
6. Experiments and Results
In this section, we will use the proposed competitive coevolutionary framework to retrieve the EP of a battle group. A character, from race A with level 3, is chosen as the defender, and with the same level, a character from race C as the attacker. Also, for convenience, we define 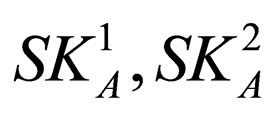 as the two skills of race A, similarly,
as the two skills of race A, similarly, 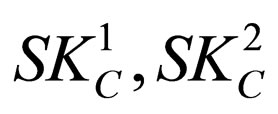 for race C. In accordance with the basic design contents mentioned before, we set the experiment environments as follows:
for race C. In accordance with the basic design contents mentioned before, we set the experiment environments as follows:
1) VA = 10, VC = 25, DRA = 0.3, DRC = 0.45, HA(3) = 100, HC(3) = 60;
2) Properties of : {SD(3) = 30, SR = 70, SCDT = 1, SCHR =0.1};
: {SD(3) = 30, SR = 70, SCDT = 1, SCHR =0.1};
3) Properties of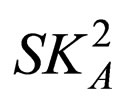 : {SD(3) = 20, SR = 70, SCDT = 2, SCHR =0.3};
: {SD(3) = 20, SR = 70, SCDT = 2, SCHR =0.3};
4) Properties of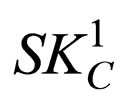 : {SD(3) = 25, SR = 190, SCDT = 13, SCHR =0.3};
: {SD(3) = 25, SR = 190, SCDT = 13, SCHR =0.3};
5) Properties of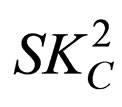 : {SD(3) = 25, SR = 190, SCDT = 14, SCHR =0.6};
: {SD(3) = 25, SR = 190, SCDT = 14, SCHR =0.6};
6) The APV of attacker is (0.2, 0.6, 0.2);
7) In CCEA, population size of each species = 100, in SEA, population size = 500;
8) Generation t = 600, Mutation Rate = 0.01.
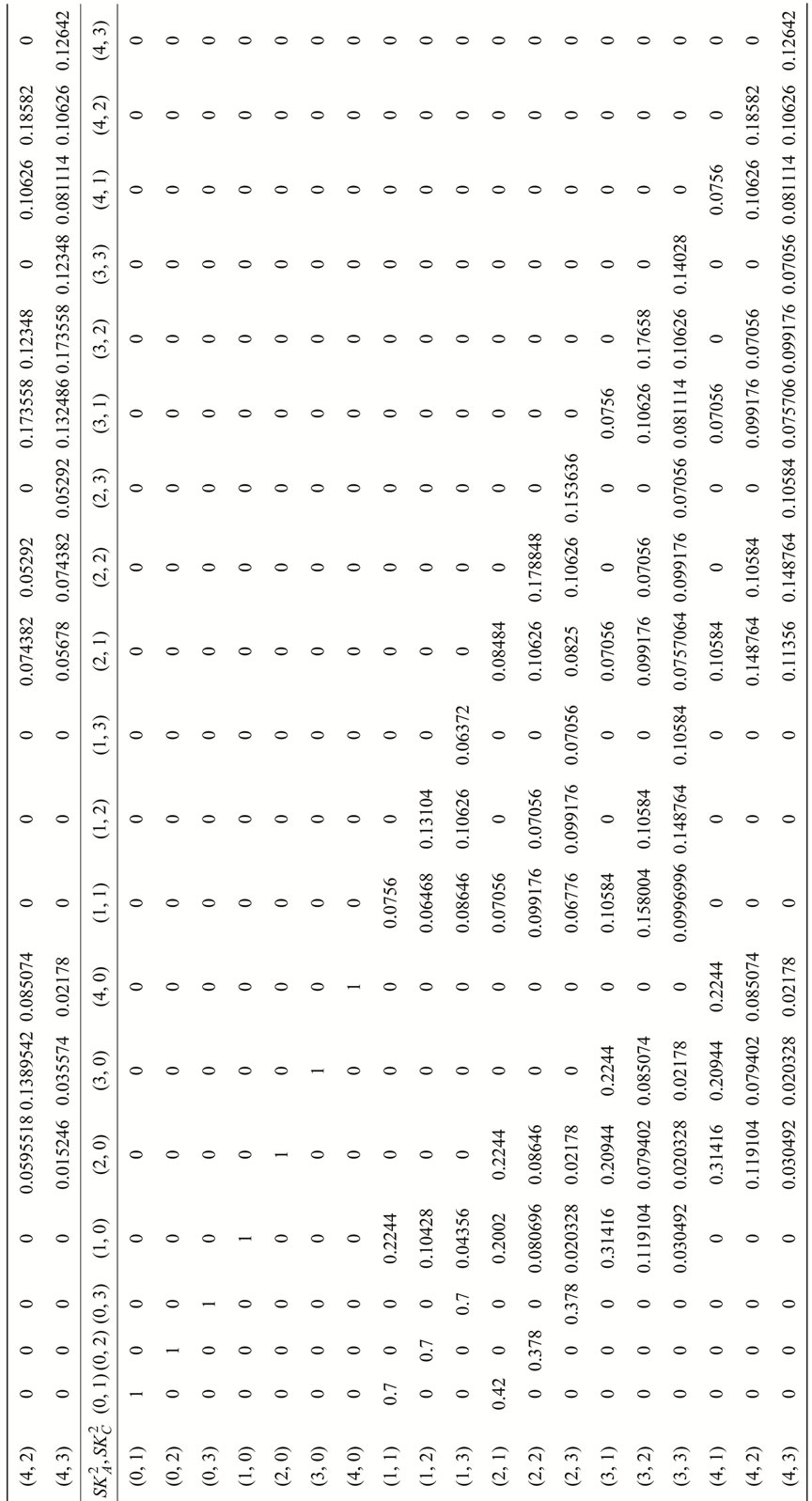
We define the fighting round, a period of time, from attacker launching an attack to the ending of his(her) waiting time. Such definition implies that attacker can attack only one time in a round. Also, based on the experiment environments, we obtain the attacking times of defender, when players chose a certain skill pair and attacker attacked in a certain range. The results are shown in Table 1.
According to those results and the optimal SM as well as the optimal SAO, the probability transition matrix defined by skill pair,  where i, j = {1, 2}, can be calculated (refer to Table 2), then according to Formula 1, we can retrieve the probability transition matrix defined by a stationary strategy pair (π1, π2). Consequently, such strategy pair can be evaluated by
where i, j = {1, 2}, can be calculated (refer to Table 2), then according to Formula 1, we can retrieve the probability transition matrix defined by a stationary strategy pair (π1, π2). Consequently, such strategy pair can be evaluated by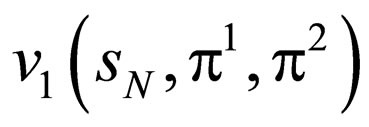 .
.
Besides the proposed algorithm, another one, whose blocks use SEA instead of CCEA, is introduced for the comparison. Considering the stochastic nature of the algorithms, each of the programs is repeated 100 times. The results are shown in Figures 5 and 6.
According to the results in Figure 5, both two algorithms can retrieve the EPs,  , and we can obtain the exception and the variance of
, and we can obtain the exception and the variance of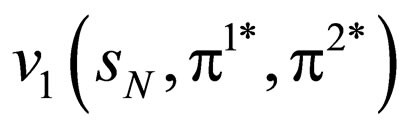 , as follows:
, as follows:
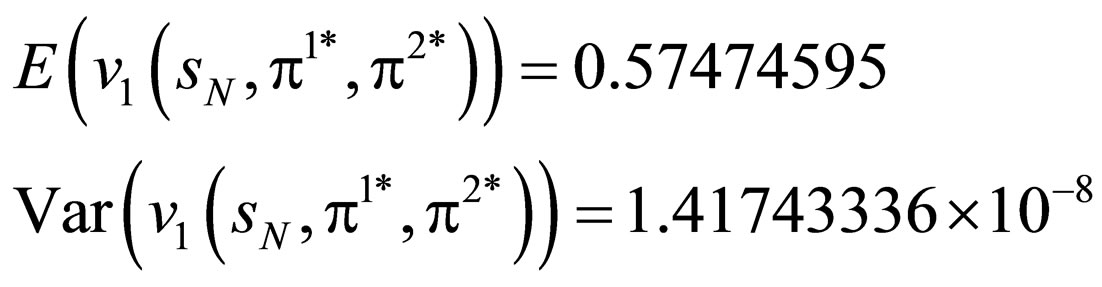 (10)
(10)

Table 1. The attacking times of defender in a round.
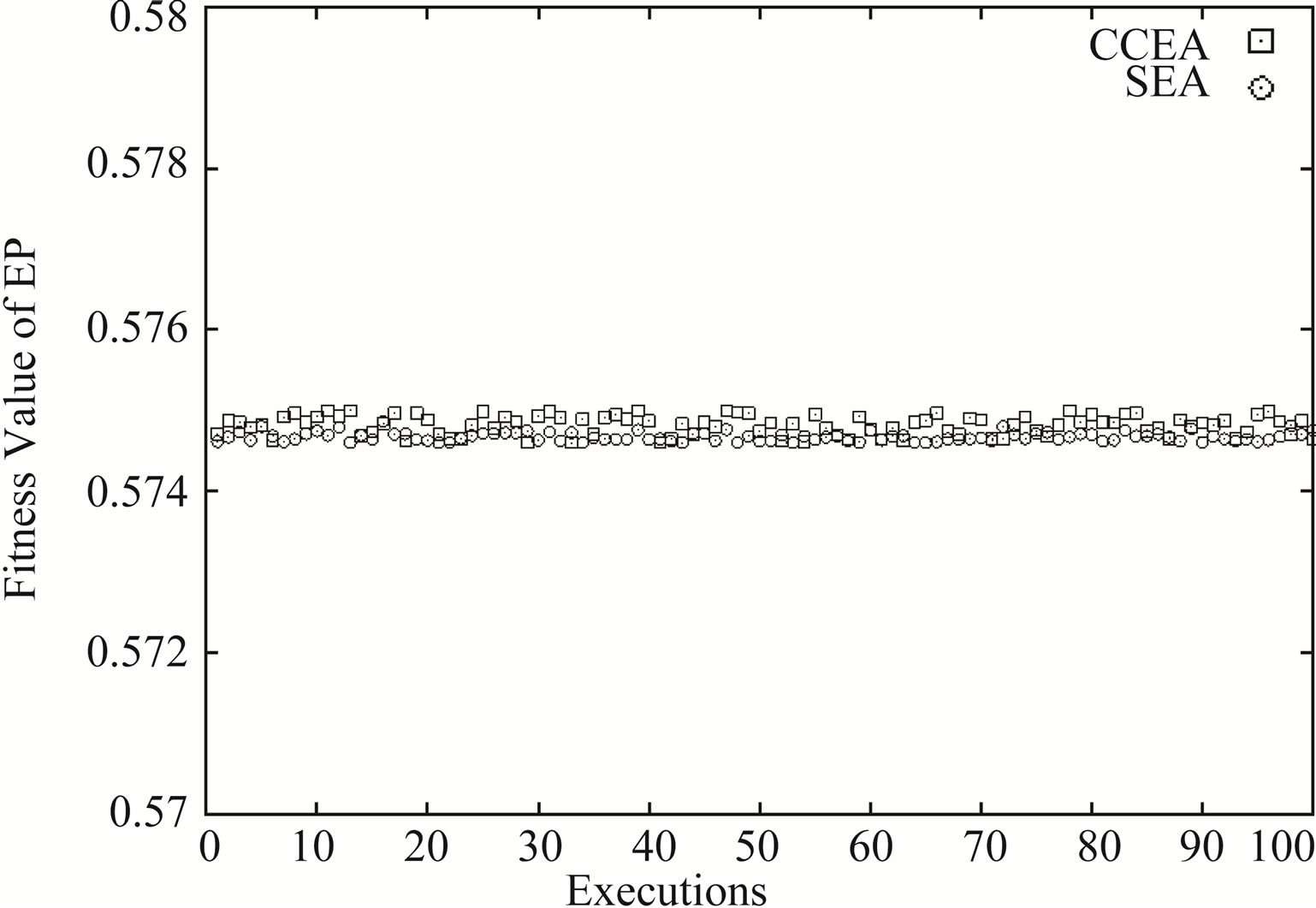
Figure 5. The fitness of the ep retrieved by each execution.
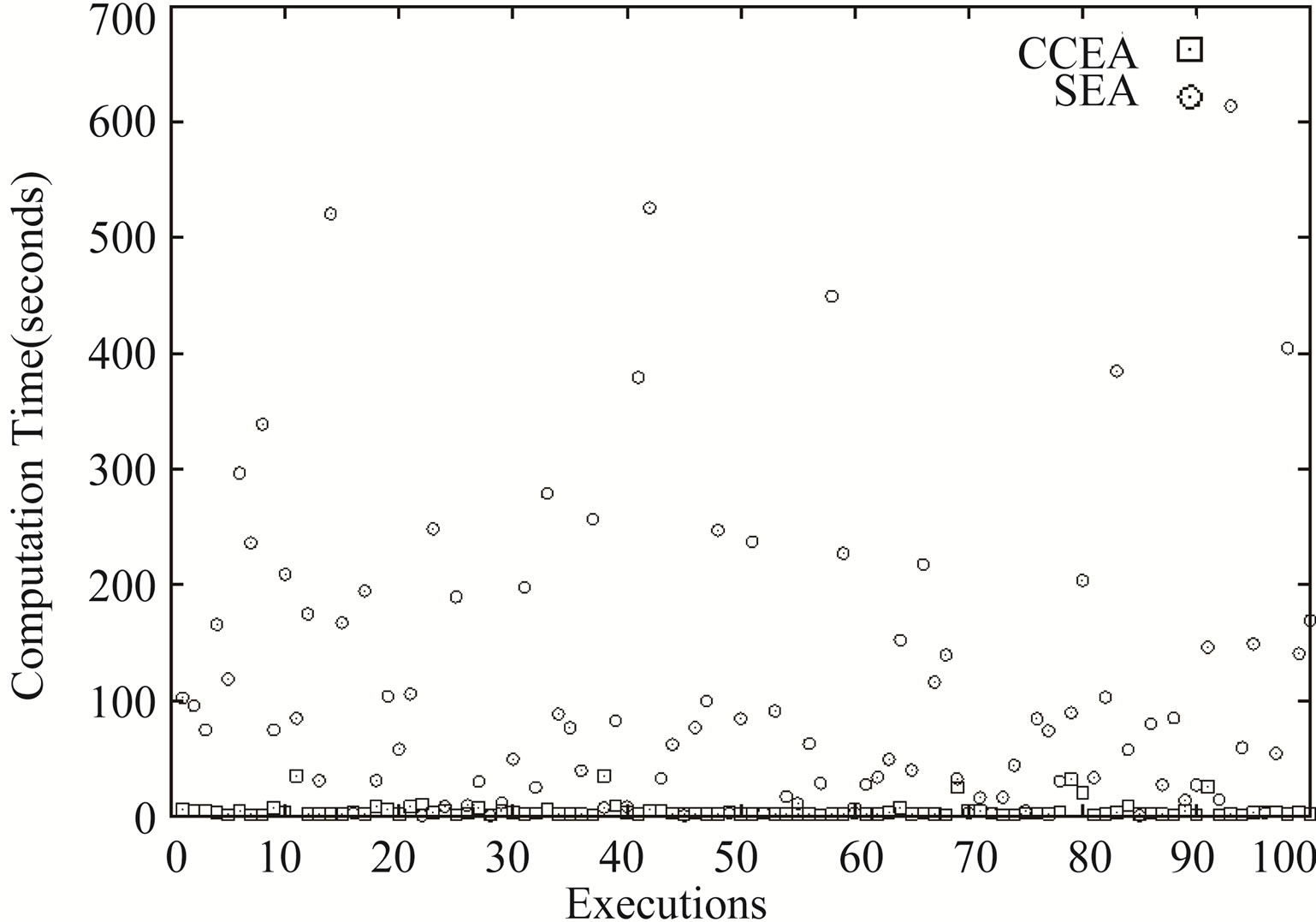
Figure 6. The computation time of retrieving EP in each execution.
Such data are very important because we can judge whether the designed contents are well-balanced based on it. Also, it can be seen from Figure 6 that the CCEA is much faster than SEA, hence a better placement solution than using SEA.
7. Conclusion and Future Work
In this paper, we constructed a basic ARPG system and modeled the combat by using the zero-sum Γβ process. We noted that in the case of zero-sum Γβ, an EP of the entire behavior strategy space can be retrieved just by searching the stationary strategy space, and all the overall discounted value vectors of the EPs are coincide. Also, an evolutionary framework, which includes integration with competitive coevolution and CCEA, has been proposed to search the SUS pairs which are the EPs of the strategy space. Based on the framework, we made some experiments with certain environments. The results showed that the EPs can be obtained, and by using CCEA, the efficiency and capability of the framework have been improved significantly.
In the future work, we will investigate another combat type in which the battle time is constrained, and in such type the strategies of players will no longer be stationary.
REFERENCES
- R. Leigh, J. Schonfeld and S. Louis, “Using Coevolution to Understand and Validate Game Balance in Continuous Games,” Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, 12-16 July 2008, pp. 1563-1570. doi:10.1145/1389095.1389394
- H. Y. Chen, Y. Mori and I. Matsuba, “Design Method for Game Balance with Evolutionary Algorithms Using Stochastic Model,” Proceedings of International Conference on Computer Science and Engineering, Shanghai, 28-31 October 2011, Vol. 7, pp. 1-4.
- H. Y. Chen, Y. Mori and I. Matsuba, “Evolutionary Approach to the Balance Problem of On-Line Action RolePlaying Game,” Proceedings of the 3rd International Conference on Computational Intelligence and Software Engineering, Wuhan, 9-11 November 2011, pp. 1039- 1042.
- J. Filar and K. Vrieze, “Competitive Markov Decision Processes,” Springer-Verlag, New York, 1996. doi:10.1007/978-1-4612-4054-9
- P. Husbands and F. Mill, “Simulated Coevolution as the Mechanism for Emergent Planning and Scheduling,” Proceedings of the 4th International Conference on Genetic Algorithms, San Diego, July 1991, pp. 264-270.
- M. Potter, “The Design and Analysis of a Computational Model of Cooperative Coevolution,” Ph.D. Dissertation, George Mason University, Fairfax, 1997.
- L. Bull, T. C. Fogarty and M. Snaith, “Evolution in Multi-Agent Systems: Evolving Communicating Classifier Systems for Gait in a Quadrupedal Robot,” Proceedings of the 6th International Conference on Genetic Algorithms (ICGA), Pittsburgh, 15-19 July 1995, pp. 382-388.
- M. Potter, L. Meeden and A. Schultz, “Heterogeneity in the Coevolved Behaviors of Mobile Robots: The Emergence of Specialists,” Proceedings of the 17th International Conference on Artificial Intelligence, Seattle, 4-10 August 2001, pp. 1337-1343.
- K. S. Hwang, J. L. Lin and H. L. Huang, “Dynamic Patrol Planning in a Cooperative Multi-Robot System,” Communications in Computer and Information Science, Vol. 212, 2011, pp. 116-123. doi:10.1007/978-3-642-23147-6_14
- M. Potter and K. D. Jong, “The Coevolution of Antibodies for Concept Learning,” Proceedings of the 5th International Conference on Parallel Problem Solving from Nature, Amsterdam, 27-30 September 1998, pp. 530-539. doi:10.1007/BFb0056895
- Y. Wen and H. Xu, “A Cooperative Coevolution-Based Pittsburgh Learning Classifier System Embedded with Memetic Feature Selection,” Proceedings of IEEE Congress on Evolutionary Computation, New Orleans, 5-8 June 2011, pp. 2415-2422.
- A. Carlos and S. Moshe, “Fuzzy CoCo: A CooperativeCoevolutionary Approach to Fuzzy Modeling,” IEEE Transactions on Fuzzy Systems, Vol. 9, No. 5, 2001, pp. 727-737. doi:10.1109/91.963759
- R. Chandra and M. Zhang, “Cooperative Coevolution of Elman Recurrent Neural Networks for Chaotic Time Series Prediction,” Neurocomputing, Vol. 86, 2012, pp. 116- 123. doi:10.1016/j.neucom.2012.01.014
- M. Potter and K. D. Jong, “A Cooperative Coevolutionary Approach to Function Optimization,” Proceedings of the 3rd International Conference on Parallel Problem Solving from Nature, Jerusalem, 9-14 October 1994, Vol. 866, pp. 249-257. doi:10.1007/3-540-58484-6_269
- M. Potter and K. D. Jong, “Cooperative Coevolution: An Architecture for Evolving Coadapted Subcomponents,” Evolutionary Computation, Vol. 8, No. 1, 2000, pp. 1-29. doi:10.1162/106365600568086
- R. P. Wiegand, W. Liles and K. D. Jong, “An Empirical Analysis of Collaboration Methods in Cooperative Coevolutionary Algorithms,” Proceedings of the Genetic and Evolutionary Computation Conference, San Francisco, 7-11 July 2001, pp. 1235-1242.
- T. Jansen and R. P. Wiegand, “Exploring the Explorative Advantage of the CC (1+1) EA,” Proceedings of the Genetic and Evolutionary Computation Conference, Chicago, 12-16 July 2003, pp. 310-321.
- R. P. Wiegand, “An Analysis of Cooperative Coevolutionary Algorithms,” Ph.D. Dissertation, George Mason University, Fairfax, 2004.
- C. Reeves and J. Rowe, “Genetic Algorithms Principles and Perspectives: A Guide to GA Theory,” Kluwer Academic Publishers, Norwell, 2002.
- L. Schmitt, “Theory of Genetic Algorithms,” Theoretical Computer Science, Vol. 259, No. 1-2, 2001, pp. 1-61. doi:10.1016/S0304-3975(00)00406-0
- M. Vose, “The Simple Genetic Algorithm,” MIT Press, Cambridge, 1999.
- P. Liviu, “Theoretical Convergence Guarantees for Cooperative Coevolutionary Algorithms,” Evolution Computation, Vol. 18, No. 4, 2010, pp. 581-615. doi:10.1162/EVCO_a_00004
NOTES
*Corresponding author.