Journal of Intelligent Learning Systems and Applications
Vol.4 No.2(2012), Article ID:19256,12 pages DOI:10.4236/jilsa.2012.42010
Prediction of the Bombay Stock Exchange (BSE) Market Returns Using Artificial Neural Network and Genetic Algorithm
![]()
1Computer Science & Information System, Jazan University, Jazan, Kingdom of Saudi Arabia (KSA); 2Department of Management, Singhnia University, Rajasthan, India.
Email: {yusufperwej, asifperwej}@gmail.com
Received April 6th, 2011; revised February 6th, 2012; accepted February 13th, 2012
Keywords: Stock Market; Genetic Algorithm; Bombay Stock Exchange (BSE); Artificial Neural Network (ANN); Prediction; Forecasting; Data; Autoregressive (AR)
ABSTRACT
Stock Market is the market for security where organized issuance and trading of Stocks take place either through exchange or over the counter in electronic or physical form. It plays an important role in canalizing capital from the investors to the business houses, which consequently leads to the availability of funds for business expansion. In this paper, we investigate to predict the daily excess returns of Bombay Stock Exchange (BSE) indices over the respective Treasury bill rate returns. Initially, we prove that the excess return time series do not fluctuate randomly. We are applying the prediction models of Autoregressive feed forward Artificial Neural Networks (ANN) to predict the excess return time series using lagged value. For the Artificial Neural Networks model using a Genetic Algorithm is constructed to choose the optimal topology. This paper examines the feasibility of the prediction task and provides evidence that the markets are not fluctuating randomly and finally, to apply the most suitable prediction model and measure their efficiency.
1. Introduction
It is nowadays a common notion that vast amounts of capital are traded through the Stock Markets all around the world. National economies are strongly linked and heavily influenced by the performance of their Stock Markets. The characteristic that all Stock Markets have in common is the uncertainty, which is related with their short and long term future state. This feature is undesirable for the investor but it is also unavoidable whenever the Stock Market is selected as the investment tool. The best that one can do is to try to reduce this uncertainty. Stock Market Prediction (or Forecasting) is one instrument in this process.
The Stock Market prediction task divides researchers and academics into two groups those who believe that we can devise mechanisms to predict the market and those who believe that the market is efficient and whenever new information comes up the market absorbs it by correcting itself, thus there is no space for prediction. Furthermore they believe that the Stock Market follows a Random Walk, which infers that the best prediction you can have about tomorrow's value is today’s value.
2. Stock Market
A place, whether physical or electronic, where stocks in listed companies are bought and sold. A stock market may be a private company, a non-profit, or a publiclytraded company. A stock market provides a regulated place where brokers and companies may meet to make investments on neutral ground. The stocks are listed and traded on stock exchanges which are entities of a corporation or mutual organization specialized in the business of bringing buyers and sellers of the organizations to a listing of stocks and securities together. The stock market in the India is the Bombay Stock Exchange. Participants in the stock market range from small individual stock investors to large hedge fund traders, who can be based anywhere. Their orders usually end with a professional at a stock exchange, who executes the order.
In 12th century France the courratiers de change were concerned with managing and regulating the debts of agricultural communities for the banks. Because these men also traded with debts, they could be called the first brokers. A common misbelieve is that in late 13th century Bruges commodity traders gathered inside the house of a man called Van der Beurze, and in 1309 they became the “Brugse Beurse”, institutionalizing what had been, until then, an informal meeting, but actually, the family Van der Beurze had a building in [1] Antwerp where those gatherings occurred, the Van der Beurze had Antwerp, as most of the merchants of that period, as their primary place for trading. The idea quickly spread around Flanders and neighboring counties and “Beurzen” soon opened in Ghent and Amsterdam.
In the middle of the 13th century, Venetian bankers began to trade in government securities. In 1351 the Venetian government outlawed spreading rumors intended to lower the price of government funds. Bankers in Pisa, Verona, Genoa and Florence also began trading in government securities during the 14th century. This was only possible because these were independent city states not ruled by a duke but a council of influential citizens. The Dutch later started joint stock companies, which let shareholders invest in business ventures and get a share of their profits or losses. In 1602, the Dutch East India Company issued the first share on the Amsterdam Stock Exchange. It was the first company to issue stocks and bonds.
2.1. Investment Theory
An investment theory suggests what parameters one should take into account before placing his (or her) capital on the market. Traditionally the investment community accepts two major theories 1st the Firm Foundation and 2nd the Castles in the Air [2]. These theories allow us to understand how the market is shaped, or in other words how the investors think and react. It is this sequence of “thought and reaction” by the investors that define the capital allocation and thus the level of the market. There is no doubt that most of the people related to stock markets are trying to achieve profit. Profit comes from investing in stocks that have a good future. What they are trying to accomplish one way or the other is to predict the future of the market. But what determines this future? The way that people invest their money is the answer and people invest money based on the information they hold. Therefore we have the following schema in Figure 1.
The factors that are under discussion on this schema is Figure 1, the content of the “Information” component and the way that the “Investor” reacts when having this information. According to the Firm Foundation theory the market is defined from the reaction of the investors, which is triggered by information that is related to the “real value” of firms. The “real value” or else the intrinsic value is determined by careful analysis of present conditions and future prospects of a firm [3]. On the other hand, according to the Castles in the Air theory the investors are triggered by information that is related to other investor’s behavior. So for this theory the only concern that

Figure 1. Investment procedure.
the investor should have is to buy today with the price of 20 and sell tomorrow with the price of 30, no matter what the intrinsic value of the firm he (or she) invests in is. Therefore the Firm Foundation theory favors the view that the market is defined mostly by logic, while the Castles in the Air theory supports that the market is defined mostly by psychology.
2.2. Data Related to the Market
The information about the market comes from the study of the relevant data. Here we are trying to describe and group into categories the data that relate to the stock markets. In this paper these data are divided into three major categories [4].
• Technical data: This type of all the data that refer to stocks only. Technical data include:
■ The price at the end of the day.
■ The highest and the lowest price of a trading day.
■ The volume of shares traded per day.
• Fundamental data: This type of data related to the intrinsic value of a company or category of companies as well as data related to the general economy. Fundamental data include:
■ Inflation.
■ Interest Rates.
■ Trade Balance.
■ Indexes of industries (e.g. Heavy industry).
■ Net profit margin of a firm.
■ Prognoses of future profits of a firm.
• Derived data: This type of data can be produced by transforming and combining technical and/or fundamental data. Some commonly used examples are:
• Returns: This type of One-step returns R(t) is defined as the relative increase in price from the previous point in a time series. Thus if y(t) is the value of a stock.
On day t, 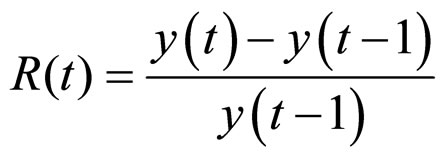
• Volatility: This type of Describes the variability of a stock and is used as a way to measure the risk of an investment.
In this paper the study (process) of these data permit us to understand the market and some of the rules it follows. In our effort to predict the future of the market we have to study its past and present and imply from them. It is this inference task that all prediction methods are trying to accomplish. The way they do it and the different subsets of data they use is what differentiates them [5].
3. Prediction of the Market
3.1. Defining the Prediction Task
Before having any further discussion about the prediction of the market we define the task in a formal way. “Given a sample of N examples {(xi, yi), I = 1,…, N} where f(xi) = yi, i, return a function g that approximates f in the sense that the norm of the error vector E = (e1,…, eN) is minimized. Each ei is defined as ei = e(g(xi), yi) where e is an arbitrary error function”. In other words the definition above shows that to predict the market you should search historic data and find relationships among these data and the value of the market. Then try to exploit these relationships you have found in future situations. This definition is based on the assumption that such relationships do exist. But do they? Or do the markets fluctuate in a totally random way leaving us no space for prediction? This is a question that has to be answered before any attempt for prediction is made.
3.2. Prediction Method
The prediction of the market is without doubt an interesting task. In the literature there are several methods applied to accomplish this task. These methods use various approaches, ranging from highly informal ways (e.g. the study of a chart with the Fluctuation of the market) in more formal ways (e.g. Linear or non-linear regressions). We have categorized these techniques as follows:
• Traditional Time Series Prediction Methods;
• Machine Learning Methods.
The criterion to this categorization is the type of tools and the type of data that each method is used to predict the market. What is common to these techniques are that they are used to predict and thus benefit from the market’s future behavior. None of them has proved to be the consistently correct prediction tool that the investor would like to have. Furthermore many analysts question the usefulness of many of these predictions techniques.
3.2.1. Traditional Time Series Prediction
The Traditional Time Series Prediction analyzes historic data and attempts to approximate future values of a time series as a linear combination of these historical data. In econometrics there are two basic types of time series forecasting: univariate (simple regression) and multivariate (multivariate regression) [6]. These types of regression models are the most common tools used in econometrics to predict time series. The way they are applied in practice is that first a set of factors that influence (or more specific is presumed that influence) the series under prediction is formed. These factors are the explanatory variables xi of the prediction model. Then a mapping between their values xit and the values of the time series yt (y is the to-be explained variable) is done, so that pairs {xit, yt} are formed. These pairs are used to define the importance of each explanatory variable in the formulation of the explained variable. In other words the linear combination of xi that approximates in an optimum way y is defined. Univariate models are based on one explanatory variable (I = 1) while multivariate models use more than one variable (I > 1). Regression models have been used to predict stock market time series. A good example of the use of multivariate regression is the work of Pesaran and Timmermann (1994) [7].
3.2.2. Machine Learning Method
Machine learning is a process that begins with the identification of the learning domain and ends with testing and using the results of the learning. It will be useful to start with an overview of how a machine learning system is developed, trained, and tested. The key parts of this process is the “learning domain,” the “training set,” the “learning system,” and “testing” the results of the learning process [8]. All these methods use a set of samples to generate an approximation of the underlying function that generated the data. The aim is to draw conclusions from these samples in such a way that when unseen data are presented to a model it is possible to infer the to be explained variable from these data. The methods we discuss here are the [9] Neural Networks Techniques. These methods have been applied to market prediction particularly for Artificial Neural Networks there is a rich literature related to the forecast of the market on a daily basis.
4. Bombay Stock Exchange (BSE)
Bombay Stock Exchange is the oldest stock exchange in Asia, today is now popularly known as the BSE was established as “The Native Share & Stock Brokers Association” in 1875. Over the past 135 years, BSE has facilitated the growth of the Indian corporate sector by providing it with an efficient capital raising platform. Today, BSE is the world’s number 1 exchange in the world in terms of the number of listed companies (over 4900). It is the world’s 5th most active in terms of number of transaction handle through its electronic trading system. And it is in the top ten of global exchanges in terms of the market capitalization of its listed companies. The companies listed on BSE command a total market capitalization of USD Trillion 1.36 as of 31st March, 2010. The BSE Index, SENSEX, is India’s first and most popular Stock Market benchmark index. Exchange traded funds (ETF) on SENSEX, are listed on BSE and in Hong Kong. SENSEX, first compiled in 1986, was calculated on a “Market Capitalization-Weighted” methodology of 30 component stocks representing large, well-established and financially sound companies across key sectors. SENSEX is being calculated on a free-float market capitalization methodology [10]. The free-float market capitalization-weighted methodology is a widely followed index construction methodology on which majority of global equity indices are based; all major index providers like MSCI, FTSE, STOXX, S&P and Dow Jones uses the free float methodology.
5. Artificial Neural Network
The artificial neural network is simplified models of the biological neuron system, is a massively parallel distributed processing system made up of highly interconnected neural computing elements that can learn and thereby acquire knowledge and make it available for use. The artificial neural network learns by example. They can therefore be trained with known examples of a problem to acquire knowledge about it. Once appropriately trained, the network can be put to effective use in solving unknown or untrained instances of the problem.
5.1. Neuron
A neuron is a processing unit that takes several inputs and gives a distinct output. The Figure 2 below depicts a single neuron with R inputs p1, p2,…, pR, each input is weighted with a value w11, wl2,…, wlR and the output of the neuron an equal to f (w11·p1 + w12·p2 +…+ w1R·pR).
Each neuron apart from the number of its input is characterized by the function f known as a transfer function. The most commonly used transfer functions are the hardlimit, the purelinear, the sigmoid and the tansigmoid function Table 1 shows. The preferences on these functions derive from their characteristics. Hardlimit maps any value that belongs with  into two distinct values {0, 1}, thus it is preferred for networks that perform classification tasks (multiplayer perceptrons MLP). Sigmoid and tansigmoid, known as squashing functions, map any value from
into two distinct values {0, 1}, thus it is preferred for networks that perform classification tasks (multiplayer perceptrons MLP). Sigmoid and tansigmoid, known as squashing functions, map any value from  to the intervals [0, 1] and [–1, 1] respectively. Lastly purelinear is used due to its ability to return any real value and is mostly used at the neurons that are related to the output of the network in Table 1.
to the intervals [0, 1] and [–1, 1] respectively. Lastly purelinear is used due to its ability to return any real value and is mostly used at the neurons that are related to the output of the network in Table 1.
5.2. Layer
Figure 3 presents the Artificial Neural network is defined as data processing system consisting of many of simple highly interconnected processing elements (artificial neurons) is an architecture inspired by the structure of the cerebral cortex of the brain. Each network has got exactly one input layer, zero or more hidden layers and one output layer. All of them apart from the input layer consist of neuron. The number of inputs to the Artificial Neural Networks equal to the dimension of our input samples Figure 3 shows, while the number of the outputs we want from the Artificial Neural Networks define the number of neurons in the output layer. In our case the

Figure 2. A simple neuron with R input.

Table 1. The most commonly used transfer function.

Figure 3. Neural Network Diagram.
output layer will have exactly one neuron since the only output we want from the network is the prediction of tomorrow’s excess return.
The mass of hidden layers as well as the mass of neurons in each hidden layer is proportional to the ability of the network to approximate more complicated functions. Of course this does not infer by any means that networks with complicated structures will always perform better. The reason for this is that the more complicated a network is the more sensitive it becomes to noise or else, it is easier to learn apart from the underlying function the noise that exists in the input data. Therefore clearly there is a trade off between the representational power of a network and the noise it will incorporate.
5.3. Weight
The weights used on the connections among different layers have much significance in the working of the Artificial Neural Networks and the characterization of a network. The procedure of adjusting the weights of a Artificial Neural Networks based on a specific dataset is referred as the training of the network on that set (training set). The basic idea behind training is that the network will be adjusted in a way that will be able to learn the patterns that lie in the training set. Using the adjusted network in future situations (unseen data) it will be able based on the patterns that learned to generalize giving us the ability to make inferences. In our case we will train the Artificial Neural Network model on a part of our time series (training set) and we will measure their ability to generalize on the remainning part (test set). The size of the test set is usually selected to be 10% of the available samples [11]. Each sample consists of two parts the input and the target path is called supervised learning. Initially the weights of the network is assigned random values (usually within [–1, 1]). Then the input part of the first sample is presented to the network. The network computes an output based on: the values of its weights, the number of its layers and the type and mass of neurons per layer.
There are two major categories of network training the incremental and the batch training. During the incremental training the weights of the network is adjusted each time that each one of the input samples are presented to the network, while in batch mode training the weights are adjusted only when all the training samples have been presented to the network.
5.4. Training Algorithm
The mechanisms of weights update are known as training algorithm. The algorithms described here are related to feed-forward networks. Artificial Neural Networks are characterized as feed-forward network if it is possible to attach successive numbers of the inputs and to all the hidden and output units such that each unit only receives connections from inputs or units having a smaller number [12]. All these algorithms use the gradient of the cost function to determine how to adjust the weights to minimize the cost function. The gradient is determined using a technique called backpropagation, which involves performing computations backwards through the network.
5.5. Gradient Descent
We will describe in detail the way that the weights of a feed forward network are updated using the backpropagation gradient descent algorithm. The following description is related to the incremental training mode. We introduce the notion we will use.
If  is the value of the error function of the sample N and
is the value of the error function of the sample N and 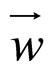 the vector with all the weights of the network then the gradient of
the vector with all the weights of the network then the gradient of 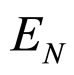 in respect to
in respect to  is
is
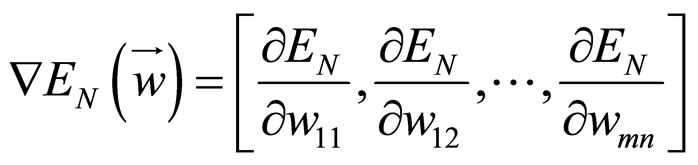
Where  is the weight that is related with the neuron j and its input i. “When interpreted as a vector in weight space, the gradient specifies the direction that produces the steepest increase in
is the weight that is related with the neuron j and its input i. “When interpreted as a vector in weight space, the gradient specifies the direction that produces the steepest increase in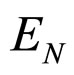 .The negative of this vector therefore gives the direction of the steepest decrease”. Based on this concept we are trying to update the weights of the network according to
.The negative of this vector therefore gives the direction of the steepest decrease”. Based on this concept we are trying to update the weights of the network according to


Here 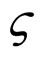 is a positive constant called the learning rate, the greater
is a positive constant called the learning rate, the greater  is the greater the change in
is the greater the change in .
.
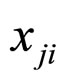 , is the i-th input of unit j, presuming that each neuron is assigns a number successively.
, is the i-th input of unit j, presuming that each neuron is assigns a number successively.
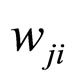 , the weight associated with the i-th input to neuron j.
, the weight associated with the i-th input to neuron j.
 (The weighted sum of inputs of neuron j)
(The weighted sum of inputs of neuron j)
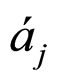 , the output computed by node j.
, the output computed by node j.
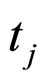 , the target of output unit j.
, the target of output unit j.
ó, the sigmoid function.
Outputs, the set of nodes in the final layer of the network.
Downstream (j), the set of neurons whose immediate inputs include the output of neuron j.
If we make the assumption that we have a network with neurons that use the sigmoid transfer function (ó) then we will try to calculate the gradient  using the chain rule we have that
using the chain rule we have that
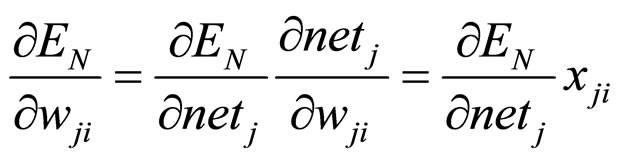
5.6. Parameter Setting
The properties related to a neuron is the transfer function it uses as well as the way it processes its inputs before feeding them to the transfer function. The Artificial Neural Networks we will create use neurons that preprocess the input data as follow, If x1,…, xN are the inputs to the neuron and w1,…, wN their weights the value fed to the transfer function would be 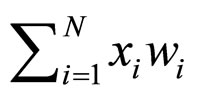
The neurons in the output layer will use the purelinear function while the neurons in the hidden layer the tansigmoid function. We select the tansigmoid and not the sigmoid since the excess return time series contains values in [–1, 1], thus the representational abilities of a tansigmoid function fit in a better way the series we attempt to predict comparable to those of the sigmoid’s. We will be following structure in Artificial Neural Networks x-y-z-1 where x, y can be any integer greater than one, while z can be any non-negative integer. So far we have fully defined the characteristics of the output layer and for the hidden layers the properties of their nodes. What remains open is the number of hidden units per layer as well as the number of inputs. Since there is no rational way of selecting one structure and neglecting the others we will use a search algorithm to help us to choose the optimum number of units per layer. The algorithm we will use is a Genetic Algorithm (GA). The Genetic Algorithms will search a part of the space defined by x-y-z-1 and will converge towards the network structures that perform better on our task.
6. Genetic Algorithm
Genetic Algorithm proposed in 1975 by Johan Holland. Genetic Algorithms are computerized search and optimization algorithms based on the mechanics of natural genetics and natural selection. Genetic algorithms performed directed random searches through a given set of alternative with the aim of finding the best alternative with respect to the given criteria of goodness as illustrated in Figure 4. The criteria are required to be expressed in terms of an objective function which is usually called a fitness function. Fitness is defined as a figure of merit, which is to be either maximized or minimized.
The biological organism to be specified is defined by one or by a set of chromosomes. The overall set of chromosomes is called genotype, and the resulting organism is called the phenotype. Every chromosome consists of genes. The gene position within the chromosome refers to the type of organism characteristic, and the coded content of each gene refers to an attribute within the organism type. In Genetic Algorithms terminology, the set of strings (chromosomes) forms a structure (genotype). Each string consists of characters (genes). Genetic Algorithms are a method for moving from one population of “chromosomes” [13] (strings of 1, 0 bits) to a new population by using a kind of “natural selection” together with the genetics inspired operators of crossover, mutation, and inversion. Each chromosome consists of “genes” (bits), each gene being an instance of a particular “allele” (0 or 1). The selection operator chooses those chromosomes in the population that will be allowed to reproduce, and on average the fitter chromosomes produce more offspring than the less fit ones. Crossover exchanges subparts of two chromosomes, roughly mimicking biological recombination among two single chromosomes (haploid) organisms; mutation randomly changes the allele values of some locations in the chromosome; and the inversion reverses the order of a contiguous section of the chromosome, thus rearranging the order in which genes are arrayed.
6.1. A Conventional Genetic Algorithm
A genetic algorithm has the three major components. The
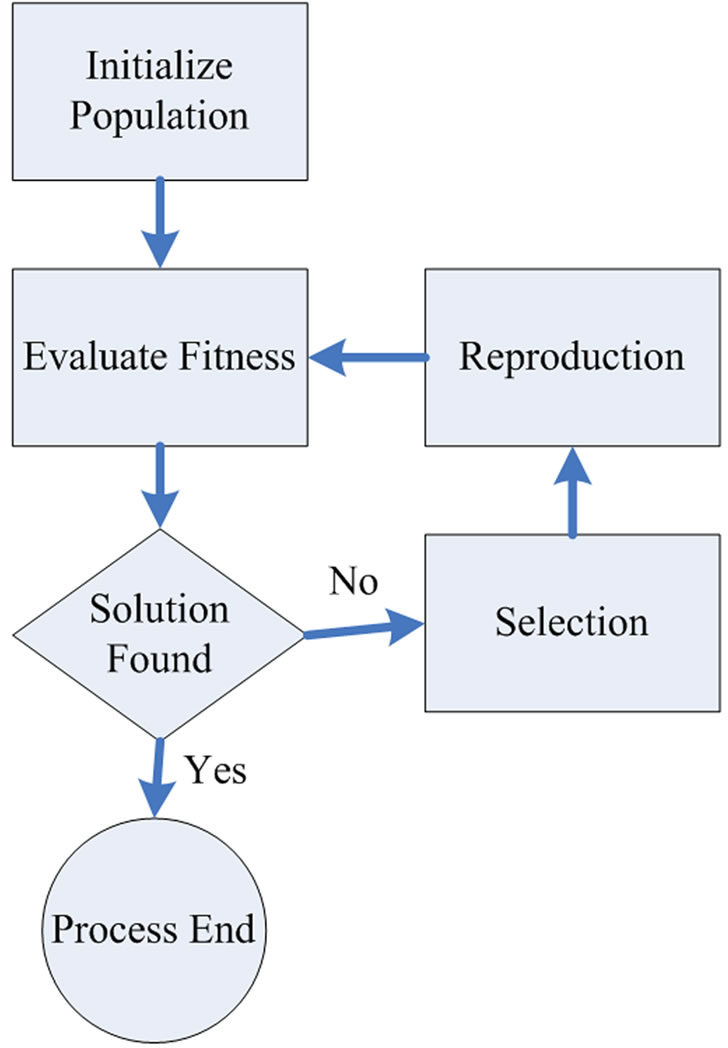
Figure 4. Flow chart of genetic algorithm iteration.
first component is related to the creation of an initial population of m randomly selected individuals. The initial population shapes the first generation. The second component inputs m individuals and gives as output an evaluation for each of them based on an objective function has known as fitness function shown in Figure 5" target="_self"> Figure 5. This evaluation describes how close to our demands each one of these m individuals is and the third component is responsible for the formulation of the next generation. A new generation is formed based on the fittest individuals of the previous one. This procedure of evaluation of generation N and production of generation N + 1 (based on N) is iterated until a performance criterion is met. The creation of offspring based on the fittest individuals of the previous generation is known as breeding. The breeding procedure includes three basic genetic operation reproduction, crossover and mutation.
Reproduction selects probabilistically one of the fittest individual of generation N and passes it to generation N + 1 without applying any changes to it. On the other hand, crossover selects probabilistically two of fittest individuals of generation N then in a random way chooses several their characteristics and exchanges them in a way that the chosen characteristics of the first individual would be obtained by the second a vice versa as illustrated in Figure 5. Following this procedure creates two new offspring that both belong with the new generation. Finally the mutation selects probabilistically one fittest individual and changes several its characteristics in a random way showed in Figure 5" target="_self"> Figure 5. The offspring that comes out of this transformation is passed to the next generation [14]. The way that a conventional Genetic Algorithm works by combining the three components described below in the following figure.
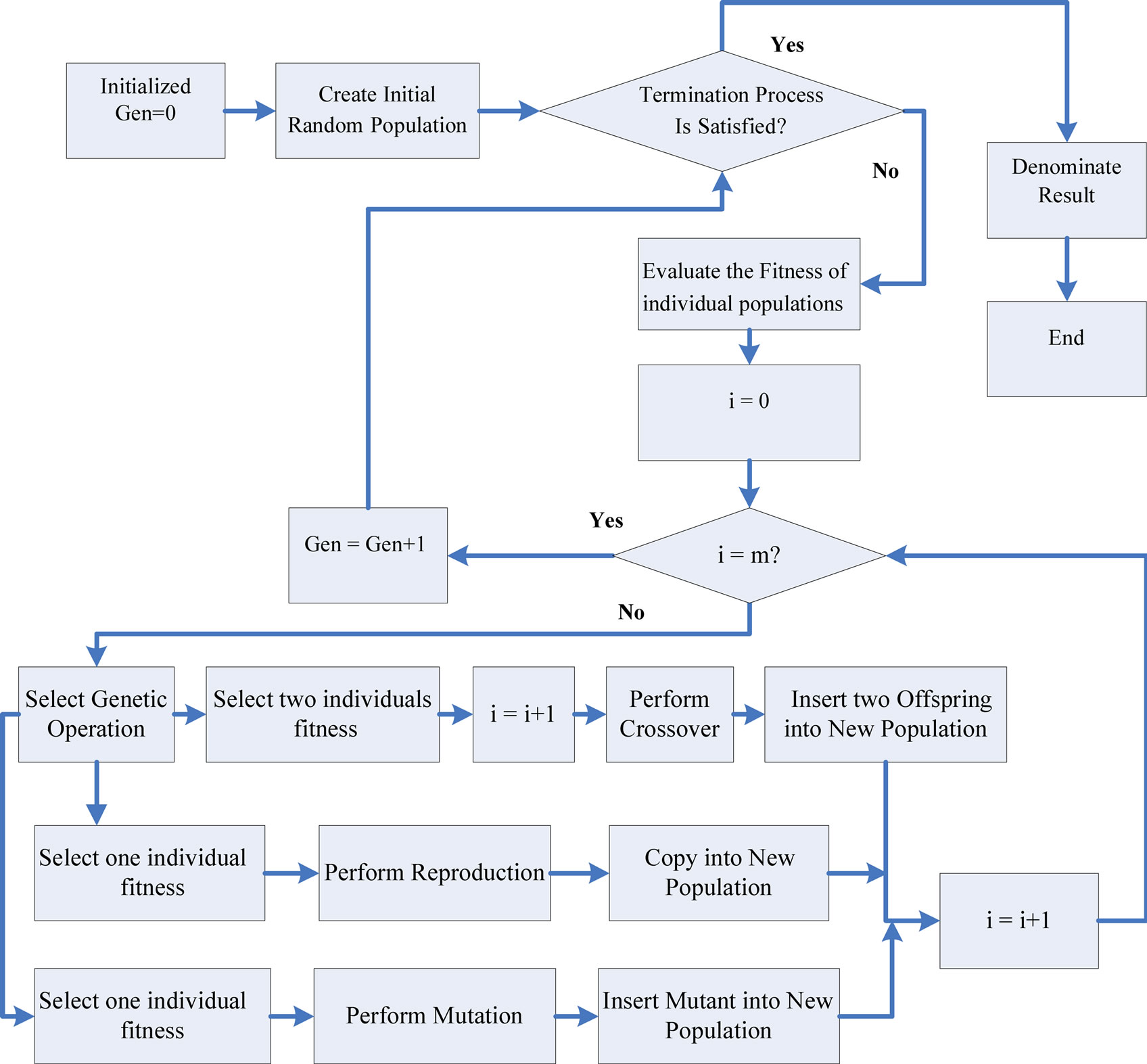
Figure 5. A conventional Genetic Algorithm.
It is clear from the flowchart of the Genetic Algorithms that each member of a new generation comes either from a reproduction, crossover or mutation operation. The operation that will be applied each time is selected based on a probabilistic schema. Each one three operations is related to a probability Preproduction, Pcrossover, and Pmutation in a way that Preproduction + Pcrossover + Pmutation = 1 Therefore the number of offspring that comes from reproduction, crossover or mutation is proportional to Preproduction, Pcrossover, and Pmutation respectively [15].
6.2. A Genetic Algorithm That Define the Artificial Neural Network Structure
We use Genetic Algorithms to search a space of Artificial Neural Network topologies and select those that match optimally our criteria. The topologies that interest us have at most two hidden layers and their output layer has the one neuron (x-y-z-1). Due to computational limitations it is not possible search the full space defined by x-y-z-1. What we can do is to search the space defined by xmax-ymax-zmax-1, where xmax, ymax and zmax are upper limits we set for x, y and z respectively.
7. Proposed Prediction Using Artificial Neural Network
The proposed prediction consisted of three phases Figure 6. In the first phase a Genetic algorithm searched the space of Artificial Neural Networks with different structures and resulted a generation with the fittest of all networks searched based on a metric which was either PreA or PreB or PreC [16]. The Genetic Algorithms search was repeated three times for each metric. Then the best three networks were selected from each repetition of the Genetic Algorithms search and for each one metrics. The output of the first phase was a set of thirty six network structures shown in Figure 6.
In the second phase for each one of the thirty six resulting network structures we applied the following procedure. We trained and validated the network. Then we
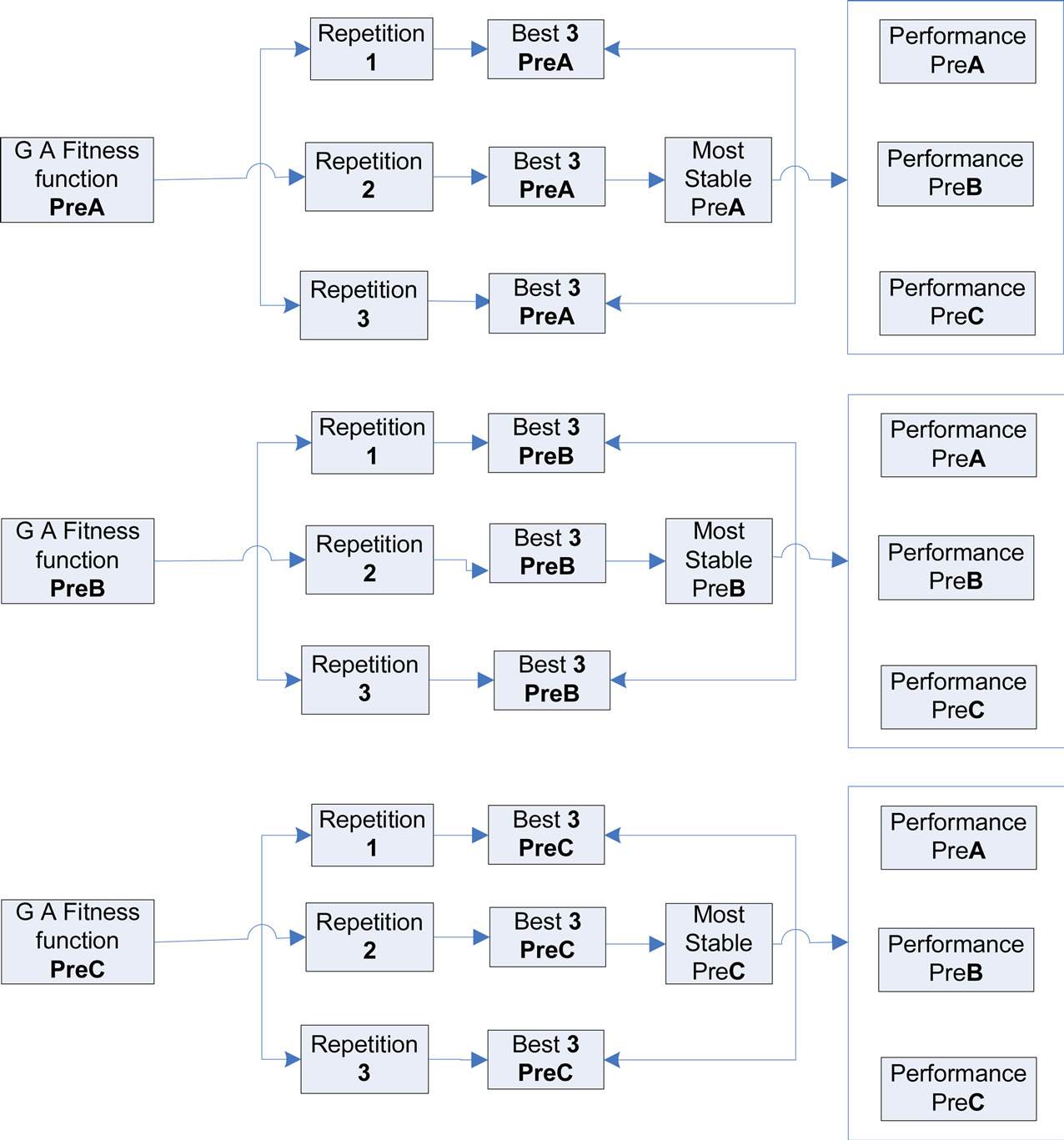
Figure 6. Experiment of BSE Data.
used the showed number of epochs from the validation procedure and based on it we retrained the network on the Training1 plus the Validation 1 set. Finally we tested the performance of the network for unseen data (Validation 2 set). This procedure was repeated 50 times for each network structure for random initializations of its weights. From the nine networks for each performance statistic, we selected the most stable in terms of standard deviation of their performance. Thus the output of the second phase was a set of four network structures. During the third phase for each one of these four networks we applied the following procedure 50 times. We trained each network on the first half of the Training Set and we used the remaining half for validation. Then, using the showed epochs by the validation procedure, we retrained the network on the complete Training Set as illustrated in Figure 6. Finally we tested the network on the Test Set calculating all four metrics. The performance for each network on each metric was measured again in terms of standard deviation and mean of its performance over 50 times that it was trained, [17] validated and tested.
In this paper first set of parameters is related to the size of the space that the Genetic Algorithm will search. We constructed this is set through variables xmax, ymax and zmax which represent the size of the input, the first hidden and the second hidden layer respectively. For all the Genetic Algorithms in this study we have used xmax = 30, ymax = 40 and zmax = 40. This decision was made having in mind that the larger the space the smaller the probability of neglecting network structures that might perform well in our task. We have selected the larger space that we could search keeping in mind our computational constraints. All the experiments proved that the most interesting part of our search space was not close to these bounds therefore we concluded that the search space needed no expansion. We observed that the Resilient Backpropagation is the algorithm that converged fastest and in fewest epochs. Our observations on the performances of these algorithms agree with the observations of Demuth and Beale [18]. They also experimented on specific network structures using different data and they found that the Resilient Backpropagation converges faster than all the other algorithms we considered in our research.
8. Experimental Results of Bombay Stock Exchange (BSE)
The Bombay Stock Exchange data we searched the space defined above 12 times using 3 repetitions for each one of our metrics (PreA, PreB, PreC).
PreA
By evaluating the networks based on PreA the Genetic algorithm search for the first repetition gave us the following results. The first two columns of shown in Table 2 describe the initial generation that contains 30 randomly selected networks and their performance (PreA), while the next two columns give the individuals [19] of the last generation with their performance. The ten network structures that were mostly visited by the algorithm as well as the frequency with which they were met in the 25th generation are shown by the following Table 2.
We have that the network with structure 6-19-3-1 was considered by the algorithm 61 times and it was not present in the final generation, while network 11-6-3-1 was considered 50 times and it was met 9 times in the 25th generation. Table 2" target="_self"> Table 2 shows that the variance of the performance of the networks in Generation 1 is small and their average is close [20] to one. The performance of the networks belongs to the last generation shows that most of them performed only as well as the random walk model based on the price of the market. This can be either because there are no structures that give significantly better results compared to the random walk model or that the path that our algorithm followed did not manage to discover these networks. Therefore, to have safer conclusions we selected to repeat the search twice. A second comment is that there are network structures that seem to perform very badly, for instance 10-29-21-1 gave us PreA of 4.5. Furthermore from Table 2 it is clear that the Genetic Algorithms did manage to converge to network with smaller in both terms of mean and standard deviation. The type of network structures we got in the final generation the only pattern we observed was a small second hidden layer and more Specifically 3 neurons for most of our structures. How fit individuals proved to be throughout the search that the algorithm performed. For instance the network 6-19-3-1 was visited 60 times, which infers that for a specific time period this individual managed to survive but a farther search of the algorithm proved that new fittest individuals came up and 6-19-3-1 did not manage to have a place at the 25th generation. The next step we repeated the Genetic Algorithms search. The results we obtained in terms of the mean and standard deviation of the first and last generations were
Repetition 3
Generation first last
Average 1.031067456 0.017527960
Std 0.043528247 0.023318392
The simulation results shown in Figure 7 were generated with Matlab following plots give the mean and the standard deviation of PreA for each generation (from 1 to 25). In addition the overall generations mean and standard deviation is reported.

Table 2. The results of the First Repetition of the Genetic Algorithms search on the Bombay Stock Exchange data.

Figure 7. Mean and STD of PreA. Mean and STD of PreA throughout all generation for the Bombay Stock Exchange data.
Repetition 3
Repetition 3 Minimum 0.9795799885 Maximum 5.3546777648 Mean 1.0365190398 StDev 0.1147578350
The above plots make clear that in all repetitions the Genetic Algorithms converged giving us networks with smaller Pres. It is also clear that the standard deviation of the Pres across generations also converted to smaller values. However in none of these experiments did we obtain a network structure that clearly beats the random walk model shown in Figure 7. Furthermore the patterns we managed to observe in the topologies of the networks that belong with the last generations are first, topologies with many neurons in both hidden layers and in the input layer were not prepared and secondly, the fittest networks proved to be those with one or three neurons in the second hidden layer. The most occurrences that a specific topology managed to have in a last generation were 9, we discovered no network that was by far better than all the others.
PreB
Similarly, we used the Genetic Algorithms to search the space of network topologies using PreB As fitness function. The means and standard deviations of the first and last generation for all repetitions are presented in the following.
Repetition 2
Generation first Last
Average 0.760946598 0.716306695
Std 0.053750167 0.015607519
These results show that the Artificial Neural Network model managed to beat clearly the predictions of the RW model (based on the excess returns) by achieving on average Pres close to 0.69. A second important comment is that the Genetic Algorithms converged significantly both in terms of mean and standard deviation. While for PreA the average performance in both the first and the last generations was close to one and the only thing that the algorithm managed to achieve was to reduce the variance of the performance, for PreB we observed a significant improvement not only to the variance but to the average of the performance as well. Furthermore in the first repetition of the Genetic Algorithms search we obtained a topology that proved to be clearly the fittest; it was present 28 times in the last generation and it was visited by the Genetic Algorithms 243 times. The topology was 6-6-1-1.
The mean and standard deviation we obtained for each generation in each one three repetition are depicted by the shown in n">Figure 8.
Repetition 2
Repetition 2 Minimum 0.7234528054
Maximum 3.1217654038
Mean 0.7544526178
StDev 0.0973071734

Figure 8. Mean and STD of PreB throughout all generation for the Bombay Stock Exchange data.
From these plots clearly the Genetic Algorithms converged in all repetitions both in terms of standard deviation and mean. This convergence was not always stable shown in Figure 8.
PreC
The Genetic Algorithms search using as fitness function PreC gave us again values close to one shown in Figure 9. Thus here it is shown that the Artificial Neural Network model did not manage to beat clearly the model which states that the gains we will have from the stock market is exactly those that we would have from bonds.
Repetition 3
Generation first Last
Average 1.175302645 1.005318149
Std 0.431630851 0.017530157
Here again in repetitions 3 we heard that the fittest network topologies had a second hidden layer that consisted of one or two nodes. The mean and standard deviation throughout the 25 generations converted to smalller values but repetitions 3 they moved asymptotically close to one; similarly to the case we used as fitness function the PreA.
Repetition 3
Repetition 3 Minimum 0.9785128058
Maximum 3.2870893626
Mean 1.0264347153
StDev 0.1078208731
From all the repetitions of the Genetic Algorithms search using both PreA and PreC it became clear that the predictive power of predictive models that are involved is similarly shown in Figure 9.
The benchmarks that the Artificial Neural Network model did not manage to the ones that compared their predictive ability with the random walk model on the value of the Bombay Stock Exchange market (PreA) and the ones that compared their predictive ability with the

Figure 9. Mean and STD of PreC throughout all generation for the Bombay Stock Exchange data.
model which states that the value of the market tomorrow will be such that will allow us to have the same benefit from the stock market as we would have from the bond market (PreC). The benchmark that compares the Artificial Neural Network model with the random walk model on the excess returns turned out to be easy to beat always. Furthermore according to all the benchmarks that involved PreA or PreC there are naive prediction models that can perform equally well with the best Neural Networks thus the Artificial Neural Networks did not manage to outperform the predictive power of these models. The comment we must make here about PreA, B and C is that the naïve predictors related with PreA and PreC compare the predictive abilities of our models with naïve models that show no change in the value of the Bombay Stock Exchange market.
However we cannot say the same for the naïve predictor we use in PreB this predictor attempt to give us a prediction other that no change in the value of the Bombay Stock Exchange market. Therefore the naive predictors that are based on the statement that will be no change to the value of the market seems to be the most difficult to beat. The exhaustive search we performed in the experiment we have no doubt as to weather their might be a network topology for which the Neural Networks will be able to give better predictions. The search we have shown that there is no specific network structure that performs significantly better than the others, instead of there is a group of structures that gave us optimal performance, even though this performance is no better than that provided by a random walk.
9. Conclusion
Finally, the Artificial Neural Network model is superior compared to the Autoregressive models because they are able to capture not only linear but also non linear patterns in the underlying data but their performance is influenced by the way that their weights are initialized. Therefore the evaluation of Artificial Neural Network model should be done not in terms of any one specific initialization of their weights, but in terms of the mean and standard deviation of several randomly selected initializations. In the current study predicted of the Bombay Stock Exchange Market excess returns on a daily basis was attempted. More specifically we attempted to predict the excess returns of Bombay Stock Exchange (BSE) Stock Market the time series data of stock prices was transformed into the returns the investor would have if he selected the Stock Market instead of placing his capital in the bond market (excess return time series). In our prediction task we used lagged values of the excess return time series to predict the excess returns of the market on a daily basis. We applied randomness tests on the excess return time series the run and the test and we rejected randomness. Thus, we proved that the prediction task is feasible. Robustness of Artificial Neural Networks to the changing structures, it can easily manage the inaccuracy and any degree of nonlinearity in the data.
REFERENCES
- O. B. Antwerpen, “6de Eeuwse Traditionele Baken Zandsteenarchitectuur,” 2010. http://www.belgiumview.com/belgiumview/tl1/view0002205.php4
- B. G. Malkei, “A Random Walk Down Wall Street,” 7th edition, W. W. Norton & Company, New York, 1999.
- R. Gupta., “Emerging Markets Diversification: Are Correlations Changing over time?” International Academy of Business and Public Administration Disciplines (IABPAD) Conference, Orlando, 3-6 January 2006, pp. 331-351.
- T. Hellstrom and K. Holmstrom, “Predictable Pattern in the Stock Return,” 1998. http://www.wbiconpro.com/2.Sandip.pdf
- P. Dennis, “Stock Splits and Liquidity: The case of the Nasdaq-100 Index Tracking Stock,” Financial Review, Vol. 38, No. 3, 2003, pp. 415-433.
- G. S. Maddala, “Introduction to econometrics,” 1st Edition, Macmillan Publishing Company, New York, 1992.
- H. M. Pesaran and A. Timmermann, “Forecasting Stock Returns: An Examination of Stock Market Trading in the Presence of Transaction Costs,” Journal of Forecasting, Vol. 13, No. 4, 1994, pp. 335-367. doi:10.1002/for.3980130402
- R. S. Michalski and G. Tecuci, “Machine Learning: A Multistrategy Approach,” Morgan Kaufmann, Waitham, 1994.
- E. Alpaydın, “Introduction to Machine Learning (Adaptive Computation and Machine Learning),” MIT Press, Cambridge, 2004.
- Reserve Bank of India, “Handbook of Statistics on Indian Economy,” 2001. http://www.rbi.org.in
- M. T. Mitchell, “Machine learning,” 1st Edition, The McGraw-Hill Companies, New York, 1997.
- M. C. Bishop, “Neural Networks for Pattern Recognition,” Oxford University Press, New York, 1996.
- E. D. Goldberg, “Genetic Algorithm in Search, Optimization, and Machine Learning,” Addison-Wesley, New York, 1989.
- M. T. Mitchell, “An Introduction to Genetic Algorithms,” MIT Press, Cambridge, 1997.
- R. J. Koza, “Genetic Programming on the Programming of Computers by Means of Natural Selection,” MIT Press, Cambridge, 1992.
- P. Healy, J. Ledyard, S. Linardi and R. J. Lowery, “Prediction Markets: Alternative Mechanisms for Complex Environments with Few Traders,” Management Science, vol. 56, no. 11, 2010, pp. 1977-1996. doi:10.1287/mnsc.1100.1226
- H. White, “Economic Prediction Using Neural Networks: The Case of IBM Daily Stock Returns,” Proceedings of the 2nd Annual IEEE Conference on Neural Networks, San Diego, 24-27 July 1988, pp. 451-458. doi:10.1109/ICNN.1988.23959
- H. Demuth and M. Beale, “Neural Network Toolbox: For Use with Matlab,” 4th Edition, The MathWorks Inc., Natick, 1997.
- O. Castillo and P. Melin, “Simulation and Forecasting Complex Financial Time Series Using Neural Networks and Fuzzy Logic,” IEEE International Conference on Systems, Man, and Cybernetics, Tucson, 7-10 October 2001, pp. 2664-2669.
- G. B. Antonio, O. U. Claudio, M. S. Manuel and O. M. Nelson, “Stock Market Indices in Santiago de Chile: Forecasting Using Neural Networks,” IEEE International Conference on Neural Networks, Washington DC, 3-6 June 1996, pp. 2172-2175.

