Wireless Sensor Network
 Vol. 4  No. 10 (2012) , Article ID: 23692 , 6 pages DOI:10.4236/wsn.2012.410036

BER of OFDM System with Multiple NBI Rejection Cascade Complex Coefficient Adaptive IIR Notch Filter

Aloys N. Mvuma

School of Informatics, The University of Dodoma, Dodoma, Tanzania

Email: mvuma@udsm.ac.tz

Received August 16, 2012; revised September 15, 2012; accepted September 30, 2012

Keywords: Multiple Narrowband Interference; Cascade Adaptive Notch Filter; OFDM System; Bit Error Ratio

ABSTRACT

In this paper, rejection of multiple narrowband interferers in a binary phase shift keying modulated orthogonal frequency division multiplexing (BPSK-OFDM) system is investigated. The BPSK-OFDM system in consideration operates in an additive white Gaussian noise (AWGN) channel. A cascade complex coefficient adaptive infinite impulse response (IIR) notch filter with gradient-based algorithm is used to reject the interferers. Bit error ratio (BER) performance of the system is studied and a general closed-form expression is derived assuming negligible steady-state leakage NBI and by estimating the decision variable as Gaussian distributed based on Central Limit Theorem (CLT). Dependence of the BER performance on the notch bandwidth coefficient is demonstrated by the analysis. Extensive simulation results are included to substantiate accuracy of the analysis.

1. Introduction

Complex coefficient adaptive notch filters (ANF) have been proposed for use in applications that require detection and rejection or enhancement of narrowband signals embedded in broadband signals with in-phase and quadrature-phase components. One such applications is in the rejection of narrowband interference (NBI) in quadriphase shift keying (QPSK) spread-spectrum communication systems [1,2]. It is well known that infinite impulse response (IIR) implementation of adaptive notch filters is more advantageous as compared to finite impulse response (FIR) with much less computation complexity. A complex coefficient adaptive notch filter implemented as a constrained IIR filter with a complex Gauss-Newton adaptation algorithm was proposed in [2]. Furthermore, its application in suppression of NBI in QPSK spread-spectrum communication system showed a substantial improvement in overall system bit error ratio (BER).

A complex coefficient adaptive IIR notch filter with a simplified gradient-based algorithm that does not require any matrix inversion was proposed in [4] and its convergence and steady state behaviors were extensively analyzed in [3] and [4]. Its application in rejection of a single NBI in a QPSK DS-SS communication system over an additive white Gaussian noise (AWGN) channel was also discussed in [5]. Cascade extension of the algorithm in [4] for detection of multiple sinusoids was further proposed and analyzed in [6]. Its application in the rejection of multiple NBI in a QPSK direct sequence codedivision multiple access (DS-CDMA) system was discussed in [7] with promising improvement in BER. However, the ANF has not been attempted in rejection of multiple NBI in an orthogonal frequency division multiplexing (OFDM) system. OFDM has recently become a preferred transmission technique in emerging broadband wireless communication systems [8,9]. It has been reported that WLAN and WMAN standards based on OFDM that operate in the unlicensed frequency bands are susceptible to NBI from other systems coexisting in the same spectrum. Such systems include Bluetooth, microwave ovens, cordless telephones, etc. The observation has challenged researchers to find NBI rejection techniques that can alleviate effects of NBI in OFDM systems [10-17].

Several NBI suppression techniques for OFDM systems are found in literature. The use of pre-coding, spread spectrum OFDM, post-detection receiver techniques involving equalizers and frequency domain subtractive cancellation using singular value decomposition have been reported [11-17]. Coulson [10] proposed an NBI suppression technique based on excision filtering. It was demonstrated by computer simulation that the technique improved ensemble average BER to about 0.001 for binary phase shift keying (BPSK) modulated OFDM with signal-to-interference ratios (SIR) as low as –30 dB [10]. However, the author did not show how excision filter parameters affect the BER performance of the OFDM system.

This paper employs similar method to that proposed in [10] whereby the multiple NBI excision filter is implemented using a cascade complex coefficient adaptive IIR notch filter with simplified gradient-based algorithm presented in [8]. The OFDM system is considered to be operating in an AWGN channel. Estimating the Fast Fourier Transform (FFT) of the ANF output for each subcarrier as Gaussian distributed based on Central Limit Theorem (CLT), a closed-form BER expression is derived for small step size constant with negligible steady-state leakage NBI. It is observed that besides the received signal-to-noise ratio (SNR), BER performance depends largely on the value of notch bandwidth coefficient. Computer simulation results are included to support analytical findings.

Main contributions of this paper are as follows: 1) It presents a systematic approach to the analysis of BER performance of OFDM systems with cascaded complex coefficient filters for multiple NBI suppression. Such approach has not been presented elsewhere; 2) It presents a simple closed-form BER expression for an OFDM system with multiple NBI suppression filters. The expression relates BER with filter notch bandwidth parameter and received signal-to-noise ratio (SNR).

The organization of this paper is as follows: In Section 2, OFDM system model and the NBI suppression cascade complex coefficient adaptive IIR notch filter are presented. Section 3 presents BER analysis while simulation results and discussions on findings are presented in Section 4. Lastly, concluding remarks and future research areas are included in Section 5.

2. System Model

Figure 1 below shows a block diagram of the BPSKOFDM system used in this paper. Received discrete-time low pass equivalent BPSK-OFDM symbol 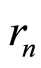is modeled as

(1)

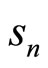is the n-th of L samples in the transmitted BPSKOFDM symbol. It is expressed as

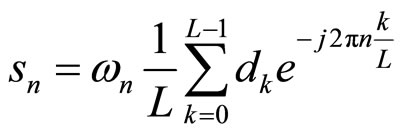(2)

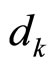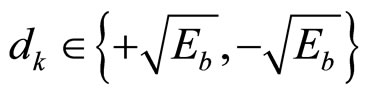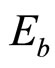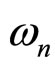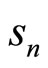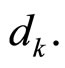
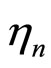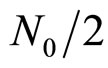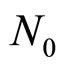is the k-th data symbol from BPSK modulation constellation, i.e., where is the signal average energy per bit and is a rectangular windowing function, i.e., It should be noted that is the inverse discrete Fourier transform (IDFT) of L data symbols is the n-th sample of a zeromean complex additive white Gaussian noise (AWGN) with variance where is the power spectral density. 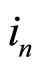is the n-th sample of the NBI which is modeled as

(3)

where are unknown amplitude, frequency and phase of the i-th of N narrowband interferers. Validity of the interference model in (3) was discussed in detail in [10].

The cascade realization of the complex coefficient adaptive IIR notch filter for detection of multiple sinusoids in noise was proposed in [8]. The equivalent transfer function Heq(z) from the ANF input signal rn to the output signal yn is given by

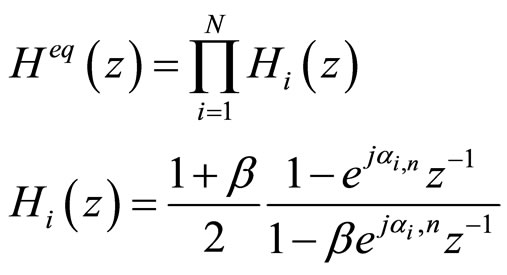(4)

Here, 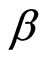is the notch bandwidth coefficient and is the notch frequency coefficient for the i-th section of

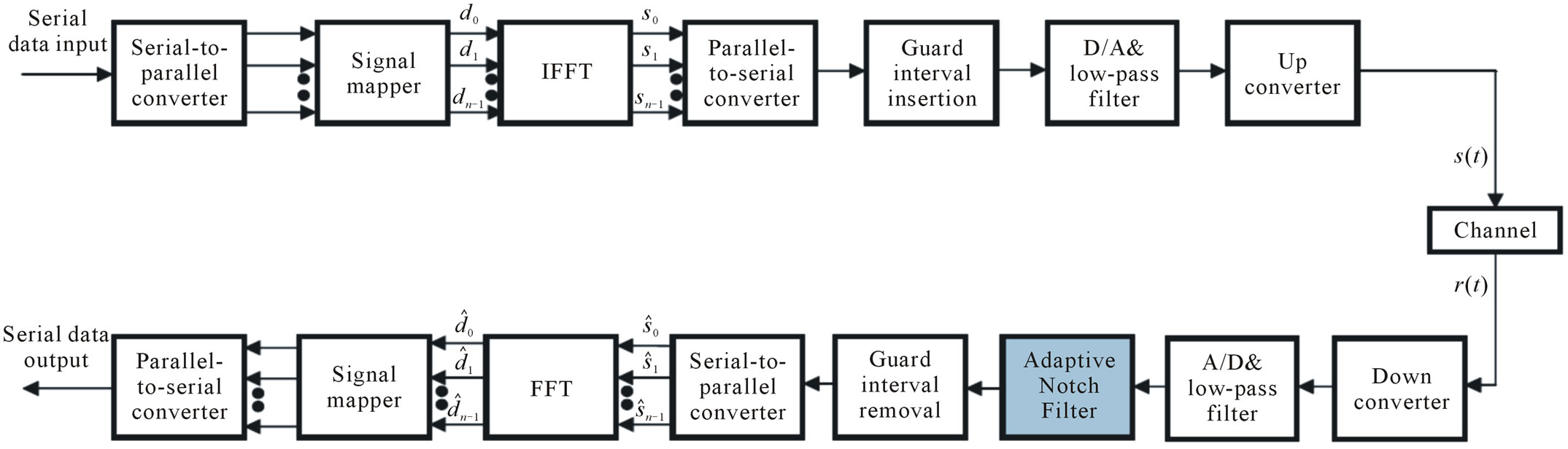
Figure 1. OFDM system model.

the cascade complex coefficient adaptive IIR notch filter at the n-th iteration, respectively.

An adaptation algorithm for the i-th notch frequency coefficient for tracking and suppressing the i-th NBI is expressed as [6]

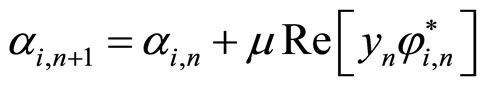(5)

where Re[.] stands for real part, 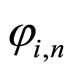is the i-th gradient signal and is its conjugate. Transfer function from rn to was obtained in [6] as

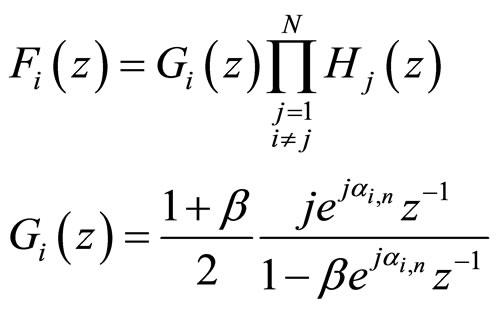(6)

Referring to (4), the unknown frequency of the i-th NBI at the n-th iteration can be estimated by where 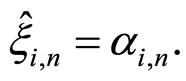The adaptation algorithm in (5) was used in [7] for suppression of multiple NBI in QPSK DS-CDMA system with significant BER improvement. Convergence behavior of the proposed adaptation algorithm is shown in Figure 2.

3. Analysis of Bit Error Ratio

This section presents analysis of BER of the BPSKOFDM system in the presence of multiple NBI with interference suppression cascaded complex coefficient ANF. The analysis ignores errors that can occur as a result of time drift or phase offset by assuming ideal time and phase synchronization. The analysis further assumes negligible steady-state leakage NBI power. This assumption is valid for small values of step size.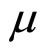

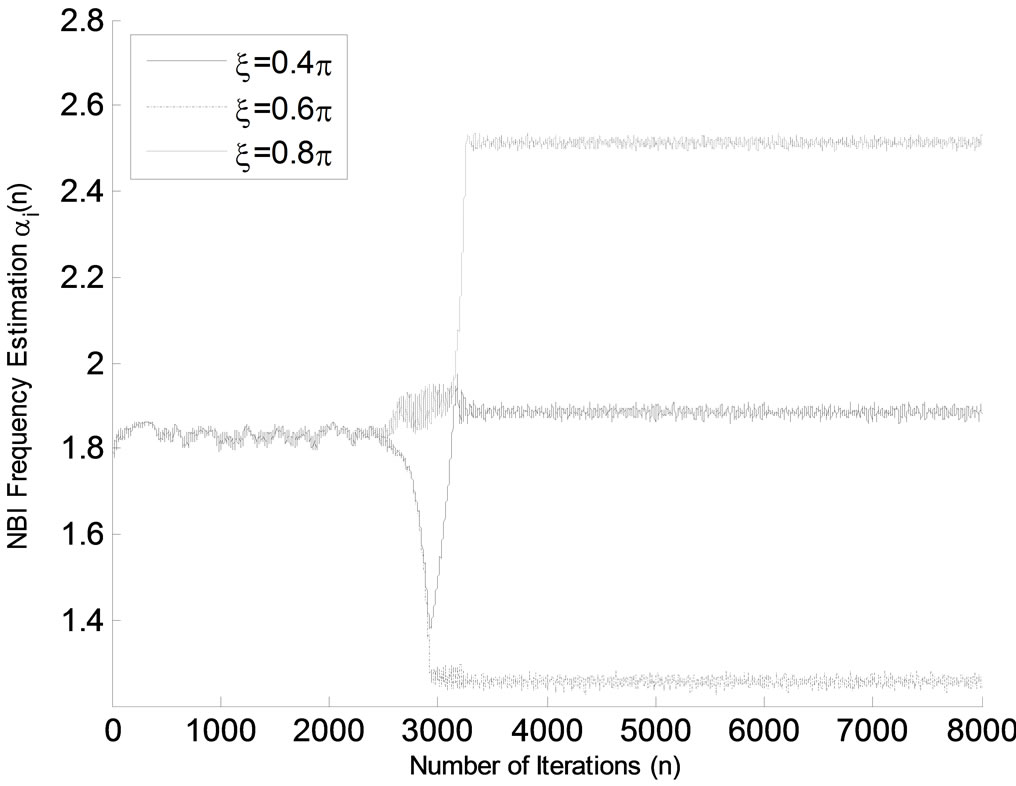
Figure 2. Convergence behavior of the cascade complex coefficient adaptive notch filter for estimating three NBI frequencies in OFDM received signal for A1 = A2 = A3 =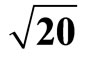, ξ1 = 0.4π rad./s, ξ2 = 0.6π rad./s, ξ2 = 0.8π rad./s, β = 0.9, μ = 10−4, L = 64, and SNR = 0 dB.

The cascade ANF output signal 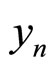is applied to an L-point discrete Fourier transform (DFT) at the receiver. The resulting k-th sample 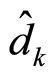is therefore given by

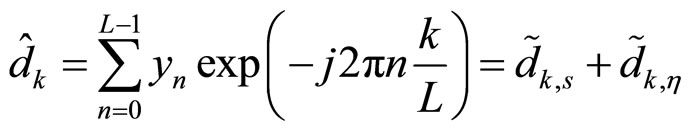(9)

The k-th sample in (9) is composed of two components i.e. and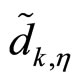. The former is the DFT of the cascade ANF output signal due to the OFDM transmitted signal while the latter is due to channel AWGN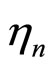. The assumption of negligible leakage steady-state NBI justifies the exclusion of the DFT of the ANF output due to NBI

3.1. Statistical Characteristics of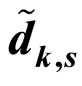

The DFT of the cascade ANF output signal due to the BPSK-OFDM transmitted signal 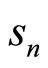is given by:

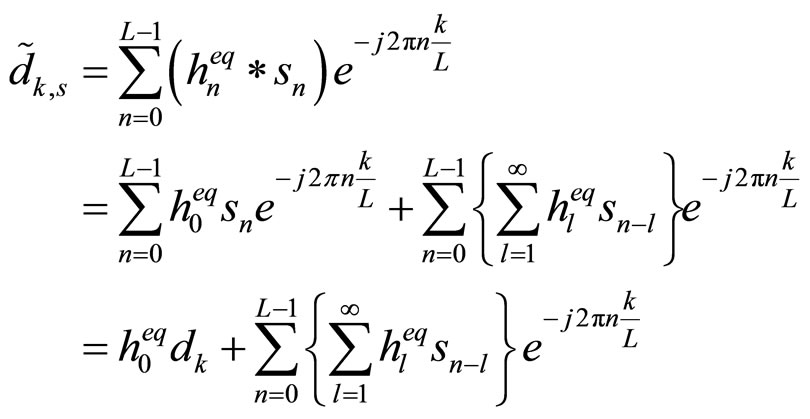(10)

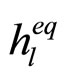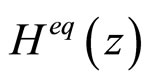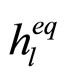where * denotes convolution sum and is a complex impulse response of in (4) that decays exponentially with l. The right hand side of (10) has two terms; the first is the desired data component while the second is due to intersymbol interference (ISI) induced by the cascade ANF. is the value of for 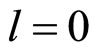and is obtained by

(11)

The expectation of 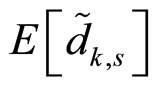is derived by referring to (10) and by assuming statistically independent and identically distributed data symbols It is expressed as

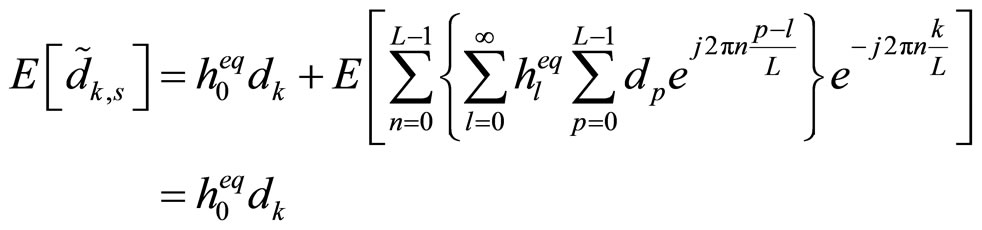(12)

It can be deduced from (12) that the cascade ANF attenuates the expectation of the k-th data symbol

by a factor proportional to which depends on the notch bandwidth coefficient 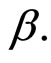Mean-square value and variance of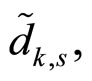 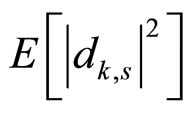and 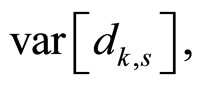respecttively, can be shown to be expressed as

(13)

3.2. Statistical Characteristics of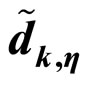

By considering the AWGN 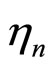the DFT of the cascade ANF output signal can be shown to be given by:

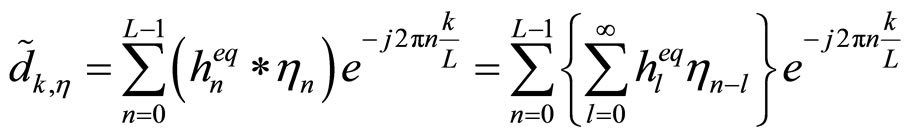(14)

Expectation of 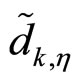is zero since 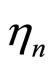is modeled as zero mean random process. Its variance is expressed as

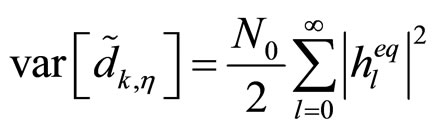(15)

which depends on the notch bandwidth coefficient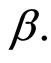

Noting that 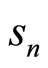and 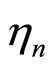are statistically independent and uncorrelated, variance of 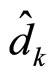denoted as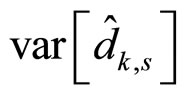

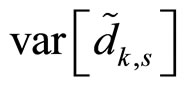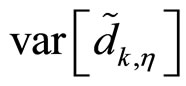becomes the total sum of and in

(13) and (15), respectively, i.e.

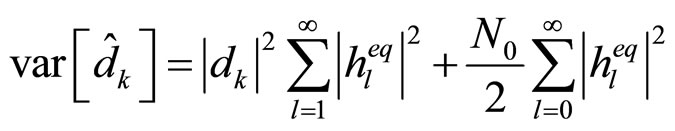(16)

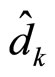in (9) can be approximated by Gaussian distribution for large 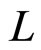using Central Limit Theorem (CLT). Average BER for the k-th frequency bin 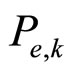is obtained by the Gaussian approximation and by referring to (12) and (16). It is given by:

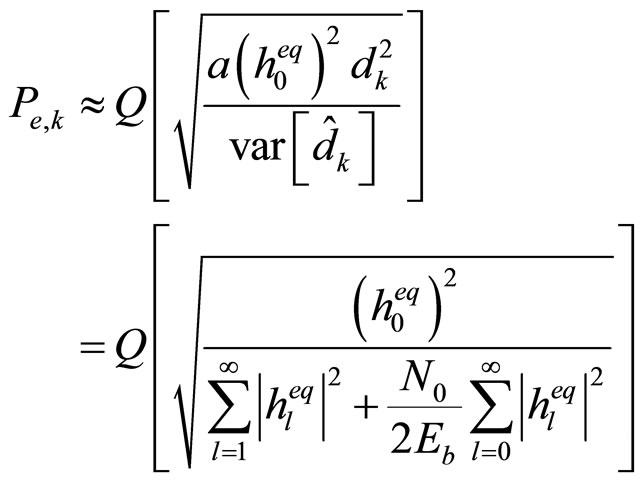(17)

Equation (17) shows the average BER to be the same for all The average BER for the OFDM symbol will therefore be the same as in (17). It is observed that the average BER depends on factors that are functions of the notch bandwidth coefficient.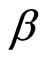

4. Simulation Results

In this section, simulation and analytical results are presented, discussed and compared to validate accuracy of the BER closed-form expression (17) derived in the previous section. All simulations results were obtained using MATLAB>® software. The results presented were obtained for the following OFDM signal parameters:

FFT size L                                          64

Number of data subcarriers           52

Number of bits per symbol             52

Number of symbols                         100

The value of step size adaptation constant 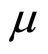in (5) was fixed to. Simulation results were obtained by averaging over ten independent computer runs after the adaptation algorithm in (5) had attained its steady state.

Analytical and simulation results for BER plotted against notch bandwidth coefficient 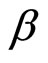with signal-tonoise ratio (SNR) as a parameter for number of NBIs N = 2 and N = 3 are shown in Figures 3 and 4, respectively. Frequencies of NBIs 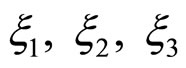in (3) were set to 0.4π, 0.6π and 0.8π, respectively. Interference-to-signal ratio for the i-th narrowband interferer (ISRi) was set to 10 dB,

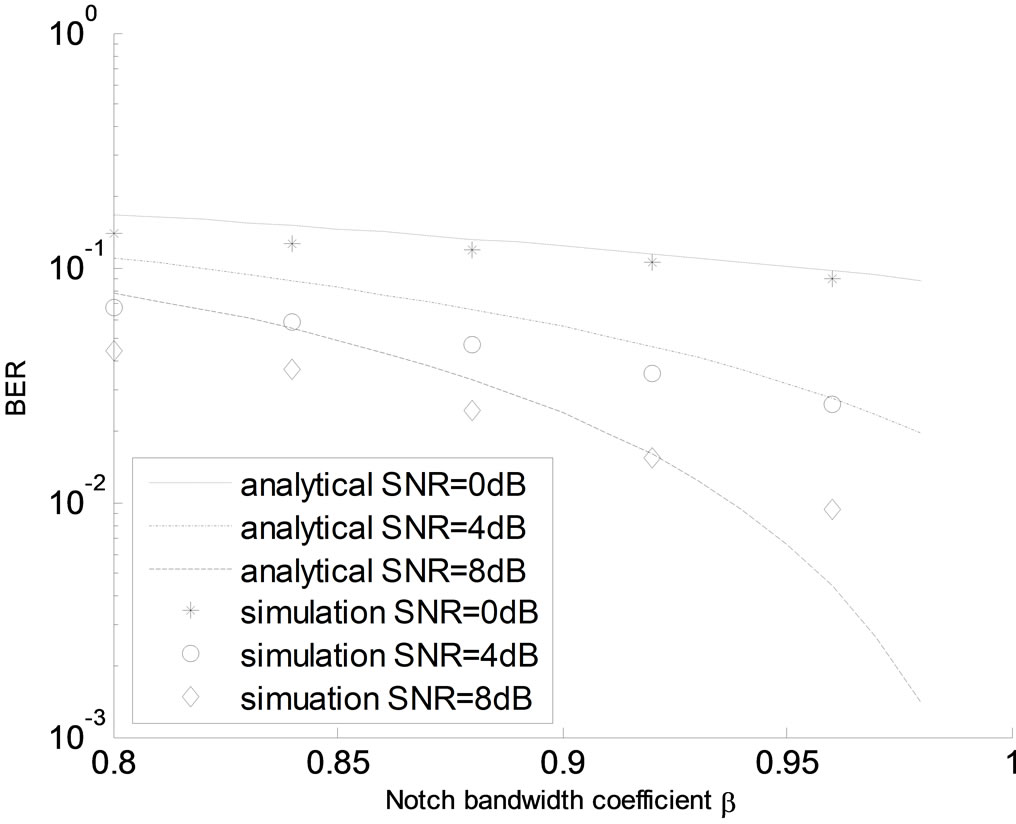
Figure 3. BER analytical and simulation results for N = 2, SNRi = 10 dBi, ξ1 = 0.4π, ξ2 = 0.6π, μ = 10−5, and L = 64.

Figure 4. BER analytical and simulation results for N = 3, SNRi = 10 dBi, ξ1 = 0.4π, ξ2 = 0.6π, ξ3 = 0.8π, μ = 10−5, and L = 64.

where

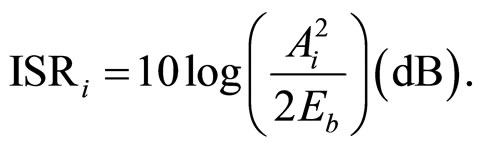
and 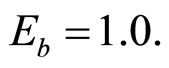The figures show that the BER decreases with in both cases. Moreover, close agreement between analytical and simulation results confirms the accuracy of the analysis carried out in Section 3.

Figures 5 and 6 show analytical and simulation BER results plotted as a function of SNR for number of NBIs N = 2 and N = 3, respectively. The value of was likewise set to 0.9 and ISR for each NBI was set to 10 dB. BER for the ideal OFDM system without NBI and that with NBI but without NBI suppression ANF are also shown for comparison purpose. Improvement of BER to about 0.001 and 0.01 for N = 2 and N = 3, respectively is

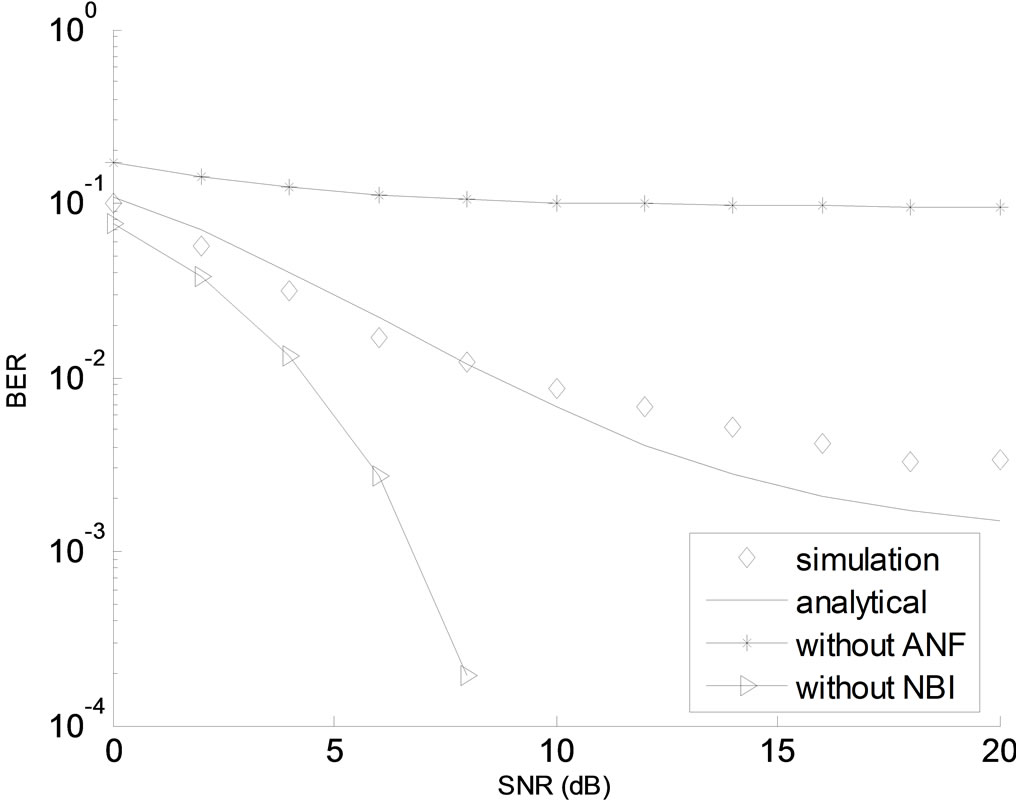
Figure 5. BER analytical and simulation results for N = 2, SNRi = 10 dBi, ξ1 = 0.4π, ξ2 = 0.6π, β = 0.9, μ = 10−5, and L = 64.

Figure 6. BER analytical and simulation results for N = 3, SNRi = 10 dBi, ξ1 = 0.4π, ξ2 = 0.6π, ξ3 = 0.8π, β = 0.9, μ = 10−5, and L = 64.

evident from the figures. Furthermore, the figures show close agreement between analytical and simulation results. Slight discrepancy between simulation and analytical results in all figures can be attributed to the Gaussian distribution assumption made on the decision variable in (9) based on CLT. Moreover, leakage NBI becomes significant as the notch bandwidth coefficient 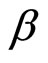approaches 1.0 that leads to slight difference between analytical and simulation results in Figures 3 and 4.

5. Conclusion

Bit error ratio (BER) of a BPSK OFDM system with multiple NBI rejection complex-coefficient cascade ANF was analyzed. A closed-form BER expression was derived using the Central Limit Theorem approximation of the decision variable. Accuracy of the derived BER expression was demonstrated by computer simulation using MATLAB® software with emphasis on its dependence on notch bandwidth coefficient. Moreover, significant BER performance improvement gained by the use of complex coefficient cascade ANF for NBI rejection was also shown. In the future, Rayleigh channel, M-ary modulation techniques and effects of leakage NBI power on the BER performance of OFDM system will be studied.

REFERENCES

  1. Y.-C. Wang and L.B. Milstein, “Rejection of multiple narrowband interference in both BPSK and QPSK DS spread spectrum systems,” IEEE Trans. Commun., vol. COM-36, pp. 195-204, Feb. 1988. doi:10.1109/26.2750
  2. S.C. Pei and C.C. Tseng, “Complex adaptive IIR notch filter algorithm and its applications,” IEEE Trans. Circuits Syst., vol. CAS-41, no.2, pp. 158-163, Feb. 1994.
  3. H.Y. Jiang, S. Nishimura, and T. Hinamoto, “Performance analysis of complex adaptive notch filters,” in Proc. ICSP: IEEE Intern. Conf. on Circ. and Syst., pp. 502-505, June 1998.
  4. H. Y. Jiang, S. Nishimura, and T. Hinamoto, “Convergence analysis of complex adaptive IIR notch filters for the detection of single sinusoid,” IEICE Trans. Fundamentals, vol.E82-A, no.6, pp. 912-915, June 1999.
  5. H. Y. Jiang, S. Nishimura, and T. Hinamoto, “Steady-state analysis of complex adaptive IIR notch filter and its application to QPSK communication systems,” IEICE Trans. Fundamentals, vol.E85-A, no.5, pp.1088-1095, May 2002.
  6. S. Nishimura and H. Y. Jiang, “Simplified realization of cascaded adaptive notch filters with complex coefficients,” in Proc. ISCAS 1998, vol.5, pp. 269-272.
  7. A.N. Mvuma, “Performance of cascade complex coefficient adaptive IIR notch filter for multiple NBI suppression in QPSK DS-CDMA system over Rayleigh channel,” Inter. Journal of Comp. and Commun. Eng., vol. 6, pp.46-54, Jan. 2012.
  8. R. V. Nee, and R. Prasad, OFDM for Wireless Multimedia Communications, Boston, The artech House, 2000.
  9. G. L. Stuber, “Orthogonal frequency division multiplexing for wireless communication,” Georgia institute of Technology, 2006.
  10. A. J. Coulson, “Bit error rate performance of OFDM in narrowband interference with excision filtering,” IEEE Trans. Wireless Commun., vol. 5, no. 9, pp. 2484-2492, September 2006. doi:10.1109/TWC.2006.1687772
  11. Z. Nikolova, G. Iliev, M. Ovtcharov, and V. Poulkov, “Narrowband interference suppression in wireless OFDM systems,” African Journal of Information and Communication Technology, Vol.5, No. 1, pp.30-42, 2009.
  12. R. W. Lowdermilk and F. J. Harris, “Interference mitigation in orthogonal frequency division multiplexing (OFDM),” in Proc. ICUPC1996: IEEE International. Conf. Universal Personal Commun., vol. 2, pp. 623–627, Oct. 1996. doi:10.1109/ICUPC.1996.562648
  13. G. J. Saulnier, Z. Ye, and M. J. Medley, “Performance of a spread spectrum OFDM system in a dispersive fading channel with interference,” in Proc. MILCOM98: IEEE Military Commun. Conf., vol. 2, pp. 679–683, Oct. 1998.
  14. S. Kapoor and S. Nedic, “Interference suppression in DMT receivers using windowing,” in Proc. ICC2000: IEEE Internat. Conf. Commun., vol. 2, pp. 778–782, June 2000.
  15. R. Nilsson, F. SjÖberg, and J. P. LeBlanc, “A narrow-band interference canceller for OFDM-based systems,” in Proc. EPMCC01: 4th European Personal Mobile Commun. Conf., Feb. 2001.
  16. A. J. Coulson, “Narrowband interference suppression for OFDM,” IEEE Trans. Wireless Commun., vol. 5, no. 9, pp. 2484–2492, December 2010. doi:10.1109/TWC.2006.1687772
  17. D. Gerakoulis and P. Salmi, “An interference suppressing OFDM system for wireless communications,” in Proc. ICC2002: IEEE Intern. Conf. Commun., vol. 1, pp. 480-484, April 2002.

Journal Menu >>