Journal of Water Resource and Protection
Vol.08 No.02(2016), Article ID:63376,11 pages
10.4236/jwarp.2016.82012
Comparison of Stochastic Models in Forecasting Monthly Streamflow in Rivers: A Case Study of River Nile and Its Tributaries
Mohammed A. Elganiny, Alaa Esmaeil Eldwer
Irrigation Eng. and Hydraulics Department, Faculty of Engineering, Alexandria University, Alexandria, Egypt
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 August 2015; accepted 15 January 2016; published 5 February 2016
ABSTRACT
The dynamic and accurate forecasting of monthly streamflow processes of a river are important in the management of extreme events such as floods and drought, optimal design of water storage structures and drainage network. Many Rivers are selected in this study: White Nile, Blue Nile, Atbara River and main Nile. This paper aims to recommend the best linear stochastic model in forecasting monthly streamflow in rivers. Two commonly hydrologic models: the deseasonalized autoregressive moving average (DARMA) models and seasonal autoregressive integrated moving average (SARIMA) models are selected for modeling monthly streamflow in all Rivers in the study area. Two different types of monthly streamflow data (deseasonalized data and differenced data) were used to develop time series model using previous flow conditions as predictors. The one month ahead forecasting performances of all models for predicted period were compared. The comparison of model forecasting performance was conducted based upon graphical and numerical criteria. The result indicates that deasonalized autoregressive moving average (DARMA) models perform better than seasonal autoregressive integrated moving average (SARIMA) models for monthly streamflow in Rivers.
Keywords:
Monthly Streamflow, River Nile, DARMA Model, SARIMA Model, Stochastic Model

1. Introduction
Streamflow forecasting is of great importance to water resources management and planning. Medium- to long- term forecasting, at weekly, monthly, seasonal, or even annual time scales, is particularly useful in reservoir operations and irrigation management, as well as institutional and legal aspects of water resources management and planning. Due to their importance, a large number of forecasting models have been developed for Streamflow forecasting, including concept-based process-driven models such as the low flow recession model and rainfall-runoff models, and statistics-based data-driven models such as regression models, stochastic time series models [1] .
The stochastic time series models are the popular and useful tools for medium-range forecasting and generating the synthetic data. A number of stochastic time series models such as the Markov, Box-Jenkins (BJ) Seasonal Autoregressive Integrated Moving Average (SARIMA), deseasonalized Autoregressive Moving Average (DARMA), Periodic Autoregressive (PAR), Transfer Function Noise (TFN) and Periodic Transfer Function Noise (PTFN), are in use for these purposes [2] -[4] . The first three of these are univariate models and the last two are multivariate models. In addition, the PAR and PTFN models are periodic in nature [5] .
The univariate time series models that deal with only one time series, including the autoregressive integrated moving average (ARIMA) model and its derivatives such as seasonal ARIMA (SARIMA), periodic ARIMA, and deseasonalized ARIMA models, have long been applied in streamflow forecasting, particularly in the modeling of monthly streamflow [4] [6] -[10] . Rabenja et al. [11] forecasted both monthly rainfall and discharge of the Namorona River in the Vohiparara River Basin of Madagascar using ARIMA and SARIMA models and also concluded that the SARIMA model was more suitable than the non-seasonal ARIMA model.
The objective of this research is to select the best linear stochastic model for modeling monthly streamflow in Rivers. Two models are selected to be compared which the best; the deasonalized autoregressive moving average (DARMA) models and seasonal autoregressive integrated moving average (SARIMA) models. It is expected that this study will provide useful information for modeling monthly streamflow in Rivers, developing the appropriate strategy for managing the surface water under consideration and forming the basis of planning of major water resources. For example, a prediction may be required for construction of a hydrologic such as a bridge or dam.
2. Methodologies
Two main approaches to model seasonal time series at main key stations are considered in this paper. In the first approach, the series is deseasonalized by subtracting the seasonal means and perhaps dividing the seasonal adjustment by the seasonal standard deviation. A non-seasonal ARMA model is then fitted to the deseasonalized series. This model is named deseasonalized autoregressive moving average (DARMA) model. In the second approach, a linear stochastic model containing both seasonal and non-seasonal parameters is fitted to the differenced series this model is called Seasonal Autoregressive Integrated Moving Average (SARIMA) model. This type of seasonal model is discussed by Box and Jenkins [12] . I t has been used by various other researchers for modeling seasonal riverflow time series. The SARIMA model is often considered the most parsimonious model.
The DARMA model is a widely used approach to model seasonal data series. In this method, first the series should be deseasonalized and then an appropriate nonseasonal stochastic ARMA(p, q) models are fitted to the deseasonalized data. Two standard deseasonalization techniques that have been widely used are:
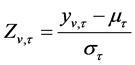 (1)
(1)
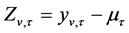 (2)
(2)
where 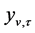 is the transformed observation for year v and season τ,
is the transformed observation for year v and season τ, 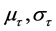 are the periodic mean and periodic standard deviation. The series may first be transformed by BOX-COX transformation, for which a logarithmic transformation is a special case, to eliminate problems with non-normality in the estimated model residuals [4] . The DARMA model is described as follow:
are the periodic mean and periodic standard deviation. The series may first be transformed by BOX-COX transformation, for which a logarithmic transformation is a special case, to eliminate problems with non-normality in the estimated model residuals [4] . The DARMA model is described as follow:
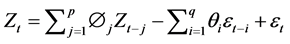 (3)
(3)
where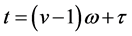 ,
, 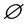 ,
, 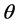 are the coefficients of the autoregressive and moving average and
are the coefficients of the autoregressive and moving average and 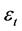 is the independent normal variable.
is the independent normal variable.
The second stochastic model, ARIMA model is constructed using a combination of moving average (MA) and autoregressive (AR) processes after differencing the data to remove nonstationarity. The general non-seasonal ARIMA(p, d, q) model, AR(p) refers to order of the autoregressive part, I(d) refers to degree of differencing involved and MA(q) refers to order of the moving average part. The equation for the simplest ARIMA(p, d, q) model is:
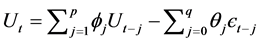 (4)
(4)
where Ut is the d-th difference of the Xt process, 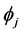 refers to ith term auto regressive parameter,
refers to ith term auto regressive parameter, 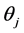 refers to ith term moving average parameter, and
refers to ith term moving average parameter, and 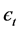 is an independent variable.
is an independent variable.
Box and Jenkins [12] obtained the multiplicative ARIMA(p, d, q) × (P, D, Q)ω model which consists of a seasonal ARMA(P, Q) fitted to the D-th seasonal difference of the data coupled with an ARMA(p, q) model fitted to the d-th difference of the residuals of the former model. The general form of the ARIMA(p, d, q) × (P, D, Q)ω model is given by:
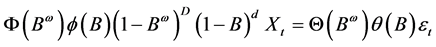 (5)
(5)
where ω refers to number of periods per season, 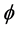 refers to non-seasonal auto regressive parameter,
refers to non-seasonal auto regressive parameter, 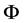
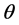
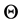

Calibration of time-series models is conducted based on the three stages of model building: identification, estimation, and diagnostic checking [4] [12] [13] . The purpose of the identification stage is to determine the order of the model using interpretation of the autocorrelation function (ACF) and the partial autocorrelation function (PACF). In the estimation stage, the approximate maximum likelihood estimates (MLEs) for the model parameters is obtained by employing the unconditional sum of squares method, as suggested by Box and Jenkins (1976). The third stage of time-series analysis consists of Diagnostic check to determine whether residuals are independent and normally distributed or not.
The residual autocorrelation function (RACF) should be obtained to determine whether residual are white noise. There are three useful applications related to RACF for independence of residual. The first one is the correlogram drawn by plotting rk(є) against lag k. If some of the RACF are significantly different from zero, this may mean that the present model is inadequate. The second one is Porte Manteau Lack of fit test (Q). The Q statistic is calculated by
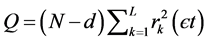
where N is the number of observations, rk is the correlogram of the residual єt, L is the maximum lag considered, and d is the number of differences. The static Q is approximately chi-square distribution with L-p-q degree of freedom. The adequacy of ARIMA(p, d, q) may be checked by comparing the static Q with the chi-square value χ2(L-p-q) of a given significance level. If Q < χ2(L-p-q), єt is an independent series and so the model are adequate , otherwise the model are inadequate.
The third approach, the Ljunge Box Q or Q(r) statistics can be employed to check independence for the model adequacy, If Q(r) < χ2-table critical value at a level of significance so the model are adequate. The Q(r) statatistic is calculated by the following equation [14] :
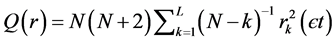
There are many standard tests available to check whether the residuals are normally distributed. Chow et al. [15] cited that if a historical data is normally distributed, the graph of the cumulative distribution for the data should appear as a straight line when it is plotted on normal probability paper. Shapiro-Wilk test, Anderson-Darling test, Jarque- Bera test and skewness tests are also used in normality test. The p value for Shapiro-Wilk test, Anderson-Darling test, and Jarque-Bera tests should be larger than the 5% level of significance and skewness measures (γ) related to residuals from each model falls within the limits for normality distributed [16] .
3. Study Area
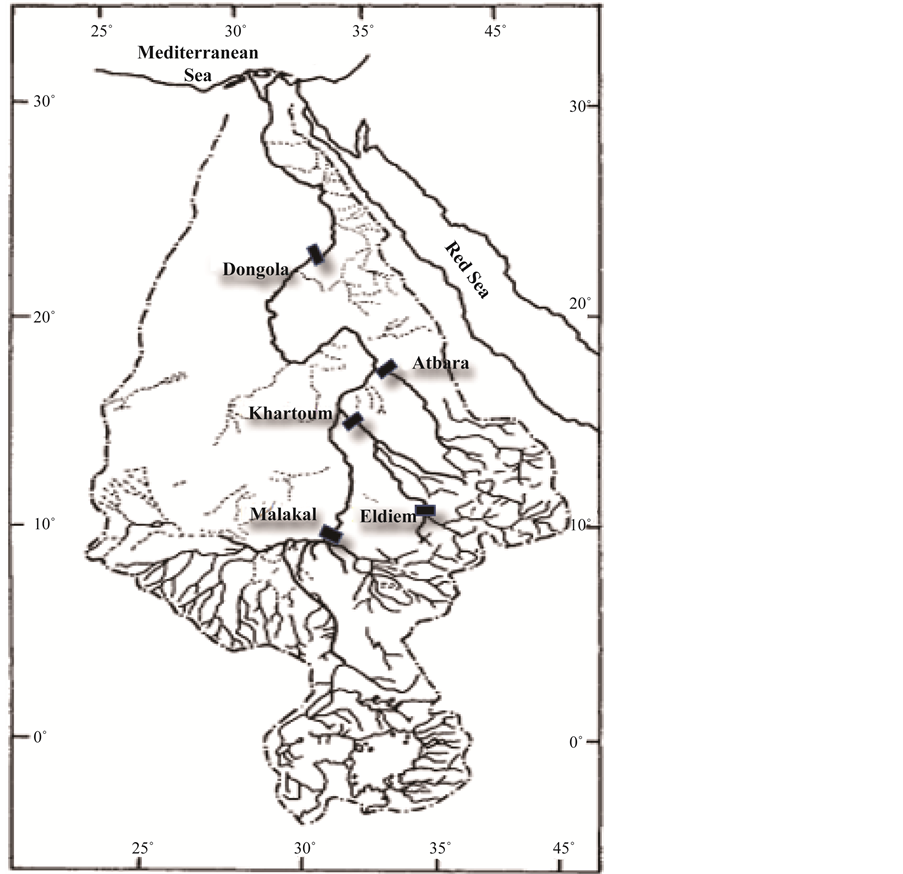
The Nile Basin covers a surface of about 2.9 million square kilometers, approximately one-tenth of the surface area of Africa. It extends from 4˚S to 31˚N latitude and from about 21˚30'E to 40˚30'E longitude as shown in Figure 1. The length of the River Nile is about 6500 kilometers [17] . The Nile basin is shared by 11 countries: Ethiopia, Sudan, South Sudan, Egypt, Tanzania, Burundi, Democratic Republic of Congo (DRC), Eritrea, Rwanda, and Uganda. The River Nile has three main branches; White Nile, Blue Nile, and River Atbra.
The data collected in this study consisted of monthly discharge at Key stations as shown in Table 1. The data were collected from volumes V of the Nile Basin. A split sample procedure was used for calibration and validation, flow data to 1997 were used for calibration and data from 1998 to 2002 for validation.
4. Results and Discussion
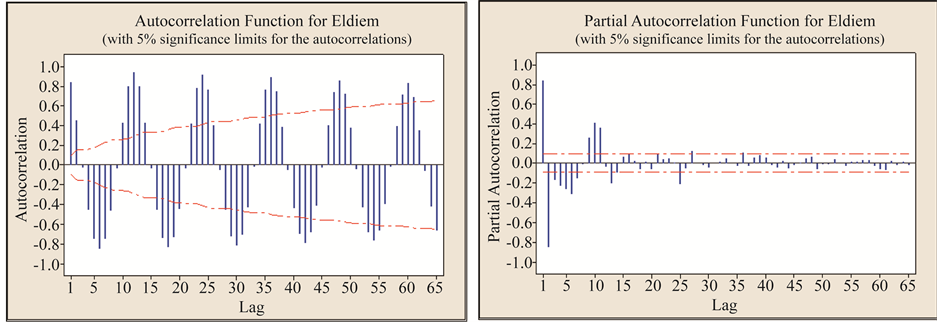
The plots of the ACF and PACF for each monthly data sequence were drawn to gather information about the seasonal and non seasonal AR and MA operators concerning the monthly series. The ACF graphs show an attenuating sine wave pattern that reflects the random periodicity of the data. For these data sequences with the cyclic seasonal component, seasonal differencing was needed by taking the seasonal differencing operator as one (1) or standardized (see Figure 2).
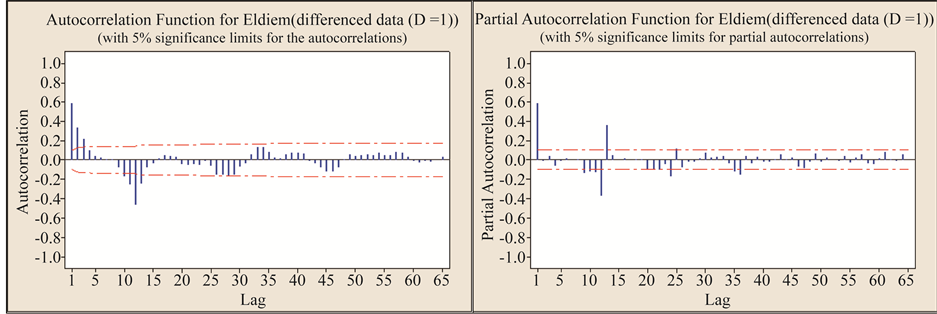
For differenced data (Figure 3), the ACFs did not cut off but rather damped out. This may suggest the presence of autoregressive (AR) terms. The ACFs have significant values at lags that are multiples of 12 this may
Figure 1. Locations of the main key stations on the Rive Nile and its tributaries.
Table 1. Summary of information about gauging station.
Figure 2. ACFs and PACFs for monthly streamflow at Eldiem stations.
Figure 3. ACFs and PACFs for seasonal differenced streamflow at Eldiem stations.
stress that seasonal AR terms are required. The PACFs possess significant values at some lags but rather tail off this may imply the presence of moving average (MA) terms. There are peaks in the graphs of the PACFs at lags that are multiples of 12, which may suggest seasonal MA terms.
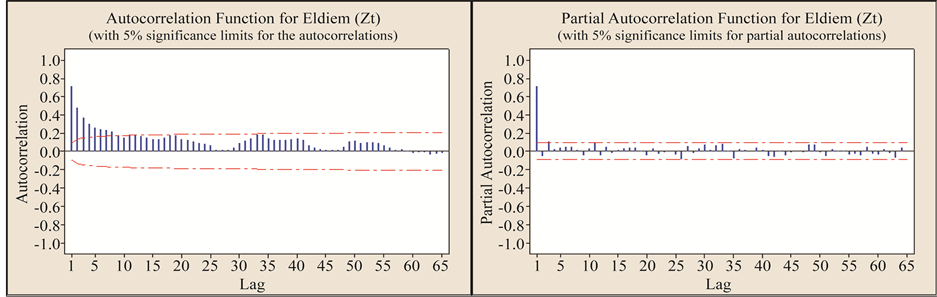
For standardized data (Zt) as shown in Figure 4, the ACFs did not cut off but rather damped out. This may suggest the presence of autoregressive (AR) terms. The ACFs possess significant values at some lags but rather tail off this may imply the presence of moving average (MA) terms.
Logarithmic transformations are made for monthly data to be approximately normally distributed for all stations except Atbara River, square root transformation is used. Alternative models were selected by inspecting ACFs and PACFs for monthly streamflow at all stations. Diagnostic checks were applied in order to determine whether the residuals of the alternative models were independent and normally distributed. All of the DARMA and SARIMA models selected from ACF and PACF graphs did not fulfill the residual assumption (independent, normality). The models that did not fulfill at least one of the diagnostic checks were eliminated. The selected best models for DARMA and SARIMA models are presented in Table 2 and Table 3.
Two approach, Porte Mnteau lack test and Ljung-Box Q (LBQ) are applied for testing the independence assumption of residuals for the best models. The results of these tests are presented in Table 4. The selected best models were consistent with the independence assumption for all tests. The test statistics were smaller than the critical values from the tables related to the tests. This implies that residuals from the best models are independence or white noise. Furthermore, the RACF drawn for the best models (Figure 5) indicated that the residuals were not significantly different from a white noise series at the 5% significance level.
For the selected best models, the results related to the normality of residuals using Shapiro-Wilk test, Anderson-Darling test, Jarque-Bera test and skewness tests are given in Table 5. As can be seen in Table 5, the p value for tests are larger than the 5% level of significance and skewness measures (γ) related to residuals from each model falls within the limits. These results suggest that the residuals of the best models are normally distributed. In addition to these tests, Figure 6 shows the probability paper of the residuals. As expected, the curves significantly reflect a normal distribution.
Figure 4. ACFs and PACFs for standardized streamflow at Eldiem stations.
Table 2. Parameters of the best fitted DARMA models for each gauging station.
Table 3. Parmeters of the best fitted SARIMA models for each gauging station.
Table 4. Independence test result of monthly streamflow data for each gauging station.
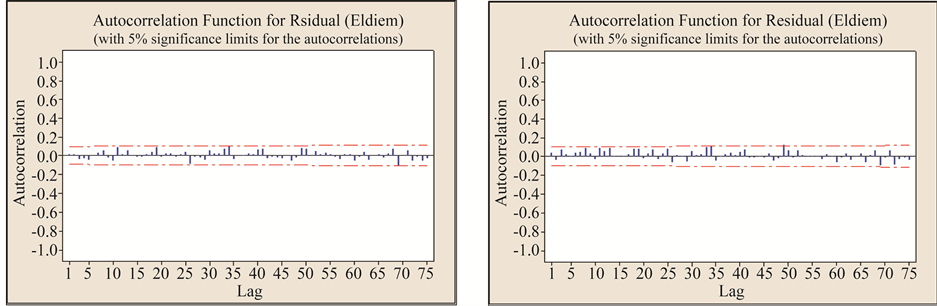
Figure 5. Residual ACF for monthly streamflow data for Eldiem station. (a) DARMA model; (b) SARIMA model.
Plotting the observed and estimated data series for each model could be used as an indication of reliability of the models at the validation stages. The scatter plots of observed monthly flow and one-month-ahead forecasts of all models from the period from 1998 to 2002 are given in Figure 7. As can be seen, all the models tend to underestimate high flows. This may due to the fact that only previous flow conditions were used as predictors in the forecasting models. Other important factors that have significant contributions to the streamflow processes such as precipitation and temperature were not included in the modeling process due to data limitation. Figure 8 displays the time series of one-month-ahead forecasting of the DARMA, SARIMA models and observed monthly flow during testing period (1998-2002).
Model Comparison
For validation the SARIMA and DARMA models described in the previous sections, one-step-ahead forecasts for the test portion of the time series were generated using the selected set of calibrated models. The forecasting performance of all the models at the validation stage was compared based on the mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R2) which indicates the strength of fit between observed and forecasted stream. The procedure having lower MAE and RMSE and upper R2 values can be assumed to be the most accurate model for flow forecasting in the study area.
Table 5. Normality test result of monthly streamflow data for each gauging station.
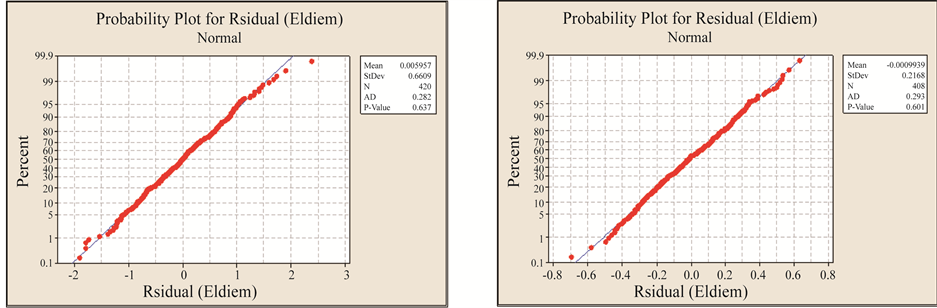
Figure 6. Residual probability paper for monthly streamflow data for Eldiem station. (a) DARMA model; (b) SARIMA model.
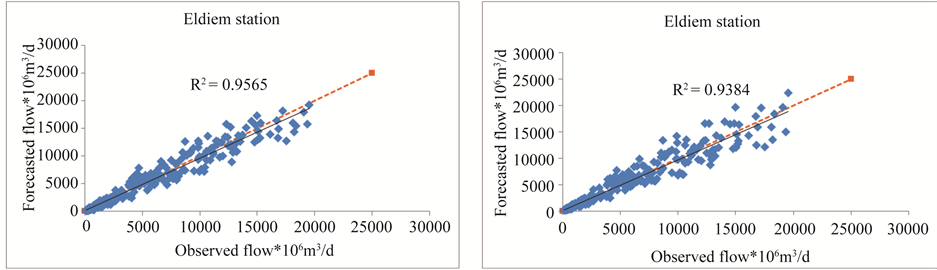
Figure 7. Observed and forecasting monthly streamflow at Eldiem station. (a) DARMA model; (b) SARIMA model.
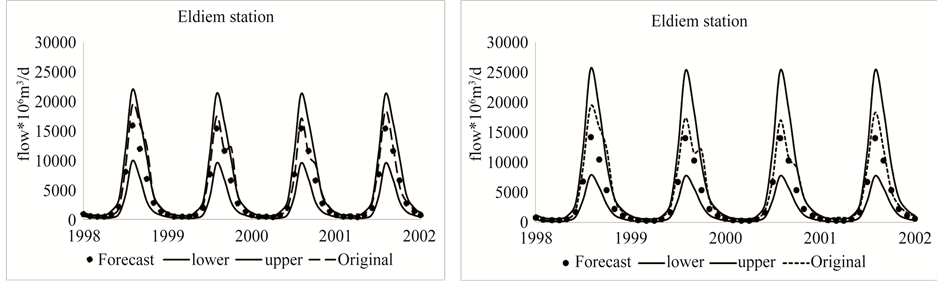
Figure 8. Comparison of observed and forecasted monthly flow at Eldiem station for validation period (1998 to 2002). (a) DARMA model; (b) SARIMA model.
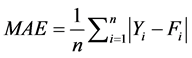
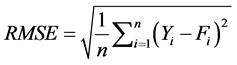
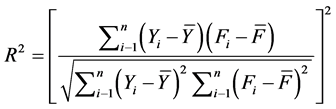
where Yi is the observed flow, Fi is the forecasted flow, n is the number of data points, 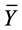
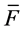
The one month ahead forecasting performances of all models for the calibration and testing periods are shown in Table 6. Based on the performance comparison of the models, the DARMA model slightly better than SARIMA models as DARMA models have lower MAE and RMSE and upper R2 values for all stations.
5. Conclusion
This study aims to select the suitable stochastic model in forecasting monthly streamflow in rivers. Many Rivers are selected: White Nile, Blue Nile, Atbara River and main Nile. In this study a comparison between DARMA and SARIMA models which are the most popular for generating stochastically synthetic data, is applied to monthly streamflow data for key stations at Rivers. Independence analysis of the residuals was examined by using Porte Mnteau lack test and Ljung-Box Q (LBQ). To determine whether the residuals are normally distributed,
Table 6. Comparison of models performance in calibration and testing (Predicted) periods.
Shapiro-Wilk test, Anderson-Darling test, Lilliefors test, Jarque-Bera test and skewness tests were used. The selected model for each data set among DARMA and SARIMA models fulfilled the diagnostic checks. Furthermore, comparisons of monthly values for observed and predicted data from DARMA and SARIMA were compared based on the mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R2). DARMA models for all stations have the lower MAE and RMSE and upper R2 values can be assumed the most accurate model for monthly streamflow forecasting in Rivers.
Cite this paper
Mohammed A.Elganiny,Alaa EsmaeilEldwer, (2016) Comparison of Stochastic Models in Forecasting Monthly Streamflow in Rivers: A Case Study of River Nile and Its Tributaries. Journal of Water Resource and Protection,08,143-153. doi: 10.4236/jwarp.2016.82012
References
- 1. Wang, W. (2006) Stochasticity, Nonlinearity and Forecasting of Streamflow Processes. IOS Press, Amsterdam.
- 2. Box, G.E.P., Jenkins, G.M. and Reinsel, G.C. (1994) Time Series Analysis: Forecasting and Control. Prentice-Hall, Upper Saddle River.
- 3. Brockwell, P.J. and Davis, R.A. (2002) Introduction to Time Series and Forecasting. Springer, New York.
http://dx.doi.org/10.1007/b97391 - 4. Hipel, K.W. and McLeod, A.I. (1994) Time Series Modeling of Water Resources and Environmental Systems. Elsevier Science, Amsterdam.
- 5. Mondal, M.S. and Wasimi, S.A. (2007) Choice of Model Type in Stochastic River Hydrology. Proceedings of the 1st International Conference on Water & Flood Management (ICWFM-2007), Dhaka, 12-14 March 2007, 633-640.
- 6. Bender, M. and Simonovic, S. (1994) Time-Series Modeling for Long-Range Streamflow Forecasting. Journal of Water Resources Planning and Management, 120, 857-870.
http://dx.doi.org/10.1061/(ASCE)0733-9496(1994)120:6(857) - 7. Ghanbarpour, M.R., Abbaspour, K.C., Jalalvand, G. and Moghaddam, G.A. (2010) Stochastic Modeling of Surface Stream Flow at Different Time Scales: Sangsoorakh karst Basin, Iran. Journal of Cave and Karst Studies, 72, 1-10.
http://dx.doi.org/10.4311/jcks2007ES0017 - 8. McKerchar, A.I. and Delleur, J.W. (1974) Application of Seasonal Parametric Linear Stochastic Models to Monthly Flow Data. Water Resources Research, 10, 246-255.
http://dx.doi.org/10.1029/WR010i002p00246 - 9. Noakes, D.J., McLeod, A.I. and Hipel, K.W. (1985) Forecasting Monthly Riverflow Time Series. International Journal of Forecasting, 1, 179-190.
http://dx.doi.org/10.1016/0169-2070(85)90022-6 - 10. Salas, J.D. (1992) Analysis and Modeling of Hydrologic Time Series. In: Maidment, D.R., Ed., Handbook of Hydrology, McGraw-Hill, New York, 19.1-19.72.
- 11. Rabenja, A.T., Ratiarison, A. and Rabeharisoa, J.M. (2009) Forecasting of the Rainfall and the Discharge of the Namorona River in Vohiparara and FFT Analyses of These Data. Proceedings of 4th International Conference in High-Energy Physics, Antananarivo, 1-12.
- 12. Box, G.E.P. and Jenkins, G.M. (1976) Time Series Analysis: Forecasting and Control. Revised Edition, Holden-Day, San Francisco.
- 13. Hipel, K.W., McLeod, A.I. and Lennox, W.C. (1977) Advances in Box-Jenkins Modeling, Part One, Model Construction. Water Resources Research, 13, 567-575.
http://dx.doi.org/10.1029/WR013i003p00567 - 14. Ljung, G.M. and Box, G.E.P. (1978) On a Measure of Lack of Fit in Time Series Models. Biometrika, 65, 297-303.
http://dx.doi.org/10.1093/biomet/65.2.297 - 15. Chow, V.T., Maidment, D.R. and Mays, L.W. (1988) Applied Hydrology. McGraw-Hill Book Company, New York, 572.
- 16. Razali, N. and Wah, Y.B. (2011) Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests. Journal of Statistical Modeling and Analytics, 2, 21-33.
- 17. Shahin, M. (1985) Hydrology of the Nile Basin. Elsevier Sciences Publishing co., New York.