Journal of Water Resource and Protection
Vol.06 No.13(2014), Article ID:50219,9 pages
10.4236/jwarp.2014.613112
Climate Based Risk Assessment for Maize Producing Areas in Rainfed Agriculture in Mexico
I. Sanchez Cohen*, G. Esquivel Arriaga, M. A. Velasquez Valle, Marco A. Inzunza Ibarra, Arcadio Muñoz Villalobos, P. Bueno Hurtado
Instituto Nacional de Investigaciones Forestales Agrícolas y Pecuarias, Centro Nacional de Investigación Disciplinaria en Relación Agua Suelo Planta Atmósfera (INIFAP-CENID RASPA), Km. 6.5 Canal Sacramento, Zona Industrial Gómez Palacio, Durango, México
Email: *sanchez.ignacio@inifap.gob.mx, esquivel.gerardo@inifap.gob.mx, velasquez.agustin@inifap.gob.mx, inzunza.marco@inifap.gob.mx, villalobos.arcadio@inifap.gob.mx, bueno.palmira@inifap.gob.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2014; revised 27 August 2014; accepted 21 September 2014
ABSTRACT

*Corresponding author.
Rainfed areas in Mexico accounts for 14 million hectares where around 23 million people live and are located in places where there is a little climatic information. The severe drought that has impacted northern Mexico in the past several years as well as other parts of the country, has forced decision takers to look for improved tools and procedures to prevent and to cope with this natural hazard. For this paper, the methodology of the Food and Agricultural Organization of the United Nations (FAO) for estimating water balance variables was modified to provide crop yield estimations under rainfed agriculture in maize producer states of Mexico. The water balance accounts for the daily variation of soil water content having main input rainfall (Pp) and main output crop evapotranspiration (Eta). The algorithm computes crop yield using two distinctive approaches: 1) one based on surplus/deficit functions for each crop considered and 2) yield estimations based on soil water balance and water function productions of the crop being analyzed. For computing water balance and crop yields, a computer model is built that incorporates the FAO method for water balance (MODEL SICTOD: Computational System for Decision Taking, acronym in Spanish) which stochastically generate precipitation based on wet/dry transition probabilities using a first order Markov chain scheme. Maps of average crop yields were obtained after interpolating model outcomes for the main maize producer states of Mexico: Jalisco, Michoacan, Guerrero, Puebla Oaxaca and Chiapas. Different planting dates were analyzed, early (90 days of length period), intermediate (120 days of length period) and late (150 days of length period). Crop yield variability correlates to the transition probability on having a wet day following a dry day. Results have shown high yield variation and probability of crop yield failure and climatic risk follows a distinctive pattern according to planting date and rainfall occurrence. The approach used is of great support for decision taking processes.
Keywords:
Risk Assessment, Water Balance, Crop Yield, Simulation, Rainfed

1. Introduction
The Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) states that the world has been more drought-prone during the past 25 years and that climate projections indicate an increased frequency in the future. This carries significant implications for the agriculture sector, especially in the developing countries. Drought is considered as an abnormal water deficit in at least one part of the land surface hydrological cycle. It can also be described in three dimensions: intensity, duration, and the area it covers; it differs from aridity, which is restricted to low rainfall regions [1] . For most people, the cause of droughts is easy to understand, but hard to prevent. Depending on the location, crop failures, famine, high food prices, and deaths can occur. The onset time is the more difficult part of a drought given the high uncertainty that characterizes arid lands. Unlike other forms of severe weather or natural disasters, droughts often develop slowly. In Mexico people who leaves their place because of a flood, as soon as the water recede, go back to their way of life; on the other hand, people moves away from their place because of a drought; there is a high probability that they will never go back searching for a new less risky place to stay changing the source of income and becoming part of the city’s poor belts. Also, when the impacts of a drought are severe, depending on people capacity to cope with the situation, the last resort is to emigrate to other states or to the US [2] .
Rainfed areas in Mexico accounts for 14 million hectares where around 23 million people live and are located in places where there is a little climatic information. The severe drought that has impacted northern Mexico in the past several years as well as other parts of the country, has forced decision takers to look for improved tools and procedures to prevent and to cope with this natural hazard. Computer models that simulate crop growth and estimate crop yields are a powerful tool for decision taking and planning when properly used. Achieving potential crop yields under irrigated conditions depends on the following agronomical recommendations, such as planting dates, use of suitable seeds, and pests and diseases control mainly; on the other hand, for having an estimation of crop yields under rainfed conditions, one must add rainfall uncertainty to the above constraints. This uncertainty may be accounted for using stochastically driven water balance models where rainfall patterns are estimated based on statistics that define the behavior of the rainfall historical data.
Soil water balance models are being utilized everywhere to compute crop yields based on the crop’s water requirements and the availability of water driven by rainfall or irrigation (e.g. [3] - [6] ). Nevertheless, the water balance method by FAO is widely used and incorporated in most simulation models [7] . The FAO method relies on the adequate computation of evapotranspiration under standard or not standard conditions. Under the latter condition, the soil water content has low potential energy and is strongly bound by capillary and absorptive forces to the soil matrix making the absorption by plants difficult. This method does not consider the randomness of rainfall inputs.
Generally these models determine the amount of water that can infiltrate into the soil profile either from rainfall or irrigation and that can be extracted from the soil by evaporation and/or crop transpiration. In rainfall driven models, normally rainfall inputs comes from water collected in rain gages on the field or at nearby weather station. Also these models are of deterministic nature rather than stochastic where probabilities of precipitation spells are considered. Stochastic models allow estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. The random variation is based on fluctuations observed in historical data. In this way, deterministic models are incapable of predicting future scenarios. They quantify actual outcomes based on historical records.
Under this framework the objective of the study is to compute maize yield in main maize producing rainfed areas in Mexico, utilizing a computer model that incorporates a modification of the soil water balance of FAO considering the precipitation as stochastic variable and computing crop yield utilizing a moisture stress factor.
2. Study Area/Materials and Methods
For computing crop yield under rainfed conditions, a computer program was developed and calibrated using observed maize crop yields in the main producing rainfed areas of Mexico. The method of FAO [7] was modified to compute maize yields under nonstandard conditions. The FAO method computes the relationship between relative yield and relative evapotranspiration as:
 (1)
(1)
where 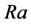 and
and 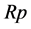 are actual and potential crop yield and
are actual and potential crop yield and 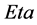 and
and 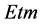 are the actual and maximum crop evapotranspiration respectively [8] . Nevertheless, the application of Equation 1 resulted in overestimations of maize yields and hence, one of the approaches for computing crop yield in this paper was that proposed by [9] instead.
are the actual and maximum crop evapotranspiration respectively [8] . Nevertheless, the application of Equation 1 resulted in overestimations of maize yields and hence, one of the approaches for computing crop yield in this paper was that proposed by [9] instead.
Figure 1 shows the general diagram of the approximation. Simulation of crop growth using a crop growth model that depends on daily weather data is a generally accepted method for assessing the effects of climatic variability on crop production [10] [11] .
The crop yield computation procedure assesses yield using two different approaches.
1) The first one consists in a classic regression approach, in which the focus is on the relationship between a dependent variable―the yield―and one or more independent parameters related to climate/weather effects
Figure 1. Flux diagram of the approach used for computing crop yield in rainfed areas of Mexico.
(Deficit-Surplus function). As a first approach, crop yield is computed according the water deficit (WD) and related to the historical crop yield for the location. WD is in turn computed as the difference between precipitation (Pp) and Potential evapotranspiration (ETo)
Similar to [2] , functional relationships between soil moisture deficit-surplus (D) and moisture stress factor (MSF) were obtained for the main maize producing areas in Mexico. D is computed as:
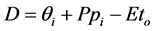 (2)
(2)
where  is the plant available soil water content at the start of the growing period, all other variables already defined. Maize yield in maize producing rainfed areas (Ra) was estimated by reducing the potential yield (Rp) with a moisture stress factor as follows:
is the plant available soil water content at the start of the growing period, all other variables already defined. Maize yield in maize producing rainfed areas (Ra) was estimated by reducing the potential yield (Rp) with a moisture stress factor as follows:
 (3)
(3)
where Ra is average crop yield observed at a particular location for all years available under non-standard conditions, Rp is the average crop yield under irrigated conditions for the same locations. Data for both Ra and Rbwere drawn from a national database of the ministry of agriculture (www.siap.gob.mx). A polynomial cubic function was fitted to the relationship between MSF and D (see Figure 2). Actual yield is computed solving Equation (2) for Ra.
2) The second approach for computing crop yield computes and accumulates actual evapotranspiration (Eta) in a daily basis taking in to account rainfall occurrence and soil water depletion by Eta. Then the water function productions of the crops are used to compute actual yield. Since the model generates stochastically daily precipitation data, the soil water balance may be thought as stochastic as well and thus subject to random variation and risk.
Risk Assessment
Stochastic weather models can be used as random number generators whose input resembles the weather data to which they have benefit. These models are convenient and computationally fast, and are useful in a number of applications where the observed climate record is inadequate with respect to length, completeness, or spatial coverage. Within the model, daily rainfall is simulated using a Markov chain-exponential model in which precipitation occurrence is described by a first-order Markov chain and the amount of rainfall for those days on which rainfall occurs is based on an exponential distribution of daily rainfall amounts as:
 (4)
(4)
Figure 2. Functional relationship between MSF and D for maize using data from the Mexican ministry of agriculture information system (SIAP).
where parameter λ = inverse of daily precipitation [12] . The first-order Markov Chain utilizes two states defined by the transition probabilities:
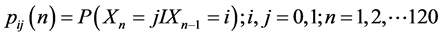 (5)
(5)
where state 0 signifies a dry day and state 1 signifies a wet day and:
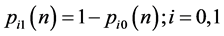 (6)
(6)
Thus these transition probabilities define four possible states as follows: P00―the probability of a day being dry given that the previous day was dry; P01―the probability of a day being dry given that the previous day was wet; P10―the probability of a day being wet given that the previous day was dry; and P11―the probability of a day being wet given that the previous day was wet [13] . Both Markov chain and exponential distribution parameters may be computed for selected periods from daily rainfall data using methods described by [14] and by [15] .
Although the computational application designed allows the user to consider different planting dates, different growing periods, contrasting initial soil water content and different soil textural class, for the purpose of this paper and in an attempt to simulate crop yield in a general manner, for computing probability of crop failure or risk assessment, model runs were performed for three planting dates, 2 lengths of growing periods, considering medium soil texture class and 25% of initial soil water content. The consideration of the 25% of initial soil water content comes from several samples in the field where we found that when the producers plant the crop in rainfed areas (maize) the soil water content in the upper soil layer (≈30 cm) is barely that amount. The yield computed with the MSF method may be thought as “global-climatic-dependent” crop yield since does not considers the actual daily change of soil water content as a function of actual evapotranspiration and rainfall occurrence, it relies on potential evapotranspiration; moreover, it considers only the initial soil water content but not further consideration is set to this variable. In Figure 2 it can be seen that even when there is neither water deficit nor surplus (D = 0) the attainable crop yield is far from its potential (MSF = 1) speculatively this is due to three main causes: 1) rainfall opportunity; 2) farmers not following recommended management practices and 3) the precision of the crop yield data that is officially reported and registered. Nevertheless, the crop yield computed with this method provides an indicator of the yield that it may be expected according the historical yield records of the region of interest. For having a more “crop-soil water balance” related yield assessment, a routine for computing crop yield considering the water functions production of the crops was included in the model source code (second approach). Crop water function productions relate crop yield to seasonal evapotranspiration or transpiration [16] . Actual evapotranspiration is function of seasonality crop water requirements and rainfall patterns opportunity; the rational way to account for this variation is performing the daily soil water balance during the crop-growing period. With this function decision makers can assess crop water needs to meet production targets or, conversely, estimate likely crop production for fixed volumes of water [17] . These functions were obtained in the field under irrigated conditions varying the timing and amount of irrigation in different crop growth stages. The crop water function obtained for maize is presented in Figure 3.
Figure 3. Water function production for maize.
3. Results and Discussion
Model Runs Design
Model runs (25 growing seasons) consisted in varying planting dates (early, intermediate and late) considering 120 days of crop growing period, medium textured soils and 25% of initial soil water content. A growing season was considered the elapsed time between planting date and harvest. Table 1 shows the timing of each planting date within the states considered. The yields shown on Table 1 are the average of the 25 growing seasons simulated. Interpolations were performed considering plating dates for each state even though they don’t necessarily match, this under the argument of presenting a continuous surface that can be used to have an appreciation of the variation of the expected yield for the different panting dates. These states produce 53.5% of the total area of maize under rainfed conditions in Mexico that during 2011 accounted for 2.9 million hectares. For the interpolation process the inverse square law was used within a geographic information system.
Model outputs were interpolated obtaining maps that depict the average crop yield for the main maize producer states in Mexico for three planting dates (Figures 4-6). Average crop yield is expected to occur once every
Table 1. Computed yield according planting date and length of growing period.
*Planting date, **E = early, I = intermediate, L = Late.
Figure 4. Average maize yield for early planting dates.
Figure 5. Average maize yield for intermediate planting dates.
two years. In practice, planting dates are set according the timing of the rainy season. For most producers, the timing of the planting dates is purely empirical since they catalog the beginning of the season when the rains provide enough moisture to hold a handful of soil without getting loose in the hand. Technically the beginning of the rainy season is based on statistics of long-term rainfall time series from where rainfall occurrence persistency is analyzed for a period of time. The latter criteria include other crop climate needs as heat hours.
According the results, late planting dates are the most suitable dates for the states of Jalisco Michoacan and Puebla; Guerrero, Oaxaca and Chiapas states obtains the best crop yields in early planting dates. Since variability of rainfall is the main cause to variability in crop yields in arid and semi-arid regions, this variation may be explained according the transition probability of having a wet day following a dry day from where rainfall occurrence is found and from where the amount of precipitation is computed based on an exponential probability density function. Figure 7 and Figure 8 shows the transition probabilities of having a wet day given that the previous day was dry (PWD) for the six states considered in the study.
4. Conclusions
Decision takers within agricultural risk prone areas should have mitigation procedures on hand to cope with this hazard. According to [18] , risk management in agriculture is now an essential tool for farmers to anticipate, avoid and react to shocks. But this should be a hand to hand procedure between policy makers and farmers. An efficient risk management system for agriculture will preserve the standard of living of those who depend on farming, strengthen the viability of farm businesses, and provide an environment which supports investment in the farming sector. The design of policies for risk management in agriculture raises multiple challenges from generating good information on types of risks and tool available to deal with these, to creating incentives to encourage farmers to adopt a proactive risk management strategy. The design of the institutional framework for the governance of catastrophic risks is crucial to delineate the boundaries of responsibility between farmers, government and stakeholders.
Figure 6. Average maize yield for late planting dates.
Figure 7. Probability of having a wet day following a dry day (PWD) for late planting dates in Jalisco, Michoacan and Puebla shows the highest yields for this planting date.
Moreover, strategies of planning and managing water resources during a drought period are not an easy task but forecast and climate monitoring persist as a necessary step towards the design of mitigation measurements. Modeling crop yield response to water stress within a region water balance is the most suitable planning tool considering different climate scenarios. For the case of Mexico, mixed strategies are the best option considering
Figure 8. Probability of having a wet day following a dry day (PWD) for early planting dates. Chiapas, Oaxaca and Guerrero show the highest yields for this planting date.
planting dates, different crop’s length periods and water harvesting techniques; the shift to less water demanding crops is also a good option.
References
- Sivakumar, M.V.K., Motha, R.P., Wilhite, D.A. and Wood, D.A. (2011) Agricultural Drought Indices. Proceedings of the WMO/UNISDR Expert Group Meeting on Agricultural Drought Indices, 2-4 June 2010, Murcia, Spain: Geneva, Switzerland: World Meteorological Organization. AGM-11, WMO/TD No. 1572; WAOB-2011, 197.
- Cohen I.S., Spring, U.O., Padilla, G.D., Paredes, J.C., Inzunza, M.A., LopezLopez, R. and Vi-llanueva Diaz, J. (2012) Forced Migration, Climate Change, Mitigation and Adaptative Policies in Mexico: Some Functional Relationships. International Migration, 51, 53-57. http://dx.doi.org/10.1111/j.1468-2435.2012.00743.x
- Brisson N., Seguin, B. and Bertuzzi, P. (1992) Agrometeorological Soil Water Balance for Crop Simulation Models. Agricultural and Forest Meteorology, 59, 267-287.
- Panigrahi, B. and Panda, S.N. (2003) Field Test of a Soil Water Balance Simulation Model. Agricultural Water Management, 588, 223-240. http://dx.doi.org/10.1016/S0378-3774(02)00082-3
- Leuven, K.U. (2002) BUDGET: A Soil Water and Salt Balance Model. Reference Manual. Faculty of Agricultural and Applied Biological Sciences, Institue for Land and Water Management, Vital Decosterstraat 102, B-3000 Leuven, Belgium.
- Bargaoui, Z.K. (2012) Estimation of evapotranspiration Using Soil Water Balance Modelling, Evapotranspiration—Remote Sensing and Modeling, Dr. AyseImark (Ed.), ISBN: 978-953-307-808-3, In Tech. http://www.intechopen.com/books/evapotranspiration-remote-sensing-and-modeling/estimation-of-evapotranspiration-using-soil-water-balance-modelling
- Allen, R.G., Pereira, L.S., Raes, D. and Smith, M. (1988) Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage Paper 56, Rome, 300.
- Doorembos, J. and Kassam A.H. (1979) Yield Response to Water. FAO Irrigation and Drainage Paper No. 33, FAO, Rome, 193.
- Bootsma, A., Boisvert, J. and Dumanski, J. (1994) Climate-Based Estimates of Potential Forage Yields in Canada Using a Crop Growth Model. Agricultural and Forest Meteorology, 67, 151-172. http://dx.doi.org/10.1016/0168-1923(94)90001-9
- Hutchinson, M.F. (1990) Climatic Analysis in Data Sparse Regions. Proceedings of the International Symposium on Climate Risk in Crop Production: Models and Management for the Semi-Arid Tropics and Subtropics, Brisbane, 2-6 July 1990, 55-71.
- JRC Scientific and Technical Reports (2007) CGMS Version 9.2. User Manual and Technical Documentation. Luxemburg.
- Hanson, C.L., Neff, E.L. and Woolhiser, D.A. (1975) Hydrologic Aspects of Water Harvesting in the Northern Great Planes. Proc., Water Harvesting Symp., ARS W-22, US Department of Agriculture-Agricultural Research Service, Water Conservation Laboratory, Phoenx, 129-140.
- Sanchez Cohen, I., Lopes, V.L., Slack, D.C. and Fogel, M.M. (1997) Water Balance Model for Small-Scale Water Harvesting Systems. Journal of Irrigation and Drainage Engineering, 123, 123-128. http://dx.doi.org/10.1061/(ASCE)0733-9437(1997)123:2(123)
- Woolhiser, D.A. and Roldan, J. (1986) Seasonal and Regional Variability of Parameters for Stochastic Daily Precipitation Models: South Dakota, U.S.A. Water Resources Research, 22, 965-978. http://dx.doi.org/10.1029/WR022i006p00965
- Wilks, D.S. (1995) Statistical Methods in the Atmospheric Sciences. Academic Press, San Diego, 467 p.
- Ikbadun, H.E., Tarimo, A.K.P.R., Salim, B.A. and Mahoo, H.F. (2007) Evaluation of Selected Crop Water Production Functions for an Irrigated Maize Crop. Agricultural Water Management, 94, 1-10.
- Brumbelow, K. and Georgakakos, A. (2007) Determining Crop-Water Production Functions Using Yield-Irrigation Gradient Algorithms. Agricultural Water Management, 87, 151-161. http://dx.doi.org/10.1016/j.agwat.2006.06.016
- OECD (2011) Managing Risk in Agriculture: Policy Assessment and Design. OECD Publishing. http://dx.doi.org/10.1787/9789264116146-en










