Journal of Water Resource and Protection
Vol.6 No.2(2014), Article ID:42880,8 pages DOI:10.4236/jwarp.2014.62012
Spatial Estimation of Rainfall Distribution and Its Classification in Duhok Governorate Using GIS
1School of Planning, Faculty of Engineering and Applied Science of the University of Duhok, Duhok, Kurdistan Region-Iraq
2Faculty of Science of the University of Zakho, Zakho, Kurdistan Region-Iraq
Email: *hosseinhamid@uod.ac
Received November 7, 2013; revised December 9, 2013; accepted January 5, 2014
ABSTRACT
Rainfall is a significant portion of hydrologic data. Rainfall records, however, are often incomplete due to several factors. In this study, the inverse distance weighting (IDW) method integrated with GIS is used to estimate the rainfall distribution in Duhok Governorate. A total of 25 rain fall stations and rainfall data between 2000 and 2010 were used, where 6 rainfall stations were used for cross-validation. In addition, the relationship between interpolation accuracy and two critical parameters of IDW (Power α value, and a radius of influence) was evaluated. Also, the rainfall distribution of Duhok Governorate was classified. As an output of this study and in most cases, the optimal parameters for IDW in interpolating rainfall data must have a radius of influence up to (15 - 60 km). However, the optimal α values varied between 1 and 5. Based on the results of this study, we concluded that the IDW is an appropriate method of spatial interpolation to predict the probable rainfall data in Duhok Governorate using α = 1 and search radius = 105 km for all the 25 rainfall stations.
Keywords:Geographic Information Systems (GIS); Inverse Distance Weighting (IDW); Spatial Interpolation; Rainfall Data
1. Introduction
This Rainfall is one of the important variables that define the climate of a region. Its spatial characterization is highly relevant. It is amongst the hydrological parameters, and is the most difficult one to be measured due to its temporal and spatial variability and discontinuity. Although the data can be fully provided in a rain gauge networks, they are still considered as a point estimate. Thus, providing an estimate of the rainfalls patial distribution within an area from rain gauge data frequently remains a problem of interpolation.
Better methods could be used to provide better resolution without interpolation, such as radar measurements. This technique, however, is costly and not often available. Hence, several spatial interpolation methods have been used that are appropriate for a rapid estimation. For example, local polynomial (LP), trend surface analysis (TSA), radial basic function (RBF), geographically weighted regression, Kriging method, and inverse distance weighting (IDW) [1-4].
Naoum and Tsanis [5] developed a Geographical Information System (GIS) based spatial interpolation module, which adopts a multiple linear regression (MLR) technique. For the assessment purpose, this method can be compared with other methods, such as splin_regularized, spline_tension, IDW, kriging, and second-order polynomial. Li et al. [6] used the annual precipitation, from 2114 meteorological stations in China, over a span of 30 years between 1961 and 1990. The data were compared with its respective adjacent regions and analyzed through spline, ordinary kriging (OK), and IDW. Their results showed a good accuracy output with the IDW. This is also carried out by Chu et al. [7] and they reported a similar trend. The field spatial rainfall data can be obtained by using IDW when the data over a catchment are interpolated. The results of such a method were significant as the stimulated data at individual sites preserved properties [8]. Moreover, Dirks et al. [9] used rainfall data from a network of 13 rain gauges on Norfolk Island to compare four spatial interpolation methods. Their study showed that the more computationally demanding method of Kriging provided no significant advantage over any of the much simpler IDW, Thiessen, or arealmean methods. This further indicates that the IDW method is the good method for interpolations using spatiallydense networks.
The aim of the study is to improve interpolation accuracy of the spatial rainfall distribution in the Duhok Governorate by using the IDW method. The important influential parameter of IDW is the distance. Therefore, the elevation of rainfall stations will not be taken into the consideration of this study.
2. Materials and Methods
2.1. Study Area
The Duhok Governorate was chosen to detect this research. It is approximately between latitudes 36˚18'12.64'' and 37˚20'33.55''N, and longitudes 42˚20'25.36'' and 44˚17'40.50''E in the northwestern of Iraq, at 430 - 2500 m above the sea level and it covers about 11,000 km2 (Figure 1). The total number of the rainfall stations is 21 and spatially distributed in the Duhok Governorate as shown in Figure 2, beside 4 stations around Duhok Go-

Figure 1. (a) Map region of Iraq; (b) Location of Duhok Governorate.

Figure 2. Location of 25 rainfall station in Duhok Governorate and its around.
vernorate. The rainfall stations are managed by the directorate of meteorology in Duhok, Erbil and Mosul cities. Historical observation of rainfall data was required to interpolate spatial rainfall using IDW. Hence, the annual rainfall data of 10 years from 2000 to 2010 were adopted in this study.
2.2. Inverse Distance Weighting (IDW)
The IDW is one of the widest used as an interpolation method. It gets the value by calculating a weighted average of known values within a specific neighbourhood. It was defined as everything is related to everything else, but near things are more related than distant things. The IDW method involves the process of assigning values to unknown points by using values from a scattered set of known points. The value at the unknown point is a weighted sum of the values of N known points. Therefore, IDW simply can be used to estimate the unknown spatial rainfall data from the known data of sites that are adjacent to the unknown site [2,10]. The IDW formulas could be defined as
 (1)
(1)
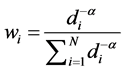 (2)
(2)
where ![]() refers to the unknown rainfall data (mm);
refers to the unknown rainfall data (mm); ![]() refers to the known rainfall data (mm),
refers to the known rainfall data (mm), ![]() is the amount of rainfall stations,
is the amount of rainfall stations, ![]() is the weighting of each rainfall stations,
is the weighting of each rainfall stations, ![]() is the distance from each rainfall stations to the unknown site,
is the distance from each rainfall stations to the unknown site, ![]() refers to the power, and is also a control parameter. Several researchers (e.g., [11,12]) have examined IDW with variations in a power, assessing its effects on the spatial distribution of information from precipitation observations. In this study, the
refers to the power, and is also a control parameter. Several researchers (e.g., [11,12]) have examined IDW with variations in a power, assessing its effects on the spatial distribution of information from precipitation observations. In this study, the ![]() value is conducted in the range of 1 to 5 with an incremental interval value of 1. Cross-validation is used to validate critical parameters, which may affect the interpolation accuracy of rainfall data by IDW method. These parameters are
value is conducted in the range of 1 to 5 with an incremental interval value of 1. Cross-validation is used to validate critical parameters, which may affect the interpolation accuracy of rainfall data by IDW method. These parameters are ![]() value and search radius. They have been chosen to insure the overall utility of the IDW models and allows optimal data prediction that is comparable to the observed data. Furthermore, the crossvalidation can be considered as a method for estimating the accuracy of an inducer. This is achieved by dividing the data into
value and search radius. They have been chosen to insure the overall utility of the IDW models and allows optimal data prediction that is comparable to the observed data. Furthermore, the crossvalidation can be considered as a method for estimating the accuracy of an inducer. This is achieved by dividing the data into ![]() mutually exclusive subsets (fold) of approximately equal size. Such an inducer is trained and evaluated
mutually exclusive subsets (fold) of approximately equal size. Such an inducer is trained and evaluated ![]() times of which at each time it is trained on the dataset minus a fold and evaluated on that fold. The accuracy estimate is the average accuracy for the
times of which at each time it is trained on the dataset minus a fold and evaluated on that fold. The accuracy estimate is the average accuracy for the ![]() times [13]. Hence, for the cross-validation purpose, 6 rainfall stations were adopted from the total of 25 rainfall stations (Figure 3).
times [13]. Hence, for the cross-validation purpose, 6 rainfall stations were adopted from the total of 25 rainfall stations (Figure 3).

Figure 3. Distribution of 6 rainfall station for cross validation.
2.3. Accuracy Assessment
The accuracy assessment of the IDW model is tested using Root Mean Square Error (RMSE). It measures frequently used on the differences between predicted (or estimated) values by a model and the actuallyobserved values from the thing being modeled or estimated. Moreover, the correlation coefficient ![]() was also used for evaluating whether the estimated data fits observed data or not. The formulas of RMSE and
was also used for evaluating whether the estimated data fits observed data or not. The formulas of RMSE and ![]() that serve this study, are given as:
that serve this study, are given as:
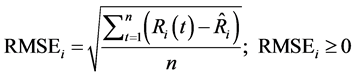 (3)
(3)
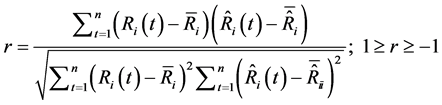 (4)
(4)
where  refers to the spatial rainfall values interpolated using IDW in the unknown rainfall station
refers to the spatial rainfall values interpolated using IDW in the unknown rainfall station![]() ;
;  is the observed rainfall data in the unknown rainfall station
is the observed rainfall data in the unknown rainfall station![]() ;
; ![]() means numbers (
means numbers (![]() in this study) of stations adopted, at year
in this study) of stations adopted, at year![]() .
.
2.4. Implementation and Analysis
To interpolate rainfall data by IDW models, a 25 rainfall stations were used, implementing cross-validation as an appropriate method to assess the accuracy of the spatial interpolated rainfall data. 25% of the total 25 rainfall stations were selected for a cross-validation process. 6 rainfall stations were selected to cover all districts with maximum search radius to increase the evaluated groups in cross-validation steps. These rainfall stations were Amedi, Darkar, Duhok, Batel, Hosseinie and Akri. The required Rainfall data were continuously recorded in the period of 2000-2010 (11 years). Table 1 shows the distance among respective rainfall stations. It is used to calculate the weighting of the individual rainfall station to the objective rainfall station. The 11 search radii (15 - 165 km) were selected and executed as shown in Table2 This is achieved to determine the Optimal Search Radii (O.S.R.) in the IDW of the 6 rainfall stations. The bold numbers in Table 2 represent the optimal number of rainfall stations close the objective that were selected for rainfall interpolation. Figure 4 shows the schematic diagram of different groups in Duhok rainfall station as an example. It is clear from Figure 4 that the different rainfall stations within different selected search radii can be used for interpolate rainfall data. For example; in Duhok station, 3 and 24 rainfall stations located within the selected search radius of 15 and 120 km for rainfall data interpolation. We compared and analyzed the data that falls within 8 groups, by assessing the relationship
Table 1 . Distance (km) between 25 rainfall stations to the 6 objective rainfall stations for calculating the individual weighting.
between prediction accuracy with a search radius; the number of selected rainfall stations. Such procedure was used for further calculations in cross validation. For such a purpose, the RMSE was used to determine the optimal parameters, ![]() value and search radius of IDW. Finally, the results of rainfall data interpolation using IDW were all validated by using correlation coefficient
value and search radius of IDW. Finally, the results of rainfall data interpolation using IDW were all validated by using correlation coefficient![]() . This was achieved to express the applicability of IDW models.
. This was achieved to express the applicability of IDW models.
3. Results and Discussion
Six rainfall stations (Table 2) were assumed as unknowns and rainfall data estimated using IDW in a
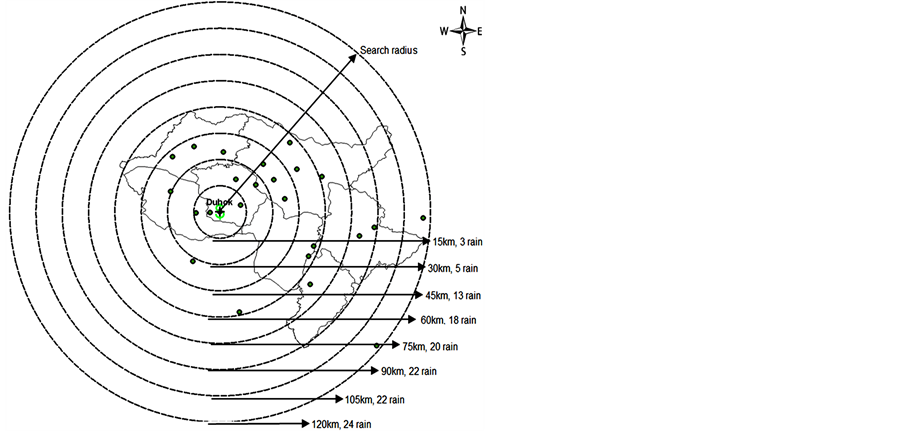
Figure 4. Schematic diagram of rainfall station groups of different search radius-use Duhok rainfall station for example.
Table 2. Optimal numbers of rainfall stations evaluated by different search radii (15 - 165 km) of 6 objective rainfall stations.
common parameter of![]() . This is achieved to interpolate the unknown rainfall data. Every different group of each rainfall station was estimated individually using the observed data respectively to individual rainfall station’s search radius (d = 15 to 165 km), where the data expressed as an annual rainfall. Moreover, to determine the optimal parameters of IDW;
. This is achieved to interpolate the unknown rainfall data. Every different group of each rainfall station was estimated individually using the observed data respectively to individual rainfall station’s search radius (d = 15 to 165 km), where the data expressed as an annual rainfall. Moreover, to determine the optimal parameters of IDW; ![]() value and O.S.R.and the minimum RMSE were calculated. Those results are shown in Table 3 in the form of annual rainfall. Simultaneously, the O.S.R. and
value and O.S.R.and the minimum RMSE were calculated. Those results are shown in Table 3 in the form of annual rainfall. Simultaneously, the O.S.R. and ![]() value were recorded in the condition of the minimum RMSE. By performing a comparison between the annual O.S.R. and the
value were recorded in the condition of the minimum RMSE. By performing a comparison between the annual O.S.R. and the ![]() values, we found two events. The first event regarding to the annual O.S.R., we found that 70% O.S.R. were within 15 - 30 km, there were two anomaly (60, 90 km) which occurred in Amedi and Akri rainfall stations. They deemed the use of several rainfall stations unnecessary for data interpolation under most conditions. On the other hand, the results revealed that the interpolation accuracy of rainfall was greater with increasing rainfall stations and to an optimal up limit.
values, we found two events. The first event regarding to the annual O.S.R., we found that 70% O.S.R. were within 15 - 30 km, there were two anomaly (60, 90 km) which occurred in Amedi and Akri rainfall stations. They deemed the use of several rainfall stations unnecessary for data interpolation under most conditions. On the other hand, the results revealed that the interpolation accuracy of rainfall was greater with increasing rainfall stations and to an optimal up limit.
The second event was that the optimal ![]() value varied from 1 to 5. There was 70% probability concurring and that the optimal
value varied from 1 to 5. There was 70% probability concurring and that the optimal ![]() was equal to 1 and 30% above that. The result in this study has identical views with several studies as in [7,]">12]. Wang et al. [14] also reported a case in China. They showed the prediction accuracy of annual rainfall had the highest significance when the
was equal to 1 and 30% above that. The result in this study has identical views with several studies as in [7,]">12]. Wang et al. [14] also reported a case in China. They showed the prediction accuracy of annual rainfall had the highest significance when the ![]() value was considered in the range of three to five. Figure 5 displays a series of 6 subdiagrams on the RMSE variation at different search radii (15 - 165 km) and
value was considered in the range of three to five. Figure 5 displays a series of 6 subdiagrams on the RMSE variation at different search radii (15 - 165 km) and ![]() value
value

Figure 5. RMSE variation of different search radii (15 - 165 km) and α value (1 - 5) of 6 rainfall stations.
from 1 to 5 with an increment interval of 1. The result was a large RMSE variation of different groups (search radius) occurred when ![]() approach one, the RMSE variation also reduced with the increase in
approach one, the RMSE variation also reduced with the increase in![]() . This showed that the minimum variation occurred at the largest
. This showed that the minimum variation occurred at the largest ![]() value, regardless of the number of rainfall stations used for interpolation. However, the minimum variation of RMSE stays uncertain on based of the optimal
value, regardless of the number of rainfall stations used for interpolation. However, the minimum variation of RMSE stays uncertain on based of the optimal ![]() and search radius. Hence, the optimal
and search radius. Hence, the optimal ![]() and search radius need to be further measured.
and search radius need to be further measured.
The relationship between the interpolated rainfall values and the actual observed data for all the 21 rainfall stations (inside Duhok Governorate) was also evaluated. Table 4 showed an estimated rainfall of 21 rainfall stations using IDW. The correlation coefficient ![]() was utilized as an indicator to evaluate the fittingness of IDW for estimating data. We found that the
was utilized as an indicator to evaluate the fittingness of IDW for estimating data. We found that the ![]() was greater than 0.74 in 21 rainfall stations in case using
was greater than 0.74 in 21 rainfall stations in case using ![]() and search radius = 105 km. It was evident that, rainfall interpolations using IDW showed significant similarities with the observed data using optimal independent annual values. Therefore, we could deduce that IDW is a suitable method for rainfall interpolation under the conditions that optimal
and search radius = 105 km. It was evident that, rainfall interpolations using IDW showed significant similarities with the observed data using optimal independent annual values. Therefore, we could deduce that IDW is a suitable method for rainfall interpolation under the conditions that optimal ![]() and search radius must be measured. Finally, Duhok Governorate was reclassified into 10 rainfall classes except some areas near Turkey and Syria borders due to the lack of data (Figure 6).
and search radius must be measured. Finally, Duhok Governorate was reclassified into 10 rainfall classes except some areas near Turkey and Syria borders due to the lack of data (Figure 6).
4. Conclusion
In this study, two major findings are drawn by using IDWfor interpolating spatial rainfall. First, the predicted
Table 4 . Estimated rainfall of the 21 rainfall station Using IDW (![]() = 1 & O.S.R = 105 km)
= 1 & O.S.R = 105 km)

Figure 6. Rainfall classification of Duhok Governorate into classes using IDW method.
accuracy of rainfall interpolated can be improved through the ![]() value adjustment. Second, the number of known rainfall station is also another influential parameter; most cases show that the prediction accuracy increases with the increasing numbers of known rainfall station. Finally, we conclude that through analyzing the optimization steps of
value adjustment. Second, the number of known rainfall station is also another influential parameter; most cases show that the prediction accuracy increases with the increasing numbers of known rainfall station. Finally, we conclude that through analyzing the optimization steps of ![]() value and radius of influence, the IDW is deemed as a suitable spatial interpolation method of rainfall.
value and radius of influence, the IDW is deemed as a suitable spatial interpolation method of rainfall.
REFERENCES
- A. S. Fotheringham, C. Brunsdon and M. Charlton, “Geographically Weighted Regression: The Analysis of Spatially Varying Relationships,” Wiley, Chichester, Hoboken, 2002.
- J. Li and A. D. Heap, “A Review of Spatial Interpolation Methods for Environmental Scientists,” Geoscience Australia, Canberra, 2008.
- H.-C. Yeh, Y.-C. Chen, C. Wei and R.-H. Chen, “Entropy and Kriging Approach to Rainfall Network Design,” Paddy and Water Environment, Vol. 9, No. 3, 2011, pp. 343-355. http://dx.doi.org/10.1007/s10333-010-0247-x
- S. S. Chinchorkar, G. R. Patel and F. G. Sayyad, “Development of Monsoon Model for Long Range Forecast Rainfall Explored for Anand (Gujarat-India),” International Journal of Water Resources and Environmental Engineering, Vol. 4, 2012, pp. 322-326.
- S. Naoum and I. K. Tsanis, “A Multiple Linear Regression GIS Module Using Spatial Variables to Model Orographic Rainfall,” Journal of Hydroinformatics, Vol. 6, 2004, pp. 39-56.
- J. L. Li, J. Zhang, C. Zhang and Q. G. Chen, “Analyze and Compare the Spatial Interpolation Methods for Climate Factor,” Pratacult Science, Vol. 23, No. 8, 2006, pp. 6-11.
- S. L. Chu, Z. Y. Zhou, L. Yuan and Q. G. Chen, “Study on Spatial Precipitation Interpolation Methods,” Pratacult Science, Vol. 25, 2008, pp. 19-23.
- M.-L. Segond, N. Neokleous, C. Makropoulos, C. Onof, and C. Maksimovic, “Simulation and Spatio-Temporal Disaggregation of Multi-Site Rainfall Data for Urban Drainage Applications,” Hydrological Sciences Journal, Vol. 52, No. 5, 2007, pp. 917-935. http://dx.doi.org/10.1623/hysj.52.5.917
- K. N. Dirks, J. E. Hay, C. D. Stow and D. Harris, “High-Resolution Studies of Rainfall on Norfolk Island: Part II: Interpolation of Rainfall Data,” Journal of Hydrology, Vol. 208, No. 3-4, 1998, pp. 187-193. http://dx.doi.org/10.1016/S0022-1694(98)00155-3
- P. Goovaerts, “Geostatistical Approaches for Incorporating Elevation into the Spatial Interpolation of Rainfall,” Journal of Hydrology, Vol. 228, No. 1-2, 2000, pp. 113- 129. http://dx.doi.org/10.1016/S0022-1694(00)00144-X
- F.-W. Chen and C.-W. Liu, “Estimation of the Spatial Rainfall Distribution Using Inverse Distance Weighting (IDW) in the Middle of Taiwan,” Paddy and Water Environment, Vol. 10, No. 3, 2012, pp. 209-222. http://dx.doi.org/10.1007/s10333-012-0319-1
- Y. Tung, “Point Rainfall Estimation for a Mountainous Region,” Journal of Hydraulic Engineering, Vol. 109, No. 10, 1983, pp. 1386-1393. http://dx.doi.org/10.1061/(ASCE)0733-9429(1983)109:10(1386)
- R. Kohavi and F. Provost, “Special Issue on Applications of Machine Learning and the Knowledge Discovery Process,” Vol. 30, Kluwer Academic Publishers, 1998.
- Y. Wang, C.-k. Li, L. Chen and S.-N. Zheng, “Analysis on Impact of Weight to Spatial Interpolation Methods,” Journal of Hunan University of Science & Technology, Vol. 28, No. 1, 2008, pp. 77-80. http://dx.doi.org/10.1007/s11596-008-0119-4
NOTES
*Corresponding author.


