Journal of Water Resource and Protection
Vol.4 No.6(2012), Article ID:19894,4 pages DOI:10.4236/jwarp.2012.46038
Optimal Reservoir Operation Using Stochastic Dynamic Programming
State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan, China
Email: *liupan@whu.edu.cn
Received April 4, 2012; revised May 4, 2012; accepted June 2, 2012
Keywords: Reservoir Operation; Stochastic Dynamic Programming; Operating Rules
ABSTRACT
This paper focused on the applying stochastic dynamic programming (SDP) to reservoir operation. Based on the two stages decision procedure, we built an operation model for reservoir operation to derive operating rules. With a case study of the China’s Three Gorges Reservoir, long-term operating rules are obtained. Based on the derived operating rules, the reservoir is simulated with the inflow from 1882 to 2005, which the mean hydropower generation is 85.71 billion kWh. It is shown that the SDP works well in the reservoir operation.
1. Introduction
Stochastic programming is a framework for modeling optimization problems that involve uncertainty [1-2]. It has been widely used in water resources planning and management [3-9]. The classic approach is the stochastic dynamic programming (SDP), which is able to tackle not only linear but also nonlinear objective function and constraints. The SDP recurrent formulation is
 (1)
(1)
where 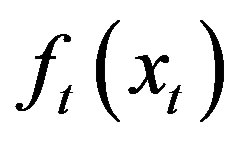 denotes the optimal benefit-to-go function from decision
denotes the optimal benefit-to-go function from decision  and g0(xt) is the benefit with a decision xt.
and g0(xt) is the benefit with a decision xt.
However, SDP needs to discrete the state space and this makes it heavy computational burden. In order to tackle this “curse of dimensionality”, there are several types of methods have been studied. 1) Method based on aggregation and decomposition. A method was proposed in which the control problem for a system of M reservoirs in series was decomposed into M sub-problems each with two reservoirs: one a reservoir from the original problem and the other an aggregate representation of the reservoirs downstream of that reservoir [3]. The solution time increases linearly with the number of reservoirs in the system and so the approach is practical for large systems [4]. This method was extended to a model consisting of that reservoir and a two-dimensional representation of the rest of the system [4]. A Benders decomposition algorithm was proposed and applied it to systems including 37 reservoirs [5]. 2) Method based on approximate of utilization function. An approach based on efficient discretization of the state space and approximation of the value functions was proposed over the continuous state space by means of a flexible feed forward neural network [6]. This method can be used for nonlinear objective function and has been applied to multi-reservoir systems with 30 reservoirs. 3) Method based on Stochastic Dual Dynamic Programming (SDDP). A sampled hyperplane was used to provide an outer approximation of the benefit-to-go function. These hyperplanes are equivalent to Benders cuts in Benders decomposition [7].
An interval-parameter multistage stochastic programming method was proposed for supporting water resources decision making, where uncertainties expressed as random variables and interval numbers could be reflected [8]. This method was improved that handles uncertainties through constructing a set of scenarios that is representative for the universe of possible outcomes, as well as reflects dynamic features of the system conditions and risk levels of violating system constraints within a multistage context [9]. They also recognized that it was a challenge to extend this method to flood control operation of reservoir due to large scenarios.
2. Methodology
The operating rules are a function between decision and observation (or prediction). Typically, single reservoir operating rules provide a release decision when inflow and current water storage have been obtained. If the operation horizon is infinite to future,
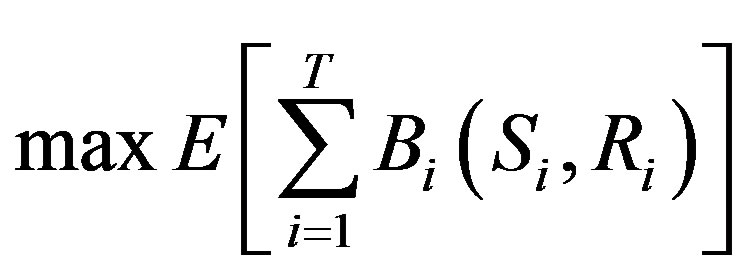
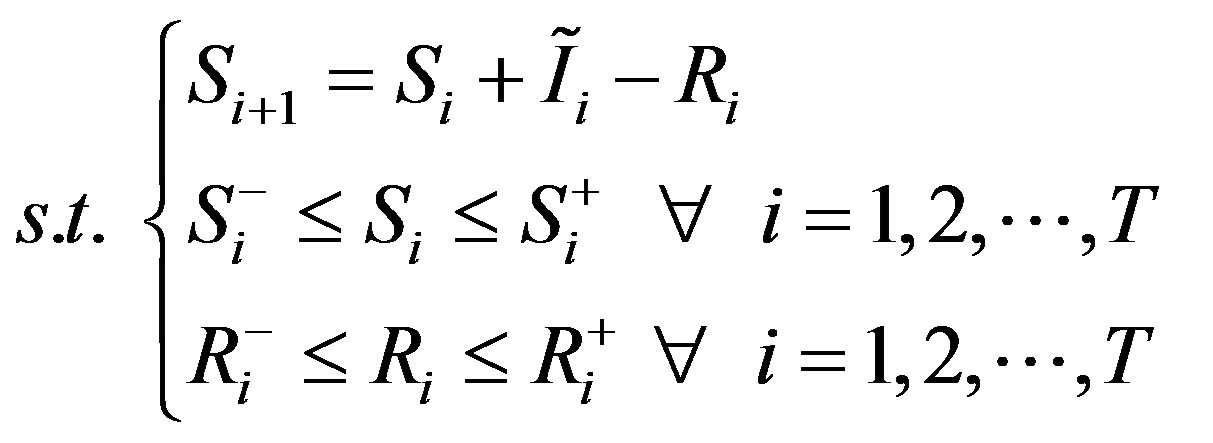 (2)
(2)
where Si is the initial water storage at time period i,  and Ri are inflow and release during time period i.
and Ri are inflow and release during time period i.  and
and 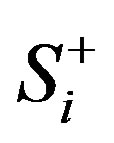 are the minimum and maximum allowable water storages during time period i, respectively.
are the minimum and maximum allowable water storages during time period i, respectively. 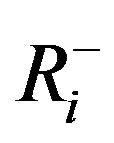 and
and 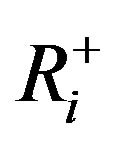 denote the minimum and maximum reservoir releases subjected to physical constraints during time period i, respectively.
denote the minimum and maximum reservoir releases subjected to physical constraints during time period i, respectively.
Since it is difficult to estimate accurately the inflow 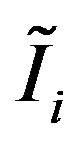 far behind (e.g., 100 years late), we estimate it by using periodic characterization. That is, during a cycle periodic time 1 to n,
far behind (e.g., 100 years late), we estimate it by using periodic characterization. That is, during a cycle periodic time 1 to n,
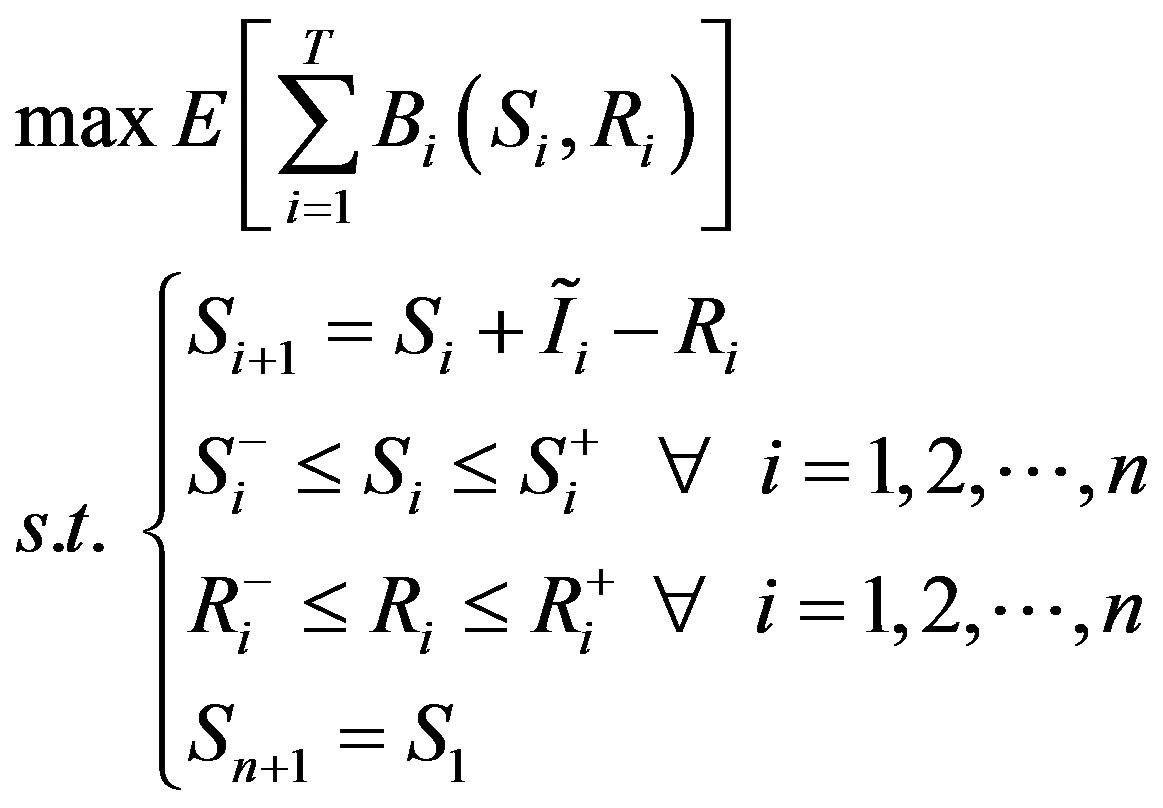 (3)
(3)
By using a two-stage stochastic programming framework,
 (4)
(4)
where 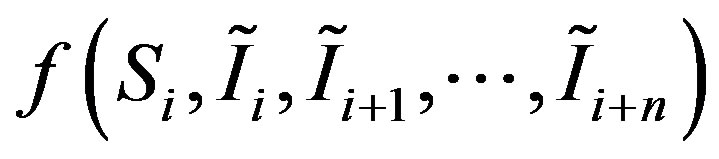 is a benefit-to-go function from
is a benefit-to-go function from 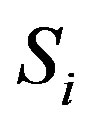 to end time
to end time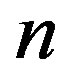 . The
. The 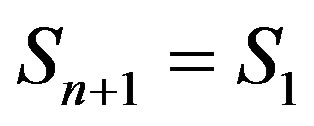 means the terminal condition of optimization.
means the terminal condition of optimization.
The utilization function 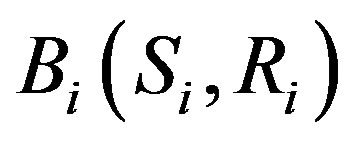 may be a linear function (e.g., for water supply) and a nonlinear function (e.g., for hydropower generation).
may be a linear function (e.g., for water supply) and a nonlinear function (e.g., for hydropower generation).
3. Case Study
3.1. The Three Gorges Reservoir
The Three Gorges Reservoir (TGR) is a vital project for water resources development of China’s largest river, the Yangtze River (Figure 1). The reservoir receives inflow from a 4.5 × 103 km long channel with a contributing
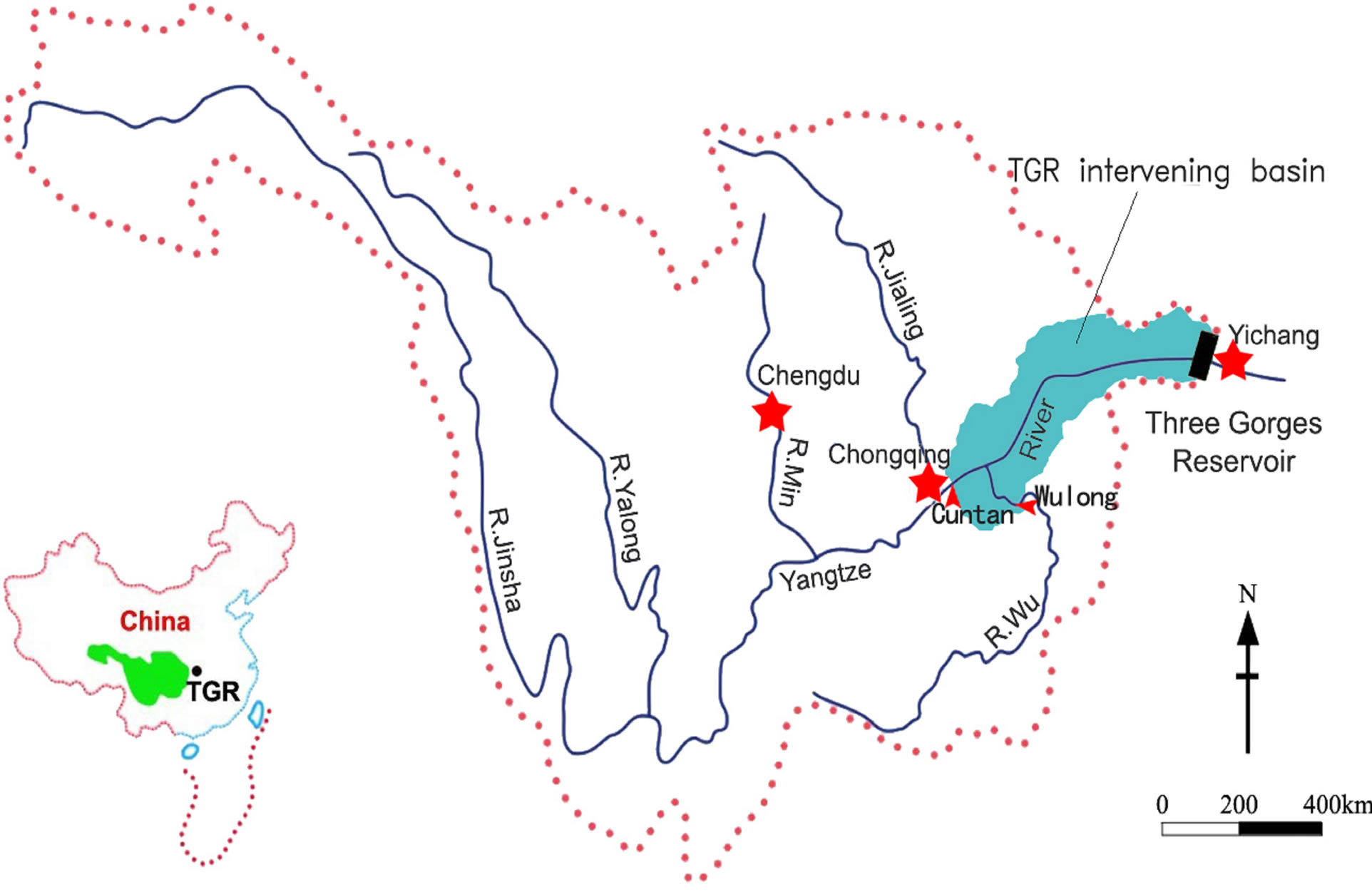
Figure 1. The location of the Three Gorges Reservoir basin in China.
drainage area of 106 km2. The mean annual runoff at the dam site is 4.51 × 1011 m3. The TGR is to date the largest multipurpose hydro-development project ever built in the world. Its benefits include flood control, power generation and navigation improvement. Streamflow records from Yichang flow gage station, located about 40 km downstream of the TGR, are used as inflow of the TGR. The interval of the time period is ten-day-long, a traditional Chinese measure of time. The streamflow series from 1882 to 2005 is used in this study.
3.2. SDP
The SDP involves two steps as follows:
1) Discretized the Inflow and Reservoir Storage: The inflow during the same time period (such as Jan), are discretized into N intervals from minimum to maximum. The probability of inflow interval i (during time period t) to inflow j (during time period t + 1) is also computed from the observed inflow series.
2) Finding the optimal solutions: By using Equation (4), the optimal solution is found and saved as optimal operating rules. The following operating rules are used in this paper.
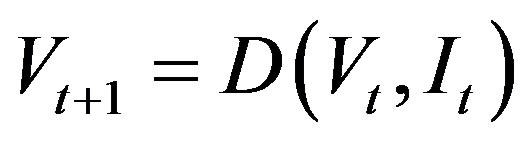 (5)
(5)
where 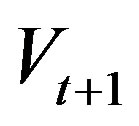 is the reservoir storage need to decide,
is the reservoir storage need to decide, 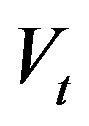 and
and 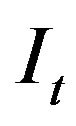 are the current reservoir storage and inflow.
are the current reservoir storage and inflow.
3.3. Results
The above SDP method is used to find the optimal operating rules, and it consumes about 3 minutes. Part of the operating rules is shown in Figure 2.
Based on the derived operating rules, the reservoir is simulated from 1882 to 2005. Finally, the mean hydropower generation is 85.71 billion kWh.
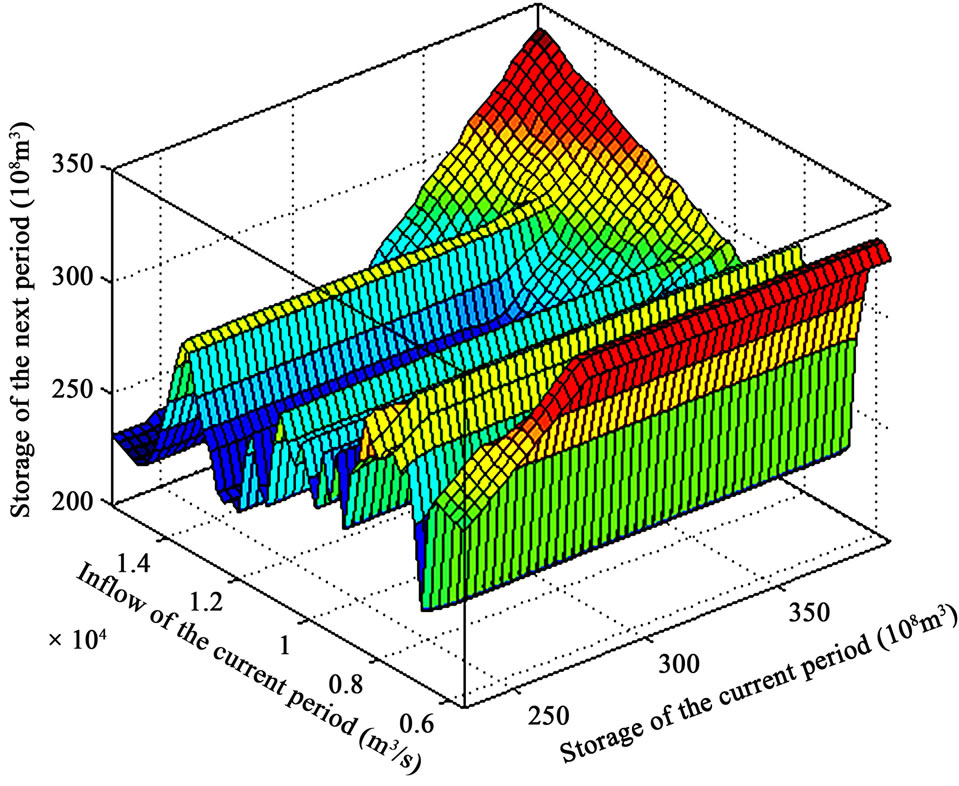
Figure 2. The optimal operating rules for the middle-tendays in April.
The above operating rules only use the current reservoir storage and inflow as variables for make-decision. In other words, this is a two-dimensional SDP problem. Indeed, SDP needs to discrete the state space and this makes it heavy computational burden.
4. Conclusion
In this paper, we focused on the applying stochastic programming to water resources management. We built one operation model for reservoir operation for operating rules derivation. With a case study of the China’s Three Gorges Reservoir, long-term operating rules are obtained. Based on the derived operating rules, the reservoir is simulated with the inflow from 1882 to 2005, which the mean hydropower generation is 85.71 billion kWh. It is shown that the SDP works well in the reservoir operation.
5. Acknowledgements
This study was supported by Program for New Century Excellent Talents in University (NCET-11-0401), the National Key Technologies Research and Development Program of China (2009BAC56B02, 2009BAC56B04) and the National Natural Science Foundation of China (50979072).
REFERENCES
- P. Kall and S. W. Wallace, “Stochastic Programming,” John Wiley & Sons, Chichester, 1994.
- H. Vladimirou, “Brief Introduction to Stochastic Programming (and Financial Modeling Applications),” University of Cyprus, 2003.
- A. Turgeon, “Optimal Operation of Multi-Reservoir Power Systems with Stochastic Inflows,” Water Resources Research, Vol. 16, No. 2, 1980, pp. 275-283. doi:10.1029/WR016i002p00275
- T. W. Archibald, K. I. M. McKinnon and L. C. Thomas, “An Aggregate Stochastic Dynamic Programming Model of Multi-Reservoir Systems,” Water Resources Research, Vol. 33, No. 2, 1997, pp. 333-340. doi:10.1029/96WR02859
- A. Tilmant, D. Pinte and Q. Goor, “Assessing Marginal Water Values in Multipurpose Multireservoir Systems via Stochastic Programming,” Water Resources Research, Vol. 44, 2008, 17p. doi:10.1029/2008WR007024
- C. Cervellera, V. Chen and A. Wen, “Optimization of a Large-Scale Water Reservoir Network by Stochastic Dynamic Programming with Efficient State Space Discretization,” European Journal of Operational Research, Vol. 171, No. 3, 2006, pp. 1139-1151. doi:10.1016/j.ejor.2005.01.022
- M. V. F. Pereira and L. M. V. G. Pinto, “Stochastic Optimization of a Multireservoir Hydroelectric System: A Decomposition Approach,” Water Resources Research, Vol. 21, No. 6, 1985, pp. 779-792. doi:10.1029/WR021i006p00779
- Y. P. Li, G. H. Huang and S. L. Nie, “An Interval-Parameter Multistage Stochastic Programming Model for Water Resources Management under Uncertainty,” Advanced in Water Resources, Vol. 29, No. 4, 2006, pp. 776-789. doi:10.1016/j.advwatres.2005.07.008
- Y. P. Li, G. H. Huang and X. Chen, “Multistage Scenario-based Interval-Stochastic Programming for Planning Water Resources Allocation,” Stochastic Environmental Research and Risk Assessment, Vol. 23, No. 2, 2009, pp. 781-792. doi:10.1007/s00477-008-0258-y
NOTES
*Corresponding author.

