Journal of Water Resource and Protection
Vol. 3 No. 8 (2011) , Article ID: 6990 , 8 pages DOI:10.4236/jwarp.2011.38068
One Dimensional Solute Transport Originating from a Exponentially Decay Type Point Source along Unsteady Flow through Heterogeneous Medium
Department of Mathematics, Banaras Hindu University, Varanasi, India
E-mail: prema.singh@rediffmail.com
Received May 27, 2011; revised June 29, 2011; accepted August 3, 2011
Keywords: Uniform Point Source, Heterogeneity, Dispersivity, Porous Media
ABSTRACT
One dimensional advection dispersion equation is analytically solved initially in solute free domain by considering uniform exponential decay input condition at origin. Heterogeneous medium of semi infinite extent is considered. Due to heterogeneity velocity and dispersivity coefficient of the advection dispersion equation are considered functions of space variable and time variable. Analytical solution is obtained using Laplace transform technique when dispersivity depended on velocity. The effects of first order decay term and adsorption are studied. The graphical representations are made using MATLAB.
1. Introduction
Managing the groundwater resources and rehabilitation of polluted aquifers, mathematical modeling is a powerful tool. The contaminant concentration distribution behaviour along/against unsteady groundwater flow in aquifer is studied through mathematical modeling as it is an important approach to formulate the geo-environmental problems and provides the best possible solution for reducing its impact on the environment. The pollutant’s solute transport from a source through a medium of air or water is described by a partial differential equation of parabolic type derived on the principle of conservation of mass, and is known as advection–diffusion equation (ADE). In one-dimension it contains two coefficients, one represents the diffusion parameter and the second represents the velocity of the advection of the medium like air or water. In case of porous medium, like aquifer, velocity satisfies the Darcy law and in non-porous medium, like air it satisfies the laminar conditions. The dispersive property differs from pollutant to pollutant.
The literature contains analytical solutions for solute transport in homogenous and heterogeneous porous media. Analytical solutions in one-, two-, and three-dimensional advection-dispersion transport equations with constant coefficients in homogeneous medium which have been collected in various compendiums [1-4]. Some more works in homogeneous medium has been compiled [5-10]. Using the theory [11] that relates dispersion directly to velocity, analytical solutions were obtained for solute transport along unsteady flow through homogeneous medium [12-15]. According to the dispersion theory [16] the dispersion parameter is proportional to square of velocity. Though much analytical solutions are not available based on this theory but some works [17,18] do occur. Some large sub-surface formations exhibit variable dispersivity properties either as a function of time or function of distance observed [19]. So the advectiondispersion equation with constant coefficients may not be appropriate for solute transport in heterogeneous media. Analytical solutions are available for space and/or time dependent coefficients manly in finite domain are very less in number. Analytical solutions for heterogeneous porous media for transport equation with time dependent coefficients [20-23]. Distance dependent analytical solution for one dimensional transport in porous media with an exponential dispersion function were solved [24,25] for uniform input condition and [26] for periodic input condition which describe the solute transport due to spatially dependent dispersion along uniform flow through heterogeneous semi-infinite media. The limitations of analytical solutions of the ADE with coefficients being function of space variables discussed [27]. Analytical solution of the advection-diffusion transport equation using a change-of-variable and integral transform technique obtained [28]. Further the technique of generalized integral transform to get analytical solutions of ADE in heterogeneous media with different spatially dependent dispersivity discussed [29]. A closed form analytical solution for spatially-varying initial conditions was derived for Dirichlet and Cauchy boundary conditions each with Bateman-type source terms [30]. Some work on distance dependent [31-40]. Longitudinal and transverse dispersion in two dimensional flows in aquifer-aquitard system have been investigated analytically [41]. The numerical solution of a fractional partial differential equation with Riesz-Space fractional derivative in a finite domain is discussed [42]. They considered two types of fractional partial differential equation, first one is the Riesz fractional diffusion equation and the second is the Riesz fractional advection-diffusion equation and provided three numerical methods to deal with the Riesz-Space fractional derivative. Also a finite difference approximation for two sided space fractional partial differential equation was provided [43].
In the present work one-dimensional advection diffusion equation is solved for dispersivity depended on square of velocity. The medium is of inhomogeneous nature and is of semi infinite extent. Due to inhomogeneous medium both the parameters dispersion and fluid velocity depends on space and time. Initially aquifer is considered to be solute free. The input point source is of exponentially decreasing nature at the origin and at the other end its concentration gradient is considered to be zero. The effect of first order decay of temporally dependent and adsorption is also considered in this work to get the physical insite of the problem. Laplace transform technique is used to obtain the analytical solution.
2. Mathematical Formulation and Its Analytical Solution
The linear Advection-Diffusion partial differential equation in one dimension in general form with absorption and decay term may be written as
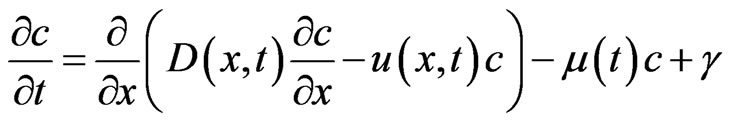 (1)
(1)
where 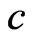 is the solute concentration at a position
is the solute concentration at a position 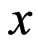 at time
at time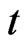 ,
, 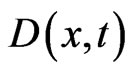 represents the solute dispersion and
represents the solute dispersion and 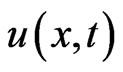 is velocity of the medium transporting the solute particles,
is velocity of the medium transporting the solute particles,  is first order decay or production term [T–1],
is first order decay or production term [T–1], 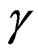 is source/sink of dimension [ML–3T–1],
is source/sink of dimension [ML–3T–1],  is empirical constant and
is empirical constant and 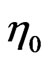 is the porosity. Initially the medium is solute free. An exponential decay type input point source concentration is assumed at the origin of the medium of uniform nature where
is the porosity. Initially the medium is solute free. An exponential decay type input point source concentration is assumed at the origin of the medium of uniform nature where  is the contaminant decay rate of dimension inverse of time [T–1]. It means that the input concentration decreases with time at the source. The second boundary condition is assumed to be of second type (flux type) of homogeneous nature. Thus the initial and two boundary conditions are as follows:
is the contaminant decay rate of dimension inverse of time [T–1]. It means that the input concentration decreases with time at the source. The second boundary condition is assumed to be of second type (flux type) of homogeneous nature. Thus the initial and two boundary conditions are as follows:
 (2)
(2)
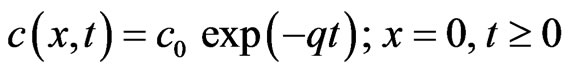 (3)
(3)
and
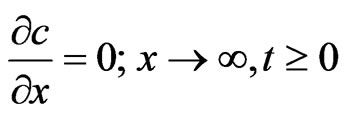 (4)
(4)
In [44] they considered the co-efficients of Equation (1) are temporally dependent and [23] assumed spatially dependent in a constant point source and derived their analytical solutions. But in this paper due to heterogeneity velocity is considered spatially dependent of linearly interpolated nature, and also velocity is assumed temporally dependent. Due to heterogeneous medium it’s not always possible that the source of contaminants is constant, so in this paper the source of contaminant at the origin is of exponentially decay type. The expressions for each coefficient velocity, dispersion and first order decay are considered in degenerate forms as follows:
 (5)
(5)
where the coefficient 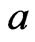 is the heterogeneity parameter of dimension inverse of that of space variable, and
is the heterogeneity parameter of dimension inverse of that of space variable, and 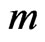 is an unsteadiness parameter of dimension inverse of that of time variable,
is an unsteadiness parameter of dimension inverse of that of time variable,  ,
, 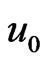 and
and 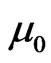 in above expressions referred as initial dispersion coefficient of dimension [L2 T–1], initial velocity of dimension [L2 T–1] and initial firs order time decay rate of dimension of inverse of time [T–1].
in above expressions referred as initial dispersion coefficient of dimension [L2 T–1], initial velocity of dimension [L2 T–1] and initial firs order time decay rate of dimension of inverse of time [T–1].
3. Dispersion through Heterogeneous Medium along Unsteady Flow
Using the expressions (5), the advection-diffusion Equation (1) can now be written as
 (6)
(6)
or
 (7)
(7)
Let us introduce a new time variable  defined by [45] by the transformation as
defined by [45] by the transformation as
 (8)
(8)
The dimension of 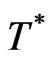 is same as dimension of
is same as dimension of , so it is referred to as a new time variable. An expression for
, so it is referred to as a new time variable. An expression for 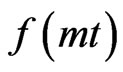 chosen such that for
chosen such that for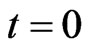 , we get the value of
, we get the value of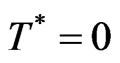 , so that the initial condition not affected in new time domain. Also a space variable transformation is introduced [23,46] as
, so that the initial condition not affected in new time domain. Also a space variable transformation is introduced [23,46] as
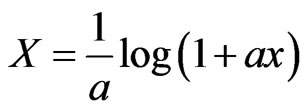 (9)
(9)
The initial value problem together with their initial and boundary conditions in new time and space variable becomes
 (10)
(10)
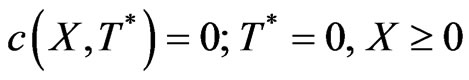 (11)
(11)
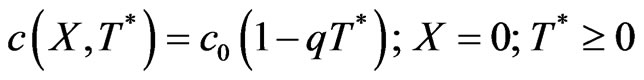 , (12)
, (12)
and
 (13)
(13)
where 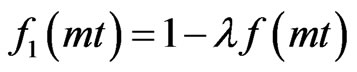 is another time dependent expression in non-dimensional variable
is another time dependent expression in non-dimensional variable  and
and  is non dimensional coefficient.
is non dimensional coefficient.
To eliminate the first order decay term form the Equation (10), introducing the transformation as:
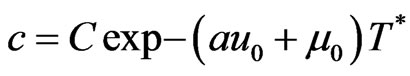 (14)
(14)
With the use of Equation (14), Equation (10) becomes
 (15)
(15)
Further using a space variable  and time variable
and time variable 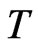 through the transformations as:
through the transformations as:
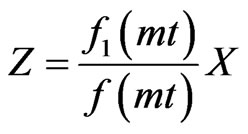 (16)
(16)
and
 (17)
(17)
The one-dimensional advection-diffusion Equation (15) with their initial condition (11) and boundary conditions (12)-(13) may now be written as
 (18)
(18)
 (19)
(19)
 (20)
(20)
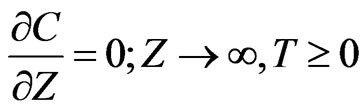 (21)
(21)
The time variable  has to be expressed explicitly in terms of
has to be expressed explicitly in terms of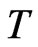 . An expression of exponentially decreasing nature is chosen as
. An expression of exponentially decreasing nature is chosen as
 (22)
(22)
So from Equation (8), we get
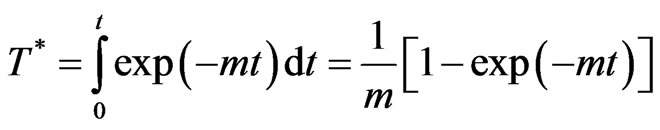
or
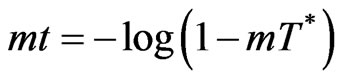
Also using the transformation in Equation (17) we get

or

or
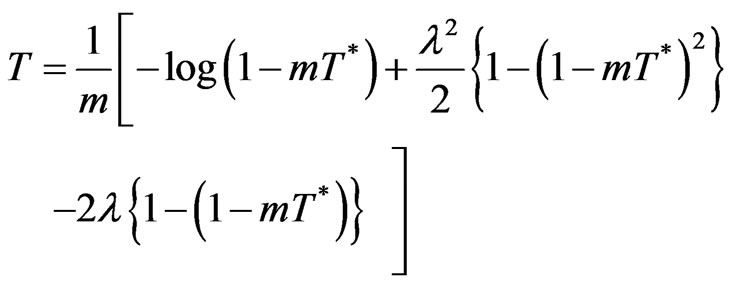
In ,
,  is much smaller than one, so its second and higher degree terms in the logarithmic and binomial expansions in above equations are omitted. So we get
is much smaller than one, so its second and higher degree terms in the logarithmic and binomial expansions in above equations are omitted. So we get
 , where
, where 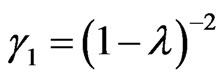 (23)
(23)
Thus the initial value problem (18) and their conditions (19)-(21), becomes
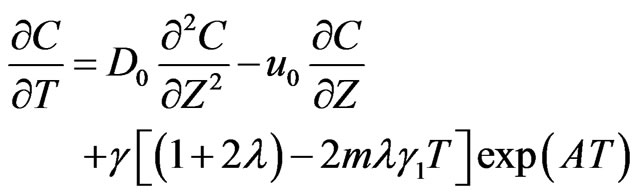 (24)
(24)
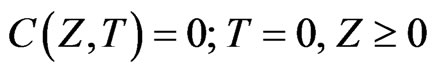 (25)
(25)
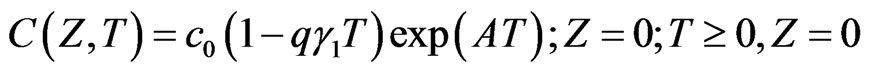 (26)
(26)
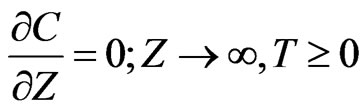 (27)
(27)
where .
.
Now to find the analytical solution for Equation (24), Laplace transform technique is used, but to apply it more conveniently the convective term from the Equation (24) is to be removed by the use of the transformation as
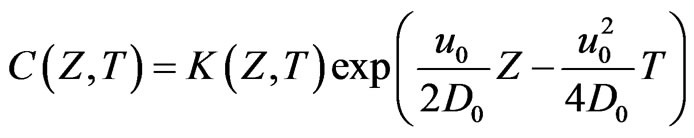 (28)
(28)
The initial and boundary value problem from (24-27) in terms of new dependent variable 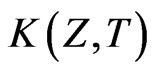 may now be written as
may now be written as
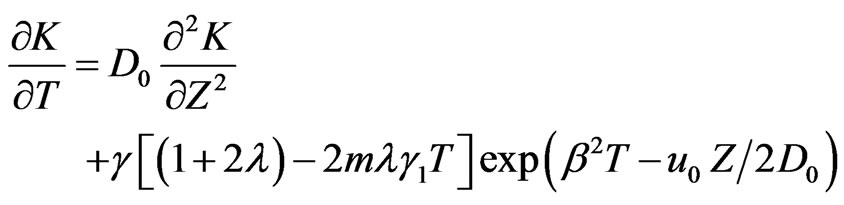 (29)
(29)
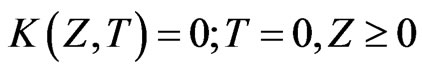 (30)
(30)
 (31)
(31)
 (32)
(32)
where  and
and 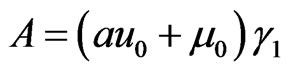
Applying Laplace transformation on the above boundary value problem, the problems become in second order ordinary differential equation in the Laplacian domain  as :
as :
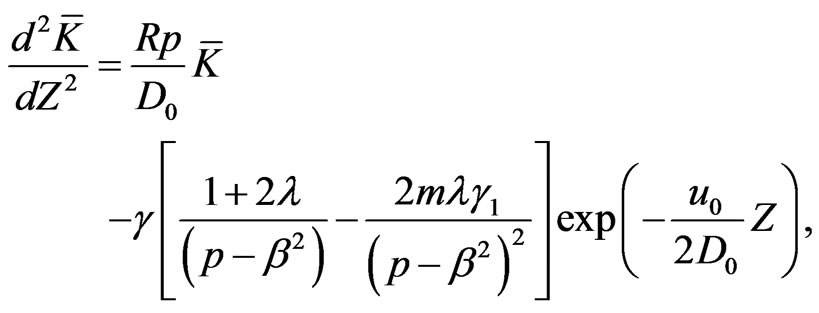 (33)
(33)
 , (34)
, (34)
and
 (35)
(35)
After using the boundary conditions (34) and (35), its particular solution may be obtained as
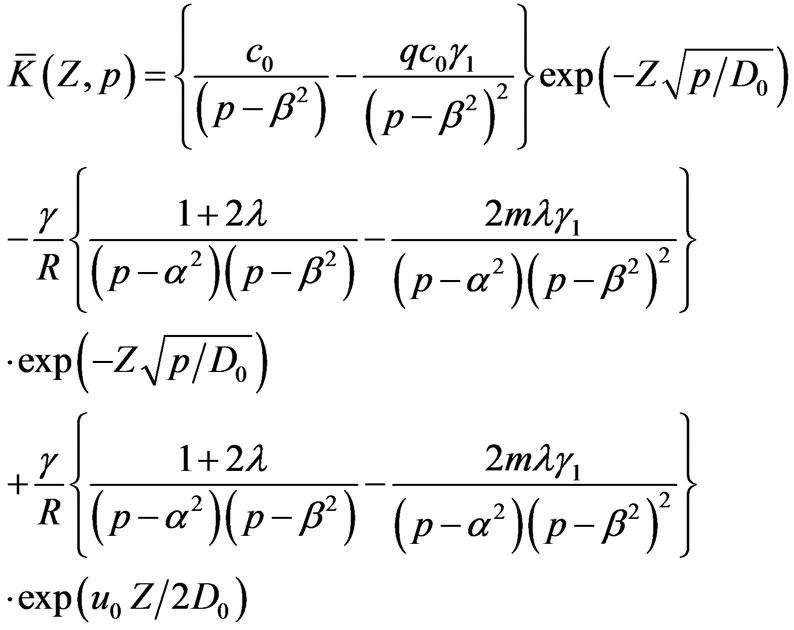 (36)
(36)
where 
Now taking the inverse Laplace transform of Equation (36), the solution in 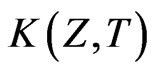 may be obtained. Using the transformation (28) and (14) the desired solution may be obtained as
may be obtained. Using the transformation (28) and (14) the desired solution may be obtained as
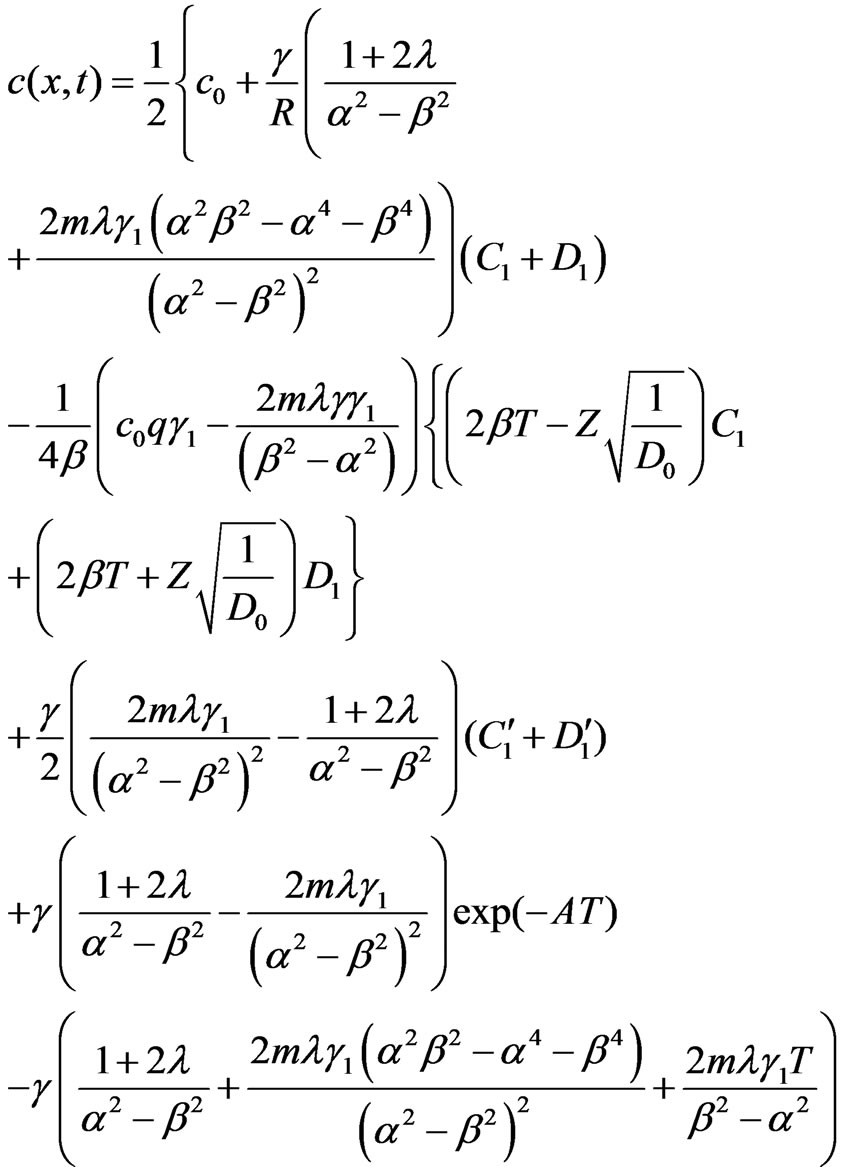 (37)
(37)
where
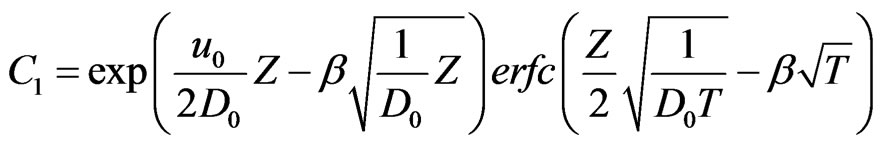 ;
;
 ;
;
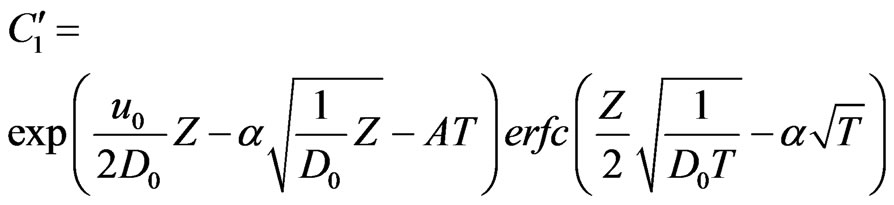 ;
;
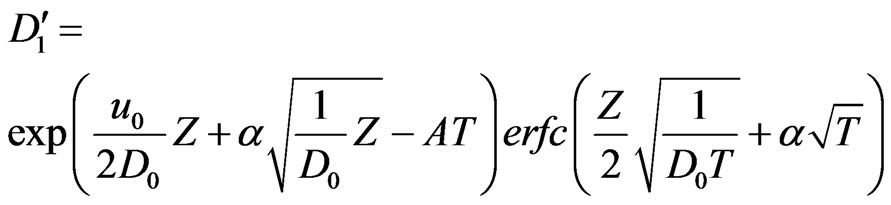 ;
;
 ;
;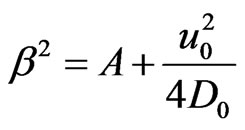 ;
; ;
; ;
;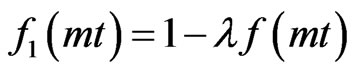 ;
; ;
; ;
; 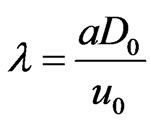 ;
; ;
;
The solution defined by Equation (37) describes the solute transport for exponential decay type input condition at origin in heterogeneous semi infinite domain.
4. Illustration and Discussion
The analytical solution of the present hydrodynamics dispersion is obtained as given in Equation (37). The concentration values  are evaluated from the solution for the input values: reference concentration
are evaluated from the solution for the input values: reference concentration  = 1, initial velocity
= 1, initial velocity 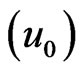 = 0.61 (km/year), initial dispersivity
= 0.61 (km/year), initial dispersivity 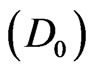 = 0.71 (km2/year), heterogeneity parameter (
= 0.71 (km2/year), heterogeneity parameter (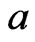 ) = 0.1 (km–1), unsteady parameter (
) = 0.1 (km–1), unsteady parameter ( ) = 0.1 (km-1), contaminant decay rate (
) = 0.1 (km-1), contaminant decay rate (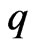 ) = 0.1 (km–1), initial first order decay (
) = 0.1 (km–1), initial first order decay (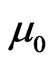 ) = 0.5 (year–1) , and the initial source/sink (
) = 0.5 (year–1) , and the initial source/sink ( ) = 0.2
) = 0.2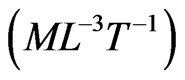 . Concentration attenuation with position and time is studied in the domain
. Concentration attenuation with position and time is studied in the domain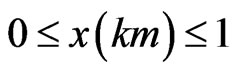 , at
, at  = 0.4, 0.7 and 1.0 (year). It is illustrated in Figure 1. Full line curves are drawn for decelerating flow filed represented by
= 0.4, 0.7 and 1.0 (year). It is illustrated in Figure 1. Full line curves are drawn for decelerating flow filed represented by 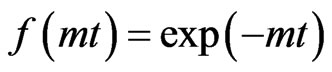 and dotted curves are drawn for accelerating flow field represented by
and dotted curves are drawn for accelerating flow field represented by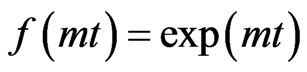 . In case input concentration, i.e.
. In case input concentration, i.e. 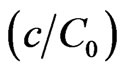 at
at  decreases with time but solute transport of lower input concentration source is faster than that of source having higher input value. It is evident that, in view of the dispersion parameter being proportional to square of velocity, solute transport is much faster in case of accelerating flow field than that along decelerating flow field. The effect of heterogeneity is studied in Figure 2. For it concentration values
decreases with time but solute transport of lower input concentration source is faster than that of source having higher input value. It is evident that, in view of the dispersion parameter being proportional to square of velocity, solute transport is much faster in case of accelerating flow field than that along decelerating flow field. The effect of heterogeneity is studied in Figure 2. For it concentration values  are evaluated from solution (37) at
are evaluated from solution (37) at 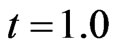 and
and 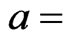 0.1, 0.2, 0.3, for both the flow field. It may be observed that solute transport faster along accelerating flow field in a medium of higher heterogeneity (causing larger increase in velocity from origin to the end
0.1, 0.2, 0.3, for both the flow field. It may be observed that solute transport faster along accelerating flow field in a medium of higher heterogeneity (causing larger increase in velocity from origin to the end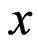 ) than that in a medium of lower heterogeneity. But the trend reverses in a decelerating flow field.
) than that in a medium of lower heterogeneity. But the trend reverses in a decelerating flow field.
The effect of first order decay and zero order production are studied through Figure 3. It is drawn at 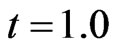

Figure 1. Illustration of solute transport at different times when ,
, 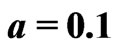 (km–1),
(km–1), 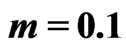 (year–1),
(year–1), 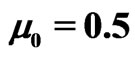 (year–1),
(year–1), 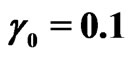 , and
, and  (km–1) described by solution (37). Solid and dotted curves are drawn for
(km–1) described by solution (37). Solid and dotted curves are drawn for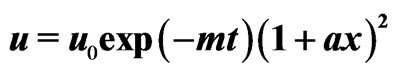 , and
, and 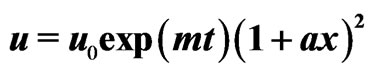 respectively.
respectively.
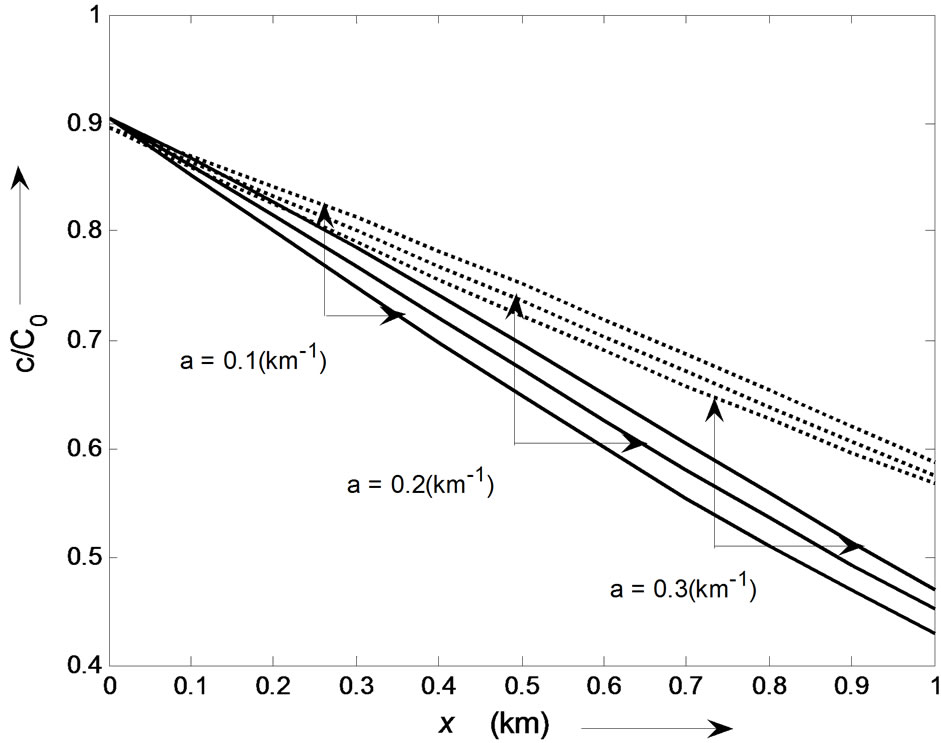
Figure 2. Illustration of the effect of heterogeneity on the solute transport when , described by solution (37), at
, described by solution (37), at 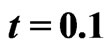 (year). Solid and dotted curves are drawn for
(year). Solid and dotted curves are drawn for 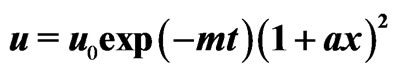 and
and 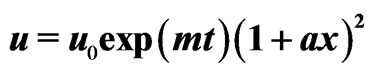 respectively,
respectively, 
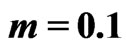 (year–1).
(year–1).
and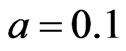 . It may be observed that solute transport is fastest in the absence of both the parameters. It is slowest in the presence of first order decay but in the absence of the production term.
. It may be observed that solute transport is fastest in the absence of both the parameters. It is slowest in the presence of first order decay but in the absence of the production term.
5. Conclusions
One-dimensional analytical solution of advection—diffusion equation with variable coefficients is obtained using Laplace transformation technique. The source con-
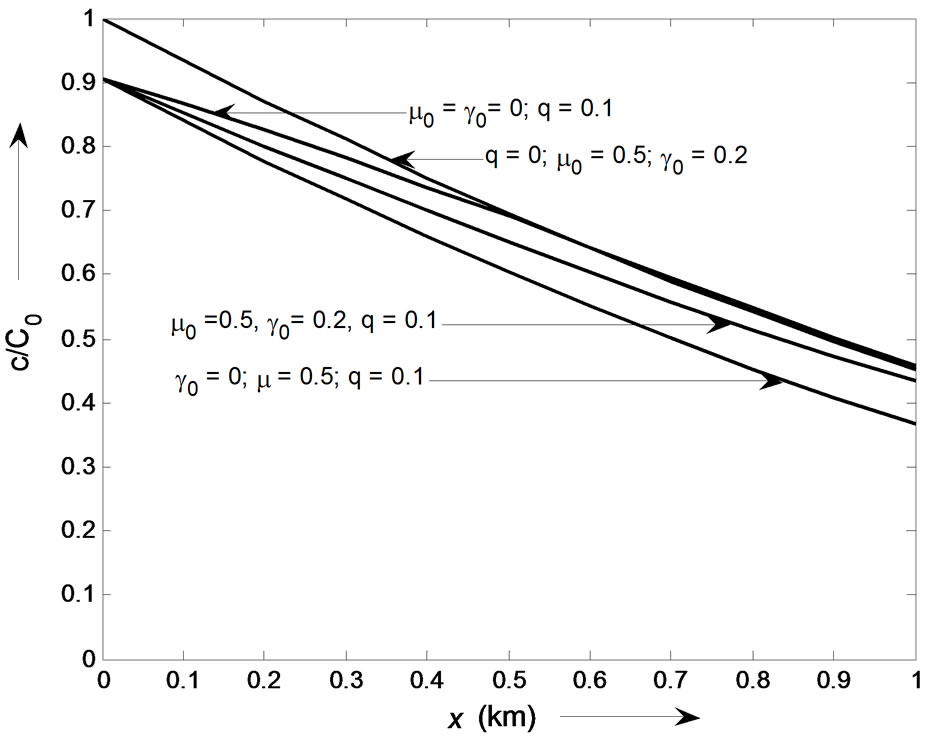
Figure 3. Illustration of solute transport for different parameters when ,
,  (km-1) and
(km-1) and  (year–1) at time
(year–1) at time 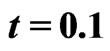 (years).
(years).
centration is a point uniform source of exponentially decay nature. The expressions for both the coefficients are considered in both the independent variables but in degenerate forms given by Equation (5). With the help of certain transformations the variable coefficients are reduced into constant coefficients. Such forms of the two coefficients are conceived which correspond to the different dispersion theory (Scheidegger, 1957). The change in velocity due to heterogeneity and unsteadiness may be varied by assigning appropriate values to the separate parameters of the both. It may be concluded from the present study that the concentration level in case of accelerating diffusive source along decelerating flow domain are the least. From engineering point of view this observation may be important to keep the emission of polluting solute particles from a source of accelerating nature. The effects of first order decay and adsorption are considered and their impact illustrated by graph.
6. Acknowledgements
The author gratefully acknowledges the financial support in the form of Dr D. S. Kothari post doctoral fellowship by the University Grants Commission, Government of India.
REFERENCES
- M. Th. Van Genuchten and W. J. Alves, “Analytical Solutions of the One–Dimensional Convective–Dispersive Solute Transport Equation,” Technical Bulletin (United States Department of Agriculture), No. 1661.
- I. Javandel, C. Doughty, and C. F. Tsang, “Groundwater Transport: Handbook of Mathematical Models,” American Geophysical Union Water Resources Monograph, Series 10, American Geophysical Union, Washington D C, 1984.
- M. K. Singh, N. K. Mahto and P. Singh, “Longitudinal Dispersion with Time Dependent Source Concentration in Semi Infinite Aquifer,” Journal of Earth System Science, Vol. 117, No. 6, 2008, pp. 945-949. http://dx.doi.org/10.1007/s12040-008-0079-x
- M. K. Singh, V. P. Singh, P. Singh, and D. Shukla, “Analytical Solution for Conservative Solute Transport in One Dimensional Homogeneous Porous Formations with Time Dependent Velocity,” Journal of Engineering Mechanics, Vol. 135, No. 9, 2009, pp. 1015-1021. doi:10.1061/(ASCE)EM.1943-7889.0000018
- F. B. Smith, “The Diffusion of Smoke from a Continuous Elevated Point Source into a Turbulent Atmosphere,” The Journal of Fluid Mechanics, Vol. 2, No. 1, 1957, pp. 49- 76. doi:10.1017/S0022112057000737
- A. Ogata, “Theory of Dispersion in Granular Media,” United States Geological Survey Professional Paper, No. 411-I, 1970, p. 34.
- M. A. Marino, “Distribution of Contaminants in Porous Media Flow,” Water Resources Research, Vol. 10, No. 5, 1974, pp. 1013-1018. doi:10.1029/WR010i005p01013
- R. A. Scriven and B. A. Fisher, “The Long Range Transport of Airborne Material and Its Removal by Deposition and Washout—II. The Effect of Turbulent Diffusion,” Atmospheric Environment, Vol. 9, 1975, pp. 59-69.
- C. Demuth, “A Contribution to the Analytical Steady Solution of the Diffusion Equation for Line Sources,” Atmospheric Environment, Vol. 12, No. 5, 1978, pp. 1255- 1258. doi:10.1016/0004-6981(78)90399-2
- V. A. Fry, J. D. Istok and R. B. Guenther, “Analytical Solutions to the Solute Transport Equation with RateLimited Desorption and Decay,” Water Resources Research, Vol. 29, No. 9, 1993, pp. 3201-3208.
- E. H. Ebach and R. White “Mixing of Fluids Flowing through Beds of Packed Solids,” Journal of American Institute of Chemical Engineers, Vol. 4, 1958, pp. 161-164.
- R. B. Banks and S. Jerasate, “Dispersion in Unsteady Porous Media Flow,” Journal of the Hydraulics Division, Vol. 88, No. HY3, 1962, pp. 1-21.
- N. Kumar, “Unsteady Flow Against Dispersion in Finite Porous Media,” Journal of Hydrology, Vol. 63, No. 3-4, 1983, pp. 345-358. doi:10.1016/0022-1694(83)90050-1
- M. M. Aral and B. Liao, “Analytical Solutions for TwoDimensional Transport Equations with TimeDependent Dispersion Coefficients,” Journal of Hydrologic Engineering, Vol. 1 No. 1, 1996 pp. 20-32. doi:10.1061/(ASCE)1084-0699(1996)1:1(20)
- M. K. Singh, P. Singh and V. P. Singh, “Analytical Solution for Two Dimensional Solute Transport in Finite Aquifer with Time Dependent Source Concentration,” Journal of Engineering Mechanics, Vol. 136, No. 10, 2010, pp. 1309-1315. doi:10.1061/(ASCE)EM.1943-7889.0000177
- A. E. Scheidegger, “The Physics of Flow through Porous Media,” 3rd Edition, University of Toronto Press, 1974.
- C. Zoppou and J. H. Knight, “Analytical Solution of a Spatially Variable Coefficient Advection–Diffusion Equation in up to Three Dimensions,” Applied Mathematical Modelling, Vol. 23, No. 9, 1999, pp. 667-685. doi:10.1016/S0307-904X(99)00005-0
- D. K. Jaiswal, A. Kumar and R. R. Yadav, “Analytical Solution to the One Dimensional Advection-Diffusion Equation with Temporally Dependent Coefficient,” Journal of Water Resource and Protection, Vol. 1, 2011, pp. 76-84.
- G. Matheron and G. deMarsily, “Is Transport in Porous Media Always Diffusive?” Water Resources Research, Vol. 16, No. 5, 1980, pp. 901-917. doi:10.1029/WR016i005p00901
- D. A. Barry and G. Sposito, “Analytical Solution of a Convection—Dispersion Model with Time Dependent Transport Coefficients,” Water Resources Research, Vol. 25, No. 12, 1989, pp. 2407-2416.
- H. A. Basha and F. S. El-Habel, “Analytical Solution of One Dimensional Time-Dependent Transport Equation.” Water Resources Research, Vol. 29, No. 9, 1993, pp. 3209-3214.
- G. Marinoschi, U. Jaekel and H. Vereecken, “Analytical Solutions of Three Dimensional Convection-Dispersion Problems with time Dependent Coefficients,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 79, No. 6, 1999, pp. 411-421. doi:10.1002/(SICI)1521-4001(199906)79:6<411::AID-ZAMM411>3.0.CO;2-6
- A. Kumar, D. K. Jaiswal and N. Kumar, “Analytical Solutions to One-Dimensional Advection-Diffusion Equation with Variable Coefficients in Semi-Infinite Media,” Journal of Hydrology, Vol. 380, No. 3-4, 2010, pp. 330- 337. doi:10.1016/j.jhydrol.2009.11.008
- S. R. Yates, “An Analytical Solution for One—Dimensional Transport in Heterogeneous Porous Media,” Water Resources Research, Vol. 26, No. 10, 1990, pp. 2331- 2338.
- S. R. Yates, “An Analytical Solution for One—Dimensional Transport in Porous Medium with an Exponential Dispersion Function,” Water Resources Research, Vol. 28, No. 8, 1992, pp. 2149-2154. doi:10.1029/92WR01006
- J. D. Logan, “Solute Transport in Porous Media with Scale—Dependent Dispersion and Periodic Boundary Conditions,” Journal of Hydrology, Vol. 184, No. 3-4, 1996, pp. 261-276. doi:10.1016/0022-1694(95)02976-1
- S. Neelz, “Limitations of an Analytical Solution for Advection—Diffusion Equation with Variable Coefficients,” Communications in Numerical Methods in Engineering, Vol. 22, No. 5, 2006, pp. 387-396.
- J. S. P. Guerrero, L. C. G. Pimental, T. H. Skaggs and M. Th. van Genucheten, “Analytical Solution of the Advection-Diffusion Transport Equation Using a Change of Variable and Integral Transform Technique,” International Journal of Heat and Mass Transfer, Vol. 52, No. 13-14, 2009, pp. 3297-3304. doi:10.1016/j.ijheatmasstransfer.2009.02.002
- J .S. P. Guerrero and T. H. Skaggs, “Analytical Solution for One-Dimensional Advection—Dispersion Transport Equation with Space-Dependent Coefficients,” Journal of Hydrology, Vol. 390, No. 1, 2010, pp. 57-65. doi:10.1016/j.jhydrol.2010.06.030
- V. Srinivasan and T. P. Clement, “Analytical Solutions for Sequentially Coupled One-Dimensional Reactive Transport Problems-Part I: Mathematical Derivations,” Advances in Water Resources, Vol. 31, No. 2, 2008, pp. 203-218. doi:10.1016/j.advwatres.2007.08.002
- C. V. Chrysikopoulos, P. K. Kitanidis and P. V. Roberts, “Analysis of One-Dimensional Solute Transport through Porous Media with Spatially Variable Retardation Factor,” Water Resources Research, Vol. 26, No. 3, 1990, pp. 437-446.
- K. Huang, M. Th. van Genuchten and R. Zhang, “Exact Solutions for One Dimensional Transport with Asymptotic Scale Dependent Dispersion,” Applied Mathematical Modelling, Vol. 20, 1996, pp. 297-308.
- B. Hunt, “Contaminant Source Solutions with scale Dependent Dispersivities,” Journal of Hydrologic Engineering, Vol. 3, No. 4, 1998, pp. 268-275. doi:10.1061/(ASCE)1084-0699(1998)3:4(268)
- B. Hunt, “Scale Dependent Dispersion from a Pit,” Journal of the Hydraulics Division, Vol. 104, 2002, pp. 75-85.
- L. Pang and B. Hunt, “Solutions and Verification of a Scale—Dependent Dispersion Model,” Journal of Contaminant Hydrology, Vol. 53, No. 1-2, 2001, pp. 21-39.
- G. Liu and B. C. Si, “Analytical Modeling of One-Dimensional Diffusion in Layered System with Position-Dependent Diffusion Coefficients,” Advances in Water Resources, Vol. 31, No. 2, 2008, pp. 251-268. doi:10.1016/j.advwatres.2007.08.008
- J. S. Chen, C. W. Liu and C. M. Liao, “Two-Dimensional Laplace-Transformed Power Series Solution for Solute Transport in a Radially Converget Flow Field,” Advances in Water Resources, Vol. 26, No. 10, 2003, pp. 1113- 1124. doi:10.1016/S0309-1708(03)00090-3
- J. S. Chen, C. F. Ni, C. P. Liang and C. C. Chiang, “Analytical Power Series Solution for Contaminant Transport with Hyperbolic Asymptotic Distance—Dependent Dispersivity,” Journal of Hydrology, Vol. 362, No. 1-2, 2008, pp. 142-149. doi:10.1016/j.jhydrol.2008.08.020
- J. S. Chen, C. S. Chen and C. Y. Chen, “Analysis of Solute Transport in a Divergent Flow Tracer Test with ScaleDependent Dispersion,” Hydrological Processes, Vol. 21, No. 18, 2007, pp. 2526-2536. doi.org/10.1002/hyp.6496
- Y. Nibori, R. Nakata, O. Tochiyama and H Mimura, “Evaluation of Solute Transport through a Fracture by Considering the Spatial Distributions of Retardartion Effect in Granule Scale,” Journal of Hydrologic Engineering, Vol. 14, No. 11, 2009, pp. 1214-1220. doi:10.1061/(ASCE)1084-0699(2009)14:11(1214)
- H. Zhan, Z. Wen, G. Huang and D. Sun, “Analytical Solution of Two-Dimensional Solute Transport in an Aquifer-Aquitard System,” Journal of Contaminant Hydrology, Vol. 107, No. 3-4, 2009, pp. 162-174. doi:10.1016/j.jconhyd.2009.04.010
- Q. Yang, F. Liu and I. Turner, “Numerical Methods for Fractional Partial Differential Equations with Riesz Space Fractional Derivatives,” Applied Mathematical Modelling, Vol. 34, No. 1, 2010, pp. 200-218. doi:10.1016/j.apm.2009.04.006
- M. M. Meerschaert and C. Tadjeran, “Finite Difference Approximations for Two-Sided Space-Fractional Partial Differential Equations,” Applied Numerical Mathematics, Vol. 56, No. 1, 2006, pp. 80-90. doi:10.1016/j.apnum.2005.02.008
- D. K. Jaiswal, A. Kumar, N. Kumar and R. R. Yadav, “Analytical Solutions for Temporally and Spatially Dependent Solute Dispersion of Pulse Type Input Concentration in One-Dimensional Semi-Infinite Media,” Journal of Hydro-Environment Research, Vol. 2, No. 4, 2009, pp. 254-263. doi:10.1016/j.jher.2009.01.003
- J. Crank, “The Mathematics of Diffusion,” Oxford University Press, Oxford, 1975.
- A. Kumar, D. K. Jaiswal and N. Kumar, “Analytical Solutions to One—Dimensional Advection—Diffusion Equation with Variable Coefficients in Finite Domain,” Journal of Earth System Science, Vol. 118, No. 5, 2009, pp. 539-549. doi:10.1007/s12040-009-0049-y

