Journal of Water Resource and Protection
Vol. 1 No. 4 (2009) , Article ID: 757 , 11 pages DOI:10.4236/jwarp.2009.14030
Optimal Extraction of Groundwater in Gaza Coastal Aquifer
1Environment Quality Authority, Al-Naser Street, Gaza-Palestine
2 Department of Mineral Engineering, Ecole Mohammadia d’Ingénieurs, Université Mohammed V-Agdal,
Agdal, Morocco
3 Department of Civil Engineering, Ecole Mohammadia d’Ingénieurs, Université Mohammed V-Agdal,
Agdal, Morocco
4 Faculty of Science, Université Abdelmalek Essaadi, Tangier, Morocco
5 Department of Civil Engineering, University of Mississippi, University, USA
E-mail: kqahman@gmail.com; {larabi, ouazar}@emi.ac.ma;
naji@dns1.fstt.ac.ma; acheng@olemiss.edu
Received June17, 2009; revised July 13, 2009; accepted September 10, 2009
Keywords: Seawater Intrusion, Genetic Algorithm, Pumping Optimization, Density-dependent Miscible Transport
ABSTRACT
Two multi-objective management models are applied on a local area selected from the regional Gaza coastal aquifer. The objectives and constraints of these management scenarios include maximizing the total volume of water pumped, minimizing the salt concentration of the pumped water, and controlling the drawdown limits. The physical model is based on the CODESA-3D density-dependent advective-dispersive solute transport model. Genetic algorithm is used as the optimization tool. The models are tested on a part of the aquifer ( ) with 9 existing pumping wells located at various depths. The results of the optimization show that the optimization/simulation approach can give better decision if there is enough information to feed to the model. It confirms that the use of the concept of safe yield alone is not enough for sustainable development of the coastal aquifer. It shows that the optimum pumping rate is in the range of 26%–34% of the total natural replenishment. The application shows that the proposed technique is a powerful tool for solving this type of management problems.
) with 9 existing pumping wells located at various depths. The results of the optimization show that the optimization/simulation approach can give better decision if there is enough information to feed to the model. It confirms that the use of the concept of safe yield alone is not enough for sustainable development of the coastal aquifer. It shows that the optimum pumping rate is in the range of 26%–34% of the total natural replenishment. The application shows that the proposed technique is a powerful tool for solving this type of management problems.
1. Introduction
Water is the most precious and valuable natural resource in the Middle East in general and in Palestine (Gaza strip) in particular. It is vital for socio-economic growth and sustainability of the environment. The development of groundwater resources in coastal areas is a sensitive issue, and careful management is required if water quality degradation, due to the encroachment of seawater, is to be avoided. In many cases, difficulties arise when aquifers are pumped at rates exceeding their natural capacity to transmit water, thus inducing seawater to be drawn into the system. Problems can also occur when excessive pumping at certain individual wells lowers the potentiometric surface locally and causes upconing of the interface between fresh water and saline water [1]. To combat these situations, saltwater intrusion management models need to be implemented to design optimal and sustainable groundwater abstraction strategies.
Optimization solutions in saltwater intrusion that consider the existence of transition zone between the freshwater and seawater are relatively few. Das and Datta [2,3] considered the multi-objective management in coastal aquifers that maximized pumping in the freshwater zone, and minimized it in the saline zone, with the pumped salt concentration as a constraint or the third objective. The nonlinear finite difference solution of the densitydependent miscible flow and transport equations was embedded in the management model as constraints. The MINOS optimization solver was used to solve the resulting large-scale problem. Gordon et al. [4] developed a model for the optimal management of a regional (two dimensional) aquifer under salinization. The sources of salinization were from irrigation water, saline waters from faults at the bottom of aquifer, and inflow from adjacent saline water bodies. The objectives were to maximize the volume of water pumped and to minimize the amount of salt extracted. The model was based on a combination of simulation and optimization. The simulation model uses finite element formulation for the flow and upwind Petrov-Galerkin formulation for the transport. The gradients of the state variables (heads and concentrations) with respect to the decision variables (pumping rates) were used in a Bundle-Trust non-smooth optimization procedure to improve the solution. Qahman et al. [5] investigated four examples for the optimal and sustainable extraction of groundwater from a coastal aquifer under the threat of seawater intrusion. The physical model is based on the density-dependent advective-dispersive solute transport model. Genetic algorithm (GA) [6] is used as the optimization tool. The models are tested on a hypothetical confined aquifer with 4 pumping wells located at various depths. These solutions establish the feasibility of simulating various management scenarios under complex three-dimensional flow and transport processes in coastal aquifers for the optimal and sustainable use of groundwater.
In this study, two multi-objective management models of saltwater intrusion was applied on a local area selected from the Gaza coastal regional aquifer and solved using the same approach presented by Qahman et al. [5]. These management schemes for the prevention of saltwater intrusion as proposed here are new for the Gaza aquifer and can be applied to other areas where there is a potential risk of saltwater intrusion. Therefore, the saltwater intrusion management problem presented in this work will give more insight in the planning and future management of the study area.
2. Genetic Algorithm
The GA is used in many engineering fields to seek optimal solutions to complex problems. A number of researchers have demonstrated that the GA can yield significant better results [7,8]. The GA is an optimization technique based on the process of biological evolution. After its introduction by Holland [9], it has gained popularity in many fields. For water resources, the GA has been applied to problems such as pipe network optimization [10], groundwater parameter determination [11], and groundwater cleanup [12,13]. A review of the GA technique in water resources applications is given by Ouazar and Cheng [14].
Goldberg [6] stated that genetic algorithms are different from other optimization and search procedures in the following aspects:
1. GA works with a coding of the parameters set, not the parameters themselves.
2. GA searches from a population of points, not a single point.
3. GA uses payoff (objective function) information, not derivatives or other auxiliary knowledge.
4. GA uses probabilistic transition rules, not deterministic rules.
In this work, a FORTRAN version of a genetic algorithm driver is adopted. The program initializes a random sample of individuals to be optimized. The selection scheme is a tournament competition with a shuffling technique for choosing pairs for mating. The genetic operators used include jump mutation, creep mutation, and the option of single-point or uniform crossover. Niching (sharing) and an option for the number of children per pair of parents have been added.
Linkage of simulation model to optimization model. An important part of this methodology is the linkage between the optimization model and the 3D variable density seawater intrusion model. Basically, an iterative procedure is followed in which GA tests new decision variables (pumping rates) for feasibility and optimality. The objective function and constraints are functions of the state variables (heads and concentrations). These values are obtained from the CODESA- 3D model. The model simulates the water movement in the aquifer, taking into account different forcing inputs such as pumping rates, and computes the heads and concentrations. The objective function calculated using the heads and concentrations are then optimized in the GA procedure.
3. Study Aquifer
The real world problem is addressed in a particular study area, selected from the coastal aquifer of the Gaza Strip. The area is intruded by saltwater with the current interface (transition zone) position located near the existing pumping wells. The selected area is located in the northeast of Wadi Gaza and is parallel to the coastline, as shown in Figure 1.
This part of the aquifer is considered unconfined, homogeneous and isotropic with respect to freshwater hydraulic conductivities, molecular diffusion, and longitudinal and transverse dispersivities. The aquifer system is subjected to seawater intrusion along the sea face boundary and a uniformly distributed lateral flow along the inland face. It is a problem of steady state saturated flow and transport in three dimension domain. The geometry and boundary conditions are shown schematically in Figure 2a. The dimensions of the aquifer are 2000 m in length, 2000 m in width parallel to sea face, and about 100 m in average thickness. The domain is discretized using three dimensional grid ( , and
, and ). The simulation code divides each rectangular cell into
). The simulation code divides each rectangular cell into

Figure 1. Location of the selected area for optimization.
two triangles to have tetrahedral elements. The flow boundary conditions consist of impermeable border along the bottom of the computational domain and recharge boundary along the top of the aquifer. The bottom side wall is also impervious for diffusive solute fluxes. Hydrostatic pressure is assumed along the vertical boundary of the sea side. The aquifer is charged with freshwater at constant flux from the inland side. At the inland side the concentration is zero (freshwater condition), while at the coastal side the relative concentration of seawater is imposed for a height of 80 m from the aquifer bottom. Initial conditions of heads and solute concentrations throughout the domain are taken from the results of the regional 3-D seawater intrusion model done in previous work [1]. Existing pumping locations (in plan view) are identified with number 1 through 9, as shown in Figure 2b. The screened portions of the well are at different vertical levels as shown.
The simulation parameters for the problem are given in Table 1. Table 2 shows the annual abstraction from the existing wells.
4. The Formulation of Optimization Problems
In groundwater management, the concept of the so called safe yield has been used for several decades by hydrogeologists all over the world to establish the limits of pumpage from a groundwater basin. Traditionally, it has been defined as the attainment and maintenance of a long-term balance between the amount of groundwater withdrawn annually and the annual amount of recharge [15]. Thus, it limits the pumpage to the amount that is replenished naturally through precipitation and surface-water seepage. Because the concept of safe yield ignores the discharge from the aquifer by evapotranspiration
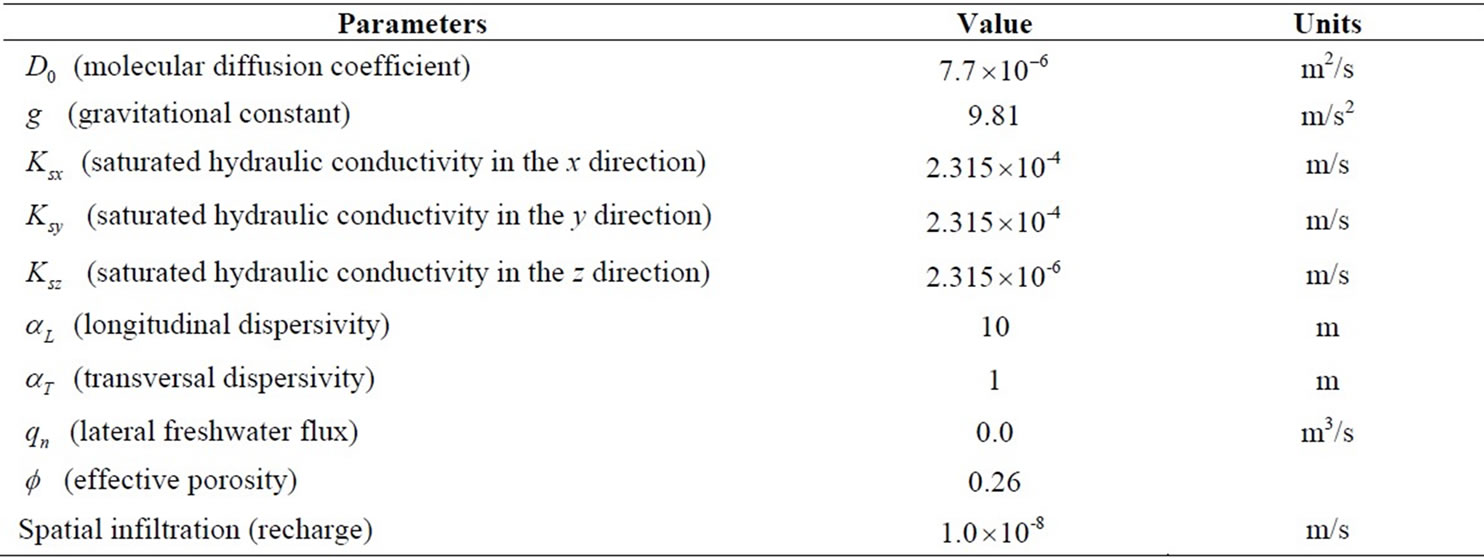
Table 1. Simulation parameter of the aquifer.

Table 2. Annual abstraction from the existing wells.
or into streams, seeps, and springs, groundwater management policies based upon it ended up with some unintended consequences, such as drying up of streams, springs and wetlands with loss of ecosystems, contamination of groundwater by polluted streams. When withdrawals exceeded the recharge on a continual basis, eventual depletion of the aquifers can lead to seawater intrusion. This has happened in a number of places in the world, including the Gaza Strip. Thus, aquifer development based upon the concept of safe yield is not safe and sustainable, as pointed out by Sophocleous [15,16] and Bredehoeft [17].

Figure 2a. Schematic elevation description of the aquifer with the projected well screens locations at the proper layer.
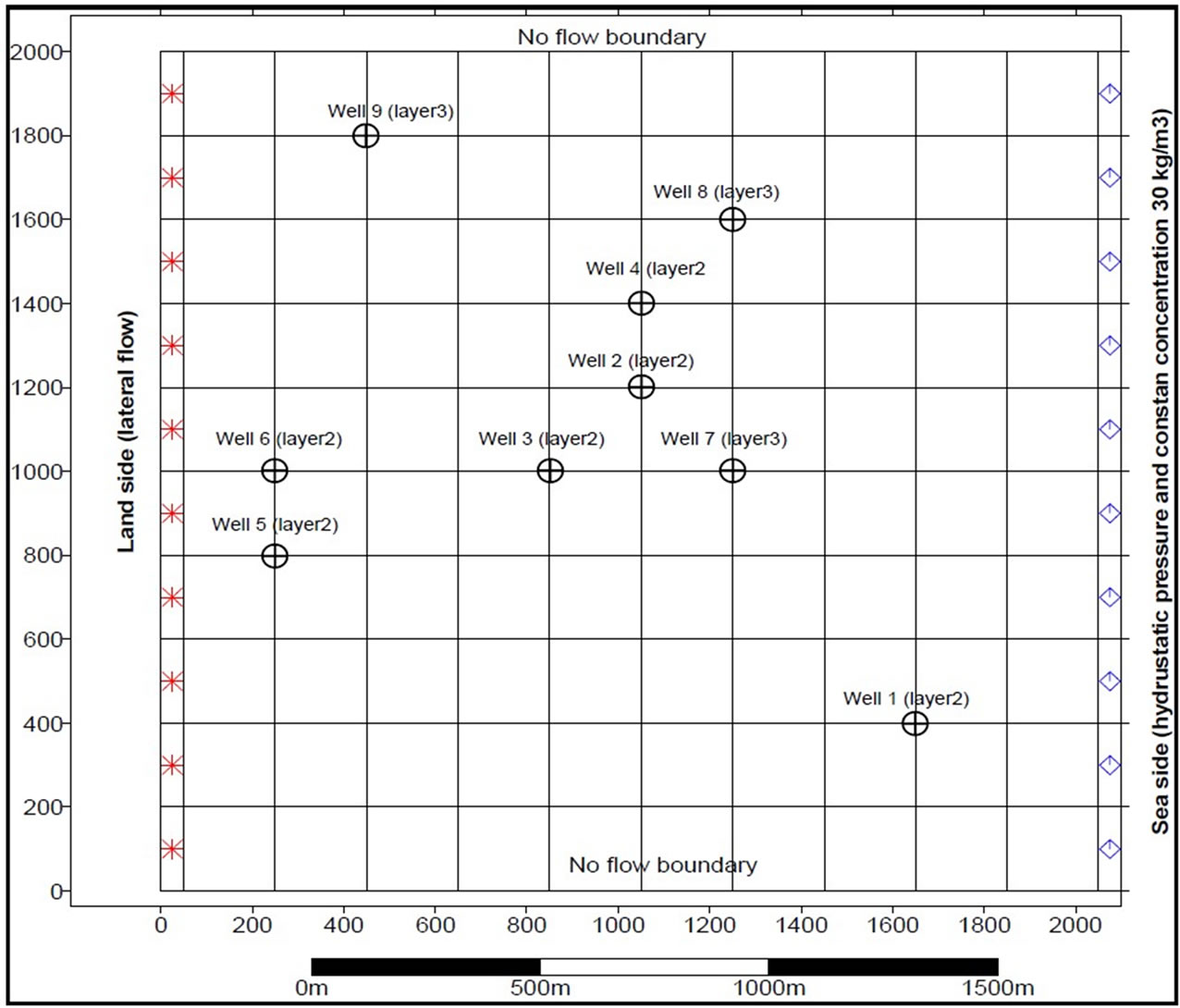
Figure 2b. Schematic Plan-view description of the aquifer with the pumping well locations.
As first elucidated by Theis [18] and eloquently reiterated by Bredehoeft et al. [19], Bredehoeft [17,19], Sophocleous [15,16] and Alley et al. [20], the source of water for pumpage is supplied by 1) increased or induced recharge, 2) decreased discharge or capture, and 3) removal of water from groundwater storage or some combinations of these three. For a sustainable groundwater development, the rate of removal of water from storage should be zero and the pumpage must be balanced by the induced recharge and/or decreased discharge [17]. Thus, it becomes mandatory to evaluate the amount of water available from changes in groundwater recharge, discharge, and storage for different levels of groundwater development. Furthermore, there is always a trade-off between the size of groundwater development and the changes that will occur in the surface and subsurface environment (i.e. changes in base-flow conditions, declines in groundwater reserves and water levels, salinity concentrations etc.). Hydrogeologists should be able to evaluate these changes and present them in a form that can be easily understood by the public and decision makers [21].
In this section we examine two management scenarios with different objectives and constraints, and find the optimal solutions for them. This study was conceived on the basis of a desire to establish a management policy for the sustainable development and management of part of the Gaza Strip aquifer system. To that end, it was envisaged to achieve the following objectives:
·Evaluation of a development strategy that will protect this part of the Gaza aquifer in terms of quantity and quality for continued use by future generations·To determine the safe and sustainable yields and the limits of utilization for this part of aquifer system by establishing trade-off curves between alternatives from which decision makers may select optimum development strategy.
To achieve these objectives the multi-objective management models (model 1 and model 2) of the aquifer system will be applied to this case of the Gaza aquifer. The full description of these models is presented in the previous work [5] and only the final mathematical representations are given as follows:
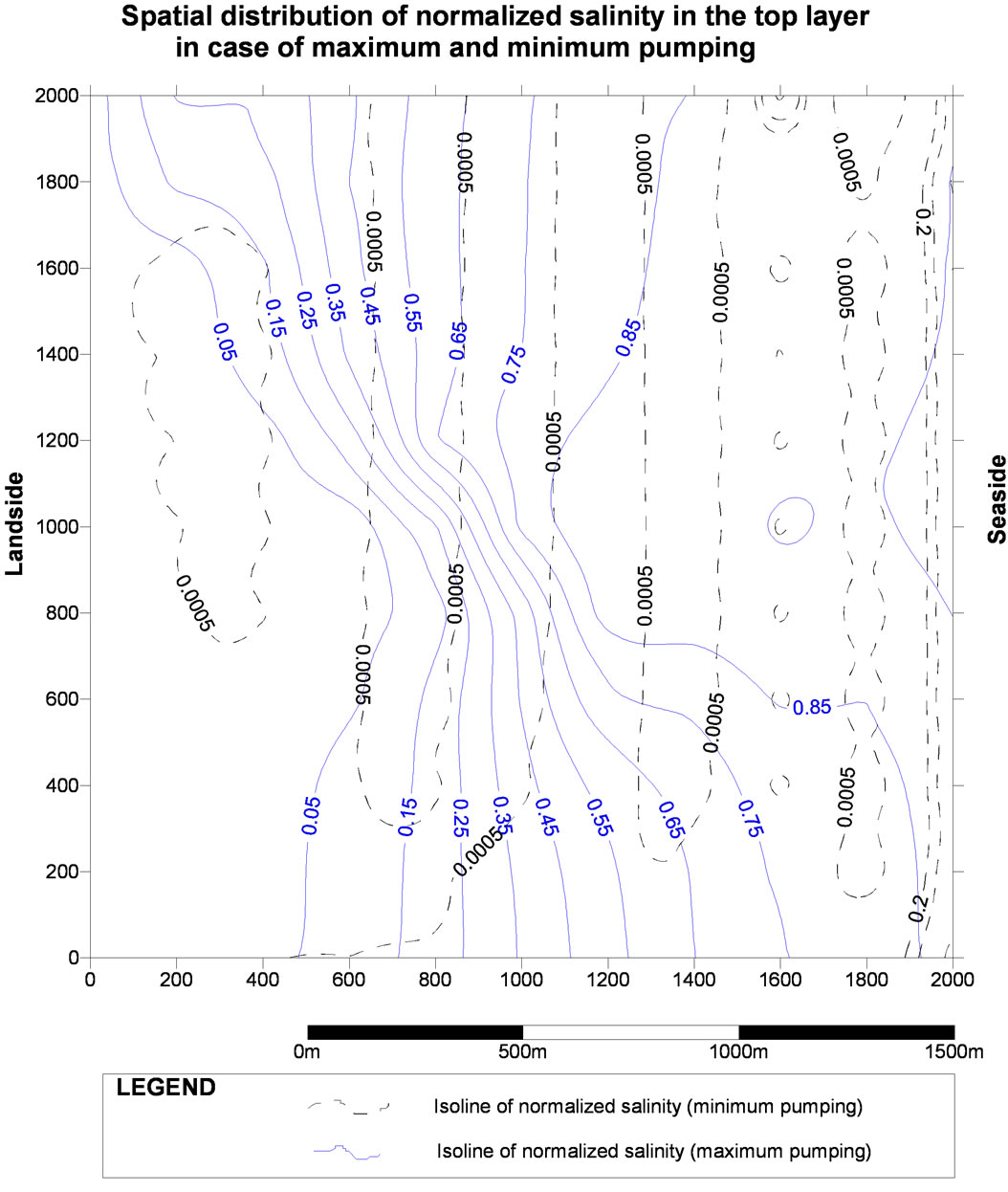
Figure 3. Simulated normalized concentration in layer 1 in case of minimum and maximum pumping.
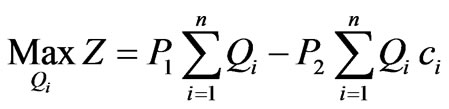 (model 1)
(model 1)
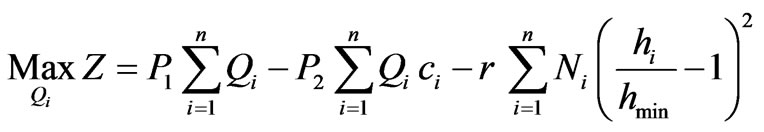 (model 2)
(model 2)
For both models, the discharge of each pumping well should stay within the specified limits; the aquifer safe yield (S) divided by the number of pumping wells (Q max =S/n) for the upper limit and no pumping (Qmin=zero) for the lower limit. This constraint is automatically satisfied by definition of population space in GA.
4.1. GA Parameters Determination
In order to specify the limits of the management models constraints (salinity), the upper and lower limits have to be determined before using the optimization process. The lower limit of the maximum salinity level (Cmax) is a solution with no water withdrawal; while the upper limit is a solution with maximum water withdrawal which is assumed to be equal the safe yield of the aquifer divided by the number of pumping wells as described previously. The results of simulation using the above mentioned conditions for steady state using the CODESA-3D (COupled variable DEnsity and SAturation 3-Dimensional model) [22,23], without optimization are shown in Figure 3. It shows the spatial distribution of normalized concentrations in layer 1 in case of no pumping and also in case of maximum pumping (total recharge/number of pumping wells) for each well, which is 0.004 m3/sec for each well and for a total of 0.036 m3/sec (3,110 m3/day=1,135,296 m3/yr). This amount of maximum pumping is about 4 times the current pumping in its maximum case (790 m3/day = 288,190m3/yr) as presented in Table 2.
In the GA optimization, there are 9 decision variables, representing the 9 pumping rates. The GA is applied using the following parameters: population size=5; maximum generations parameter is determined according to the optimization results, when the fitness value is not changed by increasing the number of generations; and the values of crossover and mutation probabilities are 0.02 and 0.5, respectively. Table 3 summarized the GA parameters used in the management models.
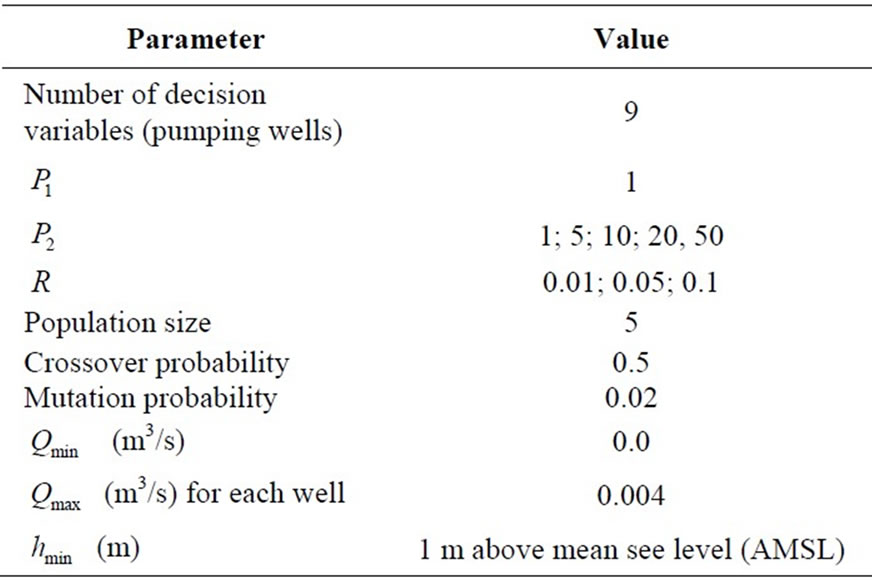
Table 3. Summary of the parameters used in solving the management models.
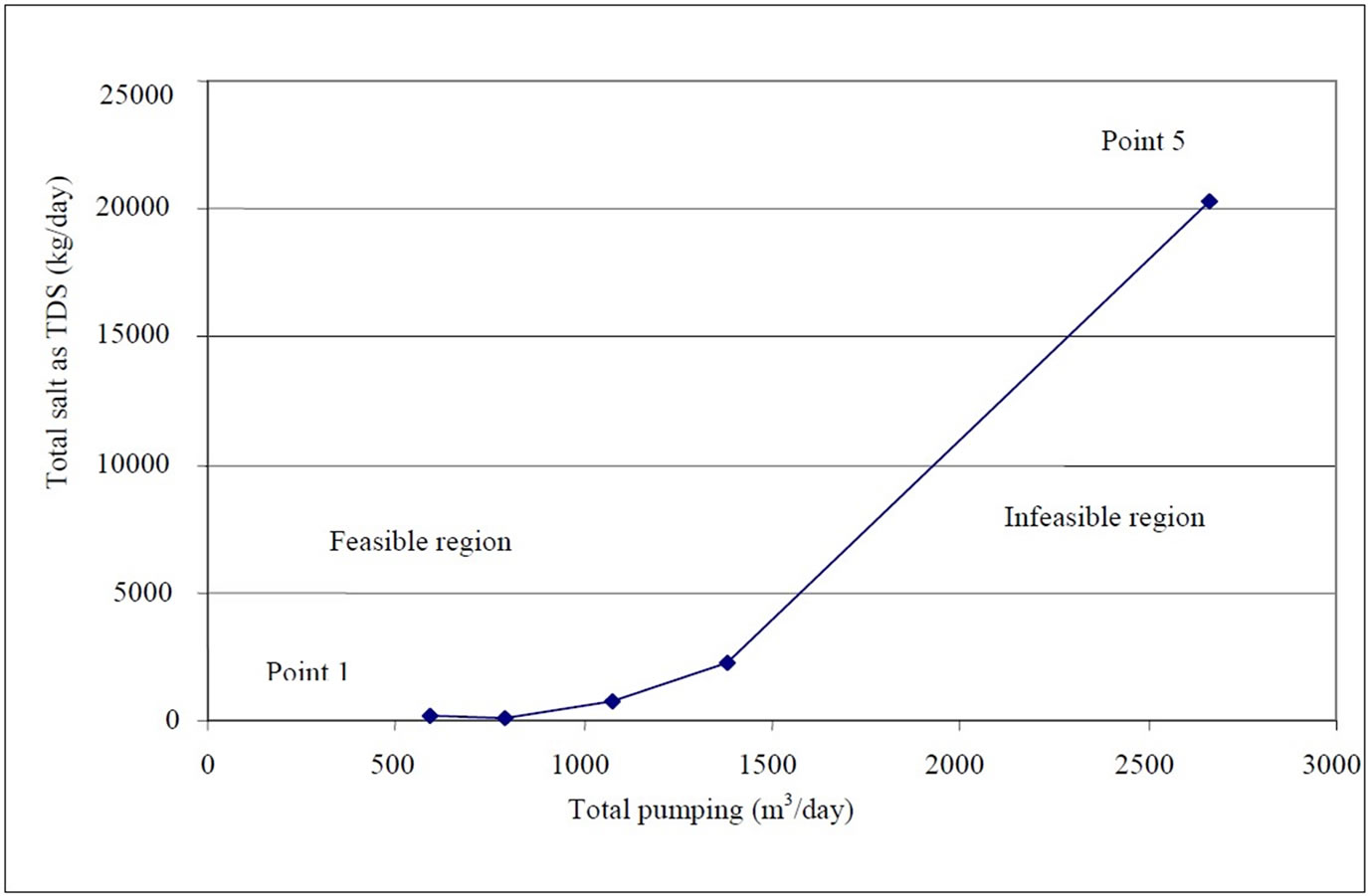
Figure 4. Two-objective trade-off curve (Model 1).
5. Results of Application of Management Model 1
The trade-off between the two objectives of maximizing pumping and minimizing extracted salts was investigated by combining them into a single objective, and then changing the relative weights parametrically to generate the trade-off curve shown in Figure 4. The results of optimal strategies and maximum concentration at the pumping wells are presented in Table 4.
As seen in Figure 4 and Table 4, the increase of pumped water amounts also increases the salt mass pumped from the aquifer because of the need to pump water from wells with higher salinity. One way of interpreting the results in Figure 4 is as follow. Between points 4 and 5 the pumping increases by 1279 m3/d,

Table 4. Results of optimal pumping rates and chloride concentration (Model 1).

Table 5. Results for three optimal solutions of Model 1.

Figure 5a" target="_self">Figure 5a. Hydraulic head distribution (meters AMSL) for point 4 of the trade-off curve.

Figure 5b" target="_self">Figure 5b. Concentration distribution (normalized) for point 4 of the trade-off curve.
while the total amount of salt increases by 180,062 kg/d. This corresponds to an average additional salinity of the added water of 4,013 mg/l, which corresponds to the slope of the trade-off curve between point 4 and 5.
At point 5 the weight of salt mass objective (P2=1), which depends on concentration, is small, so the total pumping is at its maximum value and pumping rates are high even at wells with high salinity. Thus the increase of the pumping from 1379.6 m3/d (point 4) to 2658.7 m3/d (point 5) (a rise of 93%) results in an increase of salt mass extracted by a factor of 9. For other points the changes are less drastic.
The most interesting points are probably around the middle of the curve, where the trade-off between the two objectives is significant. One of these points (point 3) is presented in Table 5. The optimal strategy for this case is to pump more at wells of low salinity, almost not to pump at wells of very high salinity and sensitive ones like well 6 and well 9, and gradually decrease pumping rates with an increase in salinity of the water pumped. The total abstracted amount is 1077 m3/d with average chloride concentration of 491 mg/l.
Figure 5a presents the hydraulic head distribution in layer 1 for the optimum solution of the trade-off curve at point 4 (Figure 4). It is clear from this figure that the increased pumping draws the head down near wells 2, 3, 4, 7, and 8, which are very close to each others.
Figure 5b presents the distribution of normalized concentration in layer 1 for the optimum solution of point 4 of the trade-off curve. Again, the figure shows that the salinity concentration is the highest near wells 5, 6, and 9 because they are very close to the coastline. Also the salinity contours are relatively high near wells 2, 3, 4, 7 and 8 because they are very close to each others and together draw a large amount of water.
6. Results of Application of Management Model 2
This model is introduced with more constraint on the hydraulic head in order to prevent unfavorable drop in water level due to groundwater abstraction. The results of solution of model 2 with the constraint of minimum head (hmin) of 1m AMSL are presented in Table 6 and Figure 6.
One way of interpreting the result in Table 6 and Figure 6 is as follows. Between points 2 and 4 the pumping increases by 323.7 m3/d, while the total amount of salt increases by 1559 kg/d. This corresponds to an average additional salinity of the added water of 655 mg/l, which is the slope of the trade-off curve between point 2 and 4.

Table 6. Results for optimal solutions (Model 2).
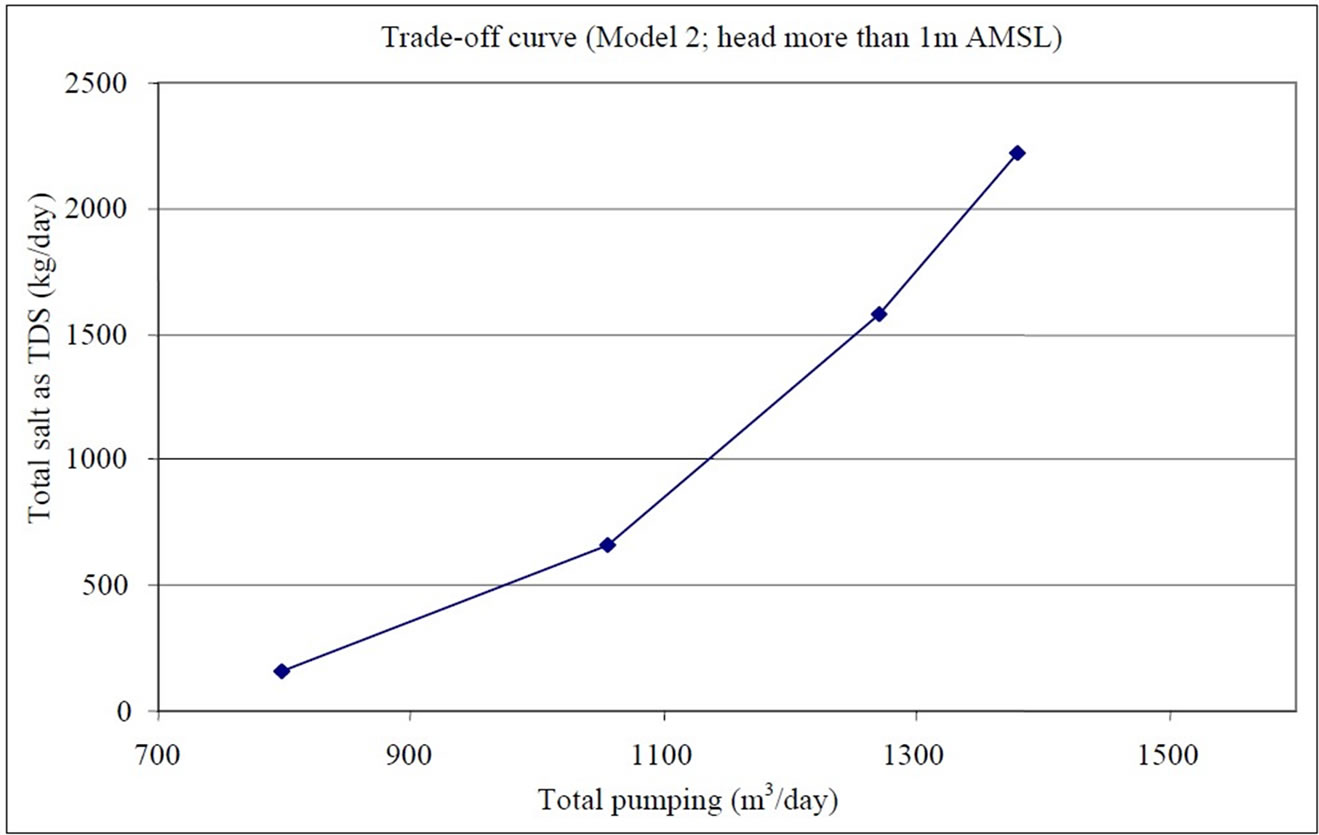
Figure 6. Two-objective trade-off curve (Model 2).
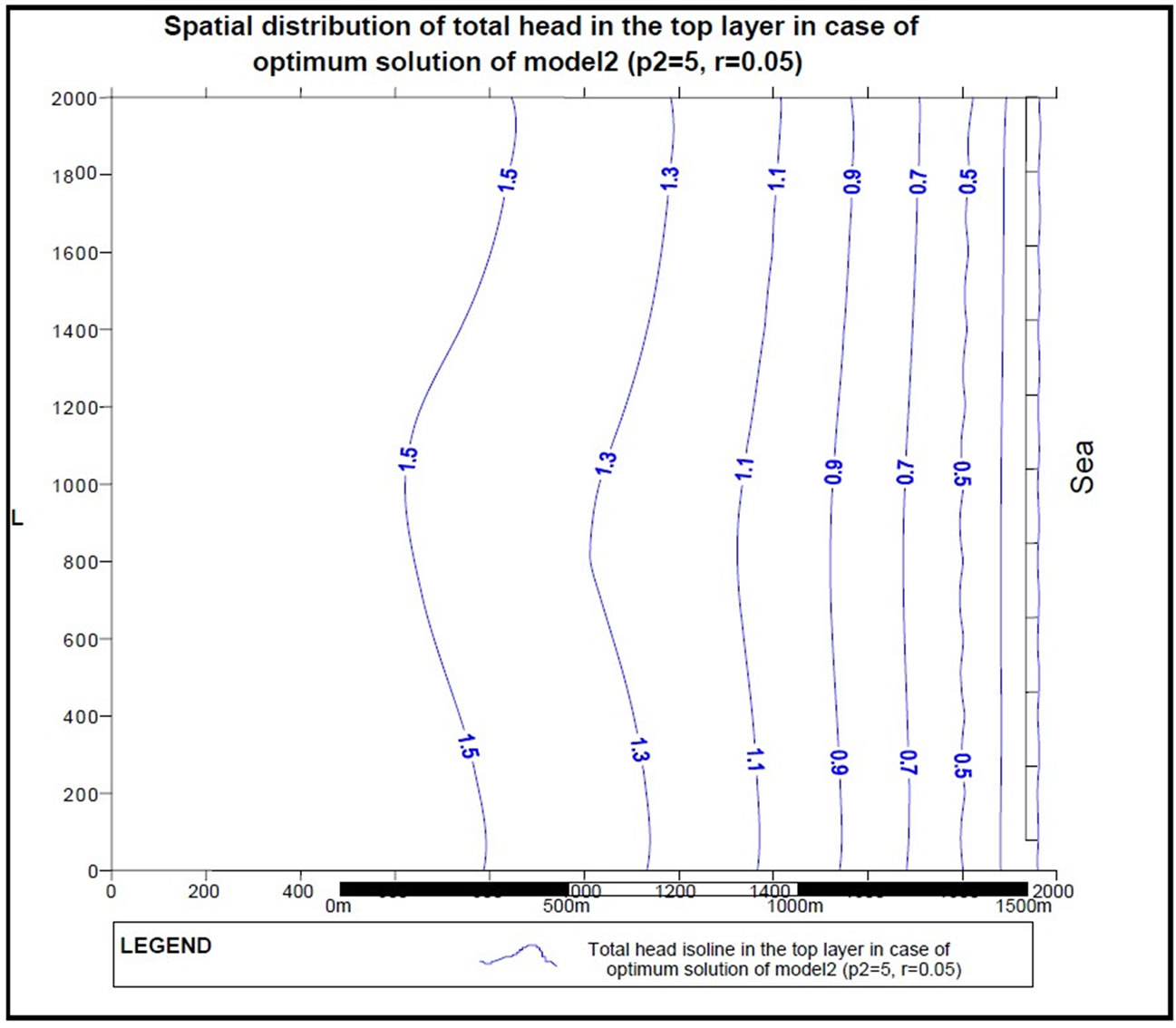
Figure 7a. Hydraulic head distribution (m AMSL) for optimum solution of model 2.
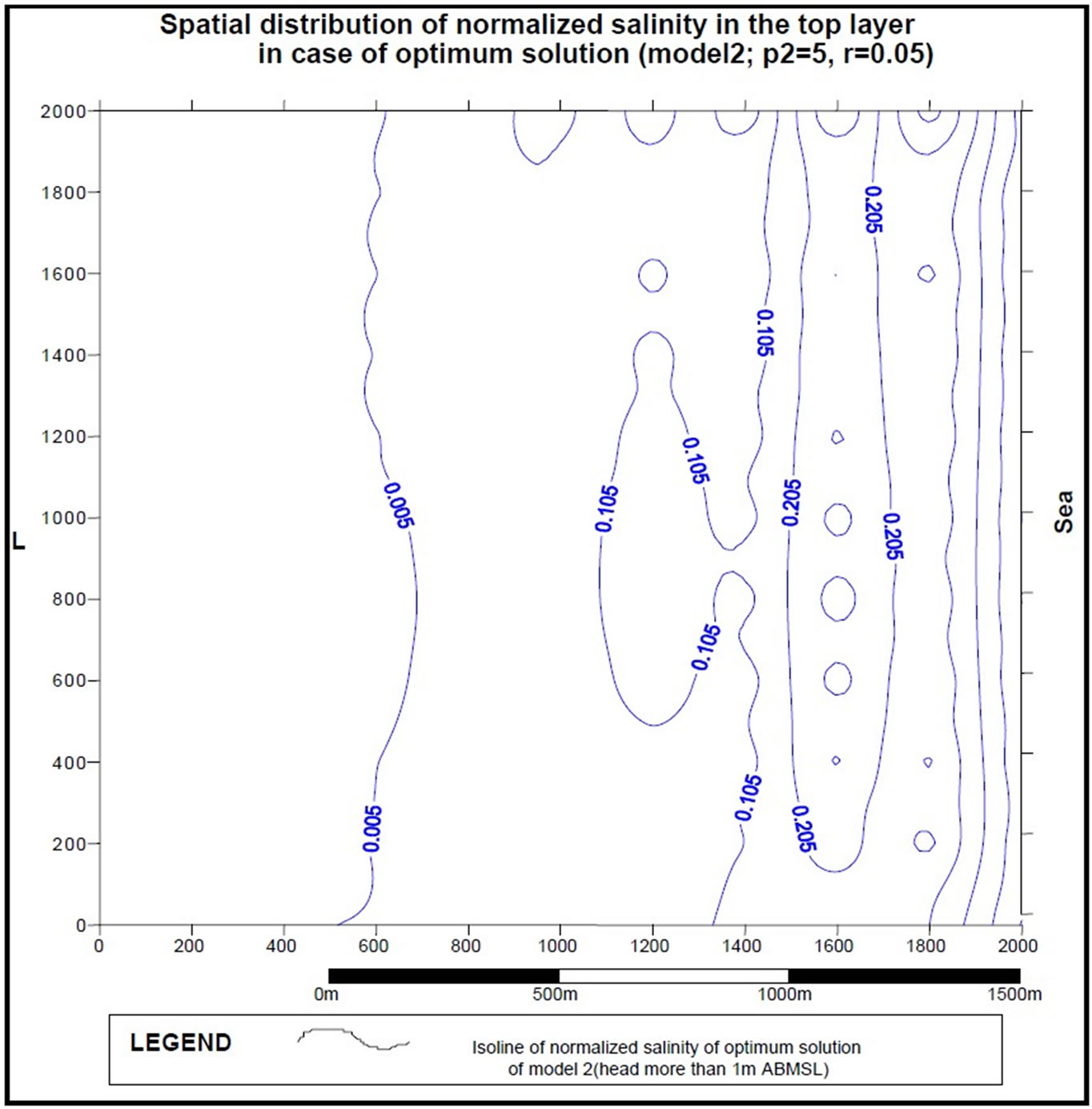
Figure 7b. Concentration distribution (normalized) for optimum solution of model 2.
Figure 7a presents the hydraulic head distribution in layer 1 for the optimum solution of model 2 with minimum head 1 m AMSL and penalty (r) of 0.05. It is clear from this figure that there is an outflow from the aquifer to the coastline boundary. Also, the major flow direction is towards the sea similar the case of no pumping.
Figure 7b presents the distribution of normalized concentration in layer 1 for the optimum solution of model 2 with minimum head 1 m AMSL and penalty (r) of 0.05.
7. Summary and Conclusions
This study presented the numerical solution of maximum pumping rate of wells located in seawater invaded coastal aquifer in the Gaza Strip. Two multi-objective management models with different objective functions are formulated and solved for sustainable exploitation of groundwater from coastal aquifer. The simulation optimization approach links the 3D simulation model with the GA optimization model.
The application to the Gaza aquifer shows that the optimization/simulation approach can assist the managers to make better decisions and to improve the planning and management policies. It confirms that the use of the concept of safe yield alone is not enough for sustainable development of the coastal aquifer. The results on this part of Gaza aquifer show that the optimum pumping rate according to model 2 is in the range of 26%–34% of the total natural replenishment.
A relatively small size problem involving a 3D aquifer with 9 pumping wells at various depths is solved. The size of the problem is only limited by the computing resources of a Pentium 4 microcomputer. If a higher computing capability is used, optimization in a regional groundwater basin with miscible salt transport might be feasible. The present management objectives are based on the sustainability of long term operation; hence only steady state conditions are examined. For short term goals, transient objectives and transient simulations are needed. In the present models, we assumed the certainty of aquifer data. In a real-world situation, aquifer data can contain a large degree of uncertainty. This factor is not yet considered in the present study. These and other improvements will be considered in future studies.
8. Acknowledgements
David L. Carroll is gratefully acknowledged for the use of his genetic algorithms driver in this study. CRS4-Italy kindly provided the CODESA-3D code. This work was conducted on behalf of Gaza Islamic University, Palestine and Ecole Mohammadia d’Ingénieurs, Université Mohammed V, Morocco within the framework of the SWIMED project under contract number ICA3- CT2002-10004 funded by EU. The second and last author’s participation is also supported by the U.S. National Science Foundation grant OISE-0422868 “Optimal groundwater models for sustainable management of coastal aquifers.” The encouragement of the program director Dr. Osman Shinaishin for this international cooperation is deeply appreciated.
REFERENCES
- K. Qahman and A. Larabi. “Evaluation and numerical modeling of seawater intrusion in the Gaza aquifer (Palestine),” Hydrogeology Journal (in press), 2005a.
- A. Das, and B. Datta, “Development of multi-objective management models for coastal aquifers,” J. Water Resour. Plann. Manage., Vol. 125, pp. 76–87, 1999a.
- A. Das and B. Datta, “Development models for sustainable use of coastal aquifers,” J. Irrig. Drain. Eng., Vol. 125, pp. 112–121, 1999b.
- E. Gordon, U. Shamir, and J. Bensabat, “Optimal extraction of water from regional aquifer under salinization,” J. Water Resour. Plann. Manage. Vol. 127, pp. 71–77, 2001.
- K. Qahman, A. Larabi, D. Ouazar, A. Naji, and A. H.-D. Cheng, “Optimal and sustainable extraction of groundwater in coastal aquifers,” Stochastic Environmental Research and Risk Assessment Journal, Vol. 19, No. 2, pp. 99–110, 2005b.
- D. E. Goldberg, “Genetic algorithms in search, optimization and machine learning,” Addison-Wesley-Longman, Reading, Mass, 1989.
- C. Huang and A. S. Mayer, “Pump-and-treat optimization using well locations and pumping rates as decision variables,” Water Resour Res, Vol. 33, pp. 1001–1012, 1997.
- D. C. McKinney and M. Lin, “Genetic algorithms solution of groundwater management models,” J. Water Resour. Res., Vol. 30, pp. 1897–1906, 1994.
- J. Holland, “Adaptation in natural and artificial systems,” University of Michigan Press, Ann Arbor, 1975.
- D. Halhal, G. A. Walters, D. Ouazar and D. A. Savic,
- “Water network rehabilitation with structured messy genetic algorithm,” J. Water Resours. Plann. Manage, Vol. 123, pp. 137–146, 1997.
- H. K. El, D. Ouazar, G. A. Walters and A.H.-D. Cheng, “Groundwater optimization and parameter estimation by genetic algorithm and dual reciprocity boundary element method,” Eng. Anal. Boundary Elem., Vol. 124, pp. 129–139, 1998.
- A. H. Aly and P. C. Peralta, “Comparison of a genetic algorithm and mathematical programming to the design of groundwater cleanup systems,” Water Resour. Res., Vol. 35, pp. 2415–2425, 1999a.
- A. H. Aly and P. C. Peralta, “Optimal design of aquifer cleanup systems under uncertainty using a neural network and a genetic algorithm,” Water Resour. Res., Vol. 35, pp. 2523–2532, 1999b.
- D. Ouazar and A.H-D. Cheng, “Application of genetic algorithms in water resources,” In: Katsifarakis KL (ed) Groundwater Pollution Control, WIT Press, Boston, pp. 293–316, 1999.
- M. Sophocleous, “Managing water resources systems: Why safe yield is not sustainable,” Ground Water, New York, NY, Vol. 35, No. 4, 1997.
- M. Sophocleous, “From safe yield to sustainable development of water resources: The Kansas experience,” Journal of Hydrology, Vol. 235, pp. 27–43, 2000.
- J. D. Bredehoeft, “The water budget myth revisited: Why hydrogeologist’s model,” Ground Water, Vol. 40, No. 4, pp. 340–345, 2002.
- C. V. Theis,. “The source of water derived from wells: Essential factors controlling the response of an aquifer to development,” Civil Eng., Vol. 10: pp. 277–280, 1940.
- J. D. Bredehoeft, S. S. Papadopulos and H. H. Jr. Cooper, “The water budget myth,” In: Scientific Basis of Water Resource Management, National Academy Press, Studies in Geophysics, pp. 51–57, 1982.
- W. M. Alley, T. E. Reilly and O. L. Frank “Sustainability of groundwater resources,” US Geological Survey Circular 1186, 1999.
- J. Sakiyan and H. Yazicigil, “Sustainable development and management of an aquifer system in western Turkey,” Hydrogeology Journal, Vol. 12, pp. 66–80, 2004.
- G. Gambolati, M. Putti , and C. Paniconi, “Three-dimensional model of coupled density-dependent flow and miscible transport in groundwater,” Chap. 10 in Seawater Intrusion in Coastal Aquifers: Concepts, Methods, and Practices, (eds.) Bear et al., Kluwer, Dordrecht, The Netherlands, pp. 315-362, 1999.
- G. Lecca, “Implementation and testing of the CODESA- 3D model for density-dependent flow and transport problems in porous media,” CRS4-TECH-REP-00/40, Cagliari, Italy, 2000.

