Journal of Software Engineering and Applications
Vol.10 No.05(2017), Article ID:76505,25 pages
10.4236/jsea.2017.105025
Tree Automata for Extracting Consensus from Partial Replicas of a Structured Document
Maurice Tchoupé Tchendji, Milliam M. Zekeng Ndadji
Department of Mathematics and Computer Science, Faculty of Sciences, University of Dschang, Dschang, Cameroon
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 14, 2017; Accepted: May 23, 2017; Published: May 26, 2017
ABSTRACT
In an asynchronous cooperative editing workflow of a structured document, each of the co-authors receives in the different phases of the editing process, a copy of the document to insert its contribution. For confidentiality reasons, this copy may be only a partial replica containing only parts of the (global) document which are of demonstrated interest for the considered co-author. Note that some parts may be a demonstrated interest over a co-author; they will therefore be accessible concurrently. When it’s synchronization time (e.g. at the end of an asynchronous editing phase of the process), we want to merge all contributions of all authors in a single document. Due to the asynchronism of edition and to the potential existence of the document parts offering concurrent access, conflicts may arise and make partial replicas unmergeable in their entirety: they are inconsistent, meaning that they contain conflictual parts. The purpose of this paper is to propose a merging approach said by consensus of such partial replicas using tree automata. Specifically, from the partial replicas updates, we build a tree automaton that accepts exactly the consensus documents. These documents are the maximum prefixes containing no conflict of partial replicas merged.
Keywords:
Structured Documents, Workflow of Cooperative Edition, Merging Partial Replicas, Conflict, Consensus, Tree Automata, Automata Product, Lazy Evaluation

1. Introduction
A significant proportion of documents handled and/or exchanged by appli- cations has a regular structure defined by a grammatical model (DTD: Document Type Definition, schema [1] ): they are called structured documents. The ever- increasing power of communication networks in terms of throughput and security, as well as efficiency is concerned, has revolutionized the way of editing such documents. Indeed, to the classical model of an author, editing locally and autonomously his document, was added the (asynchronous) cooperative editing in which, several authors located on geographically distant sites, coordinate to edit asynchronously a same structured document (Figure 1): it is an asyn- chronous cooperative editing workflow.
In such editing workflows (Figure 2), the desynchronized editing phases in which each co-author edits on his site his copy of the document, alternate with the synchronization-redistribution phases in which the different contributions (local replicas) are merged (on a dedicated site) into a single document, which is then redistributed to the various co-authors for the continuation of the edition. This pattern is repeated until the document is completely edited.
In the literature, there are several cooperative editing systems offering, for some, a concurrent collaborative edition of the same document (Etherpad [2] , Google Docs [3] , Fidus Writer [4] , …), or on the other hand, a truly distributed and asynchronous edition (Wikis [5] [6] , Git [7] [8] , …) in which the co-authors work on replicas of the document; replication techniques as well as recon- ciliation strategies must then be addressed. If the collectively edited document is structured, it may in some cases be desirable for reasons of confidentiality, for example, a co-author has access only to certain information, meaning that he only has access to certain parts of the document belonging to certain given types (sorts1) of the document model. Thus, the replica 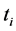 edited by co-author
edited by co-author
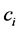 from the site i may be only a partial replica of the (global2) document t, obtained via a projection operation, which conveniently eliminates from global
from the site i may be only a partial replica of the (global2) document t, obtained via a projection operation, which conveniently eliminates from global
Figure 1. The desynchronized cooperative editing of partial replicas of a structured document.
Figure 2. An orchestration diagram of an asynchronous cooperative editing workflow.
document t parts which are not accessible to the co-author in question. We call “view” of a co-author, the set of sorts that he can access [9] . Figure 1 is an illustration of such a cooperative edition in which, the edition and the merging of the (global) document in conformity to the (global) model G of documents are perform on site 1; while on site 2 and 3, other co-authors perform the edition of the partial replicas in accordance with projected models of documents 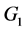 and
and 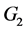 obtained from the global model G.
obtained from the global model G.
When asynchronous local editions are done on partial replicas, it can be assumed that each co-author has on his site a local document model guiding him in his edition. This local model can help to ensure that for any update 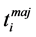 of a partial replica
of a partial replica 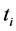 (conform to the considered (local) model), there is at least one document t conform to the global model so that
(conform to the considered (local) model), there is at least one document t conform to the global model so that 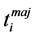 is a partial replica of t: for this purpose, the local model should be coherent towards the global one3. Thus,
is a partial replica of t: for this purpose, the local model should be coherent towards the global one3. Thus,
because of the asynchronism of the editing, the only inconsistencies that we can have when the synchronization time arrives are those from the concurrent edition of the same node4 (in the point of view of the global document) by several co-authors: the partial replicas concerned are said to be in conflict. This paper proposes an approach of detection and resolution of such conflicts by consensus during the synchronisation-redistribution phase, using a tree auto- maton said of consensus, to represent all documents that are the consensus of competing editions realised on the different partial replicas.
A structured document t is intentionally represented by a tree that possibly contains buds5 [9] (see Figure 3). Intuitively, synchronizing or merging consens-
ually the updates  of n partial replicas of a document t, consists in finding a document
of n partial replicas of a document t, consists in finding a document 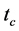 conform to the global model, integrating all the nodes of
conform to the global model, integrating all the nodes of 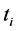 not in conflict and in which, all the conflicting nodes are replaced by buds. Consensus documents are therefore the largest prefixes without conflicts in merged documents. The algorithm of consensual merging presented in this paper is an adaptation of the fusion algorithm presented in [9] which does not handle conflicts. Technically, the process for obtaining the documents forming part of the consensus is: 1) for each update
not in conflict and in which, all the conflicting nodes are replaced by buds. Consensus documents are therefore the largest prefixes without conflicts in merged documents. The algorithm of consensual merging presented in this paper is an adaptation of the fusion algorithm presented in [9] which does not handle conflicts. Technically, the process for obtaining the documents forming part of the consensus is: 1) for each update 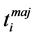 of a partial replica
of a partial replica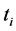 , we associate a tree automaton with exit states
, we associate a tree automaton with exit states 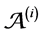 recognizing the trees (conform to the global model) for which
recognizing the trees (conform to the global model) for which  is a projection [9] . 2) The consensual automaton
is a projection [9] . 2) The consensual automaton 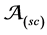 generating the consensus documents is obtained by perfor- ming a synchronous product of the automata
generating the consensus documents is obtained by perfor- ming a synchronous product of the automata 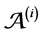 with a commutative and associative operator noted
with a commutative and associative operator noted 


In the subsequent sections, after the presentation (Section 2) of some concepts and definitions related to the cooperative editing and tree automata, we expose (Section 3) the construction process of the operator 
Figure 3. An intentional representation of a docu- ment containing buds.
2. Structured Cooperative Edition and Notion of Partial Replication
2.1. Structured Document, Edition and Conformity
In the XML6 community, the document model is typically specified using a
Document Type Definition (DTD) or a XML Schema [1] . It is shown that these DTD are equivalent to (regular) grammars with special characteristics called XML grammars [10] . The (context free) grammars are therefore a generalization of the DTD and on the basis of the studies they have undergone, mainly as formal models for the specification of programming languages, they provide an ideal framework for formal study of the transformations involved in XML technologies. That’s why we use them in our work as tools for specifying the structure of documents.
We will therefore represent the abstract structure of a structured document by a tree and its model by an abstract context free grammar; a valid structured document will then be a derivation tree for this grammar. A context free grammar defines the structure of its instances (the documents that are conform to it) by means of the productions. A production, generally denoted 


Definition 1. A abstract context free grammar is given by 






For certain treatments on trees (documents) it is necessary to designate precisely a particular node. Several indexing techniques exist, among them, the so-called Dynamic Level Numbering [11] based on identifiers with variable lengths inspired by the Dewey decimal classification (see Figure 4). According to this indexing system, a tree can be defined as follows:
Definition 2. A tree whose nodes are labelled in an alphabet 













Let t be a document and 
Figure 4. Example of an indexed tree.












There is a bijective correspondence between the set of derivation trees of one grammar and all its Abstract Syntax Tree (AST). In an AST, nodes are labelled by the names of the productions.
Definition 3. The set 






AST are used to show that a given tree labelled with grammatical symbols is an instance of a given grammar.
A structured document being edited is represented by a tree containing buds (or open nodes) which indicate in a tree, the only places where editions (i.e.
updates) are possible7. Buds are typed; a bud of sort X is a leaf node labelled by












When we look at the productions of a grammar, we can notice that each sort is associated with a set of productions. From this point of view, therefore, we can consider a grammar as an application

which associates to each sort a list of pairs formed by a production name and the list of sorts in the right hand side of this production. Such an observation suggests that a grammar can be interpreted as a (descending) tree automaton that can be used for recognition or for the generation of its instances.
Definition 4. A (descending) tree automaton defined on 




・ An element of R is denoted 



・ If 



One can interpret a grammar 








To obtain the set 






















As for automata on words, one can define a synchronous product on tree automata to obtain the automaton recognizing the intersection, the union, …, of regular tree languages [13] . We introduce below the definition of the synchronous product of k tree automata whose adaptation will be used in the next section for the derivation of the consensual automaton.
Definition 5. Synchronous product of k automata:
Let 





2.2. Notions of View, Projection, Reverse Projection and Merging
2.2.1. View, Associated Projection and Merging
The derivation tree giving the (global) representation of a structured document edited in a cooperative way makes visible the set of grammatical symbols of the grammar that participated in its construction. As we mentioned in Section 1 above, for reasons of confidentiality (accreditation degree), a co-author mani- pulating such a document will not necessarily have access to all of these gram- matical symbols; only a subset of them can be considered relevant for him: it is his view. A view 

A partial replica of t according to the view





Practically, a partial replica is obtained via a projection operation denoted



Figure 5. Example of projections made on a document and partial replicas obtained.
Let’s note 






2.2.2. Partial Replica and Reverse Projection (Expansion)
The reverse projection (also call the expansion) of an updated partial replica 






A solution to this problem using tree automata is given in [9] ; in that solution, productions of the grammar 
















The interested reader may consult [9] for a more detailed description of the process of associating a tree automaton with a view and Appendix A for an illustration.
3. Reconciliation by Consensus
3.1. Issue and Principle of the Solution of Reconciliation by Consensus
There are generally two distinct phases when synchronizing replicas of a document [14] : the updates detection phase which consists of recognizing the different replica nodes (locations) where updates have been made since the last synchronization, and the propagation phase which consists in combining the updates made on the various replicas to produce a new synchronized state (document) for each replica. In an asynchronous cooperative editing workflow of several partial replicas of a document, when you reach a synchronization point, you can end up with unmergeable replicas in their entirety as they contain
not compatible updates12 they must be reconciled. This can be done by ques- tioning (cancelling) some local editing actions in order to resolve conflicts and result in a coherent global version said of consensus.
Studies on reconciling a document versions are based on heuristics [15] insofar as there is no general solution to this problem. In our case, since all editing actions are reversible13 and it is easy to locate conflicts when trying to merge the partial replicas (see Section 3.2), we have a canonical method to eliminate conflicts: when merging, we replace any node (of the global document) whose replicas are in conflict by a bud. Thus, we prune at the nodes where a conflict appears, replacing the corresponding sub-tree with a bud of the ap- propriate type, indicating that this part of the document is not yet edited: the documents obtained are called consensus. These are the maximum prefixes without conflicts of the fusion of the documents resulting from the different expansions of the various updated partial replicas. For example, in Figure 8, the parts highlighted (blue backgrounds) in trees (f) and (g) are in conflict; they are replaced in the consensus tree (h) by a bud of type C (node labelled
The problem of the consensual merging of 

Problem of the consensual merging: Given k views 









The solution that we propose to this problem stems from an instrumenta- lization of that proposed for the expansion (Section 2.2.2). Indeed, we use an associative and commutative operator noted 



states of the automata





previously indicated (Section 2.2.2):
erator

3.2. Consensus Calculation
Before presenting the consensus calculation algorithm, let us specify using the concepts introduced in Section 2.1 the notion of (two) documents in conflict. Let 


















Figure 6. Example of documents in conflict.

Figure 6 shows two conflicting documents. In fact, at address 2.1 we have two nodes of the same type (“C”) but edited with different C-productions: pro- duction 

3.2.1. Consensus among Multiple (Two) Documents
Let 







Figure 7 present the document resulting from the consensual merging of the
Figure 7. Document resulting from the consensual merging of the documents in Figure 6.
documents in Figure 6. We have prume at the level of nodes 2.1 in both do- cuments who are in conflict.
When






Definition 6. Let 






3.2.2. Construction of Consensus Automaton
Consideration of documents with buds requires the readjustment of some models. For example, in the following, we will handle the tree automata with exit states instead of tree automata introduced in definition 4. Intuitively, a state q of an automaton is called an exit state if there is a unique transition 

A tree automata with exit states 






A type for automata with exit states can be defined in Haskell [16] [17] by:
In Section 3.2.1 above, we said that, when two nodes are in conflict, “they appear in the consensus tree as a (unique) bud”. From the point of view of automata synchronization, the concept of “nodes in conflict” is the counterpart of the concept of “states in conflict” (as we specify below) and the above extract is reflected in the automata context by “when two state are in conflict, they appear in the consensus automaton in the form of a (single) exit state”. Thus, if we consider two states of the same type 








This can be coded in Haskell by the following function:
If X is the type of two states q and 


The operator 


・ Its states are vectors of states :
・ its initial state is formed by the vector of initial states of different automata:
・ For the exit function , it is considered that when a given automaton 




・ Its transitions are given by:
a) If 

b) Else
b1) 


b2)
a) reflects the fact that if a state q is an exit one, we associate a single transition for generating a tree reduced to a bud of the type of q (see listing “Consensus Listing” below, line 11).
With (b1) we say that, if the component 










Consensus Listing
Proposition 7. The tree automaton 




Proof. A tree t is recognized by the synchronized automaton 














since a state of 

Conversely, suppose


Suppose that t is recognized by





















3.3. Illustration
Figure 8 is an illustration of an asynchronous cooperative editing process generating partial replicas (Figure 8(c) and Figure 8(e)) in conflict19 from the grammar having as productions:

Initially in the process, two partial replicas (Figure 8(b) and Figure 8(d)) are obtained by projections of the global document (Figure 8(a)). After their update (Figure 8(c) and Figure 8(e)) a synchronization point is reached and, by applying the approach described in Section 3.1 i.e, association of tree automata 




Figure 8. An edition with conflicts and corresponding consensus.
generation of consensus trees (Figure 8(h)). Remember that this example is fully unfold in Appendix A: therein, we present the different manipulated automata and a set of the simplest consensus documents (Figure 9).
4. Conclusions
We presented in this paper a reconciliation approach said by consensus, of partial replicas of a document submitted to an asynchronous cooperative editing process: so we opted for a partial optimistic replication approach [12] . The approach proposed is based on a relaxation of the synchronous product of auto- mata to construct an automaton capable of generating consensus documents.
The approach proposed in this paper is supported by mathematical proofs of the proposals. The presented algorithms have been implemented in Haskell [16] and experienced in many examples (including the one introduced in Section 3.3 and fully unfold in Appendix A) with convincing results. These algorithms can be also experienced in a truly distributed environment via the graphical editor prototype that we have built for this need; some screenshots are provided in Appendix B.
The deployment and use of this prototype will probably be better off if one incorporates a publishing environment generator which, from a specification of an asynchronous cooperative editing process describing in a DSL (Domain Specific Language) [19] , the model of licit documents (grammar), various co- authors, their publishing sites and views, etc., will generate for each co-author her dedicated publishing environment including, for example, among others: a dedicated editor with conventional facilities of currents editors (syntax high- lighting, code completion, etc.), tools for asking synchronizations, tools for back- up and restoration of partial replicas being edited etc.
Cite this paper
Tchendji, M.T. and Ndadji, M.M.Z. (2017) Tree Automata for Extracting Consensus from Partial Rep- licas of a Structured Document. Journal of Software Engineering and Applications, 10, 432-456. https://doi.org/10.4236/jsea.2017.105025
References
- 1. W3C. eXtensible Markup Language (xml) (2000) W3C Recommendation 1.0. 2nd Edition.
http://www.w3.org/TR/2000/REC-xml-20001006 - 2. Official Site of the Open Source Version of Etherpad.
http://www.etherpad.org/ - 3. Official Site of Google Docs.
https://docs.google.com/ - 4. Wilm, J. and Frebel, D. (2015) Real-World Challenges to Collaborative Text Creation. Proceedings of the 2nd International Workshop on (Document) Changes: Modeling, Detection, Storage and Visualization, New York, 1-4.
- 5. Ward Cunningham (2014) Wikiwikiweb History.
http://c2.com/cgi/wiki?WikiHistory - 6. Wikimedia. Wikipedia: The Free Encyclopedia That Anyone Can Edit.
https://en.wikipedia.org/ - 7. Scott Chacon. Official Site of Git.
https://git-scm.com/ - 8. Wikipédia. git—Wikipédia.
https://fr.wikipedia.org/wiki/git - 9. Badouel, E. and Tchoupé, M. (2008) Merging Hierarchically Structured Documents in Workflow Systems. Electronic Notes in Theoretical Computer Science, 203, 3-24.
- 10. Berstel, J. and Boasson, L. (2000) Xml-Grammars. In: Nielsen, M. and Rovan, B., Eds., Mathematical Foundations of Computer Science 2000. MFCS 2000. Lecture Notes in Computer Science, Vol. 1893, Springer, Berlin, Heidelberg, 182-191.
- 11. Timo, B. and Erhard, R. (2004) Supporting Efficient Streaming and Insertion of XML Data in RDBMS. 3rd International Workshop on Data Integration over the Web, 8 June 2004, Riga, Latvia, 70-81.
- 12. Saito, Y. and Shapiro, M. (2005) Optimistic Replication. ACM Computing Surveys, 37, 42-81.
- 13. Comon, H., Dauchet, M., Gilleron, R., Lugiez, D., Tison, S. and Tommasi, M. (2005) Tree Automata Techniques and Applications. Draft.
http://www.grappa.univ-lille3.fr/tata/ - 14. Balasubramaniam, S. and Pierce, B.C. (1998) What Is a File Synchronizer? Proceeding of 4th International Conference on Mobile Computing and Networking (MOBICOM), ACM/IEEE, Dallas, TX, 25-30 October 1998, 98-108.
https://doi.org/10.1145/288235.288261 - 15. Mens, T. (2002) A State-of-the-Art Survey on Software Merging. IEEE Transactions on Software Engineering, 28, 449-462.
https://doi.org/10.1109/TSE.2002.1000449 - 16. Haskell, A Purely Functional Language.
http://www.haskell.org - 17. Davie, A. (1992) An Introduction to Functional Programming Systems Using Haskell. Cambridge University Press, Cambridge.
- 18. Maurice Tchoupé, T. (2009) Une approche grammaticale pour la fusion des réplicats partiels d’un document structuré: Application à l’édition coopérative asynchrone. Thèse de Doctorat/PhD, Université de Rennes I/Université de Yaoundé I, Rennes/Yaoundé.
- 19. Van Deursen, A., Klint, P. and Visser, N.D.J. (2000) Domain-Specific Languages: An Annotated Bibliography. ACM SIGPLAN Notices, 35, 26-36.
https://doi.org/10.1145/352029.352035
Appendix A. An Illustration of the Merging Algorithm
We illustrate the consensual merging algorithm with the grammar of Section 3.3 (formula 8). We associate the automata 




Linearization of a Structured Document
To simplify the presentation, we represent in the following, trees by their linearization in the form of a Dyck word. To do this, we associate a (various) pair of brackets to each grammatical symbol and the linearization of a tree is obtained by performing a Depth First Search (DFS) of the resulting tree.
The Transition Schemas for the View {A, B}
A list of trees (forest) is represented by the concatenation of their lineari- zations.We use the opening parenthesis “(‘and the closing one’)” to represent Dyck symbols associated with the visible symbol A and the opening bracket “[” and closing “]” to represent those associated with the visible symbol B. Each transition of the automata associated to partial replicas according to the view 

These schemas are obtained from the grammar productions [9] and the pairs 















Figure 9. Consensual trees generated from the automaton
Construction of the Automaton 
Having associated Dyck symbols “(‘and’)” (resp. “[‘and’]”) to the grammatical symbol A (resp. B), the linearization of the partial replica 





The state 



Construction of the Automaton 
As before, by associating to the grammatical symbol C (resp. A) the Dyck symbols “[‘and’]” (resp. “(‘and’)”), we obtain the transition schemas (formula 10) for the automata associated to the partial replicas according to the view

The linearization of the partial replica 


Table 1. Automaton accepting updates of the (partial) replica tv1.
initial state 
Let’s note that, the state 

Construction of the Consensus Automaton
By application of synchronous product of several tree automata described in Section 3.2.2 to the automata 















The states 




The use of function that generates the simplest AST (with buds) of a tree language from its automaton [9] on
Appendix B. A Prototype of a Cooperative Editor Using Our Algorithms
We present below some screenshots of the cooperative editor prototype for graphic and cooperative editing of the abstract structure of structured do-
Table 2. Automaton accepting updates of the (partial) replica tv2.
cuments using our algorithms for consensus merging of edited partial replicas.
This prototype is used following a networked client-server model. Its user interface offers to the user facilities for creating workflows: grammars, actors and views, initial document, … (Figure 10), editing and validation of partial replicas, connecting to a local or remote workflow (Figure 11). Moreover, this interface also offers him functionality to experience the concepts of projection, expansion and consensual merging (Figure 12). This prototype is designed using Java and Haskell languages.
Table 3. The consensus automaton.
Figure 10. Some prototype screenshots showing windows for the creation of a cooperative editing workflow.
Figure 11. Some prototype screenshots showing the authentication window of a co-author (Auteur1) as well as those displaying the different workflows, local and remote in which he is implicated.
Figure 12. An illustration of the consensual merging in the prototype.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jsea@scirp.org
NOTES
1A sort is a datum used to define the structuring rules (syntax) in a document model. Example: a non-terminal symbol in a context free grammar, an ELEMENT in a DTD.
2We designate by global document or simply document when there is no ambiguity, the document including all parts.
3Intuitively, a local model of document is coherent towards a global model if any (partial) document ti that is conform to it, is the partial replica of at least one (global) document t conform to the global model.
4Manipulated documents are structured; they can be intentionally represented by a tree. Intuitively, a node is an identifiable part in the document (a section, a subsection, an image, a table, …): it is the instance of a sort.
5A bud is a leaf node of a tree indicating that an edition must be done at that level in the tree. Edit a bud consists to replace it by a sub-tree using the productions of the grammar of the document.
6XML is the acronym for Extensible Markup Language.
7We are interested in this paper only in the positive edition, based on a partial optimistic replication [12] of edited documents; In fact, the published documents are only increasing: there is no erasure possible as soon as a synchronization has been performed.
8Reminder: 


9A synchronization point can be defined statically or triggered by a co-author as soon as certain properties are satisfied.
10It may happen that the edition must be continued after the merging (this is the case if there are still buds in the merged document): we must redistribute to each of the n co-authors a (partial) replica 


11
12This is particularly the case if there is at least one node of the global document accessible by more than one co-author and edited by at least two of them using different productions.
13Reminder: the editing actions made on a partial replica may be cancelled as long as they do not have been incorporated into the global document.
14The binary relation 
15Trees we handle are AST and therefore, the nodes are labelled by productions names. Any node labelled by a X-production is said of type X. Furthermore, there is a function type Node such that type Node (t(w)) returns the type of the node located at the address w in t.
16It may then be noted that two documents (AST) admit no consensus if their roots are of different types. However, for applications that interest us, namely structured editing, since the editions are done from the root (which is always of the type of the axiom) to the leaves using productions, the documents we manipulate always admit at least a consensus.
17The corresponding node in the reverse projection of the document is a bud and reflects the fact that the corresponding author did not publish it. In the case that this node is shared with another co-author who published it in its (partial) replica, it is the edition made by the latter that will be retained when merging.
18Automata 

19By realising expansions of each of the replicas, we respectively obtain among others, the documents presented by Figure 8(f) and Figure 8(g) on which one can easily observe a conflict highlighted by areas having a blue background.
20We do not represent the whole set of transition schemas in this example; only the useful subset for reconciliation of closed documents is shown here because the documents to reconcile in this example are all closed (has no buds). To consider buds, one should, for each visible sort X, associate a new pair of Dyck symbols to the bud of type X then, derive the new schemas.



























