Journal of Software Engineering and Applications
Vol.08 No.10(2015), Article ID:60399,9 pages
10.4236/jsea.2015.810051
Productivity Monitoring of Land Pipelines Welding via Control Chart Using the Monte Carlo Simulation
Pedro Mattos Tabim¹, Miguel Luiz Ribeiro Ferreira²
¹Department of Graduation in Civil Engineering, Federal Fluminense University, Niterói, Brazil
²Mechanical Engineering Department, Federal Fluminense University, Niterói, Brazil
Email: pedro.tabim@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 August 2015; accepted 17 October 2015; published 20 October 2015
ABSTRACT
This article evaluates the efficacy of a tool developed in the Monte Carlo simulation and referred to as control chart. This tool is used in order to detect changes in productivity resulting from the occurrence of a given event during the welding of land pipelines with self shielded flux cored wire (FCAW). The elaboration of this control chart is based on the data from the Cumulative Probability Density Function (CDF) curve, and generated in the Monte Carlo simulation using version 6 of the Palisade Corporation’s @Risk software for Excel, in a sample with productivity data from 29 welded joints, gathered through direct observation which considers the productive and unproductive times. In order to evaluate the control chart efficacy, the performance of welding productivity with a FCAW process with low alloy steels has been assessed during 29 days, summing up to 842 welded joints registered on “Relatórios Diários de Obras” (Construction Works Daily Reports). The results show that the model developed for the control chart elaboration is effective in monitoring the productivity of the observed welding procedure.
Keywords:
Monte Carlo Simulation, Welding, Land Pipelines, Productivity

1. Introduction
Welding is the main productive process in construction works of land pipelines. Thus, the purpose of this paper is to develop a productivity monitoring methodology for the semi-automatic welding process with self shielded flux cored wire (FCAW) process of low alloy steel land pipelines. In this study, productivity data about a sample composed of 29 welded joints at a construction work in the Brazilian Northeast have been gathered in the field by direct observation.
On the gathering of these data, the times of the activities related to the welding productive process and associated downtimes during production have been measured in order to define the welding productivity. The unit used was joints/day, bearing in mind the employment in the land pipeline construction industry [1] . Virtual data and the Cumulative Probability Density Function (CDF) of Welding Productivity (WP), which takes into consideration the productive and unproductive welding times in this construction work, have been generated from actual productivity data of this sample, through Monte Carlo Method and @Risk 6 software.
A control chart for the monitoring of the productivity behavior of welding during construction has been elaborated, inspired by the traditional control charts for statistical processes control and based on the simulation CDF, aiming to detect eventual deviations of the productive process and allowing corrective action taking by the construction management. In order to check the effectiveness of such chart on production deviation detection during the construction work, production data about welded joints have been gathered during 29 days and registered in the Construction Work Daily Reports. We try to identify abnormalities for the days when the productivity is out of the limits established in the control chart.
2. Background Literature
2.1. Productivity Indicators
It is possible to define productivity as the value of the results, being those products or services, divided by the value of goods or resources [2] -[4] . In construction industries [5] , working time quantity is estimated in men- hour to yield a production or service unit. Productivity can be defined as the efficiency on transforming inputs― workforce, materials and equipment―in outputs or construction work product compliant to the required objectives [6] .
The activities that compose the work process are described as: direct or productive work, support work and unproductive work [7] [8] . Another classification [9] , the activities may be categorized in direct work, preparatory work, tools and equipment, material handling, waiting, travel, personal. In this article, direct work comprises welding and grinding activities and all the other activities are considered as nonproductive time. These activities are: wire changing, column positioning, idle time between activities, waiting time and handling of tools. A comparison between the concepts of work activities adopted in this paper with the authors aforementioned is presented in Table 1.
A data survey in a construction work at Duque de Caxias Refinery (REDUC) in Rio de Janeiro state [10] , the total indicators of equivalent joints/day, welding volume in cm3/day and couple joints/day have been considered for welding productivity. The most used method to measure welding productivity in pipeline constructions in the United States consists on the number of completed joints divided by the time span, i.e. the welding process output [1] . The joints/day unit, which is one of the most used indicators in the Brazilian industry in land pipelines construction, has been adopted for this paper.
2.2. Simulation by Monte Carlo Method
The Probability and Density Functions (PDF) and Cumulative Probability Density Function (CDF) curves are compared in order to estimate the welding productivity of carbon steel pipe tops joints achieved through the generation of random numbers via Monte Carlo simulation with parametric distributions from small samples with 10, 15 and 20 elements and the generated results originated from a 160 elements actual sample [11] -[13] .
Table 1. Work activities concept comparative.
As shown in these works, it is possible to determine that the Monte Carlo simulation is a suitable method to assess the welding productivity behavior.
The Monte Carlo simulation employment, according to most authors, consists in five steps: group the gathered data in class intervals in order to generate a frequency histogram; define a distribution for the probability density function, being a random variable that best represents the sample; implement the simulations with N repetitions; assess whether the number of simulations is suitable; after performing the simulations, generate the cumulative probability density function for results analysis [14] . @Risk software allows the modeling of functions and performing Monte Carlo simulations, presenting the simulation results graphically [15] .
The Monte Carlo method consists in generating virtual data from an actual sample. The simulation is useful to achieve a model that imitates the random sample of a population or to perform statistical experiments, but the success of this method depends on the model capacity to reproduce the distribution achieved based on the actual sample data. Whether the parameter uncertainty is defined by technical literature or data gathering, parametric distributions are used and, when it is not possible, non-parametric distributions may be used, such as triangular and uniform ones, with the aid of experts. The use of non-parametric distributions is applicable to the simulation in many segments [16] . The Monte Carlo simulation has many applications with non-parametric distributions. [17] tested and validated the uniform, triangular and Beta (PERT) non-parametric distributions in air, rail and land transportation projects. [18] used the uniform distribution in order to estimate a modern municipal solid waste landfill life, once the quality of the data did not suffice to adjust the parametric distributions. [19] developed a simulation model based on the uniform distribution in order to adjust the heterogeneity of oil production scenarios around the world. [20] applied the triangular distribution in order to select the cementing method type to be used in a construction work due to its ease of use and supported by technical literature on construction planning.
3. Experimental Procedure
3.1. Sample
Two kinds of samples have been used on conducting the study. One was composed of welding data from a real time field gathering consisting of 29 joints by direct observation. The productive and unproductive times have been registered. The productive times correspond to the estimated activities in the welding procedure where the open arc and cleaning by grinding time spans are calculated, taking into consideration the time spans passed on measuring the negligible interpasses temperatures and attributing a zero value. The unproductive time spans are the ones when the welding was in downtime for any reasons. For the joint performance on the root pass the electrode E6010 has been used and for the rib, the consumable E8010-P1. The 2mm diameter flux cored wire E-91T8-G, AWS specification 5.29 [21] , has been used on the four filling and finishing passes.
The welded pipes main characteristics are:
・ Carbon steel API 5L X70 - PSL2;
・ 28 inches or 711.2 millimeters diameter;
・ 0.406 inches or 10.3 millimeters thickness.
The second sample is composed of 842 welded joints production during 29 days, using the same procedure as the sample described in the last paragraph, registered in the Construction Work Daily Report.
3.2. Data Gathering
The field data gathering took place in two steps: phase 1―data gathering during welding in the worksite forming the basis for the Monte Carlo simulation and elaboration of control chart; phase 2―welding productive data registered during 29 production days in the Construction Work Daily Reports.
The field data gathering on phase 1 took place during three workdays, from the beginning to the end of the workday, following monitoring by the welding team in the site where the pipes have been welded. The joint runtimes, which are referred to as production time, and the unproductive times where, for any reason, the welding activity was in a downtime have been registered in this process. The weather in this region was good, sunny and around 25˚C. Accordingly, during the gathering of those data, no exceptional incidence such as rain, strike, accidents, among other incidents have been registered at the worksite. In this sense, it is possible to conclude that the performance conditions were normal.
On the other hand, these data have been gathered taking into consideration that the construction work was in a normal production stage, corresponding to a physical progress above 20%, having already surpassed the learning curve [22] . It is worth highlighting that the runtimes registers concern flux cored arc welding (FCAW) during the joint filling and finishing stages. Runtimes of root passes and rib with coated electrode process have not been considered in this paper.
On conducting this process 5 welding teams, each composed of two welders, two grinders and two helpers, have been monitored. In order to determine the timespan spent on welding each joint, it was required to define all the activities involved in this operation, that are: filler metal deposition, interpasses temperatures determination and cleaning between passes. Between these three activities a runtime has been associated, but the time spent in the interpasses temperatures determination activity was considered negligible and, thus, not measured. Thereby, the runtimes calculated were the ones related to filler metal deposition, referred to as welding time, and cleaning between passes, where the griding method was used and referred to as grinding time. To register the time spent in these activities, timing started on the opening of the welding electric arc in the filling phase and ended on the grinding after the finishing of all the welding passes with FCAW.
On the other hand, the gathering of these data prioritized the largest number of joints welded in a random manner, i.e. not prioritizing specific welders or pipeline stretches, aiming to avoid the influence of certain welders with distinguished skills, who could present a higher or lower performance. Besides the time spans considered productive, which are the welding and grinding times, the times when the workers, for any reason, were stopped and not performing any activity related to the welding process were also registered. The time spent in the start and end of the workday were not considered here. These time spans were considered unproductive in this paper.
A total of 29 welded joints runtimes have been gathered, encompassing the productive and unproductive times. Table 2 presents the statistical parameters of the sample.
The workday at the jobsite stretched from 7 AM to 5 PM. However, it was observed that a given time was spent, on starting the activities, for the mobilization and displacement to the work position of the joint to be welded and for the same movement backwards at the end of the day. In order to calculate these displacement and mobilization times at the start and end of the workday, to be deducted from the hours of working, the minimum, probable and maximum values for the effective start and end of the workday have been attributed. Accordingly, 1 hour for lunch is deducted from the workday. Table 3 presents these times in order to calculate the effective workday.
In order to determine the productivity in joints/day, we have proceeded like the following:
1) Sum of the welding and grinding runtimes and unproductive times;
2) Definition of the effective workday, where we have considered the lunch break and work start and finish times;
3) Definition of the Standard Team;
Table 2. Statistical parameters of the sample runtimes.
Table 3. Start and end times of the effective workday.
4) Definition of the number of team involved in the process;
5) Productivity calculation in joints/day of all teams in the work front.
The calculation of productivity in joints is expressed through the Equation (1) below:
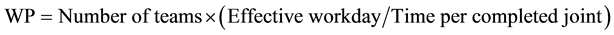 (1)
(1)
・ Welding Productivity (WP): considers the time per completed joint per welding team. This time is the denominator of the division by effective workday, producing the unit joints/day per team. To assess the productivity of the construction work with all teams, it is necessary to multiply it by the number of teams.
・ Effective workday: is the 10 daily hours of working of the studied construction work subtracted from the mobilization and displacement times where the team did not effectively started the service and the 1 hour lunch break.
・ Time per completed joint: is the sum of the opened arc time, grinding time and the unproductive times from the start of the open arc welding until the final grinding of finishing pass, in hours.
・ Joint: top, with a chamfering angle between 60˚ and 64˚, root opening between 2 mm and 2.5 mm. The weld volume deposited by FCAW is 86.7 × 10−3 dm3, calculated in similar procedure as [23] .
・ Welding team: is the composition of the team working to weld a joint. The team of the studied work was composed of 2 welders, 2 grinders and 2 helpers.
・ Number of teams―in the construction work there were 5 welding teams with the same composition.
On phase 2 we aimed at gathering the productivity values in joints/day of the studied work taking into consideration a longer production period. These data have been achieved through registers of the Construction Work Daily Report document, which is used by the contracting party and the contractor to report the main occurrences. The productive data of 29 production days have been gathered following the aforementioned procedures.
3.3. Elaboration of the Productivity Control Chart
Aiming to develop a practical monitoring tool, quick in obtaining results and easy to understand, we chose to develop a control method similar to those based on the general theory of Shewhart’s control chart rules, that esablishes a central limit, to which corresponds the sample mean, and the upper and lower limits adding or subtracting the mean of a k constant multiplied by a sample standard deviation. The control charts quickly detect anomalies in the process, once it is a real time monitoring technique [24] . Although inspired by the control charts already mentioned, the methodology developed in this work adopted its own criteria, which have been considered more suitable for productivity monitoring.
The control chart has been elaborated in the following steps: definition of the productivity model equation; conduction of a Monte Carlo simulation on the productivity model established in the Equation (1) from the productivity data gathered at the worksite via monitoring of the productive runtimes, unproductive times, start and end in order to obtain the CDF curve; definition of the control chart upper and lower limits.
The simulation of the productive model established in the Equation (1) is ran by the version 6 of the Palisade Corporation’s @Risk software for Excel [25] . Figure 1 represents a flow chart of the Monte Carlo simulation to produce the control chart.
The simulation procedure with the Monte Carlo method is conducted as in the following steps:
1st) Definition of the model input data. The input data are: welding time, grinding time, unproductive time, start time, end time, workday time deducted from lunch break, number of teams. The last two items are constant.
2nd) Definition of the output data, which in this case is the Welding Productivity (WP) defined in Equation (1).
3rd) Definition of the generating functions for the following variables: welding time, grinding time, unproductive time, start time and end time.
4th) After the definition of the generating functions and their input in the productivity model, a simulation with the Monte Carlo method is made with 1000 iterations.
5th) After the simulation, it has been verified whether the number of iterations was sufficient through convergence analysis made available by the computing software. In this case the result was positive and we proceeded to the next step. It is worth highlighting that, if the number of iterations was not sufficient, it would be necessary to raise it until a positive analysis of the convergence analysis took place, because, if it is not achieved, it is re-
Figure 1. Flow chart of the simulation.
quired the assessment of the possibility to select another generating function of each variable considered in the productivity model. Otherwise, a non-parametric distribution is used.
6th) Once the previous steps have been conducted, a CDF curve is elaborated and the statistical parameters of the data obtained via simulation calculated.
On defining the generating functions in order to conduct the productivity model simulation, 3 different criteria have been adopted for each activity, taking into consideration the specific characteristics of each of them. Thereby, on defining the generating function of the welding times, a qui-square test, tool available in the @Risk6 software, was used. The function that showed the highest compliance was the Lognormal function for a significance level of 5% with the following main parameters: µ = 747.65 and s = 253.13. Regarding the grinding time, the Weibull function presented the best compliance with the sample data, for a significance level of 5% with parameters α = 2.5198 and β = 645.79.
For unproductive times, it was impossible to adjust the data with a CDF, because there was not compliance in the Qui-square test for any function presented by the version 6 of the @Risk software [25] . In Table 2, it is possible to notice a great value dispersion, resulting in a relevant amplitude between maximum and minimum, elevated dispersion attested by the analysis of the coefficient of variation and a bimodal behavior observed on the analysis of the distribution graph of the data gathered. The coefficient of variation is a meaningful way to determine which variable, in this case unproductive, has great dispersion. The variable with the smaller coefficient of variation, near 0, is less dispersed than the variable near 1.
It has been observed that the unproductive times result from many situations, for example, idleness, consumption materials waiting time, interruptions in order to reposition the tools, among others. In this sense, it has been concluded that the differentiated nature of the generating causes for the unproductive times is the main reason for the heterogeneous behavior in the sample and the difficulty on defining a generating function that would comply with the analyzed sample. Thereby, the solution adopted was to use the uniform distribution as a generating function, which attributes the same occurrence probability for the considered events. This function, which represents the behavior of the unproductive times due to various reasons, has been defined in the interval that corresponds to the minimum of 64 seconds and maximum of 1509 seconds, which respectively correspond to the shortest and longest unproductive time registered in this case.
The triangular function has been defined as generating factor for start and end times, which correspond to the preparations for the start and end of workday activities, taking into consideration the modeling impossibility of these processes. In this case, the main parameters of this distribution are: likely time, minimum time and maximum time, both for the start times and end times, presented in Table 3.
After defining the generating functions of the times considered in the welding process, the Monte Carlo simulation was ran in with the version 6 of the @Risk software for Excel with 1000 iterations, where the CDF and the generated data main statistics were obtained.
On the other hand, in order to define the control chart Lower and Upper Limits, the Probability criterion > 0% was adopted for the first one and Probability < 90% for the second one. These values have been extracted from the CDF curve. The upper limit setting in 90% aims at avoiding the use of data generated in the CDF, where the possibility of a discrepancy between the virtual data generated in a simulation and the ones originating from a real productive process increase. On the other hand, on setting the lower limit in 0%, the minimum positive value obtained in the simulation is attributed to the minimum productivity. We would also like to highlight that a similar criterion was used successfully by [12] .
3.4. Control Chart Effectiveness Test
We gathered the production of welded joints during 29 days in the Construction Work Daily Reports in order to verify the possibility of using the productivity control chart, which has been elaborated with data resulting from real time direct observation and register of the times considered in the welding operation in the workforce. Thereby, the production from each workday in joints/day has been registered and entered in the control chart. In case the productivity registered in a given day was out of both the upper and lower limits of the control chart, it was verified if any incident or occurrence has been registered in the Construction Work Daily Report. A comparison between the construction work productivity CDF curve in joints/day and the curve obtained through simulation, respectively presented in Figure 3 and Figure 4, was conducted to complement this analysis.
4. Results Analysis
From the CDF curve―Figure 2―obtained through simulation built based on direct observation and registration of both productive and unproductive times of the productive process, establishing the 0% quota of the CDF as lower limit corresponding to a productivity of 21 joints/day, 90% of the CDF, equivalent to 49 joints/day and the mean of 39 joints/day have been inserted as control chart limits presented in Figure 3.
The establishment of the upper quota in 90% of the CDF is due to the fact that values near 100% in the curve generated in the simulation present productivity results that do not represent a real productive process. In this article it has been established that this is the maximum value for the welding productivity as it is possible to note in Table 4.
The productivity data from the Construction Works Daily Report gathered during 29 production days have been inserted to assess the Control Chart capacity to detect variations in the welding productivity. Table 5 represents
Figure 2. CDF of the welding productivity indicator.
Table 4. Statistical parameters for the WP simulation.
the statistical parameters originated in the construction report and the result of the simulation. These data have been inserted in the Control Chart presented in Figure 3.
The analysis of Figure 3 shows that 86% of the elements of the productivity measured in the construction work are between the control chart minimum and maximum values and 14% of the elements are below mini- mum. Also, it is possible to notice that most values are below central limit.
During the analysis of the occurrence of points out of the lower limit and tending to be below the simulated mean, logistics problems in the construction work, deformations on the pipes to be welded, among other problems caused by the contractor management malpractices that were affecting the welding performance have been registered in the Construction Work Daily Reports. These problems are due to factors impossible to be encompassed by the experimental data gathering, because they are either special causes or welding process anomalies. From this result it is possible to conclude that this tool is effective on detecting the productivity variations, allowing corrective actions to be taken towards problems. On the other hand, it is possible to notice the effectiveness of the Monte Carlo simulation use in predicting the welding productivity behavior in accor- dance to what [11] -[13] have determined, once this control chart has been built from the CDF generated from the simulation obtained through data gathered by direct observation of the productive process of 29 joints. The evaluation period that encompasses the example of the control chart corresponded to the production of 824 joints registered in the Construction Work Daily Reports. Accordingly, it has been verified that the productivity model adopted in the Monte Carlo simulation, as well as the premises adopted in its building, both in the behavior of the productive times and unproductive times, presented adequate results. This analysis is reinforced when comparing the behavior of the WP obtained through Monte Carlo simulation CDF (Figure 2 and Table 4) and of the 29 days production corresponding sample, registered in the Construction Work Daily Reports (Figure 4 and Table 5).
It is possible to determine that in Figure 2, which presents the CDF built from the simulation based on the 29 joints experimental data gathered through direct observation and measurement of the productive and unproductive times of the productive process, the occurrence probability of the productivity data gathered in the construction work, which vary from 11 to 44 joints/day, is placed around 75%. Figure 4 represents the behavior of the productivity registered in 29 workdays and, in this case, the occurrence probability of the productivity
Figure 3. Control chart.
Table 5. Statistical parameters of 29 days productivity in the construction work.
Source: Construction Work Daily Report.
Figure 4. The welded joints productivity CDF during 29 days in the construction work registered in the CWDR
between the values from 21 to 44 joints/day is around 77%. Thereby, on comparing Figure 2 and Figure 4, it is possible to state that the curve generated in the simulation expresses the behavior of the productive process with reasonable precision.
5. Conclusions
By the results being achieved, it is possible to determine that the CDF curve generates through Monte Carlo simulation from the small samples gathered through direct observation of the productive process represents, with a good precision margin, the productivity of low alloy steels land pipelines welding process with the shielded flux cored wire process in the construction work.
The welding productivity model develops from the worksite welding direct observation with the registration of the productive and unproductive times, as well as the distribution models adopts in it in order to conduct the Monte Carlo simulation and welding productivity CDF building is successful in representing the productivity behavior in the construction work for the welding procedure being studied in this article.
The control chart, built from the CDF generated through a Monte Carlo simulation based on the productivity model and limits established in this work, has proven to be an effective tool on monitoring the welded joints productivity during construction work.
Cite this paper
Pedro MattosTabim,Miguel LuizRibeiro Ferreira, (2015) Productivity Monitoring of Land Pipelines Welding via Control Chart Using the Monte Carlo Simulation. Journal of Software Engineering and Applications,08,539-548. doi: 10.4236/jsea.2015.810051
References
- 1. Miller, C. and Crawford, M.H. (2002) Welding-Related Expenditures, Investments, and Productivity Measurement in U.S. Manufacturing, Construction, and Mining Industries. Technical Report, American Welding Society, Miami.
- 2. Ritzman, L.P. and Krajewski, L.J. (2003) Foundations of Operations Management. 2nd Edition, Prentice Hall, Upper Saddle River.
- 3. Slack, N., Chambers, S. and Johnston, R. (2002) Operations Management. 2nd Edition, Atlas, Sao Paulo.
- 4. Gaither, N. and Frazier, G. (2002) Production and Operations Management. Thomson Learning, Sao Paulo.
- 5. Diekmann, J.E. and Heinz, J. (2001) Determinants of Jobsite Productivity. Construction Industry Institute, Austin.
- 6. de Souza, U.E.L. (2006) How to Increase Labor Efficiency: Productivity Management Manual in Construction. 1st Edition, Pini, Sao Paulo.
- 7. Adrian, J.J. (2004) Construction Productivity: Measurement and Improvement. Stipes Publishing, Champaign.
- 8. Schwartzkoft, W. (2004) Calculating Lost Labor Productivity in Construction Claims. Aspen, Austin.
- 9. Construction Industry Institute (2010) Guide to Activity Analysis. University of Texas, Austin.
- 10. Gioia, A.L.S., Silva Júnior, I.F. (2007) Assessment of Methodology for Productivity Measurement in Pipe Instalation Activity in Industrial Works. Graduation, Monograph, University Federal Fluminense, Niterói.
- 11. Martins, J.L.F. (2011) Application of Simulation with Monte Carlo and Latin Hypercube Methods to Estimate Productivity in the Welding Process of SMAW. PhD Thesis, University Federal Fluminense, Niterói.
- 12. Martins, J.L.F., Ferreira, M. and Saraiva, J.M.F. (2011) Productivity Estimation in Welding by Monte Carlo Method. Soldagem e Inspecao, 16, 204-212.
- 13. Constancio, D.S., Ferreira, M. and Freire, I.J. (2009) Welding Productivity’s Estimate of Industrial Piping, Being Used Monte Carlo’s Method. Proceedings of the XXXV CONSOLDA—Congresso Nacional de Soldagem, Piracicaba, 26-29 Outubro 2009, 26-29.
- 14. Morano, C.A.R. (2003) Application of Risk Analysis Techniques in Construction Projects. Master’s Dissertation, University Federal Fluminense, Niterói.
- 15. Grey, S. (1995) Practical Risk Assessment for Project Management. John Wiley & Sons, Chichester.
- 16. Vose, D. (2000) Risk Analysis: A Quantitative Guide. 2nd Edition, John Wiley & Sons, Chichester.
- 17. Salling, K.B. (2008) Assessment of Transport Projects: Risk Analysis and Decision Support. PhD Thesis, Technical University of Denmark, Lyngby.
- 18. Bieda, B. (2013) Stochastic Approach to Municipal Solid Waste Landfill Life Based on the Contaminant Transit Time Modeling Using the Monte Carlo (MC) Simulation. Science of the Total Environment, 442, 489-496.
http://dx.doi.org/10.1016/j.scitotenv.2012.10.032 - 19. Voudouris, V., Stasinopoulos, D., Rigby, R. and Di Maio, C. (2011) The ACEGES Laboratory for Energy Policy: Exploring the Production of Crude Oil. Energy Policy, 39, 5480-5489.
http://dx.doi.org/10.1016/j.enpol.2011.05.014 - 20. Chou, J. and Ongkowijoyo, C.S. (2015) Reliability-Based Decision Making for Selection of Ready-Mix Concrete Supply Using Stochastic Superiority and Inferiority Ranking Method. Reliability Engineering and System Safety, 137, 29-39.
http://dx.doi.org/10.1016/j.ress.2014.12.004 - 21. AWS A5.29/A5.29M (2010) Specification for Low-Alloy Steel Electrodes for Flux Cored Arc Welding. 4th Edition, American Welding Society, Miami.
- 22. Anzanello, J.M. and Fogliatto, F.S. (2007) Learning Curves: Literature Review and Further Research. Gestao e Producao, 14, 109-123.
http://dx.doi.org/10.1590/s0104-530x2007000100010 - 23. Modenesi, P.J. (2001) Estimation of Welding Costs. University Federal de Minas Gerais.
http://www.infosolda.com.br/images/Downloads/Artigos/industrial/estimativa-dos-custos-de-soldage m.pdf - 24. Montgomery, D.C. and Runger, G.C. (2007) Applied Statistics and Probability for Engineers. 4th Edition, John Wiley & Sons, New York.
- 25. Palisade Corporation (2013) @Risk Users Guide. Version 6, Palisade Corporation, New York.






