Journal of Software Engineering and Applications
Vol. 5 No. 11 (2012) , Article ID: 25118 , 9 pages DOI:10.4236/jsea.2012.511099
Performance Study of a Distributed Web Server: An Analytical Approach*
![]()
1Math and Computer Science, Eastern Connecticut State University, Willimantic, USA; 2Computer Science and Engineering, University of Connecticut, Storrs, USA.
Email: tasneems@easternct.edu
Received July 18th, 2012; revised August 16th, 2012; accepted August 25th, 2012
Keywords: Web server; CSM; Performance modeling; Performance analysis; Distributed systems; Queueing model
ABSTRACT
With the rapid expansion of the Internet, Web servers have played a major role in accessing the enormous mass of Web pages to find the information needed by the user. Despite the exponential growth of the WWW, a very negligible amount of research has been conducted in web server performance analysis with a view to improve the time a Web server takes to connect, receive, and analyze a request sent by the client and then sending the answer back to client. In this paper, we propose a multi-layer analytical approach to study the web server performance. A simple client-server model is used to represent the WWW server in order to demonstrate how to apply the proposed approach. We developed a systematic, analytical methodology to quantify the communication delay and queuing overhead in a distributed web server system. The approach uses the Computation Structure Model to derive server processing time required to process a request sent from a client and queueing model to analyze the communication between the clients and the server.
1. Introduction
With the rapid expansion of the “World Wide Web” and our increasing reliance on the information and services provided by it, indicates that the services must be offered with superior performance to retain the current users and attract new ones. For example online banking, stock exchange, remote surgery, bill payment must be secure, efficient and fast enough to be widely accepted. An essential component of WWW is the Web server which is a large computer and a program responsible to serve the HTTP requests from the clients. The most common form of client is a Web browser. The server responds to the multiple clients by sending Web pages such as HTML documents and linked objects (images, videos, etc.). One of the vital aspects of the Internet business is the performance issue of the Web server.
However, for such a system to function efficiently and cost-effectively requires that the system development be based upon careful performance analysis, because slowness can have far reaching consequences and implications in the Internet-computing. The millions of users surfing the Internet, are unwilling to spend more than few seconds waiting for a Web page to be displayed. The number of requests met per second by a Web server is one of the major metrics to be considered to a high performance Web server system. Because the content of the Web is fluid and sites change frequently, keeping up to date information is challenging [1-3]. In the design of a high performance Web server system the challenge is to keep response-time to a minimum and the generated data as up to date as possible by providing more frequent updates. Response time is calculated from the moment the server receives the request until the client starts receiving the answer back from the server. The shorter the response-time is the better the performance. Despite the popularity of the Web servers, a very negligible number of performance analysis has been done. In this paper, we have reported a partial result of a continuing research which addresses the challenging issue of quantifying the response-time and finally identifying the bottlenecks due to communication and queuing overhead in a distributed Web server system. To keep the response time to a minimum, first, we need to identify the major components of it which is accomplished by applying a systematic, analytical methodology called, Computation System Model (CSM).
In this paper, to analyze the performance of a webserver system, we have modeled a single server with multiple clients as shown in Figure 1. This is a simple
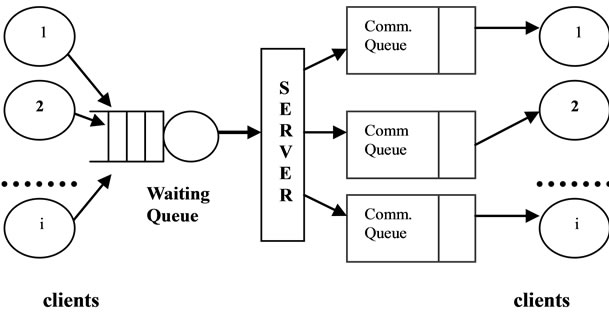
Figure 1. A single server and multiple clients model.
model for the WWW server. Our goal is to show applying our proposed analysis methodology to predict quantitative metrics describing the server performance. Studying a full WWW server is beyond the scope of this paper. The proposed performance analysis is divided into two parts: we used: 1) CSM (Computational Structure Model) to calculate the processing time cost of server processes; and 2) queueing model to study the network architecture, which includes the server’s request handling model. We will analyze the request handling within the server, as well as the communication between the server and the client, etc. At the system level we are interested in determining the time it takes for the server to connect, receive, and analyze a request sent by the client and then sending the answer back to it.
The present paper developed a systematic, analytical methodology to quantify the communication delay and queuing overhead in a distributed web server system.
The CSM derived equations will be used to determine the performance bottleneck which lies in the system architecture.
The paper is organized as follows: In Chapter 2, we discuss the related research. In Chapter 3, we describe the main components of the system architecture. In Chapter 4, we derive the equations to compute the processing time cost (without the communication time) of a request, only, using CSM analysis. In Chapter 5, we derive the response-time equations which include both the processing time as well as the time for communication between the server and the clients. In Chapter 6, we conclude.
2. Related Research
CSM: There are three principal methods for computer performance evaluation and analysis: direct measurement, simulation and analytic modeling. Direct measurement is the most accurate of the methods, but requires the system to be implemented first in order to collect specific performance information. Besides, the motivation of performance engineering is to find the performance bottleneck at the design phrase, so one can avoid an efficient design at the earliest time. Simulations are prototypes of the real system that provide a fairly accurate performance measurement, but are often time consuming and difficult to construct. Analytic modeling which exercises techniques such as queueing networks [1,4], Markov models [4], Perti-nets, state charts and CSM [5-9], is the least expensive because hardware and software do not need to be implemented. It also provides insight into the variable dependencies and interactions that are difficult to determine using other methods. In the present paper we have used the CSM analysis in which during the design phase, one builds a mathematical model to describe the system behavior. Then the performance model equations are derived as a function of different design parameters. The advantage of this model not only lies on the fact that it gives an insight of the software system but also it provides plenty of details. However, the mathematics involved may be complex. Ammar et al. [10] makes use of user model to derive the software optimization. In separate papers Ammar et al. [5] and Qin et al. [11] present techniques for deriving the time cost of parallel computations.
Webserver: With the increased popularity of Web servers, recently Web server performance modeling and analysis has become an active area of research. To the best of our knowledge there is little to no published work that presents a comprehensive analysis of performance for Web server systems. Below we briefly review the previous work on the performance analysis of Web server.
Heidemann et al. [12] present analytical performance models to characterize the interaction of HTTP with several transport protocol layers. Slothouber [13] and Vander Mei et al. [14] both uses queueing model for Web server performance. The later presents an end-to-end queueing model for the performance to study the impact of client workload characteristics, as well as communication protocols and interconnect topologies. Menasce [15] provides a classification of Web server software architectures and studies the pool size behavior using queuing networks approach. Kamra et al. [16] present a theoretical approach to control overload of a 3-tiered Web sites. Liu et al. [17] use a multi-station queuing center to model each of the 3-tiered Web services architecture including the Web, application and database servers. Kant et al. [18] describe a queuing network model based on detailed measurements of a multiprocessor system with static Web workload. Interested readers may refer to Trivedi [19] and Lipsky [4] for further detail about queueing model and its application. Lipsky expresses a systematic approach using queueing models which involves advance mathematics. Wells et al. [20], Gaeta et al. [21], Gvozdanovic et al. [22], Scarpa et al. [23] uses Petri net models for the performance analysis of various features of Web servers. Gokhale et al. [24] propose an analysis methodology based on the Stochastic Reward Net (SRN) modeling paradigm to quantify the performance and the reliability tradeoffs in the process-based and the thread-based Web server software architectures. Kohavi and Parekh [25] offer several useful practical recommendations to improve e-commerce Web sites. Kaaniche et al. [26] illustrates a hierarchical modeling framework to evaluate the availability as well as dependability of an Internet based travel agency. There are also some efforts which consider availability/dependability analysis of a Web server. Merzbacher et al. [27] first present experimentally measured availability results for selected Web sites and services, then propose a new metric for availability.
Hu et al. [28] measure and analyze the behavior of the popular Apache Web [3] server on both a uniprocessor system and a 4-CPU SMP Symmetric Multi-Processor system running the IBM AIX operating system. Their discovery shows that on an average, Apache spends about 20% - 25%, 35% - 50%, and 25% - 40% of the total CPU time, on user code, kernel system calls and interrupt handling, respectively. For systems with small RAM size, the Web server performance is limited to the disk bandwidth. For systems with reasonably large RAM size, the TCP/IP stack and the network interrupt handler are the major performance bottlenecks. They also suggest new performance improvement metric of the Apache Web server. First generation Web crawlers of Google (developed at Stanford), the most popular search engine were implemented in python and distributed in a LAN or WAN reporting to a centralized analysis server that performed all the indexing functionality on the data collected. The hardware given at the time, three Google crawlers were able to collect an average of about 48.5 pages per second while the Indexer was just fast enough to finish analyzing the data before new crawler results arrived [2]. With the development of modern high speed hardware the performance bottleneck of Web crawler system has shifted from hardware processing power to communication network latency and speeds. Crawlers of Mercator [2], another popular search engine, are similar to Google’s, except that they are implemented in Java, instead of Python. In principle, first they fetch a URL from a shared server called the “frontier”, which is then fetched and processed. By distributing the work in hundreds of worker threads in each of the five or more machines, Mercator achieved an impressive crawler page rate of 112 pages per second. By using two processors per machine running at 533 MHz and 2 GB RAM, the bottleneck shifted from processing power to network speed and latency, which in this small setup already averaged at 1682 KB/s. Also, at this point, the DNS lookups became more and more frequent, so local DNS caches were implemented.
UbiCrawler is another Web crawler that incorporates meaningful performance improvements [1] over the past two cases described where the spiders were always controlled by a central instance that coordinated the crawling process. In UbiCrawler’s case, the network line speed was the limit later on. There are several limiting factors such as, communication network delay, to the performance and scalability of complex systems like UbiCrawler yet to be addressed.
A limited amount of research has been done in performance analysis of Web server, and to the best of our knowledge this is the first approach in applying hierarchical CSM modeling technique.
3. System Description
Figure 2 depicts the main functions of the server and the client which are the two major components of the system architecture.
3.1. Server Architecture
A prototype of the server application, which respond to the different requests sent by the client is developed using C language. If the client sends a regular GET message, then the response will be based upon whether the requested file is found in the current directory or not. If yes, the response message contains the status line “HTTP/1.1 200 OK” and the requested file will be included in the message body. If the requested file is not found, then a response message contains the status line “HTTP/1.1 404 Not Found” and an empty body will be sent. If the client sends a conditional GET message, then the response will be based on whether the requested file has been modified since the specified date or not. If
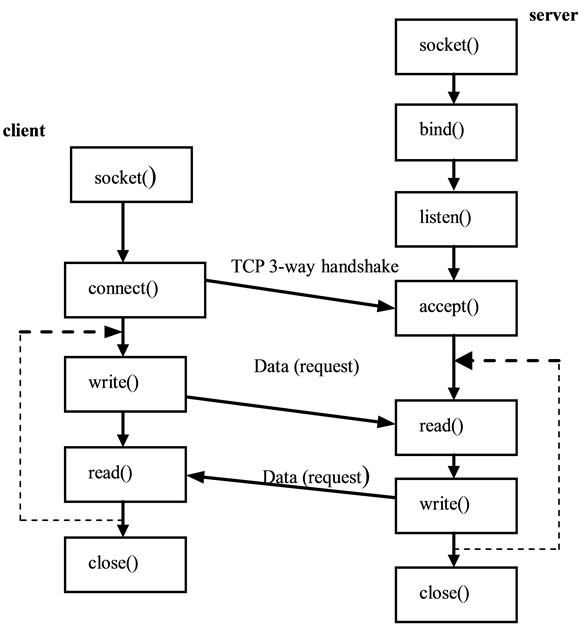
Figure 2. Flow diagram for client-server architecture.
modified then the message contains the status line “HTTP/1.1 OK” and the requested file is included in the message body. Otherwise, a response message contains the status line “HTTP/1.1 304 Not Modified” and an empty body will be sent. If the client sends a HEAD message, then the response will be based upon whether the requested file is found in the current directory or not. If yes, the response message contains the status line “HTTP/1.1 200 OK” and an empty body will be sent. If the requested file is not found, then a response message contains the status line “HTTP/1.1 404 Not Found” and an empty body will be sent.
The main functions of the server as shown in Figure 2 are illustrated below:
1) socket(): The function socket described as int socket(int domain, int type, int protocol), acts as the interface between the application and the transport layer. The domain should be set to PF_INET. The type argument tells the kernel what kind of socket is this: SOCK_STREAM or SOCK_DGRAM, and set protocol to ’0’ to have socket() choose the correct protocol based on the type.
2) bind(): This function comes after creating the socket to associate this socket with a port number on the local machine. The port number is used by the kernel to match an incoming packet to a certain process’s socket descriptor.int bind (int sockfd, struct sockaddr *myaddr, int addrlen); sockfd is the socket file descriptor returned by socket(). myaddr is a pointer to a struct sockaddr which contains information about the address, namely, port and IP address. addrlen can be set to sizeof *myaddr or sizeof(struct sockaddr).
3) listen(): The process is done in two steps: first listen(), then accept().int listen(int sockfd, int backlog); sockfd is the usual socket file descriptor from the socket() system call. backlog is the number of connections allowed on the incoming queue. Incoming connections are going to wait in this queue until accept() and this is the limit on how many can queue up. The limit is about 20 for most systems. Usually, listen() returns −1 and sets errno on error. Well, bind() needs to be called before listen() or the kernel will have one listen on a random port.
4) accept(): The accept() call will try to connect() to the machine on a port that one is listen()ing on. Their connection will be queued up waiting to be accept()ed. One calls accept() and tell it to get the pending connection. It will return a brand new socket file descriptor to use for this single connection. Suddenly there will be two socket file descriptors, the original one is still listening on the port and the newly created one is finally ready to send() and recv().int accept(int sockfd, struct sockaddr *addr, socklen t *addrlen); sockfd is the listen()ing socket descriptor. addr will usually be a pointer to a local struct sockaddr_in. This is where the information about the incoming connection will go and then one can determine which host is calling from which port. addrlen is a local integer variable that should be set to sizeof *addr or sizeof(struct sockaddr in) before its address is passed to accept(). accept() will not put more than that many bytes into addr. If it puts fewer in, it will change the value of addrlen to reflect that.
5) recv() and send(): These functions are used to receive requests from the client and send a response back according to the specified request. The send() call:int send(int sockfd, const void *msg, int len, int flags); sockfd is the socket descriptor one intends to send data to (it’s the one returned by socket()) , msg is a pointer to the data to be sent, and len is the length of that data in bytes. Just set flags to 0. The recv() call is similar to send() in many respects: int recv(int sockfd, void *buf, int len, unsigned int flags); sockfd is the socket descriptor to read from, buf is the buffer to read the information into, len is the maximum length of the buffer, and flags can again be set to 0. recv() returns the number of bytes actually read into the buffer, or −1 on error (with errno set, accordingly).
6) close(): This function will be used to close the socket connection just simply by writing close(sockfd).
3.2. Client Architecture
A persistent TCP connection will be used to connect a client process to the server. The client application will request a Web page from a Web server by using a command line including an URL with either of the two different options: “-h” and “-d”. The “-h” option will request a Web page from the Web server using the HEAD command, which sends only the header lines without the object, whereas the “-d” option will request a Web page from the Web server using the GET command, which sends only the object file if it has been modified according to a given date. If no option is included, the server will send the requested object. Then the program will be able to write the response into an output text file. The functions of the client are omitted here, as the present paper is dealing with the server performance.
4. The CSM of the System
The proposed method is based on a-priori performance model called Computation Structure Model (CSM) [11] which describes the detailed time-execution behavior of computations. A CSM is a set of two directed graphs: the Data Flow Graph (DFG) and the Control Flow Graph (CFG). These two graphs, together, model the time and space requirements of a computation. The DFG is used to model the storage requirements of a computation, and the CFG is the representation of the execution paths of a computation. The focus of the paper is on the execution time behavior, so we will not consider the DFG any further.
The CFG is a directed graph that can be used to model any computation (task). The CFG shows the way in which different subtasks fit together in a task. It is a common tool for modeling the control flow of a computation, and is used to organize the calculation of computation execution time (the time a program will take to complete). The CFG consists of nodes (elements) that represent action in the computation that consume time, and edges that depict how the thread of execution reaches these nodes. Each node is given a time cost (a single value or a distribution) and each edge a control flow count.
The control flow through an element is defined as the number of times that the element is activated, on the average, for each execution of the computation represented by the CFG.
Time equivalent CFG transformation steps: A method is described in [11] that provides a set of transformation steps which can be used to transform a given CFG, composed of elements and control flows, into a simpler, time equivalent CFG. The transformations steps are termed as time equivalent transformation steps, because, two CFG segments representing the “before” and “after” of a proposed transformation step have equivalent execution time distribution. Rules are defined to make sure that the execution time probability distribution of the two CFGs will be identical.
Probability distribution of execution time: Applying these ideas in an orderly algorithmic manner, one can obtain the overall distribution of execution time of a computation with the following form:
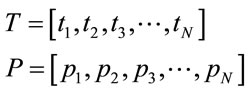
A task will take any one of time 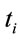 with associated probability
with associated probability 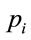 to execute.
to execute.
Next, we describe the Computation Structural Model of the present system. The CSM uses Control Flow Graphs (CFG), and Spanning Trees to model the flow of a system mathematically [5,11], which is then used to derive the cost expression of the system.
4.1. Server Control Flow Graph
The software (counts over 500 lines of C/C++ code) developed to represent the server is simplified into the CFG as shown in Figure 3. The CFG shows only the groups of continuous lines of code in a single node, as long as there is no probabilistic factor, meaning a loop or an if-else conditional statement within the groups. After performing the initialization part which is depicted as init, the program proceeds to an infinite loop, where it keeps
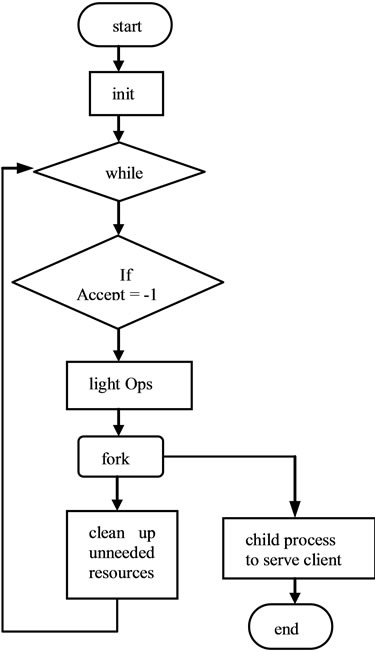
Figure 3. Main server control flow graph.
listening to any new incoming connections. Once a new connection is established, the main process first performs a few light weight operations, for example logging the time of the incoming connection etc. A child process is then created to serve the request. While the child process is serving the request, the main process continues in parallel to clean up the unneeded resources, for example open ports, go back to listen to new connections, etc. Each child process start with a few initialization operations, then proceed to analyze the server request, clean up and terminate.
4.2. Spanning Tree and Mathematical Model
In order to derive a mathematical model for the system, we first need to derive a spanning tree from the CFG and then use it to derive the cost expression. Figure 4 shows the spanning tree that corresponds to the main server system. With the spanning tree, we can use the flow balance equation: 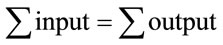 from Kirchhoff law to derive the cost expression. This normalizes the network flow and assures that the sum of the input flows would be equal to the sum of the output flows. We usually added a virtual link (edge) between the end node and the start node. However, this program does not have an end node for the main process. In order to find the cost of one cycle, we will place a cut along link (edge) e7, where we will place an end node at the end of the link and place the virtual link (e0) between the end and the start node. Using this approach, we end up with the following independent variables e0, and e4, and the following dependent variables:
from Kirchhoff law to derive the cost expression. This normalizes the network flow and assures that the sum of the input flows would be equal to the sum of the output flows. We usually added a virtual link (edge) between the end node and the start node. However, this program does not have an end node for the main process. In order to find the cost of one cycle, we will place a cut along link (edge) e7, where we will place an end node at the end of the link and place the virtual link (e0) between the end and the start node. Using this approach, we end up with the following independent variables e0, and e4, and the following dependent variables:
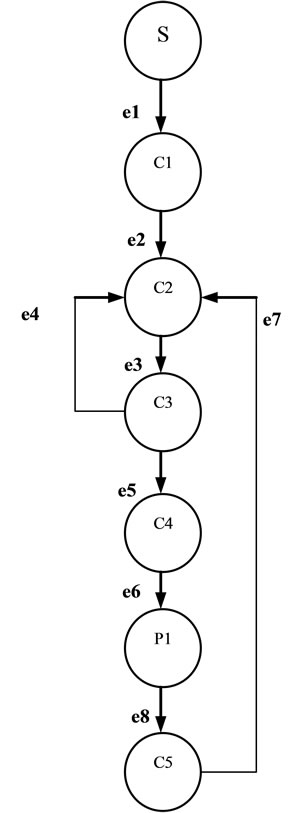
Figure 4. Main server spanning tree CFG.
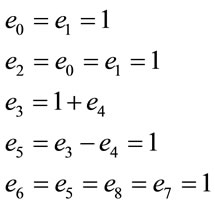
Using the above flow, the cost expression can be written as:
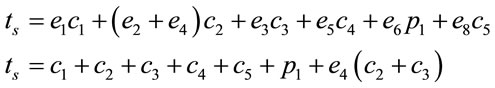 (1)
(1)
Note , is the processing time of a request sent by a client to the server as mentioned in Section 5.
, is the processing time of a request sent by a client to the server as mentioned in Section 5.
where  and
and 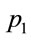 is the cost of fork.
is the cost of fork.
Using this approach, we have derived the equations for the complete system.
4.3. Client Process
The client part has six CFGs: five child functions, namely: request, parse, command, address and message, in total and one main function. We have calculated the execution time contributions from each of the functions separately in detail (which is omitted due to space limitation), using CSM technique, as shown in section 4 for the main server function.
5. Client-Server Communication
First, we illustrate the sequence of communication between the server and the client. The client initiates the communication with the server by requesting a resource (Web pages). All communication goes through the server main process which listens to incoming requests continuously. Once a request is received, the main process creates a child process to serve the request and the communication channel is therefore passed to the child process. The parent process has nothing to do with this particular client anymore. With this approach, each client will be served by a dedicated child process which terminates after serving its client. No child process will serve more than one client at a time.
This is a model with multiple sources and multiple communication channels. Where N is the maximum number of child processes that are allowed to run simultaneously at a given time. Therefore the system to analyze is an M/M/N/N, assuming that the arrival and departure rates follow Poisson process. Clients make connection to the server through a communication port (channel). All communication goes through the Network Interface Card (NIC) of the machine running the Web server application. Although the NIC might buffer (queue) data received from clients before feeding it to the server application, but for the purpose of this analysis and the sake of simplicity, we will not consider this queue.
The average response time of a request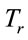 , expressed as
, expressed as
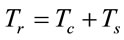 (2)
(2)
where, 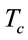 is the communication time between the server and the clients, and
is the communication time between the server and the clients, and 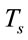 is the time to process the request.
is the time to process the request.
Here we drive equations to compute 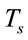 and
and , respectively. First, we derive
, respectively. First, we derive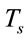 , the processing time of a request from any arbitrary client j. We assume a single processor server model. Requests from all of the j clients form a single processing queue, our objective is to evaluate
, the processing time of a request from any arbitrary client j. We assume a single processor server model. Requests from all of the j clients form a single processing queue, our objective is to evaluate  as a function of different parameters.
as a function of different parameters.
Let 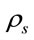 be the utilization factor for the processing queue. We assume that the utilization factor for both the processing and communication queues add up to 1.
be the utilization factor for the processing queue. We assume that the utilization factor for both the processing and communication queues add up to 1.
Therefore,
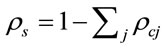 (3)
(3)
From Little’s law, we have
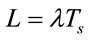 (4)
(4)
where,  is the average length of the processing queue.
is the average length of the processing queue. 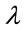 is the average arrival rate into the processing queue, and
is the average arrival rate into the processing queue, and
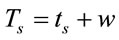 (5)
(5)
where, 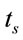 is the mean processing time (equation (1)) and
is the mean processing time (equation (1)) and 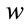 is the average waiting time in the queue.
is the average waiting time in the queue.
Note, 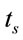 can be derived using CSM technique as mentioned in Section 4.2 (equation (1)).
can be derived using CSM technique as mentioned in Section 4.2 (equation (1)).
Let  be the average request arrival rate from client j into the server, then
be the average request arrival rate from client j into the server, then
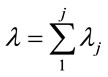 (6)
(6)
For an M/M/1 queue L can be expressed as
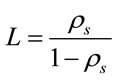 and
and 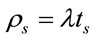
We have, 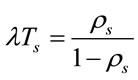
Therefore,
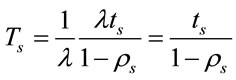 (7)
(7)
Once the request has been processed the answer is returned back from the server to the client. Here we assume one Comm. Queue for each of the j clients.
Now, we calculate communication time between the server and each of the clients (as modeled in Figure 4 by Comm. Queue) first. Let 
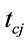 , and
, and 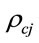 be the average service time, average arrival rate, and average utilization factor for channel of the
be the average service time, average arrival rate, and average utilization factor for channel of the  Comm. Queue (Figure 4), respectively.
Comm. Queue (Figure 4), respectively.
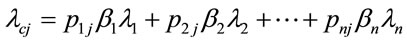 (8)
(8)
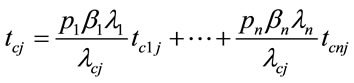 (9)
(9)
where, 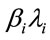 is the rate from client
is the rate from client 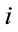 and
and 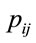 is the fraction going into channel
is the fraction going into channel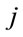 .
.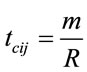 .
. 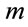 and R are the average message size and the average communication channel capacity, respectively. By definition
and R are the average message size and the average communication channel capacity, respectively. By definition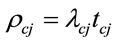 . The total communication time,
. The total communication time, 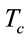 can be written as:
can be written as:
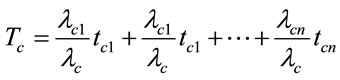 (10)
(10)
The average service time is calculated by taking in consideration the flow rate of each class of users (clients)
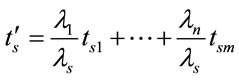 (11)
(11)
The average total execution time is:
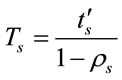 (12)
(12)
6. Utilizing the Analytical Model during Web Server Design Phase
The derived equations above describe the performance (the average response time) of the web server as a function of the used architecture (the Cs values in Equation (1) and the link capacity R for each class of users), the statistical properties of each class of users (the flow rate, the message size m, etc.) and the algorithm of handling different users’ requests (flow rate in equation (1)). The designer can utilize the analytical equations in two different ways:
1) Compare different architectures for the same design and a given set of clients’ classes.
a) Each architecture is represented by a set of operations’ execution time Cs and links’ capacities.
b) For each architecture, evaluate the average response time for the given design and the properties of clients’ classes.
c) It is also possible to evaluate the average response time as a function of the system workload (the total input flow) and repeat it for each architecture.
2) Compare different designs for the same architecture and a given set of clients’ classes.
a) Each design is represented by the flows in equation #1. The given architecture provides the Cs values and the Rs values.
b) Evaluate the average response time for each design given the statistical properties of clients’ classes (input flows, message sizes).
c) Repeat the process for each design alternative and study the system behavior with different workloads.
It is also possible to make the study for different design alternatives using a given set of architectures.
The goal is to find the best design-architecture combination that minimizes the average response time. Furthermore, the design can write the equations in a spreadsheet. This gives him a tool to study the effect of different design parameters to the objective function (the average response time in this case).
7. Conclusion
In this paper, we have reported a partial result of a continuing research which addresses the challenging issue of quantifying the response-time of a web-server system. We have modeled a web server with multiple clients and worked through the steps of deriving the performance equations to process a request, by utilizing Hierarchical Computation Structure Model (CSM). Moreover, queueing model analysis has been used to derive equations for communication between server and clients. The equations derived from the CSM and the queueing models offer far more insights in the processing time cost of a request made by a client to a server, than a simple complexity analysis expression could provide. For instance, the expression from complexity analysis would reveal the polynomial running time of the system as a whole in terms of big O notations which can give a high level idea of the system timing in general. However, by applying CSM, we developed a detailed mathematical cost expression for the request processing time from which one can identify the bottleneck in the system and suggests further improvements. The analytical model can also be utilized to select the best design-architecture combination for the web server that minimizes the average response time.
REFERENCES
- P. Boldi, B. Codenotti, M. Santini and S. Vigna, “Ubicrawler: A Scalable Fully Distributed Web Crawler,” Software-Practice & Experience, Vol. 34, No. 8, 2004, pp. 711-726. doi:10.1002/spe.587
- M. Najork and A. Heydon, “High-Performance Web Crawling,” In: J. M. Abello, P. M. Pardalos and M. G. C. Resende, Eds., Handbook of Massive Data Sets, Kluwer Academic Press, Dordrecht/Boston/London, 2002.
- Apache Software Foundation, “Apache HTTP Server Project.” http://httpd.apache.org/
- L. Lipsky, “Queueing Theory: A Linear Algebraic Approach (LAQT),” Macmillan Publishing Company, New York, 1992.
- R. A. Ammar and B. Qin, “An Approach to Derive Time Costs of Sequential Computations,” Journal of Systems and Software, Vol. 11, No. 3, 1990, pp. 173-180.
- T. L. Booth, “Performance Optimization of Software Systems Processing Information Sequences Modeled by Probabilistic Languages,” IEEE Transactions on Software Engineering, Vol. 5, No. 1, 1979, pp. 31-44. doi:10.1109/TSE.1979.226496
- B. M. MacKay and H. A. Sholl, “Communication Alternatives for a Distributed Real-Time System,” Proceedings of the ISCA Computer Applications in Industry and Engineering Conference, Honolulu, November 1995.
- H. A. Sholl and T. L. Booth, “Software Performance Modeling Using Computation Structures,” IEEE Transactions on Software Engineering, Vol. 1, No. 4, 1975, pp. 414-420. doi:10.1109/TSE.1975.6312874
- R. Ammar, “Hierarchical Performance Modeling and Analysis of Distributed Software,” In: S. Rajasekaran and J. H. Reif, Eds., Handbook of Parallel Computing: Models, Algorithms, and Applications, Chapman & Hall/CRC Press, London.
- R. A. Ammar and T. L. Booth, “Software Optimization Using User Models,” IEEE Transactions on Systems, Man, Cybernetics, Vol. 18, No. 4, 1988, pp. 552-560. doi:10.1109/21.17373
- B. Qin, H. A. Sholl and R. A. Ammar, “Micro Time Cost Analysis of Parallel Computations,” IEEE Transactions on Computers, Vol. 40, No. 5, 1991, pp. 613-628. doi:10.1109/12.88485
- J. Heidemann, K. Obraczka and J. Touch, “Modeling the Performance of HTTP over Several Transport Protocols,” IEEE/ACM Transactions on Networking, Vol. 5, No. 5, 1997, pp. 616-630. doi:10.1109/90.649564
- L. Slothouber, “A Model of Web Server Performance,” Proceedings of the 5th International World Wide Web Conference, 1996.
- R. D. Van der Mei, R. Hariharan and P. Reeser,” Web Server Performance Modeling, “Telecommunication Systems, Vol. 16, No. 3-4, 2001, pp. 361-378. doi:10.1023/A:1016667027983
- D. Menasce, “Web Server Software Architecture,” IEEE Internet Computing, Vol. 7, No. 6, 2003, pp. 78-81. doi:10.1109/MIC.2003.1250588
- A. Kamra, V. Misra and E. Nahum, “Controlling the Performance of 3-Tiered Web Sites: Modeling, Design and Implementation,” Proceedings of the Joint International Conference on Measurement and Modeling of Computer Systems, June 2004, pp. 414-415.
- X. Liu, J. Heo and L. Sha, “Modeling 3-Tiered Web Applications,” 13th IEEE International Symposium on Modeling, Analysis and Simulation of Computer Telecommunications Systems (MASCOTS’05), 2005, pp. 307-310.
- K. Kant and C. R. M. Sundaram, “ A Server Performance Model for Static Web Workloads,” IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS’00), 2000, pp. 201-206.
- K. S. Trivedi, “Probability and Statistics with Reliability, Queuing, and Computer Science Applications,” John Wiley and Sons, Chichester, 2001.
- L. Wells, S. Christensen, L. M. Kristensen and K. H. Mortensen, “Simulation Based Performance Analysis of Web Servers,” Proceedings of 9th International Workshop on Petri Nets and Performance Models, 2001, pp. 59-68. doi:10.1109/PNPM.2001.953356
- R. Gaeta, M. Gribaudo, D. Manini and M. Sereno, “A GSPN Model for the Analysis of DNS-Based Redirection in Distributed Web Systems,” Proceedings of 12th Annual International Symposium on Modeling, Analysis, and Simulation of Computer and Telecommunications Systems (MASCOTS’04), 2004, pp. 39-48.
- D. Gvozdanovic, D. Simic, U. Vizek, M. Matijasevic, K. P. Valavanis and D. Huljenic, “Petri Net Based Modeling of Application Layer Traffic Characteristics,” EUROCON’01, 2001, pp. 424-427.
- M. Scarpa, A. Puliafito, M. Villari and A. Zaia., “A Modeling Technique for the Performance Analysis of Web Searching Applications,” IEEE Transactions on Knowledge and Data Engineering, Vol. 16, No. 11, 2004, pp. 1339-1356. doi:10.1109/TKDE.2004.65
- S. S. Gokhale, P. J. Vandal and J. Lu, “Performance and Availability Analysis of Web Server Software Architecture,” Proceedings of 12th IEEE International Symposium on Pacific Rim Dependable Computing (PRDC’06), 2006, pp. 351-358. doi:10.1109/PRDC.2006.50
- R. Kohavi and R. Parekh, “Ten Supplementary Analyses to Improve E-Commerce Web Sites,” Proceedings of the 5th WEBKDD Workshop (WEBKDD’03), 2003, pp. 29- 36.
- M. Kaaniche, K. Kanoun and M. Martinello, “A UserPerceived Availability Evaluation of a Web Based Travel Agency,” Proceedings of the 2003 International Conference on Dependable Systems and Networks (DSN’03), 22-25 June 2003, pp. 709-718. doi:10.1109/DSN.2003.1209986
- M. Merzbacher and D. Patterson, “Measuring End User Availability on the Web: Practical Experience,” Proceedings of the 2002 International Conference on Dependable Systems and Networks (DSN’02), 2002, pp. 473-477.
- Y. Hu, A. Nanda and Q. Yang, “Measurement, Analysis and Performance Improvement of the Apache Web Server,” IEEE International Performance, Computing and Communications Conference (IPCCC’99), 1999, pp. 261-267.
NOTES
*Partially funded by CSU-AAUP Summer Research Grant 2011-2012.

