Journal of Biomedical Science and Engineering
Vol.08 No.08(2015), Article ID:58701,9 pages
10.4236/jbise.2015.88046
Influence of Supporting Tissue on the Deformation and Compliance of Healthy and Diseased Arteries
Biyuan Sun1, Lauren J. Vallez1, Brian D. Plourde1, John P. Abraham1, John R. Stark2
1School of Engineering, University of St. Thomas, St. Paul, USA
2The University of Kansas Department of Mechanical Engineering, Lawrence, USA
Email: jpabraham@stthomas.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 July 2015; accepted 7 August 2015; published 10 August 2015
ABSTRACT
Hemodynamics and the interaction between the components of the cardiovascular system are complex and involve a structural/fluid flow interaction. During the cardiac cycle, changes to vascular pressure induce a compliant response in the vessels as they cyclically stretch and relax. The compliance influences the fluid flow throughout the system. The interaction is influenced by the disease state of the artery, and in particular, a plaque layer can reduce the compliance. In order to properly quantify the fluid-structural response, it is essential to consider whether the tissue surrounding the artery provides a support to the vessel wall. Here, a series of calculations are provided to determine what role the supporting tissue plays in the vessel wall and how much tissue must be included to properly carry out future fluid-structure calculations. Additionally, we calculate the sensitivity of the compliance to material properties such as the Young’s modulus or to the transmural pressure difference.
Keywords:
Fluid-Structural Interaction, Blood Flow, Compliant Vessels, Finite Element Analysis

1. Introduction
During cardiac cycles, periodic heart beats cause subsequent periodic variations in cardiovascular pressure and blood flow. The cyclic pressure within the artery is exerted on the vessel wall and causes deformation because the artery wall is generally compliant. As cardiovascular disease progresses and plaque accumulates on the vessel wall, the compliance of the vessel changes [1] [2] .
Compliance, which is often measured as a change of cross section area (or diameter) for a specific change in intra-vessel pressure, can be used as a marker for the onset of disease. Cardiovascular stenosis affects the blood velocity waveforms [1] -[6] which are measured by low-invasive observational techniques such as Doppler and ultrasound [7] - [17] .
Insofar as there is a two-way interaction between the pressure wave created at the heart and the downstream vascular wall, and this interaction can alter the overall cardiovascular system performance; it is essential to calculate the importance of the interaction. The interaction may influence mass transfer processes within the artery or the progression of arterial disease, wall shear stress, or injections of medication or cells for therapeutic treatment of coronary disease [18] -[34] .
The literature dealing with fluid-structural interactions is rich [35] -[55] . During the evolution of this field, increasingly complex properties and conditions have been employed and more sophisticated simulation tools have been used. Among the literature cited here are consideration of the non-Newtonian blood properties, the elastic behavior (or hyper-elastic behavior) of tissue, the presence or absence of plaque, the laminar/turbulent nature of the blood flow, and unsteadiness.
What is less well understood is the external boundary condition of the artery wall itself. Almost all studies treat the external boundary condition as stress free however in reality; the artery is surrounded by a sheath of tissue which will respond when the vessel expands. Of the literature cited here, and to our best knowledge, only two studies have investigated the influence of surrounding tissue [54] [55] . In [54] , the presence of the surrounding tissue was incorporated into the analysis as an effective perivascular pressure. In [55] , the surrounding tissues were modeled by introduction of viscoelastic support conditions along the artery. No prior work has formally incorporated the surrounding tissue into the stress calculations.
In the present study, a fully continuous model was built which included plaque, an artery wall, and the surrounding tissue. Each layer was simulated by linear elastic properties which had been shown to sufficiently represent the hyperelastic behavior of arteries [47] . The surrounding tissue sheath was systematically increased and transmural pressures were applied which spanned the physiologic range. Calculations were continued until further increase in the tissue thickness no longer impacted the compliance of the artery wall. Analyses which do not include the minimum thickness of surrounding tissue will result in overestimates of the artery compliance.
The aforementioned calculations were carried out with a range of tissue properties and plaque thicknesses (and with no plaque) so that the minimum required tissue could be determined for a full range of potential situations. Both steady and unsteady calculations were completed; it was found that the minimum thickness of a steady structural calculation was also viable for an unsteady case where the internal pressure varied periodically.
2. The Model
The numerical model includes three layers of tissue (supporting tissue sheath, artery wall, and plaque layer). The layers are arranged in a circular and axisymmetric manner (although this arrangement is not a limitation of the method). Figure 1 shows the cross section of the geometry with descriptive annotation.
The transmural pressure difference is defined as the difference between the inner and outer pressure (inside the lumen and outside the tissue sheath). At upstream and downstream ends of the artery, tissue is allowed to expand radially but not axially. This condition essentially enforces a one-dimensional (radial) situation.
The simulations spanned the entire range of potential geometries and tissue properties. At one extreme, there was no plaque layer included (a healthy artery) while at the other extreme, the plaque nearly completely spanned the artery. As stated earlier, all materials were treated as linear and elastic with Young’s modulus values that were systematically varied to account for uncertainties in this value. In addition, Poisson ratios were varied to determine whether the results are sensitive to its value.
The surrounding tissue and artery wall Young’s modulus parameters were given values of 0.5, 1.0 and 1.5 MPa. The plaque was assigned values that ranged from 10 to 15 MPa (literature sources report its value at 12.6 MPa). Poisson ratios of both 0.3 and 0.4 were applied and the results were compared and found to be nearly identical (less than 1% effect). The inner diameter of the artery was 5.2 mm, the artery wall thickness was 1 mm. Transmural pressure differences ranged from 60 to 120 mm Hg.
Following the above-referenced static calculations, a transient simulation was performed where the transmural pressure varied sinusoidally from a value of zero to a maximum of 165 mm Hg. For those unsteady cases, the calculations had to be numerically integrated in time. Multiple time steps were used to ensure that the results were not dependent on the time step.
For each situation, the local stress, strain, and deformation were determined. The calculations used the local mechanical equilibrium equation which is provided in Equation (1).
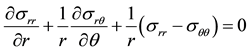 (1)
(1)
After the calculation, radial deformation (stretch) of the inner and outer surfaces of the artery were determined and the cases were compared. Most attention will be given to the inner surface of the artery because it is the surface used as a clinical indicator of compliance. The tissue layer was made thicker in sequential steps until the addition of more thickness did not alter the results. This occurrence coincided with the requisite supporting tissue for compliance calculations.
The calculations were completed using the finite element method (ANSYS v15). Throughout the solution procedure, the number of elements was systematically varied (increased by a factor of approximately 10) and results were found to be negligibly different (less than 1%).
Based on the above discussion, the radial deformation model was known to be independent of mesh size and time step size. It is now possible to show and discuss the major findings, in particular the thickness of the tissue sheath which must be included in a compliant study.
3. Results and Discussion
3.1. Simulations on Healthy Arteries
The first set of results corresponds to a healthy artery (absence of the plaque layer shown in Figure 1). The calculations are intended to quantify to extent of surrounding tissue required to constrain the artery. The list of simulations is outlined in Table 1. For these calculations, the transmural pressure difference was 120 mm Hg, the Young’s modulus of the artery and the tissue were both 1 MPa, and the Poisson ratio of the layers were 0.3. The internal lumen diameter of the artery, taken from IVUS measurements, was 5.2 mm (superficial femoral artery). The deformation listed in the table is the radial motion of the inner surface of the artery wall. The error for each case is calculated with reference to the deformation of the thickest tissue calculation. This thickness is taken to be the limit for reasonable values of tissue sheath thickness.
Figure 1. Layers of tissue with boundary conditions specified.
Table 1. Simulations performed on healthy arteries, transmural pressure difference = 120 mm Hg.
The results of Table 1 are shown graphically in Figure 2 and Figure 3. In the first image, the radial deformation (displacement) of the inner wall of the artery is shown. It is seen that for the no-tissue case (an artery with no surrounding tissue), the calculated deformation is an overestimate of that which actually occurs when supporting tissue is present. As the supporting tissue thickness increases, the deformation decreases until a constant value results.
An alternative way to present the information is displayed in Figure 3. There, results are shown as a percentage deviation from that which occurs for very thick surrounding tissue layers. In order to quantify the required amount of surrounding tissue which must be included in the calculation, some judgement has to be made with regard to the acceptable levels of error. It should be noted that the errors in deformation of the artery are directly related to errors in compliance measurements. For the present case, a 10% error is taken to be reasonable which would correspond to a 6 mm required thickness of tissue. To ensure that all following calculations are within this error limit, a tissue layer thickness of 6.5 mm will be hereafter employed.
It is also noted that neglecting the surrounding tissue results in an overestimate of the deformation (and consequently the artery compliance) by as much as 140%. This finding makes clear the need to include supporting tissue in calculations
3.2. Impact of Plaque and Tissue Properties
Next, plaque was inserted into the model as indicated by Figure 1. The plaque was given a thickness of 1 mm and two transmural pressure differences were used (120 and 60 mm Hg). Insofar as the tissue properties are not known with absolute certainty, a sensitivity study was performed. For the study, both the artery and the tissue Young’s modulus were varied systematically and the deformation of the inner wall of the artery was calculated. The key results are listed in Table 2. All of the results correspond to a plaque Young’s modulus of 12.6 MPa.
Figure 2. Radial deformation of a healthy artery wall for various supporting tissue thicknesses.
Figure 3. Error in deformation calculations of a healthy artery wall for various supporting tissue thicknesses.
Table 2. Results of property sensitivity study plaque thickness of 1 mm, plaque Young’s modulus of 12.6 MPa.
From Table 2, it is seen that generally, the results are not very sensitive to properties. All of the calculated results are approximately 0.0024 mm or 0.0047 mm for the low and high pressures, respectively. Secondly, it is seen that as the tissue or the Young’s modulus increases, the deformation decreases (an expected behavior).
To test the influence of the Poisson ratio, all values were varied from 0.3 to 0.4 and with a transmural pressure of 60 mm Hg, tissue, an artery Young’s modulus value of 1 MPa, and a plaque Young’s modulus of 12.6 MPa. There was less than 0.5% change in the results. Consequently, the results shown here are not dependent on the Poisson ratio.
A deeper review of the results in Table 2 shows that the presence of a layer of plaque significantly reduces the deformation of the artery wall during the cardiac cycle. Comparison of Table 1 with Table 2 shows that a 1 mm plaque layer reduces the deformation by a factor of approximately 13. This finding is expected and reflects prior literature which shows a reduction of compliance with increasing cardiovascular disease and stenosis.
3.3. Impact of Thickness of Plaque Layer
As stated earlier, the calculations in the prior section were carried out with a non-changing thickness of plaque. Insofar as there are various stages of arterial disease, it is important to perform calculations with increasingly levels of occlusion. Consequently, the calculations from Table 2 were repeated with a 2 mm thick layer of plaque.
The cases in Table 3 are labeled to correspond to those of Table 2. A few conclusions can be quickly drawn from a comparison of the results of the two plaque thicknesses. First, the thicker layer of plaque further reduces the deformation (and therefore the compliance) of an artery. This result is expected. Second, the thicker layer of plaque reduces the sensitivity of the results to the other material properties. This too is expected.
3.4. Transient Pressure Variations
A final set of simulations was performed using an unsteady transmural pressure to assess whether the heretofore steady calculations were valid. A sinusoidal transmural pressure was applied with a cycle time which represents a cardiac cycle. The transmural pressure peak was set to be approximately 165 mm Hg. The resulting timewise variation in the arterial radial deformation was found. The results were compared with the steady calculations at similar pressure levels (60 and 120 mm Hg). It was found that the results agreed to within 5%. That is, trans-
Table 3. Same as Table 2 with a plaque layer thickness of 2 mm.
mural pressure differences resulted in the same arterial motion regardless of whether the motion was steady or unsteady.
The unsteady calculations were completed and a time-step study was performed wherein the numerical integration was changed from 0.1 seconds to 0.01 seconds. The results were identical and therefore are independent of time step. The comparison study between steady and unsteady deformation was completed on a healthy artery with a surrounding tissue sheath of 6.5 mm.
3.5. Summary of Results
With the large volume of results presented here, a brief summary is appropriate. Calculations performed on compliance of artery walls, when subjected to a transmural pressure, reveal that neglecting the surrounding tissue leads to large overestimates in compliance. Furthermore, we find that it is necessary to include approximately 6.5 mm of surrounding tissue in order to reduce the incurred error to 10%. Next, it was seen that when a plaque layer is present the compliance is much reduced. Thicker plaque layers result in less compliance. Finally, the sensitivity of the findings to the material properties of the artery wall or the surrounding tissue is not very great when a plaque layer is present.
The most important factor determining the compliance of arteries is clearly the presence/absence of plaque and on the plaque thickness. All other parameters were second-order or less effects.
4. Concluding Remarks
The present study was focused on determining whether the supporting tissue surrounding an artery was important to the compliance of the artery. It is seen that calculations without sufficient arterial support will overestimate the artery compliance. It is further found that it is necessary to include approximately 6.5 mm of surrounding tissue in order to accurately calculate compliance.
Next, a study was made of the sensitivity of compliance calculations to the values of the mechanical properties of the tissue and the artery wall, in particular, the Young’s modulus and the Poisson ratio. It was found that the results were moderately dependent on the Young’s modulus with increasing Young’s modulus leading to lesser compliance. The results are not dependent on the Poisson ratio.
The presence of plaque has a significant effect in determining the compliance. A 1 mm layer of calcific plaque dramatically reduces the compliance compared to a healthy artery. Thicker layers of plaque (for instance 2 mm) even further reduce compliance.
The calculations were primarily steady; however, a comparison of certain unsteady and steady calculations showed that they gave nearly identical results. Consequently, it is not necessary to perform unsteady structural deformation calculations in order to predict arterial compliance, even though the transmural pressure difference may vary in time.
It is hoped that the information presented here will be useful for future studies on arterial compliance and fluid-structural interaction studies. These studies are an important area of cardiovascular research and proper accounting of supporting tissue is necessary in those studies.
Acknowledgements
This research was carried out at the request of Cardiovascular Systems Inc. No financial support was given to the authors for the research and the authors declare no financial interests in the company or conflicts of interest.
Cite this paper
BiyuanSun,Lauren J.Vallez,Brian D.Plourde,John P.Abraham,John R.Stark, (2015) Influence of Supporting Tissue on the Deformation and Compliance of Healthy and Diseased Arteries. Journal of Biomedical Science and Engineering,08,490-499. doi: 10.4236/jbise.2015.88046
References
- 1. O’Rouke, M.F., Staessen, J.A., Vlachopoulos, D., Duprez, D. and Plante, G. E. (2002) Clinical Applications of Arterial Stiffness; Definitions and Reference Values. American Journal of Hypertension, 15, 426-444.
http://dx.doi.org/10.1016/S0895-7061(01)02319-6 - 2. Pannier, B.M., Avolio, A.P., Hoeks, A., Mancia, G. and Takazawa, K. (2002) Methods and Devices for Measuring Arterial Compliance in Humans. American Journal of Hypertension, 15, 743-753.
http://dx.doi.org/10.1016/S0895-7061(02)02962-X - 3. Woodcock, J.P., Morris, S.J. and Wells, P.N.T. (1975) Significance of the Velocity Impulse Response and Cross-Correlation of the Femoral and Popliteal Blood-Velocity/Time Waveforms in Disease of the Superficial Femoral Artery. Medical and Biological Engineering, 13, 813-818.
http://dx.doi.org/10.1007/BF02478083 - 4. Baird, R.N., Bird, D.R., Clifford, P.C., Lusby, R.J., Skidmore, R. and Woodcock, J.P. (1980) Upstream Stenosis: Its Diagnosis by Doppler Signals from the Femoral Artery. Archives of Surgery, 115, 1316-1322.
http://dx.doi.org/10.1001/archsurg.1980.01380110054008 - 5. Nicholls, S.C., Kohler, T.R., Martin, R.L., Neff, R., Phillips, D.J. and Strandness, D.E. (1986) Diastolic Flow as a Predictor of Arterial Stenosis. Journal of Vascular Surgery, 3, 498-501.
http://dx.doi.org/10.1016/0741-5214(86)90115-1 - 6. Burnham, S.J., Jacques, P. and Burnham, C.B. (1992) Noninvasive Detection of Iliac Artery Stenosis in the Presence of Superficial Femoral Artery Obstruction. Journal of Vascular Surgery, 16, 445-452.
http://dx.doi.org/10.1016/0741-5214(92)90380-Q - 7. Risoe, C. and Wille S. (1978) Blood Velocity in Human Arteries Measured by a Bidirectional ultrasonic Doppler flowmeter. Acta Physiologica Scandinavica, 103, 370-378.
http://dx.doi.org/10.1111/j.1748-1716.1978.tb06230.x - 8. Mohajer, K., Zhang, H., Gurell, D., Ersoy, H., Ho, B., Kent, K.C. and Prince, M.R. (2006) Superficial Femoral Artery Occlusive Disease Severity Correlates with MR Cine Phase-Contrast Flow Measurements. Journal of Magnetic Resonance Imaging, 23, 355-360.
http://dx.doi.org/10.1002/jmri.20514 - 9. Holland, C.K., Brown, J.M., Scoutt, L.M. and Taylor, K.W. (1998) Lower Extremity Volumetric Arterial Blood Flow in Normal Subjects. Ultrasound in Medicine and Biology, 24, 1079-1086.
http://dx.doi.org/10.1016/S0301-5629(98)00103-3 - 10. Macpherson, D.S., Evans, D.H. and Bell, P.R.F. (1984) Common Femoral Artery Doppler Wave-Forms: A Comparison of Three Methods of Objective Analysis with Direct Pressure Measurements. British Journal of Surgery, 71, 46-49. http://dx.doi.org/10.1002/bjs.1800710114
- 11. Caputo, G.R., Masui, T., Gooding, G.A.W., Chang, J.M. and Higgins, C.B. (1982) Popliteal and Tibioperoneal Arteries: Feasibility of Two Dimensional Time-of-Flight MR Angiography and Phase Velocity Mapping. Cardiovascular Radiology, 182, 387-392.
- 12. Johnston, K.W., Maruzzo, B.C. and Cobbold, S.C. (1977) Errors and Artifacts of Doppler Flowmeters and Their Solution. Archives of Surgery, 112, 1335-1342.
http://dx.doi.org/10.1001/archsurg.1977.01370110069007 - 13. Johnston, K.W., Kassam, M., Koers, J., Cobbold, R.S.C. and Mac Hattie, D. (1984) Comparative Study of Four Methods for Quantifying Doppler Ultrasound Waveforms from the Femoral Artery. Ultrasound in Medicine and Biology, 10, 1-12.
http://dx.doi.org/10.1016/0301-5629(84)90056-5 - 14. Baker, J.D., Machleder, H.I. and Skidmore, R. (1984) Analysis of Femoral Artery Doppler Signals by Laplace Transform Damping Method. Journal of Vascular Surgery, 1, 520-524.
http://dx.doi.org/10.1016/0741-5214(84)90037-5 - 15. Woodcock, J.P., Gosling, R.G. and Fitzgerald, D.E. (1972) A New Non-Invasive Technique for Assessment of Superficial Femoral Artery Obstruction. British Journal of Surgery, 59, 226-231.
http://dx.doi.org/10.1002/bjs.1800590320 - 16. Spronk, S., den Hoed, P.T., de Jonge, L.C.W., van Dijk, L.C. and Pattynama, P.M.T. (2005) Value of the Duplex Waveform at the Common Femoral Artery for Diagnosing Obstructive Aortoiliac Disease. Journal of Vascular Surgery, 42, 236-242.
http://dx.doi.org/10.1016/j.jvs.2005.04.048 - 17. Skidmore, R. and Woodcock, J.P. (1980) Physiological Interpretations of Doppler-Shift Waveforms—I Theoretical Considerations. Ultrasound in Medicine and Biology, 6, 7-10.
http://dx.doi.org/10.1016/0301-5629(80)90057-5 - 18. Khakpour, M. and Vafai, K. (2008) A Critical Assessment of Arterial Transport Models. International Journal of Heat and Mass Transfer, 51, 807-822.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.04.021 - 19. Khaled, A.R.A. and Vafai, K. (2003) The Role of Porous Media in Modeling Flow and Heat Transfer in Biological Tissues. International Journal of Heat and Mass Transfer, 46, 4989-5003.
http://dx.doi.org/10.1016/S0017-9310(03)00301-6 - 20. Khanafer, K. and Vafai, K. (2006) The Role of Porous Media in Biomedical Engineering as Related to Magnetic Resonance Imaging and Drug Delivery. Heat and Mass Transfer, 42, 939-953.
http://dx.doi.org/10.1007/s00231-006-0142-6 - 21. Khakpour, M. and Vafai, K. (2008) A Critical Assessment of Arterial Transport Models. International Journal of Heat and Mass Transfer, 51, 807-822.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2007.04.021 - 22. Wang, S. and Vafai, K. (2014) Analysis of Low Density Lipoprotein (LDL) Transport within a Curved Artery. Annals of Biomedical Engineering, 43, 1571-1584.
http://dx.doi.org/10.1007/s10439-014-1219-x - 23. Ellahi, R., Rahman, S., Nadeem, U. and Vafai, K. (2015) The Blood Flow of Prandtl Fluid through a Tapered Stenosed Arteries in Permeable Walls with Magnetic Field. Communications in Theoretical Physics, 63, 353-358.
http://dx.doi.org/10.1088/0253-6102/63/3/353 - 24. Schwalbach, D.B., Plourde, B.D., Abraham, J.P. and Kohler, R.E. (2013) Drug Dispersion for Single- and Multi-Lumen Catheters. Journal of Biomedical Science and Engineering, 6, 1021-1028.
http://dx.doi.org/10.4236/jbise.2013.611127 - 25. Stark, J.R. Gorman, J.M., Sparrow, E.M., Abraham J.P. and Kohler, R.E. (2013) Controlling the Rate of Penetration of a Therapeutic Drug into the Wall of an Artery by Means of a Pressurized Balloon. Journal of Biomedical Science and Engineering, 6, 527-532.
http://dx.doi.org/10.4236/jbise.2013.65067 - 26. Gebreegziabher, T., Sparrow, E.M., Abraham, J.P. Ayorinde, E. and Singh, T. (2011) High-Frequency Pulsatile Pipe Flows Encompassing All Flow Regimes. Numerical Heat Transfer, 60, 811-826.
http://dx.doi.org/10.1080/10407782.2011.627794 - 27. Abraham, J.P., Sparrow, E.M. and Lovik, R.D. (2008) Three-Dimensional Fluid Mechanical Analysis of Blood Flow in Plaque-Narrowed and Plaque-Free Arteries. International Journal of Heat and Mass Transfer, 51, 5633-5641.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.04.038 - 28. Abraham, J.P., Sparrow, E.M., Gorman, J.M., Stark, J.R. and Kohler, R.E. (2013) A Mass Transfer Model of Temporal Drug Deposition in Artery Walls. International Journal of Heat and Mass Transfer, 58, 632-638.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2012.11.053 - 29. Abraham, J.P., Stark, J.R., Gorman, J.M., Sparrow, E.M. and Kohler, R.E. (2013) A Model of Drug Deposition within Artery Walls. Journal of Medical Devices, 7, Paper No. 020902.
- 30. Dib, N., Kohler, R.E., Abraham, J.P., Plourde, B.D. and Schwalbach, D.B. (2013) TCT-811 Stem Cell Viability Significantly Reduced after Passing through a Standard Single Lumen Over-the-Wire 0.014 Balloon Angioplasty Cather. Journal of the American College of Cardiology, 62, B246.
http://dx.doi.org/10.1016/j.jacc.2013.08.1564 - 31. Naughton, N.M., Plourde, B.D., Stark, J.R., Hodis, S. and Abraham, J.P. (2014) Impacts of Waveforms on the Fluid Flow, Wall Shear Stress, and Flow Distribution in Cerebral Aneurysms and the Development of a Universal Reduced Pressure. Journal of Biomedical Science and Engineering, 7, 7-14.
http://dx.doi.org/10.4236/jbise.2014.71002 - 32. Plourde, B.D., Schwalbach, D.B., Abraham, J.P. and Kohler, R.E. (2014) Intracoronary Injection of Medication from Multi-Lumen Injection Catheters. Journal of Medical Devices, 8, Paper No. 020901.
- 33. Dib, N., Abraham, J.P., Schwalbach, D.B., Dana, D., Myers, L., Hunkler, K., D’Silva, S.R., Flower, T.R. and Kohler, R.E. (2014) TCT-155 A Novel Multi-Lumen Compliant Balloon Catheter (ND Infusion Catheter) Preserves Stem Cell Viability and Improves Dispersion When Compared to a Standard Single Lumen Balloon Angioplasty Catheter. Journal American College of Cardiology, 64, B46-B47.
http://dx.doi.org/10.1016/j.jacc.2014.07.191 - 34. Dib, N., Schwalbach, D.B., Plourde, B.D., Kohler, R.E., Dana, D. and Abraham, J.P. (2014) Single Lumen Balloon Angioplasty Catheter Reduces Cell Viability When Compared to Multi Lumen Infusion Catheter. Cardiovascular Translation Research, 7, 781-787.
- 35. Tang, D., Yang, C., Huang, Y. and Ku, D.N. (1999) Wall Stress and Strain Analysis Using a Three-Dimensional Thick-Wall Model with Fluid-Structure Interactions for Blood Flow in Carotid Arteries with Stenosis. Computers and Structures, 72, 341-356.
http://dx.doi.org/10.1016/S0045-7949(99)00009-7 - 36. Tang, D., Yang, C. and Ku, D.N. (1999) A 3-D Thin-Wall Model with Fluid-Structure Interactions for Blood Flow in Carotid Arteries with Symmetric and Asymmetric Stenosis. Computers and Structures, 72, 357-377.
http://dx.doi.org/10.1016/S0045-7949(99)00019-X - 37. Zhao, S.Z., Xu, X.Y., Hughes, A.D., Thom, S.A., Stanton, A.V., Ariff, B. and Long, Q. (2000) Blood Flow and Vessel Mechanics in a Physiologically Realistic Model of a Human Carotid Arterial Bifurcation. Journal of Biomechanics, 33, 975-984.
http://dx.doi.org/10.1016/S0021-9290(00)00043-9 - 38. Tang, D., Yang, C., Walker, H., Kobayashi, S. and Ku, D.N. (2002) Simulating Cyclic Artery Compression Using a 3D Unsteady Model with Fluid-Structure Interactions. Computers and Structures, 80, 1651-1665.
http://dx.doi.org/10.1016/S0045-7949(02)00111-6 - 39. Tang, D., Yang, C., Kobayashi, S., Zheng, J. and Vito, R.P. (2003) Effect of Stenosis Asymmetry on Blood Flow and Artery Compression: A Three-Dimensional Fluid-Structure Interaction Model. Annals of Biomedical Engineering, 31, 1182-1193.
http://dx.doi.org/10.1114/1.1615577 - 40. Tang, D., Yang, C., Kobayashi, S. and Ku, D.N. (2004) Effect of a Lipid Pool on Stress/Strain Distributions in Stenotic Arteries: 3-D Fluid-Structure Interactions (FSI) Models. Journal of Biomechanical Engineering, 126, 363-370.
http://dx.doi.org/10.1115/1.1762898 - 41. Li, Z. and Kleinstreuer, C. (2005) Blood Flow and Structure Interactions in a Stented Abdominal Aortic Aneurysm Model. Medical Engineering and Physics, 27, 369-382.
http://dx.doi.org/10.1016/j.medengphy.2004.12.003 - 42. Torii, R., Oshima, M., Kobayashi, T., Takagi, K. and Tezduyar, T.E. (2006) Fluid-Structure Interaction Modeling of Aneurysmal Conditions with High and Normal Blood Pressures. Computational Mechanics, 38, 482-490.
http://dx.doi.org/10.1007/s00466-006-0065-6 - 43. Valencia, A. and Villanueva, M. (2006) Unsteady Flow and Mass Transfer in Models of Stenotic Arteries Considering Fluid-Structure Interaction. International Communications in Heat and Mass Transfer, 33, 966-975.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2006.05.006 - 44. Valencia, A. and Solis, F. (2006) Blood Flood Dynamics and Arterial Wall Interaction in a Saccular Aneurysm Model of the Basilar Artery. Computers and Structures, 84, 1326-1337.
http://dx.doi.org/10.1016/j.compstruc.2006.03.008 - 45. Torii, R., Oshima, M., Kobayashi, T., Takagi, K. and Tezduyar, T.E. (2007) Influence of Wall Elasticity in Patient Specific Hemodynamic Simulations. Computers and Fluids, 36, 160-168.
http://dx.doi.org/10.1016/j.compfluid.2005.07.014 - 46. Bluestein, D., Alemu, Y., Avrahami, I., Gharib, M., Dumont, K., Ricotta, J.J. and Einav, S. (2008) Influence of Microcalcifications on Vulnerable Plaque Mechanics. Journal of Biomechanics, 41, 1111-1118.
http://dx.doi.org/10.1016/j.jbiomech.2007.11.029 - 47. Torii, R., Oshima, M., Kobayashi, T., Takagai, K. and Tezduyar, T.E. (2009) Fluid-Structure Interaction Modeling of Blood Flow and Cerebral Aneurysm: Significance of Artery and Aneurysm Shapes. Computer Methods in Applied Mechanics and Engineering, 198, 3613-3621.
http://dx.doi.org/10.1016/j.cma.2008.08.020 - 48. Khanafer, K., Bull, J.L. and Berguer, R. (2009) Fluid-Structure Interaction of Turbulent Pulsatile Flow within a Flexible Wall Axisymmetric Aortic Aneurysm Model. European Journal of Mechanics B/Fluids, 28, 88-102.
http://dx.doi.org/10.1016/j.euromechflu.2007.12.003 - 49. Janela, J., Moura, A. and Sequeira, A. (2010) A 3D Non-Newtonian Fluid-Structure Interaction Model for Blood Flow in Arteries. Journal of Computational and Applied Mechanics, 234, 2783-2791.
http://dx.doi.org/10.1016/j.cam.2010.01.032 - 50. Kung, E.O., Les, A.S., Figueroa, C.A., Medina, F., Arcaute, K., Wicker, R.B., McConnell, M.V. and Taylor, C.A. (2011) In Vitro Validation of Finite Element Analysis of Blood Flow in Deformable Models. Annals of Biomedical Engineering, 39, 1947-1960.
http://dx.doi.org/10.1007/s10439-011-0284-7 - 51. Croseetto, P., Reymond, P., Deparis, S., Kontaxakis, D., Stergiopulos, N. and Quarteroni, A. (2011) Fluid-Structure Interaction Simulation of Aortic Blood Flow. Computers and Fluids, 43, 46-57.
http://dx.doi.org/10.1016/j.compfluid.2010.11.032 - 52. Malve, M., Garcia, A., Ohayon, J. and Martinez, M.A. (2012) Unsteady Blood Flow and Mass Transfer of a Human Left Coronary Artery Bifurcation: FSI vs. CFD. International Communications in Heat and Mass Transfer, 39, 745-751.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2012.04.009 - 53. Reymond, P., Crosetto, P., Deparis, S., Quarteroni, A. and Stergiopulos, N. (2013) Physiological Simulation of Blood Flow in the Aorta: Comparison of Hemodynamic Indices as Predicted by 3-D FSI, 3-D Rigid Wall and 1-D Models. Medical Engineering and Physics, 35, 784-791.
http://dx.doi.org/10.1016/j.medengphy.2012.08.009 - 54. Liu, Y., Dang, C., Garcia, M., Gregersen, H. and Kassab, G.S. (2007) Surrounding Tissues Affect the Passive Mechanics of the Vessel Wall: Theory and Experiment. American Journal of Heart and Circulatory Physiology, 293, H3290-H3300.
http://dx.doi.org/10.1152/ajpheart.00666.2007 - 55. Moireau, P., Xiao, N., Astorino, M., Figueroa, C.A., Chapelle, D., Taylor, C.A. and Gerbeau, J.F. (2012) External Tissue Support and Fluid-Structure Simulation in Blood Flows. Biomechanics and Modeling in Mechanobiology, 11, 1-18.
http://dx.doi.org/10.1007/s10237-011-0289-z





