Journal of Biomedical Science and Engineering
Vol.08 No.09(2015), Article ID:59497,10 pages
10.4236/jbise.2015.89055
The Effects of Bone Screw Configurations on the Interfragmentary Movement in a Long Bone Fixed by a Limited Contact Locking Compression Plate
Jalil Nourisa1, Amin Baseri2, Leszek Sudak3, Gholamreza Rouhi1*
1Amirkabir University of Technology, Faculty of Biomedical Engineering, Tehran, Iran
2Department of Biomedical Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran
3Department of Mechanical and Manufacturing Engineering, University of Calgary, AB, Canada
Email: *grouhi@aut.ac.ir, grouhi@uottawa.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 May 2015; accepted 6 September 2015; published 9 September 2015
ABSTRACT
The locking compression plates (LCP) are efficient tools in open reduction and internal fixation (ORIF), especially in osteoporotic bones. Two important factors of screw density and screw position can affect the functionality of the bone plate. Several studies have assessed the influence of the screw configurations on the bone-plate stiffness, but the effects of screw positions on the interfragmentary strain, εIF of LCP construct have not been investigated yet. In this study, finite element method was used to investigate the influence of screws number and position on the interfragmentary strain of LCP-femur system for a mid-shaft fracture. Results of this study showed that by insertion of screws closer to the fracture site, εIF decreases by 2nd degree polynomial function versus screw position, but by adding the screws from the ends of the plate, or by moving and placing the screws towards the fracture site, the reduction of εIF will be linear. Results of this study were compared and are in agreement with some studies in the literature, even though their scope was mostly stability of the bone-implant system, whereas our scope was focused on the interfragmentary strain.
Keywords:
Long Bone Fracture, Locking Compression Plate, Interfragmentary Strain, Screw Density, Screw Position

1. Introduction
Femur is the biggest and strongest bone, and one of the main components for load bearing in our body [1] -[3] . Mid-shaft fractures of the femur are very common and one of the most prevalent fractures, especially in car accidents [2] . Comminuted and segmental fractures of mid-shaft femur can be treated by internal fixation systems, such as orthopedic plates specially when there is extremely narrow medullary canal [4] -[7] . Locking compression plates (LCP) by taking the advantage of the threaded holes in the plate, is not pressed to the bone, which this can greatly reduce the biological damage [8] . Because of the threaded holes, the bone-plate structure turns into an integrated structure that increases in the resistance of the screws to the pullout force [3] . Thus, direct contact between the bone and plate is not needed, and the gap between the plate and bone results in a better blood supply to the fracture site, and there are also no need to plate shaping, based on the geometry of the broken bone, during surgery [3] [8] [9] .
Fracture healing process is affected by the stability of the bone-plate structure. Based on Perren’s study [3] , callus generated at the fracture site has different healing rates according to the interfragmentary strain (εIF). The strain range of 2% - 10% guarantees the production of cartilage and woven bone tissue, and smaller strains, below 2%, causes direct bone healing and lamellar bone tissue [3] . Furthermore, strains above 10% result in fibrous tissue production. The stability of fracture site and the healing time are strongly influenced by the surgical techniques, such as the number and positions of screws [3] [8] [10] -[13] . There are many studies, which investigated the influence of screw position in the conventional plates on the stability of the bone-implant system experimentally and clinically [14] -[18] . There are some other studies that investigated the effects of screw configurations on the stability of the locking plates [10] [19] -[21] .
Stoffel et al. [10] investigated the importance of the position and density of the screws on the axial stiffness and torsional rigidity of the bone-LCP construct. They demonstrated that by increasing the number of screws, the rigidity of the structure increases, and by increasing the distance of screw from the fracture site, the bone- plate construct’s stiffness decreases. MacLeod et al. [22] added the effect of bone quality on the response of construct to the screws positions and reported similar results with Stoffel and co-workers [10] . In an earlier study, Lee et al. [21] employed an optimization method to determine the best combination of number and position of screws to optimize the stability of the bone-plate system. All these studies [10] [21] [22] investigated the effects of the screw configurations on the mechanical properties of the bone-implant construct, but did not focus on the effects of screw configurations on the bone fracture healing process. The main scope of the present study was to determine the relations between the screw configurations and the interfragmentary strain (εIF), which is an indicator of the tissue phenotype during the healing process, in a femur-LCP construct.
2. Materials and Methods
2.1. Construction of the CAD Model
To create a CAD model, CT data of a 65 years old male’s left femur were used by considering the intramedullary canal, and cross-sectional images at every 1 mm slice along the longitudinal axis of the femur. The point clouds obtained by Mimics (V.10.01) were imported to Catia (V5.R19) for making the solid structure. For the sake of simplification, only the proximal fragment of femur was created by Mimics and for modeling the diaphysis, the cross section of the mid-shaft was extruded 150 mm (Figure 1(a)). To simulate a 3 mm transverse fracture gap in the mid-shaft of the femur (AO classification: 32-A3 [23] ), the distal fragment of the femur was placed 3 mm away from the proximal part.
An LCP (type = broad; 12 holes; length = 239 mm; width = 17.5 mm), along with bone screws (screw core diameter = 5 mm; outer diameter = 5.5 mm) was used to fix the fracture. In order to reduce the complexity of the finite element analysis, the threads of the screws were all neglected, and they were modeled as a cylinder with a truncated cone head (Figure 1(b), right). In accordance with the AO procedure [23] , the plate is positioned in the lateral side of the femur. In general, the locked constructs lose their stability when the distance between the bone and plate exceeds a limit [24] . Ahmad et al. [24] suggested that the distance between the LCP and bone surface should not exceed 2 mm. Based on Ahmad and co-workers’ results [24] , a band analysis was performed in Catia to make sure that the plate is located in a way, where the distance between bone surface and plate does not exceed 2 mm.
Nine different screw configurations were developed, which divided into 3 groups with 4 different configurations
Figure 1. CAD model created in Catia, (a) Assembly of bone-plate. The outer diameter of femoral shaft was around 30 mm, and the inner diameter was 20 mm; (b) Specifications of LCP and screw.
in each group (Figures 2-4). In groups 1 and 2 screws were added from the fracture gap side and lateral side, respectively (Figure 2 and Figure 3). In group 3, with constant number of the screws, the second screw stepped towards the plate ends (Figure 4). It is highly recommended that the number of screws in each main fragment of the bone should not be less than three [8] [10] [11] [19] . It was reported that the closest screw to the fracture site plays the most important role in the stiffness of the bone-plate structure [10] . Thus, in this study, all models contain the 1st screw inserted closest to the fracture site, and also not less than 3 screws were used in each fragment side.
By defining ∆L1 and ∆L2 as the interfragmentary movement in the medial and lateral side of the femur, respectively (Figure 5), the interfragmentary strain, εIF is determined as the average of ∆L1/L and ∆L2/L (Equation (1)).
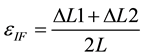 (1)
(1)
2.2. Finite Element Analysis
Bone-plate complex was constructed in Catia and then was imported to Abaqus (V 6.11-1, Simulia, Dassault Systems). The plate and screws were assumed to be made by stainless steel, with a Young’s modulus of 191 GPa, and Poisson’s ratio of 0.3 [25] . In accordance with Wang et al. [26] , the proximal fragment of the femur was divided into 3 regions with various material properties (Figure 6). Material properties of these 3 regions are listed in Table 1. It was assumed that bone is homogeneous and linear elastic, and also bone marrow and callus were disregarded in our FE model.
The contact areas of the screw-plate and screw-bone were assumed to be tied together. To simulate the different load regimes for different weights, loads of 600, 700, 800 and 900 N were applied to the femur head vertically, in X direction (see Figure 7), and the end of the distal part was fixed with no degrees of freedom (Figure 7). In order to reduce the complexity, muscle forces were neglected in our model.
The types of elements and the average number of elements for each part are listed in Table 2. The ten node tetrahedral element (C3D10) was used for all different parts of the bone-plate construct. The effect of mesh
Figure 2. Screw configurations in group 1.
Figure 3. Screw configurations in group 2.
Figure 4. Screw configurations in group 3.
Figure 5. The initial fracture gap lengths in the medial (L1) and lateral (L2) sides of the femur (L1 = L2 = L = 3 mm).
refinement was explored by increasing the local seeds in the high stressed area especially around the screw holes. The number of elements was increased until the third decimal of interfragmentary movement (mm) reached a
Figure 6. The proximal femur was divided into 3 different regions; high density spongy bone (region 1), low density spongy bone (region 2), and cortical bone (region 3) [26] .
Figure 7. Loading and boundary condition: External load was applied on the femoral head and the distal end was fully constrained.
Table 1. Material properties of different regions of femur (see Figure 6).
constant value, and the average seed size was 1mm in the refined regions.
3. Results
Results of all simulations can be seen in Table 3. For all different configurations, εIF is greater than 0.1 for the
Table 2. Number and type of elements used in the FE model for femur proximal fragment, femur distal fragment, LCP and screw.
Table 3. Interfragmentary strains (εIF) for nine different configurations of screws placement (see Figures 2-4).
external load of 900 N, and lower than 0.1 for the external loads of 600 N and 700 N (see Figure 8). Based on Perren’s theory [3] , results of this study show that for an external load between 700 N to 800 N, the screw positions are the most critical for changing the tissue phenotype (see Figure 8).
The relations between εIF and the screws configurations for different external loads in groups 2 and 3 are linear (Figure 10 and Figure 11), and in group 1 are polynomial (Figure 9) (R-square > 0.95). Figure 8 shows, there is a linear relation between the load and the interfragmentary strain for all different configurations. Furthermore, slopes of εIF versus load are steeper for the less stable bone-implant constructs, e.g. 156 configuration compared to 123456, which the latter is more stable.
4. Discussion
In this study, an investigation was made on the impact of screw position on the interfragmentary strain in a LCP-femur construct. In group 1 (see Figure 2), insertion of more than 4 screws showed a little and marginal effect on the interfragmentray strain (see Table 3 and Figure 9), in agreement with Stoffel et al. [10] and Lee et al. [21] . In group 2 (see Figure 3), because the pattern of screw insertion has been changed, increase in the number of screw more than 4 has same effect on the interfragmentray strain as from 3 to 4 (see Table 3 and Figure 10). The latter result was not reported by other investigators, since these specific patterns of screws (Figure 3) were not investigated by others, and suggests that when insertion of the screw number 2 (see Figures 2-4) is not possible, to increase the stability of the system, insertion of more screws is needed. In group 3 (see Figure 4), by stepping the second screw to the middle of plate, the interfragmentary strain will decrease, in agreement with Stoffel and co-workers’ results [10] , and the reduction pattern of εIF follows a linear function with respect to the screw position (see Figure 11).
LCP with a small number of locking screws can reduce both bone and soft tissue damage, as well as decreases bone-implant stiffness that can ultimately lead to a reduction in the stress shielding effect [27] . By comparing results of configurations 126 with 1456, and 13456 and 136 with 1456 (see Table 3), it can be concluded that proximity of the screws to the fracture site has a greater impact on the interfragmentary strain (εIF) than the number of screws itself. This result is in agreement with the finding of Lee et al. [21] , who showed that LCP
Figure 8. The interfragmentary strains (εIF) versus external load for different configurations of screw placement.
Figure 9. The interfragmentray strain (εIF) for different screw configurations of group 1.
Figure 10. The interfragmentray strain (εIF) for different screw configurations of group 2.
Figure 11. The interfragmentray strain (εIF) for different screw configurations of group 3.
with six locking screws results in the necessary fixation stability, and the optimized screw configuration is 126, three locking screws on either side of the bone fragment with two locking screws right beside the fracture line. This finding can be used by the surgeons to choose the appropriate selection of screws in order to achieve the same healing rate, but by using less screws, and consequently less damage to the soft and hard tissues, and less surgery costs. More investigations, especially well-defined in-vivo tests on animal models are needed to reinforce our findings.
The relationships between the interfragmentary strain (εIF) and the screw configurations were investigated for four different constant values of external load, i.e. 600 N, 700 N, 800 N or 900 N, which represent load bearing after surgery for 4 different weights (60 - 90 kg). Based on Perren’s theory [3] , it was shown for the majority of loads, change in the screw configurations cannot greatly affect the tissue phenotype (see Figure 8). This fact is partly due to the lack of exact relationships between the interfragmentary strain and tissue phonotype, for instance, for the strains in the range of 2% - 10%, and 10% - 30% in Perren’s theory [3] . In order to more accurately predict the impact of screws configuration on the outcome of internal fixation, more quantitative mechano- biological models, such as [28] [29] , should be employed in the future studies. Furthermore, results of this study show that the screw positions are the most influential for an external load between 700 N to 800 N (see Figures 8-11). Needless to emphasize that by changing either of the geometry and/or material properties of bone and/or implant, the critical load with the greatest impact on the tissue phenotype will be different.
Figure 8 shows the influence of the load magnitude on the interfragmentary strain (εIF). It indicates that by an increase of 200N in the load magnitude, the tissue phenotype can completely change. It is interesting to note that for vertical external loads, altering the screws positions, from the most stable configuration (configuration 123456) to the most unstableconfiguration (configuration 156), cannot alter the tissue type. This result implies that change of load regime has greater impact on the interfragmentary strain in comparison with changing the screws positions (compare Figure 8 with Figures 9-11).
The effect of gap size on interfragmentary strain (εIF) was not investigated in this study. However, in the bone-LCP construct, because there is no contact between plate and bone (biological fixation) [3] [8] , the gap size should not have considerable influence on the stiffness of the bone-implant system and the interfragmentary movement (as reported by [30] [31] ). The interfragmentary strain (εIF) that is defined by the interfragmentary displacement over the initial gap length (see Equation (1) and Figure 5), has an inverse linear relationship with the initial gap size. Based on these explanation, it can be concluded that results obtained in this study can be extended to the models with a gap greater than 3 mm by applying an appropriate coefficient. It should be noted that because of the possibility of bone contact for gap size of smaller than 3 mm, the above mentioned point might not be true.
This study has some limitations. No experimental tests were conducted in this research, and the validation of our results was done by comparing with others’ studies reported in the literature. Verification of the developed numerical model can increase the impact of the results. Moreover, as it is difficult to apply anatomical boundary condition to the condyle of femur, in most studies, boundary conditions are simplified through constraining the distal end of the femurrigidity [21] [32] -[36] . Geometrical complexity of condyle was also disregarded in this study, and the distal fragment of femur was modeled by a cylinder (see Figure 1). These simplifications reduce the computational costs and can help address convergence issues (see Figure 7) [26] [33] . To simulate the physiological condition during normal gait, the effective muscle forces, i.e. abductors and vastus lateralis [32] [34] [37] [38] should also be considered, which was another limitation of this work. Furthermore, in the present investigation, only vertical component of the hip reaction force was modeled, but according to [32] -[34] [37] -[39] , consideration of two other components of hip reaction force, i.e. loads in the z and y directions (see Figure 6), can provide us with more accurate results. In this study only axial interfragmentary movement was investigated, but it should be concerned that by considering muscle forces and other components of hip reaction forces, shear interfragmentary movement plays a more significant role in the production of the fibrous tissue [40] and consequently will result in delay in union or non-union [41] [42] , that should be investigated in the future studies.
Modeling the interaction between the bone and screw is a challenging task, which was tackled differently in various studies [36] [43] . In this study, we used tied contact in which the outer nodes of the screw were bonded to the surface of the bone holes, and subsequently there is no relative displacement between these two surfaces. This approaches imply that there was full osseointegration between bone and screw, which is not a realistic assumption especially in the early phase of bone healing process. To simulate bone-screw interaction more realistically, the quality of interconnection of the bone-screw surfaces should increase gradually from more poorest osseointegration, by considering no friction between the surfaces of the bone-screw, to low friction that implies imperfect osseointegration [43] [44] and ultimately “Tie” contact that represents full osseointegration [36] [43] - [45] . Besides, in order to have a more realistic simulation of the bone-screw construct, geometry of the screw must be modeled more realistically by considering the screw threads [43] [45] , and then stress shielding as a crucial factor in determining failure of screw-bone could be investigated [46] .
5. Conclusion
In this study, the effects of screw number and position on the interfragmentary strain, and the relations between the screw configurations and the interfragmentary strain (εIF) in a femur-LCP construct were investigated. It was shown that inserting two innermost screws is the most influential factor in interfragmentary strain, while the effects of other screws, as well as screw numbers are less important. Thus, an optimal configuration of the screws for minimizing the healing time and also the cost of surgery might be a configuration with a small number of screws, which are close to the fracture site, considering appropriate magnitude of external load, as a crucial contributor.
Acknowledgements
The authors would like to thanks Amirkabir University of Technology, Iran, University of Calgary, Canada, Natural Sciences and Engineering Council of Canada, and AB is also thankful to the Science and Research Branch Islamic Azad University (SRBIAU), Iran.
Cite this paper
JalilNourisa,AminBaseri,LeszekSudak,GholamrezaRouhi, (2015) The Effects of Bone Screw Configurations on the Interfragmentary Movement in a Long Bone Fixed by a Limited Contact Locking Compression Plate. Journal of Biomedical Science and Engineering,08,590-600. doi: 10.4236/jbise.2015.89055
References
- 1. Moore, K.L., Dalley, A.F. and Agur, A.M. (2013) Clinically Oriented Anatomy. Wolters Kluwer Health.
- 2. Bucholz, R.W. and Jones, A. (1991) Fractures of the Shaft of the Femur. The Journal of Bone and Joint Surgery American, 73, 1561-1566.
- 3. Perren, S.M. (2002) Evolution of the Internal Fixation of Long Bone Fractures. The Scientific Basis of Biological Internal Fixation: Choosing a New Balance between Stability and Biology. The Journal of Bone & Joint Surgery (Br), 84, 1093-1110.
http://dx.doi.org/10.1302/0301-620X.84B8.13752 - 4. Nork, S.E. (2006) Femural Shaft Fracture. Rockwood and Green’s Fractures in Adults. Lippincott Williams & Wilkins, Philadelphia, 14-15.
- 5. Endo, H., Asaumi, K., Mitani, S., Noda, T., Minagawa, H., Tetsunaga, T., et al. (2008) The Minimally Invasive Plate Osteosynthesis (MIPO) Technique with a Locking Compression Plate for Femoral Lengthening. Acta Medica Okayama, 62, 333-339.
- 6. Oh, C.-W., Kim, J.-J., Byun, Y.-S., Oh, J.-K., Kim, J.-W., Kim, S.-Y., et al. (2009) Minimally Invasive Plate Osteosynthesis of Subtrochanteric Femur Fractures with a Locking Plate: A Prospective Series of 20 Fractures. Archives of Orthopaedic and Trauma Surgery, 129, 1659-1665.
http://dx.doi.org/10.1007/s00402-009-0815-y - 7. Strohm, P., Reising, K., Hammer, T., Suedkamp, N., Jaeger, M. and Schmal, H. (2011) Humerus Shaft Fractures— Where Are We Today. Acta Chirurgiae Orthopaedicae et Traumatologiae Cechosl, 78, 185-189.
- 8. Miller, D.L. and Goswami, T. (2007) A Review of Locking Compression Plate Biomechanics and Their Advantages as Internal Fixators in Fracture Healing. Clinical Biomechanics, 22, 1049-1062.
http://dx.doi.org/10.1016/j.clinbiomech.2007.08.004 - 9. Kanchanomai, C., Phiphobmongkol, V. and Muanjan, P. (2008) Fatigue Failure of an Orthopedic Implant—A Locking Compression Plate. Engineering Failure Analysis, 15, 521-530.
http://dx.doi.org/10.1016/j.engfailanal.2007.04.001 - 10. Stoffel, K., Dieter, U., Stachowiak, G., Gachter, A. and Kuster, M.S. (2003) Biomechanical Testing of the LCP—How Can Stability in Locked Internal Fixators Be Controlled? Injury, 34, 11-19.
http://dx.doi.org/10.1016/j.injury.2003.09.021 - 11. Gautier, E. and Sommer, C. (2003) Guidelines for the Clinical Application of the LCP. Injury, 34, 63-76.
http://dx.doi.org/10.1016/j.injury.2003.09.026 - 12. Tan, S. and Balogh, Z.J. (2009) Indications and Limitations of Locked Plating. Injury, 40, 683-691.
http://dx.doi.org/10.1016/j.injury.2009.01.003 - 13. ElMaraghy, A., ElMaraghy, M., Nousiainen, M., Richards, R. and Schemitsch, E. (2001) Influence of the Number of Cortices on the Stiffness of Plate Fixation of Diaphyseal Fractures. Journal of Orthopaedic Trauma, 15, 186-191.
http://dx.doi.org/10.1097/00005131-200103000-00007 - 14. Ellis, T., Bourgeault, C.A. and Kyle, R.F. (2001) Screw Position Affects Dynamic Compression Plate Strain in an in Vitro Fracture Model. Journal of Orthopaedic Trauma, 15, 333-337.
http://dx.doi.org/10.1097/00005131-200106000-00005 - 15. Field, J.R., Tornkvist, H., Hearn, T.C., Sumner-Smith, G. and Woodside, T.D. (1999) The Influence of Screw Omission on Construction Stiffness and Bone Surface Strain in the Application of Bone Plates to Cadaveric Bone. Injury, 30, 591-598.
http://dx.doi.org/10.1016/S0020-1383(99)00158-8 - 16. Lindvall, E.M. and Sagi, H.C. (2006) Selective Screw Placement in Forearm Compression Plating: Results of 75 Consecutive Fractures Stabilized with 4 Cortices of Screw Fixation on Either Side of the Fracture. Journal of Orthopaedic Trauma, 20, 157-162.
http://dx.doi.org/10.1097/00005131-200603000-00001 - 17. Sanders, R., Haidukewych, G.J., Milne, T., Dennis, J. and Latta, L.L. (2002) Minimal versus Maximal Plate Fixation Techniques of the Ulna: The Biomechanical Effect of Number of Screws and Plate Length. Journal of Orthopaedic Trauma, 16, 166-171.
http://dx.doi.org/10.1097/00005131-200203000-00005 - 18. Tornkvist, H., Hearn, T. and Schatzker, J. (1996) The Strength of Plate Fixation in Relation to the Number and Spacing of Bone Screws. Journal of Orthopaedic Trauma, 10, 204-208.
http://dx.doi.org/10.1097/00005131-199604000-00009 - 19. Freeman, A.L., Tornetta III, P., Schmidt, A., Bechtold, J., Ricci, W. and Fleming, M. (2010) How Much Do Locked Screws Add to the Fixation of “Hybrid” Plate Constructs in Osteoporotic Bone? Journal of Orthopaedic Trauma, 24, 163-169.
http://dx.doi.org/10.1097/BOT.0b013e3181d35c29 - 20. Hak, D.J., Althausen, P. and Hazelwood, S.J. (2010) Locked Plate Fixation of Osteoporotic Humeral Shaft Fractures: Are Two Locking Screws per Segment Enough? Journal of Orthopaedic Trauma, 24, 207-211.
http://dx.doi.org/10.1097/BOT.0b013e3181bdd1da - 21. Lee, C.H., Shih, K.S., Hsu, C.C. and Cho, T. (2014) Simulation-Based Particle Swarm Optimization and Mechanical Validation of Screw Position and Number for the Fixation Stability of a Femoral Locking Compression Plate. Medical Engineering & Physics, 36, 57-64.
http://dx.doi.org/10.1016/j.medengphy.2013.09.005 - 22. MacLeod, A., Pankaj, P. and Simpson, H. (2012) The Effect of Varying Screw Configuration on the Mechanical Response of Locking Plate Fixators. Journal of Biomechanics, 45, S218.
http://dx.doi.org/10.1016/S0021-9290(12)70219-1 - 23. https://www2.aofoundation.org.
- 24. Ahmad, M., Nanda, R., Bajwa, A., Candal-Couto, J., Green, S. and Hui, A. (2007) Biomechanical Testing of the Locking Compression Plate: When Does the Distance between Bone and Implant Significantly Reduce Construct Stability? Injury, 38, 358-364.
http://dx.doi.org/10.1016/j.injury.2006.08.058 - 25. Kim, H.-J., Kim, S.-H. and Chang, S.-H. (2011) Finite Element Analysis Using Interfragmentary Strain Theory for the Fracture Healing Process to Which Composite Bone Plates Are Applied. Composite Structures, 93, 2953-2962.
http://dx.doi.org/10.1016/j.compstruct.2011.05.008 - 26. Wang, C., Yettram, A., Yao, M. and Procter, P. (1998) Finite Element Analysis of a Gamma Nail within a Fractured Femur. Medical Engineering & Physics, 20, 677-683.
http://dx.doi.org/10.1016/S1350-4533(98)00079-4 - 27. Benli, S., Aksoy, S., Havitcgolu, H. and Kucuk, M. (2008) Evaluation of Bone Plate with Low-Stiffness Material in Terms of Stress Distribution. Journal of Biomechanics, 41, 3229-3235.
http://dx.doi.org/10.1016/j.jbiomech.2008.08.003 - 28. Lacroix, D. and Prendergast, P. (2002) A Mechano-Regulation Model for Tissue Differentiation during Fracture Healing: Analysis of Gap Size and Loading. Journal of Biomechanics, 35, 1163-1171.
http://dx.doi.org/10.1016/S0021-9290(02)00086-6 - 29. Lacroix, D., Prendergast, P., Li, G. and Marsh, D. (2002) Biomechanical Model to Simulate Tissue Differentiation and Bone Regeneration: Application to Fracture Healing. Medical & Biological Engineering & Computing, 40, 14-21.
http://dx.doi.org/10.1007/BF02347690 - 30. Nassiri, M., MacDonald, B. and O’Byrne, J.M. (2013) Computational Modelling of Long Bone Fractures Fixed with Locking Plates—How Can the Risk of Implant Failure Be Reduced? Journal of Orthopaedics, 10, 29-37.
http://dx.doi.org/10.1016/j.jor.2013.01.001 - 31. Oh, J.K., Sahu, D., Ahn, Y.H., Lee, S.J., Tsutsumi, S., Hwang, J.H., et al. (2010) Effect of Fracture Gap on Stability of Compression Plate Fixation: A Finite Element Study. Journal of Orthopaedic Research, 28, 462-467.
- 32. Britton, J., Walsh, L. and Prendergast, P. (2003) Mechanical Simulation of Muscle Loading on the Proximal Femur: Analysis of Cemented Femoral Component Migration with and without Muscle Loading. Clinical Biomechanics, 18, 637-646.
http://dx.doi.org/10.1016/S0268-0033(03)00113-X - 33. Tsai, A.G., Reich, M.S., Bensusan, J., Ashworth, T., Marcus, R.E. and Akkus, O. (2013) A Fatigue Loading Model for Investigation of Iatrogenic Subtrochanteric Fractures of the Femur. Clinical Biomechanics, 28, 981-987.
http://dx.doi.org/10.1016/j.clinbiomech.2013.09.009 - 34. Simoes, J., Vaz, M., Blatcher, S. and Taylor, M. (2000) Influence of Head Constraint and Muscle Forces on the Strain Distribution within the Intact Femur. Medical Engineering & Physics, 22, 453-459.
http://dx.doi.org/10.1016/S1350-4533(00)00056-4 - 35. Cheung, G., Zalzal, P., Bhandari, M., Spelt, J. and Papini, M. (2004) Finite Element Analysis of a Femoral Retrograde Intramedullary Nail Subject to Gait Loading. Medical Engineering & Physics, 26, 93-108.
http://dx.doi.org/10.1016/j.medengphy.2003.10.006 - 36. Wieding, J., Souffrant, R., Fritsche, A., Mittelmeier, W. and Bader, R. (2012) Finite Element Analysis of Osteosynthesis Screw Fixation in the Bone Stock: An Appropriate Method for Automatic Screw Modelling. PLoS ONE, 7, e33776.
http://dx.doi.org/10.1371/journal.pone.0033776 - 37. Heller, M., Bergmann, G., Kassi, J.-P., Claes, L., Haas, N. and Duda, G. (2005) Determination of Muscle Loading at the Hip Joint for Use in Pre-Clinical Testing. Journal of Biomechanics, 38, 1155-1163.
http://dx.doi.org/10.1016/j.jbiomech.2004.05.022 - 38. Stolk, J., Verdonschot, N. and Huiskes, R. (2001) Hip-Joint and Abductor-Muscle Forces Adequately Represent in Vivo Loading of a Cemented Total Hip Reconstruction. Journal of Biomechanics, 34, 917-926.
http://dx.doi.org/10.1016/S0021-9290(00)00225-6 - 39. Campoli, G., Weinans, H. and Zadpoor, A.A. (2012) Computational Load Estimation of the Femur. Journal of the Mechanical Behavior of Biomedical Materials, 10, 108-119.
http://dx.doi.org/10.1016/j.jmbbm.2012.02.011 - 40. Watson-Jones, R. and Wilson, J.N. (1982) Watson-Jones Fractures and Joint Injuries. Churchill Livingstone, Edinburg.
- 41. Aro, H.T., Wahner, H.T. and Chao, E.Y. (1991) Healing Patterns of Transverse and Oblique Osteotomies in the Canine Tibia under External Fixation. Journal of Orthopaedic Trauma, 5, 351-364.
http://dx.doi.org/10.1097/00005131-199109000-00016 - 42. Yamagishi, M. and Yoshimura, Y. (1955) The Biomechanics of Fracture Healing. The Journal of Bone & Joint Surgery, 37, 1035-1068.
- 43. MacLeod, A.R., Pankaj, P. and Simpson, A. (2012) Does Screw-Bone Interface Modelling Matter in Finite Element Analyses? Journal of Biomechanics, 45, 1712-1716.
http://dx.doi.org/10.1016/j.jbiomech.2012.04.008 - 44. Yang, J. and Xiang, H.-J. (2007) A Three-Dimensional Finite Element Study on the Biomechanical Behavior of an FGBM Dental Implant in Surrounding Bone. Journal of Biomechanics, 40, 2377-2385.
http://dx.doi.org/10.1016/j.jbiomech.2006.11.019 - 45. Haase, K. and Rouhi, G. (2013) Prediction of Stress Shielding around an Orthopedic Screw: Using Stress and Strain Energy Density as Mechanical Stimuli. Computers in Biology and Medicine, 43, 1748-1757.
http://dx.doi.org/10.1016/j.compbiomed.2013.07.032 - 46. Rouhi, G., Tahani, M., Haghighi, B. and Herzog, W. (2015) Prediction of Stress Shielding around Orthopedic Screws: Time-Dependent Bone Remodeling Analysis Using Finite Element Approach. Journal of Medical and Biological Engineering,35, 545-554.
NOTES

*Corresponding author.













