Journal of Biomedical Science and Engineering
Vol.7 No.9(2014), Article
ID:47573,10
pages
DOI:10.4236/jbise.2014.79064
Helical Dielectrophoretic Particle Separator Fabricated by Conformal Spindle Printing
Nicolas Guérin, Martin Lévesque, Daniel Therriault
Laboratory for Multiscale Mechanics, Mechanical Engineering Department, École Polytechnique de Montréal, Montréal, Canada
Email: daniel.therriault@polymtl.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 May 2014; revised 17 June 2014; accepted 29 June 2014
ABSTRACT
This paper reports the fabrication and testing of a helical cell separator that uses insulator-based dielectrophoresis as the driving force of its separation. The helical channel shape’s main advantage is its constant curvature radius which generates a constant electric field gradient. The presented separator was fabricated by extruding a sacrificial ink on rotating spindles using a computer-controlled robot. After being assembled, connected to the reservoir and encapsulated in epoxy resin, the ink was removed to create a helical microchannel. The resulting device was tested by circulating polystyrene microbeads of 4 and 10 µm diameter through its channel using a voltage of 900 VDC. The particles were separated with efficiencies of 94.0% and 92.5%, respectively. However, roughness in some parts of the channel and connections that had larger diameters compared to the channel created local electric field gradients which, doubtless, hindered separation. It is a promising device that could lead the way toward portable and affordable medical devices.
Keywords:Conformal Printing, Dielectrophoresis, Particle Separator, Helix

1. Introduction
Cell separation is an essential part of the sample preparation prior to medical testing, as in the case of the concentration and separation of erythrocytes from other blood for the detection of malaria [1] . Current techniques for this key step rely on large and expensive equipment [2] [3] that cannot easily be used outside laboratories and hospitals. The miniaturization of the medical diagnostic equipment would facilitate field testing and could reduce the time between sample collection and eventual treatment. As a matter of fact, approximately 95% of the time needed to obtain molecular diagnostic data is associated to sample collection, transportation and preparation [4] .
Dielectrophoresis (DEP) is the physical process by which forces are applied to particles polarized by an inhomogeneous electric field. DEP can efficiently be used to separate particles since the magnitude and orientation of the forces depend on different properties such as the radii of the particles, the permittivities of the particles and medium as well as the electric field gradient. As such, DEP has been used to separate carbon nanotubes by chirality [5] . Moreover, DEP has been widely investigated as the operating principle for miniaturized medical devices [1] [6] -[13] .
The first type of DEP to be discovered [14] is the electrode-based DEP in which the inhomogeneity of the electric field arises from the shape of the electrodes generating the electric field such as pinlike electrodes [15] or interdigitated electrodes [16] . In a separator application, the electrodes are the driving force of the separation and must necessarily be placed where the separation occurs. This electrode placement presents some important disadvantages such as Joule heating [17] [18] and electrolysis of the suspending medium which can alter the trajectory of the particles and greatly hinder the separation [19] .
In insulator-based dielectrophoresis (iDEP), the device is non-conductive and the inhomogeneity of the electric field arises from the shape of the device itself [20] . The main advantage resides in the fact that the electrodes are located away from the separation site, usually in the input and output reservoirs of the device. Joule heating and electrolysis can still occur but they do not significantly disrupt the separation process since they take place far from the location where the separation itself occurs [17] .
Different iDEP-based separator shapes have been proposed such as an insulating hurdle [6] , a serpentine [7] and a planar spiral shape [8] . These devices were fabricated by a conventional microfabrication technique called soft lithography. These two-dimensional (2D) separators can efficiently separate many types of particles with a simple design. Spiral-shaped separators, in particular, have obtained very good separation efficiency [8] . However, in spiral-shaped separators, the force applied on a given particle is inversely proportional to the curvature radius of the channel. Hence, the center section of the separator applies relatively large forces on the particles, whereas, the periphery applies lower forces. This section of the channel is, thus, less effective.
This shortcoming could be overcome by using a three-dimensional (3D) spiral equivalent: the helix. In a helical channel, the curvature radius is constant, thus resulting in constant separation forces throughout the channel regardless of its length. Despite being very powerful for the fabrication of 2D shapes, conventional microfabrication methods, such as soft lithography, are incapable of producing complex 3D shapes such as a helical microchannel.
This article reports a new 3D iDEP particle separator relying on helical microchannels fabricated by conformal spindle printing. This method consists of a computer-controlled fugitive ink deposition on rotating spindles creating helices that are assembled and connected to reservoirs before being encapsulated into an epoxy resin. The ink is removed to create the helical channels. Although 3D devices have been reported [9] [16] [21] -[23] , this new device surpasses all existing 3D devices by the complexity of its shape.
This paper presents the operating principle of the separator, its design, its fabrication process, the particle suspension preparation and the description of the separation experiments, respectively. The fabrication capabilities and separation results are presented next, followed by concluding remarks.
2. Experimental
2.1. Dielectrophoresis Theory
Particles suspended in a medium between two electrodes under tension are polarized by the ensuing electric field. Charges inside the particles accumulate near the particle-medium interfaces and attract charges inside the medium. Charges also accumulate at the interfaces on the medium side. These accumulations of electric charges form what are called electric double layers [6] .
The polarizabilities of both medium and particles determine the relative quantity of charges inside and outside the particles. As negative and positive charges attract, and effectively cancel each other, electric dipoles are created. These relative differences determine the orientation of the dipoles [6] .
A net dipole inside an electric field is subjected to forces resulting from the attraction of opposite charges and the repulsion of identical charges. In the case of a symmetrical electric field generated by electrodes of identical sizes and shapes, for example, the forces cancel each other and no resulting force occurs. If the electric field is inhomogeneous, when electrodes of different sizes are used for example, a resulting force is applied on each particle. This force can be expressed by [24] :
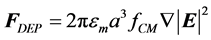 (1)
(1)
where 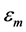 is the permittivity of the medium,
is the permittivity of the medium, 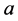 is the radius of the particle,
is the radius of the particle, 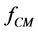 is the Clausius-Mossotti factor and
is the Clausius-Mossotti factor and  is the electric field. In a DC electric field, the Clausius-Mossoti factor is given by [25]
is the electric field. In a DC electric field, the Clausius-Mossoti factor is given by [25]
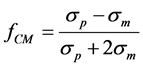 (2)
(2)
where 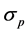 and
and 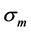 are the conductivity of each particle and the medium, respectively. This factor, which varies from −0.5 to 1, determines if the particles are attracted or repulsed by regions of high electric field intensity [26] . The Clausius-Mossotti factor also affects the value of the dielectrophoretic force. By carefully selecting the medium conductivity,
are the conductivity of each particle and the medium, respectively. This factor, which varies from −0.5 to 1, determines if the particles are attracted or repulsed by regions of high electric field intensity [26] . The Clausius-Mossotti factor also affects the value of the dielectrophoretic force. By carefully selecting the medium conductivity,  can be tailored to obtain the required force, the absolute maxima being bounded by the extreme values of −0.5 and 1.
can be tailored to obtain the required force, the absolute maxima being bounded by the extreme values of −0.5 and 1.
Particles being acted upon by dielectrophoresis accelerate inside the medium. The acceleration is dictated by the dielectrophoretic force and by the drag. As the velocity of the particles increase, so does the drag. When those two forces become equal, the particles reach their terminal velocity. Usually, the particles reach their terminal velocities inside the medium in a very short time (in the order of 10−4 s for 10 μm particles) [19] . The acceleration phase can then be neglected and velocity can be used instead of force to provide a clearer understanding of the particle behavior. The velocity of particles subjected to DEP is given by [27]
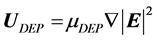 (3)
(3)
where , a measure of the impact of the electric field gradient on the particle velocity, is called the dielectrophoretic mobility. It is given by [27]
, a measure of the impact of the electric field gradient on the particle velocity, is called the dielectrophoretic mobility. It is given by [27]
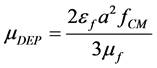 (4)
(4)
where 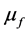 is the fluid viscosity.
is the fluid viscosity.
2.2. Helical Separator Operation Principle and Design
Figure 1(a) shows the design of the 3D separator that consisted of one inlet reservoir, two outlet reservoirs and a channel connecting the inlet to the outlet. In order to separate a bimodal particle dispersion, the channel and output reservoirs were filled with a conductive aqueous sodium chloride solution. The input reservoir was filled with the particle dispersion. Three electrodes made of 250 µm diameter gold wire, were immersed in the reservoirs. A DC voltage was then applied between the inlet and outlet as shown in Figure 1(a).
The electric field distribution for a voltage of 900 VDC is shown in Figure 1(b). The field values were obtained using COMSOL Multiphysics (Comsol, Burlington, MA, USA). Under the influence of the electric field, the particles were subjected to tangential forces resulting from electrically-induced phenomena called electroosmosis and electrokinesis and the resulting particle velocities are noted . Figure 1(c) shows the separator from the side with the three particle arrangement during the separation experiments. First, the particles entered the channel leading to the first helix in a random arrangement as shown in Figure 1(d). Upon entering the first helix, the particles were subjected to radial dielectrophoretic forces resulting in velocities noted
. Figure 1(c) shows the separator from the side with the three particle arrangement during the separation experiments. First, the particles entered the channel leading to the first helix in a random arrangement as shown in Figure 1(d). Upon entering the first helix, the particles were subjected to radial dielectrophoretic forces resulting in velocities noted  and given by equation (3). These velocities were toward the outside wall of the channel and their magnitude depended on the size of the particles. The larger particles had a larger radial velocity than the smaller particles. Due to the sufficient length of the first helix, both types of particles reached the outside wall and were aligned when exiting the first helix, as shown in Figure 1(e). This first step was crucial in order to separate the particles because their random positions would nullify the effect of the difference in
and given by equation (3). These velocities were toward the outside wall of the channel and their magnitude depended on the size of the particles. The larger particles had a larger radial velocity than the smaller particles. Due to the sufficient length of the first helix, both types of particles reached the outside wall and were aligned when exiting the first helix, as shown in Figure 1(e). This first step was crucial in order to separate the particles because their random positions would nullify the effect of the difference in  rendering separation nearly impossible.
rendering separation nearly impossible.
After the alignment, the particles entered the second helix which was coiled in the opposite direction and in which the outside wall became the inside wall. The electric field gradient pushed the particles with the same respective velocities toward the outside wall. The difference in velocities separated the particles until they reached
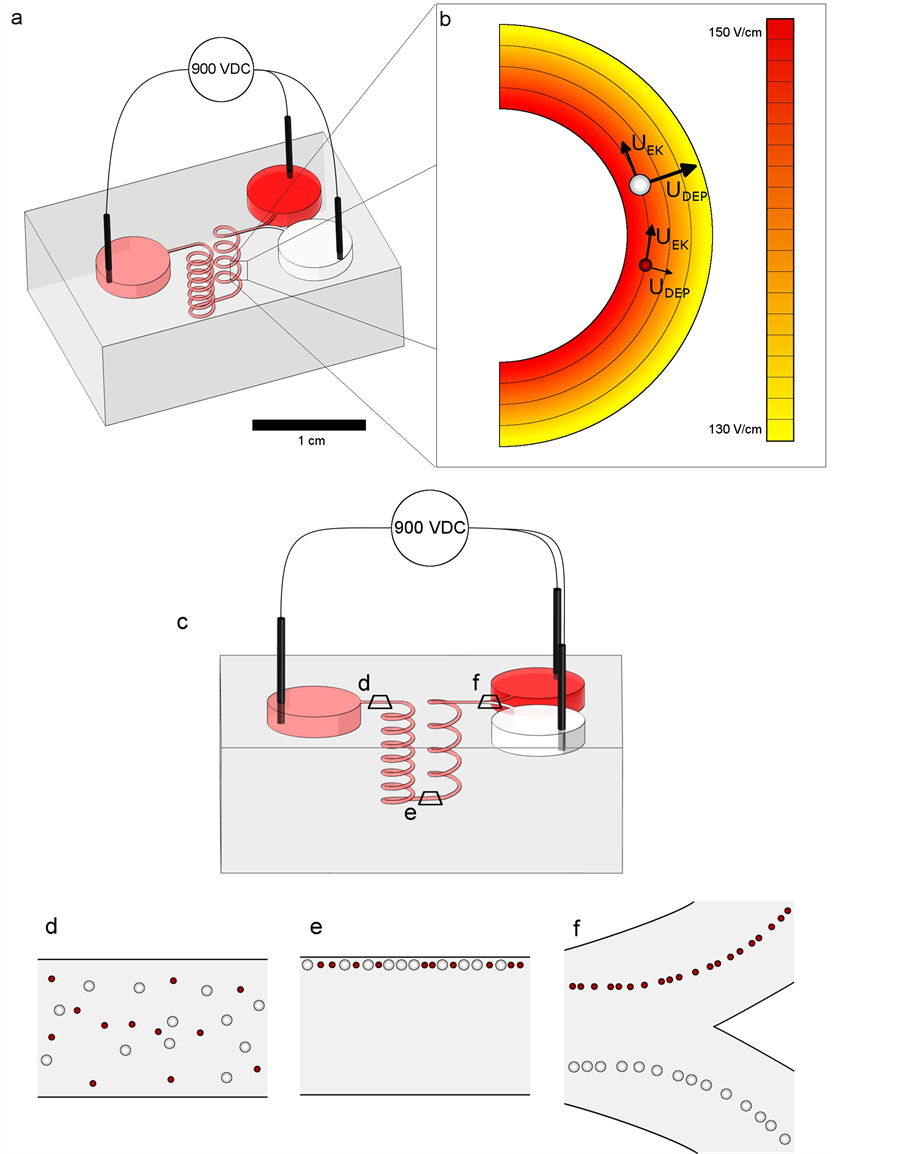
Figure 1. Schematics of the design and operation of the helical separator. (a) Isometric view of the separator. The inlet reservoir contains a mixed suspension which is separated into its two constituents which are present in the outlet reservoirs. (b) Illustration of the electric field intensity in the curved channel for a voltage of 900 VDC and its effect on particles. (c) Slightly inclined side view of the separator showing three stages of particle separation with a 900 VDC voltage. (d) Randomly distributed particles enter the first helix. (e) Particles are aligned after their transit through the first helix. (f) Separated particles exit the second helix and are split toward the two output reservoirs.
the end of the second helix. That length was shorter than that of the first helix to insure that the particles did not reach the outside wall but were properly positioned with respect to the bifurcation shown in Figure 1(f). The particles were then collected in the outlet reservoirs.
2.3. Separator Fabrication
The microchannels were fabricated using the direct-write fabrication method [28] . The sacrificial ink, which was made of 70 wt% of petroleum jelly (Unilever, Toronto, Canada) and 30 wt% microcrystalline wax (Strahl & Pitsch, West Babylon, NY, USA), was extruded through a steel nozzle by the piston.
Fugitive ink was deposited on rotating epoxy 1.2 mm diameter spindles with the direct-write method to create the helices, as shown on Figure 2(a). This diameter of spindle, which determined the curvature radius, was chosen because of ease of fabrication. These spindles were rotated using a precision electric motor (VT-80, Pi Micos GmbH, Eschbach, Germany). For each helix, a straight section was deposited first to facilitate the connection of the channels. The helix was deposited on the rotating spindle and followed by another straight section. The first helix had 6 coils and the second had 4. These numbers of coils were determined by analysis of the results of previous prototypes. They were both made using a 100 μm nozzle and a pressure of 550 kPa. This nozzle size was chosen because of its availability.
The two epoxy spindles were glued upright on a glass slide. The inlet and outlet channels were deposited and connected to the lower part of the helices as shown on Figure 2(b). The bifurcation was completed by depositing its second branch. The reservoirs were fabricated by depositing circular walls 1.5 mm high and with a diameter of 5 mm which were subsequently filled with fugitive ink to prevent resin infiltration during the encapsulation step. The entire apparatus was encapsulated with a two-part liquid epoxy (Epon 862/Epikure 3274, Momentive, Colombus, OH, USA) and left to cure as illustrated in Figure 2(c). The top section of the epoxy was then carefully cut using a precision saw (Isomet Low Speed Saw, Buehler Canada, Whitby, ON, Canada) to prevent the introduction of foreign particles that could clog the channels. The two exposed filaments were connected with a filament of fugitive ink deposited with a 100 µm nozzle thus completing the connection of all the filaments as shown on Figure 2(d). This last filament was encapsulated with epoxy and left to cure. The glass slide was removed to expose the filaments. The encapsulated model was heated in boiling water to melt the ink that was then removed by applying vacuum to one end of the channel. Any remaining ink residue was dissolved and removed by circulating hexane through the channel. The remaining epoxy block had empty channels and reservoirs and constituted a finished and functional separator.
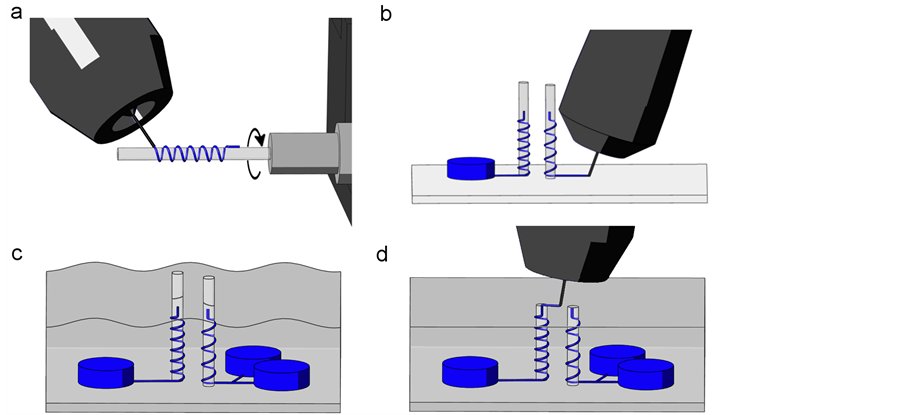
Figure 2. Fabrication steps of the helical separator. (a) Deposition of the fugitive ink on a rotating spindle. (b) Deposition of the reservoirs and filaments linking the upright helices to the reservoirs. (c) Encapsulation of the reservoirs and filaments in liquid epoxy resin. (d) After curing, the top part of the epoxy is cut to expose the filaments that are connected with another fugitive ink filament.
2.4. Suspension Preparation
The particle suspension was prepared by mixing 4 and 10 µm polystyrene microbeads (Fluka Analytical, Buchs, Switzerland) with an aqueous solution of 100 ppm of sodium chloride. The solution was also used without particles to fill the channel and the outlet reservoirs. The final suspension had a conductivity measured of 210 µS/cm and contained approximately 5 × 106 particles per mL of each type for a total of 107 particles per mL. The conductivities of the particles were 10 µS/cm and 4 µS/cm for the 4 µm and 10 µm particles, respectively (these conductivities were calculated using the surface conductance recommended by Ermolina and Morgan [29] ). The Clausius-Mossotti factor of both particle types were computed as −0.465 and −0.486 for the 4 µm and 10 µm particles, respectively, from Equation (2). These values are very close to the theoretical minimum of the Clausius-Mossotti factor of −0.5, which means that, during separation experiments, the particles were pushed toward the regions of low electric field value with forces very close to the maxima allowed by a negative ClausiusMossotti factor. The specific gravity of polystyrene being 1.05, the particles tended to settle. Manual stirring was required before the particle introduction in the inlet reservoir.
2.5. Separation Experiments
The outlet reservoirs and channel were filled with the NaCl solution using a syringe. The inlet reservoir was then filled with approximately 30 µL of particle suspension using a pipette. The gold electrodes were immersed inside the reservoirs. The voltage was supplied by a 1000 VDC electrophoresis power supply (FB1000Q, ColeParmer, Montréal, Canada). The inlet reservoir received the positive potential and the outlet reservoirs were grounded. The reservoirs were carefully filled to the same level to avoid the interference of a pressure induced flow.
2.6. Image Analysis
Particle motion was captured using an Evolution VF Camera (MediaCybernetics, Rockville, MD, USA) and an SZX12 stereomicroscope (Olympus, Richmond Hill, Ontario, Canada). Close-up fluorescent optical images were taken using an Evolution VF camera and a BX61 microscope (Olympus). Pictures were treated with Image Pro 7 (MediaCybernetics). Close-up images were assembled from several images with different focus heights to extend the depth of field.
3. Results and Discussion
3.1. Analysis of Fabricated Separator Geometry
Figure 3(a) shows the completed 3D separator having a total microchannel length of 65 mm and a planar footprint is 2.6 cm2, which is a 35% reduction compared to a reported spiral-shaped separator [8] . The effective separation length, which was comprised of the two helices and their connection, was 42 mm. The curvature radius of the helices at the center of the channels, which takes into account the channel roughness, was 0.650 ± 0.004 mm. The channel in the helical part of the separator, which is shown in Figure 3(b), had a diameter of 111 ± 6 µm. The three straight channel parts were fabricated with the same procedure. Their width should have been similar. Two of the three were similar with a width of 147 ± 4 µm. However, the top channel (shown in Figure 3(c)) had a width of 215 ± 15 µm. This difference can be seen in Figure 3(c) where the angled part is smooth and the horizontal part is wider and more jagged. The junction between the different parts of the channel, such as those visible at the bottom of Figure 3(b) and the top of Figure 3(d), had a diameter of 216 ± 54 µm.
The overall dimensions and shape of the designed separator were respected. The curvature radius was relatively constant in the device and the channel dimensions had variations of less than 7%. Despite the overall smoothness, one part of the output channel had some visible roughness that induced local electric field gradients and could potentially have hindered the separation. The difference between the total length and the effective length did not contribute to the separation but reduced the available voltage in the helices. The connections between the different parts of the channel had diameters that were nearly twice that as large as the average diameter of the helices, which also created local electric field distortions. Finally, the fabrication process is complex and heavily reliant on manual operations.
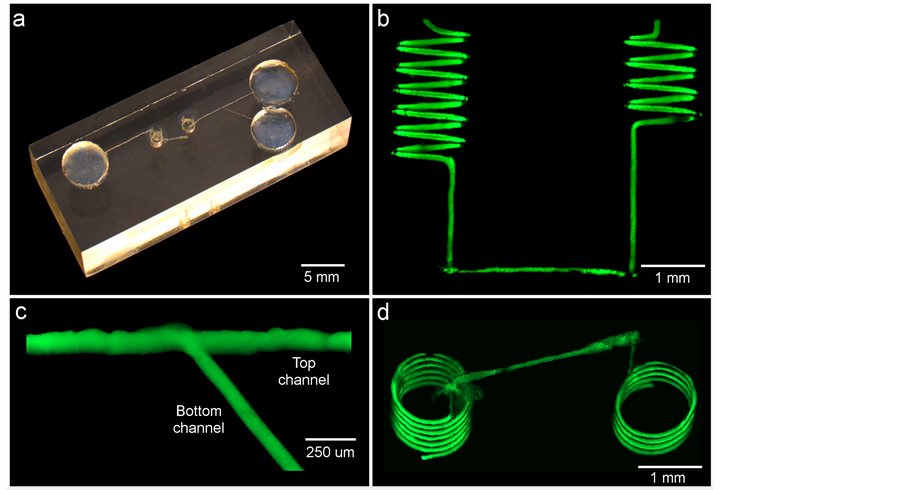
Figure 3. (a) Optical image of the fabricated separator. (b) Fluorescent side view image of the two helices. (c) Fluorescent top view image of the bifurcation. (d) Fluorescent slightly inclined bottom view of the two helices.
3.2. Separation Efficiency
Separation experiments have been performed with the method described in Section 2.5. Voltages between 800 and 1000 VDC were tested. The highest separation efficiency was obtained using a voltage of 900 VDC.
Figure 4(a) shows the particles before separation. The particles accumulated in both output reservoirs after their separation using a voltage of 900 VDC. Figure 4(b) shows a still image from the video captured of the bifurcation during a test using a voltage of 900 VDC. The 4 and 10 µm particles can be seen being separated and entering both branches of the bifurcation which lead them to the output reservoirs. Figure 4(c) and Figure 4(e) show representative images of the separated particles in each of the reservoirs after the test. Figure 4(d) shows the separation efficiency calculated by counting the proportion of each type of particle that reached the expected reservoir. After their transit through the separator, 94.0% of the 4 µm particles reached the reservoir at the end of the top channel and 92.5% of the 10 µm particle reached the reservoir at the end of the bottom channel. The particles were tracked and counted from recorded videos of the separation experiments.
Difficulties were encountered during the separation experiments. The results were difficult to reproduce because valid tests were challenging to obtain. The fine adjustment of the level of solution in each reservoir was especially difficult to make. An uneven level of solution led to pressure-induced flow which deviated the particles and prevented efficient separation. The settling of the particles during the short initial period between the introduction of the particle in the input reservoir and the beginning of the separation experiments was also a problem observed. Since the 10 µm particles settled more rapidly than the 4 µm particles, the smaller particles were more numerous altogether during the experiments even though the same number of each type of particle was introduced in the input reservoir.
Reported 2D separators have efficiencies varying between 90% and 98% [7] [8] . These results are comparable to the results obtained in the experiments with the helical-shaped separator. The fabrication process generated geometrical flaws, such as channel roughness and increased cross-section in the connections, which most probably hindered the separation. Considering these shortcomings, the results, and how they compare with other devices, are promising.
4. Conclusion
The fabrication of a functional dual helix dielectrophoretic separator was presented in this paper. Separation
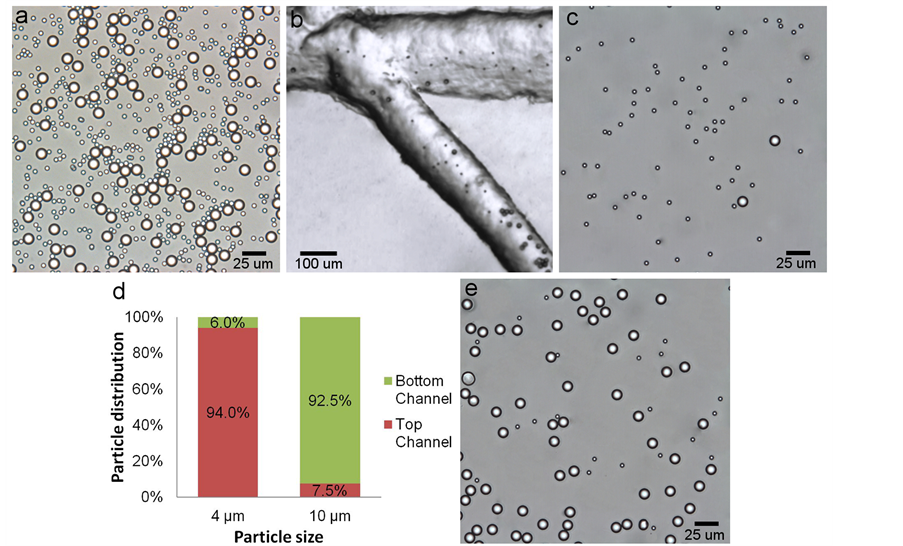
Figure 4. Separation results of the 3D separator using a voltage of 900 VDC. (a) Optical image of the 4 µm and 10 µm particles before separation. (b) Bifurcation of the channel during a separation at 900 VDC. (c) Particles collected from the top reservoir after separation. (d) Proportion of the particles reaching the expected reservoir (e) Particles collected from the bottom reservoir after separation.
tests at 900 VDC obtained separation efficiencies of 94.0% and 92.5% for 4 µm and 10 µm particles respectively. These results are similar to those obtained with 2D DEP-based separator that were reported in the literature. In order to prove the applicability of this device to the biomedical field and to better compare it with other existing devices, further separation experiments will have to be performed using living cells. As polystyrene separation is very common in the literature as a proving ground for new separation devices, these results constitute a definite and encouraging proof of concept for the helical DEP separator because even with some geometrical flaws, the prototype was able to obtain separation efficiencies comparable to 2D devices. A spiral-shaped separator has two intertwined spirals, thus binding the length of the two spirals. Having two independent helices, the dual helix shape also lends a flexibility in the number of coils that a 2D separator does not have. This allows a precise tailoring of the number of coils for each helix to optimize the separation efficiency. The helical separator also has a smaller planar footprint than 2D separators. The efficient length of the helices is not limited because of its constant curvature radius. Helical DEP separators thus have the potential to outperform 2D separators while being more flexible and occupying less space.
References
- Gascoyne, P., Mahidol, C., Ruchirawat, M., Satayavivad, J., Watcharasit, P. and Becker, F.F. (2002) Microsample Preparation by Dielectrophoresis: Isolation of Malaria. Lab on a Chip, 2, 70-75. http://dx.doi.org/10.1039/b110990c
- Lewpiriyawong, N., Kandaswamy, K., Yang, C., Ivanov, V. and Stocker, R. (2011) Microfluidic Characterization and Continuous Separation of Cells and Particles Using Conducting Poly(dimethyl siloxane) Electrode Induced Alternating Current-Dielectrophoresis. Analytical Chemistry, 83, 9579-9585. http://dx.doi.org/10.1021/ac202137y
- Yu, C., Vykoukal, J., Vykoukal, D.M., Schwartz, J.A., Shi, L. and Gascoyne, P.R.C. (2005) A Three-Dimensional Dielectrophoretic Particle Focusing Channel for Microcytometry Applications. Journal of Microelectromechanical Systems, 14, 480-487. http://dx.doi.org/10.1109/JMEMS.2005.844839
- Gascoyne, P.R.C. and Vykoukal, J.V. (2004) Dielectrophoresis-Based Sample Handling in General-Purpose Programmable Diagnostic Instruments. Biomedical Applications for Mems and Microfluidics, 92, 22-42.
- Rao, C.N.R., Voggu, R. and Govindaraj, A. (2009) Selective Generation of Single-Walled Carbon Nanotubes with Metallic, Semiconducting and Other Unique Electronic Properties. Nanoscale, 1, 96-105. http://dx.doi.org/10.1039/b9nr00104b
- Kang, Y., Li, D., Kalams, S.A. and Eid, J.E. (2008) DC-Dielectrophoretic Separation of Biological Cells by Size. Biomedical Microdevices, 10, 243-249. http://dx.doi.org/10.1007/s10544-007-9130-y
- Church, C., Zhu, J. and Xuan, X. (2011) Negative Dielectrophoresis-Based Particle Separation by Size in a Serpentine Microchannel. Electrophoresis, 32, 527-531. http://dx.doi.org/10.1002/elps.201000396
- Zhu, J. and Xuan, X. (2011) Curvature-Induced Dielectrophoresis for Continuous Separation of Particles by Charge in Spiral Microchannels. Biomicrofluidics, 5, 024111-024113. http://dx.doi.org/10.1063/1.3599883
- Zellner, P.A., Sahari, A., Hosseini, Y., Behkam, B. and Agah, M. (2012) Selective E. coli Trapping with 3D Insulator-Based Dielectrophoresis Using DC-Biased, AC Electric Fields. 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS 2012, 28 August-1 September 2012, San Diego, 6285-6288.
- Cen, E.G., Dalton, C., Li, Y., Adamia, S., Pilarski, L.M. and Kaler, K.V.I.S. (2004) A Combined Dielectrophoresis, Traveling Wave Dielectrophoresis and Electrorotation Microchip for the Manipulation and Characterization of Human Malignant Cells. Journal of Microbiological Methods, 58, 387-401. http://dx.doi.org/10.1016/j.mimet.2004.05.002
- Gascoyne, P.R.C., Wang, X.-B., Huang, Y. and Becker, F.F. (1997) Dielectrophoretic Separation of Cancer Cells from Blood. IEEE Transactions on Industry Applications, 33, 670-678. http://dx.doi.org/10.1109/28.585856
- Hu, X., Bessette, P.H., Qian, J., Meinhart, C.D., Daugherty, P.S. and Soh, H.T. (2005) Marker-Specific Sorting of Rare Cells Using Dielectrophoresis. Proceedings of the National Academy of Sciences of the United States of America, 102, 15757-15761. http://dx.doi.org/10.1073/pnas.0507719102
- Lapizco-Encinas, B.H., Simmons, B.A., Cummings, E.B. and Fintschenko, Y. (2004) Dielectrophoretic Concentration and Separation of Live and Dead Bacteria in an Array of Insulators. Analytical Chemistry, 76, 1571-1579. http://dx.doi.org/10.1021/ac034804j
- Pohl H. A. (1951) Motion and Precipitation of Suspensoids in Divergent Electric Fields. Journal of Applied Physics, 22, 869-871. http://dx.doi.org/10.1063/1.1700065
- Pohl, H.A. and Crane, J.S. (1971) Dielectrophoresis of Cells. Biophysical Journal, 11, 711-727. http://dx.doi.org/10.1016/S0006-3495(71)86249-5
- Yamamoto, M., Yasukawa, T., Suzuki, M., Kosuge, S., Shiku, H., Matsue, T., et al. (2012) Patterning with Particles Using Three-Dimensional Interdigitated Array Electrodes with Negative Dielectrophoresis and Its Application to Simple Immunosensing. Electrochimica Acta, 82, 35-42. http://dx.doi.org/10.1016/j.electacta.2012.02.109
- Srivastava, S.K., Gencoglu, A. and Minerick, A.R. (2011) DC Insulator Dielectrophoretic Applications in Microdevice Technology: A Review. Analytical and Bioanalytical Chemistry, 399, 301-321. http://dx.doi.org/10.1007/s00216-010-4222-6
- Suehiro, J., Zhou, G., Imamura, M. and Hara, M. (2003) Dielectrophoretic Filter for Separation and Recovery of Biological Cells in Water. IEEE Transactions on Industry Applications, 39, 1514-1521. http://dx.doi.org/10.1109/TIA.2003.816535
- Hyoung Kang, K., Xuan, X., Kang, Y. and Li, D. (2006) Effects of dc-Dielectrophoretic Force on Particle Trajectories in Microchannels. Journal of Applied Physics, 99, Article ID: 064702.
- Ai, Y., Park, S., Zhu, J., Xuan, X., Beskok, A. and Qian, S. (2010) DC Electrokinetic Particle Transport in an l-Shaped Microchannel. Langmuir, 26, 2937-2944. http://dx.doi.org/10.1021/la902711x
- Voldman, J., Gray, M.L., Toner, M. and Schmidt, M.A. (2002) A Microfabrication-Based Dynamic Array Cytometer. Analytical Chemistry, 74, 3984-3990. http://dx.doi.org/10.1021/ac0256235
- Huang, C.-T., Weng, C.-H. and Jen, C.-P. (2011) Three-Dimensional Cellular Focusing Utilizing a Combination of Insulator-Based and Metallic Dielectrophoresis. Biomicrofluidics, 5, 044101-044111. http://dx.doi.org/10.1063/1.3646757
- Hyunjung, C., Il, D. and Young-Ho, C. (2009) A Three-Dimensional (3D) Particle Focusing Channel Using the Positive Dielectrophoresis (pDEP) Guided by a Dielectric Structure between Two Planar Electrodes. Lab on a Chip, 9, 686-691. http://dx.doi.org/10.1039/b812213j
- Pohl, H., Pollock, K. and Crane, J. (1978) Dielectrophoretic Force: A Comparison of Theory and Experiment. Journal of Biological Physics, 6, 133-160. http://dx.doi.org/10.1007/BF02328936
- Morgan, H. and Green, N.G. (2003) AC Electrokinetics: Colloids and Nanoparticles. Research Studies Press Limited.
- Jones, T.B. (2005) Electromechanics of Particles. Cambridge University Press, England.
- Zhu, J., Tzeng, T.-R.J., Hu, G. and Xuan, X. (2009) DC Dielectrophoretic Focusing of Particles in a Serpentine Microchannel. Microfluidics and Nanofluidics, 7, 751-756. http://dx.doi.org/10.1007/s10404-009-0432-7
- Therriault, D., White, S.R. and Lewis, J.A. (2003) Chaotic Mixing in Three-Dimensional Microvascular Networks Fabricated by Direct-Write Assembly. Nature Materials, 2, 265-271. http://dx.doi.org/10.1038/nmat863
- Ermolina, I. and Morgan, H. (2005) The Electrokinetic Properties of Latex Particles: Comparison of Electrophoresis and Dielectrophoresis. Journal of Colloid and Interface Science, 285, 419-428. http://dx.doi.org/10.1016/j.jcis.2004.11.003

