Journal of Biomedical Science and Engineering
Vol. 5 No. 8 (2012) , Article ID: 21464 , 10 pages DOI:10.4236/jbise.2012.58054
Influence of the aspect ratio on the endovascular treatment of intracranial aneurysms: A computational investigation
![]()
1Department of Mechanical Engineering, University of Hong Kong, Hong Kong, China
2Department of Neurosurgery, Kwong Wah Hospital, Hong Kong, China
3Division of Neurosurgery, Department of Surgery, Li Ka Shing Faculty of Medicine, University of Hong Kong, Queen Mary Hospital, Hong Kong, China
Email: *kwchow@hku.hk
Received 15 May 2012; revised 12 June 2012; accepted 28 June 2012
Keywords: Intracranial Aneurysm; Endovascular Treatment; Stent; Aspect Ratio; Computational Fluid Dynamics
ABSTRACT
Intracranial aneurysm, a localized dilation of arterial blood vessels in the Circle of Willis and its branches, is potentially life threatening, due to massive bleeding in the subarachnoid space upon rupture. In clinical practice, one minimally invasive surgical procedure is the implantation of a metallic stent to cover the aneurysm neck. This flow diverting device can reduce the flow into the aneurysm and enhance the prospect of thrombosis, a condition expected to reduce the risk of growth and rupture. The biomechanical and haemodynamic factors in stented and nonstented situations are studied by computational fluid dynamics. Unlike earlier models with straight or curved parent blood vessels, the aneurysm is now located near an arterial bifurcation. The influence of the aspect (depth to neck) ratio of the aneurysm on the flow dynamics will be emphasized, especially in the post-operation stages. More precisely, the maximum flow velocity, the variations of wall shear stress, the risk of stent migration and volumetric flow rate after endovascular treatment will be studied. Aneurysms with larger aspect ratios (i.e. smaller neck sizes for constant depth) generally pose a greater risk in terms of these flow parameters. These results will assist the applications and design of stents in future neurosurgical therapy. The approach is limited to a nonelastic model, without taking into account of questions like stent expansion and interaction with tissue.
1. INTRODUCTION
The formation of an intracranial aneurysm in the arteries at the base of the brain is a serious cerebrovascular disorder [1], occurring in roughly 2% to 5% of the population [2,3]. Rupture of such aneurysm may result in massive bleeding, with an incidence rate of about 6 to 8 cases per 100,000 persons [4]. Treatment by surgical clipping aims to isolate the aneurysm from the normal blood circulation, but such open surgical procedure may lead to complications such as brain injury, infection and seizures.
Recently, endovascular coiling has been developed [5,6], but the procedure may fail for wide-necked aneurysms, as the coil would extrude into the parent blood vessel. The promising alternative is then endovascular stenting [7], where a metallic stent, serving as a flow diverter, will drastically reduce the flow into the aneurismal sac. Nearly stagnant blood facilitates thrombus formation [8]. Risks of growth and rupture are thus vastly mitigated.
Intracranial aneurysms are usually saccular in shape. Mechanisms for their formation and growth are still controversial, but haemodynamic and biomechanical factors are believed to play a crucial role [9-11].
Computational fluid dynamics has been utilized extensively to assess endovascular treatment quantitatively. Both idealized models, i.e. those with a straight or curved parent artery, and patient specific cases have been employed. For idealized models, the effect of stents on blood flow patterns in steady flow conditions was investigated [12]. The efficiency of different stent configurations (helix and mesh patterns) under pulsatile flow conditions was compared [13]. The impact of stent porosity on the volume flow rate entering the aneurysm was analyzed [14]. Models with curved parent vessel had been studied too [15].
For patient-specific models created from medical image processing techniques [16,17], many technological challenges exist, e.g. irregular geometric shapes, difficulty of virtual stent deployment and relatively large computational efforts. The aspect ratio of the aneurysm, the ratio of depth to neck width, will prove to be crucial [18-20]. Another clinical concern is stent migration [21-23]. Dynamics of flow diversion and prospect of delaying rupture were also investigated [24-26].
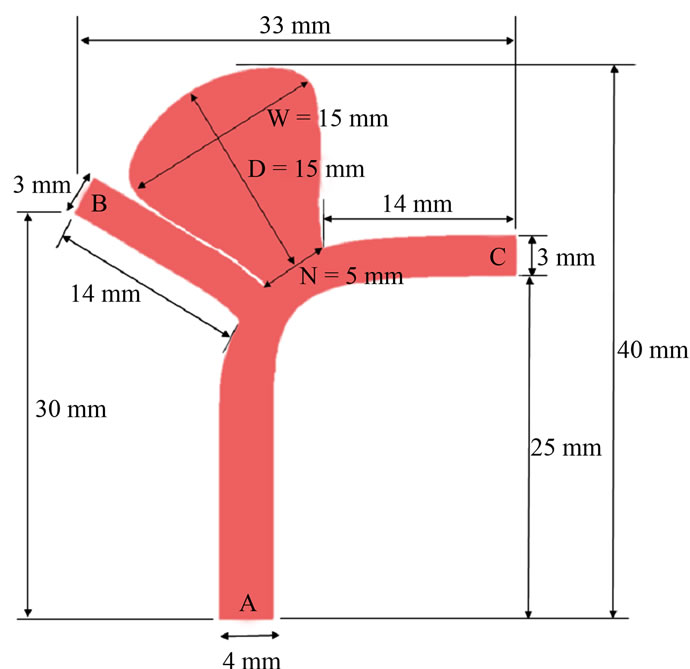
Despite these intensive efforts, many critical phenomena remain poorly understood, and the focus here is the aspect ratio [18-20]. For simplicity, we take the width and depth of the aneurysm as identical, and vary the dimension of the neck (Figure 1). Thus the aspect ratio becomes the single geometric factor governing the haemodynamics.
The first goal is to assess the blood velocity and flow rates as the aspect ratio varies. Secondly, the magnitude of the shear forces acting on the stent tangentially in the post-operative stage will depend on the dimensions of the aneurysm necks (aspect ratio). A large shear force may lead to stent migration and effectively causes the failure of endovascular treatment. Finally, the shear stress inside the aneurysm will play an important role too. In cardiovascular mechanics, a huge literature has concentrated on the magnitude of shear stress on blood vessels and endothelial cells alignment/damage [27]. The aspect ratio will affect this biomechanical factor too.
The structure of this paper is organized as follows. A three dimensional (3D) model of a saccular aneurysm is first constructed based on the imaging data of a patient. Computational fluid dynamics (CFD) analysis (Section 2) [28,29] is conducted 1) to compare the nonstented (preoperative) and stented (post-operative) configurations, and 2) to measure the effectiveness of endovascular intervention by examining flow parameters (Section 3). Conclusions are drawn (Section 4).
2. METHODOLOGY AND MODEL
2.1. Software
SOLIDWORKS 2010 (Concorde, Massachusetts, USA) was used to build a high quality model. GAMBIT 2.4.6 (developed by FLUENT) was adopted to carry out the task for mesh generation and quality control. FLUENT 6.3.26 (ANSYS, Canonsburg, Pennsylvania, USA) was utilized to conduct the simulations.
2.2. Geometric Configuration
Y-shaped configurations are highly relevant in the haemodynamics of intracranial aneurysms. Ford et al. [30] considered the angle between the parent vessel and the nominal center of the aneurysm, and the effect on flow dynamics. Ujiie et al. [31] conducted flow visualization experiments with different aspect ratios. Wang et al. [32] analyzed the flow fields inside the stented model with aspect ratio being unity. Babiker et al. [33] examined the influence of different stent deployment approaches on the flow near the bifurcation region. While these and earlier studies generally focused mainly on haemodynamic properties and aneurysm geometries, this paper addresses the potential risks of post-stenting aneurysm rupture and stent migration problems as well.
The geometry of intracranial aneurysms is complex and irregular in real patients, hence idealized models where the aneurysm was located at the intersection point of the daughter vessels had been considered [30,31]. Here we consider an asymmetric Y-shaped model with the aneurysm located near the bifurcation point of the cerebral arteries [34] (Figure 1(a)). If endovascular repair is performed, a metallic stent will cover the aneurysm neck and the left branch vessel (Figure 1(b)).
In the numerical simulations, the diameters of the parent artery and two bifurcating vessels were selected as 4 mm and 3 mm respectively. The depth (D) and width (W) of the aneurysm were taken to be identical at 15 mm,
 (a)
(a) (b)
(b)
Figure 1. Intracranial aneurysm model: (a) geometry and dimensions; (b) stent deployment.
and the aneurysm neck size (N) would take on values of 5, 7.5 and 10 mm (Figure 2). The aspect ratios (AR = D/N) for these neck sizes were thus equal to 3, 2 and 1.5 respectively. The inclinations of the outlets “B” and “C” were 30˚ and 0˚ respectively.
For the post-operative configurations, the computational stent was constructed by SOLIDWORKS as a mesh-like configuration with regular patterns of closed-cell, where each closed-cell assumed the shape of a rhombus (0.5 mm × 1 mm). The porosity of the stent was 77%, and the strut width and thickness were 0.07 mm and 0.1 mm respectively. The stent was assumed to be a rigid structure in tight contact with the vessel wall. Blood flowed from the parent artery (inlet “A”) to the two branch vessels (outlets “B”, “C”) and the aneurysm.
2.3. Fluid Properties
Blood plasma is regarded as a continuum. Suspended particles are ignored, as typical diameters of red blood cells (7.6 mm) and platelets (2.5 mm) [35] are small relative to the size of the blood vessel (3 - 4 mm). Blood is assumed to be an incompressible, Newtonian fluid [36], with density and dynamic viscosity being taken as 1060 kg·m–3 and 0.0035 kg·m–1·s–1 respectively [37].
2.4. Governing Equations
Using tensor notations (repeated indices implying summation), the continuity (mass conservation) and NavierStokes equations (momentum) are given respectively as [35]:
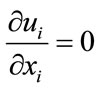 (1)
(1)
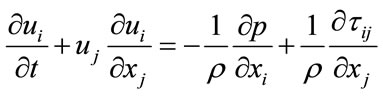 (2)
(2)
where ui (i = 1, 2, 3) are the components of the velocity vector, ρ = fluid density, p = pressure, and τij = normal and shear stresses. These equations were treated by an unsteady flow solver of FLUENT with a time step of 0.001 second, and a residual error of 10–6.
2.5. Spatial Grid Sizes
The spatial grid size ranged from 0.027 mm to 0.3 mm, depending on the complexity of stented and nonstented models. Tetrahedral/hybrid elements were employed and T-grids were used. To maintain proper resolution, the number of spatial grids must increase for the aneurysm (pre-operative case) with larger neck size as follows:
· 429,135 grids for the aneurysm with AR = 3;
· 499,845 grids for the aneurysm with AR = 2;
· 565,193 grids for the aneurysm with AR = 1.5.
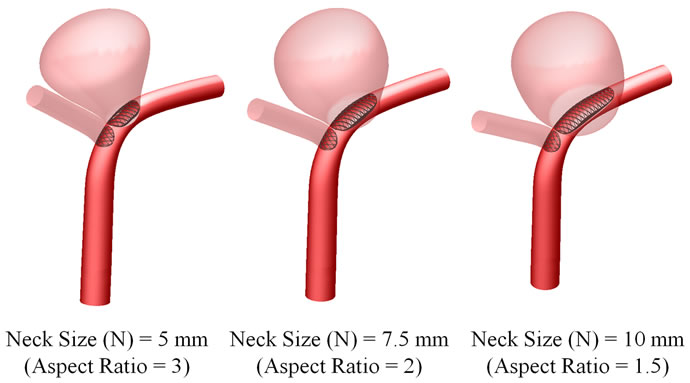

Figure 2. Three-dimensional perspective of intracranial aneurysm model with stent placement.
For the post-operative case, the spatial grid size must be refined further to sustain the mesh quality and compatibility of the aneurysm model treated with stents:
· 1,175,698 grids for the aneurysm with AR = 3;
· 1,501,084 grids for the aneurysm with AR = 2;
· 2,037,419 grids for the aneurysm with AR = 1.5.
To verify the accuracy of the simulation results, mesh independence tests were also performed. As an illustrative example, we used three different grid sizes to compute the maximum flow velocity inside the aneurysm for the post-operative case AR = 3. The results are 0.205 m·s–1 (789,433 grids), 0.211 m·s–1 (1,175,698 grids) and 0.211 m·s–1 (1,442,070 grids). Consequently, the model with 1,175,698 grids was taken as accurate, as further mesh refinement did not affect the accuracy of the results to leading order.
2.6. Boundary Conditions
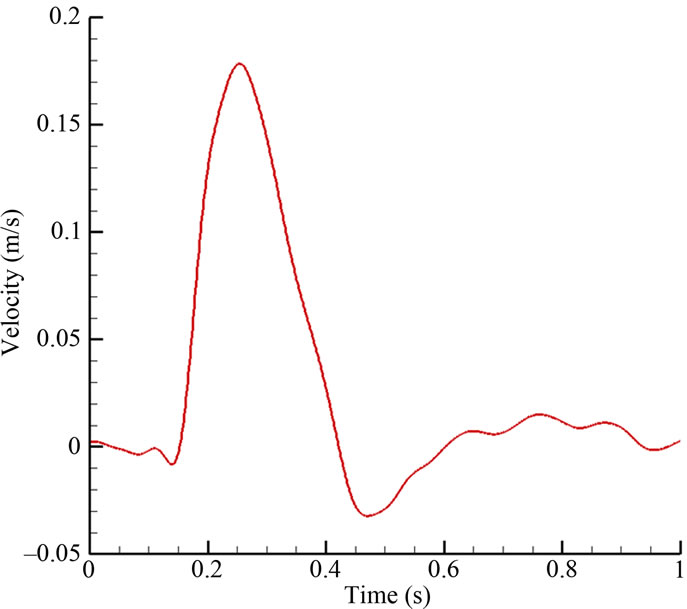
The no slip boundary conditions were applied at all vessel walls. The walls were assumed to be rigid, with effects of elasticity deferred to a future study. A pulsatile velocity waveform (Figure 3(a)), which resembled realistic patient conditions, was imposed at the inlet (position “A” in Figure 1(a)). The time-dependent waveform at the inlet was taken as a spatially parabolic velocity profile. The outlet boundaries (positions “B” and “C” in Figure 1(a)) were subjected to a pulsatile pressure waveform with 122/82 mmHg (1 mmHg = 133.332 Pa) (Figure 3(b)). The full cardiac cycle (T) was taken as 1 second.
 (a)
(a)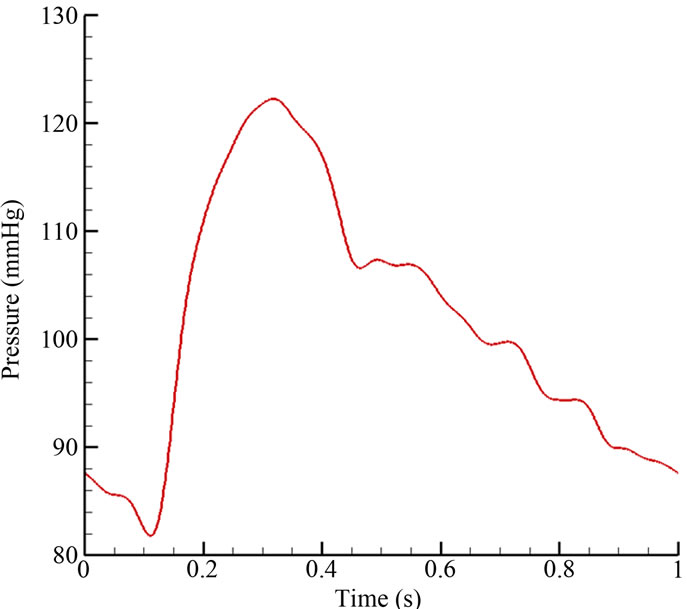 (b)
(b)
Figure 3. Pulsatile blood flow waveform: (a) velocity inlet; (b) pressure outlet.
At the peak systole (t/T = 0.25), the Reynolds number was 215, based on the inlet arterial diameter (4 mm) and the systolic velocity (0.178 m·s–1). The Reynolds number remained small throughout the cardiac cycle, and thus the flow could be treated as laminar. Typically, a periodic output was generated after just two cycles of computations, and data for the third cycle were reported. Unless otherwise specified, the subsequent results referred to those at the systolic phase of the cardiac cycle, i.e. t/T = 0.25.
3. RESULTS AND DISCUSSIONS
The aspect ratio of intracranial aneurysms is one critical factor in determining the timing of medical intervention. We focus on values of aspect ratio (AR) and neck size which are of medical interests. Clinical studies [19,20] reported that an aspect ratio larger than 1.6 poses a higher than average risk for aneurysmal rupture. To analyze quantitatively, three different aspect ratios are selected, i.e. aspect ratio AR = 3, 2 and 1.5. Since the depth and width (Figure 1(a)) are kept constant, a greater neck size will imply a smaller aspect ratio.
3.1. Velocities and Pressure
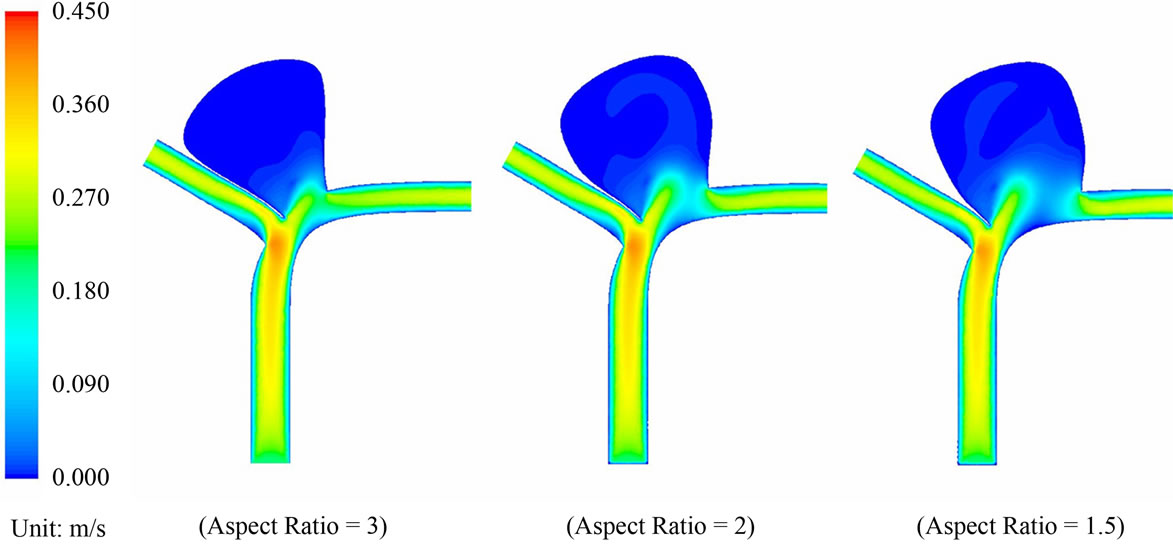
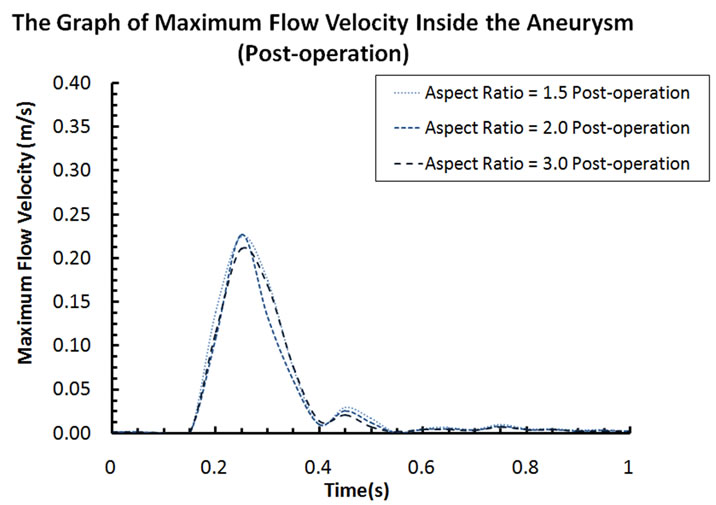
Blood flow patterns within the intracranial aneurysm can be altered considerably after the implantation of stents. Figure 4 depicts the velocity contours of blood flow for different aspect ratios. Before stent treatment, blood flow can reach the upper part of the aneurysm (i.e. aspect ratio AR = 2 and 1.5 in Figure 4). In this pre-operative case, the maximum flow velocities inside the aneurysm at systole are 0.259 m·s–1 (AR = 3), 0.297 m·s–1 (AR = 2), and 0.291 m·s–1 (AR = 1.5). For the post-operative case, the maximum velocities decrease to 0.211 m·s–1 (AR = 3), 0.227 m·s–1 (AR = 2), and 0.225 m·s–1 (AR = 1.5). The percentage reductions are 18.5% (AR = 3), 23.6% (AR = 2), and 22.7% (AR = 1.5) after stent placement.
The three dimensional sketch of the particle paths in the pre-operative and post-operative configurations of the AR = 3 case is also shown in Figure 5. The highest flow velocities inside the aneurysm throughout the full cardiac cycle for both cases are presented in Figure 6. These results clearly show that the stent is capable of decelerating the blood flow, which renders the aneurysm more prone to thrombus formation, and hopefully enhances the safety of the patient. A state of complete thrombosis can isolate aneurysms from the blood circulation. Without treatment, complete thrombosis seldom occurs. Due to this velocity reduction after flow diversion, a high speed flow jet acting on the aneurysm wall when blood passes through the tiny gap between the stent struts is unlikely, confirming the merit of endovascular stenting in the treatment of aneurysms.
Pressure drop within the aneurysm: Regarding pressure, the contour plots for the pre-operative and post-operative cases are portrayed in Figures 7 and 8. The pressure distribution patterns with different aspect ratios are similar to each other. In the pre-operative case (AR = 1.5), the maximum and minimum pressures within the aneurysm are 15,815.8 Pa and 15,796.8 Pa respectively. The absolute difference of the blood pressure is 19 Pa. In the post-operative case (AR = 1.5), the maximum and minimum pressures within the aneurysm become 15,835.2 Pa and 15,831.3 Pa respectively. These maxima and minima in pressure occur at the moment of systole.
The maximum differential in blood pressure in the interior of the sac is thus only 3.9 Pa, a reduction of 79%
 (a)
(a)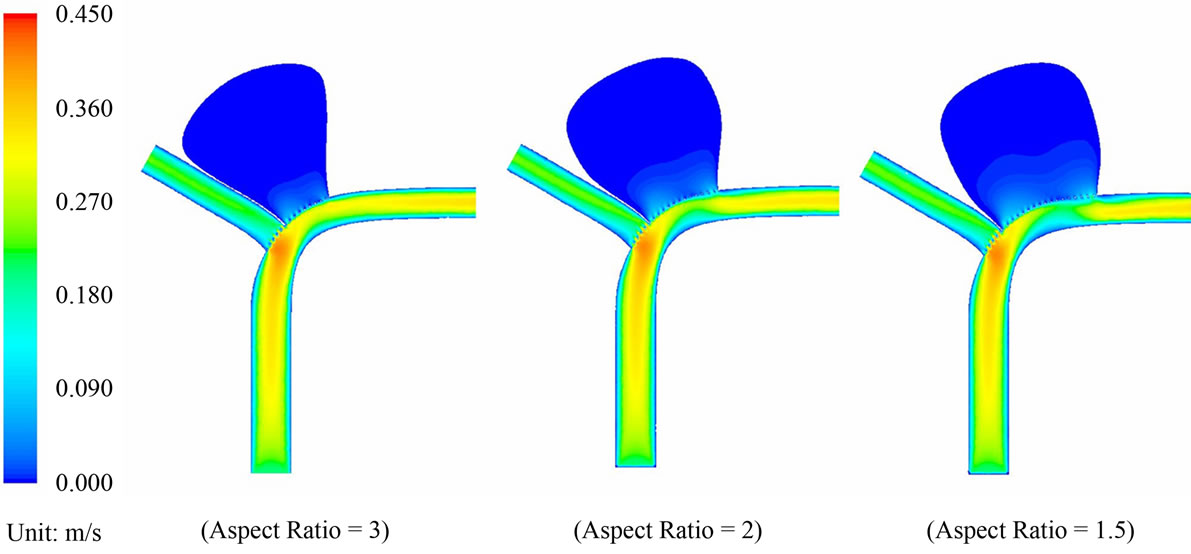 (b)
(b)
Figure 4. (a) Velocity contour plots for the pre-operative cases with aspect ratio = 3, 2 and 1.5; (b) Velocity contour plots for the post-operative cases with aspect ratio = 3, 2 and 1.5.

Figure 5. Three dimensional sketch of the particle paths in the pre-operative and post-operative configurations (AR = 3).
 (a)
(a)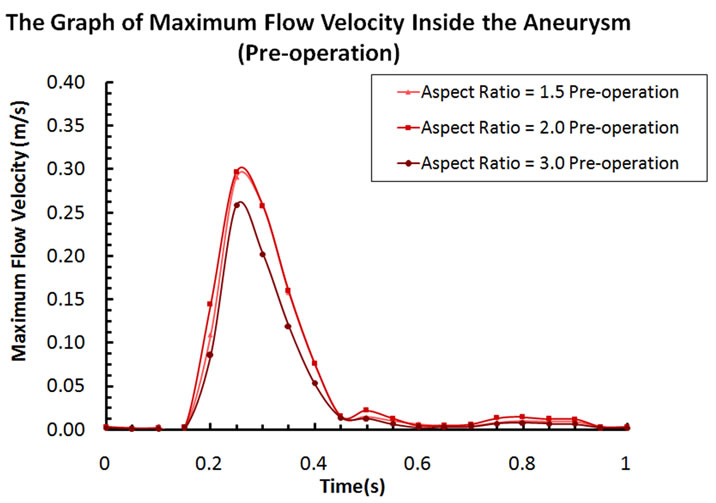 (b)
(b)
Figure 6. (a) Maximum flow velocity inside the aneurysm (pre-operation); (b) Maximum flow velocity inside the aneurysm (post-operation).
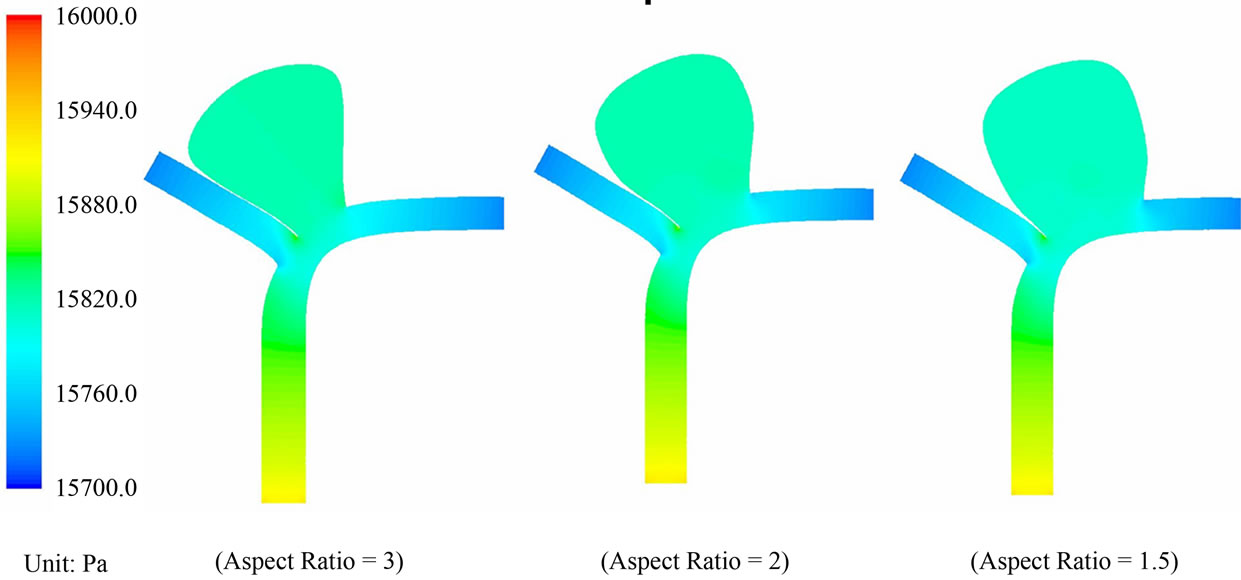
Figure 7. Pressure contour plots for the pre-operative cases with AR = 3, 2 and 1.5.
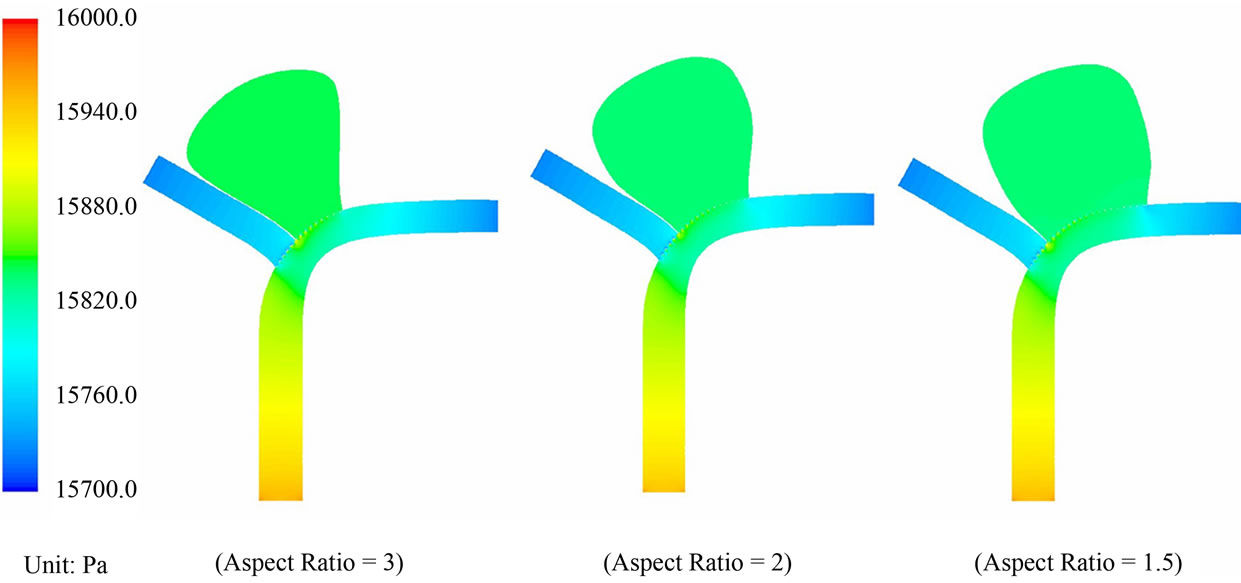
Figure 8. Pressure contour plots for the post-operative cases with AR = 3, 2 and 1.5.
as compared with the configuration before stent placement. This drastic reduction in the pressure differential will imply that blood flow in the sac is considerably reduced after the operation. Furthermore, the maximum blood pressure in the aneurysm goes up only slightly, from 15,815.8 Pa to 15,835.2 Pa, a 19.4 Pa (»0.145 mmHg) increase in the presence of stent deployment. This small increment of blood pressure is unlikely to cause the rupture of aneurysms, consolidating another merit of this endovascular stenting procedure.
Pressure drop across the vessel: The pressure drop between the inlet and the outlet will increase after the placement of the stent, as the stent will pose an additional resistance to fluid motion.
Moreover, the percentage drop in fluid velocity in the left branch is higher for the larger aspect ratio case, confirming that these cases are more difficult to treat clinically.
3.2. Wall Shear Stress
Wall shear stress (WSS) is another key factor in studying vascular biology [38]. Clinical studies indicated that low WSS can trigger the growth and rupture of aneurysms due to the degeneration of endothelial cells [39,40], which line the luminal surface of the intima. In the postoperative cases (Figure 4(b)), sluggish flow in the upper part of the aneurysm induces thrombus formation, which then protects the most weakened upper part of the aneurysm from rupture.
Here we focus on the variation of the shear stress in the vicinity of the aneurysm neck. The shear stress level there is low except for a brief period (about 20%) of the cardiac cycle. During that short instant, the shear stress rises to a maximum and then subsides. Generally, this maximum shear stress will increase significantly at both the proximal and distal regions (Figures 1(b) and 9) with stent placement. For instance, the maximum shear stress at the proximal neck goes up from 6.09 Pa (AR = 1.5) to 10.57 Pa (AR = 1.5), representing a 73.6% increase in shear stress magnitude. In the distal neck, the maximum shear stress changes from 6.47 Pa (AR = 1.5) to 10.64 Pa (AR = 1.5), with a 64.5% increase. However, the maximum shear stress for AR = 3 does not have a significant change at the distal neck as compared to AR = 1.5 and 2.
Since low WSS creates an undesirable haemodynamic environment related to the growth and rupture of aneurysms [39,40], the decision to perform stenting for aneurysms with high aspect ratios should be made with due considerations of the potential risk of rupture. The need for frequent and long-term post-operative follow-up should be emphasized.
Outside of the aneurismal sac, the shear stress in the

Figure 9. Maximum shear stress at the proximal and distal regions for various aspect ratios.
left/right branch vessel decreases/increases due to the reduced/enhanced flow respectively. Earlier works in the literature established that a shear stress falling below the threshold of 0.4 N·m–2 might trigger adverse consequences. Future works will concentrate on changes in shear stress levels with respect to variations in both the aspect ratio and porosity of the stent.
3.3. Stent Migration
The “shear force”, haemodynamic force acting parallel to the stent, may lead to stent migration with serious consequence. During the systole phase, the shear force per unit area on the stent amounts to 10.49 N·m–2 (AR = 3), 8.74 N·m–2 (AR = 2), and 8.00 N·m–2 (AR = 1.5), with the first two values higher than the last one by 31.1% and 9.3%. This implies that a stented aneurysm with a greater aspect ratio may have a higher risk of stent migration. Clinically, the use of follow-up angiographic studies in mitigating risk of stent migration and aneurysm recurrence should be given proper consideration. The actual length of the stent deployed in surgical treatment, which depends on the geometry of the local vasculature, must be taken into account.
3.4. Volume Flow Rates
Generally, a critical issue for clinicians is the efficiency of flow-diverting devices in preventing blood from entering the aneurysm. This question can be addressed quantitatively by considering the pre-operative and postoperative stages of the present model. Since results so far have indicated that an aneurysm with a greater aspect ratio is subject to a more undesirable haemodynamic environment, we shall focus on the case AR = 3. The volume flow rate can be determined by calculating an integral of the axial velocity multiplied by the neck area over the complete cardiac cycle. Since the aneurysm is a blind sac, the volume flow rate of blood entering the aneurysm, defined as:
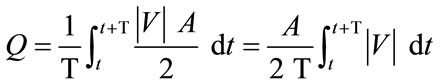 (3)
(3)
must be equal to that leaving the aneurysm at every time instant according to the conservation law of mass, where Q is the volume flow rate (m3·s–1), T is the cardiac cycle (=1 second), |V| is the spatial-averaged absolute axial velocity at the cross section of the neck (m·s–1), A is the cross-sectional area of the neck (m2), and t is a time instant. The following spatial grids are used for computation:
· 780,903 grids for the pre-operative case with AR = 3;
· 1,442,070 grids for the post-operative case with AR = 3.
In Figure 10, the absolute axial velocity |V| of blood passing through the neck (neck size N = 5 mm) is plotted. The volume flow rates Q into the aneurysm for one cardiac cycle are 31.51 mm3·s–1 (pre-operation) and 15.29 mm3·s–1 (post-operation). Despite the stent porosity of 77%, the computational results show that only 48.5% of the pre-operative volume flow rate can enter the aneurysm after stenting. This analysis verifies that endovascular stenting with flow diverters constitutes a feasible form of treatment.
Furthermore, the implantation of stent may also affect the volume flow rate of blood in the two smaller (daughter) vessels. In the pre-operative case, the volume flow rates in the left and right bifurcating vessels are 178.9 mm3·s–1 and 194.2 mm3·s–1 respectively. In the post-operative case, the rates for the left and right vessels are 128.3 mm3·s–1
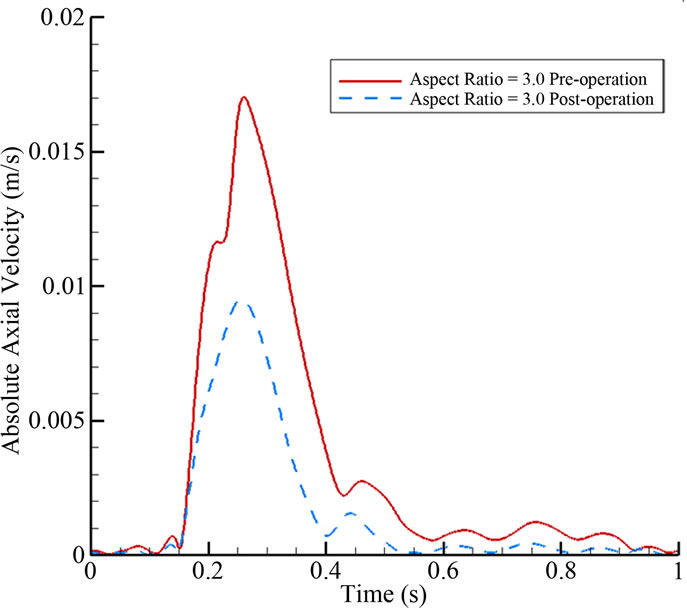
Figure 10. Absolute axial velocity of blood passing through the neck over the full cardiac cycle for AR = 3.
and 244.8 mm3·s–1 respectively. In terms of percentages, the ratios are 47.9%:52.1% (pre-operation), and 34.4%: 65.6% (post-operation). The reduction of blood supply of the left branch vessel is 13.5% of the total blood flow volume. This is reasonable as the flow diversion stent covers the entrance of the left blood vessel at the bifurcation point.
A rough clinical estimate is that a reduction of 15% to 20% would still be acceptable, i.e. providing enough blood supply to prevent cells and organs downstream of the left branch from suffering long term damage. A comprehensive examination on the relation between porosity and bifurcating blood vessels will be left for future studies.
4. CONCLUSIONS
Endovascular repair is a novel treatment modality for intracranial aneurysms. To examine the effectiveness of stenting quantitatively, a computational model with an aneurysm located near a bifurcation point of blood vessels is investigated. The focus is to assess the impact of aspect ratios (depth/neck, smaller neck means a larger ratio) on the haemodynamics in the post-operative stage. Generally, the results here indicate that aneurysms with a larger aspect ratio will pose a greater risk.
Computational fluid dynamics data supporting this claim include:
· The maximum fluid velocity inside the aneurysm after endovascular surgery will generally be reduced, as compared with the value before the operation. This reduction becomes less substantial as the aspect ratio increases, meaning that the volume flow rate reduction mechanism becomes less effective.
· The shear force (per unit area) on the stent, and thus the risk of stent migration, are higher for an aneurysm model with a greater aspect ratio.
· Damages to the endothelial cells at low shear stress have been well documented in the literature [38]. After endovascular treatment, shear stress at the distal and proximal junctions generally increases to reasonable values, offering protecting against long term damage and rupture potential. This increase fails to materialize for the case of high aspect ratio, indicating again problematic scenario for these aneurysms with narrow necks.
Other factors of general medical interests:
· The volume flow rate of blood in the two branch vessels is altered after stent placement, thus the use of low stent porosity (e.g. <65%) for endovascular treatment may notably affect the blood supply to the bifurcating branches adjacent to the aneurysm.
· The maximum flow velocity inside the aneurysm at the systolic phase is decreased by about 18% - 24% after stent deployment, hence the creation of a high speed flow jet acting on the aneurysm wall is unlikely to occur when blood passes through the tiny gap between stent struts.
· The pressure gradient within the aneurysm is reduced drastically after stent deployment, retarding the likelihood of flow and promoting chance of thrombosis.
· The volume flow rate of blood entering into the aneurysm over the entire cardiac cycle can be reduced by more than 50% after endovascular operation.
In an attempt to verify the computational results, the next step is to pursue an in-vitro experimental investigation using phantoms fabricated with rapid prototyping techniques. The fluid flow will be measured with highframe-rate ultrasound imaging. Such investigations will provide further insights into the diagnosis and treatment of this cerebrovascular disease.
5. ACKNOWLEDGEMENTS
Partial financial support has been provided by the Innovation and Technology Commission (ITS/083/11) of the Hong Kong Special Administrative Region Government.
![]()
![]()
REFERENCES
- Schievink, W.I. (1997) Medical progress—intracranial aneurysms. New England Journal of Medicine, 336, 28- 40. doi:10.1056/NEJM199701023360106
- Sekhar, L.N. and Heros, R.C. (1981) Origin, growth, and rupture of saccular aneurysms: a review. Neurosurgery, 8, 248-260. doi:10.1227/00006123-198102000-00020
- Rinkel, G.J.E., Djibuti, M., Algra, A. and van Gijn, J. (1998) Prevalence and risk of rupture of intracranial aneurysms: a systematic review. Stroke, 29, 251-256. doi:10.1161/01.STR.29.1.251
- Linn, F.H.H., Rinkel, G.J.E., Algra, A. and van Gijn, J. (1996) Incidence of subarachnoid hemorrhage: role of region, year, and rate of computed tomography: a metaanalysis. Stroke, 27, 625-629. doi:10.1161/01.STR.27.4.625
- Guglielmi, G., Viñuela, F., Dion, J. and Duckwiler, G. (1991) Electrothrombosis of saccular aneurysms via endovascular approach. Part 2: preliminary clinical experience. Journal of Neurosurgery, 75, 8-14. doi:10.3171/jns.1991.75.1.0008
- Molyneux, A.J., Kerr, R.S.C., Yu, L.M., Clarke, M., Sneade, M., Yarnold, J.A. and Sandercock, P. (2005) International subarachnoid aneurysm trial (ISAT) of neurosurgical clipping versus endovascular coiling in 2143 patients with ruptured intracranial aneurysms: a randomised comparison of effects on survival, dependency, seizures, rebleeding, subgroups, and aneurysm occlusion. Lancet, 366, 809-817. doi:10.1016/S0140-6736(05)67214-5
- Pierot, L. (2011) Flow diverter stents in the treatment of intracranial aneurysms: where are we? Journal of Neuroradiology, 38, 40-46. doi:10.1016/j.neurad.2010.12.002
- Wanke, I. and Forsting, M. (2008) Stents for intracranial wide-necked aneurysms: more than mechanical protection. Neuroradiology, 50, 991-998. doi:10.1007/s00234-008-0460-0
- Lasheras, J. C. (2007) The biomechanics of arterial aneurysms. Annual Review of Fluid Mechanics, 39, 293-319. doi:10.1146/annurev.fluid.39.050905.110128
- Humphrey, J.D. and Taylor, C.A. (2008) Intracranial and abdominal aortic aneurysms: similarities, differences, and need for a new class of computational models. Annual Review of Biomedical Engineering, 10, 221-246. doi:10.1146/annurev.bioeng.10.061807.160439
- Sforza, D.M., Putman, C.M. and Cebral, J.R. (2009) Hemodynamics of cerebral aneurysms. Annual Review of Fluid Mechanics, 41, 91-107. doi:10.1146/annurev.fluid.40.111406.102126
- Yu, S.C.M. and Zhao, J.B. (1999) A steady flow analysis on the stented and non-stented sidewall aneurysm models. Medical Engineering & Physics, 21, 133-141. doi:10.1016/S1350-4533(99)00037-5
- Liou, T.M., Liou, S.N. and Chu, K.L. (2004) Intra-aneurysmal flow with helix and mesh stent placement across side-wall aneurysm pore of a straight parent vessel. ASME Journal of Biomechanical Engineering, 126, 36-43. doi:10.1115/1.1644566
- Liou, T.M. and Li, Y.C. (2008) Effects of stent porosity on hemodynamics in a sidewall aneurysm model. Journal of Biomechanics, 41, 1174-1183. doi:10.1016/j.jbiomech.2008.01.025
- Meng, H., Wang, Z., Kim, M., Ecker, R.D. and Hopkins, L.N. (2006) Saccular aneurysms on straight and curved vessels are subject to different hemodynamics: implications of intravascular stenting. American Journal of Neuroradiology, 27, 1861-1865.
- Chow, M.M., Woo, H.H., Masaryk, T.J. and Rasmussen, P.A. (2004) A novel endovascular treatment of a wide-necked basilar apex aneurysm by using a Y-configuration, double stent technique. American Journal of Neuroradiology, 25, 509-512.
- Cekirge, H.S., Yavuz, K., Geyik, S. and Saatci, I. (2011) A novel “Y” stent flow diversion technique for the endovascular treatment of bifurcation aneurysms without endosaccular coiling. American Journal of Neuroradiology, 32, 1262-1268. doi:10.3174/ajnr.A2475
- Ujiie, H., Tachibana, H., Hiramatsu, O., Hazel, A.L., Matsumoto, T., Ogasawara, Y., Nakajima, H., Hori, T., Takakura, K. and Kajiya, F. (1999) Effects of size and shape (aspect ratio) on the hemodynamics of saccular aneurysms: a possible index for surgical treatment of intracranial aneurysms. Neurosurgery, 45, 119-130. doi:10.1097/00006123-199907000-00028
- Ujiie, H., Tamano, Y., Sasaki, K. and Hori, T. (2001) Is the aspect ratio a reliable index for predicting the rupture of a saccular aneurysm? Neurosurgery, 48, 495-503. doi:10.1097/00006123-200103000-00007
- Nader-Sepahi, A., Casimiro, M., Sen, J. and Kitchen, N.D. (2004) Is aspect ratio a reliable predicator of intracranial aneurysm rupture? Neurosurgery, 54, 1343-1348. doi:10.1227/01.NEU.0000124482.03676.8B
- Kelly, M.E., Turner IV, R.D., Moskowitz, S.I., Gonugunta, V., Hussain, M.S. and Fiorella, D. (2008) Delayed migration of a self-expanding intracranial microstent. American Journal of Neuroradiology, 29, 1959-1960. doi:10.3174/ajnr.A1224
- Pavlisa, G., Ozretic, D., Rados, M. and Pavlisa, G. (2009) Migration of enterprise stent in treatment of intracranial aneurysms: a report of two cases. Radiology and Oncology, 43, 233-239.
- Lobotesis, K., Gholkar, A. and Jayakrishnan, V. (2010) Early migration of a self expanding intracranial stent: case report. Neurosurgery, 67, E516-E517. doi:10.1227/01.NEU.0000372094.75062.D4
- Hampton, T., Walsh, D., Tolias, C. and Fiorella, D. (2011) Mural destabilization after aneurysm treatment with a flow-diverting device: a report of two cases. Journal of Neurointerventional Surgery, 3, 167-171. doi:10.1136/jnis.2010.002873
- Turowski, B., Macht, S., Kulcsár, Z., Hänggi, D. and Stummer, W. (2011) Early fatal hemorrhage after endovascular cerebral aneurysm treatment with a flow diverter (SILK-stent): do we need to rethink our concepts? Neuroradiology, 53, 37-41. doi:10.1007/s00234-010-0676-7
- Kulcsár, Z., Houdart, E., Bonafé, A., Parker, G., Millar, J., Goddard, A.J.P., Renowden, S., Gál, G., Turowski, B., Mitchell, K., Gray, F., Rodriguez, M., van den Berg, R., Gruber, A., Desal, H., Wanke, I. and Rüfenacht, D.A. (2011) Intra-aneurysmal thrombosis as a possible cause of delayed aneurysm rupture after flow-diversion treatment. American Journal of Neuroradiology, 32, 20-25.
- Hu, J., Zhang, E.Y., Wu, J., Xu, W.L., Chen, H.Q., Shi, Y.K. and Guo, Y.Q. (2010) Pressure shift mediated anoikis of endothelial cell in the flow field in vitro. Journal of Biomedical Science and Engineering, 3, 206-212. doi:10.4236/jbise.2010.32027
- Fung, G.S.K., Lam, S.K., Cheng, S.W.K. and Chow, K.W. (2008) On stent-graft models in thoracic aortic endovascular repair: a computational investigation of the hemodynamic factors. Computers in Biology and Medicine, 38, 484-489. doi:10.1016/j.compbiomed.2008.01.012
- Cheng, S.W.K., Lam, E.S.K., Fung, G.S.K., Ho, P., Ting, A.C.W. and Chow, K.W. (2008) A computational fluid dynamic study of stent graft remodeling after endovascular repair of thoracic aortic dissections. Journal of Vascular Surgery, 48, 303-310. doi:10.1016/j.jvs.2008.03.050
- Ford, M.D., Lee, S.W., Lownie, S.P., Holdsworth, D.W. and Steinman, D.A. (2008) On the effect of parent-aneurysm angle on flow patterns in basilar tip aneurysms: towards a surrogate geometric marker of intra-aneurismal hemodynamics. Journal of Biomechanics, 41, 241-248. doi:10.1016/j.jbiomech.2007.09.032
- Ujiie, H., Shinohara, C., Higa, T., Kato, K., Yoshimoto, S. and Hori, T. (2009) Intraaneurysmal flow and aspect ratio (Dome/Neck). Journal of Biorheology, 23, 41-48. doi:10.1016/j.jbiomech.2007.09.032
- Wang, S., Ding, G., Zhang, Y. and Yang, X. (2011) Computational haemodynamics in two idealised cerebral wide-necked aneurysms after stent placement. Computer Methods in Biomechanics and Biomedical Engineering, 14, 927-937. doi:10.1080/10255842.2010.502531
- Babiker, M.H., Gonzalez, L.F., Ryan, J., Albuquerque, F., Collins, D., Elvikis, A. and Frakes, D.H. (2012) Influence of stent configuration on cerebral aneurysm fluid dynamics. Journal of Biomechanics, 45, 440-447. doi:10.1016/j.jbiomech.2011.12.016
- Perktold, K., Kenner, T., Hilbert, D., Spork, B. and Florian, H. (1988) Numerical blood flow analysis: arterial bifurcation with a saccular aneurysm. Basic Research in Cardiology, 83, 24-31. doi:10.1007/BF01907101
- Fung, Y.C. (1997) Biomechanics: Circulation. 2nd Edition, Springer, New York.
- Sweetman, B., Xenos, M., Zitella, L. and Linninger, A.A. (2011) Three-dimensional computational prediction of cerebrospinal fluid flow in the human brain. Computers in Biology and Medicine, 41, 67-75. doi:10.1016/j.compbiomed.2010.12.001
- Fan, Y., Cheng, S.W.K., Qing, K.X. and Chow, K.W. (2010) Endovascular repair of type B aortic dissection: a study by computational fluid dynamics. Journal of Biomedical Science and Engineering, 3, 900-907. doi:10.4236/jbise.2010.39120
- Malek, A.M., Alper, S.L. and Izumo, S. (1999) Hemodynamic shear stress and its role in atherosclerosis. Journal of the American Medical Association, 282, 2035-2042. doi:10.1001/jama.282.21.2035
- Shojima, M., Oshima, M., Takagi, K., Torii, R., Hayakawa, M., Katada, K., Morita, A. and Kirino, T. (2004) Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke, 35, 2500-2505. doi:10.1161/01.STR.0000144648.89172.0f
- Boussel, L., Rayz, V., McCulloch, C., Martin, A., Acevedo-Bolton, G., Lawton, M., Higashida, R., Smith, W.S., Young, W.L. and Saloner, D. (2008) Aneurysm growth occurs at region of low wall shear stress: patient-specific correlation of hemodynamics and growth in a longitudinal study. Stroke, 39, 2997-3002. doi:10.1161/STROKEAHA.108.521617
NOTES
*Corresponding author.

