Journal of Biomedical Science and Engineering
Vol.10 No.03(2017), Article ID:74857,14 pages
10.4236/jbise.2017.103010
Feature Conditioning Based on DWT Sub-Bands Selection on Proposed Channels in BCI Speller
Bahram Perseh1*, Majid Kiamini2, Sepideh Jabbari2
1Department of Biophysics, Zanjan University of Medical Sciences, Zanjan, Iran
2Department of Electrical Engineering, University of Zanjan, Zanjan, Iran

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 16, 2017; Accepted: March 20, 2017; Published: March 23, 2017
ABSTRACT
In this paper, we present a novel and efficient scheme for detection of P300 component of the event-related potential in the Brain Computer Interface (BCI) speller paradigm that needs significantly less EEG channels and uses a minimal subset of effective features. Removing unnecessary channels and reducing the feature dimension resulted in lower cost and shorter time and thus improved the BCI implementation. The idea was to employ a proper method to optimize the number of channels and feature vectors while keeping high accuracy in classification performance. Optimal channel selection was based on both discriminative criteria and forward-backward investigation. Besides, we obtained a minimal subset of effective features by choosing the discriminant coefficients of wavelet decomposition. Our algorithm was tested on dataset II of the BCI competition 2005. We achieved 92% accuracy using a simple LDA classifier, as compared with the second best result in BCI 2005 with an accuracy of 90.5% using SVM for classification which required more computation, and against the highest accuracy of 96.5% in BCI 2005 that used SVM and much more channels requiring excessive calculations. We also applied our proposed scheme on Hoffmann’s dataset to evaluate the effectiveness of channel reduction and achieved acceptable results.
Keywords:
Brain Computer Interface, P300 Component, Optimal Sub-Bands, Optimal Channels, Linear Discriminant Analysis

1. Introduction
The electroencephalogram (EEG) is a recording of brain activity. It is widely used as an important diagnostic tool for neurological disorders. Many BCIs utilize EEG signals to translate these signals into users’ commands, which can control some external systems. Some BCI systems, such as the P300 oddball event response, are based on the analysis of the EEG event related potentials (ERPs) [1] [2] . The P300 component of the ERP, which is a positive deflection in the EEG around 300 ms after stimuli, is utilized as a control signal in BCI systems.
A BCI system critically depends on several factors such as its cost, accuracy, how fast it can be trained and so on. The main goal of this paper is to propose an algorithm for achieving above factors. Utilizing proper channels and efficient features are two key factors that play an important role in enhancing the BCI systems. The effective features are obtained by eliminating poor features from extracted ones. In this study, we used wavelet decomposition for feature extraction, which was an efficient tool for multi-resolution analysis of non-stationary signals such as the EEG. Also, we applied Mahalanobis’s criteria to choose wavelet coefficients which were more discriminated. Optimal channels are selected by removing unnecessary channels based on Mahalanobis’s criteria and applying forward-backward selection (FBS) algorithm. In classification section, linear dis- criminant analysis (LDA) was used as a classifier because it had suitable factors such as fast training and simple implementation; hence, it brought high accuracy in output as well.
In the following sections of the paper, the P300 speller data and preprocessing phases are described in Section 2. In Section 3, we present feature extraction based on wavelet transform, optimal channel selection, optimal sub-bands selection and classification algorithm. Experimental results and conclusions are given in Sections 4 and 5, respectively.
2. P300 Speller Paradigm and Dataset
2.1. Data Description
The P300 speller paradigm described by Farwell and Donchin [3] presents a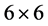 matrix of characters as shown in Figure 1. Each row and each column are flashed in a random sequence. The subject’s task was to focus on characters in a word that was prescribed by the investigator (i.e., one character at a time). Two out of 12 intensifications of rows or columns contained the desired letter (i.e., one particular
matrix of characters as shown in Figure 1. Each row and each column are flashed in a random sequence. The subject’s task was to focus on characters in a word that was prescribed by the investigator (i.e., one character at a time). Two out of 12 intensifications of rows or columns contained the desired letter (i.e., one particular
Figure 1. Screen of P300 speller paradigm.
row and one particular column). Thus, a P300 can be achieved when the row/co- lumn flashes with attended symbol.
We applied proposed method on data set II from the third edition of the BCI Competition, which was recorded for two different subjects, A and B [4] . Each subject consists of 64 channels sampled at 240 Hz with 15 repetitions per character. Signals were band-pass-filtered from 0.1 - 60 Hz [5] .
The training and the testing sets were made of 85 and 100 characters, respectively. As such, the number of corresponding epochs for each subject was 85 × 12 × 15 = 15,300 and 100 × 12 × 15 = 18,000, respectively.
2.2. Preprocessing
First, some preprocessing must be done on the signal to improve the signal to noise ratio and make it appropriate for using in BCI systems. To this end, all data were normalized as bellow:
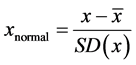 . (1)
. (1)
where x denotes the original signal, 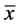 is the mean and
is the mean and  is the standard deviation of the signal. Then, we extracted the first 168 samples of each epoch, corresponding to the first 700 ms after each illumination in the P300 speller paradigm. Finally, all signals were filtered by using a band-pass filter between [0.5 - 40 Hz] and down sampled by a factor of 3.
is the standard deviation of the signal. Then, we extracted the first 168 samples of each epoch, corresponding to the first 700 ms after each illumination in the P300 speller paradigm. Finally, all signals were filtered by using a band-pass filter between [0.5 - 40 Hz] and down sampled by a factor of 3.
3. Methods
3.1. Feature Extraction
The Discrete Wavelet Transform (DWT) has been extensively used in ERP analysis due to its ability to effectively explore both the time-domain and the frequency-domain features of ERPs [6] [7] . Therefore, we used DWT to decompose a recorded EEG signal into coefficients to form a suitable feature vector. We chose the Daubechies 4 (db4) mother wavelet as it resembles the P300 component in ERPs and is very smooth. The effective frequency components of the ERPs specified the number of decomposition levels. Since the ERPs do not have any useful frequency components above 15 Hz, the effective wavelet coefficients were in the frequency range [0 - 15] Hz. Therefore, each EEG signal was decomposed into four levels and all five resulted sub-bands coefficients (i.e. A4, D4, D3, D2, D1) were candidate to form the feature vector.
3.2. Channel Selection Algorithm
The spelling accuracy in P300 speller depends on utilizing effective channels. It is obvious that less important channels leads to extraction of poor features. So, removing ineffective channels can decrease the computation time, implementation cost, and increase the output performance as well. To achieve this purpose, we used a hybrid method which extracts the optimal channels in two stages. In the first stage, we investigated the channels which had more discrimination ability of target signals from non-target signals based on Mahalanobis’s distance (MD) [8] :
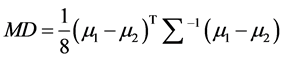 (2)
(2)
where μ1 is the mean for target class, μ2 is the mean for non-target class, and 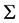 is the covariance matrix of all two classes together.
is the covariance matrix of all two classes together.
The procedure of channel selection starts with computing the MD of each of 64 channels. First, we chose 44 channels with larger MD which were about 66% of all channels. Figure 2 shows the MD for all 64 channels of subjects A and B.

Figure 2. Mahalanobis distance for all channels of (a) Subject A and (b) Subject B.
In the next stage, we used the FBS algorithm to find optimal channels. First of all, just one channel which had the highest accuracy on validation set was selected. In each running stage of the FBS algorithm, three channels were added and two channels were eliminated. So, one channel was added in each stage. The classification accuracy was assessed on the validation set described in the appendix. The FBS algorithm was implemented by defining the initial channel set which included the channel with highest accuracy on validation set. The FBS algorithm’s steps are described below:
1) Forward procedure:
・ Add each channel separately to the channel set (includes k channels).
・ Find a channel which the maximum validation set accuracy can be obtained by adding it. So, the number of channels will be .
.
・ Run all the above process two times.
・ In this case, 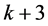 channels are obtained.
channels are obtained.
2) Backward procedure:
・ Calculate validation set accuracy by removing each channel of selected channel set at forward procedure (includes  channels).
channels).
・ Find channel which it has the maximum bypass accuracy and eliminate it.
・ Run all the above process again. So, the number of remained channels would be equal to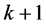 .
.
As you see, one channel in each stage of the FBS algorithm was added to the channel set. This process continued until the optimal channel set was obtained.
Figure 3 presents validation set accuracy for first 20 channels which were obtained by FBS algorithm. For a proper performance, we chose channels which could create higher accuracy in validation set. According to Figure 3, 17 and 13 channels are selected for subjects A and B, respectively. Scalp position of the
Figure 3. Accuracy of the first 20 channels which were selected by the FBS algorithm for subject A and subject B.
selected channel set for each subject is shown in Figure 4.
Figure 4. The scalp position of optimal channels for (a) Subject A and (b) Subject B.
3.3. Sub-Band Selection Algorithm
P300 component doesn’t appear at the same sub-bands for different channels. On the other hand, all sub-bands in wavelet analysis don’t make enough discrimination between two classes. So, using an algorithm for choosing the optimal sub- bands seems to be necessary. In this situation, not only the redundancy gotreduced in feature dimension, discrimination between two classes can increase as well. For meeting these requirements, we used Mahalanobis’s criterion which was defined in Equation (2).
Figure 5 shows the MD of sub-bands for selected channels in previous section. Notice that in Figure 5(a) numbers 1 to 17 of X axisreferto channels F1, F6, FC3, FCZ, C3, CZ, CP2, CPZ, CP3, P2, PZ, PO7, POZ, PO8, O1, OZ and O2, respectively. Also, in Figure 5(b) numbers 1 to 13 of X axis refer to channels FZ, FC6, C3, CZ, CPZ, P2, PO3, PO4, POZ, PO8, O1, OZ and IZ, respectively.
After computing MD of sub-bands, it is necessary to use threshold limit for optimal sub-bands selection. In order to select suitable threshold, four steps should be considered as below:
・ Computing the MD of sub-bands for selected channels. Dividing area of max (MD) and min (MD) to five levels which were defined as threshold levels.
・ Eliminating poor sub-bands whose MD are smaller than thresholds.
・ Evaluating output accuracy on validation data set.
・ Choosing the threshold corresponding to the best validation performance.
By applying the threshold level, one can use important sub-bands with nonzero values to construct the effective features. The appropriate threshold levels were 78.36 and 45.9 for subject A and B, respectively.
Figure 5. Mahalanobis distance of different sub-bands A4, D4, D3, D2, D1 versus optimal channels for (a) Subject A and (b) Subject B.
3.4. Classification Algorithm
We used the LDA classifier based on linear transform y = WTx to classify the feature vectors of two classes. Here, W is the discriminant vector, x is the feature vector and y is output of the LDA classifier. Fisher’s LDA defined in Equation (3), tries to obtain transformation matrix W by maximizing the ratio of between- class scatter [9] :
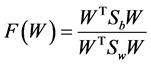 (3)
(3)
where Sb and Sw are between-class scatter matrix and within-class scatter matrix. By computing the derivative of F and setting it to zero, one can show the optimal W is determined by below equation [10] :
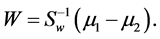 (4)
(4)
4. Experimental Results
4.1. Results of Dataset 1
For evaluation of the proposed method in selecting optimal channel set, our channel set was compared with three other channel sets. Their list is illustrated in Table 1. Classification performances for all channel sets were computed on data set II of BCI competition [4] . This data was recorded for two different subjects A and B. So, the performance of each channel set is averaged between two classifiers. Results are shown in Figure 6. According to the figure, we can see that results of channel set proposed in this study are much better than others.
To show that our proposed scheme extracts effective features, we compared the classification accuracies for all sub-bands and the optimal sub-bands as feature vectors in Table 2. According to the table, the classification accuracy of the use
Figure 6. Comparison of accuracy between the three channel sets and optimal channel set obtained by proposed method.
of the optimal sub-bands in all trials, except in single trial, is higher than that of using all sub-bands. Besides, the feature vector dimension reduced up to 40%.
Table 3 shows a comparison between output accuracy of the two best results of the BCI competition 2005 [11] , our previous work [12] and also the results obtained in this paper. As it is clear, our results are better than the second ranked competitors using SVM classifier. Although the results of this paper are somewhat lower than presented results in [12] , here we utilized a simple classifier and less EEG channels.
4.2. Results of Dataset 2
To investigate the robustness of the proposed method, we employed Hoffmann’s dataset [13] , which was comprised of four healthy subjects and four subjects
Table 1. List of electrode positions in different channel sets.
Table 2. Evaluation the feature vector obtained by Mahalanobis’s criteria.
Table 3. Classification accuracy of our algorithm, the two best competitors in BCI competition 2005 and [12] based on the number of channels and classification algorithms.
with neurological deficits. The recorded EEG data were based on visual stimuli (TV, telephone, lamp, door, window, and a radio) that evoked the P300 component. Each subject had to complete four sessions. In each session, having six runs, subjects were asked to focus on a specific image for each run, while the sequence of stimuli was randomly presented. The number of blocks inside each run was randomly chosen between 20 and 25. During every block, each image was flashed one time. The data contained 32 channels of EEG signals recorded at sampling rate of 2048. We used the data recorded in the first three sessions as the training and the last session as the test data for all eight subjects.
First, EEG signals were preprocessed according to Section 2. For each session, the single trial features corresponding to the first 20 blocks of flashes were extracted via DWT decomposition. For each subject, we reduced the number of channels from 32 to 20 by using the sorted MD values in decreasing order. We ran the FBS algorithm (as described in Section 3.2) to choose the most effective channels from the pre-selected 20 channels. Table 4 shows the number of selected final channels by the proposed method for eight subjects. It is important to note that the mean number of selected channels is 8.5 per subject. In order to select the best sub-bands of decomposed coefficients (A4, D4, D3, D2, D1), the selected channels were used to compute the efficient threshold by using the Mahalanobis criteria as described in Section 3.3. For each subject, we ran the sub-band selection procedure and reduced the feature vector dimension as nearly 45%. The results showed that by eliminating those sub-bands whose MD values were smaller than the threshold, the number of features was reduced without decreasing the accuracy. Moreover, in some cases, the classification accuracy was improved. Figure 7 presents the mean accuracy for 8 subjects in our proposed scheme and Hoffman method with 8 and 32 channels.
4.3. Run Time and Computational Complexity
We compared the computation time in our approach with our previous works [12] [17] and two best results in the BCI competition [4] [11] . The results revealed that the training time of our procedure was significantly lower than the first and the second ranked competitors using SVM classifier. The fact is that when training data dimension is too large, tuning of the SVM classifier is very difficult and its performance is reduced. So as to reduce the dimension of the training data in [11] , the data was divided into 17 partitions, and for each partition, final channels were selected among all of the 64 channels by using backward selection algorithm. The decision on target or non-target test data was made by voting on the outputs of 17 parallel SVM classifiers. Although this method has better accuracy as compared to our scheme, it extremely increases the
Table 4. Number of selected channels for each subject.
Figure 7. The mean accuracy for 8 subjects of second dataset in our proposed method and Hoffman method for 8 and 32 channels.
computational requirements and training time. It is worth mentioning that we used fewer channels than the first ranked competitor. Additionally, we used the LDA classifier that needs less calculation as compared to the SVM. We observed that the training phase in this paper was nearly 2 and 1.5 times faster than the previous works in [12] and [17] , respectively. The procedure of feature and channel selection in [17] is more complex and needs more computations than this work. The LDA outperforms the BLDA that used in [12] [17] in small size data because of parameters tuning requirements of BLDA and its complexity.
5. Conclusion
Three main features of a suitable BCI system are defined as low cost, real time responses and high accuracy. To achieve these objectives, we proposed a scheme for selecting minimal channels and effective features. Proper channels were obtained by utilizing Mahalanobis’s criteria and FBS algorithm. To extract effective features, we used discrete wavelet decomposition via mother wavelet db4 and reduced the number of coefficients by utilizing Mahalanobis’s criteria. The set of minimal features and effective channels resulted in less computation, and reasonable accuracy. We achieved 92% accuracy using a simple classification algorithm based on LDA, as compared with our previous works [12] [17] using the BLDA classifier, requiring more computation, and much more channels requiring excessive computation. Also, our results in all trials were better than the se- cond best result in BCI 2005 using SVM classifier, with low computational speed, not having enough robust performance. The results on two different P300-BCI datasets including 10 disabled and able-bodied subjects indicated that our proposed scheme needed less features and channels, and significantly reduced calculations, despite providing similar or better accuracy compared with other existing schemes.
Cite this paper
Perseh, B., Kiamini, M. and Jabbari, S. (2017) Feature Conditioning Based on DWT Sub-Bands Selection on Proposed Channels in BCI Speller. J. Biomedical Science and Engineering, 10, 120-133. https://doi.org/10.4236/jbise.2017.103010
References
- 1. Wolpaw, J.R., Birbaumer, N. and Heetderks, W.J. (2000) Brain Computer Interface Technology: A Review of the First International Meeting. IEEE Trans Rehab Engineering, 8, 64-73.
https://doi.org/10.1109/tre.2000.847807 - 2. Wolpaw, J.R., Birbaumer, N., McFarland, D., Pfurtscheller, G. and Vaughan, T. (2002) Brain-Computer Interfaces (BCIs) for Communication and Control. Clinical Neurophysiology, 113, 767-791.
- 3. Farwell, L.A. and Donchin, E. (1988) Talking off the Top of Your Head: Toward a Mental Prosthesis Utilizing Event-Related Brain Potentials. Electroen-Cephalography and Clinical Neurophysiology, 70, 510-523.
- 4. BCI Competition III Webpage.
http://www.bbci.de/competition/iii/#data_set_iiib - 5. Schalk, G., McFarland, D., Hinterberger, T., Birbaumer, N. and Wolpaw, J.R. (2004) BCI2000: A General-Purpose Brain-Computer Interface (BCI) System. IEEE Transactions on Biomedical Engineering, 51, 1034-1043.
https://doi.org/10.1109/TBME.2004.827072 - 6. Markazi, S.A., Stergioulas, L.K. and Ramchurn, A. (2007) Latency Corrected Wavelet Filtering of the P300 Event-Related Potential in Young and Old Adults. Proceeding of the 3rd International IEEE EMBS Conferences on Neural Engineering, Hawaii, 2-5 May 2007, 582-586.
- 7. Fatourechi, M., Birch, G.E. and Ward, R.K. (2007) Application of a Hybrid Wavelet Feature Selection Method in the Design of a Self-Paced Brain Interface System. Journal of Neuro Engineering and Rehabilitation, 4, 11.
https://doi.org/10.1186/1743-0003-4-11 - 8. Theodoridis, S. and Koutroumbas, K. (2003) Pattern Recognition. 2nd Edition, Academic Press, San Diego.
- 9. Fisher, R.A. (1936) The Use of Multiple Measurements in Taxonomic Problems. Annals of Human Genics, 7, 179-188.
- 10. Martinez, A. and Aka, A. (2001) PCA versus LDA. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23, 228-233.
https://doi.org/10.1109/34.908974 - 11. Rakotomamonjy, A. and Guigue, V. (2008) BCI Competition III: Dataset II-Ensemble of SVMs for BCI P300. IEEE Transactions on Biomedical Engineering, 55, 1147-1154.
https://doi.org/10.1109/TBME.2008.915728 - 12. Perseh, B. and Kiamini, M. (2013) Optimizing Feature Vectors and Removal Unnecessary Channels in BCI Speller Application. Journal of Biomedical Science and Engineering, 6, 973-981.
https://doi.org/10.4236/jbise.2013.610121 - 13. Hoffmann, U., Vesin, J.M., Ebrahimi, T. and Diserens, K. (2008) An Efficient P300-Based Brain-Computer Interface for Disabled Subjects. Journal of Neuroscience Methods, 167, 115-125.
- 14. Kaper, M. and Ritter, H. (2004) Generalizing to New Subjects in Brain-Computer Interfacing. Proceedings of the 26th Annual Conference in EMBS, San Francisco, 1- 4 September 2004, 4363-4366.
https://doi.org/10.1109/iembs.2004.1404214 - 15. Thulasidas, M. and Guan, C. (2005) Optimization of BCI Speller Based on P300 Potential. Proceedings of the 27th Annual Conference in Medicine and Biology, Shanghai, 1-4 September 2005, 5396-5399.
- 16. Yang, L., Li, J., Yao, Y. and Li, G. (2007) An Algorithm to Detect P300 Potentials Based on F-Score Channel Selection and Support Vector Machines. 3rd International Conference on Natural Computation, Haikou, 24-27 August 2007, 280-284.
https://doi.org/10.1109/ICNC.2007.172 - 17. Perseh, B. and Sharafat, A.R. (2012) An Efficient P300-Based BCI Using Wavelet Features and IBPSO-Based Channel Selection. Journal of Medical Signals & Sensors, 2, 128-142.
Appendix
We applied validation process based on five-fold cross-validation method to obtain proper channels. The procedure follows items below:
・ Training data with 85 × 12 × 15 × Channel Count signals (where, 85: characters, 12: stimuli, 15: time repetitions, and Channel Count: number of channels) averaged over all signals by 3 times repetitions. So, training data contained 85 × 12 × 5 × Channel Count signals.
・ We divided 85 characters to five partitions and built validation set from N × 12 × 5 × Channel Count signals, where, N contains 17 characters and used residual data to form a training set.
・ Feature vectors were created based on wavelet coefficients (approximate coefficients level 4 and detail coefficients levels 1 to 4 (A4, D4, D3, D2, D1).
・ The LDA classifier was trained and output precision was evaluated based on
validation set. The precision is defined as:
FN are the number of true positive, false positive and false negative respectively.
・ Validation performance was assessed by averaging between five precisions.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jbise@scirp.org










