Journal of Biomedical Science and Engineering
Vol. 5 No. 3 (2012) , Article ID: 18096 , 7 pages DOI:10.4236/jbise.2012.53015
Quantification of the distribution of blood flow pressure with postures*
![]()
1Science and Technology on Human Factors Engineering Laboratory, China Astronaut Research and Training Center, Beijing, China
2Instrument Science and Technology, Harbin Institute of Technology, Harbin, China
3School of Biological Science and Medical Engineering, Beijing University of Aeronautics and Astronautics, Beijing, China
4State Key Lab of Space Medicine Fundamentals and Application, China Astronaut Research and Training Center, Beijing, China
Email: #shanguang_chen@126.com, #paper_c@163.com
Received 18 November 2011; revised 6 January 2012; accepted 29 January 2012
Keywords: Distribution of Blood Flow Pressure (DBFP); Posture; Gravity; Numerical Simulation
ABSTRACT
At a different angle, this study analyzed the contour chart of blood flow pressure, extreme pressure and its position to quantify DBFP in thirteen different postures with gravity considered or not (G ≠ 0 or G = 0). The aim was to determine the suitable body positions, in which the postural model of a single vessel could be simplified to two-dimensional (2D) symmetrical one while only considering such factors as posture and gravity. Computational fluid dynamic simulations were performed. Numerical results demonstrated that the DBFP showed 2D axisymmetry at ±90˚ and three-dimensional (3D) asymmetry at any other posture with G ≠ 0, and 2D axisymmetrical one at any posture with G = 0. Therefore, modeling a vessel as a 2D model is feasible in space and at ±90˚ posture on earth. In addition, the maximum pressure occurred between the inlet and the middle of the vessel, and its position variation mainly happened in the range of 0˚ - 15˚. For a single vessel, this study provides the first theoretical evidence for cardiovascular modeling in microgravity and may help guide the researchers in designing defense devices for astronauts or patients clinically.
1. INTRODUCTION
Hemodynamic parameters, especially the blood pressure, vary with postures. Sudden postural change will bring out the large fluctuation of the blood pressure, which may lead to hypotension, syncope, even falls [1]. These symptoms are the manifestations of orthostatic intolerance (OI). OI does harm not only to the astronauts in the aerospace field [2], also to the patients in the clinical medicine [3].
In recent years many researches have focused on the blood pressure variation with the postural change. There are two main types of methods. One is test method [4-7], and the other is modeling and simulation one [2,8-10]. Olufsen et al. [2] performed the study of blood pressure and blood flow variation during the postural change from sitting to standing by presenting a mathematical model. This model utilized 11 compartments to predict the dynamic changes of the arterial blood pressure and some other haemodynamic parameters. It included two types of control mechanisms: autonomic regulation and autoregulation. The effects of gravity on venous blood pooling during the postural change was described by a physiologybased submodel, one dimensional model. Heusden et al. [9] developed a baroreflex model combined with a lumped-parameter model of the circulation. Gravity was introduced into the model as the formulation of the hydrostatic column. During the first 5 s after head-up tilt (HUT) and tilt back, the direct effect of gravity on the pulmonary circulation influenced the blood pressure (BP) response, and the response to HUT was mainly determined by the response of the venous system. JYA Foo [10] introduced a mathematical model using only a few empirical parameters and the measured lower limb vascular path length. The aim was to monitor blood pressure with different postures by estimating the pulse transit time, which was inversely correlated to the BP change. The reliability of the model was assessed by measuring the value of the pulse transit time at the sitting and supine positions at discrete intervals from 23 healthy children.
The previous studies did not quantitatively analyze the DBFP in so many different postures because gravity, as a scalar, was introduced into these studies.
The present study was focused on the simulation of the pressure contour, extreme pressure and its position to quantify the DBFP in the inner carotid artery with single definite posture. Gravity was taken into consideration as a vector. It is worthy to study this issue so as to assist the researchers in postural/hemodynamical model simplification and in identifying the effective range to defense for astronauts or patients clinically.
2. METHODS
The postural model for the single vessel has been developed in a previous paper [11]. As a body force in this model, gravity was first introduced as a term to reflect the postural change. Therefore, it could realistically reflect the effect of gravity.
Equation of continuity
 (1)
(1)
Equation of motion for fluid
 (2)
(2)
where  represents the inertial force,
represents the inertial force, 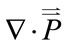
represents the surface force, 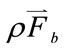 represents the body force, which was identified as the key term to reflect the postural change,
represents the body force, which was identified as the key term to reflect the postural change, 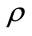 is the blood density,
is the blood density, 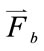 is the body force per unit mass of blood,
is the body force per unit mass of blood, 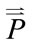 is the second order stress tensor of the blood pressure,
is the second order stress tensor of the blood pressure, 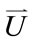 is the blood velocity, and A is the cross-sectional area of the vessel.
is the blood velocity, and A is the cross-sectional area of the vessel.
In the large systemic artery such as the inner carotid artery, the blood flow can be assumed to be homogeneous, incompressible, viscous and Newtonian fluid [12,13]. The vascular wall is assumed to be rigid [14,15]. The dimension of the vessel [16] and the property of the blood [13,17] are listed in Table 1, where L is the length of the vessel, D1 and D2 are the inlet and outlet diameters of the vessel, respectively, ρ is the blood density, and μ is the blood viscosity. The boundary conditions used in this postural model were as follows. The inlet and outlet pressures were set to constants, respectively, and the pressure difference was 199.98 Pa (1.5 mmHg). The rigid wall condition was given.
A commercial finite element software package ADINA (ADINA R & D, Inc., Watertown, MA, USA) was used as the tool for simulation in this study. The software has been used by many researchers such as Tang et al. [18,19] and Kaazempur-Mofrad et al. [20] for various biological systems in the last several years. 3D fluid element was meshed. Mesh analysis was performed until the relative error between solutions from two consecutive meshes was less than 1%. Numerical computational model-FE model is shown in Figure 1.
In this study, thirteen different postures were considered. The schematic diagram of the different postures is shown in Figure 2. The 0˚ posture corresponded to supine one, 90˚ to upright, –90˚ to upside-down, the postures between –90˚ and 0˚ were denoted as the negative tilting ones, and the postures between 0˚ and 90˚, as the positive tilting ones. More postures were included in this study than before. Therefore, more comprehensive hemo-

Table 1. Geometric and material parameters of the single vessel.
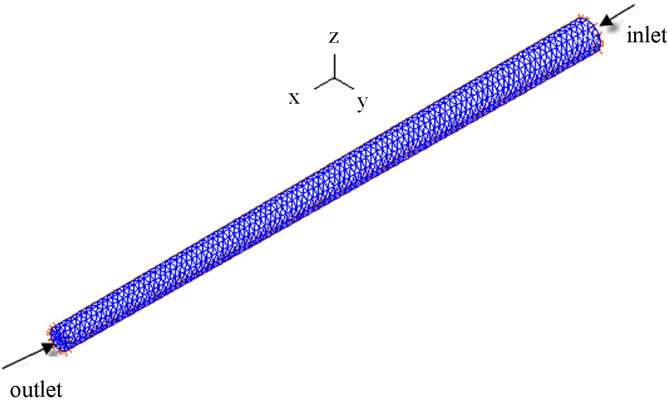
Figure 1. FE model of a single vessel.
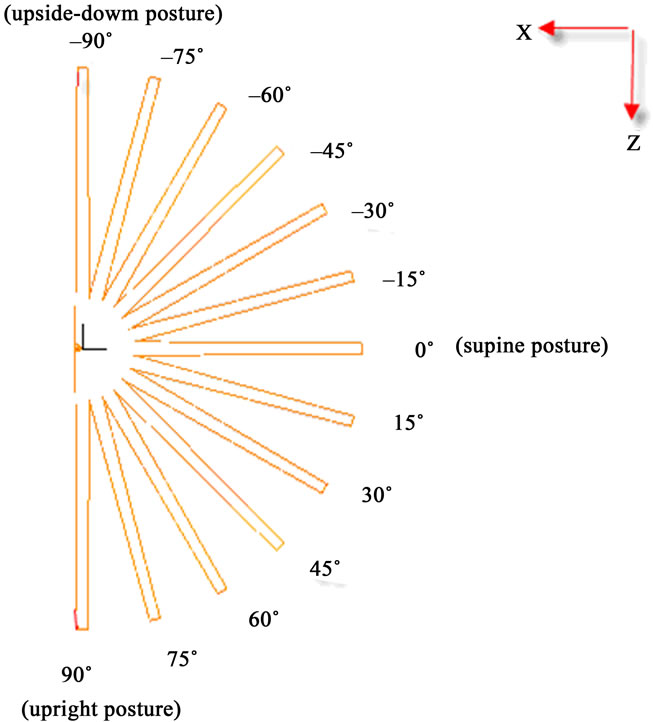
Figure 2. Schematic diagram of different postures of a single vessel.
dynamic responses could be obtained in different postures.
3. RESULTS
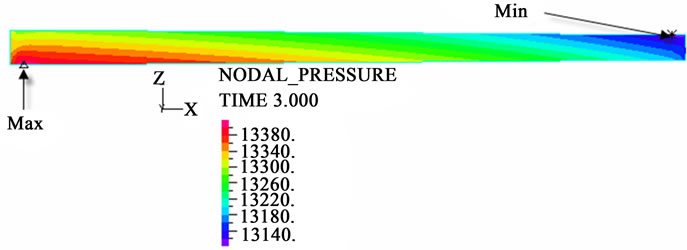
The contour charts of the blood flow pressure in different postures in the inner carotid artery are shown in Figure 3 with G ≠ 0. The DBFP varied with the posture and gravity. As G ≠ 0, at upright (90˚) and upside-down (–90˚) postures, the DBFP took on 2D axisymmetrical one, and
 (a)
(a)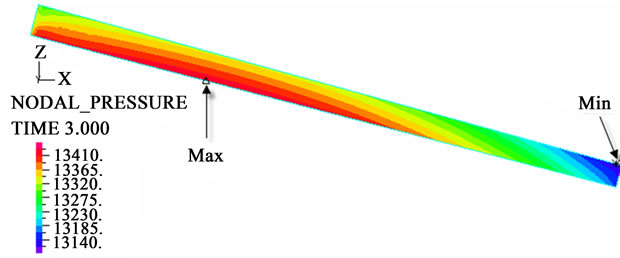 (b)
(b)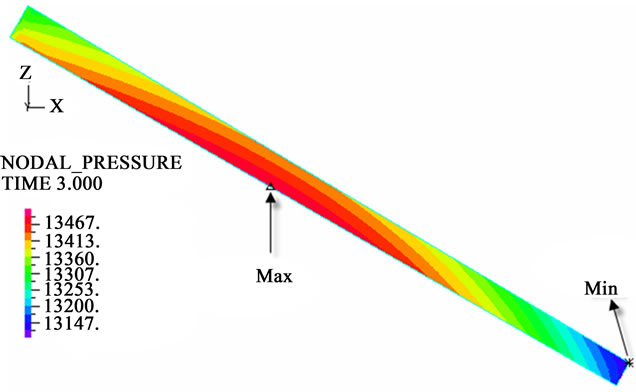 (c)
(c) (d)
(d)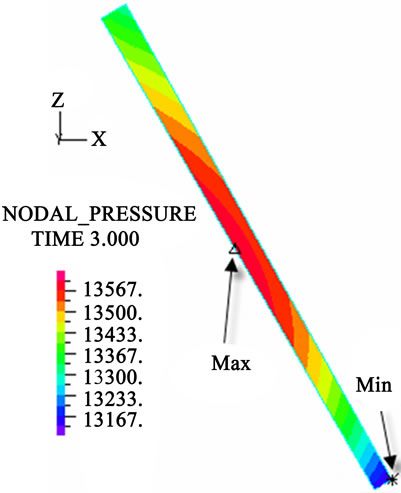 (e)
(e) (f)
(f)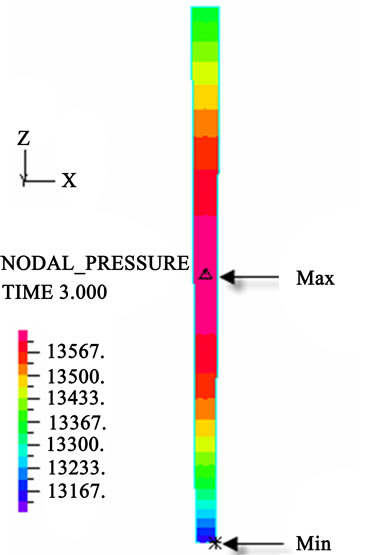 (g)
(g)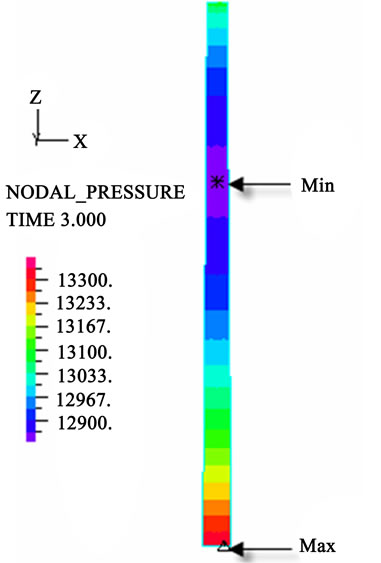 (h)
(h)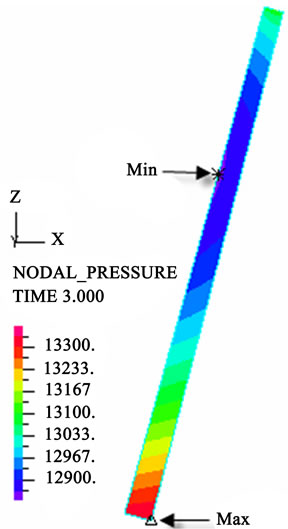 (i)
(i)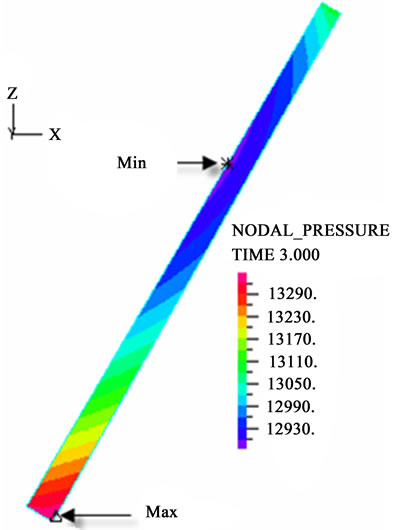 (j)
(j)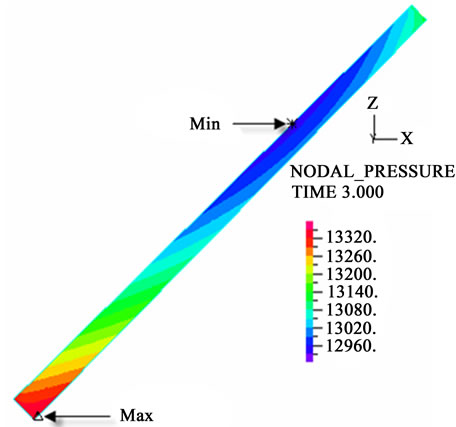 (k)
(k) (l)
(l)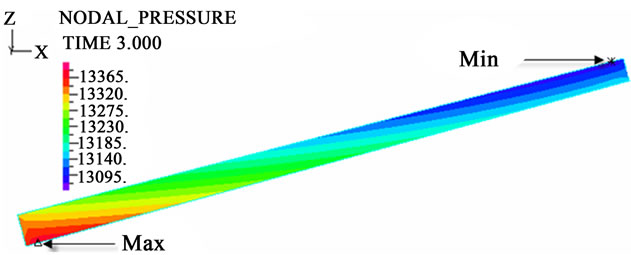 (m)
(m)
Figure 3. Longitudinal section contour chart of distribution of blood flow pressure in different postures (△P = 199.98 Pa, G ≠ 0): (a) 0˚ supine posture; (b) 15˚ positive tilting posture; (c) 30˚ positive tilting posture; (d) 45˚ positive tilting posture; (e) 60˚ positive tilting posture; (f) 75˚ positive tilting posture; (g) 90˚ upright posture; (h) –90˚ upside-down posture; (i) –75˚ negative tilting posture; (j) –60˚ negative tilting posture; (k) –45˚ negative tilting posture; (l) –30˚ negative tilting posture; (m) –15˚ negative tilting posture.
3D asymmetrical distribution at any other posture (0˚, ±15˚, ±30˚, ±45˚, ±60˚, ±75˚). From –90˚ to 0˚, the asymmetrical degree of the DBFP increased step by step, and gradually decreased from 0˚ to +90˚. As G = 0, the 2D axisymmetrical distribution existed at all single definite postures. This indicates that modeling a single vessel as a 2D model is reasonable in space.
The extreme values of the blood flow pressure in different postures are shown in Figure 4. Both the maximum pressure (Pmax, corresponding to SBP) and the minimum pressure (Pmin, to DBP) increased with increasing postures from –90˚ to +90˚ as G ≠ 0. The increase rate of Pmax was significantly different from that of Pmin. To Pmax, the increase rate from –90˚ to 0˚ was smaller than that from 0˚ to 90˚. To Pmin, vice versa. Comparing the increase rate between Pmax and Pmin, the one of Pmin was larger than that of Pmax from –90˚ to 0˚. From 0˚ to 90˚, however, vice versa. With G = 0, Pmax and Pmin kept invariant although the posture varied.
Figure 5 shows that the position obviously differs between Pmax and Pmin with postures as G ≠ 0. At the negative tilting postures, Pmin moved from the 2/3 length
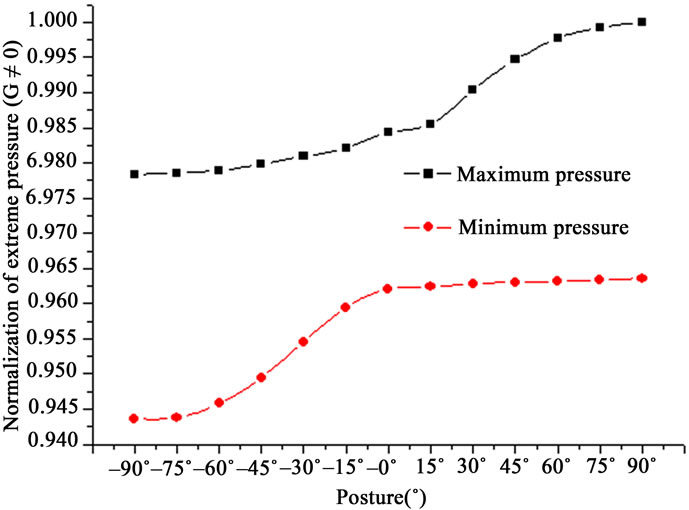
Figure 4. Extreme values of pressure in different postures in the single vessel (G ≠ 0).

Figure 5. Positions of extreme pressure in different postures in the single vessel (G ≠ 0).
to the outlet of the vessel, and its position variation mainly happened from –30˚ to –15˚ posture. At the positive ones, Pmax come out from the inlet to the middle, and its position variation peaked from 0˚ to 15˚ posture. However, the corresponding Pmax or Pmin remained inactive at the inlet or outlet of the vessel, respectively. As G = 0, the position of Pmax or Pmin remained constant at all postures.
4. DISCUSSIONS
This study quantified the DBFP by analyzing the contour chart of blood flow pressure, extreme pressure and its position in a single vessel. Thirteen different postures (from –90˚ to 90˚) with G ≠ 0 or G = 0 were investigated by numerical simulation. According to previous studies, the postural change causes blood redistribution, then blood pressure variation (systolic blood pressure/diastolic blood pressure/pulse pressure/mean aortic pressure (SBP/DBP/ PP/MAP)) [21]. No matter whether other hemodynamic parameters change or not due to the postural change, blood pressure, which is usually measured on the body surface non-invasively, is determined by the space distribution of the blood flow pressure in the vessel, i.e., the contour chart of blood flow pressure.
The contour chart of the DBFP can provide more elaborate expression than blood pressure obtained non-invasively. In this study, results demonstrated that the DBFP for all postures was 2D axisymmetrical distribution with G = 0, and with G ≠ 0, the same as the above at ±90˚, 3D asymmetrical one at any other posture. Therefore, gravity and posture, as a whole, is a determinant factor in the nature of the DBFP in a single vessel, and if a vessel is simplified to a 2D axisymmetrical model, the cost of computation will be significantly decreased, especially to the cardiovascular system. Peterson et al. [22] performed a simulation study about the influence of posture and gravity on cardiac performance, and obtained the similar results that, for G = 0, the computing results were the same for supine, launch, sitting and standing postures.
The extreme values of the blood flow pressure varied with postures as G ≠ 0 (Figure 4). Hemodynamic variables, such as SBP/DBP, are significantly different from supine values at each tilting angle [5]. Head up tilt has produced progressive increases in SBP (12% - 21%) and DBP (20% - 33%) with increasing tilt angle. The overall trend is in agreement with the result of this study about the variation of Pmax/Pmin, i.e., SBP (Pmax) or DBP (Pmin) increased with increasing tilt angle. This result indicated that gravity pushes the blood to flow forward at the positive postures and pulls blood backward at the negative postures. However, the difference still exists. In this study, the variation of SBP was larger than that of DBP. This result is in the opposite direction to Zaidi et al.’s [5]. The difference may be due to the effect of the nervous control.
Numerical investigation of critical flow and stress/ strain conditions for human atherosclerotic plaque rupture has been conducted [19]. Not only the magnitude of critical strain/stress and flow is important, also so is the position of critical strain/stress and flow. A small fluctuation of the hemodynamic variables may be crucial to the critical value. As shown in Figure 5, with G ≠ 0 or G = 0, Pmax occurred in the range from the inlet to the middle, and Pmin, from the 2/3 length to the outlet of the vessel at any posture. Moreover, the position variation of Pmax peaked from 0˚ to 15˚ posture. This result quantitatively explained Webster et al.’s further. Webster et al. [23] suggested that the position of the subject’s arm influenced the measurement of the blood pressure. In addition, this result may help determine the critical range of the position and posture to defense for astronauts or patients clinically.
This present study excludes the effect of the nervous control in the simulation, and it is focused only on the effects of different postures and gravity on hemodynamics. In fact, neuroregulation couples with gravity during the postural change. So the real physiological effect is a compound one. If minus the effect of posture and gravity from the total effect, this research may help clarify the real function of nervous control during the postural change.
In future study, based on the research, a simplified cardiovascular system (CVS) model (used for simulated weightlessness) will be presented while only considering posture and gravity. On earth, any artery in the CVS model could be simplified to 2D model as long as it is in upright or upside-down position. While in space, all the arteries could be done the same as the above at any posture. This will lessen the computational cost apparently. However, more precise hemodynamic response could still be obtained on earth because of gravity as a vector. So this study may provide a theoretical reference for further study into the hemodynamic response of the cardiovascular system in different postures on earth or in space.
Overall, in so many different postures, rare studies were reported to quantitatively investigate the DBFP based on the contour charts of the pressure, extreme pressure and its position with gravity as a vector.
5. CONCLUSION
The present numerical simulation demonstrates that the DBFP varies with different postures, and is closely related to gravity. In terms of the effect of single posture and gravity on the DBFP of a single vessel, simplifying the single vessel to a 2D model is reasonable in space and at ±90˚ on earth. At any other posture except ±90˚, there is a substantial difference in the DBFP if doing so despite real 3D distribution on earth. In addition, Pmax occurs in the range from the inlet to the middle of the vessel with G ≠ 0 or G = 0, and its position variation peaks from 0˚ to 15˚ posture. Thus the key location and posture to defense for a single vessel might lie in the range. The results may help provide the researchers with theoretical reference in model simplification in cardiovascular simulation in microgravity, and also in identifying the effective range of defense for astronauts or patients.
6. ACKNOWLEDGEMENTS
The authors would like to thank Dr. Liu Da’an, An Guangming of Institute of Geology and Geophysics, Chinese Academy of Sciences for providing us with the computational tool freely. We also thank Dr. Yu G. and Prof. Yang C. for their helpful advice. This work was supported by National Basic Research Program of China (NO.2011CB711000).
![]()
![]()
REFERENCES
- Ooi, W.L., Barrett, S., Hossain, M., Kelley-Gagnon, M. and Lipsitz, L.A. (1997) Patterns of orthostatic blood pressure change and their clinical correlates in a frail, elderly population. Journal of the American Medical Association, 277, 1299-1304. doi:10.1001/jama.1997.03540400049030
- Olufsen, M.S., Ottesen, J.T., Tran, H.T., Ellwein. L.M., Lipsitz, L.A. and Novak, V. (2005) Blood pressure and blood flow variation during postural change from sitting to standing: Model development and validation. Journal of Applied Physiology, 99, 1523-1537. doi:10.1152/japplphysiol.00177.2005
- Sullivan, S.D., Hanauer, J., Rowe, P.C., Barron, D.F., Darbari, A. and Oliva-Hemker, M. (2005) Gastrointestinal symptoms associated with orthostatic intolerance. Journal of Pediatric Gastroenterology and Nutrition, 40, 425- 428. doi:10.1097/01.MPG.0000157914.40088.31
- Rossum, A.C., Ziegler, M.G. and Meck, J.V. (2001) Effect of spaceflight on cardiovascular responses to upright posture in a 77-year-old astronaut. The American Journal of Cardiology, 88, 1335-1337. doi:10.1016/S0002-9149(01)02104-X
- Zaidi, A., Benitez, D., Gaydecki, P.A., Vohra, A. and Fitzpatrick, A.P. (2000) Haemodynamic effects of increasing angle of head up tilt. Heart, 83, 181-184. doi:10.1136/heart.83.2.181
- László, Z., Rössler, A. and Hinghofer-Szalkay, H.G. (2001) Cardiovascular and hormonal changes with different angles of head-up tilt in men. Physiological Research, 50, 71-82.
- Schrage, W.G. (2008) Not a search in vein: Novel stimulus for vascular dysfunction after simulated microgravity. Journal of Applied Physiology, 104, 1257-1258. doi:10.1152/japplphysiol.00174.2008
- Singleton, C.D., Robertson, D., Byrne, D.W. and Joos, K.M. (2003) Effect of posture on blood and intraocular pressures in multiple system atrophy, pure autonomic failure, and baroreflex failure. Circulation, 108, 2349- 2354. doi:10.1161/01.CIR.0000097114.11038.26
- Heusden, K.V., Gisolf, J., Stok, W.J., Dijkstra, S. and Karemaker, J.M. (2006) Mathematical modeling of gravitational effects on the circulation: Importance of the time course of venous pooling and blood volume changes in the lungs. American Journal of Physiology-Heart and Circulatory Physiology, 291, H2152-H2165. doi:10.1152/ajpheart.01268.2004
- Foo J.Y.A. (2007) A computational approach to predict pulse transit time variations during postural change. Cardiovascular Engineering, 7, 121-126. doi:10.1007/s10558-007-9034-8
- Mu, W.Y., Yu, G., Zhuang, F.Y. and An, G.M. (2009) Mathematical model of hemodynamics with posture. Journal of Medical Biomechanics, 23, 441-445, 458.
- Caro, C.G., Pedley, T.J., Schroter, R.C. and Seed, W.A. (1978) The systemic arteries. The Mechanics of the Circulation, 243-346.
- Fung, Y.C. (1981) The flow properties of blood. Biomechanics: Mechanical Properties of Living Tissues, SpringerVerlag, New York, 62-98.
- Kwak, D., Kiris, C. and Kim, C.S. (2005) Computational challenges of viscous incompressible flows. Computers & Fluids, 34, 283-299. doi:10.1016/j.compfluid.2004.05.008
- Taylor, C.A. and Draney, M.T. (2004) Experimental and computational methods in cardiovascular fluid mechanics. Annual Reviews of Fluid Mechanics, 36, 139-231. doi:10.1146/annurev.fluid.36.050802.121944
- Matthys, K.S., Alastruey, J., Peiró, J., Khir, A.W., Segers, P., Verdonck, P.R., Parker, K.H. and Sherwin, S.J. (2007) Pulse wave propagation in a model human arterial network: Assessment of 1-D numerical simulations against in vitro measurements. Journal of Biomechanics, 40, 3476-3486. doi:10.1016/j.jbiomech.2007.05.027
- Caro, C.G., Pedley, T.J., Schroter, R.C. and Seed, W.A. (1978) Blood. The Mechanics of the Circulation, 151- 180.
- Tang, D., Yang, C., Zheng, J. and Raymond, P.V. (2003) Effects of stenosis asymmetry on blood flow and artery compression: A 3-D FSI model. Annals of Biomedical Engineering, 31, 1182-1193. doi:10.1114/1.1615577
- Tang, D., Yang, C., Zheng, J., Woodard, P.K., Sicard, G.A., Saffitz, J.E. and Yuan, C. (2004) 3D MRI-based multicomponent FSI models for atherosclerotic plaques. Annals of Biomedical Engineering, 32, 947-960. doi:10.1023/B:ABME.0000032457.10191.e0
- Kaazempur-Mofrad, M.R., Bathe, M., Karcher, H., Younis, H.F., Seong, H.C., Shim, E.B., Chan, R.C., Hinton, D.P., Isasi, A.G., Upadhyaya, A., Powers, M.J., Griffith, L.G. and Kamm, R.D. (2003) Role of simulation in understanding biological systems. Computers & Structures, 81, 715-726. doi:10.1016/S0045-7949(02)00481-9
- Ward, R.I., Danziger, F., Bonica, J.I., Allen, G.D. and Tolas, A.G. (1966) Cardiovascular effects of change of posture. Aerospace Medicine, 37, 257-259.
- Peterson, K., Ozawa, E.T., Pantalos, G.M. and Sharp, M.K. (2002) Numerical simulation of the influence of gravity and posture on cardiac performance. Annals of Biomedical Engineering, 30, 247-259. doi:10.1114/1.1451075
- Webster, J., Newnham, D., Petrie, J.C. and Lovell, H.G. (1984) Influence of arm position on measurement of blood pressure. British Medical Journal, 288, 1574-1575. doi:10.1136/bmj.288.6430.1574
NOTES
*There are no conflicts of interest for the authors of this study.
#Corresponding author.

