Journal of Biomedical Science and Engineering
Vol. 5 No. 2 (2012) , Article ID: 17626 , 6 pages DOI:10.4236/jbise.2012.52008
Comparative study of the mechanical behavior of the superior thoracic artery and abdominal arteries using the finite elements method
![]()
Laboratory of Industrial Méchanic, University of Badji Mokhtar, Annaba, Algeria
Email: salim.kadri@yahoo.fr
Received 23 May 2011; revised 20 August 2011; accepted 19 December 2011
Keywords: Biomechanics; Finite-Element; Modeling; Thoracic Aorta; Deformation (Strain) of the Arteries
ABSTRACT
The human body has been the subject of thorough researches—not only from medical perspective but from a technical one as well—are very rich, amongst them we find blood circulation system comprising: the heart, the arteries and the veins. The overriding role of these researches is to explain some cardiovascular pathology and provide an aid tool for the endoprothesis positioning in blood vessels while treating them. In this study we have developed a digital pattern using the common (engineering technique of the) finite element method (FEM) to simulate the mechanical behavior of the thoracic aorta and the abdominal aorta below the kidney under blood pressure effect. This pattern calculates the displacements, the stresses (constraints) and the deformations of the two arteries’ walls enabling us to know their experimentally determined mechanical and geometric properties. This pattern could be applied to detect the aneurysm and dissection phenomena.
1. INTRODUCTION
The mechanical behavior of the thoracic aorta is linked to the blood pressure (artery pressure) [1] where the pulsating feature triggers dilatations and deformations of the wall which is constituted of three coats (layers) (the tunica intima, the tunica media and the tunica adventitia). This dilatation may multiply the risk of developing some pathology such as: the aneurysm and the dissection [2, 3].
In fact, the blood flows with a diastolic pressure (minimum pressure) then this latter increases to attain a systolic pressure (maximum blood pressure), the artery wall is then expanded owing to a radial traverse.
Due to the wall’s weak elasticity (advanced age) and the alternating pressure affecting this wall per se, this could trigger a aneurysm thoracic which is a very critical phenomenon because it doesn’t deform only the aorta but other adjacent organs as well if the dilatation is very severe. Besides it also alters the pulse wave’s value which causes a rupture (break) within another artery or a delay in blood distribution [4,5].
What’s more, the dissection is also a serious phenomenon since it is tightly linked to the rupture of the arterial layer depending on its length; the latter could trigger the above mentioned phenomena on the other layers. In order to simulate the mechanical behavior of the thoracic aorta under blood pressure effect and make similarities with the abdominal aorta below the kidney—very known for specialists by its pathological phenomena—a pattern based on the finite element method has been adjusted. While situating ourselves in the small-deformation theory and considering the isotropic materials, the compressible of E Young’s modulus and Poisson 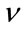 coefficient [4], this pattern allows for calculating the displacements, the constraints and the deformations rates in the plan based on the mechanical properties of the thoracic aorta. Lots of researches had been carried out over the past several years in the arteries mechanical properties field, Wang, J. J. Parker, K. H, have calculated the Young’s modulus in addition to geometries of 55 arteries in the human body [6].
coefficient [4], this pattern allows for calculating the displacements, the constraints and the deformations rates in the plan based on the mechanical properties of the thoracic aorta. Lots of researches had been carried out over the past several years in the arteries mechanical properties field, Wang, J. J. Parker, K. H, have calculated the Young’s modulus in addition to geometries of 55 arteries in the human body [6].
2. BASIC EQUATIONS
Considering the arteries as a cylinder of an infinite length with an internal radius R1 and external radius R2 within which blood circulates at Pint pressure. Under blood pressure effect, the aorta’s wall undergoes radial displacement Ur and radial deformation rates εrr and angular εθθ which are given respectively bellow [4,5]:
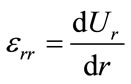 (1)
(1)
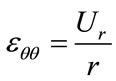 (2)
(2)
and
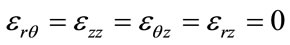
Applying Hooke’s relation we can readily obtain the constraints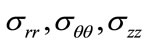 :
:
 (3)
(3)
In order to obtain the radial displacement function Ur we apply Navier-Lamé relation:
 (4)
(4)
with f = 0 (gravity forces are considered negligible).
In order to apply the finite element method we perform a shift from cylindrical coordinates system to Cartesian coordinates using:
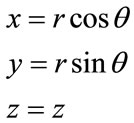
In this case, the displacement becomes bi-dimensional (U, V) as well as the deformations and constraints (see Figure 1) [7].
Problem data: geometries and mechanical properties of two arteries are given in the Table 1.
3. DIGITAL RESOLUTION
The finite element method consists in dividing the geometry into many elements then monitor element geometry alterations in a thorough manner. These stages could be summarized as follow [8]:
Step 1: mesh sizing: it is about putting nodes in the geometry, and then numbering every and each node which allows the automatic determination of the triangular element associated with three nodes (Figure 2).
• Identify the coordinates of each node according to one parameter which is the number of nodes (internal and external of the aorta).
• Find the connection between then nodes’ numbering from one hand and the elements from another.
For symmetry reason we carry out the mesh sizing except for a quarter of a pipe and considering the conditions of the limits (setting against x & y).
Step 2: calculate the three nodal coordinates of each element (N1, N2, N3) in accordance with the coordinates of each node.
• Calculate the surface of each element.
Step 3: work out the elementary stiffness matrix  using the following formula:
using the following formula:
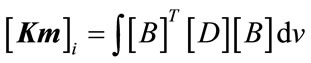 (5)
(5)
Step 4: assemblage of the elementary stiffness matrix

Figure 1. Geometry of the thoracic aorta.
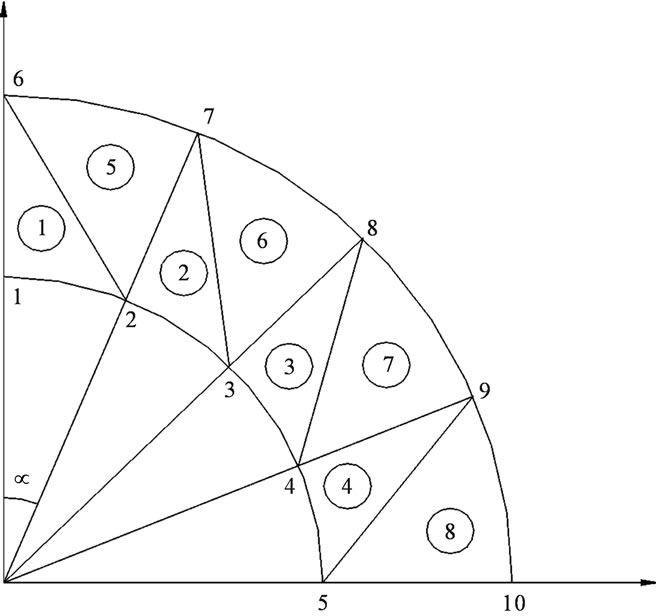
Figure 2. Mesh sizing of the arterial wall.

Table 1. Geometrical and mechanical characteristics of two arteries.
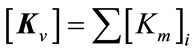 (6)
(6)
• Assemblage of the force vectors.
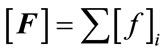 (7)
(7)
where 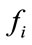 in our case is the force resulting from pressure Pint.
in our case is the force resulting from pressure Pint.
Step 5: work out the displacement vector (U, V) using the following system matrix resolution.
 (8)
(8)
Stage 6: calculate the deformation and the constraint in every and each element using the same system applying the elasticity hypothesis.
4. RESULTS AND DISCUSSION
We have carried out our calculation following the same example of Figure 2 i.e. 10 nodes (5 on the R1 arc and 5 on the R2 arc), referring to our example we have also 8 elements.
The curves bellow are displacement and constraint curves according to blood pressure Figure 3.
5. OBSERVATION
Constraints values of elements 4, 7 and 8 are negligible if compared to other constraints (see Figures 4 to 10).
Thoracic Aorta Situation
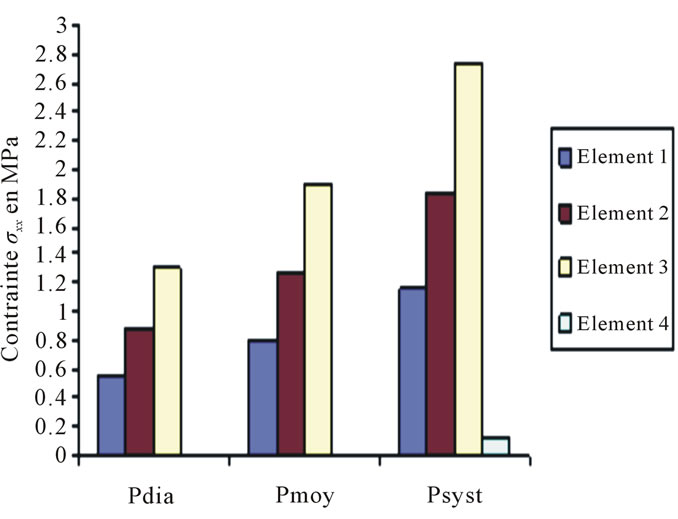
Figure 3. Constraints values σx applied on elements 1, 2, 3, 4 according to blood pressure.

Figure 4. Constraints values σy applied on elements 1, 2, 3, 4 according to blood pressure.
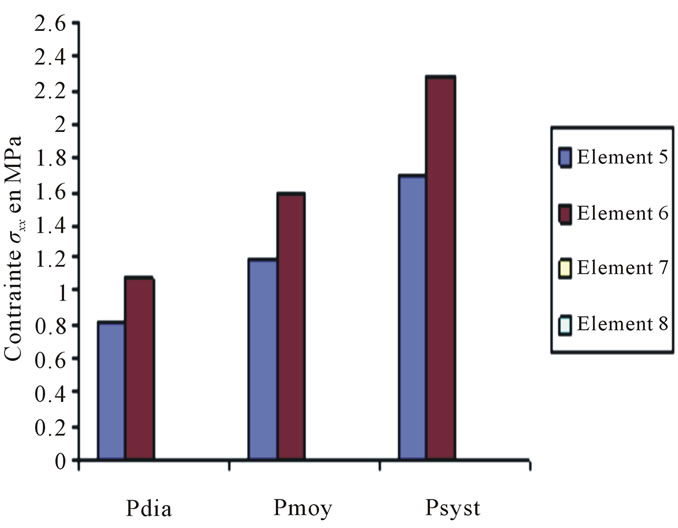
Figure 5. Constraints values σx applied on elements 5, 6, 7, 8 according to blood pressure.
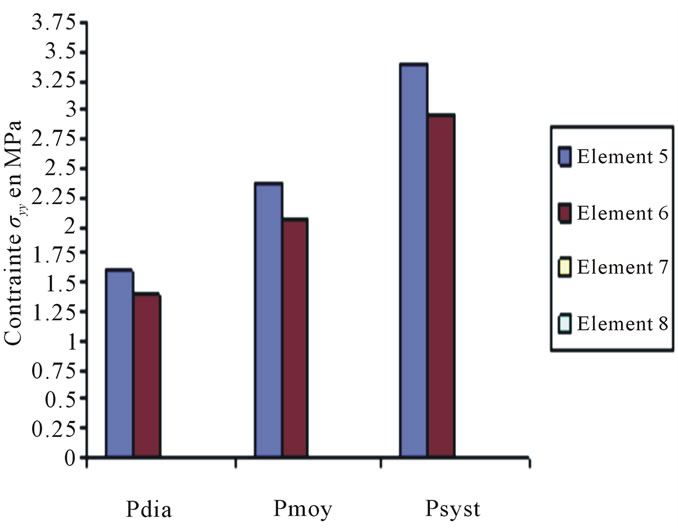
Figure 6. Constraints values σy applied on elements 5, 6, 7, 8 according to blood pressure.
Abdominal Aorta Situation
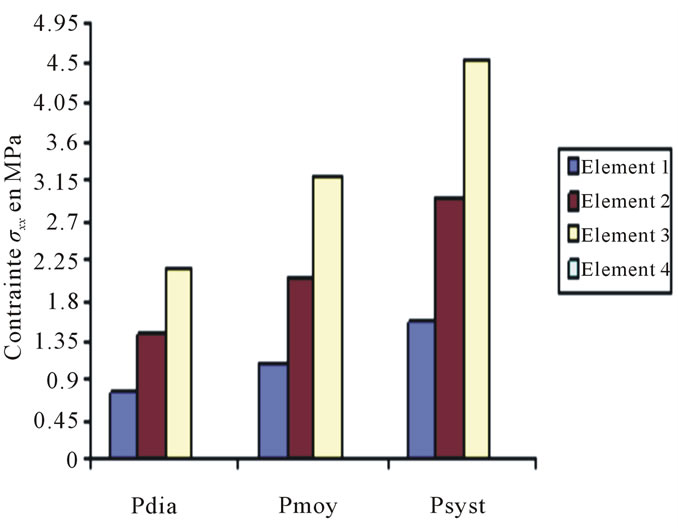
Figure 7. Constraints values σx applied on elements 1, 2, 3, 4 according to blood pressure.
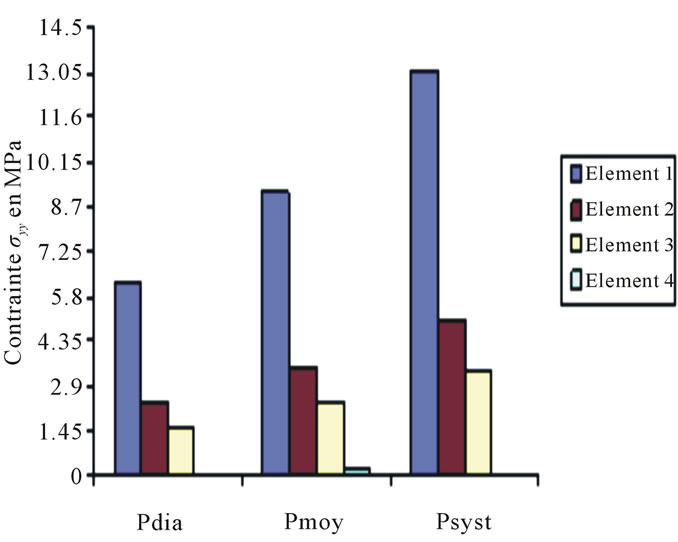
Figure 8. Constraints values σy applied on elements 1, 2, 3, 4 according to blood pressure.
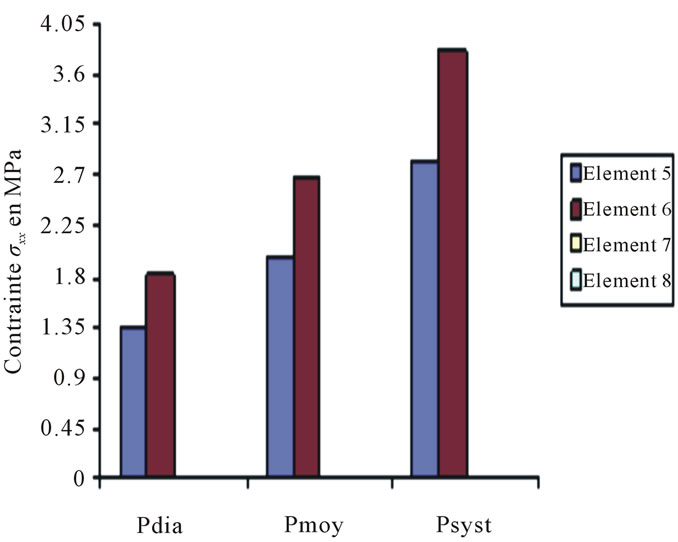
Figure 9. Constraints values σx applied on elements 5, 6, 7, 8 according to blood pressure.
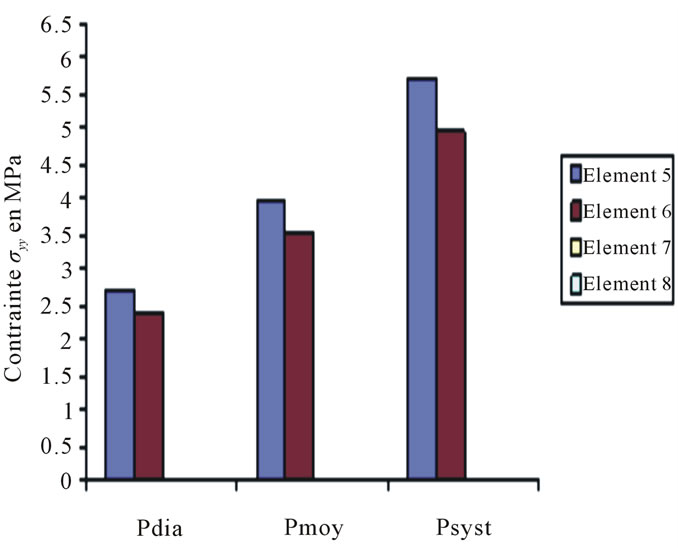
Figure 10. Constraints values σy applied on elements 5, 6, 7, 8 according to blood pressure.
These curves depict the increase of the applied constraints as per x & y, this increase which is very much remarkable in the case of the internal wall (Tunica Intima) is very high—compared to the thoracic aorta—on the abdominal aorta below the kidney, which explains the emergence of those two pathologies.
The bellow curves depict the position change of aorta walls under systolic pressure effect.
6. CONCLUSIONS
On the basis of the results of the present study, the nodes movement in the second arch, representing the outer layer of the thoracic aorta, rang from 6 to 10 mm, while those of the abdominal aorta range from 3 to 5 mm. These movements are not so important if one takes into account the respective geometry of the arteries, particularly their outer radius.
The nodes movement in the first arch that represents the inner layer of the thoracic aorta, is about 10.8 cm, while those of the abdominal aorta is 11.2 cm (see Figures 11 to 14).
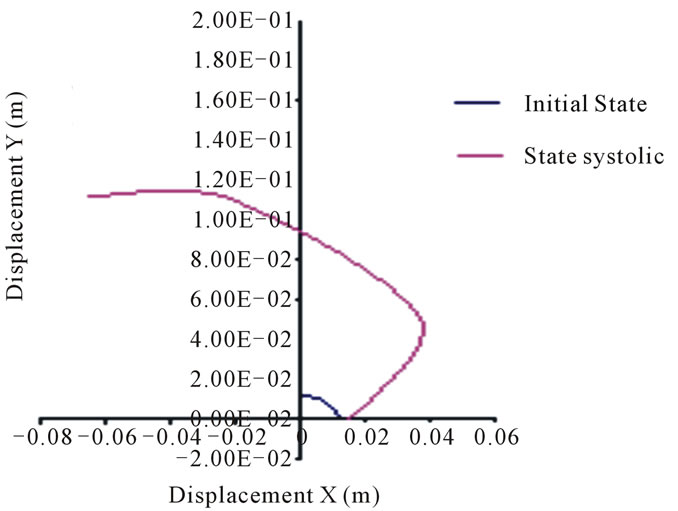
Figure 11. Positions of the thoracic aorta internal wall nodes.
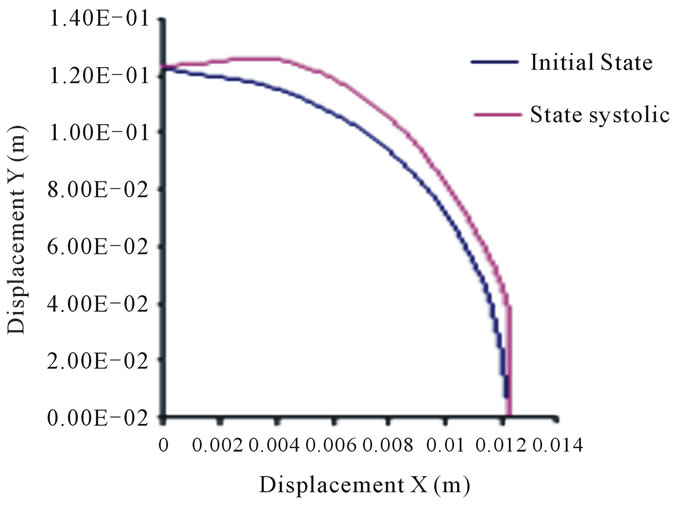
Figure 12. Positions of the thoracic aorta external wall nodes.

Figure 13. Positions of the abdominal aorta internal wall nodes.

Figure 14. Positions of the abdominal aorta external wall nodes.
In terms of the inner layer, the displacements are considered very important to their in relation to geometry.
We deduce that the arterial wall does not react in the same way as blood pressure: the inner layer or intima moves more significantly than the outer layer or adventitia. Unlike the movements of layers in the case of diastolic pressure and in the case of systolic pressure is high. This difference, applied alternately as in real life where the systolic peak is oscillating, a break may appear in this area.
The stress (constraint) distribution increases as blood pressure does, but this increase is concentrated on the internal elements (see Figure 2). Hence, the requirement of elastic nature intima firstly helps to prevent the break of this layer (dissection), and secondly to avoid the displacement of the three layers together at the same time which does not guarantee the return of one of the layers (aneurysm phenomenon).
Assuming that the aorta is rally circular, the change of that pace after the systolic pressure is enormous; therefore this change affects the entire blood circulatory system, since it involves blood flow and distribution alteration.
The results show that the risk of the above mentioned pathologies arising is greater for the abdominal aorta than for the thoracic one.
![]()
![]()
REFERENCES
- Asmar, R. (2007) Préssion artérielle régulation et épidé- miologie, mesures et valeurs normales. Néphrologie & Thé- rapeutique, 21, 163-184. http://www.sciencedirect.com/science/article/pii/S1769725507001204 doi:10.1016/j.nephro.2007.03.008
- Roudant, R., Laurent, F. and Roques, X. (2002) Anévrisme de l’aorte thoracique. Edition Scientifiques et Médicales, 17, 11-500-A-10.
- Veyssier-Belot, C. (1998) Dissection aortique. La Revue de Médcine Interne, 4, 704-708. doi:10.1016/S0248-8663(98)80704-2
- Wang, X., Wache, P., Navibakhsh, M., Lucius, M. and Stoltz, J.F. (1999) Simulation numérique tridimensionnelle de l’écoulement sanguin dans un anévrisme. Mécanique Industrielle et Matériaux, 3, 71-74.
- Carli, F. and Martelli, M. (1999) Mechanical model of net reinforced blood vessel. Advances in Engineering Software, 9, 673-681. doi:10.1016/j.jbiomech.2003.09.007
- Wang, J.J. and Parker, K.H. (2004) Wave propagation in a model of the arterial circulation. Journal of Biomechanics, 13, 457-470. doi:10.1016/j.jbiomech.2003.09.007
- Leslie, P., Gartner, J. and Hiatt, L. (1997) Atlas en couleur d’histologie. Pradel, Paris.
- Zienkiewicz, O.C. (2005) The finit element method for solid and structural mechanics. Elsevier Butterworth-Heinemann, Maryland Heights.
NOMENCLATURE
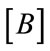 : Deformation matrix
: Deformation matrix
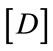 : Matrix containing the elastic properties of the material (Hooke’s relationship)
: Matrix containing the elastic properties of the material (Hooke’s relationship)
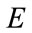 : Young’s modulus
: Young’s modulus
 : Elementary stiffness matrix
: Elementary stiffness matrix
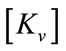 : Global stiffness matrix
: Global stiffness matrix
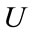 : The displacement function
: The displacement function
 : The radial displacement of the aorta Pint: Blood pressure N1, N2, N3: The coordinates of each nodal element R1, R2: Inner and outer radius of the aorta
: The radial displacement of the aorta Pint: Blood pressure N1, N2, N3: The coordinates of each nodal element R1, R2: Inner and outer radius of the aorta
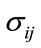 : The constraints according to the coordinates (x, y) or (r, θ)
: The constraints according to the coordinates (x, y) or (r, θ)
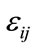 : Deformation depending on the coordinates (x, y) or (r, θ)
: Deformation depending on the coordinates (x, y) or (r, θ)
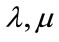 : The Lame coefficients
: The Lame coefficients
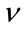 : Coefficient of fish (Poisson coefficient)
: Coefficient of fish (Poisson coefficient)

