Intelligent Information Management
Vol.07 No.06(2015), Article ID:61426,26 pages
10.4236/iim.2015.76025
Development and Comparison of Hybrid Genetic Algorithms for Network Design Problem in Closed Loop Supply Chain
Muthusamy Aravendan1, Ramasamy Panneerselvam2
1Department of Leather Design (Footwear & Products), National Institute of Fashion Technology, Chennai, India
2Department of Management Studies, School of Management, Pondicherry University, Pondicherry, India
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 18 October 2015; accepted 21 November 2015; published 24 November 2015

ABSTRACT
This paper presents four different hybrid genetic algorithms for network design problem in closed loop supply chain. They are compared using a complete factorial experiment with two factors, viz. problem size and algorithm. Based on the significance of the factor “algorithm”, the best algorithm is identified using Duncan’s multiple range test. Then it is compared with a mathematical model in terms of total cost. It is found that the best hybrid genetic algorithm identified gives results on par with the mathematical model in statistical terms. So, the best algorithm out of four algorithm proposed in this paper is proved to be superior to all other algorithms for all sizes of problems and its performance is equal to that of the mathematical model for small size and medium size problems.
Keywords:
Closed Loop Supply Chain, Genetic Algorithms, HGA, Meta-Heuristics, MINLP, Model, Network Design, Optimization

1. Introduction
Supply chain management system has been being practiced as one of the main applications and research areas in the Industrial Engineering and Management discipline for the past two decades. A supply chain system is a complex network of business distribution channel which includes suppliers, manufacturers, distributors or wholesalers, warehouses, retailers, service providers and customers involved in the upstream and downstream flows of goods or services, information and finances. The effective and efficient management of the flows among these channel partners ensures the successive implementation of the entire supply chain. This can be achieved by adopting a coherent supply chain strategy with an appropriate network design, planning and implementation of the network for the execution of the flows in the supply chain system. The integration of entire supply chain flows into a closed loop network is the need of the hour now to ensure a business to be economically and environmentally sustainable with the changing trends in business and social environments, growing environmental consciousness in the society and government legislations to protect the environment as well as the business.
The integrated supply chain network design problems involve the decisions on the configuration of the network like, locating the right facilities, allocating the right capacity to the facilities, selection of the right mode of transportation and the route or path and optimizing the entire shipment of goods among the facilities or nodes in the entire distribution channel. These network design problems are often solved by using large optimization models. As these CLSC network design problems are combinatorial and complex in nature, handling of these problems with conventional optimization techniques like exact algorithms is quite difficult. Meta-heuristics algorithms like genetic algorithms and their hybrids are more suitable for these problems. In this context, this research work deals with a multi-echelon closed loop supply chain network design with forward and reverse logistics chains. In this research, an attempt has been made to develop a set of hybrid genetic algorithms and then select the best using through a complete factorial experiment.
The structure of this research paper is organized as follows. The next section gives the overview of the GAs and the third section deals with the literature review of the research works carried out in the past and recent periods and summarizes with the research gaps. The fourth section presents the statement of the problem identified and the fifth section presents the appropriate research methods adopted to solve the problem. The sixth section discusses the development and implementation of the mathematical model and the seventh section discusses the design, development and implementation of the hybrid genetic algorithms and its source codes. The eighth section discusses the comparison of the variants of hybrid genetic algorithms and determines the best HGA among them. The ninth section compares the best HGA with the mathematical model in terms of their performance measure for the optimization of the network. The last section concludes this research work with the summary of the main research outcome, scope and future research directions.
2. Genetic Algorithms―An Overview
Genetic Algorithm (GA) is inspired by the theory of natural evolution and its principles. It is one of the directed random search techniques, employed to find a near-optimal solution for many larger problems in complex multi-dimensional search spaces. These algorithms encode a potential solution for complex problems on a simple chromosome like data structure and using techniques of natural evolution like inheritance, selection, mutation and crossover. After coding the solution in an appropriate way, GA iteratively works and evolves to get the global optimum without getting restricted at a local optimum. The individuals or chromosomes in a population are manipulated by the genetic operators to improve their fitness values while searching for global optimum solutions.
2.1. Stages of Genetic Algorithm
The steps involved in the formulation of Genetic Algorithms are mentioned as follows.
Chromosome Representation or Encoding: The individuals or the chromosomes are encoded or represented with a coding system to enable the computational processing of GA.
Initiation: Choose the initial population of the individuals.
Evaluation: Evaluate the fitness of each individual in population.
Breeding: Breeding is the process of reproduction with the following sub-steps which gets repeated until the termination condition gets satisfied.
Selection: Process of selecting the individuals with greater fitness for reproduction.
Crossover: Perform the crossover of selected individuals with a crossover probability for breeding new individuals which are offsprings.
Mutation: Perform the mutation process with a mutation probability on new individuals or offsprings for getting better offsprings.
Reevaluation: Evaluation the fitness of the each offspring created to find out the best or optimum fitness.
Termination: Terminate the process.
2.2. Classification of Genetic Algorithms
Genetic algorithms are theoretically and empirically proven to provide robust search and global solutions in complex scenarios for all sizes of problems. The Genetic Algorithms are capable of giving and efficient search in the problem domain and are finding wider range of applications in business, science, engineering and technology. These algorithms are more powerful in their search for improvement which has enabled the researchers to form different approaches of genetic algorithm. The genetic algorithms are classified as simple GA, parallel GA, hybrid GA, distributed GA, messy GA and adaptive GA etc., as given in Figure 1.
3. Literature Review
The literature is surveyed for the past 25 years and the varied research papers like concept papers, review papers, case studies, model papers and algorithmic research papers related to the principles, concepts of genetic algorithms, their application in the various closed loop and reverse supply chain network design problems are reviewed and presented in this section.
Goldberg and Deb [1] presented a comparative analysis of selection schemes used in Genetic Algorithms. They considered the commonly used selection schemes in GA viz. proportionate reproduction, ranking selection, tournament selection and Genitor (steady state) selection and compared them on the basis of solutions to deterministic difference or differential equations and verified it through computer simulations. Srinivas and Deb [2] presented their research on multi-objective optimization using non-dominated sorting in genetic algorithms. They investigated Goldberg’s notion of non-dominated sorting in GAs along with a niche and speciation method to find multiple pareto-optimal points simultaneously. Golub [3] presented an implementation of binary and floating point chromosome representation in genetic algorithm. In both representations, the algorithm is based on steady-state reproduction, roulette-wheel bad individuals’ selection and has the same parameters. The researcher concluded that the GA with floating point chromosome representation is simpler for implementation and it is faster than GA with binary representation. Deb [4] presented an introduction to Genetic Algorithm its concepts and scope of application. He presented the extension of simple GA and its population approach and ability to solve other search and optimization problems efficiently, including multimodal, multi-objective and scheduling problems, as well as fuzzy-GA and neuro-GA implementations. Lin et al. [5] proposed a generic scheme for adapting the crossover and mutation probabilities and presented an adaptive genetic algorithm for automatically adjusting suitable crossover and mutation rates to reduce the effort of searching for generation probability. Sim et al. [6] considered an extended supply chain network design model with reverse logistics and proposed an LP-based genetic algorithm that uses the LP-based solution and genetic operators. Yeh [7] presented a hybrid heuristic algorithm for the multistage supply chain network problem. The researcher employed a simple greedy method and a hybrid local search method combining the linear programming technique (LP), the pairwise exchange procedure (XP), the insert procedure (IP) and the remove procedure (RP) to solve the MSCN
Figure 1. Classification of genetic algorithms.
problem, in the proposed algorithm.
Altiparmak et al. [8] presented a mixed integer non-linear programming model for multi-objective optimization which considers the three objectives: 1) minimization of total cost comprised of fixed costs of plants and distribution centers (DCs), inbound and outbound distribution costs, 2) maximization of customer services that can be rendered to customers in terms of acceptable delivery time(coverage), and 3) maximization of capacity utilization balance for DCs (i.e. equity on utilization ratios). They implemented two different weight approaches (i.e. GA_A1 and GA_A2) in the proposed GA at the first stage to evaluate the alternate solutions and compared the Pareto optimal solutions obtained with that of the multi-objective simulated annealing (MO_SA) at the second stage. It was found that GA_A1 outperformed the MO_SA in terms of the quantity and quality of the Pareto optimal solutions obtained. Min, et al. [9] dealt with the reverse logistic problem involving spatial and temporal consolidation of returned products in a closed-loop supply chain network. They proposed a mixed-in- teger, nonlinear programming model and a genetic algorithm to solve the problem. El-Mihoub et al. [10] reviewed the Hybrid Genetic Algorithms. The different forms of integration between genetic algorithms and other search and optimization techniques are presented. They discussed that hybridization has been utilized to construct competent genetic algorithms that belong to two of the three main approaches for building competent algorithms, i.e., perturbation, linkage adaptation, and probabilistic model-building. Zhou et al. [11] proposed a mixed integer non-linear programming model and a hybrid genetic algorithm to solve the supply chain distribution problem with uncertain demands and product returns, simultaneously. The proposed HGA was verified with a series of computational experiments and showed efficiency in obtaining a near-optimal solution for the distribution system problem. Schultmann et al. [12] presented modeling of reverse logistics tasks within closed loop supply chains based on an example considering the end of life vehicle (ELV) treatment practiced in the automobile industry of Germany. They proposed different design options for a closed loop supply chain concentrating on the handling of the reverse material flows to reintegrate them into their genuine supply chains. They modeled the reverse logistics aspects with vehicle routing planning and developed a problem-tailored algorithm.
Altiparmak et al. [13] proposed a steady state genetic algorithm (ssGA) with a new encoding structure and a new greedy heuristics for the single-source, multi-product, multi-stage supply chain network design problem. They investigated the effectiveness the ssGA by comparing the results with those obtained by CPLEX, Lagrangean heuristics, hybrid GA and simulated annealing on two sets of test problems with different sizes. Lin, et al. [14] presented flexible multistage logistics network (fMLN) design with location allocation problems. They proposed an effective hybrid genetic algorithm to solve the problem, by adding some guiding information into the chromosome of the existing pGA in the literature and also employed local optimization based decoding method and proposed a new combinatorial crossover to improve the performance of rpGA. Staikos and Rahimifard [15] presented a decision-making model for waste management in the footwear industry through reverse logistics model which investigated into the steps required to consider the end-of-life implication of shoes and promote post-consumer recycling practices in the industry. In the product recovery process, they included the recycle, repair/reuse, land-filling and incineration operations to minimize the cost and EOL wastage for an environmentally sustainable network model. Ko and Evans [16] developed an optimization model and associated algorithm to design an integrated logistics network for 3PL providers with the simultaneous flows of forward and reverse logistics network and presented a mixed integer nonlinear programming model which is a multi-period, two-echelon, multi-commodity, capacited network design problem. They proposed a GA-based heuristic with genetic operations and transshipment algorithm to solve the problem.
Min and Ko [17] presented a proposed a mixed-integer programming model and a genetic algorithm for solving a reverse logistics design problem which includes the location and allocation of repair facilities for 3PLs. The researchers suggested the comparison of proposed GA with other heuristics like Lagrangian relaxation and Tabu search methods for future investigations. Belgasmi et al. [18] considered a multi-location transshipment model with limited storage capacity with an objective to minimize the aggregate cost function where decision variables are the constrained up-to-date quantities. The researchers proposed a real coded genetic algorithm (RCGA) with a new crossover operator to approximate the optimal solution. The GA proved its ability to solve instances of the problem with high accuracy. Farahania and Elahipanaha [19] developed a new model in a multi-objective mixed integer linear programming for a three-echelon supply chain network to minimize the total costs and service level for just-in-time distribution purposes for the real world situations. They developed a genetic algorithm (GA) to find the pareto optimal solutions for the large sized instances of this problem. Lee and Don [20] developed a mathematical model for the integration of forward and reverse distribution network design and the locations of facilities jointly used by forward and reverse logistics operations. They developed a two-stage heuristic algorithm as the first attempt in solving the integrated forward and reverse logistics network design problem using meta-heuristics. A tabu search is also applied to obtain the improved solution of shipping the returned products.
Yun et al. [21] designed a multi-stage supply chain model and proposed a hybrid genetic algorithm (hGA) with adaptive local search scheme which determines the usage of local search technique in GA loop. They suggested two multi-stage based supply chain models with complicated routes and compared the proposed hGA with other conventional algorithms like GA, enumeration method, using numerical examples for their performances. The proposed hGA outperformed the competing algorithms. Sourirajan et al. [22] presented a two stage supply chain with a production facility that replenishes a single product retailer with an objective to locate distribution centers in the network such that the sum of facility location, pipeline inventory, and safety stock costs is minimized. They used genetic algorithm to solve the model and compared the performance to that of a Lagrangian heuristic in earlier work. They applied a new chromosome representation that combines binary vectors with random keys provides solutions of similar quality to those from the Lagrangian heuristic. Lee et al. [23] proposed a model for optimization of reverse logistics network using hybrid genetic algorithm. They proposed a genetic algorithm with priority-based encoding method consisting of 1st and 2nd stages combined a new crossover operator called as weight mapping crossover (WMX). They applied a heuristic in the 3rd stage to transportation of parts from processing center to manufacturer.
Gen et al. [24] dealt with bi-criteria network design (bND) problem using multi objective hybrid genetic algorithm (mo-hGA) to minimize the total cost and maximize the total flow. They proposed a new chromosome representation based on priority based encoding method and a new crossover operator called as weight mapping crossover (WMX), and adopted insertion mutation operator and hybrid approach by fuzzy logic control (FLC) and local search (LS). Lin et al. [25] formulated an integrated multi-stage logistics network model by considering the direct shipment and direct delivery of logistics and inventory. A mixed integer programming model is formulated to to minimize the sum of transportation cost, inventor holding cost, fixed ordering cost and open cost of facilities. An effective hybrid evolutionary algorithm is proposed to solve the location-allocation problem combined with lot sizing problem which is a more complex and NP hard in nature. Salema et al. [26] presented a strategic and tactical model for closed loop supply chain. They integrated the strategic network design decisions with the tactical decisions like production, storage and distribution planning and achieved the integration by considering the micro and macro time scales. They formulated a mixed integer linear programming and solved the model using standard branch & bound techniques.
Costa et al. [27] proposed a new efficient encoding-decoding procedure for chromosome representation in genetic algorithm to minimize the total logistic cost resulting from the transportation of goods and the location and opening of the facilities in a single product three-stage supply chain network. The procedure is based on a parsimonious permutation decoding of the string representing the network and a three steps decoding procedure allowing the occurrence of unfeasible transportation trees to be reduced. Pishvaee et al. [28] proposed a model for integrated logistic network design to address the issues due to increasing network costs and network responsiveness in supply chain and reverse logistics. They presented a bi-objective mixed integer non-linear programming (MINLP) model for the integrated forward and reverse logistics network design. The researchers designed a multi-objective memetic algorithm with dynamic local search mechanism (MOMA) to solve the model with non-dominated set of solutions. On comparison with LINGO, MOMA obtained a reasonable quality of solutions on the multiple capacity test problems.
Zarei et al. [29] designed a conceptual model of a logistics network including forward and reverse chains for the production of new vehicles and recovery of used ones. They developed a mathematical model to minimize the cost of setting up the network and also the relevant transportation costs. They designed a genetic algorithm to deal with the complexity of the problem. Kannan et al. [30] presented the case of a battery recycling in which a closed loop mixed integer linear programming model was developed to determine the raw material level, production level, distribution and inventory level, disposal level, and recycling level at different facilities with the objective of minimizing the total supply chain costs. The researchers proposed heuristics based genetic algorithm (GA) for solving the problems and computational results obtained through GA are compared with the solutions obtained by GAMS optimization software. They found that for smaller size problems the GAMS software provides better results but with worst computational time and also found that some larger-size real-world problems which cannot be solved by GAMS or other commercial software are only solved by the proposed heuristics based GA. The result comparison between GA and GAMS shows that the heuristics based GA as a solution methodology is reliable for the larger problem sizes. El-Sayed et al. [31] developed a multi-period, multi- echelon forward-reverse logistics network design under risk. The network structure includes three echelons in the forward direction(suppliers, facilities and distribution centers) and two echelons in the reverse direction (disassembly and redistribution centers), first customer zones in which the demands are stochastic and second customer zones in which the demand is assumed to be deterministic. They formulated the problem in a stochastic mixed integer linear programming (SMILP) decision making form as a multi-stage stochastic program to maximize the total expected profit.
Kaya et al. [32] presented a novel crossover operator for genetic algorithms called ring crossover. In order to evaluate the efficiency and feasibility of the proposed operator, a comparison between the results of this study and results of different crossover operators used in GAs is made through a number of test functions with various levels of difficulty. The most important advantage of the proposed method is that more variety is presented in possible number of children according to SPC and TPC operators. Khajavi et al. [33] presented an integrated forward/reverse logistics network optimization model for multi-stage capacited supply chain network. The model is proposed by formulating the generalized logistics network problem into a bi-objective mixed-integer programming model to minimize the total costs and maximize the responsiveness of the CLSC network simultaneously. The proposed model was able to integrate the forward and reverse logistics network design decisions to avoid the sub-optimality resulted from separated and sequential designs. Nandita [34] proposed a reverse logistics model for the apparel product acquisition via two channels viz., used garment collectors and used garment importers in the Indian apparel market. The author also presented the recovery process of the used garments as per their value potential and the level of reconditioning required. Further, reconditioning, reconstruction and recycling processes in the reverse logistics chain for the redistribution and sales in the apparel aftermarket in India have been examined.
Hosseinzadeh and Roghanian [35] presented an optimization model for reverse logistics network under stochastic environment using genetic algorithm. The researchers developed a probabilistic mixed integer linear programming model for multi-product, multistage reverse logistics network design problem which considers minimizing of total shipping cost and fixed opening costs of the disassembly centers and the processing centers in the reverse network. A priority based genetic algorithm was applied to solve the problem using a numerical example. Kumar and Jyotishree [36] studied different encoding techniques and their genetic operations and proposed a new encoding scheme to overcome the limitations of existing encoding techniques. The proposed encoding scheme is independent of order or value, represents genes in the chromosome as its fitness contribution value and the order of genes is immaterial. The encoding scheme supports one point crossover as in binary encoding and PMX crossover as in permutation encoding. The proposed encoding scheme is also apt for inversion operation which is restricted to some encoding schemes. Bozorgirad et al. [37] proposed Route Based Genetic Algorithm (RBGA) to find the minimum cost of flexible multi stage logistic network. They considered a multi- source multi product flexible multistage logistic network and presented the comparison of numerical results of RBGA and standard GA. They applied the penalty method in GA and new representation of GA to satisfy all existing constraints.
Mehdizadeha and Afrabandpeia [38] presented a multi-stage and multi product logistic network design problem for which they formulated a mixed integer nonlinear programming model (MINLP) to minimize the transportation and holding costs. Then they developed a hybrid priority based genetic algorithm (pb-GA) and simulated annealing algorithm (SA) in two phases. The researchers determined the amount of products to be carried between the sources and depots in the first phase and determined the vehicles for transporting products in the second phase. The researchers used Response Surface Methodology (RSM) to adjust the significant parameters of the algorithm. Iris and Serdarasan [39] presented the applications of genetic algorithms to solve the supply chain network design problem. The researchers introduced different GA approaches that are used at different steps of the algorithm, such as encoding/decoding techniques, initialization strategies, fitness function determination, selection techniques, crossover and mutation strategies. Zaki et al. [40] presented an efficient algorithm for solving multi-objective transportation, assignment and transshipment problems. The researchers proposed an integrated approach of both genetic algorithm (GA) and local search (LS) scheme. The algorithm is an iterative multi-objective genetic algorithm with an external population of pareto optimal solutions that best confirm a Pareto front. Then the algorithm implements GA to provide the initial set (close to the pareto set as possible followed by local search method to improve the quality of the solutions. Ozkir and Basligil [41] proposed modeling of product recovery processes in closed loop supply chain network design, where a mixed integer linear programming model was applied to obtain CLSC network design in which the recovery process occurs as material recovery, component recovery and product recovery.
Rafsanjani and Eskandari [42] proposed a genetic algorithm (GA) approach with segment based operators combined with a local search technique (SHGA) to solve the multi stage supply chain network design problem. The researchers evaluated the performance of the proposed algorithm (SHGA) by comparing the results with that of several other algorithms like simulated annealing (SA), a simple genetic algorithm without segment based operators (GA), hybrid genetic algorithm with local search and without segment based operators (HGA) and also with a proposed segment based GA without the local search (SGA) on different MSCN design problems. Lee et al. [43] considered single product and two stage reverse logistics problem with two objectives of minimizing the total transportation cost (includes fixed opening cost, transportation cost and inventory cost) and minimizing the total tardiness in all time periods. The researchers proposed a multi objective hybrid genetic algorithm (mo-hGA) combined with Fuzzy Logic Controller (FLC) for efficiently dealing with multi-objective logistics (mo-RLN) problem. They applied a priority based chromosome representation and adaptive weight approach in the hybrid GA for solving the problem. Soleimani et al. [44] proposed a multi-echelon multi-period and multi product CLSC model using genetic algorithm. They solved the proposed model using CPLEX optimization software and by a developed genetic algorithm. They compared the results of proposed pre-tuned genetic algorithm with a global optimum of CPLEX solver. Then they generated a sufficient large number of large-size instances and solved them by the proposed GA. The results proved the constancy and acceptable performances of the proposed GA and its applicability in real-size situations. Lee and Lee [45] developed a closed loop supply chain model for saving the cost of integrating the forward and reverse supply chains with by considering the uncertainties in demand and supply in forward chain, and uncertainties in the time frame of recovery and the amount of recovered materials in reverse chain. The optimal costs are determined by applying an optimization algorithm using the priority based genetic algorithm and the modified genetic algorithm. This modified hybrid genetic algorithm (mhGA) provides an improved search-ability of best solution and the convergence speed. Teodoro et al. [46] proposed a new hybrid operator for genetic algorithm used to optimize the purchase of products in stores geographically separated in order to obtain solutions that combine the purchase of products with the lowest possible total cost, considering the route between each store. They described the development of a strategy based on GA, emphasizing the proposition of a new hybrid genetic crossover operator, to provide a set of optimized solutions for a SCM specific problem. The proposed operator has proven to be effective in situations where the aim is to ensure solutions with high genetic diversity, but with the same best fitness value. For problems where the goal is to achieve the best solution, the two-point and/or uniform crossover can be used. Ramezani et al. [47] presented a new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level. They included three echelons in forward flow viz. suppliers, plants and distribution centers and two echelons in the backward flow viz. collection centers and disposal centers. They evaluated the systematic supply chain configuration maximizing the profit, customer responsiveness and quality to achieve the objectives of the network. Rosa et al. [48] presented a robust sustainable bi-directional logistics network design under uncertainty which handles a network of multiple supply stages, including production allocations, uncertain data development, facility locations and flexible capacity adjustments. They first introduced a detailed deterministic model assessing the impact of incorporating reverse logistics into a forward-oriented supply chain then extended it to a robust capacited facility location model, which minimizes the expectations of relative regrets for a set of scenarios over a multi-period planning horizon, by considering uncertainty in supplying and collecting goods.
Mahmoudi et al. [49] proposed mathematical modeling for minimizing costs in a multi-layer, multi-product reverse supply chain. They presented an integer linear programming model for multi-layer, multi-product reverse supply chain that minimizes the products and parts transportation costs among centers and also sites launch, operation parts, maintenance and remanufacturing costs at the same time. The model was solved and validated using LINGO 9 software. Hafeti and Jolai [50] proposed a robust and reliable network design for forward-reverse logistics design which simultaneously takes care of uncertain parameters and facility disruptions in the network. They proposed a mixed integer linear programming model with augmented p-robust constraints considered to control the reliability of the network during disruptions thereby reducing the nominal cost and disruptions risks. They compared the performance of the augmented p-robust criterion with that of the other conventional robust criteria. Cardoso et al. [51] developed a mixed integer linear programming for the design and planning of supply chains with reverse flows by simultaneously considering the production, distribution and reverse logistics activities for which the product demand is uncertain. The model defines the maximization of the expected net present value and provides details on sizing and location of plants, warehouses and retailers, definition of processes to install, establishment of forward and reverse flows and inventory levels to achieve.
Devika et al. [52] presented the design of a sustainable closed loop supply chain network to cover the gap in the quantitative modeling by considering the social impacts, environmental impacts and economic impacts in the network design problem. They developed three new hybrid meta-heuristic methods based on adapted imperialist competitive algorithms and variable neighbourhood research, to solve this NP hard problem. They compared the algorithms with each other and also with other strong algorithms to assess the efficiency and effectiveness of the proposed algorithms. Asghari and Nezhadali [53] considered a design of reverse logistics network development for recycling waste products to reduce harmful emissions due to storage, transportation and various processes. They proposed a multi objective model using mixed integer linear programming and solved the problem by applying a hybrid method based on non-dominated sorting genetic algorithm (NSGA II). Aggarwal et al. [54] discussed the general principles of Genetic algorithm, its structure and mechanism in their paper. They presented different encoding schemes like binary encoding, permutation encoding, value encoding and octal encoding schemes used in genetic algorithm. Demirel et al. [55] proposed a mixed integer programming model for a closed loop supply chain (CLSC) network with multi-periods and multi-parts under two main policies as secondary market pricing and incremental incentive policies. The researchers developed a fuzzy multi-objective extension in addition to the base case (crisp) formulation to solve CLSC network problem with fuzzy objectives to represent vagueness in real-world problems. A genetic algorithm (GA) approach was applied to solve the real size crisp and fuzzy CLSC problems. The researchers investigated and illustrated the effectiveness of the proposed meta-heuristic approach by comparing the results with GAM-CPLEX on a set of crisp/fuzzy problems with different sizes. Dzupire and Gyeke [56] developed a multi-stage supply chain network optimization using genetic algorithms. The developed model minimizes system wide costs of the supply chain and delays on delivery of products to distribution centers for a three echelon supply chain. The researchers used NSGA-II through the Global Optimization Toolbox in MATLAB. The algorithm clearly provides the Pareto fronts which are efficient solutions for improving the supply chain design problems. The researchers proved that the proposed multi objective evolutionary algorithms are successful in dealing with multi-objective optimization problems and have potential to solve combinatorial problems. Rad et al. [57] formulated a bi-criteria multi source single product fMLN model that considers the minimization of the total transportation cost and total product delivery time simultaneously. A meta-heuristic technique i.e. genetic algorithm with an enhancement to solve the complex fMLN is proposed. A set of pareto optimal solution is obtained using new chromosome representation capable of improving the constraints of the problem by a considerable ratio and with the defined crossover and mutation techniques. The results showed that the solutions of the proposed GA are better than that of the standard GA. Aravendan and Panneerselvam [58] considered a multi-echelon closed loop network design problem with an objective to minimize the total cost of the network and increasing the quality of service. They developed a mixed integer non-linear programming model to solve the CLSCND problem. The researchers simulated the experiments and solve the model using the optimization software LINGO14.
Sarrafhaa et al. [59] presented a bi-objective integrated procurement, production and distribution problem of a multi-echelon supply chain network design in order to minimize the total cost of the supply chain and the average tardiness of the products delivered to DCs by factories. The authors developed a multi periodic structure in the network design involving suppliers, factories, distribution centers (DCs) and retailers. A novel Pareto based algorithm MOBBO was developed to find pareto optimal solutions. They validated the results using existing NSGA-II and MOSA, where the parameters of all algorithms were tuned using the Taguchi method. The results showed that the proposed MOBBO is a compatible alternative to the competing algorithms. Pasandideh et al. [60] presented a bi-objective optimization of a multi-product multi-period three echelon supply chain under uncertain environments. The researchers first formulated the problem into the framework of a single objective stochastic mixed integer linear programmimg model (MILP) then reformulated the problem into a bi-objective deterministic mixed integer nonlinear programming model (MINLP). They used a non-dominated sorting genetic algorithm (NSGA-II) to solve the problem and applied another GA based algorithm called non-dominated ranking genetic algorithm (NRGA) to validate the results obtained. A modified priority based encoding is proposed in both algorithms. The researchers showed the applicability of the proposed method by providing numerical illustrations and applied t test along with the simple additive weighting (SAW) method to select the best method. The results showed that NSGA-II acted better than NRGA for all problem instances.
3.1. Review Summary
The literature is reviewed for the design of reverse supply chain systems as well as the closed loop supply chain systems i.e. the reverse supply chain networks in conjunction with forward supply chain networks under the following nine categories, viz. models, branch and bound algorithms, heuristics, genetic algorithms, simulated annealing algorithms, Petri net algorithms, simulation approaches and general approaches. The review outcome shows that the Meta heuristics particularly the Genetic Algorithm and its hybrids were applied majorly by the researchers to deal with the supply chain network design problems. The models developed were majorly based on MILP and a few were also on MINLP, depends on the complexity of the problems. The research gaps with respect to modeling and algorithmic approaches are identified and furnished as follows.
3.2. Research Gaps with Respect to Model
Most of the researches carried out in the prior periods deal with the CLSCND model very specific to a supply chain problem of a particular industry or a product category or a type of distribution network. There is a less or lack of research on the generic integrated closed loop network design model which can be applicable to a majority of the Industries or to the vast range of product categories or all kinds of distribution network. So, there is a need for the generic integrated model proposed in this research. This integrated model can be applicable to majority of the industries or product category or any kind of distribution network just by making minor addition or deletion in the stages or levels or echelons involved in the integrated model. Thus, this model can be applicable to various industrial sectors like Automobiles, Leather products, Textile products, Footwear, Consumer Electronics, Home appliances and Industrial equipment or machines, etc.
3.3. Research Gaps with Respect to Algorithms
The past researches in the supply chain network design deal with the development of heuristics / meta heuristics mostly for forward chain network designs. A fair amount of research has been carried out to develop heuristics for reverse supply chain network designs. A very less research has been done to develop heuristics /Meta heuristics for the closed loop supply chains which are gaining importance in recent times. Also most of genetic algorithms developed in the past were designed with a specific set of GA parameters. A very less research has been done to study the performance of the GA with respect to changing GA parameters like selection methods, cross over methods, parent replacement methods etc., for the same problem. This gap is addressed in this research by developing new variants of hybrid genetic algorithm with different combination of GA parameters like using Elitism & Rank Selection methods, Chromosome Cross over techniques and Chromosome Replacement techniques.
4. Statement of the Problem
The closed loop supply chain network model considered in this research work is a multi-echelon and multi stage network which includes manufacturers, wholesalers, retailers and first customers in the forward chain and service/repair centers, collector/dismantler/re-furbisher (CDR), remanufacturers, recyclers, disposal centers/land- fillers, resellers and second customers in the reverse chain. The network deals with the two types of product returns i.e. product returns due to repair and product returns due to end of use or life, in its reverse chain. The repair products are sent directly to the repair/service centre by the first customer for getting them repaired and the end of life products are returned either directly or through the retailer to the collector/dismantler/re-furbisher by the first customer for re-processing. The returned products thus collected in the CDR locations are sorted; parts are dismantled and segregated into recoverable and non-recoverable or waste items. The recoverable items are again segregated into re-furbishable, remanufacturable, recyclable items and shipped to the respective facilities or locations for recovery process. The non-recoverable or the waste items are shipped to the disposal centers/ Land-fillers and disposed through land filling or incineration. The recovered products through the process of refurbishing and remanufacturing are shipped to the second customers via resellers. The items recovered through recycling process are shipped to the raw material suppliers market by the recycler. Based on these discussions, it is clear that the returned products due to EOL are shipped from the first customers to the recovery facilities through a push mechanism and recovered products are shipped from the recovery facilities to the second customers through a pull logistics mechanism. In this context, the objective of this research work is to minimize the total cost which is the sum of the costs of both forward and reverse supply chains there by increasing the total profit of the closed loop network. After the text edit has been completed, the paper is ready for the template. Duplicate the template file by using the Save As command, and use the naming convention prescribed by your journal for the name of your paper. In this newly created file, highlight all of the contents and import your prepared text file. You are now ready to style your paper.
5. Research Methods
The research methods adopted for solving the research problem stated in the previous section are Modeling and Algorithmic research methods which are briefed as follows.
Modeling Research: A model is an abstraction of reality applied to the real life problems of business situations. Among the three types of modeling research methods, viz. symbolic model, mathematical model and simulation model, mathematical modeling research method is applied to design and develop the appropriate model for the specific CLSCND problem. The model is based on the Multi-Integer Non-Linear Progrmme (MINLP) as the problem is combinatorial and NP Hard in nature.
Algorithmic Research: An algorithm is a well-defined sequence of steps to solve a problem of interest in industry, business, etc. Exact algorithms, heuristics/meta-heuristics are applied to solve these problems based on whether the problem is polynomial or combinatorial in nature. In this research work, since the problem is combinatorial, complex and NP hard in nature, a Meta-heuristic i.e. Genetic Algorithm is applied to design and develop the appropriate algorithm for the specific CLSCND model. A Genetic Algorithm with hybrid architecture is planned due to its:
・ Global search nature leading to more accurate global optimal solutions rather than local optimal solutions by exact algorithms/heuristics;
・ Random pick up of chromosomes from the wider population and longer generations;
・ Faster in solving the problems and efficient in dealing the combinatorial NP hard problems.
6. Development of Mathematical Model (Aravendan and Panneerslvam [58] )
Aravendan and panneerslvam [58] proposed a model for the closed loop network design problem which integrates both forward and reverse logistics in the supply chain. The closed loop network presented in their research paper is a single product, single period and multi-echelon supply chain which channelizes manufacturers, wholesalers, retailers and first customers in the forward chain and channelizes repair/service centers, collectors/ dismantlers/re-furbishers, remanufacturers, recyclers, land fillers, resellers and second customers in the reverse chain.
In the closed loop network design model, in the forward supply chain, the manufacturers are responsible for manufacturing new or virgin products and supplying them to the wholesalers for distribution. The wholesalers are responsible for the distribution of new products to the retailers in their region. The retailers are responsible for selling the new products to the first customers as per their demands and also responsible for facilitating the after sales service. The customers’ nodes represent one or more customers or a group of customers. The first customers are responsible to return the products supplied to them as per the demand, either during the usage or after the usage of the products as either repair product returns or end of life product returns (EOL) respectively. In the reverse supply chain, the first customers return the repair products to the service/repair centre for getting them repaired and to reuse. The repair/service centers are responsible for providing the quality service to the customers and to ensure the prompt delivery of the repaired products to the first customers for reuse. The end of life products are returned to the collector/dismantler/re-furbisher (CDR) either directly or via retailers by the first customers. These CDR locations are responsible for collecting, dismantling and sorting the returned products and dismantled parts for refurbishing, remanufacturing, recycling and disposing via landfill or incineration. They are also responsible for supplying the remanufacturable to the manufacturers, recyclable to the recyclers, disposables to the land-fillers/incinerators. The CDR locations recondition the refurbishable products and distributing them directly to the resellers. The resellers also receive the remanufactured products from the remanufacturers and they sell both remanufactured and refurbished products to the second customers as per their demands. The recyclers are responsible for recycling the recyclable items received from CDR locations. The disposal centers/land-fillers are responsible for the safe disposal of the unusable wastes received from CDR locations either by landfilling or incinerations.
The assumptions and limitations of the proposed model are considered as follows: 1) The model is for a single product and single period network design, 2) The locations of the first customers and second customers are known and are with certain demands, 3) The quantities of products returned are certain and all the products supplied are returned as EOL products and repair products, 4) 60% of the products supplied are returned as EOL products and 40% are returned as repair product, 5) 50% of the EOL products are returned via retailers and remaining 50% of the EOL products are returned directly, to the Collectors/Dismantlers/Re-furbishers (CDR), 6) Out of the total returned EOL products, 30% are re-furbishable items, 45% are re-manufacturable items, 20% are recyclable items and 5% are non-recoverable and disposed by land-filler, 7) The quality of the remanufactured, refurbished and repaired products is different from that of the new product, 8) The potential locations of manufacturers, wholesalers, retailers, collectors/dismantlers/re-furbishers, repair/service centers, recyclers, land fillers and resellers are assumed, 9) The capacity of each location is known, 10) The costs parameters considered (viz., opening costs, operating costs, un-utilized capacity costs and transportation costs) are known for all the facilities and node, 11) The measure of quantity of products transported per trip is defined in the form of number of units per trip and 12) There is no shipment happening between the nodes in the same stage.
6.1. Costs Associated with the Closed Loop Supply Chain Network Design Model
The various costs incurred at different nodes in the multi-echelons of the closed loop supply chain network are opening costs, operation costs and transportation costs for manufacturers, wholesalers and retailers in the forward chain, and the same costs are applied for repair/service centers, collectors/dismantlers/re-furbishers, land fillers, recyclers, remanufacturers and resellers in the reverse chain. An un-utilized capacity cost is also considered and added only to the hybrid centers manufacturers/remanufacturers. There is no cost considered for first customers and second customers as the products are picked up by them at the retail points in this particular model.
6.2. The Mathematical Model
The proposed model has the objective of minimizing the total cost i.e. the cost of the shipment flows in both forward and reverse supply chains as given in Figure 2 for which the objective function is defined and described as follows:


Figure 2. Shipment flows of CLSCND before optimization.
Subject to
Demand Constraints (DC):
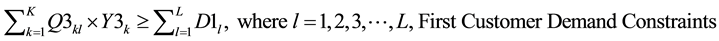 (1)
(1)
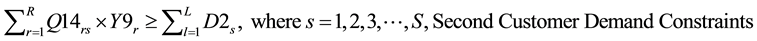 (2)
(2)
Capacity Constraints (CC):
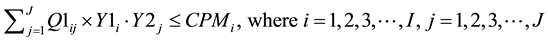 (3)
(3)
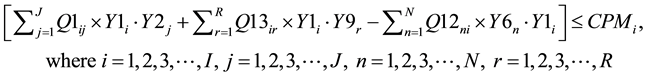 (4)
(4)
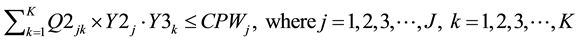 (5)
(5)
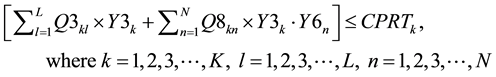 (6)
(6)
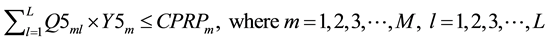 (7)
(7)
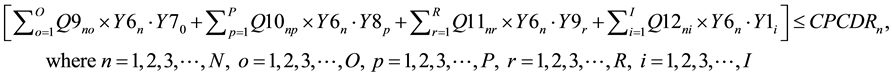 (8)
(8)
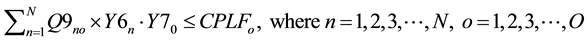 (9)
(9)
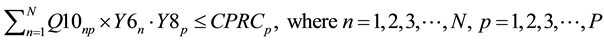 (10)
(10)
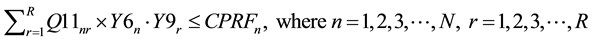 (11)
(11)



Balance Constraints (BC):














where,
Constraints (1) and (2) correspond to the demands of the first customers and second customers respectively. Constraint (3) makes sure that the sum of the outflows from each manufacturer to all the wholesalers does not exceed the capacity of the manufacturers. Constraint (4) makes sure that the sum of the outflows from each manufacturer to all the wholesalers plus sum of the outflows from the each manufacturer to all the resellers minus sum of the outflows from each CDR to all the manufacturers for remanufacturing does not exceed the capacity of the manufacturers. Constraint (5) makes sure that the sum of the outflows from each wholesaler to all the retailers does not exceed the capacity of the wholesalers. Constraint (6) makes sure that the sum of the outflows from each retailer to all the first customers and CDRs does not exceed the capacity of the retailers. Constraint (7) makes sure that the sum of the outflows from each repair center to all the first customers does not exceed the capacity of the repair centers. Constraint (8) makes sure that the sum of the outflows from each CDR to all the remanufacturers, resellers, recyclers and land fillers does not exceed the capacity of the CDRs. Constraint (9) makes sure that the sum of the inflows to land fillers from all CDRs does not exceed the capacity of the land fillers. Constraint (10) makes sure that the sum of the inflows to recyclers from all CDRs does not exceed the capacity of the recyclers. Constraint (11) makes sure that the sum of the outflows from each re-furbisher under CDRs to all the resellers does not exceed the refurbishing capacity of CDRs. Constraint (12) makes sure that the sum of the outflows from each remanufacturer to all the resellers does not exceed the capacity of the remanufacturers. Constraint (13) makes sure that the sum of the inflows to resellers from all the CDRs (refurbished items) and from all the remanufacturers does not exceed the capacity of the resellers. Constraint (14) makes sure that the sum of the outflows from each reseller to all the second customers does not exceed the capacity of the resellers. Constraint (15) makes sure that the sum of the quantities produced by the manufacturers is equal to the sum of the demands of the first customers. Constraint (16) makes sure that the sum of the quantities produced by the manufacturers is equal to the sum of the outflows from the manufacturers. Constraint (17) makes sure that the sum of the inflows to the wholesalers from each manufacturer is equal to the sum of outflows from the wholesalers to the retailers. Constraint (18) makes sure that the sum of the inflows to the retailers from each wholesaler is equal to the sum of the outflows from the retailers to first customers. Constraint (19) makes sure that the sum of the inflows to each first customer from retailer is greater than or equal to the sum of the outflows from each first customers to repair centers and CDRs. Constraint (20) makes sure that the sum of the outflows from each first customer to the repair center is less than or equal to the demand fraction for repair returns of the sum of the demands of the first customers. Constraint (21) makes sure that the sum of the inflows to each repair center from all the first customers is equal to the sum of the outflows from each repair center to all the first customers. Constraint (22) makes sure that the sum of the outflows from each first customer as EOL via retailer or directly to the CDRs is less than or equal to the demand fraction for EOL returns of the sum of the demands of the first customers. Constraint (23) makes sure that the sum of the outflows from each first customer as EOL via retailer to the CDRs is less than or equal to its return fraction of the sum of the EOL returns. Constraint (24) makes sure that the sum of the outflows from each first customer as EOL directly to the CDRs is less than or equal to its return fraction of the sum of the EOL returns. Constraint (25) makes sure that the sum of the EOL returns inflows to each CDR from first customer via retailer and directly is equal to the sum of the flow of CDR fractions exiting from each CDR to all the land fillers, recyclers, resellers and remanufacturers. Constraint (26) makes sure that the sum of the inflows to all the remanufacturers from each CDR is less than or equal to the sum of the outflows from the remanufacturers to resellers. Constraint (27) makes sure that the sum of the inflows to all the resellers from each CDR and each remanufacturer is equal to the sum of the outflows from the resellers to the second customers. Constraint (28) makes sure that the sum of the outflows from each reseller to all the second customers is equal to the sum of the demands of all the second customers.
Thus the mathematical model for the CLSC network design problem formulated as Multi Integer Non-Linear Programming model has been solved by Aravendan and Panneerselvam (2014) [58] using Lingo 14 and the optimized shipment flows of the solved CLSCND model is illustrated in Figure 3. The results of this model are compared with the best hybrid genetic algorithm out the set of four different genetic algorithms proposed in this research.
7. Development of Hybrid Genetic Algorithms
A hybrid genetic algorithm is the fusion or combination of two algorithmic structures i.e. the structure of the main genetic algorithm and a special algorithm specifically incorporated according to the nature of the problem. In this problem, the computation of total cost also includes the transshipment cost of the network in which the main genetic algorithm is fused with the transshipment algorithm which is the combination of VAM and U-V method Algorithms. This hybrid genetic algorithm is also developed with a combination of two selection methods i.e. Elitism and Rank selection. These combinations lead to the formation of variants of HGA developed.
7.1. Preliminaries of Hybrid Genetic Algorithm (HGA)
This section presents the preliminaries of genetic algorithm adopted to develop the variants of .hybrid genetic algorithms.
Figure 3. Shipment flows of CLSCND after optimization.
7.1.1. Chromosome Encoding Method
Chromosome Encoding is a process of representing the individual genes in the chromosomes. The representation can be performed using bits, numbers, trees, arrays, lists or any other objects. In this particular problem, binary encoding (using bits) is performed as given as follows.
Binary Encoding
The most common way of encoding is a binary string in which each chromosome is encoded with a binary (bit) string. Each bit in the string represents a gene i.e. node or facility in the CLSC network design. So, every bit string is a solution but not necessarily the best solution. The binary encoding applied in this hybrid genetic algorithm for the example problem is illustrated in Table 1.
7.1.2. Selection Methods
A combination of elitism selection method and rank selection method are applied in all the HGA variants developed. The methods are briefly explained below.
1) Elitism Selection Method
In this method, the first best chromosome or the few best chromosomes are copied to the new population. The rest is done in a classical way. Such individuals can be lost if they are not selected to reproduce or if crossover or mutation destroys them. This method significantly improves the GA’s performance.
2) Rank Selection Method
Rank selection method ranks the population and every chromosome receives fitness from the ranking. The worst fitness has the last rank and the best fitness has the first rank. It results with slow convergence but prevents too quick convergence. It also keeps up selection process when the fitness variance is low. It preserves diversity and hence leads to a successful search.
7.1.3. Crossover Methods
An advantage of having more crossover points is that the problem space may be searched more thoroughly. The crossover methods applied for developing the variants of hybrid genetic algorithms are: 1) Two-point crossover method and 2) Uniform crossover method which are discussed as given in Figure 4 and Figure 5 respectively.
7.1.4. Chromosome Replacement Methods
The HGA variants are also developed by varying the chromosome replacement methods applied after crossover and mutation processes. The two methods, viz. both parent replacement method and weak parent replacement method, adopted in this research are briefed as follows.
1) Both Parent Replacement Method
In this method, the fitness values of the off-spring are replaced with that of the parent chromosomes irrespective of the nature of the fitness values. The fitness values of the parent chromosomes are not checked whether they are weaker or stronger than their corresponding offspring.
2) Weak Parent Replacement Method
In this method, the fitness values of the offspring are replaced only if they are stronger than the fitness values of the parent chromosomes. So, the subsequent generations will have chromosomes with better fitness values.
Table 1. Binary encoding of chromosomes in HGA.
M―Manufacturer, W―Wholesaler, RT―Retailer, FC―First Customer, RP―Repair Center, CDR―Collector/Dismantler/Re-furbisher, LF―Land Filler, RC―Re-Cycler, RM―Re-Manufacturer, RS―Re-Seller, and SC―Second Customer.
Figure 4. Two-point crossover method. In two-point crossover, two crossover points are chosen and the chromosomes between these points are exchanged between two mated parents. In the above figure, the two thick lines indicate the two crossover points. Thus the contents between these points are exchanged between the parents to produce new children for mating in the next generation.
Figure 5. Uniform crossover method. In this method, each gene in the offspring is created by copying the corresponding gene from one or the other parent chosen according to a random generated binary crossover mask of the same length as the chromosomes. Where there is a 1 in the crossover mask, the gene is copied from the first parent, and where there is a 0 in the mask the gene is copied from the second parent. A new crossover mask is randomly generated for each pair of parents. Offspring, therefore, contains a mixture of genes from each parent.
7.2. Steps of Hybrid Genetic Algorithms
The various steps implemented sequentially to develop the hybrid genetic algorithms are furnished as follows.
Step 1: Input the following:
Number of stages = 11 (Manufacturers, Wholesalers, Retailers, First Customers, Repair Centers, Collector/ Dismantler/Re-furbisher, Recycler, Land filler, Remanufacturers, Resellers and Second Customers);
Maximum number of units/nodes in each stage from first to last stage. Ex. 3, 3, 3, 6, 2, 2, 2, 2, 3, 2, 3 (Medium size);
Maximum number of successive populations to be generated (N) = 50;
Maximum number of Chromosomes in Each Population-Population size (L) = 100;
The Generation Count GC = 1.
Step 2: Apply the binary encoding method for the chromosomes to decide on the status (open or close) of the genes (units) in the Chromosomes.
Step 3: Generate a random initial population of n chromosomes (suitable solutions for the problem). Let it be the larger population L = 100.
Step 4: Evaluate the Fitness function f(x) of each chromosome x in the population L. The fitness function is as used in the mathematical proposed by Aravendan and Panneerselvam [58] .
Fitness Function Value FFV = OPC + OPRC + UCC + TC, Where OPC = Opening Cost, OPRC = Operation Cost, UCC = Un-utilized Capacity Cost and TC = Transportation cost. (The Transshipment Algorithm, a combination of VAM and U-V algorithms is incorporated to evaluate the transshipment cost in the Fitness function)
Step 5: Sort the population L by the objective function (fitness function) value in the ascending order for minimization problem.
Step 6: Apply Elite Count (say top 2) and Rank selection; Select a given percentage (say 30%) from the top of the larger population L leaving the elite count, to form a sub-population S.
Step 7: Randomly pick up any two unselected parent chromosomes from the sub-population S. Let them be the parents xand y.
Step 8: Perform the crossover of the parents x and y for a crossover probability Pc (say Pc = 0.3) to form their two new offspring x1 and y1. If no crossover is performed, then assume the offspring x1 and y1 as the exact copies of the parent chromosomes x and y respectively. (Two point crossover and Uniform crossover methods are applied to form hybrids)
Step 9: Perform the mutation of each of the offspring x1 and y1 for a mutation probability Pm (say Pm = 0.06).
Step 10: Evaluate the fitness function value of each of the offspring x1 and y1.
Step 11: Replace the FFV of parent chromosomes x and y in the larger population L, with the FFV of their respective offspring x1 and y1. (Both parent replacement and Weak parent replacement methods are applied to form hybrids)
Step 12: Repeat Step 7 to Step 11 until all the chromosomes in the sub-population S are selected to create offspring.
Step 13: Increase the Generation Count (GC) by 1, i.e. GC = GC + 1.
Step 14: If GC ≤ N, then go to Step 5, else go to Step 15.
Step 15: Identify the chromosome in the larger population L, which has the best fitness function valueand printthe corresponding results.
Step 16: Stop.
7.3. Development of Variants of Hybrid Genetic Algorithms
The variants of hybrid genetic algorithm are developed by varying the GA parameters like selection method, crossover method and replacement method. Four hybrid genetic algorithms are thus constructed, viz. HGA1, HGA2, HGA3 and HGA4 with the following combination.
HGA1 has the combination of 2 point crossover method and both parent replacement method.
HGA2 has the combination of 2 point crossover method and weak parent replacement method.
HGA3 has the combination of uniform crossover method and both parent replacement method.
HGA4 has the combination of uniform crossover method and weak parent replacement method.
The configurations of these four hybrid genetic algorithms are illustrated in Figure 6.
7.4. Development of Source Codes for Hybrid Genetic Algorithms
The programme source codes for the four HGAs are developed using C#. Input data are fed by developing and implementing the store procedures in Microsoft SQL server. The whole programme is implemented in the Visual Basic. NET ver. 4.5 platform. This strategy has remarkably reduced the running time of the hybrid genetic algorithm for solving the problem.
8. Comparison of Hybrid Genetic Algorithms
The four hybrid genetic algorithms presented in this paper are compared using a complete factorial experiment with two factors, viz. “Problem Size” and “Algorithms”. The number of levels for the problem size is three, viz. small, medium and large. In all the three size problems, the number of nodes at manufacturer, wholesaler, retailer, first customers and second customers are varied according to the size of the problems. The number of levels for the algorithm is 4, viz. HGA1, HGA2, HGA3 and HGA4. In all these four algorithms, the selection method applied is common i.e. the combination of Elitism and Rank methods, but the crossover methods and chromosome replacement methods are different as illustrated in Figure 6 of previous section. The number of replications under each experimental combination is 6. The descriptions of the problems are shown in Table 2 and those of the algorithms are shown in Table 3.
Figure 6. Configuration of the four variants of hybrid genetic algorithm.
Table 2. Experiments/replications with respect to problem sizes.
M―Manufacturer, W―Wholesaler, RT―Retailer, FC―First Customer, RP―Repair Center, CDR―Collector/Dismantler/Re-furbisher, LF―Land Filler, RC―Re-Cycler, RM―Re-Manufacturer, RS―Re-Seller, and SC―Second Customer.
Table 3. Experiments/replications with respect to HGA parameters.
The replications of the experiment were carried out in the above combinations for all the three problem sizes vis-à-vis the four HGAs and the results are plotted in Table 4.
The different hypotheses proposed are as listed below.
・ Whether there are significant differences among the problem sizes in terms of the total cost;
・ Whether there are significance differences among the algorithms in terms of the total cost;
・ Whether there are significance differences among the interaction terms of problem size and algorithm in terms of the cost.
The results of ANOVA for the data given in Table 4 are shown in Table 5. From Table 5, it is clear that there are significant differences among the algorithms, HGA1, HGA2, HGA3 and HGA4, because the corresponding p value is less than 0.05 (significance level).
Hence, the best algorithm is obtained using Duncan’s multiple range tests. The result of Duncan’s multiple range tests are shown in Figure 7. From this figure, it is clear that the algorithm HGA4 is significantly different
Table 4. Experiment results for HGAs.
Table 5. Results of ANOVA for comparison of algorithms.
Figure 7. Results of Duncan’s multiple range test.
from other algorithms and its total cost is the least among the total costs all the algorithms. Hence, the hybrid genetic algorithm HGA4 is proved the best among all the four proposed hybrid genetic algorithms.
9. Comparison of Best Hybrid Genetic Algorithm with Mathematical Model
In the previous section, it is proved that the hybrid genetic algorithm 4 (HGA4) is proved to be the best among all the four proposed algorithms. Hence, in this section, it is benchmarked against the results of the mathematical model presented in section 6 using a complete factorial experiment in which the problem size is considered as one factor and the method of solving a problem is considered as another factor. The number of levels for the problem size is 3, viz. small, medium and large and the number of levels for the method is 2, viz. HGA4 and Model. The number of replications carried out under each experimental combination is 6. The results as per this complete factorial experiment are shown in Table 6. It is seen that the model did not give results even after long time execution for large size problems. Hence, the number of levels of problem size is reduced to 2, viz. small and medium.
The different hypotheses of this comparison are listed below.
・ Whether there are significant differences among the problem sizes in terms of the total cost;
・ Whether there are significant differences among the two methods in terms of the total cost;
・ Whether there are significant differences among the interaction terms of problem size and method in terms of the cost.
The results of ANOVA executed for the experimental results shown in Table 6 are shown in Table 7. From the results shown in Table 6, it is clear that there is no significant difference between the levels of the factor “method”, which means that the there is no significant difference between the results of HGA4 and the model. So, HGA4 can be equated to model in terms of given solution for small size and medium size problems.
Table 6. Experimental results of HGA4 and model.
Table 7. Results of ANOVA for the comparison of HGA4 with model.
10. Conclusions
In this paper, four different hybrid genetic algorithms have been proposed and they are compared through a complete factorial experiment with two factors, viz. problem size (three problem sizes) and Algorithm (four algorithms). It is found that there are significant differences among the four algorithms, viz. HGA1, HGA2, HGA3 and HGA4. Hence, using Duncan’s Multiple Range Test, it is found that the algorithm HGA4 is the best. In the next stage, HGA4 is compared with model using a complete factorial experiment with two factors, viz. Problem Size (Two sizes) and Method (HGA4 and Model). It is found that there is no significant difference between HGA4 and Model. So, HGA4 is proved to be superior in terms of giving very near optimal solution for small and medium size problems and provides the best solution when compared to all other hybrid genetic algorithms, viz. HGA1, HGA2 and HGA3.
Scope and Future Research Directions
The model and the hybrid genetic algorithm developed have good scope in the industrial application as they can be applied to a wide range of industries like automobiles, consumer electronics, textile apparels, fashion leather garments, luxury goods, footwear, home appliances, industrial equipment and machines, etc. As the incorporation of hybrid centers/facilities at the same location in the forward and reverse chains eliminates the establishment and maintenance costs of the separate facilities at different locations, the overall cost of the closed loop supply chain is minimized remarkably. The model and algorithm are proposed for the single product and single period system. Further research on the network design for multi-products and multi-periods CLSC system would be beneficial to the business sector. The future direction of research could also be an extension of this research work towards developing CLSC network design with incapacitated facilities to deal with the stochastic/uncertain demands of the customers.
Acknowledgements
The authors profusely thank M/S. Lindo Systems Inc., Chicago, USA for their technical support by providing the license of the extended version of LINGO 15 optimization software package. The authors also thank the anonymous referees for their constructive comments and suggestions, which have been incorporated in this research paper.
Cite this paper
MuthusamyAravendan,RamasamyPanneerselvam, (2015) Development and Comparison of Hybrid Genetic Algorithms for Network Design Problem in Closed Loop Supply Chain. Intelligent Information Management,07,313-338. doi: 10.4236/iim.2015.76025
References
- 1. Goldberg, D.E. and Deb, K. (1991) A Comparative Analysis of Selection Schemes Used in Genetic Algorithms. In: Rawlins, G., Ed., Foundations of Genetic Algorithms, Morgan Kaufmann Publishers, San Francisco, 69-93.
- 2. Srinivas, N. and Deb, K. (1994) Multi-Objective Optimization Using Non-Dominated Sorting in Genetic Algorithms. Journal of Evolutionary Computation, 2, 221-248.
http://dx.doi.org/10.1162/evco.1994.2.3.221 - 3. Golub, M. (1996) An Implementation of Binary and Floating Point Chromosome Representation in Genetic Algorithm. Proceedings of the 18th International Conference ITI, Pula, 18-21 June 1996, 417-422.
- 4. Deb, K. (1999) An Introduction to Genetic Algorithm. Sadhana, 24, 293-315.
- 5. Lin, W.-Y., Lee, W.-Y. and Hong, T.-P. (2003) Adapting Crossover and Mutation Rates in Genetic Algorithms. Journal of Information Science and Engineering, 19, 889-903.
- 6. Sim, E., Jung, S., Kim, H. and Park, J. (2004) A Generic Network Design for a Closed-Loop Supply Chain Using Genetic Algorithm. Lecture Notes in Computer Science, 3103, 1214-1225.
http://dx.doi.org/10.1007/978-3-540-24855-2_129 - 7. Yeh, W.-C. (2005) A Hybrid Heuristic Algorithm for the Multistage Supply Chain Network Problem. International Journal of Advanced Manufacturing Technology, 26, 675-685.
- 8. Altiparmak, F., Gen, M., Lin, L. and Paksoy, T. (2006) A Genetic Algorithm Approach for Multi-Objective Optimization of Supply Chain Networks. Computers & Industrial Engineering, 51, 196-215.
http://dx.doi.org/10.1016/j.cie.2006.07.011 - 9. Min, H., Ko, C.S. and Ko, H.J. (2006) The Spatial and Temporal Consolidation of Returned Products in a Closed-Loop Supply Chain Network. Computers & Industrial Engineering, 51, 309-320.
http://dx.doi.org/10.1016/j.cie.2006.02.010 - 10. El-Mihoub, T.A., Hopgood, A.A., Nolle, L. and Battersby, A. (2006) Hybrid Genetic Algorithms: A Review. Engineering Letters, 13, 124-137.
- 11. Zhou, G., Cao, Z., Qi, F. and Cao, J. (2006) A Genetic Algorithm Approach on a Logistics Distribution System with Uncertain Demand and Product Return. World Journal of Modelling and Simulation, 2, 99-108.
- 12. Schultmann, F., Zumkeller, M. and Rentz, O. (2006) Modeling Reverse Logistic Tasks within Closed-Loop Supply Chains: An Example from the Automotive Industry. European Journal of Operational Research, 171, 1033-1050.
http://dx.doi.org/10.1016/j.ejor.2005.01.016 - 13. Altiparmak, F., Gen, M., Lin, L. and Karaoglan, I. (2007) A Steady-State Genetic Algorithm for Multi-Product Supply Chain Network Design. Computers & Industrial Engineering, 56, 521-537.
http://dx.doi.org/10.1016/j.cie.2007.05.012 - 14. Lin, L., Gen, M. and Wang, X. (2007) A Hybrid Genetic Algorithm for Logistics Network Design with Flexible Multistage Model. International Journal of Information Systems for Logistics and Management, 3, 1-12.
- 15. Staikos, T. and Rahimifard, S. (2007) A Decision-Making Model for Waste Management in the Footwear Industry. Journal of Production Research, 45, 4403-4422.
http://dx.doi.org/10.1080/00207540701450187 - 16. Ko, H.J. and Evans, G.W. (2007) A Genetic Algorithm-Based Heuristic for the Dynamic Integrated Forward/Reverse Logistics Network for 3PLs. Computers & Operations Research, 34, 346-366.
http://dx.doi.org/10.1016/j.cor.2005.03.004 - 17. Min, H. and Ko, H.-J. (2008) The Dynamic Design of a Reverse Logistics Network from the Perspective of Third-Party Logistics Service Providers. International Journal of Production Economics, 113, 176-192.
http://dx.doi.org/10.1016/j.ijpe.2007.01.017 - 18. Belgasmi, N., Said, L.B. and Ghedira, K. (2008) Genetic Optimization of the Multi-Location Transshipment Problem with Limited Storage Capacity. Proceedings of the 18th European Conference on Artificial Intelligence, Patras, 21-25 July 2008, 563-567.
- 19. Farahania, R.Z. and Elahipanaha, M. (2008) A Genetic Algorithm to Optimize the Total Cost and Service Level for Just-in-Time Distribution in a Supply Chain. International Journal of Production Economics, 111, 229-243.
http://dx.doi.org/10.1016/j.ijpe.2006.11.028 - 20. Lee, D.H. and Dong, M. (2008) A Heuristic Approach to Logistics Network Design for End-of-Lease Computer Products Recovery. Transportation Research Part E, 44, 455-474.
http://dx.doi.org/10.1016/j.tre.2006.11.003 - 21. Yun, Y.S., Moon, C. and Kim, D. (2009) Hybrid Genetic Algorithm with Adaptive Local Search Scheme for Solving Multi-Stage Based Supply Chain Problems. Computers & Industrial Engineering, 56, 821-838.
http://dx.doi.org/10.1016/j.cie.2008.09.016 - 22. Sourirajan, K., Ozsen, L. and Uzsoy, R. (2009) A Genetic Algorithm for a Single Product Network Design Model with Lead Time and Safety Stock Considerations. European Journal of Operational Research, 197, 599-608.
http://dx.doi.org/10.1016/j.ejor.2008.07.038 - 23. Lee, J.-E., Gen, M. and Rhee, K.-G. (2009) Network Model and Optimization of Reverse Logistics by Hybrid Genetic Algorithm. Computers & Industrial Engineering, 56, 951-964.
http://dx.doi.org/10.1016/j.cie.2008.09.021 - 24. Gen, M., Lin, L. and Jo, J.-B. (2009) Evolutionary Network Design by Multi Objective Hybrid Genetic Algorithm. Intelligent and Evolutionary Systems, SCI 187, 105-121.
- 25. Lin, L., Gen, M. and Wang, X. (2009) Integrated Multistage Logistics Network Design by Using Hybrid Evolutionary Algorithm. Computers & Industrial Engineering, 56, 854-873.
http://dx.doi.org/10.1016/j.cie.2008.09.037 - 26. Salema, M.I.G., Povoa, A.P.B. and Novais, A.Q. (2009) A Strategic and Tactical Model for Closed-Loop Supply Chains. OR Spectrum, 31, 573-599.
http://dx.doi.org/10.1007/s00291-008-0160-5 - 27. Costa, A., Celano, G., Fichera, S. and Trovato, E. (2010) A New Efficient Encoding/Decoding Procedure for the Design of a Supply Chain Network with Genetic Algorithms. Computers & Industrial Engineering, 59, 986-999.
http://dx.doi.org/10.1016/j.cie.2010.09.011 - 28. Pishvaee, M.S., et al. (2010) A Memetic Algorithm for Bi-Objective Integrated Forward/Reverse Logistics Network Design. Computers & Operations Research, 37, 1100-1112.
http://dx.doi.org/10.1016/j.cor.2009.09.018 - 29. Zarei, M., Mansour, S., Kashan, A.H. and Karimi, B. (2010) Designing a Reverse Logistics Network for End-of-Life Vehicles Recovery. Mathematical Problems in Engineering, 2010, 1-16.
http://dx.doi.org/10.1155/2010/649028 - 30. Kannan, G., Sasikumar, P. and Devika, K. (2010) A Genetic Algorithm Approach for Solving a Closed Loop Supply Chain Model: A Case of Battery Recycling. Applied Mathematical Modeling, 34, 655-670.
http://dx.doi.org/10.1016/j.apm.2009.06.021 - 31. El-Sayed, M., Afia, N. and El-Kharbotly, A. (2010) A Stochastic Model for Forward-Reverse Logistics Network Design under Risk. Computers & Industrial Engineering, 58, 423-431.
http://dx.doi.org/10.1016/j.cie.2008.09.040 - 32. Kaya, Y., Uyar, M. and Tekdn, R. (2011) A Novel Crossover Operator for Genetic Algorithms: Ring Crossover.
http://arxiv.org/ftp/arxiv/papers/1105/1105.0355.pdf - 33. Khajavi, L.T., Seyed-Hosseini, S.M. and Ahmad Makui, A. (2011) An Integrated Forward/Reverse Logistics Network Optimization Model for Multi-Stage Capacitated Supply Chain. iBusiness, 3, 229-235.
http://dx.doi.org/10.4236/ib.2011.32030 - 34. Nandita, A. (2011) The Apparel Aftermarket in India—A Case Study Focusing on Reverse Logistics. Journal of Fashion Marketing and Management, 15, 211-227.
http://dx.doi.org/10.1108/13612021111132645 - 35. Hosseinzadeh, M. and Roghanian, E. (2012) An Optimization Model for Reverse Logistics Network under Stochastic Environment Using Genetic Algorithm. International Journal of Business and Social Science, 3, 249-264.
- 36. Kumar, R. and Jyotishree, (2012) Novel Encoding Scheme in Genetic Algorithms for Better Fitness. International Journal of Engineering and Advanced Technology (IJEAT), 1, 214-218.
- 37. Bozorgirad, S., Desa, M.I. and Wibowo, A. (2012) Genetic Algorithm Enhancement to Solve Multi Source Multi Product Flexible Multistage Logistics Network. IJCSI International Journal of Computer Science Issues, 9, 157-164.
- 38. Mehdizadeha, E. and Afrabandpeia, F. (2012) Design of a Mathematical Model for Logistic Network in a Multi-Stage Multi-Product Supply Chain Network and Developing a Meta Heuristic Algorithm. Journal of Optimization in Industrial Engineering, 10, 35-43.
- 39. Iris, C. and Serdarasan, S. (2012) A Review of Genetic Algorithm Applications in Supply Chain Network Design. In: Kahraman, C., Ed., Computational Intelligence Systems in Industrial Engineering, Atlantis Press Book, Paris, 209-236.
http://dx.doi.org/10.2991/978-94-91216-77-0_10 - 40. Zaki, S.A., Mousa, A.A.A., Geneedi, H.M. and Elmekawy, A.Y. (2012) Efficient Multi-Objective Genetic Algorithm for Solving Transportation, Assignment and Transshipment Problems. Applied Mathematics, 3, 92-99.
http://dx.doi.org/10.4236/am.2012.31015 - 41. Ozkir, V. and Basligil, H. (2012) Modeling Product-Recovery Processes in Closed-Loop Supply-Chain Network Design. International Journal of Production Research, 50, 2218-2233.
http://dx.doi.org/10.1080/00207543.2011.575092 - 42. Rafsanjani, M.K. and Eskandari, S. (2013) Using Segment Based Genetic Algorithm with Local Search to Find Approximate Solution for Multi-Stage Supply Chain Network Design Problem. Cankaya University Journal of Science and Engineering, 10, 185-201.
- 43. Lee, J.-E., Chung, K.-Y., Lee, K.-D. and Gen, M. (2015) A Multi-Objective Hybrid Genetic Algorithm to Minimize the Total Cost and Delivery Tardiness in a Reverse Logistics. Multimedia Tools and Applications, 74, 9067-9085.
http://dx.doi.org/10.1007/s11042-013-1594-6 - 44. Soleimani, H., Esfahani, M.H. and Shirazi, M.A. (2013) Designing and Planning a Multi Period Multi Product Closed-Loop Supply Chain Utilizing Genetic Algorithm. International Journal of Advanced Manufacturing Technology, 68, 917-931.
http://dx.doi.org/10.1007/s00170-013-4953-6 - 45. Lee, J.-E. and Lee, K.-D. (2013) Modeling and Optimization of Closed-Loop Supply Chain Considering Order or Next Arrival of Goods. International Journal of Innovative Computing, Information and Control, 9, 3639-3654.
- 46. Teodoro, F.G.S., Lima, C.A.M. and Peres, S.M. (2013) Supply Chain Management and Genetic Algorithm: Introducing a New Hybrid Genetic Crossover Operator.
http://www.lbd.dcc.ufmg.br/colecoes/eniac/2013/0023.pdf - 47. Ramezani, M., Bashiri, M. and Moghaddam, R.T. (2013) A New Multi-Objective Stochastic Model for a Forward/Reverse Logistic Network Design with Responsiveness and Quality Level. Applied Mathematical Modeling, 37, 328-344.
http://dx.doi.org/10.1016/j.apm.2012.02.032 - 48. Rosa, V.D., Gebhard, M., Hartmann, E. and Wollenweber, J. (2013) Robust Sustainable Bi-Directional Logistics Network Design under Uncertainty. International Journal of Production Economics, 145, 184-198.
http://dx.doi.org/10.1016/j.ijpe.2013.04.033 - 49. Mahmoudi, H., Fazlollahtabar, H. and Mahdavi, I. (2013) Mathematical Modeling for Minimizing Costs in a Multilayer Multi-Product Reverse Supply Chain. Industrial Engineering Management, 2, 1-6.
- 50. Hafeti, S.M. and Jolai, F. (2013) Robust and Reliable Forward-Reverse Logistics Network Design under Demand Uncertainty and Facility Disruptions. Applied Mathematical Modeling, 38, 2630-2647.
- 51. Cardoso, S.R., Paula, F.D.A., Povoa, B. and Relvas, S. (2013) Design and Planning of Supply Chains with Integration of Reverse Logistics Activities under Demand Uncertainty. European Journal of Operational Research, 226, 436-451.
http://dx.doi.org/10.1016/j.ejor.2012.11.035 - 52. Devika, K., Jafarian, A. and Nourbakhash, V. (2014) Designing a Sustainable Closed-Loop Supply Chain Network Based on Triple Bottom Line Approach: A Comparison of Metaheuristics Hybridization Techniques. European Journal of Operational Research, 235, 594-615.
http://dx.doi.org/10.1016/j.ejor.2013.12.032 - 53. Asghari, M. and Nezhadali, S. (2014) A Non-Dominated Sorting Genetic Algorithm for Sustainable Reverse Logistics Network Design. Proceedings of the 2014 International Conference on Industrial Engineering and Operations Management, Bali, 7-9 January 2014, 2426-2436.
- 54. Aggarwal, S., Garg, R. and Goswami, P. (2014) A Review Paper on Different Encoding Schemes Used in Genetic Algorithms. International Journal of Advanced Research in Computer Science and Engineering, 4, 596-600.
- 55. Demirel, N., Ozceylan, E., Paksoy, T. and Gokcen, H. (2014) A Genetic Algorithm Approach for Optimizing a Closed-Loop Supply Chain Network with Crisp and Fuzzy Objectives. International Journal of Production Research, 52, 3637-3664.
http://dx.doi.org/10.1080/00207543.2013.879616 - 56. Dzupire, N.C. and Gyekye, Y.N. (2014) A Multi-Stage Supply Chain Network Optimization Using Genetic Algorithms. Mathematical Theory and Modeling, 4, 18-28.
- 57. Rad, S.Y.B., Desa, M.I. and Azari, S.D. (2014) Model and Solve the Bi-Criteria Multi Source Flexible Multistage Logistics Network. International Journal of Advanced Computer Science and Information Technology (IJACSIT), 3, 50-69.
- 58. Aravendan, M. and Panneerselvam, R. (2014) An Integrated Multi-Echelon Model for a Sustainable Closed Loop Supply Chain Network Design. Intelligent Information Management, 6, 257-279.
http://dx.doi.org/10.4236/iim.2014.66025 - 59. Sarrafhaa, K., Rahmatia, S.H.A., Niaki, S.T.A. and Talab, A.Z. (2015) A Bi-Objective Integrated Procurement, Production, and Distribution Problem of a Multi-Echelon Supply Chain Network Design: A New Tuned MOEA. Computers & Operations Research, 54, 35-51.
http://dx.doi.org/10.1016/j.cor.2014.08.010 - 60. Pasandideh, S.H.R., Niaki, S.T.A. and Kobra, A. (2015) Bi-Objective Optimization of a Multi-Product Multi-Period Three-Echelon Supply Chain Problem under Uncertain Environments: NSGA-II and NRGA. Information Sciences, 292, 57-74.
http://dx.doi.org/10.1016/j.ins.2014.08.068



















