Received 5 December 2014; accepted 27 January 2015; published 28 January 2015

ABSTRACT

Data exchange is a goal-oriented social communications system implemented through computerized technology. Data definition languages (DDLs) provide the syntax for communicating within and between organizations, illocutionary acts, such as informing, ordering and warning. Data exchange results in meaning-preserving mapping between an ensemble (a constrained variety) and its external (unconstrained) variety. Research on unsupervised structured and semi-structured data exchange has not produced any significant successes over the past fifty years. As a step towards finding a solution, this article proposes a new look at data exchange by using the principles of complex adaptive systems (CAS) to analyze current shortcomings and to propose a direction that may indeed lead to workable and mathematically grounded solution. Three CAS attributes key to this research are variety, tension and entropy. We use them to show that older and contemporary DDLs are identical in their core, thus explaining why even XML and Ontologies have failed to a create fully automated data exchange mechanism. Then we show that it is possible to construct a radically different DDL that overcomes existing data exchange limitations―its variety, tension and entropy are different from existing solutions. The article has these major parts: definition of key CAS attributes; quantitative examination of representative old and new DDLs using these at- tributes; presentation of the results and their pessimistic ramification; a section that proposes a new theoretical way to construct DDLs that is based entirely on CAS principles, thus enabling unsupervised data exchange. The theory is then tested, showing very promising results.

Keywords:

Software Engineering, Data Definition, Schema Matching, Data Integration, Complex Adaptive Systems

1. Introduction

Data exchange is a pervasive challenge faced in applications that need to query across multiple autonomous and heterogeneous data sources. It is also a major challenge for companies entering into mergers or acquisitions. Indeed, data exchange is crucial for large enterprises that own a multitude of data sources, for progress in large- scale scientific projects (where data sets are produced independently by multiple researchers), for better cooperation among government agencies (each with its own data sources), and for offering good search quality across the millions of structured data sources on the worldwide web.

Data structures are used to organize and represent related facts with the aim to ultimately satisfy a particular goal. Computerized data structures are constructed using a given syntax, which is usually referred to as the data definition language (DDL). The DDL specifies how to organize and interconnect related elementary pieces of data into useable structures, i.e., it codifies messages to be sent or received by computerized systems or their components. There are three types of DDLs: “structured” (e.g., COBOL and SQL), “semi-structured” (e.g., web pages and word documents), and “unstructured” (e.g., images and digital audio recording). Data structures can differ in three aspects: their structure (which also implies the level of detail), field or tag names, and the syntax used to define the data structure.

Scores of DDLs have been developed over the years. Examples include Cobol’s structured File Description (FD) section, delimited flat files such as Comma Separated Values (CSV) and Data Interchange File Format (DIFF) for data exchange, Structured Query Language (SQL) for relational databases, Extensible Markup Language (XML) for semi-structured data and metadata, and ontologies expressed in a variety of DDLs such as Resource Description Framework (RDF) and Web Ontology Language (OWL). Standards such as Electronic Data Interchange (EDI) and the standards of the Society for Worldwide Interbank Financial Telecommunication (SWIFT) also define data structures and syntax. EDI is the computer-to-computer exchange of routine business data among trading partners in standard data formats. The EDI standard is strictly enforced by its users and its custodians, the American National Standards Institute (ANSI) and the Accredited Standards Committee (ASCX12). Similarly, the SWIFT has created a common “language” for exchanging monetary-related computerized transactions via the creation and strict enforcement of standards.

Data exchange may be described as a goal-oriented social communications system implemented through computerized technology. The DDL provides the syntax for communicating actions within and among organizations. Data structures built using DDLs can communicate illocutionary acts, such as informing, ordering and warning [1] . Locutionary acts [1] are fundamental in data exchange, as they facilitate the informing of other users or systems. If a recipient system “understands” the message and takes action (or avoids taking action) as a result, then the data exchange is said to have performed a perlocutionary act [1] .

From a socio-technical perspective, data exchange may be regarded as a goal-oriented process for combining data represented by dynamic structures. Since data take the form of non-identical structures, their integration requires precise mapping from one or more source structures to a destination structure. Such mapping is far from trivial, as shown by Batini et al. [2] , Hunter and Liu [3] and others [4] [5] . Both supervised and fully automatic data exchange from autonomous and heterogeneous sources take place in a dynamic, ever-changing environment. Therefore, data exchange is viewed here not as a closed system but rather as an open system, that is, in essence, an adaptive information processing system. Such systems do not simply engage in an interchange of data or information with their environments, but rather the interchange is an essential factor underlying the system’s viability and continuity and its ability to change further. Hence, the suitability of mechanisms, such as DDLs, for data exchange should be analyzed using matching paradigms, namely, Complex Adaptive Systems (CAS).

It is vital to recognize that―from a CAS perspective―data exchange is, in essence, the creation of a meaning-preservation mapping or a relation between an ensemble and its external constrained variety. Such a mapping preserves the meaning of the variety vis-à-vis information systems, whose goal is to integrate at least some external data. Mappings, or relations, which last for the duration for which they are needed, are held together by tension. In symbols-mediated CAS, this tension can be measured by formal meaning-preservation requirements [6] [7] . The level of organization created by a specific set of relations (tension) out of all the possible sets (complexion) may be measured in terms of entropy, as described below.

To date, existing data exchange approaches do not implement a robust regulation mechanism [8] - [10] and do not yield tension without human intervention in the mapping process and upkeep, i.e., people are required to invest mental energy to create relations and then keep them from falling apart when the structure of a data source is changed. Such failures are, in part, due to semantic heterogeneity among data structures, where semantic heterogeneity is a manifestation of the theoretically infinite variety that exists in the environment. The “resolution” of semantic heterogeneity, in CAS terminology, is an attempt to constrain the variety. All the data exchange methods proposed in the literature take the form of regulators, in the sense explained by Ashby [9] and Casti [11] . For example, an EDI implementation requires skilled personnel and specialized software to map data from an organization’s internal data formats to EDI and vice-versa. Without such mapping, the system’s weakness grows. The mapping requires human input (mental energy) to reduce such weaknesses, hopefully eliminating them. Therefore, correct mapping of data elements is required to create (or sustain) the tension mentioned above. All EDI implementations rely upon industry consensus, implemented as standards. This is a form of a regulator in Ashby’s sense. However, we note that adaptation to a changing environment is not a characteristic of EDI systems. We also note here that social (business) agreements provide an Ashby regulation mechanism.

2. Relevant CAS Attributes

CAS are dynamic systems able to adapt in and evolve with a changing environment. There is no separation between a system and its environment in the idea that a system always adapts to a changing environment if it is to survive. The complexity of such systems results from the inter-relationship, inter-action and inter-connectivity of elements within a system and between a system and its environment. CAS has several attributes, among them are four that play a significant role in this research and proposed theoretical DDL construct: variety, tension, entropy and regulator (A.K.A. Law of Requisite Variety). Each is explained below.

2.1. Variety

In its simplest form, given a set of elements, the variety of the set is the number of distinguishable elements, for example, the set {w, n, b, c, b, b, c, c, b, s, c, n, n} has a variety of four letters {b, c, n, w}. The variety may be more conveniently expressed as the logarithm of this number. If the logarithm is taken to the base 2, the unit is the bit, e.g., log₂(4) = 2. Thus, for any given system, the variety is the number of meaningful different states and disturbances of that system, where disturbances are irregular inputs or system states outside normal values or boundaries. To handle disturbances without breaking down, a system must have a sifting and response mechanism. Inputs that are irrelevant to the system are ignored where filtering is a function of the regulator. The remaining inputs must be dealt with using a regulator that generates a proper response, i.e., the irregularity is mapped into the system, because it helps the system to achieve its goals. If more than one response is possible, the regulator should use the one that best meets the system’s goals.

2.2. Tension

Tension in physical (mechanical) systems can be expressed as the interaction of the parts of the system, which is measurable in some unit of energy. Suspension bridges provide a prime example of tension. The tension on their cables is designed to preserve the relation between the state of the bridge and some aspects of its environment. Similarly, in information theory, the degree of sensitivity of a CAS towards its environment is its tension; this tension preserves, at least temporarily, the relation between the inner state of the CAS and some aspects of its environment. The mapping corresponds closely with the current conception of “information”, viewed as “the process of selection of a variety that has meaning” [12] .

2.3. Entropy

A thermodynamic system is one that interacts and exchanges energy with its environment through transfer of heat. If the system is in equilibrium, there is no exchange with the environment. The system is thus static, i.e., its entropy is zero because the system has no activity, specifically no random activity, which is measured by entropy. The more active a system, the higher its entropy. Von Bertalanffy demonstrated (according to Raymond [13] ) that thermodynamics entropy and information theory entropy are equivalent. Thus, entropy can be used to measure an information system’s order.

A system is made up of interacting elements. A complexion is any specific set of choices out of all the possible sets, made by each element. The number of complexions in an arrangement is the number of possible alternatives from which one can choose. This is equivalent to an ensemble of variety in information theory [14] . If elements of a complexion are entirely independent and have no interaction constraints, then all combinations have equal probability, resulting in maximal entropy and zero organization. On the other hand, if the constraints are such that only one set of complexions is allowed, then there is zero entropy and maximum organization in that system. Organization measures the amount of constraint introduced to a collective. As stated earlier, a totally constrained system has entropy of zero, because it does not interact with the environment.

A source of information whose output has an alphabet of distinct letters is termed ergodic source.Such sources can generate n symbols whose probabilities of occurrence is identical (e.g.,) are said to have maximum entropy, which can be expressed as log₂n. Rolling a fair dice or flipping a fair coin is examples of ergodic sources. However, many ergodic sources generate sequences of symbols whose probabilities of occurrence are not identical. That is,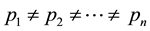. As we can see later, this is the case with data structures we examined. Therefore, its actual entropy needs to account for the different probabilities, which is what

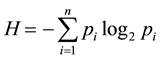does.

2.4. Law of Requisite Variety

If a system aims to successfully adapt, achieve or survive, it requires a certain amount of flexibility. That amount of flexibility must be proportional to the variety with which the system must contend. We can illustrate this idea by analogy with a chess game, in which the number of responses to a threat of a pawn is more limited than that of the queen: the queen’s variety of allowed moves is far greater than that of the pawns, and therefore the queen can better adapt to the threat to assure its survival, thereby reducing the player’s chances of losing. This required flexibility is known as Ashby’s law of requisite variety (LRV) (Ashby, 1956).

3. DDLs and CAS Attributes

This section explains how CAS attributes are used to quantify and analyze existing (old and new) DDLs. The section starts with pointing to the foundations of the question “why is unsupervised data exchange stuck for over 5o years”. It continues with the methodology used to answer the question. For brevity’s sake, we combine the description of the methods with their operationalization and results.

3.1. The Research Question

Designers and advocates of contemporary DDLs claim that recently proposed DDLs are better designed for―or entirely solve the challenge of―automatic data exchange from heterogeneous sources. However, despite such claims, unsupervised data exchange has still not been achieved [15] [16] . In their 2013 article, Vincent et al. state “a facing challenge is how to interoperate among different systems by overcoming the gap of conceptual heterogeneity” [17] . In other words, there has not been a real advancement in DDL design towards unsupervised data exchange. To find out why, we asked whether there is a real difference between older and more recent DDLs with regard to the specific CAS attributes mentioned above. If there is, in fact, no difference, we have an explanation for the stalemate, thereby opening the door to a subsequent question: How should a DDL be designed such that it will support, at least potentially, unsupervised data exchange from sources that can (and do) shape-shift one-sidedly without notice?

3.2. Data Collection Methodology

We gathered thirteen schemas expressed in a variety of DDLs from publicly available resources. We examined two protocols (EDI, SWIFT), two data dictionaries (NCREIF and a bank dictionary), one structured programming language (Cobol FD sections), three markup languages (XML, DTD, XSD) and two ontologies (OWL, RDF). All the schemas contained tags, either in English or in Hebrew, to preclude a possible validation challenge due to the natural language component of each DDL.

Each data structure collected had been originally published by its owners. We had no control over the data structures, length, composition, or complexity. Out of the tens of thousands (if not more) data structures that exist in the world, we thus limited the collection to a handful of data structures faithfully representing different approaches and DDL generations spanning five decades.

Each schema underwent a normalization process to prepare it for CAS analysis. This process included extraction of field or tag names from the data structure, discovery of atomic symbols (“alphabet”), alphabet counting, and calculations of local attributes with the aim to arrive at their underlying CAS constructs.

We isolated atomic symbols in each of the schema samples and obtained holophrase symbols engineered in natural language, which we broke down into their building blocks, i.e., single words. For instance, for the XML tag , the attribute’s name (CloseDate) was first extracted and then broken down into its atomic components, Close and Date. The same process was repeated for each composite symbol. This process created a list of words, most of which are valid terms in English or Hebrew. The list constituted the input for the subsequent calculation or assessment of the CAS parameters, variety, tension, and entropy.

3.2.1. Variety Quantification Method

Contemporary data structures are engineered using natural language, implying variety and ambiguity. We analyzed the distribution of words using Zipf’s approach [18] and counted the number of occurrences of each word. We then counted the number of meanings for each word, using WordNet [19] [20] , a lexical database for the English language. Measuring the distribution of words and the distribution of meanings provided a ratio scale measure of variety.

3.2.2. Tension Quantification Method

Successful mapping of a data structure, expressed in any DDL, to some autonomous and heterogeneous data structure needs to “make sense”, in other words, to preserve the meaning of the external variety vis-à-vis the internal structure of the system According to CAS theory, such a mapping produces tension. A formal treatment of meaning-preserving translation from a language L1 to a language L2 has been proposed by Sowa [6] . It has been noted that meaning preservation must satisfy inevitability. If an inverse function is not supported, then meaning cannot be preserved, and tension will not be created. For the purpose of the current research, it was sufficient to measure tension as a nominal variable that assumes a “true” or “false” value rather than to assess its strength on some numerical scale.

3.2.3. Entropy Quantification Method

“The important distinction between open and closed systems has often been expressed in terms of entropy” [12] . The level of entropy [14] in a given data structure is an indication of its fitness for automatic integration. According to CAS theory, morphogenic systems have reduced local entropy and increased order. The current research utilized entropy [14] as a direct measure of the level of order achieved by a given DDL. The level of entropy in a given data structure is an indication of its fitness for automatic integration, i.e., the entropy of a DDL was measured to assess the probability that it would successfully facilitate the integration of data structures.

4. Results

4.1. Variety

The variety quantification method explained above proves that the distribution of words in each of the schemas (except SWIFT and EDI) follow a typical Zipf distribution (Figure 1). Very few words are used very frequently, while others are used once or twice only.

The variety quantification method (explained above) was used to quantify meanings of words. They too follow a typical Zipf distribution (Figure 2). Several words have a very large number of meanings each, exhibiting enormous ambiguity. Words with fewer meanings exhibit much less ambiguity. However, ambiguity is never reduced to zero. This is often referred to as “semantic ambiguity”. One needs to note that SWIFT and EDI did not exhibit such a distribution. We note that these standards are engineered without using a natural language.

The variety in the size of the schemas examined also followed a Zipf distribution (Figure 3). We see one very large schema, with 1862 elements that stands by itself, the next one is about half its size, and the rest form a long tail as their number of elements becomes smaller. This should not be surprising because power law probability distribution has been observed in social, scientific, geophysical, actuarial, and many other types of observable phenomena.

4.2. Tension

We qualitatively assessed whether homomorphism exists as a DDL design constraint among the schemas

examined in this research. We counted the number of nodes in each data structure and compared that number to the number of nodes in the data structure that was the candidate for integration in the same domain. All data structures, even closely related ones, had a different number of nodes. This precludes structure preservation, a Sowa requirement for meaning preservation. Therefore, we found that no natural tension exists. Further, any manual mapping would break down if the source schema were to change suddenly, requiring manual repair by an IT professional, i.e., the human operator acts as the Ashby regulator.

Entropy

Figure 4 reports, in ascending order, the relative entropies calculated for each data structure examined. All the DDLs exhibited similar entropy levels, ranging from 0.82 to 0.96, with the exception of the two standards, EDI and SWIFT. There was no correlation between entropy levels and computing generation of the DDL, i.e., if one had expected to see an improvement in the DDLs’ ability to export a system’s entropy and increase order as the computing industry matures, this expectation was not met.

We see here that contemporary DDLs are no different from older ones when they are stripped of marketing hyperbole and invented synonyms of older concepts. All DDL generations analyzed in this study had similar power distributions of word usage and similar power distributions of meanings; all had indistinguishable expressive power measured in information bits.

5. An Alternative Approach to Building a DDL

Since the analysis of the LRV, tension and entropy leads to pessimistic conclusions about the current technologies, we explore whether it is theoretically possible to create a DDL that does not suffer from the above-de- scribed shortcomings that preclude automatic data exchange. However, we assert that designing a DDL meeting all the requirements for data exchange is possible. This paper does not pretend to propose the best solution possible, rather merely to demonstrate it is feasible to do so.

A DDL that is designed for automatic data exchange of heterogeneous sources must satisfy the following CAS characteristics: the abilities to selectively map to the system’s variety in its environment; to autonomously maintain the mapping as long as it is needed; and to dynamically add, remove or update its internal elements and relations. These demands require the ability to build a regulator that has at least the same variety as the variety it needs to regulate, via the LRV. To “make sense” it should have a perfect disambiguation mechanism. Alternatively it should be built on foundations with no ambiguity; and, the solution should have perfect entropy (H = 1).

We propose here that expectations be lowered, i.e., that the regulator be limited to handling an enumerable finite set, thereby providing constrained variety that can be generated using some relatively simple derivation rule. Such a regulator should be a canonical control system that is completely reachable and completely observable [11] [21] [22] .

An existing implementation of a canonical system that comes to mind is the symbolic language of chemistry. It could provide a working solution offering an intriguing idea for a DDL that supports automatic data exchange and satisfies LRV. Mendeleev’s Periodic Table offers unambiguous building blocks that have meaning for chemists and make some sense of the world. There are fewer than 100 elements in it, and they suffice to describe all known matter in our universe. Using a set of rather simple rules, one can combine two or more building blocks―atoms―to create new concepts, namely molecules. As long as the rules are understood and followed, a transmitter of information can create a new concept that does not exist up to that point, and the recipient will be able to process the concept using the same rules that created the new concept. For example, oxygen (O) and hydrogen (H) are two such building blocks, and each carries a meaning. Their combination into H₂O is “legal” according to the rules of chemistry, i.e., a new concept that does not exist in the Periodic Table is understood by anyone with some knowledge of chemistry. However, the same person would reject the concept H_2.5O (2.5 particles of H) because the newly created complex concept violates the set of rules.

To be more precise, a DDL designed for automatic data exchange of heterogeneous sources may be viewed as an entity D that has an automatic intelligent control system con(D) with a phase (or state) space sp(D) with an associated finite set of relations rel(D) satisfying the following properties: 1) The control system con(D) is completely observable and completely reachable (Sontag 1998) so that all elements of sp(D) can be compared, corrected and integrated (when they are identified with heterogeneous data sources); 2) The phase space is denumerable and generated by a finite set of rules or operations from a small finite set of atoms or building blocks; 3) The set of relations is finite; 4) D is able to dynamically modify both sp(D) and rel(D); 5) All the dynamical data processes of D are performed with maximum (Shannon) entropy; 6) D is universal for a large class of data sources S in the sense that it is capable of creating, maintaining and inverting an injective (one-to-one) meaning-preservation mapping (homomorphism or monomorphism) for any A in the class S such that φ: A → sp(D).

6. GlossoMote

The DDL proposed here is termed GlossoMote, a portmanteau word created from Glosso (“of the tongue”) and Mote (“a small particle”). It is a mathematically sound solution that satisfies the requirements set forth above. GlossoMote provides a regulator that can handle all possible rules-derived variety; it provides for built-in homomorphism mappings, thereby producing the necessary tension to preserve meaning. Its entropy equals 1, which means it is very efficient and does not require (or allow for) redundancy. For GlossoMote to operate, the following simple axioms and rules must be followed:

・ An atomic vocabulary exists of a finite number tokens having zero redundancy. This means it has one meaning for each token, resulting in maximum entropy;

・ Concatenation of atomic tokens is allowed, creating more complex concepts;

・ To convey the maximum amount of information, any message X should have H(X) = 1 (maximum entropy);

・ Meanings of tokens can be represented as a one-to-one mapping from symbol to meaning and vice versa, creating isomorphism.

Intuitive Proof

As intuitive proof we demonstrate an implementation using a GlossoMote language comprised of ten tokens. Unlike EDI and SWIFT, one can combine any number of tokens to create a meaningful data field (or an XML tag). For our purposes, repetition of tokens is neither allowed nor necessary. The following are the characteristics of this GlossoMote proof of concept:

・ Size of alphabet: 10 atomic tokens;

・ Number of meanings per token = exactly 1;

・ Token repetition: tokens cannot be repeated;

・ Entropy = 1.

The number of permissible combinations for a subset of k tokens out of a set of 10 tokens, where the subset is picked without replacement and without regard to the order in which the tokens of the subset are placed (or picked) is denoted as nCk = n!/(k!(n-k)!). Since k may take any value (0, 10), the total number of possible expressions is (the “extra” 1 is for the empty expression). This gives 1024 meaningful and unique complex expressions.

So we see that the set’s possible variety is constrained; each member in the set can be generated using simple rules at any given time. This allows for the creation of a regulator whose variety matches that of any data structure implemented using the GlossoMote language rules and axioms. Such a regulator satisfied the LRV, a condition that has not been achieved to date by any other approach we know of. The proposed approach offers a number of advantages: There is no need for a data dictionary or an ontology to “make sense” of newly created concepts using atomic tokens; There is no need for a complex lexicon such as WordNet; thus the complexity is reduced, as is the effort required for disambiguation, relation guessing and erroneous mapping. Having one meaning per concept satisfies the most demanding of Sowa’s requirements, i.e., having a mapping from a symbol “s” to a meaning “m” and vice versa: f(s) ® m and g(f(s)) ® s. Finally, GlossoMote has a maximum entropy of 1, the most desired level, as the calculation in Figure 5 proves.

Figure 5 lists the 10 tokens and shows the entropy calculation for a sample “toy language”. Using any permissible combination of tokens, one can create a large number of new concepts that can be understood without the aid of a dictionary. The rules are as follows:

・ The tokens represent atomic concepts relating to the weather (such as location, wind, time, precipitation, etc.);

・ Location, magnitude, and time are expressed in whole numbers, to the right of the token.

Using the rules, a token (which is also a data structure) such as SDE1RUACH100ZMN3 is a permissible token, comprised of the following atomic concepts and values: SDE1RUACH100ZMN3. To “make sense” of this information, one needs to refer to the tokens’ equivalent of the “Periodic Table”. Suppose that SDE represents the concept of location, RUACH represents the concept of wind, and ZMN represents the concept of time, then we have RUACH100 (very strong wind) SDE1 (location number 1) and ZMN3 (03:00 am). Similarly, RUACH12ZMN23SDE2 means mild wind at 10:00 pm at location “2”. The order of the tokens has no meaning, making the language less restrictive.

This approach provides the variety vital for a CAS. It provides a mechanism for the creation and maintenance of tension that is free of human intervention. And, it has the desired level of entropy, which is 1. The approach satisfies the definition of a canonical control system, thus satisfying the law of requisite variety.

7. Discussion

Sustainable unsupervised data exchange from autonomous heterogeneous sources requires that, at least, the target system should adapt itself to a constantly changing environment. This requirement means to maintain existing tension and to create additional tension when and where appropriate. In other words, there must be a regulator that mediates between the DDL’s internal variety and the variety in its changing environment. In the absence of such an Ashby regulator, the system will experience a loss of tension and will break down.

None of the DDLs reviewed in the study has a regulator to assist in dealing with a changing environment. The values of the three principle attributes of the CAS were indistinguishable across computing generations of DDLs. Variety, tension and entropy have thus remained invariant over the years. Only standards such as EDI and SWIFT provide a regulation mechanism whose output variety equals the variety in the input―solely by virtue of

social agreements and strict adherence to them. The DDLs examined are closed systems that do not have a regulator to address the LRV, are unable to maintain tension, and lack proper levels of entropy. These characteristics preclude unsupervised data exchange, thereby indicating that a new approach for the construction of DDLs is necessary.

A DDL that is designed for automatic data exchange of heterogeneous sources should satisfy some CAS characteristics, i.e., the abilities to selectively map to the variety presented by the system’s environment; to autonomously maintain the mapping as long as is needed; and to add, remove or update its own elements and relations dynamically. These demands require the ability to build a regulator that has at least the same variety as the variety it needs to regulate, such that it satisfies the law of requisite variety. In CAS terminology, the DDL should be able to “make sense”, at least, of some of the variety in the environment by means of some mediator (regulator) and to create and sustain tension (preserve meaning). To “make sense”, it should have a perfect disambiguation mechanism or be built on foundations with no ambiguity and therefore perfect entropy (H = 1).

8. Conclusion

Analyzing the challenge of unsupervised data exchange from heterogeneous autonomous sources through the lens of CAS is a radical departure from existing viewpoints and their associated methods. The new approach, termed GlossoMote, is a mathematically sound solution that satisfies all four requirements defined above. It provides a regulator for built-in homomorphism mappings, thus eliminating ambiguity. Its entropy equals 1, which means that it is very efficient and does not require (or allow for) redundancy thus eliminating semantic heterogeneity. This approach has the potential of yielding novel insights that will help direct basic research efforts in directions that will be more fruitful than the efforts of the past fifty years.

References