Intelligent Information Management
Vol.07 No.03(2015), Article ID:56184,6 pages
10.4236/iim.2015.73011
Support Vector Machines Networks to Hybrid Neuro-Genetic SVMs in Portfolio Selection
N. Loukeris, I. Eleftheriadis
Department of Business Administration, University of Macedonia, Thessaloniki, Greece
Email: nloukeris@uom.edu.gr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 December 2014; accepted 5 May 2015; published 8 May 2015
ABSTRACT
Corporate net value is efficiently described on its stock price, offering investors a chance to include a potentially surplus value to the net worth of the overall investment portfolio. Financial analysis of corporations extracted from the accounting statements is constantly demanded to support decisions making of portfolio managers. Econometrics and Artificial Intelligence methods aim to extract hidden information from complex accounting and financial data. Support Vector Machines hybrids optimized in their components by Genetic Algorithms provide effective results in corporate financial analysis.
Keywords:
Support Vector Machines, Genetic Algorithms, Corporate Finance, Financial Markets

1. Introduction
Stocks volatility in financial markets and the real economic conditions in a company―partially expressed in accounting statements―demand effective financial analysis. Portfolio managers require precise information on the economic health of corporation to secure lucrative portfolios to their investors. Econometric models mostly of Moving Average (MA), Auto Regression Moving Average (ARMA), Capital Asset Pricing Model (CAPM), or Arbitrage Pricing Theory (APT) and Artificial Intelligence in a nonlinear approach are capable to support corporate financial analysis [1] -[9] . Support Vector Machines in a hybrid with Genetic Algorithms optimization provide efficient results of financial analysis in companies.
2. Support Vector Machines
Support Vector Machines (SVM) aim to create functions from a set of labeled training data [10] [11] . The main categories are the general regression functions and the classification functions, where output is binary given that input belongs to a category. SVM during classification process seek a hypersurface which is nonlinearly related to the very high dimensional feature space of possible inputs. This hypersurface diverges the examples in a positive group and a negative one, in a way that the split achieves the largest distance from the hypersurface to the nearest of the positive and negative examples. Classification therefore is appropriate only to test the nearest data and the training data. Support Vector Machines (SVM) are trained in short time by sequential minimal optimization technique, whilst their output is an unmarked value, not a posterior probability of a class given an input. Usually SVM have a slow learning procedure in extended data set with many classes [12] [13] . SVM avoid heavy computations in the high dimensional space by using kernels that perform processing directly in the input space. According to [14] , for instances, xi,
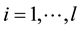 with labels
with labels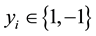 , Support Vector Machines (SVM) are trained optimizing the
, Support Vector Machines (SVM) are trained optimizing the
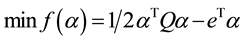 (1)
(1)
under the restrictions:
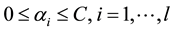
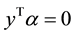
where e is the vector of all ones, C is the upper bound of all variables, Q is an l by l symmetric matrix with
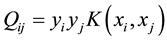 (2)
(2)
and
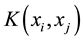 is the kernel function. Q matrix is usually fully dense and may be too large to be stored. SVM algorithms elaborate detection and exploitation of complex patterns in data performing clustering, classifications, rankings, and cleaning to the data. In case of unstable patterns SVM reject them, as an indication of over fitting, providing a statistically acceptable solution. In general, SVM provide solutions in pattern recognition, in regressions, and in learning ranking function problems. Support Vector Machine (SVM) use kernel Adatron algorithm in the Neuro Solutions software which was implemented to perform only classifications, without being able to approximate functions. The kernel Adatron maps inputs to a high-dimensional feature space, with an optimization process separates data into their respective classes by isolating those inputs which fall close to the data boundaries. Consequently the kernel Adatron acts effectively in separating sets of data which share complex boundaries. Figure 1 is represented a SVM, where the first three components expand the dimensionality corresponding a Gaussian function to each input, whilst next three components (connected to blue synapses) deploy the large margin classifier that trains the parameters of the Adatron kernel.
is the kernel function. Q matrix is usually fully dense and may be too large to be stored. SVM algorithms elaborate detection and exploitation of complex patterns in data performing clustering, classifications, rankings, and cleaning to the data. In case of unstable patterns SVM reject them, as an indication of over fitting, providing a statistically acceptable solution. In general, SVM provide solutions in pattern recognition, in regressions, and in learning ranking function problems. Support Vector Machine (SVM) use kernel Adatron algorithm in the Neuro Solutions software which was implemented to perform only classifications, without being able to approximate functions. The kernel Adatron maps inputs to a high-dimensional feature space, with an optimization process separates data into their respective classes by isolating those inputs which fall close to the data boundaries. Consequently the kernel Adatron acts effectively in separating sets of data which share complex boundaries. Figure 1 is represented a SVM, where the first three components expand the dimensionality corresponding a Gaussian function to each input, whilst next three components (connected to blue synapses) deploy the large margin classifier that trains the parameters of the Adatron kernel.
The Support Vector Machine (SVM) initially transforms data from a space of high-dimensionality, in cases with complex decision surfaces, to simpler problems with linear discriminant functions. SVM is trained and implemented only inputs that are near the decision surface since they provide the most information about the classification. SVM initially transforms the data into a high-dimensional space, using a Radial Basis Function (RBF) network which inserts a Gaussian function at each data sample, creating a feature space of which the dimension is dependent on the number of samples. The RBF network elaborates back propagation to train a linear combination of Gauss functions, providing the overall output. Furthermore the NeuroSolutions software is used to
Figure 1. The support vector machine. Source: NeuroDimensions Inc.
deploy SVM in large margin classifiers for training, offering a good generalization, making independent the capacity of the classifier from the input space, and consequently supports a fine classification [15] . The learning algorithm elaborates the Adatron algorithm adjusted to a Radial Basis Function (RBF) network, by substituting the inner product of patterns in the input space by the kernel function, leading to the optimization problem:
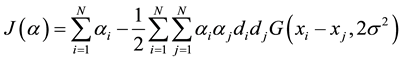 (3)
(3)
under the restrictions:
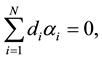 (4)
(4)
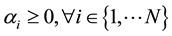
where the function g(xi) is defined:
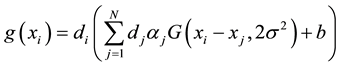 (5)
(5)
and
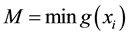 (6)
(6)
selecting a common starting multiplier αi, a small threshold t, and a low learning rate h. Since M > t a pattern xi is selected, finding update Δαi, determining the update as:
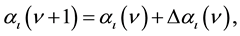 (7)
(7)
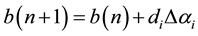 (8)
(8)
if
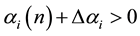


if
The adaptation of the previous system produces a few αi that are different from zero, that are the support vectors. The support vectors correspond to the closest samples of the boundary between classes.
The previous kernel Adatron algorithm adapts an RBF to an optimal margin. It consists an on-line form of the quadratic optimization approach in SVM, being able to find identical solutions to the original algorithm of Vapnik in Support Vector Machines (SVM) [15] . The kernel Adatron algorithm can be deployed easily since g(xi) is processed locally to each multiplier, when the desired response is available in input vector. The Adatron algorithm essentially prunes the RBF network so that its output for testing is:

i Î support vectors
Each of the 16 financial inputs doesn’t have a predefined importance in the hybrid neuro-genetic SVM network, and the implementation of Genetic Algorithms activates the selection of important inputs, requiring that the network must be trained multiple times to determine the combination of inputs which produce the lowest error. Genetic Algorithms were used on each layer in SVM with different topologies. On-line learning updated the weights of hybrid neuro-genetic SOFM after the presentation of each exemplar, rejecting Batch learning which updates the weights after the presentation of the entire training set. Genetic Algorithms were used providing solution to the problem of optimal values in
a) Processing Elements,
b) Step Size, and
c) Momentum Rate,
demanding a training of the network by multiple times to find the settings with the lowest error. Output layer was chosen to implement Genetic Algorithms to optimize the value of the Step size and the Momentum.
Data were produced by the financial indices of 1411 companies, given from the credit department of a Greek commercial bank, with the following 16 financial indices:
1) EBIT/Total Assets,
2) Net Income/Net Worth,
3) Sales/Total Assets,
4) Gross Profit/Total Assets,
5) Net Income/Working Capital,
6) Net Worth/Total Liabilities,
7) Total Liabilities/Total assets,
8) Long Term Liabilities/(Long Term Liabilities + Net Worth),
9) Quick Assets/Current Liabilities,
10) (Quick Assets-Inventories)/Current Liabilities,
11) Floating Assets/Current Liabilities,
12) Current Liabilities/Net Worth,
13) Cash Flow/Total Assets,
14) Total Liabilities/Working Capital,
15) Working Capital/Total Assets,
16) Inventories/Quick Assets,
and the 17th index with initial classification, was done by bank executives. Test set was 50% of overall data and training set 50%.
3. Results
The Support Vector Machines of 1000 epochs, on the in-sample results (Table 1 ), had a full convergence into the classification matrix, revealing a very low MSE at 0.026, a similar NMSE at 0.05, whilst the correlation coefficient r was the highest at 0.985, the percentage error was low at 4.53, unfortunately the Akaike Information Criterion (AIC) as a measure of the relative quality of fitness of the statistical model has very high value at 22844.43 indicating over fitting in this model that fails to explain some substantial structural variation in the data, whilst the computing time was the fastest at 3 minutes and 56 seconds.
Regarding the hybrid networks, the Hybrid Support Vector Machines with Genetic Algorithms optimization on the input layer only had a significant convergence to the experts’ decisions, though with a slight difference on the healthy companies, with the highest MSE error 84.9%, a high convergence to the data since r was 0.724, a high AIC at 10971.3 indicating over fitting, and a huge computing time of 31 hours 40 minutes and 26 seconds.
Hybrid SVM with GA optimization in all layers with no hidden layers and 500 epochs in maximum had a successful convergence in the confusion matrix, where the initially characterized as healthy companies by loan executives were classified in the category of healthy companies at a rate of 100%, and the companies initially categorized as in distress were classified in the group of the distressed companies, whilst the cost function expressed in the form of Mean Square Error was 0.707 revealing an unsatisfactory fitness of the network output to the desired output, and the average value of correlation r at 0.132 indicating a very low partial correlation between the variables, thus fitness of the model to the data is inadequate, the AIC is the lowest at −25.78 revealing an efficient fitness and the computation time is 2 hours and 43 minutes.
The Hybrid neuro-genetic Support Vector Machine with 1000 epochs and no hidden layer converged successfully as well, since the initially characterized healthy companies by bank executives were classified as healthy in a proportion of 100%, and the companies grouped in the distress category at the first place were classified as in distress at a rate of 100%. The cost in the form of MSE was very high at 0.849 denoting an inadequate fitness of the network output to the desired output, and the correlation coefficient r at 0.677 made obvious good partial correlation between the variables with a well fitted model to the data, having the highest percentage error, and a medium level AIC value at 427.58, indicating a possible over fitting whilst processing time is 4 hours and 13 minutes, appearing a possible linear dependence of the epochs number to the computing time.
On the out-of-sample results (Table 2), the SVM of 1000 epochs, maintained its superiority, in a full classification convergence, with a very low MSE at 0.035, an almost identical NMSE at 0.066, the highest r at 0.980, the lowest Error at 4.857, but in high partiality exposure as AIC was 23016.76, in a very fast time of 1 minute and 58 seconds. Next in performance from the Hybrids was the Hybrid Support Vector Machines of 1000 epochs with GAs on the input layer only, on a fine convergence in a low MSE at 0.063, a high model-data convergence of r at 0.967, a significant partiality in AIC at 9334.31, and a vast processing time of 16 hours 4 minutes and 45 seconds. The third rank was taken by the Hybrid SVM of 1000 epochs in GAs at all layers in an excellent convergence, with a low MSE at 0.159, NMSE at 0.305, a high r at 0.948, AIC at 14217.54 and a computation time of 2 hours 50 minutes and 40 seconds. Finally the Hybrid SVM of 500 epochs, in a fine classification convergence, MSE was very high at 1.019, NMSE was 1.949, r was 0.877, and the highest AIC value was at 15523.37, and a processing time of 2 hours 7 minutes and 5 seconds.
Regarding the overall results (Table 3), the SVM of 1000 epochs, was the optimal model, in a full classification convergence, with the lowest MSE at 0.030, NMSE at 0.058, the highest r at 0.999, the lowest Error at 4.694, in the highest partiality exposure in AIC of 22975.56, and the fastest time of 2 minutes and 57 seconds.
The second rank was given to the Hybrid Support Vector Machines of 1000 epochs with GAs on the input layer only, in a fine convergence, with a low MSE at 0.347, NMSE at 0.664, a high r at 0.999, a high partiality in AIC at 10152.80, and a high computing time of 23 hours 52 minutes and 35 seconds.
The third rank was given to the Hybrid SVM of 1000 epochs in GAs at all layers in an fine convergence, with a low MSE at 0.504, NMSE at 1.488, a high r at 0.999, medium AIC at 7322.53 and a computation time of 3 hours 31 minutes and 35 seconds.
Finally the fourth rank gas taken by the Hybrid SVM of 500 epochs, in an excellent classification convergence, with a high error of MSE at 0.863, NMSE was 2.852, r at 0.999, a medium AIC at 7322.56, in a computing time of 2 hours 25 minutes and 2 seconds.
Table 1. Results of support vector machines and their hybrids.
Table 2. Results of support vector machines and their hybrids, out-of-sample.
Table 3. Overall results of support vector machines and their hybrids.
4. Conclusions and Future Research
The Support Vector Machines of 1000 epochs in On-Line Learning had the optimal convergence, with a classification outcome identical to the bank experts decisions, a very high fitness of the model to the data, the lowest MSE and in the fastest processing time, on every case: the in-sample, the out-of-sample and the overall results, and this holds for the rest of the models.
The Hybrid SVM with Genetic Algorithms optimization on the input layers only had an efficient analysis result, converging to bank experts’ initial classifications, with 1000 epochs in each processing cycle, with an inadequately fitted network output to the desired output and an acceptable fitness of the model to the data.
The hybrid SVM of GAs optimisation in all layers, and 1000 epochs, although it converged, performed an unsatisfactory fitness of the network to the desired output expressed in higher errors, but in the least partiality exposure and a relatively low processing time.
Finally the hybrid SVM with GAs in all layers and 500 epochs had the worst performance in terms of errors, although it had an excellent classification, exposed in a high error, fine convergence to the data, medium partiality exposure, in a low processing time. All the models were also exposed to over fitting performance.
In conclusion the SVM of 1000 epochs in On-Line Learning network can be considered as an optimal method of financial analysis in corporations. In the future, models with an increased number of epochs may be considered for financial management, if a decrease of the MSE is achieved maintaining the fitness of the model to the data in higher levels.
References
- Loukeris, N. and Eleftheriadis, I. (2011) Support Vector Machines Neural Networks to a Hybrid Neuro-Genetic SVM form in Corporate Financial Analysis, Included in ISI/SCI Web of Science and Web of Knowledge. 15th International Conference on Computers CSCC, Corfu, 14-17 July 2011, 410-416.
- Loukeris, N., Wang, X. and Eleftheriadis, I. (2010) Optimal Portfolio Selection under a New Perspective of the Three Factor Model. 10th Special Conference of the Greek Federation of Operational Research, 5rd Meeting of Multicriteria Analysis, Democretian University of Thrace, Alexandroupolis, 30 September-1 October 2010.
- Loukeris, N., Khuman, A. and Eleftheriadis, I. (2010) Default Prevention under the Value at Risk and Expected Shortfall, 10th Special Conference of the Greek Federation of Operational Research, 5rd Meeting of Multicriteria Analysis, Democretian University of Thrace, Alexandroupolis, 30 September-1 October 2010.
- Loukeris, N. and Eleftheriadis, I. (2010) Default Prediction and Bankruptcy Hazard Analysis into Recurent Neuro- Genetic Hybrid Networks to AdaBoost M1 Regression and Logistic Regression models in Finance, Included in ISI/SCI Web of Science and Web of Knowledge,14th International Conference on Computers CSCC, Corfu, 22-25 July 2010, 35-41.
- Loukeris, N., Donelly, D., Khuman, A. and Peng, Y. (2009) A Numerical Evaluation of Meta-Heuristic Techniques in Portfolio Optimisation, Operational Research, 9, 81-103. http://dx.doi.org/10.1007/s12351-008-0028-0
- Loukeris, N. and Matsatsinis, N. (2006) Corporate Financial Evaluation and Bankruptcy Prediction implementing Artificial Intelligence methods. WSEAS Transactions of Business and Economics, 3, 343-347.
- Matsatsinis, N. and Loukeris, N. (2006) Hybrid Neuro-Genetic Principle Component Analysis as Networks of Corporate Financial Evaluation. Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization, Lisbon, 22-24 September 2006, 152-156.
- Loukeris, N. and Matsatsinis, N. (2006) Hybrid Neuro-Genetic Systems as Effective Analysis Schemes of Financial statements. Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization, Lisbon, 22-24 September 2006, 135-140.
- Loukeris, N. and Matsatsinis, N. (2006) Recurrent Hybrid Neural-Genetic Networks in Corporate Financial Evaluation. Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization, Lisbon, 22-24 September 2006, 147-151.
- Boser, B.E., Guyon, I.M. and Vapnik, V.N. (1992) A Training Algorithm for Optimal Margin Classifiers. Proceedings of the 5th Annual Workshop on Computational Learning Theory, Pittsburgh, 27-29 July 1992, 144-152. http://dx.doi.org/10.1145/130385.130401
- Cortes, C. and Vapnik, V. (1995) Support-Vector Network. Machine Learning, 20, 273-297. http://dx.doi.org/10.1007/BF00994018
- Platt, J. Cristianini, N. and Shawe-Taylor, J. (2000) Large Margin DAGs for Multiclass Classification. Advances in Neural Information Processing Systems, 12, 547-553.
- Cristianini, N. and Shawe-Taylor, J. (2000) An Introduction to Support Vector Machines: And Other Kernel-Based Learning Methods. Cambridge University Press, New York.
- Fan, R.E., Chen, P.H. and Lin, C.J. (2005) Working Set Selection Using Second Order Information for Training Support Vector Machines. Journal of Machine Learning Research, 6, 1889-1918.
- Principe, J.C., Euliano, N.R. and Lefebvre, W.C. (2000) Neural and Adaptive Systems: Fundamentals through Simulations. John Wiley & Sons, Inc., Hoboken.




