Intelligent Information Management
Vol.2 No.8(2010), Article ID:2501,18 pages DOI:10.4236/iim.2010.28056
Literature Review of Single Machine Scheduling Problem with Uniform Parallel Machines
1Program Management Office, Product Development, Mahindra & Mahindra Ltd., Farm Division, Mumbai, India
2VIT University, Vellore, India
E-mail: psenthilpondy@gmail.com, snarayanan@vit.ac.in
Received May 2, 2010; revised June 4, 2010; accepted July 18, 2010
Keywords: Uniform Parallel Machines, Measure of Performance, Heuristic, Model, Competitive Ratio
Abstract
This paper presents a survey of single machine scheduling problem with uniform parallel machines. The single machine scheduling problem with uniform parallel machines consists of n jobs, each with single operation, which are to be scheduled on m parallel machines with different speeds. These parallel machines are also called proportional machines or related machines. There are several measures of performance which are to be optimized in uniform parallel machines scheduling. Since, this scheduling problem is a combinatorial problem; usage of a heuristic is inevitable to obtain solution in polynomial time. This paper gives a classification of the literatures of this scheduling problem in three major categories, viz. offline scheduling, online scheduling and miscellaneous scheduling. In total, the available literatures are classified into 17 subgroups. Under each of the first two categories, the available literatures are discussed under different groups based on different measures of performance and non-preemptive/preemptive nature of the jobs. In the last category, the literatures are discussed under three subgroups, namely non-preemptive jobs, preemptive jobs and periodic jobs.
1. Introduction
In any company, production scheduling is an essential activity, which aims to prepare a schedule to produce a mix of products as per the production plan of the company. This in turn helps the company to improve its productivity.
Production scheduling can be classified into the following categories.
1) Single machine scheduling with single processor
2) Single machine scheduling problem with parallel processors (machines)
3) Flow shop scheduling 4) Job shop scheduling 5) Open shop scheduling 6) Batch scheduling Single Machine Scheduling with Single Processor The single machine scheduling problem with single processor (machine) consists of single machine to process n jobs. The objective of this problem is to schedule these n jobs on the single machine such that a given measure of performance is minimized. The jobs may be independent or dependent. If the set-up times of the jobs are independent of the process sequence of the jobs in the schedule, then the problem is termed as the single machine scheduling problem with independent jobs; otherwise it is termed as single machine scheduling problem with dependent jobs.
The different measures of performance of the single machine scheduling problem with independent jobs are as listed below.
•Minimizing the mean flow time
• Minimizing the maximum lateness
•Minimizing the total tardiness
•Minimizing the number of tardy jobs
In this scheduling problem, the makespan will be the same for all the sequences. Hence, it is not a part of the list of measures of performance.
Single Machine Scheduling with Parallel Machines In the single machine scheduling problem, if the number of machines is more than one, then it is called as single machine scheduling problem with parallel machines. The parallel machines scheduling problem can be classified in to the following types.
1) Identical parallel machines scheduling problem.
2) Uniform/proportional parallel machines scheduling problem.
3) Unrelated parallel machines scheduling problem.
Let, tij be the processing times of the job j on the machine i, for i = 1, 2, 3, …., m and j = 1 2, 3, …, n.
Then the three types of parallel machines scheduling problem are defined using this processing time.
1) If tij = t1j for all i and j, then the problem is called as identical parallel machines scheduling problem.
This means that all the parallel machines are identical in terms of their speed. Each and every job will take the same amount of processing time on each of the parallel machines.
2) If tij = t1j/si for all i and j, where si is the speed of the machine i and t1j is the processing time of the job j on the machine 1, then the problem is termed as uniform (proportional) parallel machines scheduling problem.
This means that the parallel machines will have different speeds. Generally, we assume s1, s2, s3, …., and sm for the parallel machines 1, 2, 3, …, and m, respectively with the relation s1 < s2 < s3 < …. < sm. That is the machine 1 is the slowest machine and the machine m is the fastest machine. For a given job, its processing times on the parallel machines will be in the ratios as listed below.
1/s1 : 1/s2 : 1/s3 : …. : 1/sm
3) If tij is arbitrary for all i and j, then the problem is known as unrelated parallel machines scheduling problem.
In this type of scheduling, there will not be any relation amongst the processing times of a job on the parallel machines. This may be due to technological differences of the machines, different features of the jobs, etc.
The measures of performance of this scheduling problem include the minimization of the makespan along with all the measures of performance as listed in Subsection 1.1. When n jobs with single operation are scheduled on m parallel machines, then each parallel machine will have its completion time of the last job in it. The maximum of such completion times on all the parallel machines is known as the makespan of the parallel machines scheduling problem, which is an important measure of performance, Panneerselvam [1].
Flow Shop Scheduling Problem The flow shop scheduling problem consists of n jobs which require processing on m different machines. Each job has a process sequence. Further, the process sequences of all the jobs are one and same. The measures of performance of this problem are as listed below.
• Minimizing the mean flow time
• Minimizing the maximum lateness
• Minimizing the total tardiness
• Minimizing the number of tardy jobs
• Minimizing the makespan
Job Shop Scheduling
The job shop scheduling problem consists of n jobs which require processing on m different machines. Each job has process sequence. Further, the process sequences of the jobs are different from one another. The measures of performance of this problem are as listed under the flow shop scheduling problem.
Open Shop Scheduling The open shop scheduling problem consists of n jobs which are to be scheduled on m different machines. There is no process sequence for each job, which means that the operations of that job can be performed in any order. The measures of performance of this problem are as listed under the flow shop scheduling problem.
Batch Scheduling Consider the loading of a batch of jobs in a furnace for the purpose of heat treatment. The furnace will continuously function over a period of time. In between, different batches of jobs will be loaded into the furnace and taken out at different points in time. Frequent opening and closing of the door of the furnace will amount dissipation of heat from the furnace. To avoid such heat loss, one should group the jobs into different batches based on their periods of heat treatment and load them into the furnace accordingly. This will facilitate minimal disturbance (opening and closing of the door) to the furnace and thus reducing the heat loss in the furnace. Such scheduling is known as batch scheduling.
In this paper, a survey of a special case of the single machine scheduling problem which is known as uniform parallel machines scheduling is considered.
2. Uniform Parallel Machines Scheduling
The essential characteristics of the uniform parallel machines scheduling problem are as listed below.
• It has n single operation jobs.
• It has m parallel machines with different speeds (s1 < s2 < s3 < ….. < sm).
• m machines are continuously available and they are never kept idle while work is waiting.
• t1j is the processing time of the job j on the machine 1 for j = 1, 2, 3, …, n.
• For each job, its processing times on the uniform parallel machines are inversely proportional to the speeds of those parallel machines (1/s1 : 1/s2 : 1/s3 : ….. : 1/sm), where s1 is the unit speed.
• tij = t1j/si for j = 1, 2, 3, …., n and i = 2, 3, ….., m.
A sample data of the uniform parallel machines scheduling problem is shown in Table 1, in which the ratio between the machine 1 and the machine 2 is 1:2.

Table 1. Processing times of jobs on uniform parallel machines.
The jobs may be classified into non-preemptive jobs and preemptive jobs. If the processing on a job which is assigned to a machine is continued till its completion, then such job is called non-preemptive job. If the processing of that job on a machine is discontinued before its completion and reassigned to either to the same machine or some other machine, that type of job is called preemptive job. If the processing times of the jobs do not depend on the sequence of assignment of the jobs on the machines, then the jobs are called independent jobs; otherwise, they are called as dependent jobs.
Further, if there is any dependency among the jobs which are to be scheduled on a set of uniform parallel machines, then they are called jobs with precedence constraints.
Periodic task is a recurring process/task which is characterized by two parameters, viz. execution requirement and a period. The execution time may be any non-negative number, deadline is assumed to be non-negative relational number. A periodic task Ti = (ei, pi) with execution requirement parameter ei and period parameter pi generates a job at each instant k.pi, which needs to execute for ei units by a deadline of (k+1).pi, for all nonnegative integers k.
2.1. Basic Measures of Performance
The basic measures of performance of the single machine scheduling problem with uniform parallel machines are as listed below.
- Minimizing mean flow time
- Minimizing total tardiness
- Minimizing maximum lateness
- Minimizing number of tardy jobs
- Minimizing the maximum of the completion times of the last jobs on the uniform parallel machines (makespan)
- Maximizing minimum of the completion times of the last jobs on the uniform parallel machines Mean flow time is the average of the completion times of the jobs. The minimization of total tardiness is an important measure, which means the minimization of the mean tardiness.
Let, n be the number of jobs with single operation
dj be the due date of the job j Cj be the completion time of the job j.
Tj be the tardiness of the job j.
Tardiness, Tj = Max[0, Cj – dj], if Cj > dj
= 0, otherwise
Total tardiness = 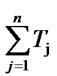
Maximum lateness is defined as the maximum of the lateness values of the jobs. The lateness of a job is the difference between the completion time and the promised due date (deliver date) of a job, if the completion time is more than the due date.
The lateness of the job j be Tj or Lj.
Tardiness, Lj = Tj = Max[0, Cj – dj], if Cj > dj
= 0, otherwise.
Here, the objective is to minimize the maximum lateness/tardiness (Lmax) of the jobs.
That is, Min Lmax = Min {Max Lj}
Minimizing the number of tardy jobs (NT) is also another measure of performance in single machine scheduling problem. This means the minimum of the number of late jobs. A job is said to be late if it is completed beyond its due date.
The minimization of the maximum of the completion times of the last jobs on the uniform parallel machines is known as the makespan of the schedule.
The problem in which the maximization of the minimum of completion times of the last jobs on the parallel machines is known as machine covering problem. The objective of this measure is to keep all the machines alive (in working mode) during the makespan of the schedule of a given batch of jobs on the set of parallel machines.
2.2. Offline Scheduling vs. Online Scheduling
The scheduling problems are broadly classified into offline scheduling and online scheduling. In offline scheduling, the release time, processing time, due date and other necessary data of each of the jobs are known before determining the schedule of jobs on the uniform parallel machines. Online scheduling algorithms make scheduling decisions at each time-instant based upon the characteristics of the jobs that have arrived thus far with no knowledge of jobs that may arrive in the future.
The online scheduling is classified into the following types.
Scheduling jobs one by one
In this type of scheduling, the jobs which are available are ordered in some list. Then each of the jobs will be assigned to some uniform parallel machine or to some time slot one by one from the list before the next jobs are seen.
Unknown running time:
In some scheduling situation, the running time of each job may be unknown until the job finishes. An online algorithm only knows whether a job is still running or not. At any time, all currently available jobs are at the disposal of the algorithm.
Jobs arrive over time
In this type of scheduling, the running time of each job is known at the time of arrival of that job, but the arrival time of each job is not known in advance.
Interval Scheduling:
In this type of scheduling, each job is to be executed in a predetermined time interval. If it is impossible to execute the job in that time interval, then the job will be rejected. Here, the objective is to maximize the number of accepted jobs.
3. Classification of Uniform Parallel Machines Scheduling Problems
By taking the offline/online features, measures of performance and non-preemptive/preemptive nature of the jobs into account, the uniform parallel machines scheduling problems can be classified into the following categories.
1) Offline scheduling of non-preemptive jobs to minimize makespan.
2) Offline scheduling of preemptive jobs to minimize makespan.
3) Offline scheduling of non-preemptive jobs to minimize the sum of total completion times.
4) Offline scheduling of preemptive jobs to minimize the sum of total completion times.
5) Offline scheduling of non-preemptive jobs to minimize total earliness/tardiness.
(Offline scheduling of preemptive jobs to minimize total earliness/tardiness is not included due to lack of reference)
6) Offline scheduling of non-preemptive jobs to minimize maximum lateness.
7) Offline scheduling of preemptive jobs to minimize the maximum lateness.
8) Offline scheduling of non-preemptive jobs to minimize the number of tardy jobs.
9) Offline scheduling of preemptive jobs to minimize the number of tardy jobs.
10) Online scheduling of non-preemptive jobs to minimize the makespan.
11) Online scheduling of preemptive jobs to minimize the makespan.
12) Online scheduling of preemptive jobs to minimize the total tardiness/earliness.
13) Online scheduling of non-preemptive jobs to maximize the minimum completion time (machine covering problem).
14) Online scheduling of preemptive jobs to maximize the minimum completion time (machine covering problem).
15) Miscellaneous problems with non-preemptive jobs.
16) Miscellaneous problems with preemptive jobs.
17) Miscellaneous problems with periodic tasks/jobs.
A comparison of the above problems as per this classification is shown in Table 2.
4. Review of Literature
Identical parallel machines scheduling forms the basics for uniform parallel machines scheduling. Coffman and Graham [2] have formulated a general model of computation structures and exhibited an efficient algorithm for finding optimal non-preemptive schedules for the identical parallel machines scheduling with the objective of minimizing the makepsan. They proved that their algorithm gives optimal solution.
4.1. Offline Uniform Parallel Machines Scheduling
In this section, the literature review of the following classifications of the offline parallel machines scheduling problem is presented.
1) Offline scheduling of non-preemptive jobs to minimize makespan.
2) Offline scheduling of preemptive jobs to minimize makespan.
3) Offline scheduling of non-preemptive jobs to minimize sum of total completion times.
4) Offline scheduling of preemptive jobs to minimize sum of total completion times.
5) Offline scheduling of non-preemptive jobs to minimize total earliness/tardiness.
6) Offline scheduling of non-preemptive jobs to minimize maximum lateness.
7) Offline scheduling of preemptive jobs to minimize maximum lateness.
8) Offline scheduling of non-preemptive jobs to minimize number of tardy jobs.
9) Offline scheduling of preemptive jobs to minimize number of tardy jobs.
4.1.1. Offline Scheduling of Non-Preemptive Jobs to Minimize Makespan
Horowitz and Sahni [3] first presented dynamic programming algorithms for scheduling independent tasks in a multiprocessor environment in which the processors have different speeds. In this research, the objective is minimize the finish time (makespan) and weighted mean flow time on two processors. These algorithms have worst-case complexity functions which are exponential in the number of tasks. Hence, they next presented approximation algorithms of low polynomial complexity for the above problem. Ibarra and Kim [4] have developed a heuristic for scheduling independent tasks on nonidentical processors. In their study, particularly, for m = 2, an n log n time-bounded algorithm is given which
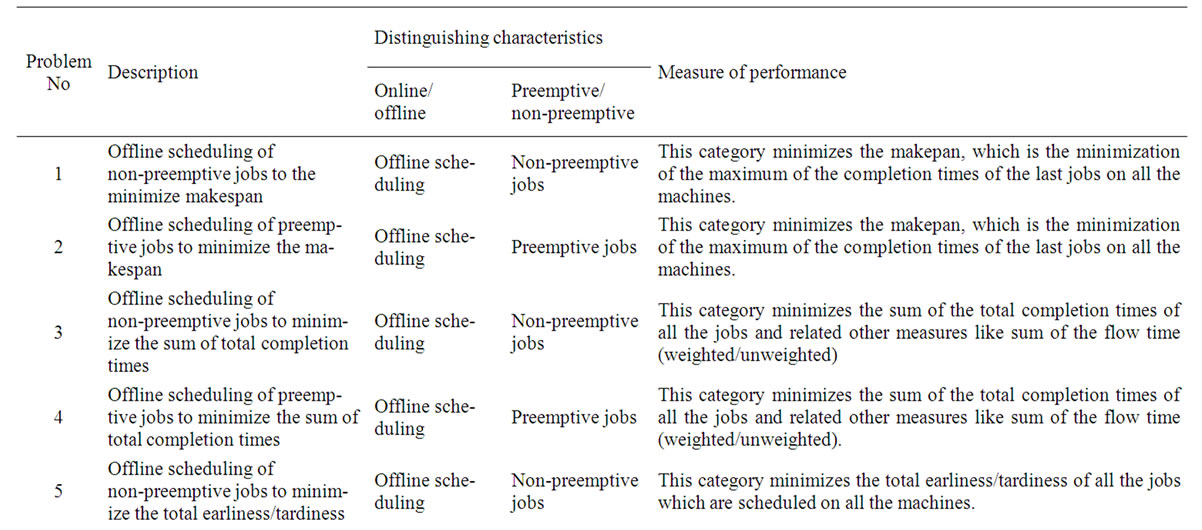
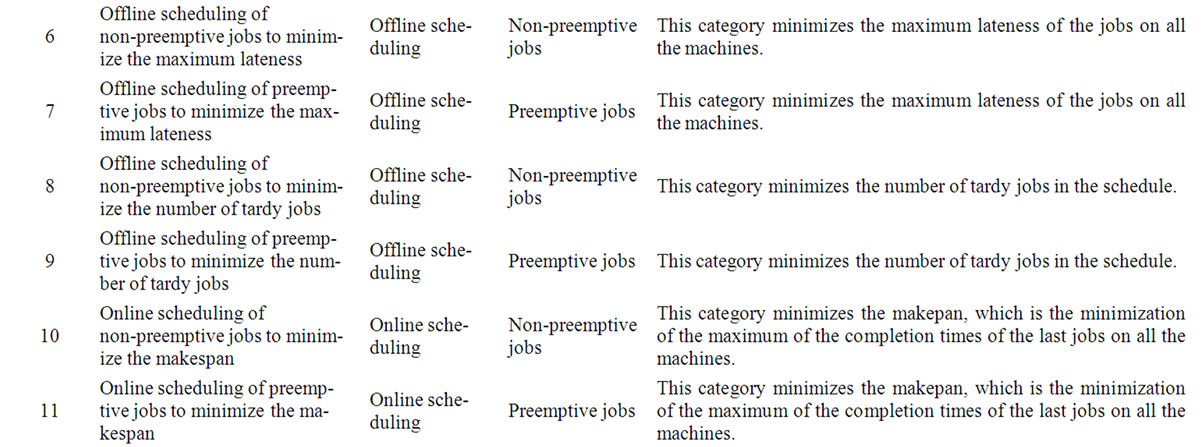

Table 2. Comparison of single machine scheduling problems with uniform parallel machines.
generates a schedule having a finishing time of at most (√5 + 1)/2 of the optimal finishing time. They verified that the LPT algorithm applied to this problem gives schedules which are near optimal for larger n. Prabuddha De and Thomas E. Morton [5] have developed a new heuristic to schedule jobs on uniform parallel processors to minimize makespan. It is tested on a large number of problems for both uniform and identical processors. They found that the solutions given by the heuristic for the uniform parallel machines scheduling are within 5% of the solutions given by the branch and bound algorithm. Bulfin and Parker [6] have considered the problem of scheduling tasks on a system consisting of two parallel processors such that the makespan is minimized. In particular, they treated a variety of modifications to this basic theme, including the cases of identical processors, proportional (uniform) processors and unrelated processors. In addition, they suggested a heuristic scheme when precedence constraints exist.
Friesen and Langston [7] examined the non-preemptive assignment of n independent tasks to a system of m uniform processors with the objective of reducing the makespan. It is known that LPT (longest processing time first) schedules are within twice the length of the optimum makespan. Graham [8], they analyzed a variation of the MULTIFIT algorithm derived from the algorithm for bin packing problem and proved that its worst-case performance bound on the makespan is within 1.4 times of the optimum makepsan. Gregory Dobson [9] has given a worst-case analysis while applying the LPT (longest processing Time) heuristic to the problem of scheduling independent tasks on uniform processors with the minimum makepsan. In this research, a bound of 19/12 is derived on the ratio of the heuristic to the optimal makespan. Also, a generalization of the classic result of Graham [8] for the case of identical processors is given. The author has derived tight bounds for the ratio of the heuristic makespan to the optimal makespan which depends on the ratio of the longest task to the makespan. Friesen [10] examined the nonpreemptive assignment of independent tasks to a system of uniform processors with the objective of minimizing the makespan. The author showed that the worst case bound for the largest processing time first (LPT) algorithm for this problem is tightened to be in the interval (1.52 to 1.67). Hochbaum and Shmoys [11] devised a polynomial approximation scheme for the minimizing makespan problem on uniform parallel processors. They gave a family of polynomial-time algorithms such that each algorithm gives a solution that is within 40% relative error of the optimum. The technique employed is the dual approximation approach, where infeasible but super-optimal solutions for a related (dual) problem are converted to the desired feasible but possibly suboptimal solution.
Chen [12] has examined the non-preemptive assignment of independent tasks to a system of m uniform processors with the objective of minimizing the makespan. The author has examined the performance of LPT (largest processing time) schedule with respect to optimal schedules, using the ratio of the fastest speed to the slowest speed of the system as a parameter. Two wellknown heuristics LPT (largest processing time first) and MULTIFIT obtains schedules having makespan with ¾ and 11/13, respectively, of the minimum possible makespan, when the m parallel processors are identical. The best known worst-case performance ratio bounds are 1.583 and 1.40, respectively. The author has tightened bound to 1.382 for MULTIFIT algorithm for the uniform parallel processors system.
Mireault, Orlin, Vohra [13] have considered the problem of minimizing the makespan when scheduling independent tasks on two uniform parallel machines. Out of the two machines, the efficiency of one machine is q times as that of the other machine. They computed the maximum relative error of the LPT (largest processing time first) heuristic as a function of q. For the special case in which the two machines are identical (q = 1), their problem and heuristic are identical to the problem and heuristic analyzed by Graham [8], respectively.
Burkard and He [14] derived the tight worst case bound √6/2 + (1/2)k for scheduling jobs using the MULTIFIT heuristic on two parallel uniform machines with k calls of FFD (first fit decreasing) within MULTIFIT. As per FFD, the tasks are sorted in non-increasing order from left to right. They concluded that when MULTIFIT is combined with LPT as an incumbent algorithm, the worst case bound decreases to √2 + ½ + (1/2)k.
Kovalyov and Shafransky [15] have studied the uniform machine scheduling of unit-time jobs subject to resource constraints. Some jobs may require a unit of an additional single resource during their execution. The resource is renewable, but the total resource consumption is limited by the same value at each time instant. They presented an O(m log m) algorithm for the problem with no machine idle times to minimize the maximum job completion time, that is the makespan. They also presented a linear time algorithm for the problem with identical machines to minimize the maximum job completion time. Burkard, He and Kellerer [16] have developed a linear compound algorithm for scheduling jobs on uniform parallel machines with the objective of minimizing makespan. This algorithm has three subroutines, which run independently in order to choose the best assignment among them. Panneerselvam and Kanagalingam [17] have presented a mathematical model for parallel machines scheduling problem with varying speeds in which the objective is to minimize the makespan. Also, they discussed industrial applications of such scheduling problem. Panneerselvam and Kanagalingam [18] have given a heuristic to minimize the makespan for scheduling n independent jobs on m parallel processors with different speeds.
Chandra Chekuri and Michael Bender [19] designed a new and efficient polynomial 6 approximation algorithm for scheduling precedence-constrained jobs on uniform parallel machines. In their work, the objective is to find a non-preemptive schedule to minimize the makespan. From their work, Woeginger [20] combined some straightforward observations and thereby derived an extremely simple 2 approximation algorithm for this problem. Chudak and Shmoys [21] gave an algorithm with an approximation ratio of O(log m), significantly improving the earlier ratio of O(√m) due to Jaffe [22]. Their algorithm is based on solving a linear programming relaxation. Building on some of their ideas, Chandra Chekuri and Michael Bender [23] have presented a combinatorial algorithm that achieves a similar approximation ratio but in O(n3) time. Ching-Jong Liao and Chien-Hung Lin [24] have considered the two uniform parallel machines problem with the objective of minimizing makespan. In this work, the two uniform parallel machines problem is converted into a special problem of two identical parallel machines from the viewpoint of workload instead of completion time. An optimal algorithm is developed for the transformed special problem. The proposed algorithm has an exponential time complexity. Inspite of this fact, the authors claim that their algorithm can find the optimal solution for large sized problems in a short time.
Epstein and Sgall [25,26] derived a polynomial approximation scheme for the problem of scheduling on uniformly related parallel machines for a large class of objective functions as listed below that depend only on the machine completion times This generalizes and simplifies many previous results in this area.
1) Minimize the sum of the completion times on all the machines.
2) Minimize the maximum of the completion times on all the machines, which amounts to minimizing the makespan.
3) Maximize the sum of the completion times on all the machines.
4) Maximize the minimum of the completion times on all the machines.
Christos Koulamas and George J. Kyparisis [27] investigated the makespan minimization problem on uniform parallel machines in the presence of release times. They developed a heuristic for this NP-hard problem and derived a tight worst-case ratio bound for this heuristic independent of the machines speeds. Agarwal, Colak, Jacob and Pirkul [28] have proposed new heuristics along with an augmented-neural-netwrok (AugNN) formulation for solving the makespan minimization taskscheduling problem for the non-identical machine environment. They explored four task and three machinepriority rules, resulting in 12 combinations of single-pass heuristics. They gave the AugNN formulation for each of the 12 heuristics and showed computational results on 100 randomly generated problems of sizes ranging from 20 to 70 tasks and 2 to 5 machines. The results clearly showed that AugNN provides significant improvement over single-pass heuristics. The reduction in the gap between the obtained solution and the lower bound due to AugNN over single-pass heuristics ranges from 24.4% to 50%. Chein-Hung Lin and Ching-Jong Liao [29] have considered a classical scheduling problem with makespan minimization on uniform parallel machines. From the viewpoint of workload, instead of completion time, two important theorems are developed for the problem. The first theorem provides an improved lower bound as the starting point of the search and the second theorem further accelerates the search speed in the algorithm. Incorporating the two useful theorems, an algorithm is developed for obtaining the optimal solution. Although the developed algorithm has an exponential time complexity, extensive computational experiments demonstrate that it is quite efficient for various sizes of the problem. With the optimal algorithm, they also examined the effectiveness of the popular LPT heuristic.
Kis and Kapolnai [30] researched the scheduling of groups of identical jobs on uniform machines with sequence independent setup times. They provide a 2-approximation algorithm for minimizing the makespan. The second result is truthful, polynomial time, randomized mechanism for the batch scheduling problem with a deterministic approximation guarantee of 4.
For this scheduling problem, most of the authors aimed at developing dynamic programming algorithm, mathematical model, branch and bound algorithm, heuristics based on LPT ordering, etc. Since, this problem comes under combinatorial category, obtaining the optimal solution will take exponential time. But, one can try metaheuristics, viz. simulated annealing algorithm, genetic algorithm, etc., which will give better solution tending towards global optimum, when compared to the single pass heuristics. Further, the researchers may consider multi-objective function for this problem. The possible combinations of the multi-objective problems are as listed below.
• Minimization of makespan and mean flow time
•Minimization of makespan and total tardiness
•Minimization of makespan and number of tardy jobs
While investigating such problems, enough care is to be taken to fix weights for the components of the objective functions, because they have differences in terms of interpretations.
4.1.2. Offline Scheduling of Preemptive Jobs to Minimize Makespan
McCormic and Pinedo [31] have considered the uniform parallel machines scheduling problem with preemption at no cost. They have generated the entire tradeoff curve of schedules which are Pareto-optimal (undominated) for the flow time and makespan objectives. To achieve this, they first developed an O(mn) algorithm that produces a schedule with minimum flow time, subject to a fixed makespan deadline. This algorithm alternates between the Shortest Processing Time on Fastest Machine (SPTFM) rule and the Longest Remaining Processing Time on Fastest Machine (LRPT-FM) rule. Their knowledge of the structure of optimal schedules allows them to characterize breakpoints on the tradeoff curve, and then to compute all of the O(mn) breakpoints in O(m3n) time.
Martel [32] describes a fast parallel algorithm for preemptive scheduling of independent jobs on uniform machines to minimize the makepsan. Gonzalez and Sahni [33] have developed a sequential algorithm which solves this problem in O(n + m log m) time. Martel [32] has developed a parallel version of this algorithm for a concurrent Read Exclusive Write (CREW) shared memory computer. This algorithm runs in O(log n + log3 m) time using n processors. Shachnai, Tamir and Woeginger [34] studied the problem of minimizing the makespan with preemption costs on a system of uniform machines scheduling. Pandelis [35] has considered the problem of scheduling independent jobs on uniform parallel machines. Each job has a deterministic processing time and a weight associated with it. In this research, the objective is to minimize the sum of the discounted flow time of the jobs. The author has shown that for scheduling on uniform machines, assigning the job with the shortest remaining time to the fastest available machine (SRPT-FM rule) is optimal in the case preemptive schedules. The author’s straightforward extension of this result is that if jobs are assigned weights that satisfy a certain agreeability condition (shortest processing time corresponds to largest weight, second shortest processing time corresponds to second largest weight, and so on), the SRPTFM rule minimizes discounted weighted flow time.
Though the researchers have used Pareto-optimal planes and other heuristics, only limited researches are carried out in this category of scheduling problem. So, the researchers may concentrate on using the advanced algorithms to the problems with single as well as multiobjective function.
4.1.3. Offline Scheduling of Non-Preemptive Jobs to Minimize Sum of Total Completion Times
Dessouky and Marcellus [36] have developed methods to optimize the expected sum of weighted completion times and the probability of meeting a common due date while scheduling identical jobs on a set of uniform parallel machines with random processing times. Meral Azizoglu and Omer Kirca [37] have considered the NP-hard problem of scheduling jobs on identical parallel machines to minimize total weighted flow time. They also discussed the properties that characterize the structure of an optimal solution, presented a lower bound and proposed a branch and bound algorithm. They also extended the algorithm to uniform parallel machines. Zhi-Long Chen and Warren B. Powell [38] have considered a class of problems of scheduling n jobs on m identical, uniform, or unrelated parallel machines with an objective of minimizing an additive criterion, viz. the total weighted completion times of the jobs. They proposed a decomposition algorithm for solving there problems exactly. The decomposition algorithm first formulates these problems as an integer program, and then reformulates the integer program, using Dantzig-Wolfe decomposition, as a set partitioning problem.
The minimization of the sum of the total completion times of the jobs in turn minimizes the mean flow time, for which there is an exact algorithm namely SPT rule in the single machine scheduling problem with single processor. The minimization of this measure under parallel machines environment makes the problem combinatorial in nature. Hence, the researchers may concentrate on the development of meta-heuristics for this problem. If one uses simulated annealing, an improved version of SPT rule may be designed as the seed generation algorithm.
4.1.4. Offline Scheduling of Preemptive Jobs to Minimize Sum of Total Completion Times
Gonzalez, Leung and Pinedo [39] have analyzed n independent jobs and m uniform machines in parallel. Each job has a processing time and a due date. Job j may complete its processing before or after its due date and preemptions are allowed. A set of jobs is said to be feasible if there exists a schedule that meets all the due dates. They presented a polynomial-time algorithm that given a feasible set of jobs, which constructs a schedule that minimizes the total completion time of the jobs.
Leung, Li, Pinedo and Jiawei Zhang [40] researched the scheduling of orders in an environment with m uniform machines in parallel. Each order requests certain amounts of k different product types. Each product type can be produced by any one of the m machines. No setup is required if a machine switches over from one product type to another. Different product types intended for the same order can be produced at the same time (concurrently) on different machines. Each order is released at time zero and has a positive weight. The completion time of an order is the finish time of the product type that is completed last for that order. The objective of this research is to minimize the total weighted completion time of orders. They proposed heuristics for the non-preemptive as well as preemptive case and obtained worstcase bounds that are functions of the number of machines as well as the difference in the speeds of the machines.
As discussed in the previous section, the indirect objective of this problem is to minimize the mean flow time. Since, this is less complex problem, when compared to the non-preemptive type, the researchers may try to develop mathematical models for different cases of the problem. In turn, the optimal solutions through a model for small or moderate size problems may be used for bench marking purpose while developing heuristics.
4.1.5. Offline Scheduling of Non-Preemptive Jobs to Minimize Total Earliness/Tardiness Kun-si Lin [41] developed an integer programming algorithm to solve the parallel machines problem with the objective of minimizing total tardiness in which different machines are allowed to have different processing speeds on a job. In this work, a solution procedure is introduced beginning with the single machine problem and then extended to the general case of m machines. Alain Guinet [42] considered the problem of scheduling n jobs on m uniform parallel machines with the objective of minimizing the mean tardiness or the weighted sum of tardiness with weights based on jobs, periods or both. For the mean tardiness criterion in the non-preemptive case, the problem is NP-hard, except for the cases with equal job processing times or with job due dates equal to job processing times. They have developed a heuristic to solve the non-preemptive scheduling problem with unrelated job processing times. The heuristic was experimented with 576 problems which consist of 18 problem sizes.
Meral Azizoglu and Omer Kirca [43] have considered the NP-hard problem of scheduling jobs on identical parallel machines to minimize the total tardiness. They presented the properties that characterize the structure of an optimal schedule. They proposed a branch and bound algorithm that incorporates the properties along with an efficient lower bounding scheme. They found that optimal solutions can be obtained in reasonable times for problems with size up to 15 jobs. In the last part of the study, they extended the results to uniform parallel machines. Naofumi, Shunji and Mitsuhiko [44] have considered a class of problems to minimize total tardiness on uniform parallel machines with human resource constraints, in which each machine requires an operator to process a job. They constructed a branch and abound algorithm for this problem and examined the efficiency of it by numerical examples.
Viniclus Amaral Armentano and Moacir Fellzardo de Franca Fllho [45] have considered the problem of scheduling jobs in uniform parallel machines with sequence dependent setup times in order to minimize the total tardiness of the jobs. They proposed GRASP versions that incorporate adaptive memory principles to solve the problem. Long-term memory is used in the construction of an initial solution and in a post optimization procedure which connects high quality local optima by means of path re-linking. They carried out computational tests on a set of benchmark instances and compared the proposed GRASP versions with heuristic methods from the literature. Toung, Soukhal and Jean-Charless Billaut [46] have developed algorithm for uniform parallel machines scheduling problem with a common due date to minimize total weighted tardiness. Gur Mosheiov and Assaf Sarig [47] have shown that the two machines case of the uniform parallel machines scheduling with earliness and tardiness and due-date costs is solvable in constant time. Also, they stated that the problem remains polynomially solvable for a fixed number of machines.
The minimization of the total earliness/tardiness is considered to be a challenging measure of performance even in the single machine scheduling problem with single processor. This magnifies the complexity of the algorithm to obtain the optimal solution. The researchers have used integer programming technique, branch and bound technique, single pass heuristic, GRASP, etc to minimize the measures of performance of this problem. As mentioned earlier, since it is a challenging measure, which magnifies the complexity of the problem, use of any exact algorithms like integer programming, branch and bound technique, etc. will take too much computational time. So, the researchers should concentrate on the development of meta-heuristics to obtain near-optimal/global optimum solutions for this scheduling problem.
4.1.6. Offline Scheduling of Non-Preemptive Jobs to Minimize Maximum Lateness
Federgruen and Groenevelt [48] considered the problem of scheduling n jobs, each with a specific processing requirement, release time and due date on m uniform parallel machines. They have obtained a feasible schedule by using network flow technique which determines the maximum flow in network. The complexity of the procedure used by them is O(tn3) operations, where t is the number of distinct machine types. Previous algorithm solves the feasibility problem in O(m + log n) (m2n3 + n4) operations. In this research, they further described algorithms for minimizing the maximum lateness.
Dessouky [49] has considered the problem of scheduling n identical jobs with unequal ready times on m parallel uniform machines to minimize the maximum lateness. In this research, a branch and bound procedure and six simple single-pass heuristic procedures are presented. The branch and bound procedure uses the heuristics to establish an initial upper bound. On sample problems, the branch and bound procedure in most instances was able to find an optimal solution within 100,000 iterations when the number of jobs is less than or equal to 80 and the number of machines is less than or equal to 3. For larger values of the number of machines, this heuristics provided approximate solutions close to optimal values.
Chhajed [50] has analyzed the problem of simultaneous determination of a common due-date and a sequence of n jobs to minimize the maximum deviation of job completion time around the common due-date. It is assumed that all the jobs are available at time zero and their processing times are known in advance. He gave some results for the case when splitting and preemption are allowed.
Chudak and Shmoys [51] presented new approximation algorithms for the problem of scheduling precedence-constrained jobs on parallel machines that are uniformly related without preemption. Here, they considered two objective functions: Cmax = maxjCj, where Cj denotes the completion time of the job j and ∑wjCj, where wj is a weight that is given for each job j. For the first objective, the best previously known result is an O(√m)-approximation algorithm, which was shown by Jaffe [22]. They have given an O(log m) approximation algorithm. They also showed how to extend this result to obtain an O(log m)-approximation algorithm for the second objective. There results also extend to settings in which each job has a release date rj before which the job may not begin processing.
Christos Koulamas and George J. Kyparisis [52] considered the uniform parallel machines scheduling problem with the objective of minimizing maximum lateness. They showed that an extension of EDD rule to a uniform parallel machines setting yields a maximum lateness value which does not exceed the optimal value by more than pmax, where pmax is the maximum job processing time.
The researchers have used network flow technique, branch and bound technique, heuristics, etc in the past. The minimization of the maximum lateness improves the goodwill of the customers, because the maximum delay is minimized, for which there is an exact algorithm namely EDD rule in the single machine scheduling problem with single processor. The minimization of this measure under parallel machines environment makes the problem combinatorial in nature. Hence, the researchers may concentrate on the development of meta-heuristics for this problem. If one uses simulated annealing, an improved version of EDD rule may be designed as the seed generation algorithm.
4.1.7. Offline Scheduling of Preemptive Jobs to Minimize Maximum Lateness
Drozdowski, Blazewicz, Formanowicz, Kubiak and Schmidt [53] have studied the problem of scheduling n preemptive tasks with ready times and due-dates on m uniform processors available in q time windows for minimizing maximum lateness criterion. The problem is reduced to a sequence of network flow problems. The complexity of the algorithm is O(n+q)3(log n + log q + log m + log max{bi}), where bi is speed of the processor i.
Only few researchers have concentrated on this problem. The researchers may extend the contributions made in the non-preemptive case to this problem.
4.1.8. Offline Scheduling of Non-Preemptive Jobs to Minimize Number of Tardy Jobs
As already stated in one of the earlier sections, Zhi-Long Chen and Warren B.Powell [38] have considered a class of problems of scheduling n jobs on m identical, uniform, or unrelated parallel machines with an objective of minimizing an additive criterion, viz. the total weighted completion times of the jobs. In addition to this measure, they also considered the objective of minimizing the weighted number of tardy jobs. They proposed a decomposition algorithm for solving these problems exactly.
Ruiz-Torres, Lopez and Ho [54] investigated the uniform parallel machines scheduling problem subject to a secondary resource constraint to minimize the number of tardy jobs. The secondary resource is fixed in quantity and is to be allocated to the machines at the start of the schedule. Two versions of the problem are analyzed. The first version assumes that the jobs are pre-assigned to the machines, while the second one takes into consideration the task of assigning jobs to the machines. They proposed an integer programming formulation to solve the first case and a set of heuristics for the second case.
One can use Hodgson’s algorithm to optimize the number of tardy jobs in the single machine scheduling problem with single processor with un-weighted jobs. When the jobs are with weights, the optimality is not guaranteed. Since, this measure is a derived measure from tardiness, it is a challenging measure. So, the researchers may use meta-heuristics to obtain global optimal solution. Further, the seed generation algorithm for the simulated annealing algorithm may be designed using an improved version of Hodgson’s algorithm.
4.1.9. Offline Scheduling of Preemptive Jobs to Minimize Number of Tardy Jobs
Lawler and Martel [55] have considered the problem of scheduling n preemptive jobs on uniform parallel machines. In this research, they formed a schedule such that the number of tardy jobs is minimized. They presented an algorithm with the complexity of O(n3) for the special case of two uniform machines. Also, they gave a fully polynomial scheme for the weighted case.
A very few researches have been carried out in this problem. So, there is a scope for further work in this problem with the guidelines as given in the previous section.
4.2. Review of Online Uniform Parallel Machines Scheduling
The performance of an online algorithm is measured by its competitive ratio which is the ratio of its worst case performance and the performance of an optimal algorithm with total prior knowledge. If the makespan is the measure of performance, alternatively, competitive ratio is the ratio between the cost of online schedule (makespan) and the cost of offline schedule (optimal makepsan).
The literature review of the following online uniform parallel machines scheduling problems is presented in this section.
1) Online scheduling of non-preemptive jobs to minimize makespan.
2) Online scheduling of preemptive jobs to minimize makespan.
3) Online scheduling of preemptive jobs to minimize total tardiness/earliness 4) Online scheduling of non-preemptive jobs to maximize the minimum completion time (machine covering problem).
5) Online scheduling of preemptive jobs to maximize the minimum completion time (machine covering problem).
4.2.1. Online Scheduling of Non-Preemptive Jobs to Minimize Makespan
Wein and Williamson [56] have studied the problem of scheduling jobs on parallel machines in an online fashion in which the processing requirement of a job is not known until that job is completed. For this problem, they scheduled jobs such that the makespan is minimized. They studied the following two models, viz. scheduling on identical parallel machines and scheduling on uniform parallel machines. Their results include the following.
- Matching upper and lower bounds on the competitive ratio for the case of identical machines.
- Upper and lower bounds that differ by a constant factor for uniformly related machines.
- A lower bound for randomized algorithms for identical machines that nearly matches the deterministic upper bound.
- Several upper and lower bounds for variations on these models.
A study on establishing a lower bound for makespan in on-line scheduling on uniformly related machines was done by Epstien and Sgall [57]. They considered the problem of on-line scheduling of jobs one by one on uniformly related machines, with or without preemption. They proved a lower bound of 2, both with and without preemption for randomized algorithms working for an arbitrary number of machines.
Tan and He [58] have investigated the semi-online scheduling problem with ordinal data on two uniform machines where the order of jobs by their processing times is known as priori. They presented a comprehensive lower bound which is a piecewise function of the speed ratio s. The algorithm gives optimal makespan for majority of s (1, ∞). In this paper, the total length of the intervals of s where the competitive ratio does not match the lower bound is less than 0.7784 and the biggest gap between them never exceeds 0.0521. Kontogiannis [59] has studied the problem of assigning unit size tasks to related machines when only limited online information is provided to each task. The author has proved that the missing information for an oblivious scheduler to perform almost optimally is the amount of tasks to be inserted into the system. In particular, the author provided an oblivious scheduler that only uses O(log log n) polls along with the additional information of the size of the input sequence, in order to achieve a constant competitive ratio. Finally, this oblivious scheduler is used in an adaptive scheduler that does not demand the knowledge of the input sequence and yet achieves almost the same performance. Epstein and Favrholdt [60] have considered non-preemptive semi-online scheduling problem in which jobs with non-increasing sizes arrive one by one which are to be scheduled on two uniformly related machines, with the goal of minimizing the makespan. They analyzed both the optimal overall competitive ratio and the optimal competitive ratio as a function of the speed ratio (s ≥ 1) between the two machines. They showed that the greedy algorithm LPT has optimal competitive ratio of ¼(1+√17) ≈ 1.28 overall, but does not have optimal competitive ratio for every value of s. They gave a tight analysis of the competitive ratio for every speed ratio.
Cheng, Ng and Vladirmir Kotov [61] have researched the online scheduling problem with m-1, m ≥ 2, uniform machines each with a processing speed of 1 and one machine with a speed of s, 1 ≤ s ≤ 2, to minimize the makespan. The well known list scheduling (LS) algorithm has a worst-case bound of (3m-1)/(m+1) (Sahni and Cho, [62]). An algorithm with a better competitive ratio was proposed by Li and Shi [63]. It has a worstcase bound of 2.8795 for large value of m and n = 2. In the note by Cheng, Ng and Vladirmir Kotov [61], they presented an algorithm with a competitive ratio of 2.45 for m ≥ 4 and any s, 1 ≤ s ≤ 2.
Angelelli, Speranza and Tuza [64] have considered the problem of online scheduling on two uniform processors where the total sum of the tasks is known in advance. In this research, tasks arrive one at a time and each task is to be assigned to one of the two processors before the next task arrives. The assignment can be changed later. The objective is the minimization of the makespan. By assuming s as the speed of the fast processor and 1 as the speed of the slow processor, they derived general lower bounds on the competitive ratio achievable with respect to offline optimum and designed on-line algorithms with guaranteed upper bound on their competitive ratio.
The researchers have concentrated on the analysis of lower bound for the makespan of this problem as well as on the development of heuristics with different competitive ratios. In future, researchers may aim to develop algorithms which yield better competitive ratio.
4.2.2. Online Scheduling of Preemptive Jobs to Minimize Makespan
Wen and Du [65] have considered the problem of preemptive on-line scheduling for two processors in which one of the processors has speed 1 and the speed of the other processor is greater than or equal to 1. In this research, the objective is to minimize the makespan. They proposed an algorithm with competitive ratio of (1+s)2/ (1+s+s2) for this problem.
Vestjens [66] considered the online scheduling problem in which n jobs, where n is unknown are to be scheduled on m uniform parallel machines with preemption of jobs such that the makespan is minimized. The processing time of the job is known on its arrival. The author has shown that if only a finite number of preemptions is allowed, then there exists an algorithm that solves the problem if and only if si-1/si ≤ si/si+1 for all i = 2, …, m-1, si is the largest machine speed. It is shown that if this condition is to be satisfied, then O(mn) preemptions are necessary.
Epstein, Noga, Seiden, Sgall and Woeginger [67] [68], studied the problem of on-line scheduling on two uniform machines with speeds 1 and s ≥ 1. Here, the objective is to obtain a schedule, which minimizes the makespan. First, they presented randomized results for this problem. Then, they showed a simple memory-less algorithm with competitive ratio (4-s)(1+s)/4 ≤ 1.5625. Also, they analyzed other randomized algorithms which demonstrate that the randomized competitive ratio is at most 1.52778 for any s. Finally, they presented a deterministic algorithm with competitive ratio of 1+s/(s2 + s + 1) for the preemptive version of this problem. Epstein [69,70] studied the preemptive scheduling on uniformly related processors, where jobs are assigned one by one in an on-line fashion such that the makespan is minimized. This paper discusses the class of machine sets where the speed ratios are non-decreasing as speed increases. For each set of machines in this class, an algorithm of optimal competitive ratio is deigned in this paper. This generalizes the known result for identical machines and solves other interesting cases.
A study on preemptive semi-online scheduling was carried out by Epstein and Favrholdt [71]. In this study, jobs with non-increasing sizes arrive one by one which are to be scheduled on two uniformly related machines. They analyzed the algorithms as a function of the speed ratio (s ≥ 1) between the two machines. Here, the objective is to minimize the makespan. Then, they designed algorithms of optimal completive ratio for all values of s and showed that for s > 2, idle time needs to be introduced. This is the first preemptive scheduling problem over list, where idle time is provably required. Donglei Du [72] also investigated the same problem within a certain range [1,r] (r ≥ 1) with the objective of minimizing the makespan. The author has characterized the optimal competitive ratio as a function of both s and r by devising a deterministic on-line scheduling algorithm.
The researchers have concentrated on the development of algorithms with different competitive ratios. In future, researchers may aim to develop algorithms which yield better competitive ratio.
4.2.3. Online Scheduling of Preemptive Jobs to Minimize Sum of Tardiness/Earliness
Balakrishnan, Kanet and Sridharan [73] have researched the problem of scheduling jobs uniform parallel machines to minimize the sum of earliness and tardiness costs. Jobs are assumed to arrive in a dynamic albeit deterministic manner and have non-identical due dates. Any job completion beyond its due date results in earliness or tardiness penalty, which may be different for different jobs. Setup times are job-sequence dependent and may be different on different machines based on the characteristics of the machines. For this problem, they presented a mixed integer formulation that has substantially fewer zero-one variables than typical formulations for scheduling problems of this type. They have reported their computational experience in using this model to solve small size problems and presented solution procedures for solving larger size problems. Bilge, Kirac, Kurtulan and Pekgun [74] have considered the problem of scheduling a set of dependent jobs with sequence dependent setups on a set of uniform parallel machines such that the total tardiness is minimized. Jobs have non-identical due dates and arrival times. They have used tabu search based algorithm for this problem. They have used several key components of tabu search such as candidate list strategies, tabu classifications, tabu tenure and intensification and diversification strategies in their algorithm. Alternate approaches to each of these issues are developed and extensively tested on a set of problems obtained from the literature. The results obtained are considerably better than those reported previously and constitute the best solutions known for the benchmark problems up to date.
As stated earlier, the minimization of the total earliness/tardiness is considered to be a challenging measure of performance even in the single machine scheduling problem with single processor. This magnifies the complexity of the algorithm to obtain the optimal solution. The researchers have concentrated on the development of mathematical model and tabu search based algorithm for this problem. As mentioned earlier, since it is a challenging measure magnifying the complexity of the problem, use of any model will take too much computational time. So, the researchers should concentrate on the development of meta-heuristics to obtain near-optimal/global optimum solutions for this scheduling problem.
4.2.4. Online Scheduling of Non-Preemptive Jobs to Maximize Minimum Completion Time (Machine Covering Problem)
Azar and Epstein [75,76] have considered the problem of scheduling a sequence of jobs on m parallel machines such that the minimum load over the machines is maximized in an online environment. Such problem is called as machine covering problem. This situation corresponds to a case that a system consists of m machines. They have given several theorems for identical parallel machines as well as for related parallel machines along with proofs. It is well known that any on-line deterministic algorithm for identical machines has a competitive ratio of at least m. In contrast they designed an on-line randomized algorithm which is O(√m) competitive and a matching lower bound of √m for any online randomized algorithm. In the case where the jobs are polynomially related, they designed an optimal O(log m) competitive randomized algorithm and a matching tight lower bound for any on-line randomized algorithm. For related machines, they showed that there is no online algorithm, whose competitive ratio is a function of the number of machines. However for the case where the value of the optimal assignment is known in advance and for the case where jobs arrive in non-increasing order, they showed that the exact competitive ratio is m. Azar and Epstein [77] have developed a polynomial approximation scheme for the machine covering problem. They reported that the previous best approximation algorithm has a performance ratio of 2. They provided an approximation scheme for the related machines scheduling. Their algorithm can be adapted to provide a simpler approximation scheme for the related machines scheduling too.
Tan, He and Epstein [78] have considered the nonpreemptive ordinal on-line scheduling of n independent jobs (p1, p2, p3, …pn) on two uniform related machines. They have developed optimal algorithms for maximizing the minimum machine completion time and minimizing the lp norm of the completion times. They assumed that the values of the processing times of the jobs are unknown at the time of assignment. However, it is known in advance that processing times of arriving jobs are sorted in a non-increasing order. They have constructed an assignment of all jobs to the machines at time zero by utilizing only ordinal data rather than actual magnitudes of jobs. For the problem of maximizing the minimum completion time, they first presented a comprehensive lower bound on the competitive ratio which is a piecewise function of machine speed ratio s. Then they proposed an algorithm which is optimal for any s which is greater than or equal to 1. For minimizing the lp norm, they studied the case of identical machines (s = 1) and present tight bounds as a function of p.
This is special class of problem. The researchers have concentrated on the development of algorithms with different competitive ratios. In future, researchers may aim to develop algorithms which yield better competitive ratio.
4.2.5. Online Scheduling of Preemptive Jobs to Maximize Minimum Completion Time (Machine Covering Problem)
He and Jiang [79] considered the semi-online preemptive scheduling problem with decreasing job sizes on two uniform machines. The goal of this paper is to maximize the continuous period of time (starting from time zero) when both machines are busy, which is equivalent to maximizing the minimum machine completion time if idle time is not introduced before all the jobs are completed. They designed optimal deterministic semi-online algorithms for every machine speed ratio s in the range from 1 to ∞ and showed that idle time is required during the assignment procedure of algorithms for any s greater than √6/2.The competitive ratio ratios of the algorithms match the randomized lower bound for every s in the range from 1 to 3.
A very few researchers have concentrated on this problem on the development of algorithms and analysis of competitive ratio. In future, researchers may aim to develop algorithms which yield better competitive ratio.
4.3. Miscellaneous Uniform Parallel Machines Scheduling
This section gives the review of articles on uniform parallel machines scheduling problem which are not grouped under any of the Subsection 4.1 and Subsection 4.2. Since, miscellaneous problem are discussed in the subsections, no specific comment is given in each of them.
4.3.1. Miscellaneous Problems with Non-Preemptive Jobs
Bahram Alidaee and Ahmad Ahmadian [80] have considered the problem of scheduling n single-operation jobs on 2 non-identical parallel machines where the sequencing of the jobs and their processing times are decision variables. In this research, the authors have assumed that the cost of processing a job is directly proportional to its processing time. The objectives of their research are as listed below.
1) Minimizing the total processing cost plus total flow time.
2) Minimizing the total processing cost plus weighted earliness and weighted tardiness.
They have reduced each of these problems to a transportation problem, which can be solved by a polynomial time algorithm.
Bahram Alidaee and Ahmad Ahmadian [81] have considered the single machine scheduling problem with variable speed. They have established polynomial time algorithms to minimize the makespan, total flow time and sum of the deviations of jobs from a common due date.
Vahid, Mahmoud and Mohsen [82] have presented a new deadline-based algorithm for the online uniform parallel machines scheduling problem with overloading situations. Then, they compared its performance with that of earliest due date first (EDF) algorithm. It is shown that their algorithm not only demonstrated a performance close to that of EDF in non-overloaded conditions but also has supremacy over EDF in overloaded situations in many aspects. Furthermore, it imposes much less overhead on the system. Bekki and Meral Azizoglu [83] studied an operational fixed interval scheduling problem on uniform parallel machines. Here, the objective is to maximize the total weight of the jobs processed. They showed that the problem is NP-hard in the strong sense and develop polynomial time algorithms for some special cases. They proposed a branch and bound algorithm that employs dominance conditions and tight bounds. He and Min [84] have considered the problem of online uniform machine scheduling with rejection. For the two machine case and a special three machine case, they presented the best possible online algorithms for certain values of speed ratio s.
4.3.2. Miscellaneous Problem with Preemptive Jobs
Blazewicz [85] has considered the problem of minimizing mean weighted information loss. In this paper, the preemptive case for identical as well as for a fixed number of uniform processors was considered. Blazewicz and Finke [86] have proposed a strongly polynomial algorithm based on a network flow technique, which minimizes the mean weighted execution time loss for an arbitrary number of identical processors as well as uniform processors. The upper bound on the number of preemptions in each of the cases is also reported.
Ishi, martel, Masuda and Nishida [87] considered a scheduling problem in which the objective is to determine both the optimal speeds of processors and an optimal schedule in a preemptive multiprocessor environment. The jobs are independent and each processor can be assigned any speed. The cost associated with each processor is a function of the speed of the processor. They presented polynomial algorithms to find the optimal speed assignments for a variety of cost functions such that the total cost is minimized in each case. Blazewicz, Bouvry, Guinand and Trystram [88] presented an optimal algorithm for scheduling a complete k-ary tree on two uniform processors of different speeds in order to minimize the makespan. They considered the basic case of unit standard execution times and unit communication times.
Shakhlevich and Strusevich [89] have provided a unified approach to solve preemptive scheduling problems with uniform parallel machines and controllable processing times. They demonstrated that a single criterion problem of minimizing total compression cost subject to the constraint that all due dates should be met can be formulated in terms of maximizing a linear function over a generalized polymatriod. This justified the applicability of the greedy approach and allowed them to develop fast algorithms for solving the special case with zero release dates and a common due date. For the bicriteria counterpart of the latter problem, they developed an efficient algorithm that constructs the trade-off curve for minimizing the compression cost and the makepsan.
Kubiak, Penz and Trystram [90] showed that the problem of scheduling chains of unit execution time (UET) jobs on uniform processors with communication delays to minimize the makespan is NP-hard in the strong sense. They also presented a heuristic that generates solutions with known and relatively small, absolute error for this problem. The NP–hardness result holds even for the case without communication delays and complements the earlier result of Gonzalez and Sahni [33] who gave a polynomial time algorithm for preemptive jobs of arbitrary length. They also studied the structure of optimal solutions for the two processor problem scheduling chains of UET jobs with communication delays, where one processor is an integer times faster than the other. This investigation resulted with a linear time optimization algorithm for this case.
4.3.3. Miscellaneous Problem with Periodic Tasks
Baruah [91] has considered scheduling systems of realtime tasks that are specified according to periodic model. In the periodic model of hard real-time tasks, a task T is characterized by two integer parameters – an execution requirement T.e and a period T.p with the interpretation that the task generates a job at each integer multiple of T.p and such job has an execution requirement of T.e execution units, which should be met by a deadline equal to the next integer multiple of T.p. A periodic task system consists of several such periodic tasks that are to execute on specified processor architecture. In this research, the job execution on a processor may be preempted. The author has designed an optimal algorithm for scheduling such periodic tasks on uniform parallel machines. Goossens and Baruah have considered the online scheduling of hard-real-time systems in which all jobs must be completed by specified deadlines on uniform multiprocessor machines. In this paper, they provided resource-augmentation techniques that permit on-line algorithms to perform better given the inherent limitations. Results derived here are applied to the scheduling of periodic task systems on uniform multiprocessor machines. Baruah and Goossens [92] considered the rate-monotonic scheduling on uniform multiprocessors. For systems comprised of periodic tasks that are to execute upon a single shared processor, a very popular static-priority run-time scheduling algorithm is the rate-monotonic scheduling algorithm (Algorithm RM). It assigns each task a priority inversely proportional to its period. The authors have obtained the first non-trivial feasibility test for a static-priority scheduling algorithm that adopts a global approach to task allocation on uniform multiprocessors. They have obtained simple sufficient conditions for determining whether any given periodic task system will be successfully scheduled by Algorithm RM upon a given uniform multiprocessor platform.
5. Conclusions
In this paper, an extensive review of literature of the single machine scheduling problem with uniform parallel processors is presented. First, an introduction of this problem is presented with its different measures of performance, viz. minimizing mean flow time, minimizing total tardiness, minimizing maximum lateness, minimizing the number of tardy jobs and maximizing the minimum of the completion times of the last jobs on the uniform parallel machines. This problem is reviewed with the primary classification of offline scheduling and online scheduling. Under each such scheduling, the next classification is non-preemptive scheduling and preemptive scheduling. Under each of the above combinations, the applicable measures of performance are considered to classify the literatures. In this way, the authors have classified the literatures into 14 categories. Finally, under miscellaneous problems, three problems, viz. non-preemptive, preemptive and periodic tasks are considered. This resulted with a total of 17 categories. For each category of literatures, a comprehensive review of literature has been presented.
In different cases of the offline scheduling problems, in future, the researchers may concentrate the following.
• For the problem under non-preemptive and preemptive cases to minimize the makespan, the researchers may concentrate on the development of meta-heuristics, viz. simulated annealing algorithm, genetic algorithm, etc., which will give better solution tending towards global optimum, when compared to the single pass heuristics. Further, effort may be directed on the development of algorithms with multi-objective function.
• For the problems under preemptive case with the minimization of the sum of the total completion times, the researchers may concentrate on the development of meta-heuristics for this problem. If one uses simulated annealing, an improved version of SPT rule may be designed as the seed generation algorithm. For the non preemptive case of this problem, the researchers may try to develop mathematical models for different cases of the problem. In turn, the optimal solutions through a model for small or moderate size problems may be used for benchmarking purpose while developing heuristics.
• Since, the minimization of the total earliness/tardiness under non-preemptive case is a challenging measure magnifying the complexity of the problem, use of any exact algorithms like integer programming, branch and bound technique, etc will take too much computational time. So, the researchers should concentrate on the development of meta-heuristics to obtain near-optimal/global optimum solutions for this scheduling problem.
• The minimization of the maximum lateness under the non-preemptive case under parallel machines environment makes the problem combinatorial in nature. Hence, the researchers may concentrate on the development of meta-heuristics for this problem. If one uses simulated annealing, an improved version of EDD rule may be designed as the seed generation algorithm. Under the preemptive case of this problem, only few researchers have concentrated on this problem. The researchers may extend the contributions made in the non-preemptive case to this problem.
•For the problems with non-preemptive jobs to minimize number of tardy jobs, the researchers may use meta-heuristics to obtain global optimal solution. Further, the seed generation algorithm for the simulated annealing algorithm may be designed using an improved version of Hodgson’s algorithm. For the problems with preemptive case, researchers may aim to develop algorithms which yield better competitive ratio.
In different cases of the online scheduling problems, the directions for future are as listed below.
• For the problems of scheduling with non-preemptive as well as preemptive jobs to minimize makespan, the researchers may aim to develop algorithms which yield better competitive ratio.
• For the problem of scheduling with preemptive jobs to minimize sum of tardiness/earliness, the researchers should concentrate on the development of meta-heuristics to obtain near-optimal/ global optimum solutions.
• For the machine covering problem with nonpreemptive as well as preemptive jobs, the researchers may aim to develop algorithms which yield better competitive ratio.
6. Acknowledgements
We sincerely thank the anonymous referees for their constructive suggestions, which helped us to improve the paper.
7. References
[1] R. Panneerselvam, “Production and Operations Management,” 2nd Edition, Prentice-Hall of India, New Delhi, 2005.
[2] E. G. Jr. Coffman and R. L. Graham, “Optimal Scheduling for Two-Processor Systems,” Acta Informatica, Vol. 1, No. 3, 1972, pp. 200-213.
[3] E. Horowiz and S. Sahni, “Exact and Approximate Algorithms for Scheduling Nonidentical Processors,” Journal of the ACM, Vol. 23, No. 2, 1976, pp. 317-327.
[4] O. H. Ibarra and C. E. Kim, “Heuristic Algorithms for Scheduling Independent Tasks on Nonidentical Processors,” Journal of the ACM, Vol. 24, No. 2, 1977, pp. 280-289.
[5] D. Prabuddha and E. M. Thomas, “Scheduling to Minimize Makespan on Unequal Parallel Processors,” Decision Sciences, Vol. 11, No. 4, 1980, pp. 586-602.
[6] R. L. Bulfin, and R. G. Parker, “Scheduling Jobs on Two Facilities to Minimize Makespan,” Management Science, Vol. 26, No. 2, 1980, pp. 202-214.
[7] D. K. Friesen and M. A. Langston, “Bounds for Multifit Scheduling on Uniform Processors,” SIAM Journal on Computing, Vol. 12, No. 1, 1983, pp. 60-70.
[8] R. L. Graham, “Bounds for Multiprocessing Timing Anomalies,” SIAM Journal of Applied Mathematics, Vol. 17, No. 2, 1969, pp. 416-429.
[9] D. Gregory, “Scheduling Independent Tasks on Uniform Processors,” SIAM Journal of Computing, Vol. 13, No. 4, 1984, pp. 705-716.
[10] D.K. Friesen, “Tighter Bounds for LPT Scheduling on Uniform Processors,” SIAM Journal on Computing, Vol. 16, No. 3, 1987, pp. 554-560.
[11] D. S. Hochbaum and D. B. Shmoys, “A Polynomial Approximation Scheme for Scheduling on Uniform Processors: Using the Dual Approximation Approach,” SIAM Journal on Computing, Vol. 17, No. 3, 1988, pp. 539- 551.
[12] B. Chen, “Parametric Bounds for LPT Scheduling on Uniform Processors,” Acta Mathematicae Applicateae, Sinica, Vol. 7, No. 1, 1991, pp. 67-73.
[13] P. Mireault, J. B. Orlin and R. V. Vohra, “A Parametric Worst Case Analysis of the LPT Heuristic for Two Uniform Machines,” Operations Research, Vol. 45, No. 1, 1997, pp. 116-125.
[14] R. E. Burkard and Y. He, “A Note on MULTIFIT Scheduling for Uniform Machines,” Computing, Vol. 61, No. 3, 1998, pp. 277-283.
[15] M. Y. Kovalyov and Y. M. Shafransky, “Uniform Machine Scheduling of Unit-Time Jobs Subject to Resource Constraints,” Discrete Applied Mathematics, Vol. 84, No. 1-3, 1998, pp. 253-257.
[16] R. E. Burkard, Y. He and H. Kellerer, “A Linear Compound Algorithm for Uniform Machine Scheduling,” Computing, Vol. 61, No. 1, 1998, pp. 1-9.
[17] R. Panneerselvam and S. Kanagalingam, “Modelling Parallel Processors with Different Processing Speeds of Single Machine Scheduling Problem to Minimize Makespan,” Industrial Engineering Journal, Vol. 17, No. 6, 1998, pp. 16-19.
[18] R. Panneerselvam and S. Kanagalingam, “Simple Heuristic for Single Machine Scheduling Problem with Two Parallel Processors Having Varying Speeds to Minimize Makespan,” Industrial Engineering Journal, Vol. 18, No. 6, 1999, pp. 2-8.
[19] C. Chekuri and M. Bender, “An Efficient Approximation Algorithm for Minimizing Makespan on Uniformly Related Machines,” Proceedings of IPCO’99, LNCS, 1999, pp. 383-393.
[20] G. J. Woeginger, “A Comment on Scheduling on Uniform Machines under Chain-Type Precedence Constraints,” Operations Research Letters, Vol. 26, No. 3, 2000, pp. 107-109.
[21] F. A. Chudak and D. B. Shmoys, “An Efficient Approximation Algorithm for Minimizing Makespan on Uniformly Related Machines,” Proceedings of the 8th Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, 1997, pp. 581-590.
[22] J. Jaffe, “Efficient Scheduling of Tasks without Full Use of Processor Resources,” Theoretical Computer Science, Vol. 26, No. 1, 1980, pp. 22-35.
[23] C. Chekuri and M. Bender, “An Efficient Approximation Algorithm for Minimizing Makespan on Uniformly Related Machines,” Journal of Algorithms, Vol. 41, No. 2, 2001, 212-224.
[24] C. J. Liao and C.-H. Lin, “Makespan Minimization for Two Uniform Parallel Machines,” International Journal of Production Economics, Vol. 84, No. 2, 2003, pp. 205- 213.
[25] L. Epstein and J. Sgall, “Approximation Schemes for Scheduling on Uniformly Related and Identical Parallel Machines,” Proceedings of 7th Annual European Symposium on Algorithms, 1999, pp. 151-162.
[26] L. Epstein and J. Sgall, “Approximation Schemes for Scheduling on Uniformly Related and Identical Parallel Machines,” Algorithmica, Vol. 39, No. 1, 2004, pp. 43- 57.
[27] C. Koulamas and G. J. Kyparisis, “Makespan Minimization on Uniform Parallel Machines with Release Times,” European Journal of Operational Research, Vol. 157, No. 1, 2004, pp. 262-266.
[28] A. Agarwal, S. Colak, V. S. Jacob and H. Pirkul, “Heuristics and Augmented Neural Networks for Task Scheduling with Non-Identical Machines,” European Journal of Operational Research, Vol. 175, No. 1, 2006, pp. 296- 317.
[29] C.-H. Lin and C.-J. Liao, “Makespan Minimization for Multiple Uniform Machines,” Computers & Industrial Engineering, Vol. 54, No. 4, 2008, pp. 983-992.
[30] T. Kis and R. Kapolnai, “Approximation and Auctions for Scheduling Batches on Related Machines,” Operations Research Letters, Vol. 35, No. 1, 2007, pp. 61-68.
[31] S. T. McCormic and M. inedo, “Scheduling n Independent Jobs on m Uniform Machines with both Flow Time and Makespan Objectives: A Parametric Analysis,” ORSA Journal of Computing, Vol. 7, No. 1, 1995, pp. 63- 77.
[32] C. U. Martel, “A parallel Algorithm for Preemptive Scheduling of Uniform Machines,” Journal of Parallel and Distributed Computing, Vol. 5, No. 6, 1988, pp. 700- 715.
[33] T. Gonzalez and S. Sahni, “Preemptive Scheduling of Uniform Processor Systems,” Journal of Association of Computing Machinery, Vol. 25, No, 1, 1978, pp. 92-101.
[34] H. Shachnai, T. Tamir and G. J. Woeginger, “Minimizing Makespan and Preemption Costs on a System of Uniform Machines,” Proceedings of the 10th European Symposium on Algorithms, 2002, pp. 859-871.
[35] D. G. Pandelis, “Optimal Preemptive Scheduling on Uniform Machines with Discounted Flow Time Objectives,” European Journal of Operational Research, Vol. 177, No. 1, 2007, pp. 630-637.
[36] M. I. Dessouky and R. L. Marcellus, “Scheduling Identical Jobs on Uniform Parallel Machines with Random Processing Times,” Computers and Industrial Engineering, Vol. 35, No. 1-2, 1998, pp. 109-112.
[37] M. Azizoglu and O. Kirca, “On the Minimization of Total Weighted Flow Time with Identical and Uniform Parallel Machines,” European Journal of Operational Research, Vol. 113, No. 2, 1999, pp. 91-100.
[38] Z.-L. Chen and W. B. Powell, “Solving Parallel Machine Scheduling Problems by Column Generation,” INFORMS Journal on Computing, Vol. 11, 1999, pp. 78-94.
[39] T. F. Gonzalez, Y. T. L. Joseph and M. Pinedo, “Minimizing Total Completion Time on Uniform Machines with Deadline Constraints,” ACM Transactions on Algorithms, Vol. 2, No. 1, 2006, pp. 95-115.
[40] J. Y. T. Leung, H. B. Li, M. Pinedo and J. W. Zhang, “Minimizing Total Weighted Completion Time when Scheduling Orders in a Flexible Environment with Uniform Machines,” Information Processing Letters, Vol. 103, No. 3, 2007, pp. 119-129.
[41] K.-S. Lin, “Scheduling with Parallel Machines to Minimize Total Job Tardiness,” Engineering Costs and Production Economics, Vol. 5, No. 3-4, 1981, pp. 289-296.
[42] A. Guinet, “Scheduling Independent Jobs on Uniform Parallel Machines to Minimize Tardiness Criteria,” Journal of Intelligent Manufacturing, Vol. 6, No. 2, 1995, pp. 95- 103.
[43]; M. Azizoglu and O. Kirca, “Tardiness Minimization on Parallel Machines,” International Journal of Production Economics, Vol. 55, No. 2, 1998, pp. 163-168.
[44] I. Naofumi, T. Shunji and A. Mitsuhiko, “Minimizing Total Tardiness on Uniform Parallel Machines under Human Resource Constraint,” Proceedings of the Annual Conference of the Institute of Systems, Control and Information Engineers, Vol. 47, 2003, pp. 419-420,.
[45] V. A. Armentano and M. F. de F. Filho, “Minimizing Total Tardiness in Parallel Machine Scheduling with Setup Times: An Adaptive Momory-Based GRASP Approach,” European Journal of Operations Research, Vol. 183, No. 1, 2007, pp. 100-114.
[46] N. H. Tuong, A. Soukhal and J.-C. Billaut, “Uniform Parallel Machine Scheduling Problem with a Common Due Date to Minimize Total Weighted Tardiness,” MAPSP Conference, 2007.
[47] G. Mosheiov and A. Sarig, “Due-Date Assignment on Uniform Machines,” European Journal of Operational Research, Vol. 193, No. 1, 2009, pp. 49-58.
[48] A. Federgruen and H. Groenevelt, “Preemptive Scheduling of Uniform Machines by Ordinary Network Flow Techniques,” Management Science, Vol. 32, No. 3, 1986, pp. 341-349.
[49] M. M. Dessouky, “Scheduling Identical Jobs with Unequal Ready Times on Uniform Parallel Machines to Minimize the Maximum Lateness,” Computers & Industrial Engineering, Vol. 34, No. 4, 1998, pp. 793-806.
[50] D. Chhajed, “A Note on Minimizing the Maximum Deviation of Job Completion Time about a Common DueDate,” Applied Mathematics Letters, Vol. 1, No. 2, 1988, pp. 161-163.
[51] F. A. Chudak and D. B. Shmoys, “Approximation Algorithm for Precedence-Constrained Scheduling Problems on Parallel Machines that Run at Different Speeds,” Journal of Algorithms, Vol. 20, No. 2, 1999, pp. 323-343.
[52] C. Koulamas and G. J. Kyparisis, “Scheduling on Uniform Parallel Machines to Minimize Maximum Lateness,” Operations Research Letters, Vol. 26, No. 3, 2000, pp. 175-179.
[53] M. Drozdowski, J. Blazewicz, P. Formanowicz, W. Kubiak and G. Schmidt, “Scheduling Preemptable Tasks on Uniform Processors with Limited Availability for Maximum Lateness Criterion,” 7th International Workshop on Project Management Scheduling, Osnabrück, 2000, pp. 118-120.
[54] A. J. Ruize-Torres, F. J. Lopez and J. C. Ho, “Scheduling Uniform Parallel Machines Subject to a Secondary Resource to Minimize the Number of Tardy Jobs,” European Journal of Operational Research, Vol. 179, No. 2, 2007, pp. 302-315.
[55] E. L. Lawler and C. U. Martel, “Preemptive Scheduling of Two Uniform Machines to Minimize the Number of Late Jobs,” Operations Research, Vol. 37, No. 2, 1989, pp. 314-318.
[56] J. Wein and D. P. Williamson, “On-Line Scheduling of Parallel Machines,” Technical Report, Institute of Technology, Cambridge Lab for Computer Science, Massachusetts, 1990, p. 18.
[57] L. Epstein and J. Sgall, “A Lower Bound for On-Line Scheduling on Uniformly Related Machines,” Operations Research Letters, Vol. 26, No. 1, 2000, pp. 17-22.
[58] Z. Tan and Y. He, “Semi-On-Line Scheduling with Ordinal Data on Two Uniform Machines,” Operations Research Letters, Vol. 28, No. 5, 2001, pp. 221-231.
[59] S. Kontogiannis, “Multiple-Choice Assignments on Uniformly Related Machines,” ALCOM-FT Technical Report Series, 2002, pp. 2-39.
[60] L. Epstein and L. M. Favrholdt, “Optimal Non-Preemptive Semi-Online Scheduling on Two Related Machines,” Journal of Algorithms, Vol. 57, No. 1, 2005, pp. 49-73.
[61] T. C. E. Cheng, C. T. Ng and V. Kotov, “A New Algorithm for Online Uniform-Machine Scheduling to Minimize the Makespan,” Information Processing Letters, Vol. 99, No. 3, 2006, pp. 102-105.
[62] S. Sahni and Y. Cho, “Scheduling Independent Tasks with Due Times on a Uniform Processor System,” Journal of the ACM, Vol. 27, No. 3, 1980, pp. 550-563.
[63] R. Li and L. Shi, “An On-Line Algorithm for Some Uniform Processor Scheduling,” SIAM Journal of Computer, Vol. 27, No. 2, 1998, pp. 414-422.
[64] E. Angelelli, M. G. Speranza and Z. Tuza, “Semi-Online Scheduling on Two Uniform Processors,” Theoretical Computer Science, Vol. 393, No. 1-3, 2008, pp. 211-219.
[65] J. Wen, and D. Du, “Preemptive On-Line Scheduling for Two Uniform Processors,” Operations Research Letters, Vol. 23, No. 3, 1998, pp. 113-116.
[66] A. Vestjens, “Scheduling Uniform Machines On-Line Requires Nondecreasing Speed Ratios,” Mathematical Programming, Vol. 82, No. 2, 1998, pp. 225-234.
[67] L. Epstein, J. Noga, S. S. Seiden, J. Sgall and G. J. Woeginger, “Randomized On-Line Scheduling on Two Uniform Machines,” Proceedings of the 10th Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, 1999, pp. 317-326.
[68] L. Epstein, J. Noga, S. S. Seiden, J. Sgall and G. J. Woeginger, “Randomized On-Line Scheduling on Two Uniform Machines,” Journal of Scheduling, Vol. 4, No. 2, 2001, pp. 71-92.
[69] L. Epstein, “Optimal Preemptive On-Line Scheduling on Uniform Processors with Non-Decreasing Speed Ratios,” Operations Research Letters, Vol. 29, No. 2, 2001(a), pp. 93-98.
[70] L. Epstein, “Optimal Preemptive Scheduling on Uniform Processors with Non-Decreasing Speed Ratios,” Proceedings of 18th STACS, Dresden, 2001(b), pp. 230-237.
[71] L. Epstein and L. M. Favrholdt, “Optimal Preemptive Semi-Online Scheduling to Minimize Makespan on Two Related Machines,” Operations Research Letters, Vol. 30, No. 4, 2002, pp. 269-275.
[72] D. L. Du, “Optimal Preemptive Semi-Online Scheduling on Two Uniform Processors,” Information Processing letters, Vol. 92, No. 5, 2004, pp. 219-223.
[73] N. Balakrishnan, J. J. Kanet and S. Sridharan, “Early/ Tardy Scheduling with Sequence Dependent Setups on Uniform Parallel Machines,” Computers & Operations Research, Vol. 26, No. 2, 1999, pp. 127-141.
[74] U. Bilge, F. Kirac, M. Kurtulan and P. Pekgun, “A Tabu Search Algorithm for Parallel Machine Total Tardiness Problem,” Computers and Operations Research, Vol. 31, No. 3, 2004, pp. 397-414.
[75] Y. Azar and L. Epstein, “On-Line Machine Covering,” Proceedings of 5th ESA conference, Graz, 1997, pp. 23- 36.
[76] Y. Azar and L. Epstein, “On-Line Machine Covering, Journal of Scheduling,” Vol. 1, No. 2, 1998(a), pp. 67-77.
[77] Y. Azar and L. Epstein, “Approximation Schemes for Covering and Scheduling on Related Machines,” Proceedings of the 1st Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX’98), in Lecture Notes in Computer Science, Springer-Verlag, Berlin, Vol. 1444, 1998(b), pp. 39-47.
[78] Z. Tan, Y. He and L. Epstein, “Optimal On-Line Algorithms for the Uniform Machine Scheduling Problem with Ordinal Data,” Information and Computation, Vol. 196, No. 1, 2005, pp. 57-70.
[79] Y. He and Y. Jiang, “Optimal Semi-Online Preemptive Algorithms for Machine Covering on Two Uniform Machines,” Theoretical Computer Science, Vol. 339, No. 2-3, 2005, pp. 293-314.
[80] B. Alidaee and A. Ahmadian, “Two Parallel Machine Sequencing Problems Involving Controllable Job Processing Times,” European Journal of Operational Research, Vol. 70, No. 3, 1993, pp. 335-341.
[81] B. Alidaee and A. Ahmadian, “Scheduling on a Single Processor with Variable Speed,” Information Processing Letters, Vol. 60, No. 4, 1996, pp. 189-193.
[82] S. Vahid, N. Mohmoud and K. Mohsen, “Deadline Scheduling with Processor Affinity and Feasibility Check on Uniform Machines,” Computer and Information Technology, Vol. 16-19, 2007, pp. 793-798.
[83] O. B. Bekki and M. Azizoglu, “Operational Fixed Interval Scheduling Problem on Uniform Parallel Machines,” International Journal of Production Economics, Vol. 112, No. 2, 2008, pp. 756-768.
[84] Y. He and X. Min, “On-Line Uniform Machine Scheduling with Rejection,” Computing, Vol. 65, No. 1, 2000, pp. 1-12.
[85] J. Blazewicz, “Minimizing Mean Weighted Information Loss with Preemptable Tasks and Parallel Processors,” Technology and Science of Informatics, Vol. 3, No. 6, 1984, pp. 415-420.
[86] J. Blazewicz and G. Finke, “Minimizing Mean Weighted Execution Time Loss on Identical and Uniform Processors,” Information processing Letters, Vol. 24, No. 4, 1987, pp. 259-263.
[87] H. Ishi, C. Martel, T. Masuda and T. Nishida, “A Generalized Uniform Processor System,” Operations Research, Vol. 33, No. 2, 1985, pp. 346-362.
[88] J. Blazewicz and P. Bouvry, F. Guinand and D. Trystram, “Scheduling Complete Intrees on Two Uniform Processors with Communication Delays,” Information Processing Letters, Vol. 58, No. 5, 1996, pp. 255-263.
[89] N. V. Shakhlevich and V. A. Strusevich, “Preemptive Scheduling on Uniform Parallel Machines with Controllable Job Processing Times,” Algorithmica, Vol. 51, No. 4, 2007, pp. 451-473.
[90] B. Kubiak, B. Penz and D. Trystram, “Scheduling Chains on Uniform Processors with Communication Delays,” Journal of Scheduling, Vol. 5, No. 6, 2002, pp. 459-476.
[91] S. Baruah, “Scheduling Periodic Tasks on Uniform Multiprocessors,” Information Processing Letters, Vol. 80, No. 2, 2001, pp. 97-104.
[92] S. Baruah and J. Goossens, “Rate-Monotonic Scheduling on Uniform Multiprocessors,” IEEE Transactions on Computers, Vol. 57, No. 7, 2003, pp. 966-970.

