Intelligent Information Management
Vol.2 No.7(2010), Article ID:2215,11 pages DOI:10.4236/iim.2010.27050
Design and Comparison of Simulated Annealing Algorithm and GRASP to Minimize Makespan in Single Machine Scheduling with Unrelated Parallel Machines
1Department of Mechanical Engineering, VIT University, Vellore, India
2Department of Mechanical Engineering, Thiagarajar College of Engineering, Madurai, India
3Department of Management Studies, School of Management, Pondicherry University, Pondicherry, India
E-mail: {Sivasankaran.panneerselvam, sornakumar2000}@yahoo.com, panneer_dms@yahoo.co.in
Received April 11, 2010; revised May 15, 2010; accepted June 20, 2010
Keywords: makespan, simulated annealing Algorithm, GRASP, unrelated parallel machines, mathematical model
Abstract
This paper discusses design and comparison of Simulated Annealing Algorithm and Greedy Randomized Adaptive Search Procedure (GRASP) to minimize the makespan in scheduling n single operation independent jobs on m unrelated parallel machines. This problem of minimizing the makespan in single machine scheduling problem with uniform parallel machines is NP hard. Hence, heuristic development for such problem is highly inevitable. In this paper, two different Meta-heuristics to minimize the makespan of the assumed problem are designed and they are compared in terms of their solutions. In the first phase, the simulated annealing algorithm is presented and then GRASP (Greedy Randomized Adaptive Search procedure) is presented to minimize the makespan in the single machine scheduling problem with unrelated parallel machines. It is found that the simulated annealing algorithm performs better than GRASP.
1. Introduction
The production scheduling is classified into single machine scheduling, flow shop scheduling, job shop scheduling, open shop scheduling and batch scheduling. The single machine scheduling is classified into single machine scheduling with single machine and with parallel machines.
The single machine scheduling problem with parallel machines is further classified into single machine scheduling with identical parallel machines and with nonidentical parallel machines. The single machine scheduling problem with non-identical parallel machines is further classified into single machine scheduling problem with uniform parallel machines and with unrelated parallel machines.
Let, tij be the processing time of the job j on the machine i, for i = 1, 2, 3,…, m and j = 1, 2, 3,…, n. The three types of single machine scheduling problems with parallel machines are defined as follows.
1) If tij = t1j for all i and j, then the problem is called as identical parallel machines scheduling problem.
This means that all the parallel machines are identical in terms of their speed. Each and every job will take the same amount of processing time on each of the parallel machines.
2) If tij = t1j/si for all i and j, then the problem is termed as uniform (proportional) parallel machines scheduling problem. Here, si is the speed of the machine i and t1j is the processing time of the job j on the machine 1.
This means that the parallel machines will have different speeds. Generally, we assume s1, s2, s3,…, and sm for the parallel machines 1, 2, 3,…, and m, respectively such that s1 < s2 < s3 < … < sm. That is the machine 1 is the slowest machine and the machine m is the fastest machine. For a given job, its processing times on the parallel machines will be as per the following relation: 1/s1 > 1/s2 > 1/s3 > … > 1/sm
3) If tij is arbitrary for all i and j, then the problem is known as unrelated parallel machines scheduling problem.
In this type of scheduling, there will not be any relation amongst the processing times of a job on the parallel machines. This may be due to technological differences of the machines, different features of the jobs, etc.
In this paper, the single machine scheduling problem with unrelated parallel machines is considered. The essential characteristics of the single machine scheduling problem with unrelated parallel machines are as listed below.
• It has n single operation jobs.
• It has m unrelated parallel machines.
• m machines are continuously available and they are never kept idle while work is waiting.
• tij is the processing time of the job j on the machine i, for i = 1, 2, 3,..., m and j = 1, 2, 3,..., n.
• tij is arbitrary for different combinations of i and j, for i = 1, 2, 3,..., m and j = 1, 2, 3,…, n. This means that there is no relationship between the processing times of a job on different parallel machines.
• The ready time of each job is assumed to be zero (rj = 0, j = 1, 2, 3,…, n)
• Once processing begins on a job, it is processed to its completion without interruption. This means that the preemption of the jobs is not permitted.
There are many measures in single machine scheduling problem [1]. In this paper, the minimization of the makespan of scheduling n independent jobs on m unrelated parallel machines is considered, because it is considered to be an integrated measure of performance, which represents the earliest completion time of the given batch of jobs.
2. Literature Review
This section presents review of literature of scheduling n independent jobs on m unrelated parallel machines to minimize the makespan. As already stated, this problem comes under NP-hard category. Hence, any attempt to obtain the optimal solution through exact algorithm may end with failure for most of the instances, because of exponential computational time for such problem [2]. Hence, researchers are focusing on the development of heuristics.
Lawler and Labetoulle [3] developed a linear programming model to minimize the makespan of scheduling n jobs on m unrelated parallel machines with preemption of jobs.
Potts [4] developed a heuristic coupled with linear programming to schedule n jobs on m unrelated parallel machines for minimizing the makespan. This heuristic uses linear programming in the first phase to form a partial solution at most with m – 1 jobs unscheduled. In the second stage, these unscheduled jobs are scheduled using an enumeration method. Van De Velde [5] considered the single machine scheduling problem with unrelated parallel machines. The author aimed to minimize the maximum job completion time which means the minimization of makespan. He presented an optimization and an approximation algorithm that are both based on surrogate relaxation and duality to solve this NP hard problem. The idea behind surrogate relaxation is to replace a set of nasty (complex) constraints with a single constraint that is a weighted aggregate of these constraints. Glass, Potts and Shade [6] have applied meta-heuristics to the problem of scheduling jobs on unrelated parallel machines to minimize the makespan and reported that genetic algorithm gives poor results. Also, they reported that a hybrid method in which a descent is incorporated into the genetic algorithm is comparable in performance with simulated annealing. Hariri and Potts [7] developed heuristic, which consists of two phases to minimize the makespan of scheduling n independent jobs on m unrelated parallel machines. In the first phase, a linear programming model is used to schedule some of the jobs and then a heuristic is used in the second phase to schedule the remaining jobs. They have stated that some improvement procedure is necessary to have good solutions.
Piersma and Van Dijk [8] have proposed new local search algorithms to minimize the makespan of scheduling jobs in unrelated parallel machines. In these algorithms, the neighbourhood search of a solution uses the efficiency of the machines for each job. They claimed that this approach gives better results when compared to general local search algorithms. Martello, Soumis and Toth [9] have considered the scheduling of jobs on unrelated parallel machines in which the makespan is minimized. They proposed lower bounds based on Lagrangian relaxations and additive techniques. They then introduced new cuts which eliminate infeasible disjunctions on the cost function value, and prove that the bounds obtained through such cuts dominate the previous bounds. These results are used to obtain exact and approximation algorithms.
Klaus and Lorant [10] have presented polynomial-approximation schemes for preemptive and non-preemptive schemes with polynomial time complexity functions to schedule jobs on unrelated parallel machines for minimizing the makepsan. Sourd [11] has developed two approximation algorithms for minimizing the makespan of independent tasks assigned on unrelated parallel machines. The first one is based on a partial and heuristic exploration of a search tree. The second implements a new large neighbourhood improvement procedure to an already existing algorithm. He reported that the computational efficiency is equivalent to the best local search heuristics.
Serna and Xhafa [12] have developed an approach to schedule jobs on unrelated parallel machines to minimize the makespan. There approach shows how to relate the linear program obtained by relaxing the integer programming formulation of the problem with a linear program formulation that is positive and in the packing/ covering form. They also demonstrated the application of the same technique to the general assignment problem.
Mokotoff and Chretienne [13] have developed a cutting plane algorithm for the unrelated parallel machine scheduling problem in which the objective is to minimize the makespan. This algorithm deals with the polyhedral structure of the scheduling problem stated above. In their work, strong inequalities are identified for fixed values of the maximum completion time and are used to build a cutting plane scheme from which exact algorithm and an approximation algorithm are developed. Mokotoff and Jimeno [14] developed heuristics based on partial enumeration for the unrelated parallel machines scheduling problem. Given the mixed integer linear model with binary decision variables, they presented heuristics based on partial enumeration. Computational experiments are reported for a collection of test problems, showing that some of the proposed algorithms achieve better solutions than other relevant approximation algorithms published up to that time.
Pfund, Fowler and Gupta [15] have carried out a survey of algorithms for single and multi-objective unrelated parallel-machine deterministic scheduling problems. Under single objective case, they have considered the following.
1) Minimization of makespan
2) Minimization of the sum of the weighted completion times
3) Minimization of maximum tardiness
4) Minimization of total tardiness
5) Minimization of the sum of the weighted total earliness and weighted total tardiness
Under multi-objective case, they have discussed some select combinations of the above measures.
Ghirardi and Potts [16] have considered the problem of scheduling jobs on unrelated parallel machines to minimize the makespan. They developed recovering beam search method to minimize the makespan in the unrelated parallel machines. The traditional beam search method is a truncated version of branch and bound method. The recovering beam search allows the possibility of correcting wrong decisions by replacing partial solutions with others. It has polynomial time complexity function for the NP hard problem of this research. Further, they reported the computational results of this method.
Shchepin and Vakhania [17] presented a polynomialtime algorithm for non-preemptive scheduling of n-independent jobs on m unrelated parallel machines to minimize the makespan. The algorithm employs rounding approach. Monien and Woclaw [18] have presented an experimental study on the unspittable-Truemper algorithm to minimize the makespan of scheduling jobs on unrelated parallel machines. This computes 2-approximate solutions in the best worst-case running time known so far. The goal of their simulations was to prove its efficiency in practice. They compared their technique with algorithms and heuristics in practice, especially with those based on two-step approach.
Efraimidis and Spirakis [19] have given a new rounding approach that yields approximation schemes for multi-objective minimum makespan scheduling with a fixed number of linear cost constraints in unrelated parallel machines. The same approach can be used to maximize the minimum load on any machine and for assigning specific or equal loads to the machines. Gairing, Monien and Woclaw [20] presented a combinatorial approximation algorithm that matches an integral 2-approximation quality. It is generic minimum cost flow algorithm, without any complex enhancements, tailored to handle unsplittable flow. In their approach, they replaced the classical technique of solving LP-relaxation and rounding afterwards by a completely integral approach. Christodoulou, Koutsoupias and Vidali [21] gave an improved lower bound for the approximation ratio of truthful mechanisms for the unrelated parallel machines scheduling. The objective of the mechanism is to schedule tasks on the machines to minimize the makespan.
From these literatures, it is clear that the development of an efficient heuristic to minimize the makespan of scheduling n independent jobs on m unrelated parallel machines is a challenging task. Various authors have proposed different methodologies. Since, this problem comes under combinatorial category, development of an efficient heuristic for this problem is highly essential. Hence, in this paper, an attempt has been made to develop a simulated annealing algorithm and GRASP to minimize the makespan of scheduling jobs on unrelated parallel machines.
3. Mathematical Model to Minimize Makespan
In this section, a mathematical model is presented to minimize the makespan of the single machine scheduling problem with unrelated parallel machines.
Let, n be the number of independent jobs with single operation m be the number of unrelated parallel machines tij be the processing time of the job j on the machine i and it is arbitrary for different combinations of i and j.
Minimize Z = M M –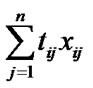 ≥ 0, i = 1, 2, 3,…, m
≥ 0, i = 1, 2, 3,…, m
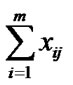 = 1, j = 1, 2, 3,…, n where, xij = 1, if the job j is assigned to the machine i = 0, otherwise, for i = 1, 2, 3, …., m and j = 1, 2, 3, …, n M ≥ 0 and it is the makespan of the schedule.
= 1, j = 1, 2, 3,…, n where, xij = 1, if the job j is assigned to the machine i = 0, otherwise, for i = 1, 2, 3, …., m and j = 1, 2, 3, …, n M ≥ 0 and it is the makespan of the schedule.
The number of variables in this model is mn + 1 and the total number of constraints is m + n.
4. Simulated Annealing Algorithm to Minimize Makespan
This section presents a simulated annealing algorithm to minimize the makespan in the single machine scheduling problem with unrelated parallel machines.
In a shop floor, to give shape and size for a component, either hammering or any other equivalent operation will be carried out, which will increase the internal energy of the component. This amounts to increasing the internal stress of the component. This will misalign the internal grains of the component, which will offer resistance to work further on it. Hence, the component is to be heat treated using a process called annealing. The component will be heated to a high temperature and the temperature will be kept constant at that value for sometime. Then, it will be reduced to a next lower temperature and it will be kept constant at that value for sometime. This process will continue until the temperature is reduced to the room temperature. This heat treatment process is called annealing, which will release the internal stress of the component, there by changing the misaligned grain structure to its original structure.
The above process of annealing is mapped to solve optimization problems, especially combinatorial problems and it is termed as “simulated annealing algorithm” [22]. The parameters of the simulated annealing algorithm are given as:
T―a temperature r―a range from 0 to 1 which is used to reduce the temperature
δ―a small positive number provided by the user (terminating criterion)
In simulated annealing algorithm, a feasible solution S1 in the neighbourhood of So is generated. Such generation of a feasible schedule is obtained using perturbation. The initial seed consists of groups of jobs and each group consists of the jobs which are scheduled on one of the m unrelated parallel machines.
In simulated annealing, there are three schemes of perturbation as listed below.
1) Exchanging jobs between two machines.
2) Shifting a job from one machine to another machine.
3) Transferring a job from one of the existing machines to a new machine (In this type of scheduling, it is an infeasible scheme).
Under the perturbation schemes, the third scheme is to form a new group of jobs by transferring a job from any one of the existing machines. Under such case, a new machine will have to be included to accommodate the job which is transferred from any of the existing machines. But, the given problem of scheduling has a fixed number of machines (m). This prevents the usage of the third scheme of perturbation. So, in this paper, only the first two schemes of perturbation are used.
Caution for Perturbation: While using the second scheme of perturbation, that is shifting a job from any one of the machines to another machine, care should be taken such that the number of jobs on the machine from which a job will be shifted is at least one.
4.1. Seed Generation Heuristic
The quality of the solution of the simulated annealing algorithm depends on the effectiveness of the seed generation algorithm. The steps of the seed generation algorithm used in this paper to obtain the initial solution, So are presented below.
Step 1: Input the data:
Number of independent jobs, n Number of unrelated parallel machines, m Processing time TIJ, I = 1 to m and J = 1 to n.
Step 2: Assign each of the jobs to the machine on which it takes the least processing time.
Step 3: Find the machine whose last job completion time is the maximum, CMAX.
Step 4: Shift the jobs on the machine with CMAX to some other machines which give maximum reduction in makespan.
Set STATUS_INDEX = 0 For each job K on the machine with CMAX, do the following:
1) a) Find the machine other than the machine with CMAX which requires least processing time for the current job (K).
b) Find the maximum of the completion times of the machines after the current job (K) temporarily scheduled on that machine. Let it be MAXMCT1.
2) a) Find the machine other than the machine with CMAX, on which the completion time of the last job is the minimum.
b) Find the maximum of the completion times of the machines after the current job (K) temporarily scheduled on that machine. Let it be MAXMCT2.
3) Find the minimum of MAXMCT1 and MAXMCT2 [MIN_MAXMCT).
4) If MIN_MAXMCT < CMAX, then
{Transfer the job K to the corresponding identified machine and update the results.
Set STATUS_INDEX = 1}
Step 5: If STATUS_INDEX = 1, then go to Step 4;
otherwise go to Step 6.
Step 6: Print the results: Machine Completion Time, Assignments of the jobs on machines and Minimized makespan.
4.2. Steps of Simulated Annealing Algorithm to Minimize Makespan
In this section, the steps of simulated annealing algorithm are presented. After an extensive experimentation, the parameters of the simulated annealing algorithm applied to the minimization of the makespan in the single machine scheduling problem with unrelated parallel machines are as follows.
T = 60, r = 0.85 and δ = 0.01 Step 1: Obtain an initial schedule using the seed generation algorithm given in Section 4.1. Let this initial schedule be initial feasible solution So and the makespan of the schedule of the initial feasible solution be f (So).
Step 2: Set the initial temperature, T = 60.
Step 3: Generation of feasible solution S1 in the neighbourhood of So and computation of corresponding makespan, f (S1).
Step 3.1: Generate a random number, R in between 0 to 0.99.
Step 3.2: If R ≤ 0.49 then go to Step 3.3; else go to Step 3.4.
Step 3.3: Exchanging jobs between two machines.
Step 3.3.1: Randomly select a machine (M1), which is assigned with at least one job for transferring a job from that machine.
Step 3.3.2: Randomly select a job from the machine M1 and let it be J1.
Step 3.3.3: Randomly select another machine (M2), which is assigned with at least one job for transferring a job from that machine.
Step 3.3.4: Randomly select a job from the machine M2 and let it be J2.
Step 3.3.5: Exchange the jobs J1 and J2 between the machines M1 and M2.
Step 3.3.6: Compute the makespan of this schedule, f(S1).
Go to Step 4.
Step 3.4: Transferring a job from one machine to another machine.
Step 3.4.1: Randomly select a machine (M1), which is assigned with at least one job for transferring a job from that machine.
Step 3.4.2: Randomly select a job from the machine M1 and let it be J1.
Step 3.4.3: Randomly select another machine (M2) to which the job J1 is to be transferred.
Step 3.4.4: Transfer the job J1 from the machine M1 to the machine M2.
Step 3.4.5: Compute the makespan of this schedule, f(S1).
Go to Step 4.
Step 4: Compute d = f(S0) – f(S1).
Step 5: Updating So.
Step 5.1: If d > 0, set So = S1 and go to Step 6; else go to Step 5.2.
Step 5.2: Generate uniformly distributed random number (R) in the range 0 to 1.
Step 5.3: If R < e(d/T), then set So = S1 and go to Step 6; else go to Step 6.
Step 6: Set T = r × T
Step 7: If T > δ, then go to Step 3; otherwise go to Step 8.
Step 8: Use the seed generation algorithm (local optimum procedure) to reach a local optimum starting from the last S0 value and print the final schedule along with the corresponding makespan.
Step 9: Stop.
5. Greedy Randomized Adaptive Search Procedure (GRASP) to Minimize Makespan
In this section, another heuristic based on Greedy Randomized Adaptive Search Procedure (GRASP) for the single machine scheduling problem with unrelated parallel machines is presented. The GRASP is an iterative procedure, which has two phases, namely construction phase and local search phase. In the construction phase, a feasible solution is constructed by choosing the next element randomly from the Candidate List (CL). The candidate list contains only the best elements selected by greedy function.
The Candidate List technique makes it possible to obtain different solution in each of the iterations. Since the solutions generated by the GRASP construction phase are not guaranteed to be the local optimum, it is recommended to apply the local search phase, which is the second phase of the GRASP. In this paper, a greedy heuristic is applied for the local search phase. At the end of each GRASP-iteration, the better solution is updated. The latest best solution becomes the final solution, when the given termination criterion is reached [23].
5.1. Steps of GRASP to Minimize Makespan
The steps of GRASP to minimize the makespan of the single machine scheduling problem with unrelated parallel machines are presented below.
Step 1: Input the data:
Number of independent jobs, n Number of unrelated parallel machines, m Processing time T(I, J), I = 1 to m and J = 1 to n.
Greedy parameter used in Step 9, γ (In this case, it is assumed as 10)
Step 2: Set the Candidate List, LC = Null Set.
Step 3: Use the following Greedy heuristic to find the feasible solutions and add it to the Candidate List (CL).
Step 3.1: Assign each of the jobs to the machine on which it takes the least processing time.
Step 3.2: Find the machine whose last job completion time is the maximum, CMAX. Update the Best Makespan, BMS = CMAX
Step 4: Select the lone member of the Candidate List (CL)Let it be M.
Step 5: Generation of Current Pool of Solution (CPS).
Step 5.1: I = 1 Step 5.2: Set the termination criterion index, k = 0.
Step 5.3: Randomly select any one of the following:
1) Exchange of jobs between machines
2) Transfer of jobs from one machine to another machine.
If the selected option is “Exchange of jobs between machines”, then go to Step 5.4; otherwise, go to Step 5.5.
Step 5.4: Exchanging jobs between two machines.
Step 5.4.1: Randomly select a machine (M1), which is assigned with at least one job for transferring a job from that machine.
Step 5.4.2: Randomly select a job from the machine M1 and let it be J1.
Step 5.4.3: Randomly select another machine (M2), which is assigned with at least one job for transferring a job from that machine.
Step 5.4.4: Randomly select a job from the machine M2 and let it be J2.
Step 5.4.5: Whether the exchange is feasible? If yes, go to Step 5.4.6; otherwise, go to Step 5.6.
Step 5.4.6: Exchange the jobs J1 and J2 between the machines M1 and M2.
Step 5.4.7: Compute the makespan of this schedule, f(S1) and add the solution to the Current Pool of Solution (CPS).
Update k = 1 and go to Step 5.6.
Step 5.5: Transferring a job from one machine to another machine.
Step 5.5.1: Randomly select a machine (M1), which is assigned with at least one job for transferring a job from that machine.
Step 5.5.2: Randomly select a job from the machine M1 and let it be J1.
Step 5.5.3: Randomly select another machine (M2) to which the job J1 is to be transferred.
Step 5.5.4: Whether the transfer is feasible? If yes, go to Step 5.5.5; otherwise, go to Step 5.6.
Step 5.5.5: Transfer the job J1 from the machine M1 to the machine M2.
Step 5.5.6: Compute the makespan of this schedule, f(S1) and add the solution to Current Pool of Solution (CPS).
Set k = 1 and go to Step 5.6.
Step 5.6: I = I + 1 Step 5.7: If I ≤ γ then go to Step 5.3, or else go to Step 6.
Step 6: If k = 0 then go to Step 10, or else go to Step 7.
Step 7: Find best solution from the Current Pool of Solution (CPS) and add it to the Candidate List (CL).
Step 8: Find the best solution from the Candidate List (CL) and let it be M.
Step 9: Go to Step 5.
Step 10: Print the lastly used best solution (M) in Step 5.
Step 11: Stop.
6. Comparison of Solutions of Simulated Annealing Algorithm and GRASP
In this section, the solutions obtained through the simulated annealing algorithm are compared with the solutions obtained through GRASP using a complete factorial experiment. In the factorial experiment, two factors are assumed, viz., “Method (M)” and “Problem Size (P)”. The number of levels for “Method” is 2, viz., “Simulated Annealing Algorithm” and “GRASP”. The number of levels for “Problem Size” is 90 which are 3 × 11, 3 × 12, 3 × 13,..., 3 × 25, 4 × 11, 4 × 12, 4 × 13,..., 4 × 25, 5 × 11, 5 × 12, 5 × 13,..., 5 × 25,…, 8 × 11, 8 × 12, 8 × 13,…, and 8 × 25. For each of 180 experimental combinations, the data for three replications have been randomly generated. The values of the makespan of these problems using the simulated annealing algorithm (SA algorithm) and GRASP are presented in Table 1.
The respective ANOVA model [24] is presented below.
yijk = μ + Mi + Pj + MPij + eijk
where, μ is the overall mean of the makespan yijk is the response in terms of the makespan for the kth replication under the ith level of the factor M and the jth level of the factor P.
Mi is the effect of the ith level of the factor M on the response yijk
Pj is the effect of the jth level of the factor P on the response yijk
MPij is the effect of the ith level of the factor M and the jth level of the factor P on the response yijk
eijk is the error in the kth replication under the ith level of the factor M and the jth level of the factor P.
The results of the corresponding ANOVA model are shown in Table 2.
The hypotheses of this ANOVA model are as listed below.
6.1. Factor “Method (M)”
H0: There is no significant difference between the methods (Simulated Annealing Algorithm and GRASP) in terms of makespan.
H1: There is significant difference between the methods (Simulated Annealing Algorithm and GRASP) in terms of makespan.
In the Table 2, the calculated F ratio of the factor
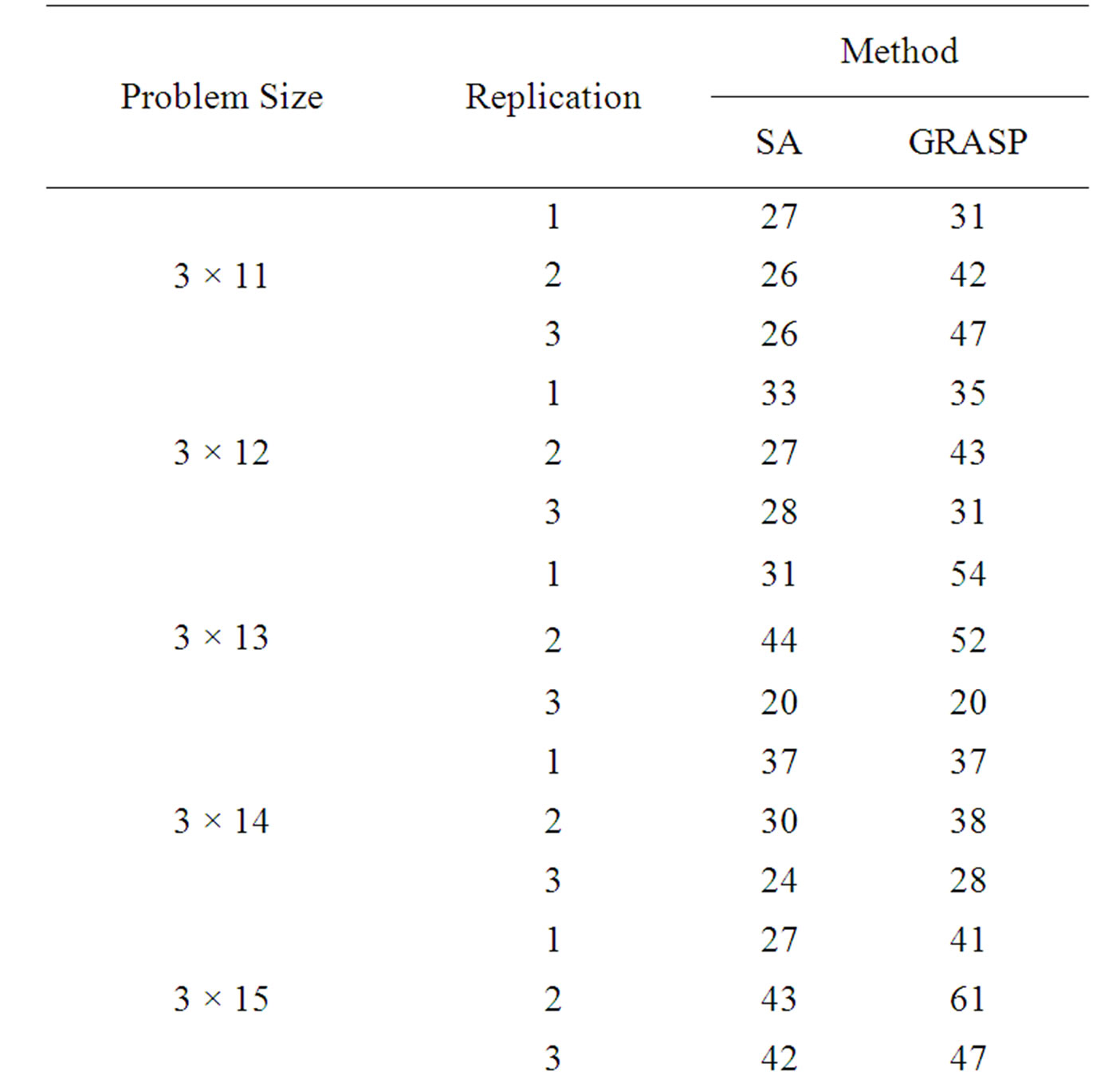
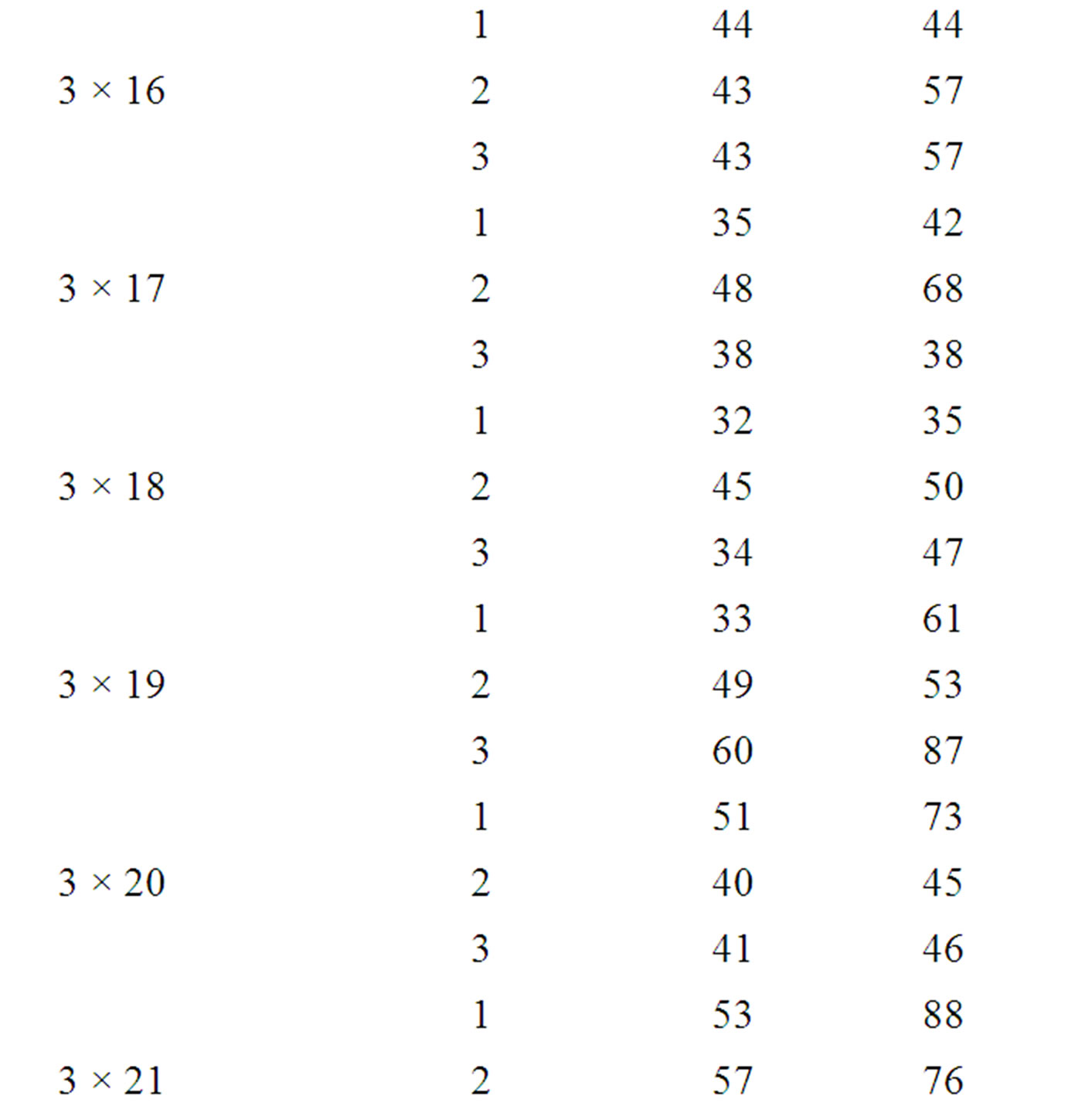
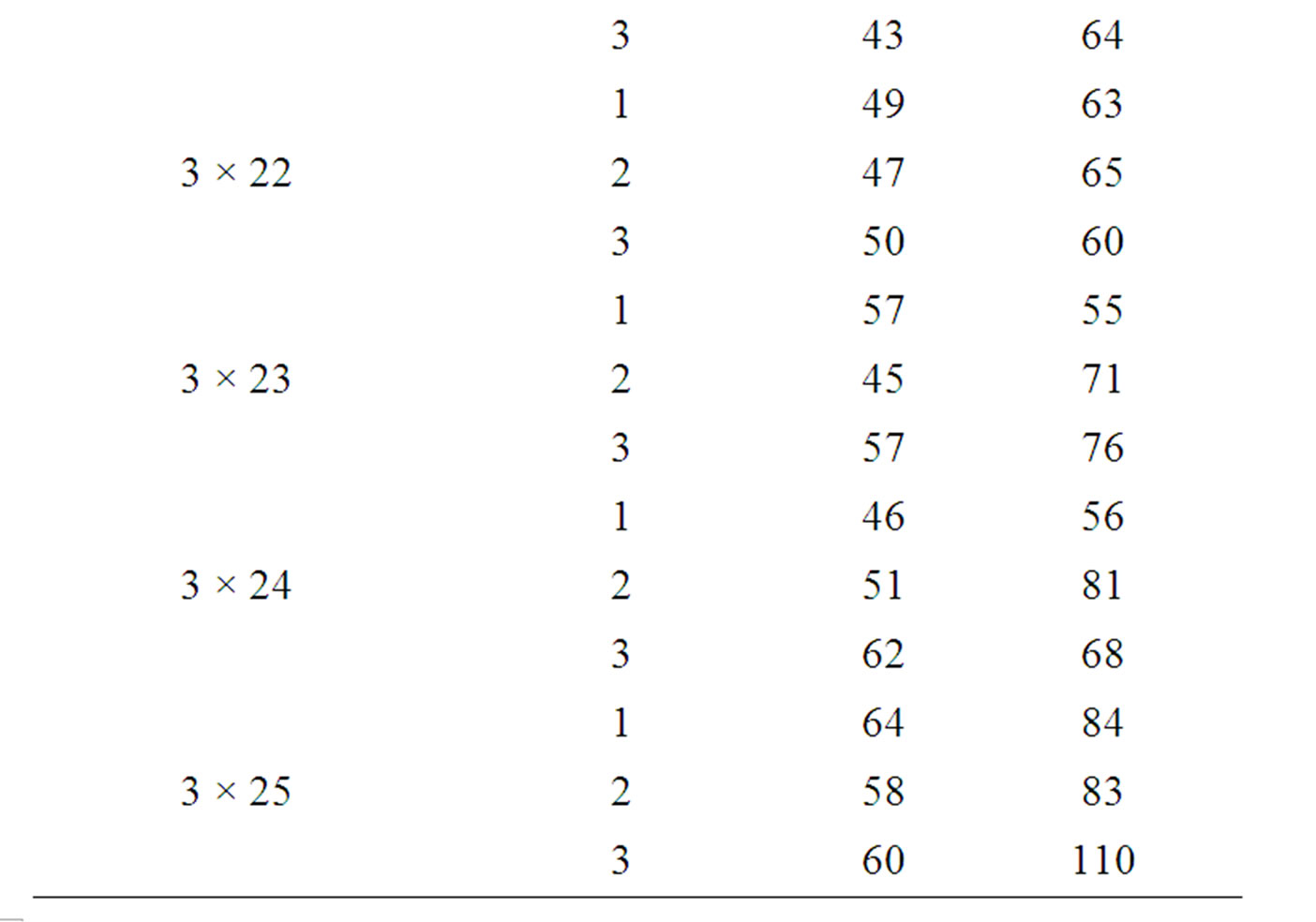

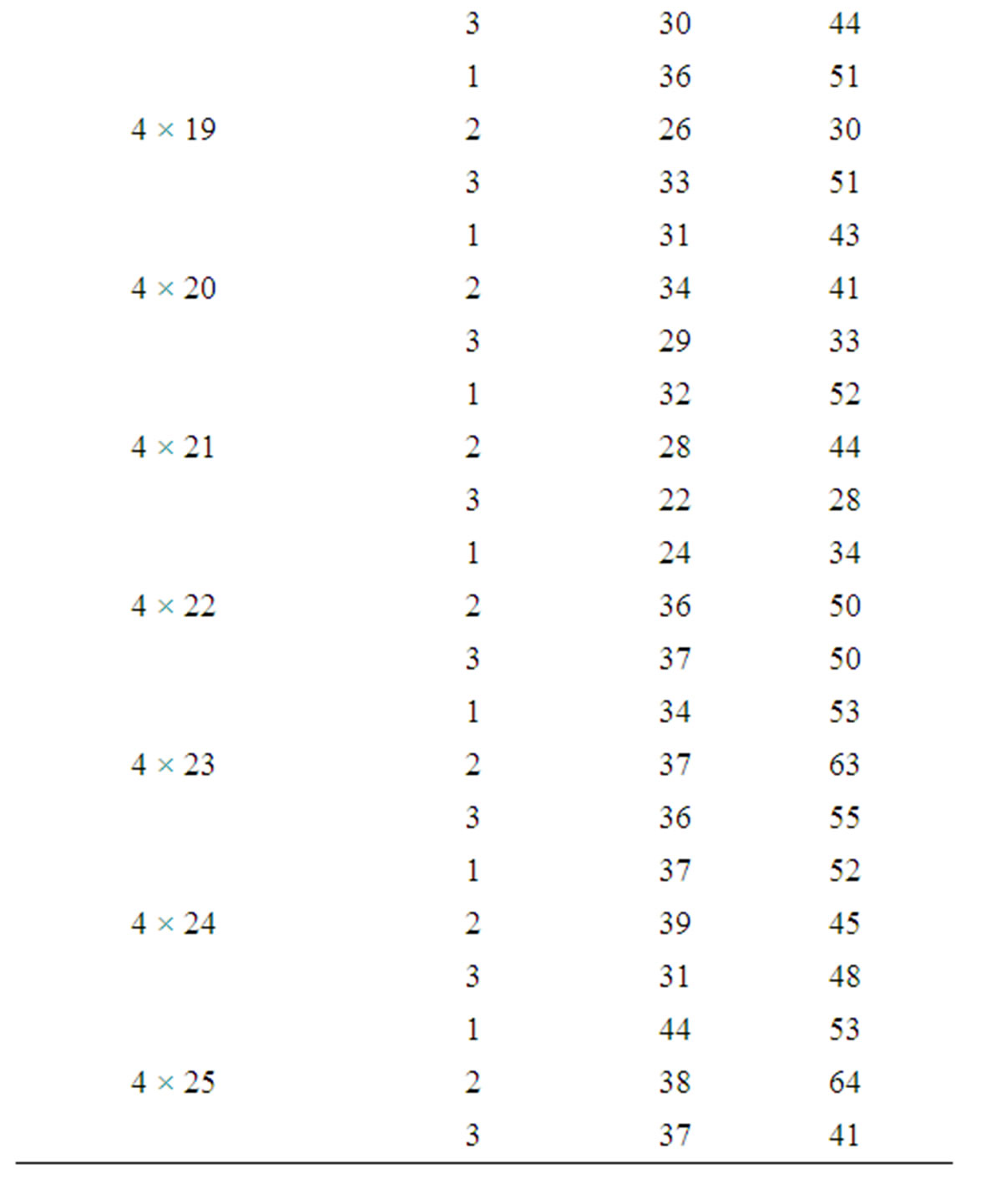

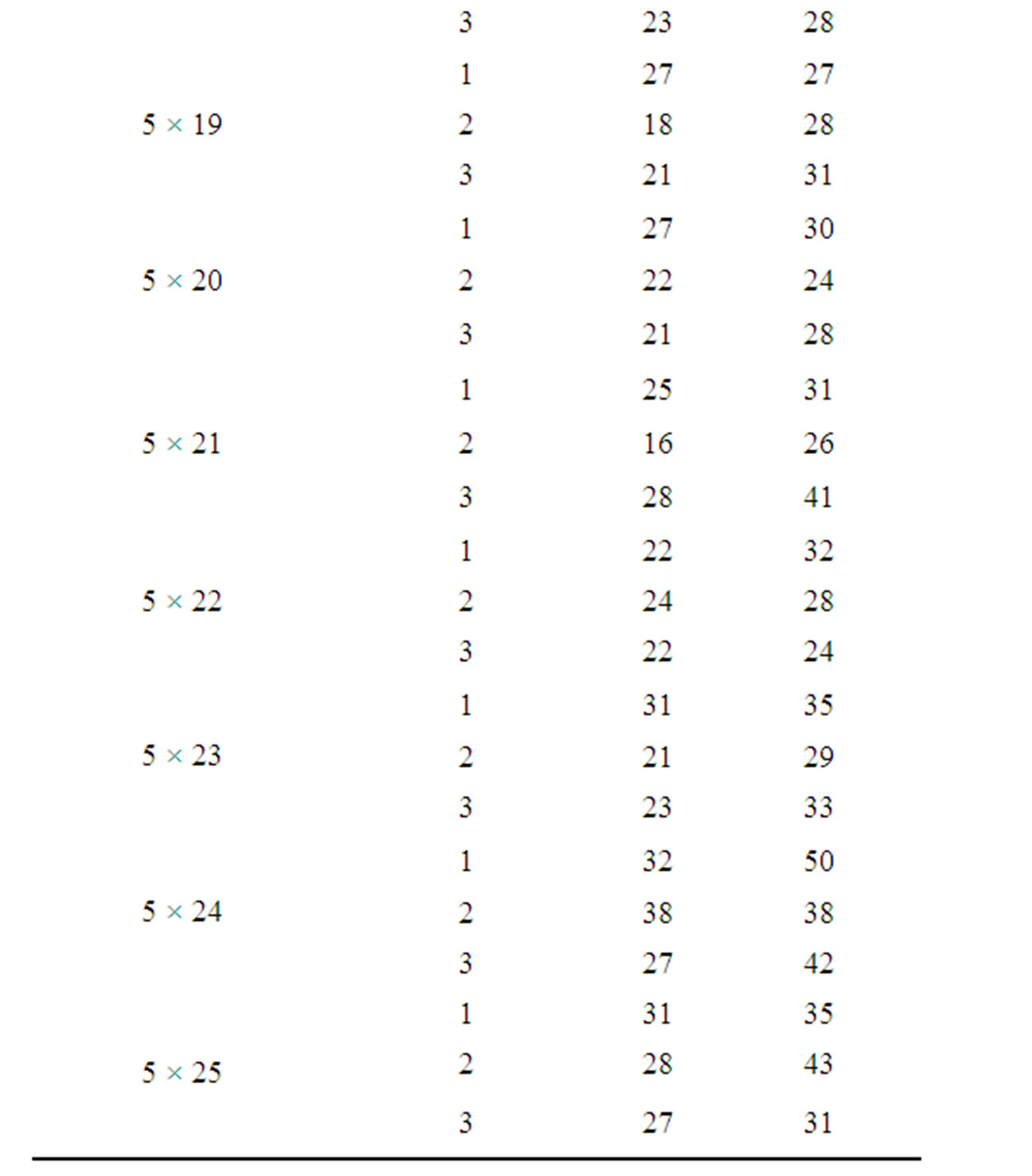


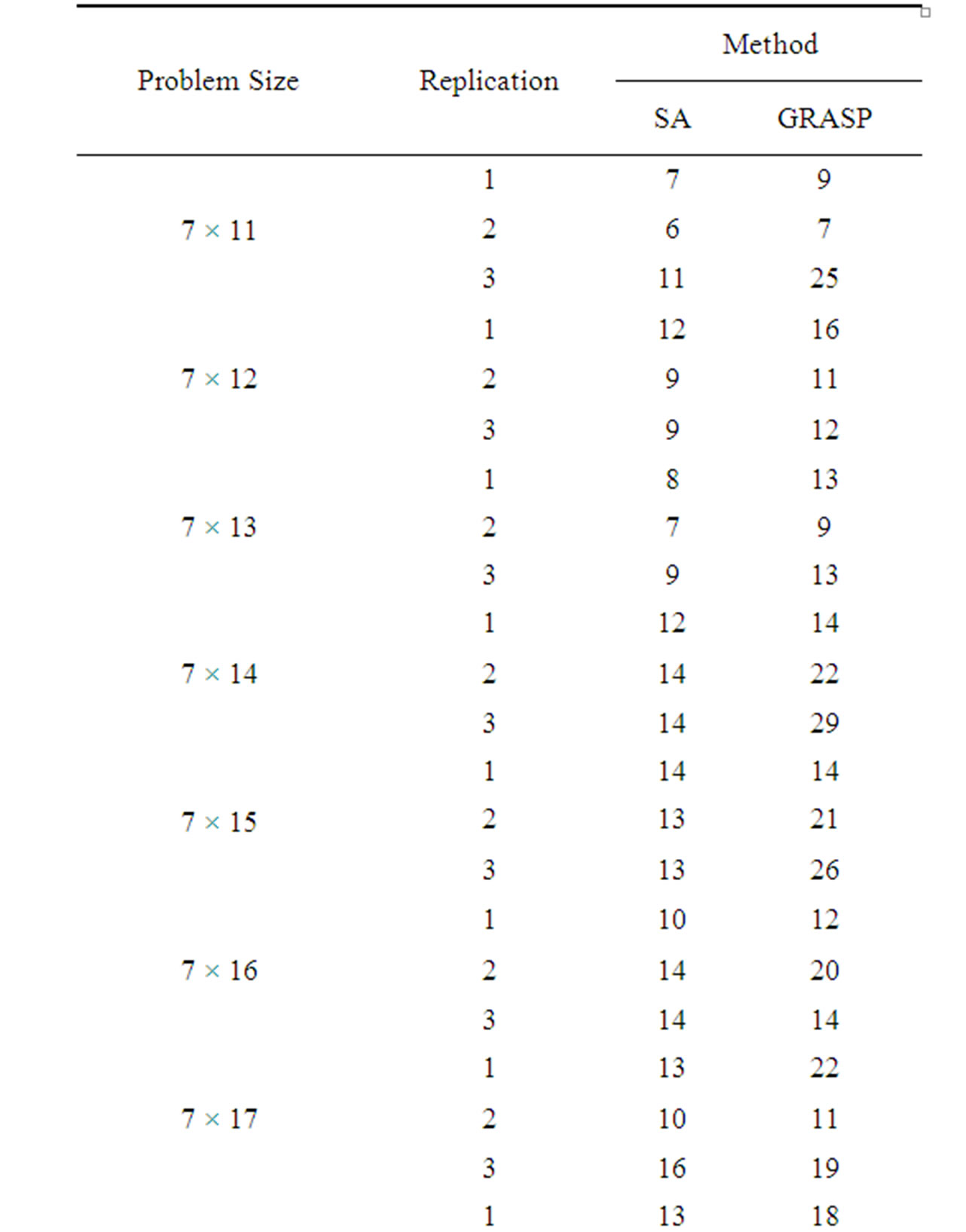



Table 1. Makespan results of SA algorithm and GRASP.
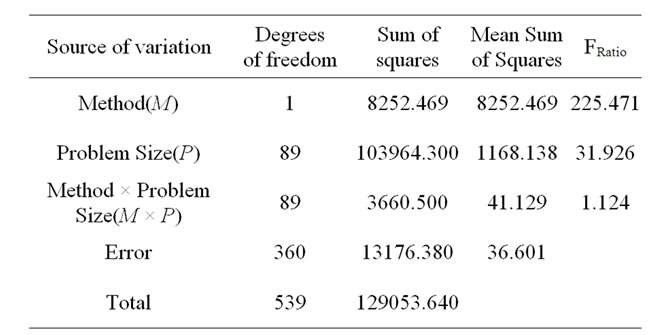
Table 2. ANOVA results for comparison of simulated annealing algorithm and GRASP.
“Method (M)” is 225.471, which is more than the corresponding table F value (3.84) for (1,360) degrees of freedom at a significance level of 0.05. Hence, the null hypothesis is to be rejected. This means that there is significant difference between the methods (Simulated Annealing Algorithm and GRASP) in terms of makespan.
The mean of the makespan values of all 270 problems is 22.30741 using the simulated annealing algorithm and that is 30.12593 using GRASP. By combining the above two facts, it is clear that the Simulated Annealing Algorithm performs better than the Greedy Randomized Adaptive Search Procedure (GRASP).
6.2. Factor “Problem Size” (P)
H0: There is no significant difference between the problems in terms of makespan [Problem size (P)].
H1: There is significant difference between the problems in terms of makespan [Problem size (P)].
In the Table 2, the calculated F ratio of the factor, “Problem Size (P)” is 31.916, which is more than the table F value (1.27) for (89,360) degrees of freedom at a significance level of 0.05. Hence, the corresponding null hypothesis is to be rejected. This means that there is significant difference between the problems in terms of makespan.
6.3. Interaction “Method × Problem Size” (M × P)
H0: There is no significant difference between the interaction terms in terms of makespan.
H1: There is significant difference between at least one pair of the interaction terms in terms of makespan.
In the Table 2, the calculated F ratio of the interaction “Method × Problem Size” is 1.124, which is less than the table F value (1.27) for (89,360) degrees of freedom at a significance level of 0.05. Hence, the corresponding null hypothesis is to be accepted. This means that there is no significant difference between the interaction terms in terms of makespan.
7. Conclusions
Production scheduling paves ways for effective calendar of production for day to day requirements in industries. The single machine scheduling problem with unrelated parallel machines which is considered in this paper is a challenging problem because it is a combinatorial problem. The design of two different meta-heuristics, viz., simulated annealing algorithm and greedy randomized adaptive search procedure (GRASP) are presented. Then, their performances are compared through a complete factorial experiment with 270 randomly generated problems with different sizes (small to big sizes: 3 × 11, 3 × 12,…, 3 × 25, 4 × 11, 4 × 12,…, 4 × 25,..., 8 × 11, 8 × 12,..., 8 × 25, each size with three replications). Based on the ANOVA results, it is found that there is significant difference between the simulated annealing algorithm and GRASP, in terms of their performance. The mean of the makespan values of all 270 problems is 22.30741 using the simulated annealing algorithm and that is 30.12593 using GRASP. By combining the above two facts, it is clear that the simulated annealing performs better than the Greedy Randomized Adaptive Search Procedure (GRASP).
8. References
[1] R. Panneerselvam, “Production and Operations Management,” 2nd Edition, PHI Learning Private Limited, New Delhi, 2005.
[2] R. Panneerselvam, “Design and Analysis of Algorithms,” PHI Learning Private Limited, New Delhi, 2007.
[3] E. L. Lawler and J. Labetoulle, “On Preemptive Scheduling on Unrelated Parallel Processors by Linear Programming,” Journal of the ACM, Vol. 25, No. 4, 1978, pp. 612-619.
[4] C. N. Potts, “Analysis of a Linear Programming Heuristic for Scheduling Unrelated Parallel Machines,” Discrete Applied Mathematics, Vol. 10, No. 2, 1985, pp. 155-164.
[5] S. L. Van De Velde, “Duality-Based Algorithms for Scheduling Unrelated Parallel Machines,” ORSA Journal of Computing, Vol. 5, No. 2, 1993, pp. 182-205.
[6] C. A. Glass, C. N. Potts and P. Shade, “Unrelated Parallel Machine Scheduling Using Local Search,” Mathematical and Computer Modelling, Vol. 20, No. 2, 1994, pp. 41-52.
[7] A. M. A. Hariri and C. N. Potts, “Heuristics for Scheduling Unrelated Parallel Machines,” Computers and Operations Research, Vol. 18, No. 3, 1991, pp. 323-331.
[8] N. Piersman and W. Van Dijk, “A Local Search Heuristic for Unrelated Parallel Machine Scheduling with Efficient Neighbourhood Search,” Mathematical and Computer Modelling, Vol. 24, No. 9, 1996, pp. 11-19.
[9] S. Martello, F. Soumis and P. Toth, “Exact and Approximation Algorithms for Makepsan Minimization on Unrelated Parallel Machines,” Discrete Applied Mathematics, Vol. 75, No. 2, 1997, pp. 169-188.
[10] J. Klaus and P. Lorant, “Improved Approximation Schemes for Scheduling Unrelated Parallel Machines,” Mathematics of Operations Research, Vol. 26, No. 2, 2001, pp. 324-338.
[11] F. Sourd, “Scheduling Tasks on Unrelated Machines: Large Neighbourhood Improvement Procedures,” Journal of Heuristics, Vol. 7, No. 6, 2001, pp. 519-531.
[12] M. Serna and F. Xhafa, “Approximating Scheduling Unrelated Parallel Machines in Parallel,” Computational Optimization and Applications, Vol. 21, No. 3, 2002, pp. 325-338.
[13] E. Mokotoff and P. Chretienne, “A Cutting Plane Algorithm for the Unrelated Parallel Machine Scheduling Problem,” European Journal of Operational Research, Vol. 141, No. 3, 2002, pp. 515-525.
[14] E. Mokotoff and J. L. Jimeno, “Heuristics Based on Partial Enumeration for the Unrelated Parallel Processor Scheduling Problem,” Annals of Operations Research, Vol. 117, No. 1-4, 2002, pp. 133-150.
[15] M. Pfund, J. W. Fowlwr and J. N. D. Gupta, “A Survey of Algorithms for Single Machine and Multi-Objective Unrelated Parallel-Machine Deterministic Scheduling Problems,” Journal of the Chinese Institute of Industrial Engineers, Vol. 21, No. 3, 2004, pp. 230-241.
[16] M. Ghirardi and C. N. Potts, “Makespan Minimization for Scheduling Unrelated Parallel Machines: A Recovering Beam Search Approach,” European Journal of Operational Research, Vol. 165, No. 2, 2005, pp. 457-467.
[17] E. V. Shchepin and N. Vakhania, “An Optimal Rounding Gives a Better Approximation for Scheduling Unrelated Machines,” Operations Research Letters, Vol. 33, No. 2, 2005, pp. 127-133.
[18] B. Monien and A. Woclaw, “Scheduling Unrelated Parallel Machines Computational Results,” Proceedings of the 5th International Workshop on Experimental Algorithms, Menorca, Spain, 2006, pp. 195-206.
[19] P. S. Efraimidis and P. G. Spirakis, “Approximation Schemes for Scheduling and Covering on Unrelated Machines,” Theoretical Computer Science, Vol. 359, No. 1, 2006, pp. 400-417.
[20] M. Gairing, B. Monien and A. Woclaw, “A Faster Combinatorial Approximation Algorithm for Scheduling Unrelated Machines,” Theoretical Computer Science, Vol. 380, No. 1-2, 2007, pp. 87-99.
[21] G. Christodoulou, E. Koutsoupias and A. Vidali, “A Lower Bound for Scheduling Mechanisms,” Algorithmica, Vol. 55, No. 4, 2009, pp. 729-740.
[22] S. Kirkpatrick, Jr. C. D. Gelatt and M. P. Vecchi, “Optimization by Simulated Annealing,” Science, Vol. 220, No. 4598, 1983, pp. 671-680.
[23] T. A. Feo and M. G. C. Resende, “Greedy Randomized Adaptive Search Procedures,” Journal of Global Optimization, Vol. 6, No. 2, 1995, pp. 109-133.
[24] R. Panneerselvam, “Research Methodology,” PHI Learning Private Limited, New Delhi, 2004.

