Intelligent Information Management
Vol.2 No.6(2010), Article ID:2018,10 pages DOI:10.4236/iim.2010.26044
Steady-State Queue Length Analysis of a Batch Arrival Queue under N-Policy with Single Vacation and Setup Times
1School of Management and Economics, University of Electronic Science and Technology of China, Chengdu, China 2School of Management, Chongqing Jiaotong University, Chongqing, China
E-mail: liumingwu2007@yahoo.cn
Received March 10, 2010; revised April 20, 2010; accepted May 23, 2010
Keywords: Queue length, recursion expressions, N policy, setup
Abstract
This paper investigates the steady state property of queue length for a batch arrival queue under N-policy with single vacation and setup times. When the system becomes empty, the server is turned off at once and takes a single vacation of random length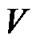 . When he returns, if the queue length reaches or exceeds threshold
. When he returns, if the queue length reaches or exceeds threshold , the server is immediately turned on but is temporarily unavailable due to a random setup time
, the server is immediately turned on but is temporarily unavailable due to a random setup time 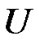 before offering service. If not, the server stays in the system until the queue length at least being
before offering service. If not, the server stays in the system until the queue length at least being . We derive the system size distribution and confirm the stochastic decomposition property. We also derive the recursion expressions of queue length distribution and other performance measures. Finally, we present some numerical examples to show the analytical results obtained. Sensitivity analysis is also performed.
. We derive the system size distribution and confirm the stochastic decomposition property. We also derive the recursion expressions of queue length distribution and other performance measures. Finally, we present some numerical examples to show the analytical results obtained. Sensitivity analysis is also performed.
1. Introduction
This paper pays attention to a batch arrival queueing system under N-policy with a single vacation and setup times, which can model queue-like manufacturing/production/inventory system. Consider a system of processing in which the operation does not start until some predetermined number (N) of semi-finished products waiting for processing. To be more realistic, the machine need a setup time for some preparatory work before starting processing. When all the semi-finished products in the system are processed, the machine is shut down and leaves for a vacation. The operator performs machine repair, preventive maintenance and some other jobs during the vacation. After these extra operations, the operator returns and checks the number of semi-finished products in the queue determining whether or not start the machine.
Queueing system with vacations has been attracted considerable attention to many authors. It has effectively been applied in computers and communication systems, production/inventory system. Doshi [1] and Takagi [2] presented an excellent survey of queueing system with server vacations. One of the important achievements for vacation queueing system is the famous stochastic decomposition results, which was first established by Fuhrmann and Cooper [3].
The N-policy was first introduced by Yadin and Naor [4], which is a control policy turning the server on whenever N (a predetermined value) or more customers in the system, turning off the server when system is empty. Lee et al. [5] successfully combined the batch arrival queue with N-policy and obtained the analytical solutions. Later, Lee et al. [6,7] analyzed in detail a batch arrival Mx/G/1 queue under N-policy with a single vacation and repeated vacation respectively. They derived the system size distribution which confirmed the famous stochastic decomposition property, and the optimal stationary operating policy was also investigated. At the present day, batch arrival queueing system under N-policy with different vacation policies have been received considerable attention because of its practical implication in production/inventory system. A number of searchers, such as Choudhury et al. [8-10], Ke [11,12], and Reddy et al. [13], and many authors not be listed above have considered batch arrival queueing system under N-policy with various vacation policies.
It is to be noted that few authors involved above considered the probability distribution of the number of customers in the system for batch arrival queue under N-policy with different vacations policies. Recently, Wang et al. [14] analyzed the behaviors of queue length distributions of a batch arrival queue with server vacations and breakdowns based on a maximum entropy approach [15,16]. Ke et al. [17] also used the maximum entropy solutions for batch arrival queue with an un-reliable server and delaying vacations. They all derived the approximate formula for the probability distribution of the number of customers in the system. Tang and his co-author [18,19] paid attention to the queue length distribution for queueing system, because it is an important performance measure for the system design and optimization. For example, the queue-length distribution has been applied for the communication system buffer design [20].
To the best of our knowledge, fewer researchers have derived the queue length distribution under N-policy batch arrival queueing system. Although, the batch arrival under N-policy have been studied extensively, but the exact analytical solutions for queue length distribution do not be obtained. This motives us to develop an approach for the queue length distribution of the N-policy batch arrival queueing system. In this paper, we study the steady state queue length for an Mx/G/1 under N policy with single vacation and setup times. First, we derive the system size distribution by the supplementary variables method. Second, using the Leibniz formula of derivation combing some knowing results, we obtain the additional queue length distribution and the recursion expressions of the queue length distribution. Finally, we present several examples for application of these recursion expressions. Also, the effect of different system parameters on the queue length distribution is investigated.
2. The Mathematical Model and Notations
This paper considers an Mx/G/1 queueing system where the arrival occurs according to a compound Poisson process with random batch size . Arriving customers in the queue form a single waiting line and the service discipline is assumed to be FCFS. The service time is an independent and identically distributed random variable with a general distribution function
. Arriving customers in the queue form a single waiting line and the service discipline is assumed to be FCFS. The service time is an independent and identically distributed random variable with a general distribution function , and with finite mean service time. The server can only process one customer at a time. The server is turned off each time if there is no customer in the queue and leaves for a vacation of random length
, and with finite mean service time. The server can only process one customer at a time. The server is turned off each time if there is no customer in the queue and leaves for a vacation of random length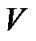 . When he returns from the vacation and finds the queue length is no less than
. When he returns from the vacation and finds the queue length is no less than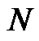 , the server starts to setup with random length
, the server starts to setup with random length . Otherwise, he stays in the system and does not start setup until the customers reaches and exceeds N. When the setup is completed, the server begins to serve the customers until there is no customer in the system.
. Otherwise, he stays in the system and does not start setup until the customers reaches and exceeds N. When the setup is completed, the server begins to serve the customers until there is no customer in the system.
Throughout the analysis, the following notations and the variables will be adopted.
![]() threshold (
threshold ( )
)
 mean arrival rate
mean arrival rate
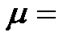 mean service rate
mean service rate
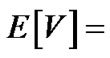 mean vacation time
mean vacation time
 mean setup time
mean setup time
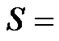 service time random variable
service time random variable
 vacation times random variable
vacation times random variable
![]() setup times random variable
setup times random variable
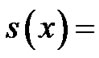 the probability density function
the probability density function ![]()
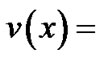 the probability density function
the probability density function 
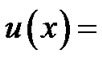 the probability density function
the probability density function 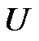
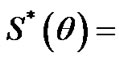 the laplace-Stieltjies transform (LST) of
the laplace-Stieltjies transform (LST) of ![]()
 the LST of
the LST of 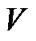
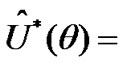 the LST of U
the LST of U
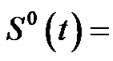 remaining service time of the customer in service at time
remaining service time of the customer in service at time 
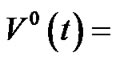 remaining vacation time of the customer in vacation at time
remaining vacation time of the customer in vacation at time 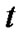
 remaining setup time of the customer in setup at time
remaining setup time of the customer in setup at time 
 , the number of customers in the queue at time
, the number of customers in the queue at time 
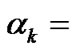 probability that
probability that 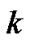 customers arrival during a vacation
customers arrival during a vacation
 , where
, where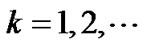
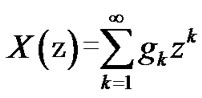 , the p.g.f. of each batch size
, the p.g.f. of each batch size

 if the server is on vacation
if the server is on vacation
 if the server is in dormancy
if the server is in dormancy
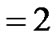 if the server is in setup
if the server is in setup
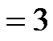 if the server is busy
if the server is busy
 traffic intensity,
traffic intensity,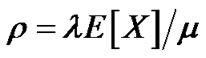 . In the steady state
. In the steady state 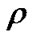 should be assumed to be less than unity
should be assumed to be less than unity
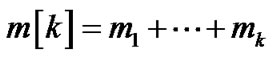 , the number of customers presents the sum of
, the number of customers presents the sum of  batches of customers
batches of customers
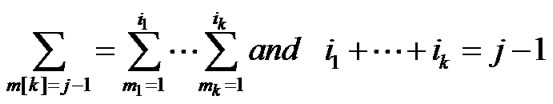 , the sum of
, the sum of 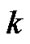 batches of customer equals to
batches of customer equals to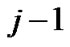 .
.
3. Preliminary Formula for Mx/G/1 Queueing System
Before discussing our model, let us recall some results in the ordinary Mx/G/1 queueing system. Let 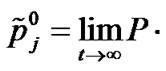
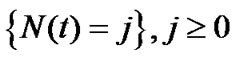 be the steady state queue length distribution for the Mx/G/1 queueing system. From Tang et al. [19], the recursion expressions of queue-length distribution are as follows:
be the steady state queue length distribution for the Mx/G/1 queueing system. From Tang et al. [19], the recursion expressions of queue-length distribution are as follows:
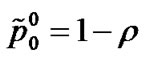 (1)
(1)
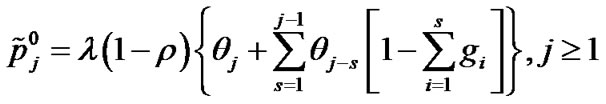 (2)
(2)
where
 ;
; ;
;
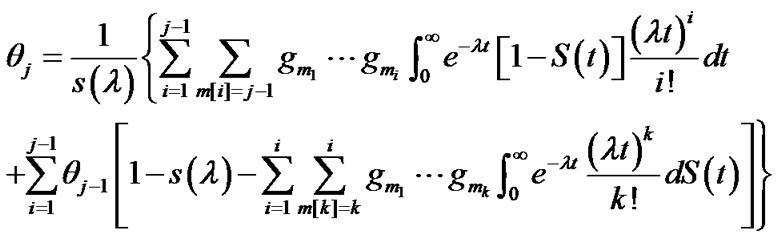
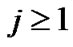 .
.
Let 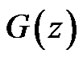 be the p.g.f. of the number of customers in the queue at stationary. We have
be the p.g.f. of the number of customers in the queue at stationary. We have
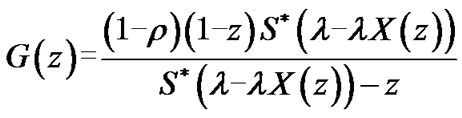 (3)
(3)
4. The System Size Distribution
This section, we set up the system equation for the system size distribution at stationary and derive the p.g.f. of the system size distribution. We introduce the supplementary variables ,
,  and
and for obtaining a Markov process
for obtaining a Markov process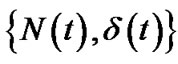 , where
, where 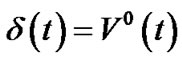 if
if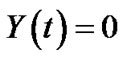 ,
,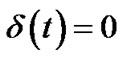 , if
, if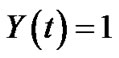 ,
, , if
, if  and
and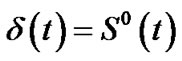 , if
, if . Denote
. Denote

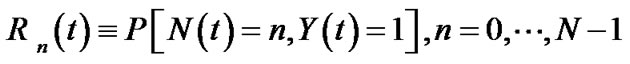

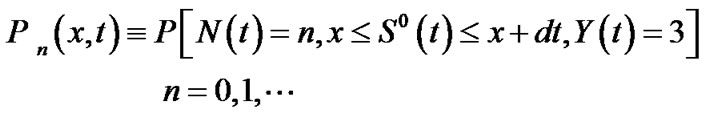
Following the argument of Lee et al. [5-7], we can easily set up the following steady state system equations the supplementary variables technique.
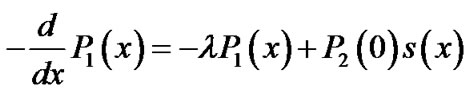 (4)
(4)
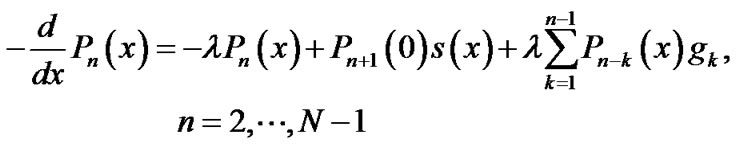 (5)
(5)
 (6)
(6)
 (7)
(7)
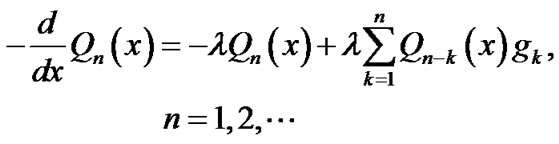 (8)
(8)
 (9)
(9)
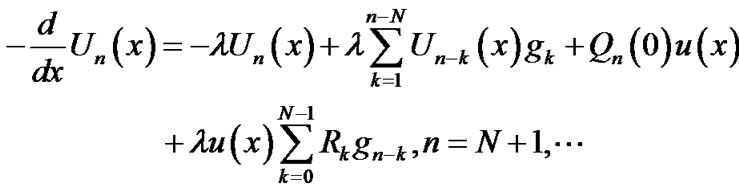 (10)
(10)
 (11)
(11)
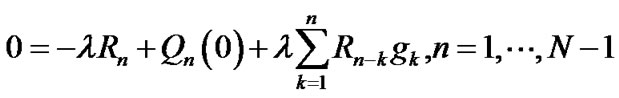 (12)
(12)
Taking the LST of both sides of Equations (4)-(10), we get
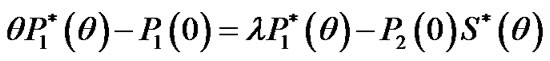 (13)
(13)
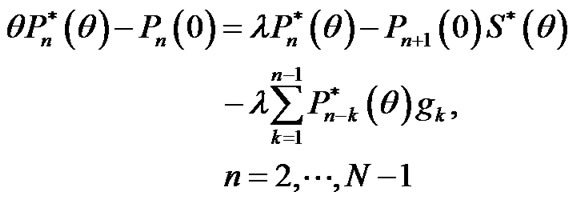 (14)
(14)
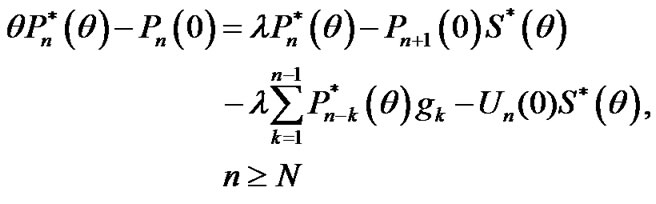 (15)
(15)
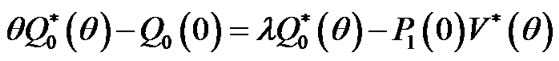 (16)
(16)
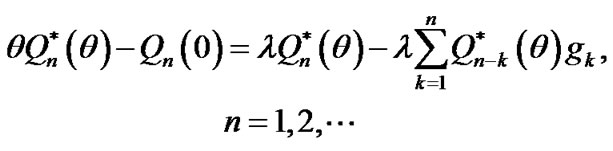 (17)
(17)
 (18)
(18)
 (19)
(19)
Noted that the LST of ,
, 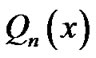 and
and  is defined as follows:
is defined as follows:
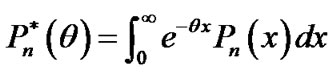 ,
, 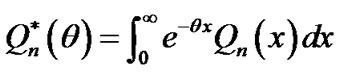 ,
, .
.
Now, we define the following p.d.f.
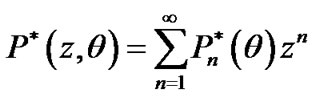 ,
, 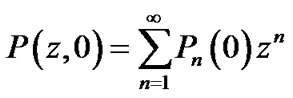
 ,
, 
 ,
, 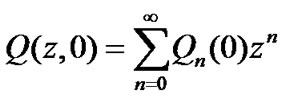
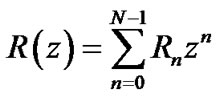 .
.
From equations (13)-(15), we have
 (20)
(20)
Letting , we get
, we get
 (21)
(21)
Substituting (21) into equation (20), we have
 (22)
(22)
Similarly, from (16), (17) and (18), (19) respectively and combining (11) and (12), we have
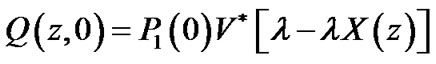 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
Let  be the p.g.f. of the queue size at an arbitrary time epoch. Then,
be the p.g.f. of the queue size at an arbitrary time epoch. Then,
 (27)
(27)
Using Equations (21)-(26) in , we have
, we have
 (28)
(28)
Following Lee et al. [7], we have
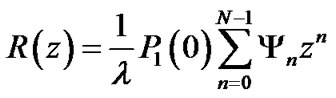 (29)
(29)
where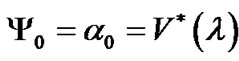 ,
, 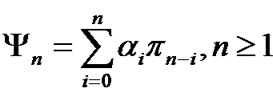 ,
, 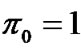 , and
, and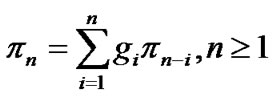 .
.  is the probability that system state visit
is the probability that system state visit ![]() during an idle period in the Mx/G/1/ N-policy queue [5].
during an idle period in the Mx/G/1/ N-policy queue [5].
Taking (29) into (28), we have
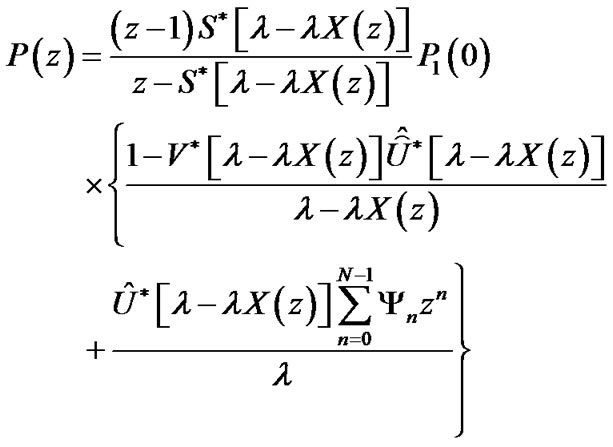 (30)
(30)
From equation (30) and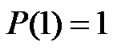 , we get
, we get
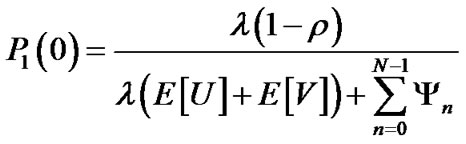 (31)
(31)
Thus, the p.d.f. of the system size distribution in the steady state becomes
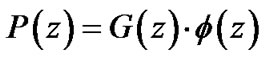 (32)
(32)
where

Remark 4.1
Note that for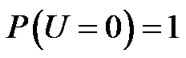 ,
, 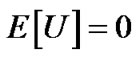 and
and 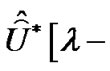
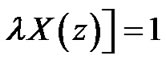 , then the equation (32) agrees with Equation (25) of Lee et al. [7].
, then the equation (32) agrees with Equation (25) of Lee et al. [7].
Remark 4.2
Let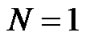 , our model can be reduced to the batch arrival queue under a single vacation policy with startup. In this case the result (32) coincides with Equation (30) of Ke [21], in which the closedown time is assumed to be zero.
, our model can be reduced to the batch arrival queue under a single vacation policy with startup. In this case the result (32) coincides with Equation (30) of Ke [21], in which the closedown time is assumed to be zero.
5. The Queue Length Distribution
5.1. The Additional Queue Length Distribution
This section, we will derive the additional queue length distribution. From (32), we see that the stationary queue length distribution of the Mx/G/1queue under N policy with a single vacation and setup times decomposes into two independent random variables: one is the stationary queue length distribution of the ordinary Mx/G/1 queue; another is the additional queue length ( ) distribution due to N policy with a single vacation and setup times.
) distribution due to N policy with a single vacation and setup times.
From the definition of p.d.f., the additional queue length distribution 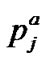 is given by
is given by
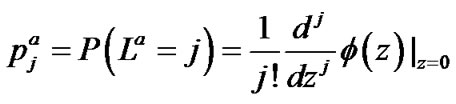 (33)
(33)
Obviously, the probability of additional queue length being zero is as follows
 (34)
(34)
When , we can get the probability distribution of the additional queue length
, we can get the probability distribution of the additional queue length 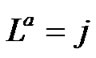 by direct derivative of
by direct derivative of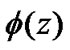 .
.
 (35)
(35)
Following Leibniz formula, we have
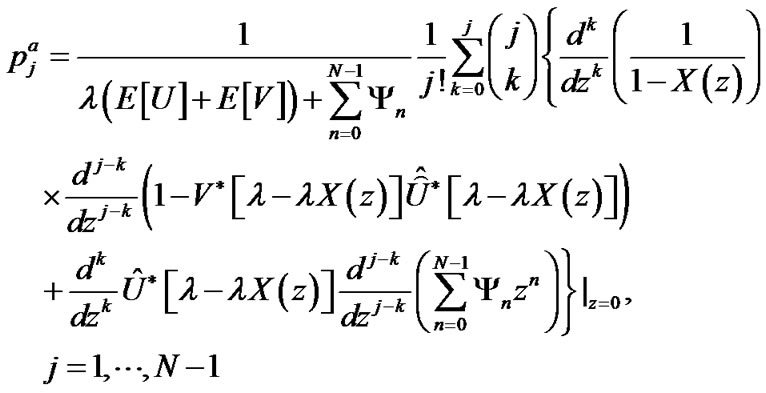 (36)
(36)
First, let us define the following functions 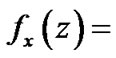
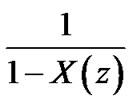 ,
, 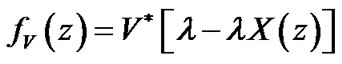 and
and 
 . For sake of convenience, we note
. For sake of convenience, we note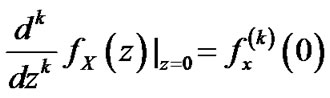 . It is to be noted that the following recursion expressions hold.
. It is to be noted that the following recursion expressions hold.
 (37)
(37)
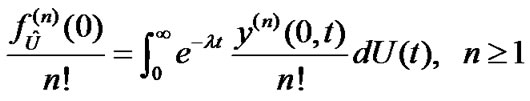 (38)
(38)
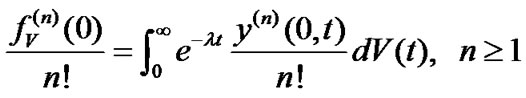 (39)
(39)
where
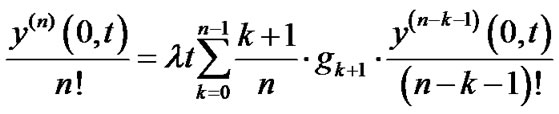 ,
,
 .
.
Substitute (37)-(39) into (36), after some manipulations, we have
 (40)
(40)
When , in the similar manner proceeding with (36), we get the following additional queue length distribution.
, in the similar manner proceeding with (36), we get the following additional queue length distribution.
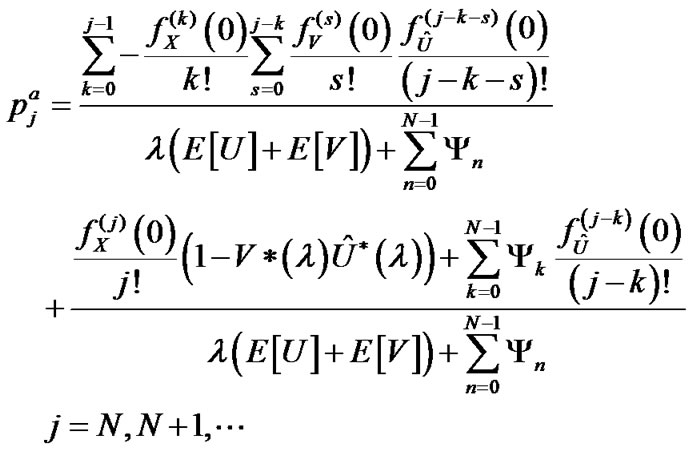 (41)
(41)
With a direct method, we have derived the additional queue length distribution presented by (34), (40) and (41). Also, following the stochastic decomposition (32), the analytical queue length distribution can be derived.
5.2. The Queue Length Distribution in Equilibrium
Let 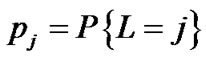 be the steady state probability distribution of queue length (
be the steady state probability distribution of queue length (![]() ) for the Mx/G/1 queueing system under N-policy with a single vacation and setup times. From (32), (1) and (34), we have
) for the Mx/G/1 queueing system under N-policy with a single vacation and setup times. From (32), (1) and (34), we have
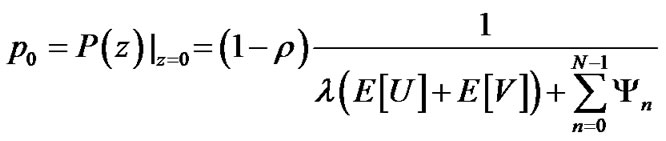 (42)
(42)
When , the probability of queue length
, the probability of queue length 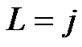 is given by
is given by
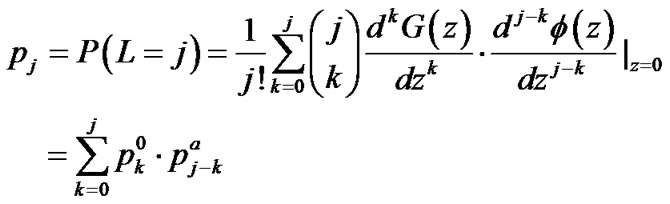 (43)
(43)
where 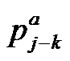 is given by (40).
is given by (40).
When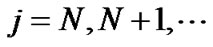 , we first analyze the following two cases:
, we first analyze the following two cases:
1) If , that is
, that is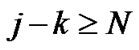 ,
, 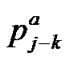 is given by (41).
is given by (41).
2) If , that is
, that is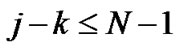 ,
, 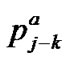 is given by (40).
is given by (40).
So, the probability of queue length 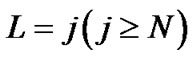 is given by
is given by
 (44)
(44)
The recursion expressions (42), (43) and (44) present the steady state queue length distribution for the Mx/G/1 queueing system under N-policy with a single vacation and setup times. We can see that linking 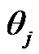 with (37)- (39) the queue length distribution could be calculated by these recursion expressions.
with (37)- (39) the queue length distribution could be calculated by these recursion expressions.
6. Numerical Experiments
This section we try to illustrate the application of these recursion expressions by taking several numerical examples. Here we assume that the batch size distribution is displaced geometric distribution i.e.
 . From (37), we have
. From (37), we have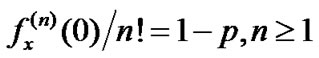 , which can be derived by the mathematical induction. The service time distributions are assumed to follow the exponential distribution with mean
, which can be derived by the mathematical induction. The service time distributions are assumed to follow the exponential distribution with mean . Furthermore, we take the vacation time distributions and setup time distributions are 3-stage Erlang distribution with finite mean
. Furthermore, we take the vacation time distributions and setup time distributions are 3-stage Erlang distribution with finite mean  and 4-stage Erlang distribution
and 4-stage Erlang distribution 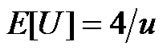 respectively. For the sake of convenience, we take
respectively. For the sake of convenience, we take 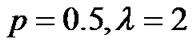 and
and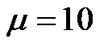 . We will investigate the effects of
. We will investigate the effects of ![]() and
and ![]() on the queue length distribution with constant other system parameters.
on the queue length distribution with constant other system parameters.
We present the results of the queue length distribution in Tables 1-3 with different 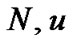 and
and![]() . Observing the table 1, it is clear that: 1) the probability of the system being empty (P0) decreases as
. Observing the table 1, it is clear that: 1) the probability of the system being empty (P0) decreases as  increases; 2) when
increases; 2) when 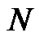 is constant, the probability increases from P1 to P3 and then decreases and converges to zero.
is constant, the probability increases from P1 to P3 and then decreases and converges to zero.

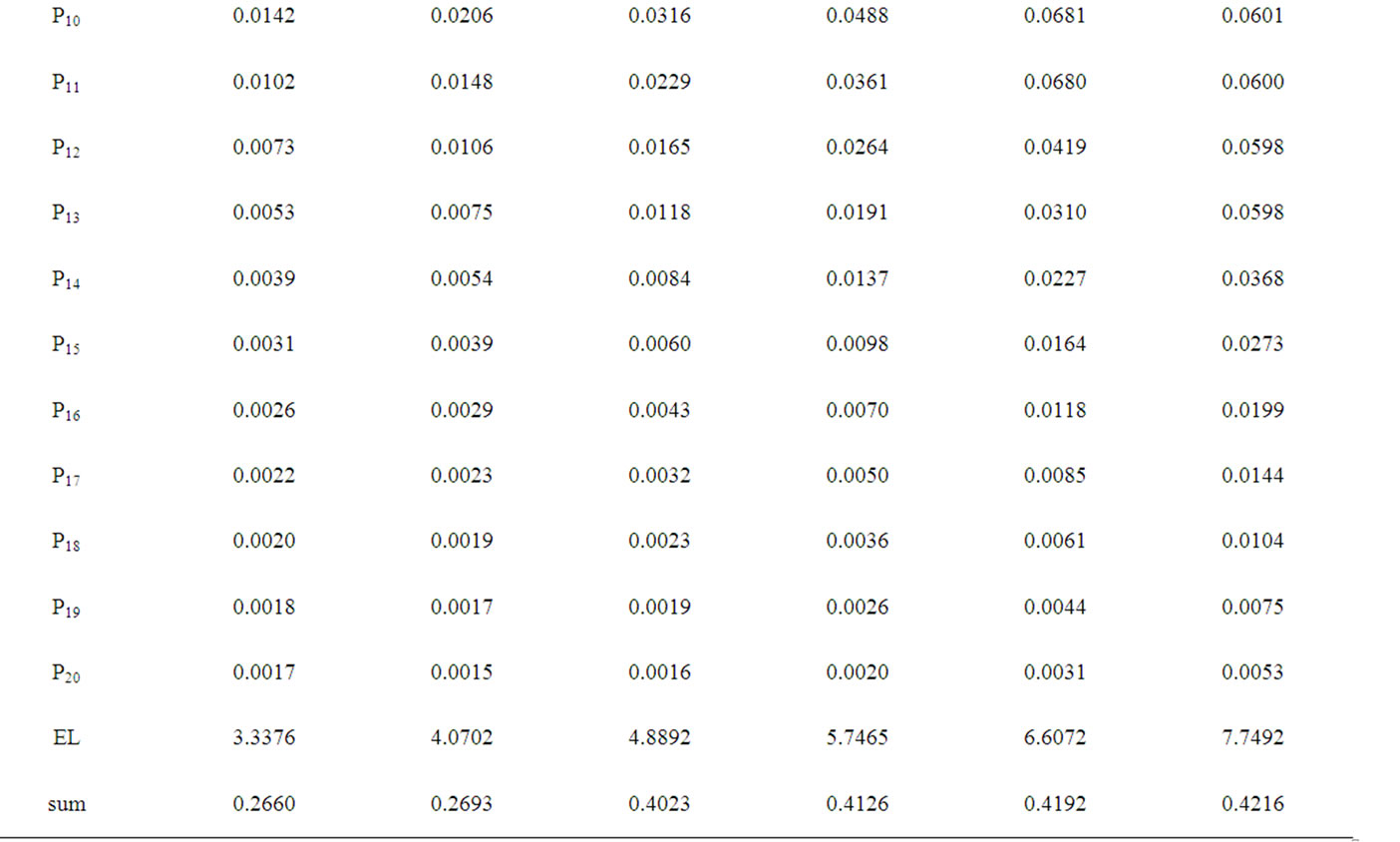
Table 1. Queue length distribution vs the threshold N.

Table 2. Queue length distribution vs the parameter u.
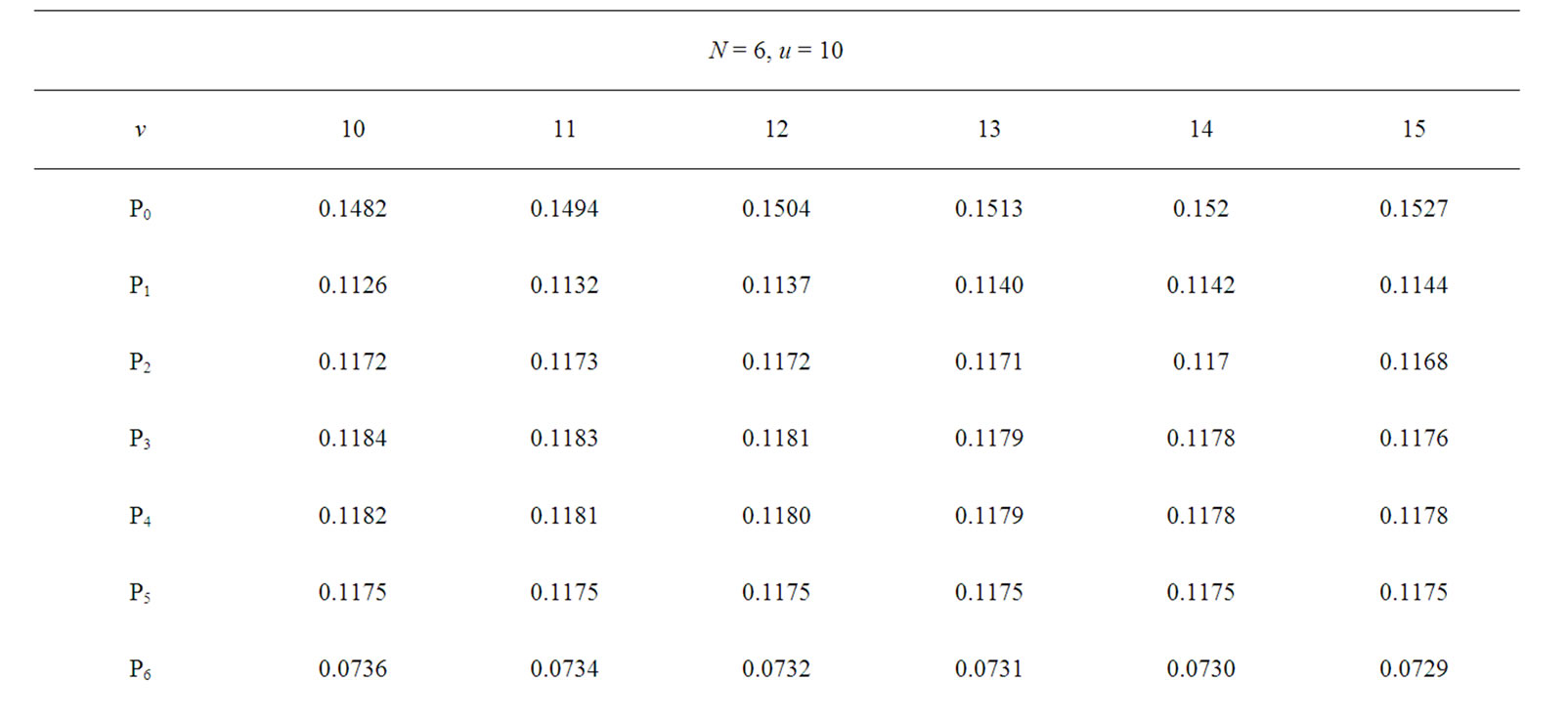
Table 3. Queue length distribution vs the parameter v.
From tables 2-3, one sees that 1) the probability of the system being empty increases as ![]() or
or ![]() increases; 2) the probability
increases; 2) the probability 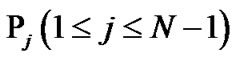 increases as
increases as ![]() or
or ![]() increases, while the probability
increases, while the probability  decreases as
decreases as ![]() or
or ![]() increases; 3) the probability
increases; 3) the probability 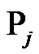 increases from
increases from 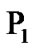 to
to 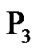 and then decreases and converges to zero under constant
and then decreases and converges to zero under constant ![]() or
or![]() .
.
The mean queue length (EL) is also presented in tables 1-3 respectively. It is shown that as  increases mean queue length increases, while mean queue length decreases as
increases mean queue length increases, while mean queue length decreases as ![]() or
or ![]() increases. It is worth mentioning that the mean queue length could not being the only one performance measure for the system design and optimization. For example, when
increases. It is worth mentioning that the mean queue length could not being the only one performance measure for the system design and optimization. For example, when 

 , the mean queue length is 4.8892, but the total of the probability (sum) when the queue length exceeding 5 is 0.4023, which could not be neglected.
, the mean queue length is 4.8892, but the total of the probability (sum) when the queue length exceeding 5 is 0.4023, which could not be neglected.
7. Conclusions
In this paper we have derived the additional queue length distribution and the recursion expressions of the queue length distribution for the Mx/G/1 queueing system under N-policy with a single vacation and setup times. Furthermore, we present the numerical results of the queue length distribution and the distribution properties are also investigated. The results in this paper would be significant and useful to system designers and others. The approach developed in this paper is powerful and can be used to analyze more complex queueing system.
8. References
[1] B. T. Doshi, “Queueing Systems with Vacations–a Survey,” Queueing System, Vol. 1, No. 1, 1986, pp. 29-66.
[2] H. Takagi, “Queueing Analysis: A Foundation of Performance Evaluation, Vacation and Priority System,” Elsevier, Amsterdam, Vol. 1, 1991.
[3] S. W. Fuhrmann and R. B. Cooper, “Stochastic Decompositions in the M/G/1 Queue with Generalized Vacations,” Operations Research, Vol. 33, No. 5, 1985, pp. 1117-1129.
[4] M. Yadin and P. Naor, “Queueing Systems with a Removable Service Station,” Operational Research Quarterly, Vol. 14, No. 3, 1963, pp. 393-405.
[5] H. W. Lee, S. S. Lee and K. C. Chae, “Operating Characteristics of Mx/G/1 Queue with N-Policy,” Queueing Systems, Vol. 15, No. 1-4, 1994, pp. 387-399.
[6] H. W. Lee, S. S. Lee, J. O. Park and K. C. Chae, “Analysis of Mx/G/1 Queue with N Policy and Multiple Vacations,” Journal of Applied Probability, Vol. 31, No. 2, 1994, pp. 467-496.
[7] S. S. Lee, H. W. Lee, S. H. Yoon and K. C. Chae, “Batch Arrival Queue with N Policy and Single Vacation,” Computers and Operations Research, Vol. 22, No. 2, 1995, pp. 173-189.
[8] G. Choudhury and M. Paul, “A Batch Arrival Queue with an Additional Service Channel under N-Policy,” Applied Mathematics and Computation, Vol. 156, No. 1, 2004, pp. 115-130.
[9] G. Choudhury and K. C. Madan, “A Two-Stage Batch Arrival Queueing System with a Modified Bernoulli Schedule Vacation under N-Policy,” Mathematical and Computer Modelling, Vol. 42, No. 1-2, 2005, pp. 71-85.
[10] G. Choudhury and M. Paul, “A Batch Arrival Queue with a Second Optional Service Channel under N-Policy,” Stochastic Analysis and Applications, Vol. 24, No. 1, 2006, pp. 1-21.
[11] J.-C. Ke, “The Control Policy of an Mx/G/1 Queueing System with Server Startup and Two Vacation Types,” Mathematical Methods of Operations Research, Vol. 54, No. 3, 2001, pp. 471-490.
[12] J.-C. Ke, “Optimal Strategy Policy in Batch Arrival Queue with Server Breakdowns and Multiple Vacations,” Mathematical Methods of Operations Research, Vol. 58, No. 1, 2003, pp. 41-56.
[13] R. G. V. Krishna, R. Nadarajan and R. Arumuganathan, “Analysis of a Bulk Queue with N-Policy Multiple Vacations and Setup Times,” Computers and Operations Research, Vol. 25, No. 11, 1998, pp. 957-967.
[14] K.-H. Wang, M.-C. Chan and J.-C. Ke, “Maximum Entropy Analysis of the Mx/M/1 Queueing System with Multiple Vacations and Server Breakdowns,” Computers & Industrial Engineering, Vol. 52, No. 2, 2007, pp. 192- 202.
[15] J. E. Shore, “Information Theoretic Approximations for M/G/1 and G/G/1 Queueing Systems,” Acta Informatica, Vol. 17, No.1, 1982, pp. 43-61.
[16] M. A. El-Affendi and D. D. Kouvatsos, “A Maximum Entropy Analysis of the M/G/1 and G/M/1 Queueing Systems at Equilibrium,” Acta Informatica, Vol. 19, No. 4, 1983, pp. 339-355.
[17] J.-C. Ke and C.-H. Lin, “Maximum Entropy Solutions for Batch Arrival Queue with an Unreliable Server and Delaying Vacations,” Applied Mathematics and Computation, Vol. 183, No. 2, 2006, pp. 1328-1340.
[18] Y. H. Tang, “The Transient Solution for M/G/1 Queue with Server Vacations,” Acta Mathematica Scientia, Vol. 17, No. 3, 1997, pp. 276-282.
[19] Y. H. Tang and X. W. Tang, “The Queue-Length Distribution for Mx/G/1 Queue with Single Server Vacation,” Acta Mathematica Scientia, Vol. 20, No. 3, 2000, pp. 397-408.
[20] Y. H. Tang, X. Yun and S. J. Huang, “Discrete-Time Geox/G/1 Queue with Unreliable Server and Multiple Adaptive Delayed Vacations,” Journal of Computational and Applied Mathematics, Vol. 220, No. 1-2, 2008, pp. 439-455.
[21] J.-C. Ke, “Batch Arrival Queues under Vacation Policies with Server Breakdowns and Startup/Closedown Times,” Applied Mathematical Modelling, Vol. 31, No. 7, 2007, pp. 1282-1292.
NOTES
The authors also thank the National Nature Science Foundation of China for its support (contract: 70672104).

