Intelligent Information Management
Vol.2 No.9(2010), Article ID:2780,26 pages DOI:10.4236/iim.2010.29062
Filters and Ultrafilters as Approximate Solutions in the Attainability Problems with Constraints of Asymptotic Character
Institute of Mathematics and Mechanics UrB RAS
E-mail: chentsov@imm.uran.ru
Received April 1, 2010; revised June 2, 2010; accepted July 15, 2010
Keywords: Control problems, Ultrafilters, Topology
Abstract
Abstract problems about attainability in topological spaces are considered. Some nonsequential version of the Warga approximate solutions is investigated: we use filters and ultrafilters of measurable spaces. Attraction sets are constructed. AMS (MOS) subject classification. 46A, 49 K 40.
1. Introduction
This investigation is devoted to questions connected with attainability under constraints; these constraints can be perturbed. Under these perturbations, jumps of the attained quality can arise. If perturbation is reduced to a weakening of the initial standard constraints, then we obtain some payoff in a result. Therefore, behavior limiting with respect to the validity of constraints can be very interesting. But, the investigation of possibilities of the abovementioned behavior is difficult. The corresponding “straight” methods are connected with constructions of asymptotic analysis. Very fruitful approach is connected with the extension of the corresponding problem. For example, in theory of control can be used different variants of generalized controls formalizable in the corresponding class of measures very often. In this connection, we note the known investigations of J. Warga (see [1]). We recall the notions of precise, generalized, and approximate controls (see [1]). In connection with this approach, we recall the investigations of R.V. Gamkrelidze [2]. For problems of impulse control, we note the original approach of N.N. Krasovskii (see [3]) connected with the employment of distributions. If is useful to recall some asymptotic constructions in mathematical programming (see [4,5]). We note remarks in [4,5] connected with the possible employment of nonsequential approximate (in the Warga terminology) solutions-nets.
The above-mentioned (and many other) investigations concern extremal problems. But, very important analogs are known for different quality problems. We recall the fundamental theorem about an alternative in differential games established by N.N. Krasovskii and A.I. Subbotin [6]. In the corresponding constructions, elements of extensions are used very active. Moreover, approximate motions were used. The concrete connection of generalized and approximate elements of the corresponding constructions was realized by the rule of the extremal displacement of N.N. Krasovskii.
In general, the problem of the combination of generalized and approximate elements in problems with constraints is very important. Namely, generalized elements (in particular, generalized controls) can be used for the representation of objects arising by the limit passage in the class of approximate elements (approximate solutions). These limit objects can be consider as attraction elements. Very often these elements suppose a sequential realizetion (see [1]). But, in other cases, attraction elements should be defined by more general procedures.
So, we can consider variants of generalized representtation of asymptotic objects. This approach is developed by J. Warga in theory of control.
Similar problems can arise in distinct sections of mathematics. For example, adherent points of the filter base in topological space can be considered as attraction elements. Of course, here nonsequential variants of the limit passage are required very often.
In the following, the attainability problem with constraints of asymptotic character is considered.
Fix two nonempty sets 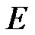 and H, and an operator h from
and H, and an operator h from  into H. Elements of
into H. Elements of 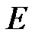 are considered as solutions (sometimes controls) and elements of H play the role of estimates. We consider h as the aim mapping. If we have the set
are considered as solutions (sometimes controls) and elements of H play the role of estimates. We consider h as the aim mapping. If we have the set  of admissible (in traditional sense) solutions, then
of admissible (in traditional sense) solutions, then  play the role of an attainability domain in the estimate space. But, we can use another constraint: instead of
play the role of an attainability domain in the estimate space. But, we can use another constraint: instead of 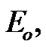 a nonempty family
a nonempty family  of subsets of E is given. In this case, we can use sequences
of subsets of E is given. In this case, we can use sequences 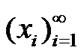 in
in  with a special property in the capacity of approximate solutions. Namely, we require that the sequence
with a special property in the capacity of approximate solutions. Namely, we require that the sequence  has the following property: for any
has the following property: for any 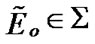 the inclusion
the inclusion 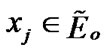 takes place from a certain index (i.e. for
takes place from a certain index (i.e. for  where
where  is a fixed index depending on
is a fixed index depending on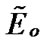 ). For such solutions we obtain the sequences
). For such solutions we obtain the sequences  in H. If H is equipped with a topology t, then we can consider the limits of such sequences
in H. If H is equipped with a topology t, then we can consider the limits of such sequences  as attraction elements (AE) in (H,t) Of course, our AE are “sequential”: we use the limit passage in the class of sequences. This approach can be very limiting. The last statement is connected both with our family
as attraction elements (AE) in (H,t) Of course, our AE are “sequential”: we use the limit passage in the class of sequences. This approach can be very limiting. The last statement is connected both with our family  and with topology
and with topology  The corresponding examples are known: see [7,8]. In many cases, the more general variants of the limit passage are required. Of course, we can consider nets
The corresponding examples are known: see [7,8]. In many cases, the more general variants of the limit passage are required. Of course, we can consider nets 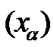 in
in 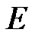 and, as a corollary, the corresponding nets
and, as a corollary, the corresponding nets 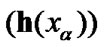 in H. In addition, the basic requirement of admissibility it should be preserved: for any
in H. In addition, the basic requirement of admissibility it should be preserved: for any  the inclusion
the inclusion 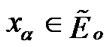 is valid starting from a certain index. With the employment of such nets, we can realize new AE; this effect takes place in many examples.
is valid starting from a certain index. With the employment of such nets, we can realize new AE; this effect takes place in many examples.
But, the representation of the “totality” of above-mentioned ( -admissible) nets as a set is connected with difficulties. Really, any net in the set
-admissible) nets as a set is connected with difficulties. Really, any net in the set 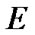 is defined by a mapping from a nonempty directed set (DS)
is defined by a mapping from a nonempty directed set (DS) 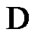 into
into 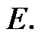 the concrete choice of
the concrete choice of  is arbitrary (
is arbitrary (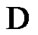 is a nonempty set). Therefore we have the very large “totality” of nets with the point of view of traditional Zermelo axiomatics. But, this situation can be corrected by the employment of filters of
is a nonempty set). Therefore we have the very large “totality” of nets with the point of view of traditional Zermelo axiomatics. But, this situation can be corrected by the employment of filters of 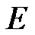 it is possible to introduce the set of all
it is possible to introduce the set of all 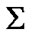 -admissible filters of the set
-admissible filters of the set  In addition, the
In addition, the 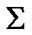 -admissibility of a filter
-admissibility of a filter 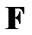 is defined by the requirement
is defined by the requirement 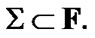 So, we can consider nonsequential approximate solutions (analogs of sequential approximate solutions of Warga) as filters
So, we can consider nonsequential approximate solutions (analogs of sequential approximate solutions of Warga) as filters  of
of  with the property
with the property  Moreover, we can be restricted to the employment of only ultrafilters (maximal filters) with the above-mentioned property. In two last cases, we obtain two variants of the set of admissible nonsequential approximate solutions defined in correspondence with Zermelo axiomatics. In our investigation, such point of view is postulated. And what is more, we give the basic attention to the consideration of ultrafilters. Here, the important property of compactness arises. Namely, the corresponding space of ultrafilters is equipped with a compact topology. This permits to consider ultrafilters as generalized elements (GE) too (we keep in mind the above-mentioned classification of Warga).
Moreover, we can be restricted to the employment of only ultrafilters (maximal filters) with the above-mentioned property. In two last cases, we obtain two variants of the set of admissible nonsequential approximate solutions defined in correspondence with Zermelo axiomatics. In our investigation, such point of view is postulated. And what is more, we give the basic attention to the consideration of ultrafilters. Here, the important property of compactness arises. Namely, the corresponding space of ultrafilters is equipped with a compact topology. This permits to consider ultrafilters as generalized elements (GE) too (we keep in mind the above-mentioned classification of Warga).
The basic difficulty is connected with realizability: the existence of free ultrafilters (for which effects of an extension are realized) is established only with the employment of axiom of choice. Roughly speaking, free ultrafilters are “invisible”. This property is connected with ultrafilters of the family of all subsets of the corresponding “unit”. But, we can to consider ultrafilters of measurable spaces with algebras and semialgebras of sets. We note that some measurable spaces admitting the representation of all such ultrafilters are known (see, for example, [9,§7.6]; in addition, the unessential transformation with the employment of finitely additive (0,1)-measures is used).
2. General Notions and Designations
We use the standard set-theoretical symbolics including quantors and propositional connectives; as usually,  replaces the expression “there exists and unique”,
replaces the expression “there exists and unique”, 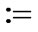 is the equality by definition. In the following, for any two objects
is the equality by definition. In the following, for any two objects 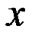 and
and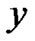 ,
, 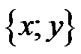 is the unordered pair of x and y (see [10]). Then,
is the unordered pair of x and y (see [10]). Then, 
 is singleton containing an object x. Of course, for any objects x and
is singleton containing an object x. Of course, for any objects x and  the object
the object 
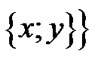 is the ordered pair of objects x and y; here, we follow to [10]. By
is the ordered pair of objects x and y; here, we follow to [10]. By 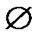 we denote the empty set. By a family we call a set all elements of which are sets.
we denote the empty set. By a family we call a set all elements of which are sets.
By  we denote the family of all subsets of a set
we denote the family of all subsets of a set  then,
then, 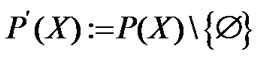 are the family of all nonempty subsets of X. Of course, for any set
are the family of all nonempty subsets of X. Of course, for any set  in the form of
in the form of 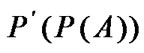 and
and 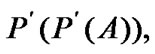 we have the family of all nonempty subfamilies of
we have the family of all nonempty subfamilies of  and
and 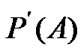 respectively.
respectively.
If  is a set, then we denote by
is a set, then we denote by 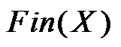 the family of all finite sets of
the family of all finite sets of  then
then 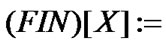
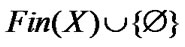 is the family of all finite subsets of
is the family of all finite subsets of 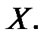
For any sets  and
and  we denote by
we denote by  the set of all mappings from
the set of all mappings from  into
into  If
If 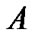 and
and 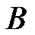 are sets,
are sets, 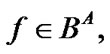 and
and 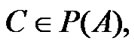 then
then
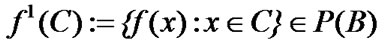
(the image of  under the operation f) and
under the operation f) and 
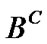 is the usual
is the usual  -restriction of
-restriction of 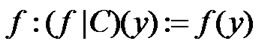
 . In the following,
. In the following,  and
and  is the real line;
is the real line;  Of course, we use the natural order
Of course, we use the natural order 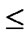 of
of . If
. If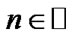 , then
, then
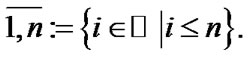
Transformations of families. For any nonempty family  and a set
and a set  we suppose that
we suppose that

If X and Y are sets and , then we suppose that
, then we suppose that
 (2.1)
(2.1)
of course, in (2.1) nonempty families are defined.
If 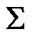 is a family, then we suppose that
is a family, then we suppose that

(we keep in mind that  is a nonempty set
is a nonempty set 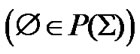 and, for
and, for ,
,  is a family) and
is a family) and
(of course, for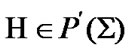 ,
,  is a nonempty family); moreover
is a nonempty family); moreover

So, for any nonempty family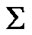 , we obtain that
, we obtain that

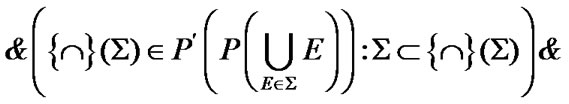

of course, .
.
Special families. Let I be a set. Then, we suppose that
 (2.2)
(2.2)
elements of (2.2) are called 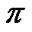 -systems with “zero” and “unit”. Moreover,
-systems with “zero” and “unit”. Moreover,
 (2.3)
(2.3)
elements of (2.3) are lattices of subsets of I (with “zero”). Finally,
 (2.4)
(2.4)
Of course, in (2.4) lattices of sets with “zero” and “unit” are introduced. We note that

Of course,
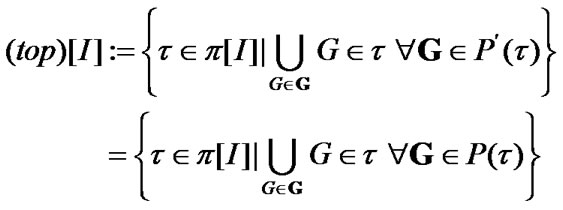 (2.5)
(2.5)
is the set of all topologies of I. If 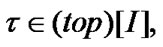 then the pair
then the pair 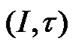 is a topological space (TS);
is a topological space (TS);
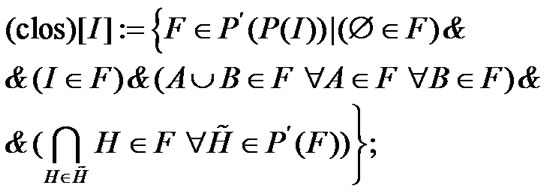 (2.6)
(2.6)
in (2.6) we have families dual with respect to topologies. It is obvious that
 (2.7)
(2.7)
We suppose that  is the mapping for which
is the mapping for which
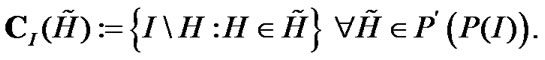 (2.8)
(2.8)
From (2.5) – (2.8), we obtain the following properties:
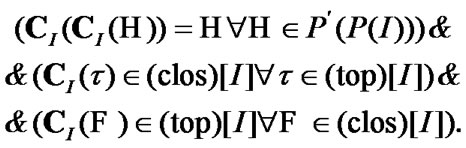 (2.9)
(2.9)
We note that  in addition,
in addition,

Of course, in (2.9), we have (in particular) the natural duality used in general topology. Let

(the set of all compact topologies of I) Now, we introduce in consideration algebras of sets. Namely,
 (2.10)
(2.10)
In connection with (2.10), we note that
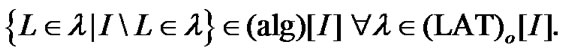
If 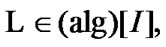 then
then  is a measurable space with an algebra of sets.
is a measurable space with an algebra of sets.
If  and
and  then by
then by 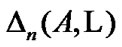 we denote the set of all mappings
we denote the set of all mappings
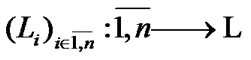
for each of which:
1) 
2) 
Then
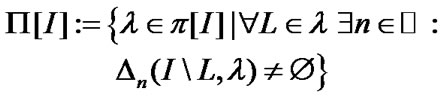 (2.11)
(2.11)
is the set of all semialgebras of subsets of I. Of course,

see (2.10). If we have a semialgebra of subsets of I, then algebra generated by the initial semialgebra is realized very simply: for any 
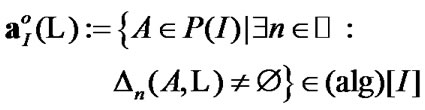
has the properties: 1) 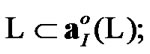 2)
2) 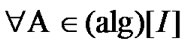
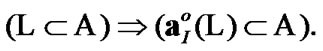
Now, we introduce some notions important for constructions of general topology. Namely, we consider topological bases of two types:
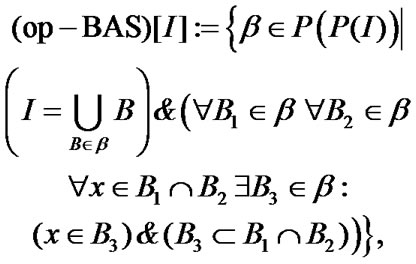 (2.12)
(2.12)
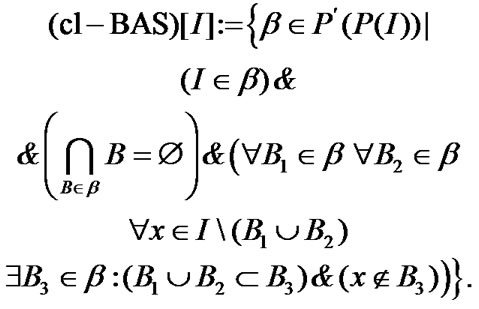 (2.13)
(2.13)
Of course,
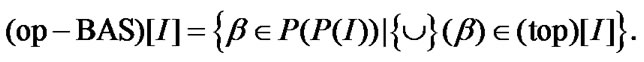
In connection with (2.12), we suppose that
 ,
,
 ;
;
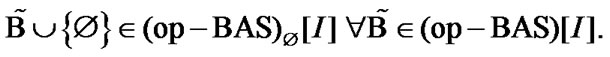
Moreover, the following obvious property is valid:
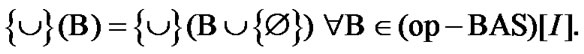
We note the natural connection of open and closed bases:
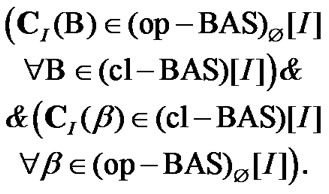 (2.14)
(2.14)
Along with (2.14), we note the following important property:
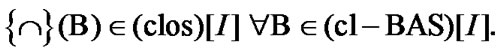 (2.15)
(2.15)
From (2.9) and (2.15), we obtain the obvious statement:
 (2.16)
(2.16)
So, closed bases can be used (see (2.16)) for topologies constructing. We note the following obvious property (here we use (2.14) and (2.16)):
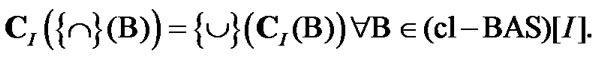 (2.17)
(2.17)
Of course, in (2.17), we use the usual duality property connected with (2.14) – (2.16).
Some additions. In the following, we suppose that
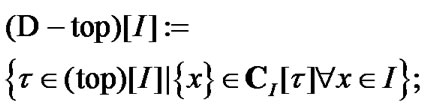 (2.18)
(2.18)
if  then TS
then TS  is called
is called 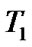 -space. We use (2.18) under investigation of properties of topologies on ultrafilter spaces.
-space. We use (2.18) under investigation of properties of topologies on ultrafilter spaces.
Finally, we suppose that
 . So, we introduce “continuous” lattices.
. So, we introduce “continuous” lattices.
3. Nets and Filters as Approximate Solutions under Constraints of Asymptotic Character
In this section, we fix a nonempty set 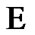 considered (in particular) as the space of usual solutions. We consider families
considered (in particular) as the space of usual solutions. We consider families 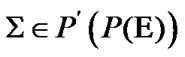 as constraints of asymptotic character. Of course, in this case, we use asymptotic version of solutions. The simplest variant is realized by the employment of sequences in
as constraints of asymptotic character. Of course, in this case, we use asymptotic version of solutions. The simplest variant is realized by the employment of sequences in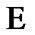 : in the set
: in the set  the set of
the set of 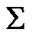 -admissible sequences (see Section 1) is selected. It is logical to generalize this approach: we keep in mind the employment of nets. Later, we introduce some definitions connected with the Moore-Smith convergence. But, before we consider the filter convergence.
-admissible sequences (see Section 1) is selected. It is logical to generalize this approach: we keep in mind the employment of nets. Later, we introduce some definitions connected with the Moore-Smith convergence. But, before we consider the filter convergence.
We denote by 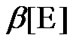 (by
(by  the set of all families
the set of all families  (families
(families ) for which
) for which

 Then,
Then,  is the set of all filter bases on
is the set of all filter bases on . By
. By  we denote the set of all filters on
we denote the set of all filters on :
:
 (3.1)
(3.1)
Using (3.1), we introduce the set 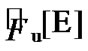 of all ultrafilters on
of all ultrafilters on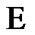 :
:
 (3.2)
(3.2)
In connection with (3.1) and (3.2), see in particular [11, ch. I]. In addition,
 (3.3)
(3.3)
By (3.3) we define the filter on 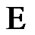 generated by a base of
generated by a base of 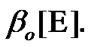
If 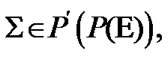 then by
then by 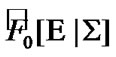 (by
(by 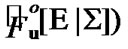 we denote the set of
we denote the set of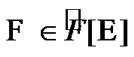 all filters (ultrafilters
all filters (ultrafilters 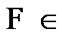
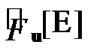 ) such that
) such that . Then, for any filter
. Then, for any filter 
 , we have
, we have 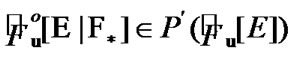 and what is more
and what is more  is the intersection of all ultrafilters
is the intersection of all ultrafilters 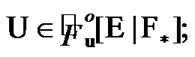 see [11].
see [11].
If a family 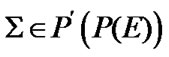 is considered as the constra int of asymptotic character, then ultrafilters
is considered as the constra int of asymptotic character, then ultrafilters 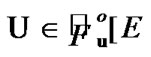
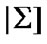 are considered as (nonsequential) approximate solutions; of course, filters
are considered as (nonsequential) approximate solutions; of course, filters  can be considered in this capacity also. But, ultrafilters have better properties; therefore, now we are restricted to employment of ultrafilters as approximate solutions.
can be considered in this capacity also. But, ultrafilters have better properties; therefore, now we are restricted to employment of ultrafilters as approximate solutions.
The filter of neighborhoods. If 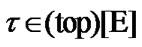 and
and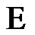
 , then
, then
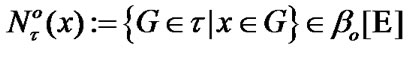
and 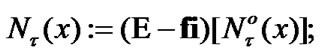 of course,
of course,  in correspondence with (3.3). We were introduce the filter of neighborhoods of
in correspondence with (3.3). We were introduce the filter of neighborhoods of  in the sense of [11,ch.I]. In the following,
in the sense of [11,ch.I]. In the following,

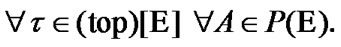
So, we introduce the closure operation in a TS. Moreover, we suppose that
 (3.4)
(3.4)
The filter convergence. We follow to [11]. Suppose that 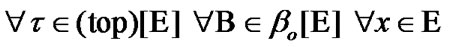
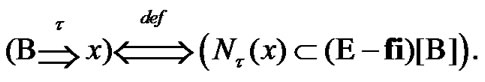 (3.5)
(3.5)
In addition, 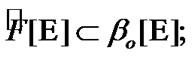 see (3.1). Therefore, we can use (3.5) in the case of
see (3.1). Therefore, we can use (3.5) in the case of  where
where 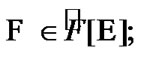 we note that
we note that 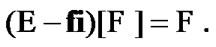 Then, by (3.5)
Then, by (3.5) 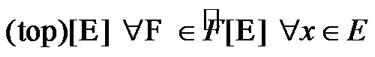
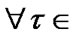
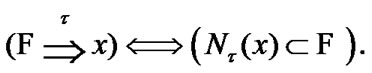 (3.6)
(3.6)
Of course, it is possible to use the variant of (3.6) corresponding to the case  where
where 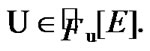
Nets and the Moore-Smith convergence. On the basis of (3.6), we can to introduce the standard MooreSmith convergence of nets. We call a net in the set 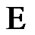 arbitrary triplet
arbitrary triplet 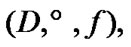 where
where  is a nonempty DS and
is a nonempty DS and 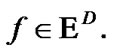 If
If 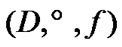 is a net in the set
is a net in the set  then
then
 (3.7)
(3.7)
we obtain the filter of  associated with
associated with  Now, for any topology
Now, for any topology  a net
a net 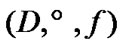 in the set
in the set  and
and  we suppose that
we suppose that
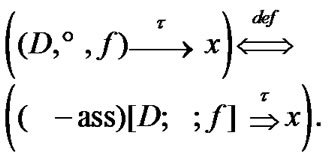 (3.8)
(3.8)
From (3.6) and (3.7), we obtain that (3.8) is the “usual” Moore-Smith convergence (see [12]). Of course, any sequence 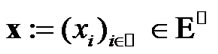 generates the net
generates the net  where
where  is the usual order of
is the usual order of .
.
If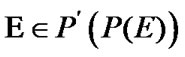 , then a net
, then a net 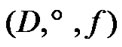 in
in 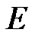 is called
is called  -admissible if
-admissible if  In this case,
In this case, 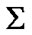 can be considered as a constraint of asymptotic character and
can be considered as a constraint of asymptotic character and 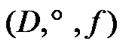 plays the role of nonsequential (generally speaking) approximate solution.
plays the role of nonsequential (generally speaking) approximate solution.
In conclusion, we note that
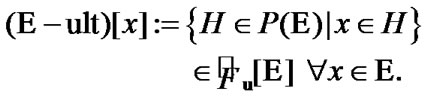 (3.9)
(3.9)
In (3.9), trivial ultrafilters are defined.
4. Attraction Sets
In this section, we construct nonsequential (generally speaking) attraction sets (AS) using different variants of the representation of approximate solutions. Since nets are similar to sequences very essential, we begin our consideration with the representation (of AS) using nets.
For brevity, in this section, we fix following two nonempty sets: 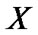 and
and 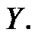 In addition, under
In addition, under 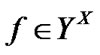 and
and 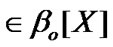

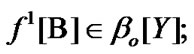 (4.1)
(4.1)
of course, in (4.1), we can use a filter or ultrafilter instead of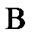 . In addition, the important property takes place: if
. In addition, the important property takes place: if 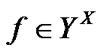 and
and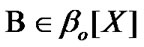 , then
, then
 (4.2)
(4.2)
So, by (4.2) image of an ultrafilter base is an ultrafilter base. Of course, the image of an ultrafilter is an ultrafilter base also.
Introduce AS: if 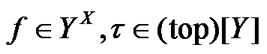 and
and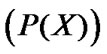
 , then by
, then by  we denote the set of all
we denote the set of all  for each of which there exists a net
for each of which there exists a net  in the set X such that
in the set X such that
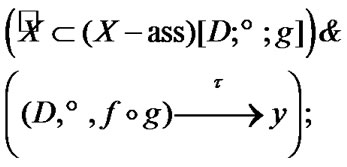 (4.3)
(4.3)
we consider 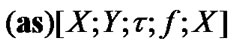 as AS. In this definition, we use nets. But, for any filter
as AS. In this definition, we use nets. But, for any filter  there exists a net
there exists a net  in the set X for which
in the set X for which 
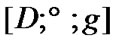 (see [13]).
(see [13]).
Proposition 4.1. For any  and
and 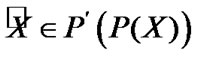
 (4.4)
(4.4)
Proof. Fix  and
and 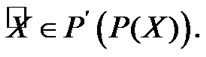 Suppose that
Suppose that 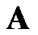 and
and 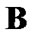 are the sets on the left and right sides of (4.4) respectively. Let
are the sets on the left and right sides of (4.4) respectively. Let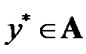 . Then
. Then  and, for a net
and, for a net  in X, the relation (4.3) is valid under
in X, the relation (4.3) is valid under 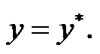 Then, by (4.3)
Then, by (4.3)
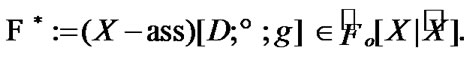 (4.5)
(4.5)
Moreover, by (3.8) and (4.3)  So, by (3.6)
So, by (3.6)
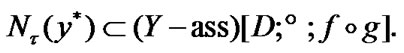 (4.6)
(4.6)
Let  Then by (3.7) and (4.6), for some
Then by (3.7) and (4.6), for some 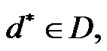 the following property is valid:
the following property is valid: 
 (4.7)
(4.7)
In addition,  and by (3.7) and (4.5)
and by (3.7) and (4.5)
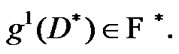
As a corollary, 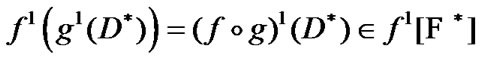 But, by (4.7)
But, by (4.7) 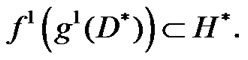 By (3.3)
By (3.3) 
 Since the choice of
Since the choice of  was arbitrary, the inclusion
was arbitrary, the inclusion  is established. By (3.5)
is established. By (3.5)
 (4.8)
(4.8)
By (4.5) and (4.8) 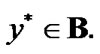 The inclusion
The inclusion  is established.
is established.
Let 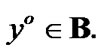 Then, for
Then, for  we have a filter
we have a filter 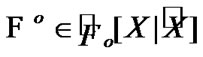 such that
such that
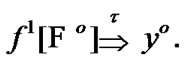 (4.9)
(4.9)
Choose a net 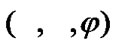 in X for which
in X for which
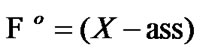 . By (4.1)
. By (4.1) 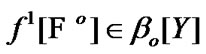 and, as a corollary, by (3.5) and (4.9)
and, as a corollary, by (3.5) and (4.9)
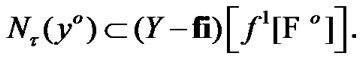 (4.10)
(4.10)
Then by (3.3) and (4.10) we obtain that
 . Using (2.1) we have the property:
. Using (2.1) we have the property: 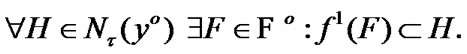 Choose arbitrary
Choose arbitrary 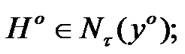 then, for some
then, for some 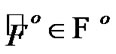 the inclusion
the inclusion 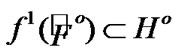 is valid. By (3.7) and the choice of
is valid. By (3.7) and the choice of  for some
for some  the following property is realized:
the following property is realized: 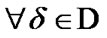
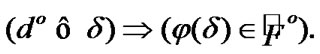
By the choice of  we obtain that
we obtain that 
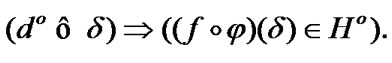
Then,  So, the important inclusion
So, the important inclusion
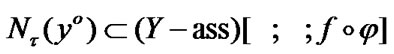
is valid. Then 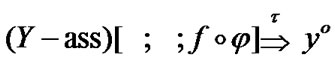 (see (3.6)). By (3.8)
(see (3.6)). By (3.8)
 (4.11)
(4.11)
Moreover, by the choice of 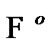 and
and  the inclusion
the inclusion

is valid. From (4.11), we have the inclusion 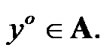 So,
So, 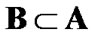 and, as a corollary,
and, as a corollary, 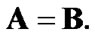
Proposition 4.2. For any 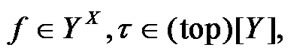 and
and 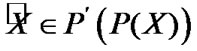
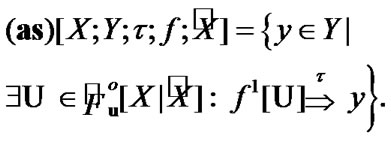 (4.12)
(4.12)
Proof. We denote respectively by  an
an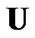 the sets on the left and right sides of (4.12). Since
the sets on the left and right sides of (4.12). Since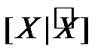
 , we have the obvious inclusion
, we have the obvious inclusion 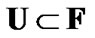 (see Proposition 4.1). Let
(see Proposition 4.1). Let 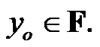 Then by Proposition 4.1
Then by Proposition 4.1 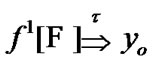 for some
for some  Then
Then 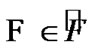
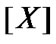 and
and 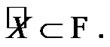 We recall (see Section 3) that
We recall (see Section 3) that . Choose arbitrary
. Choose arbitrary 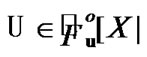
 Then
Then 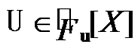 and
and 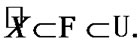 Therefore,
Therefore, 
 Moreover, by (2.1)
Moreover, by (2.1) 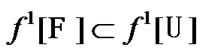 and, as a corollary,
and, as a corollary,
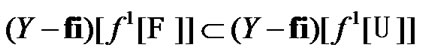 (4.13)
(4.13)
(we recall that by (4.1) 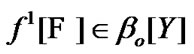 and
and 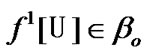
 ). By the choice of
). By the choice of  we have the inclusion
we have the inclusion
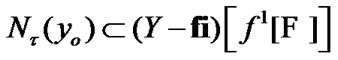
(see (3.5)). Then by (4.13) 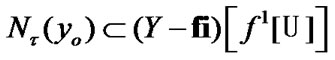 and, as a corollary (see (3.5)),
and, as a corollary (see (3.5)),
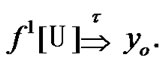
Then,  The inclusion
The inclusion 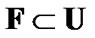 is established.
is established.
Recall that, for any family 
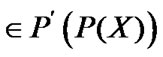 and
and 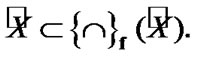 We note the following obvious.
We note the following obvious.
Proposition 4.3. For any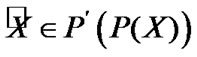 , the equality
, the equality 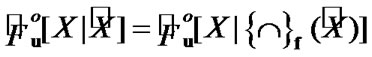 is valid.
is valid.
Proof. Recall that 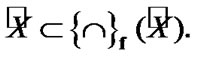 Therefore,
Therefore,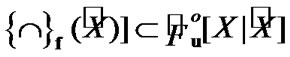
 ; on the other hand, from (3.1), we obtain that
; on the other hand, from (3.1), we obtain that  Then, for an ultrafilter
Then, for an ultrafilter 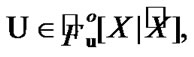

and, as a corollary,  So, since the choice of
So, since the choice of  was arbitrary,
was arbitrary, 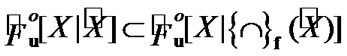 and, as a corollary,
and, as a corollary, 
Corollary 4.1. If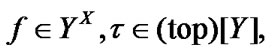 and
and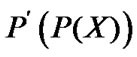
 , then
, then
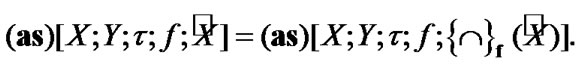
The corresponding proof is realized by the immediate combination of Propositions 4.2 and 4.3. We note that, by definitions of Section 2
 (4.14)
(4.14)
In connection with (4.14), we note the following general property. Namely, 
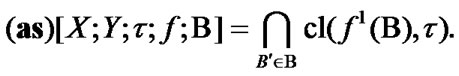 (4.15)
(4.15)
Then, by (4.14), (4.15), and Corollary 4.1
 (4.16)
(4.16)
In connection with (4.16), we note that 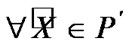

 (4.17)
(4.17)
Remark 4.1. By analogy with Proposition 4.3 we have that
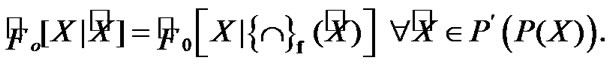
Really, fix  Then
Then  Therefore,
Therefore, 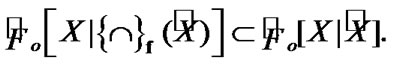 Let
Let
 . Then,
. Then,  and
and 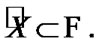 But, from (3.1), we have the equality
But, from (3.1), we have the equality 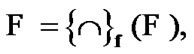 where by the choice of
where by the choice of . So,
. So, 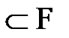
 and, as a corollary,
and, as a corollary, 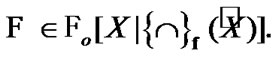 The inclusion
The inclusion 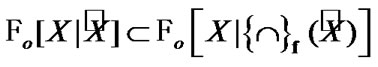 is established. So,
is established. So, 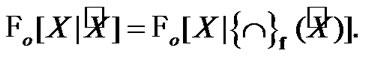
Returning to (4.17), we note that by Proposition 4.2 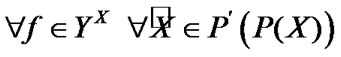
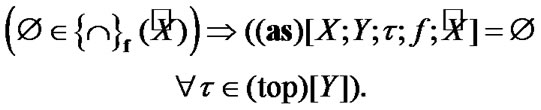 (4.18)
(4.18)
Remark 4.2. We have that, for the case 
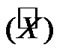 it is possible that
it is possible that
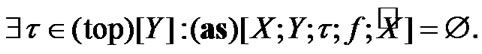
Indeed, consider the case 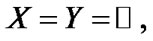
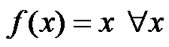
 is the usual
is the usual  -topology of real line
-topology of real line , and
, and

Then, 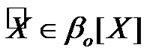 and
and  But, by (4.15)
But, by (4.15)
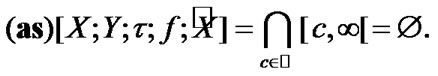
It is obvious the following.
Proposition 4.4. If 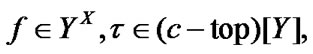 and
and 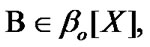 then
then
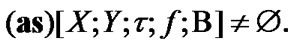
Proof. The corresponding proof follows from known statements of general topology (see [11]). But, we consider this proof for a completeness of the account. In our case, we have (4.15). In addition,
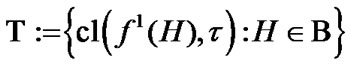 (4.19)
(4.19)
is nonempty family of sets closed in the compact topological space (TS) 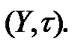 Moreover,
Moreover,  (we use known properties of the closure operation and the image operation). Since
(we use known properties of the closure operation and the image operation). Since 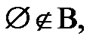 we obtain that
we obtain that 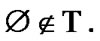 In addition,
In addition,  Therefore, by [9] we have the following property: if
Therefore, by [9] we have the following property: if  and
and

then  As a corollary,
As a corollary, 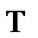 is the non empty centered system of closed sets in a compact TS. Then, the intersection of all sets of
is the non empty centered system of closed sets in a compact TS. Then, the intersection of all sets of  is not empty. By (4.19)
is not empty. By (4.19)
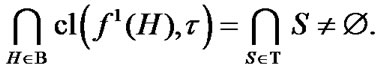
Using (4.15), we obtain the required statement about the nonemptyness of attraction set.
Corollary 4.2. If  and
and  then
then
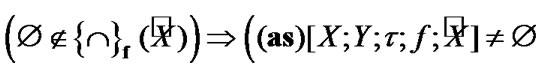
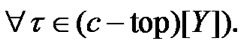
Proof. Let  Choose arbitrary topology
Choose arbitrary topology 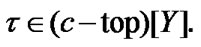 By (4.14)
By (4.14) 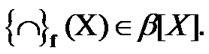 Moreover,
Moreover, 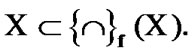 Therefore,
Therefore, 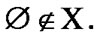 Then,
Then, 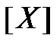
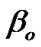
 and by Proposition 4.4
and by Proposition 4.4
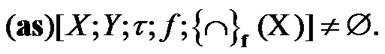
Using Corollary 4.1, we obtain that 

In the following, we use the continuity notion. In this connection, suppose that
 (4.20)
(4.20)
So, continuous functions are defined. In the following, we use bijections, open and closed mappings, and homeomorphisms. Let
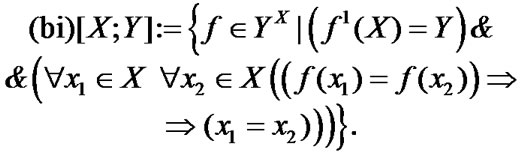 (4.21)
(4.21)
In (4.21), the set of all bijections from  onto
onto  is defined. If
is defined. If 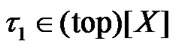 and
and  then
then
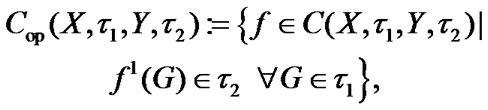 (4.22)
(4.22)
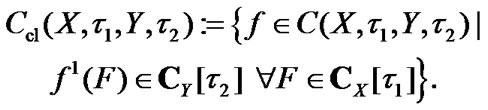 (4.23)
(4.23)
In (4.22) (in (4.23)), we consider open (closed) mappings. In addition,
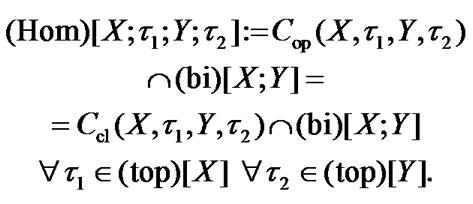 (4.24)
(4.24)
So, in (4.24), the set of homeomorphisms is defined.
5. Some Properties of Ultrafilters of Measurable Spaces
In this section, we fix a nonempty set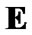 . We consider the very general measurable space
. We consider the very general measurable space  where
where 
 is fixed also. According to necessity, we will be supplement the corresponding suppositions with respect to
is fixed also. According to necessity, we will be supplement the corresponding suppositions with respect to . We suppose that
. We suppose that 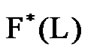 is the set of all families
is the set of all families 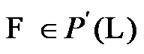 such that
such that
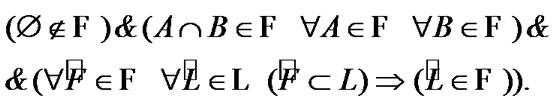
Elements of the set 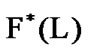 are filters of
are filters of . In addition,
. In addition,
 (5.1)
(5.1)
is the set of all ultrafilters of  Recall that (see [16])
Recall that (see [16])
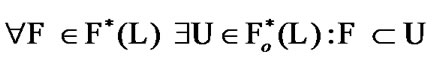 (5.2)
(5.2)
In the following, (5.2) plays the very important role.
We introduce the mapping 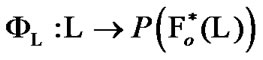 by the following rule:
by the following rule:
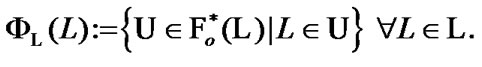 (5.3)
(5.3)
We note that 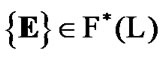 and by (5.2)
and by (5.2) 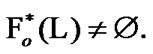 In addition, we recall that (see Section 2)
In addition, we recall that (see Section 2)
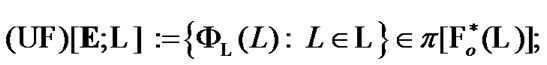 (5.4)
(5.4)
by (5.4) the pair ( ) is a nonempty multiplicative space. We note some simplest general properties. We obtain that
) is a nonempty multiplicative space. We note some simplest general properties. We obtain that
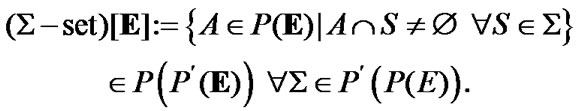
We note that
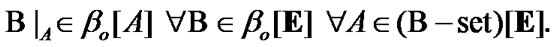
In addition, for  the inclusion
the inclusion 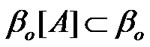
 takes place. Therefore,
takes place. Therefore,
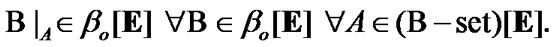 (5.5)
(5.5)
With the employment of (5.5), we obtain that, for any 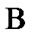
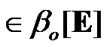 and
and 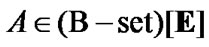
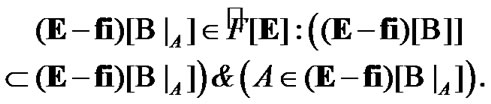 (5.6)
(5.6)
Now, we return to the space  Suppose that
Suppose that
 (5.7)
(5.7)
(the set of filter bases of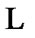 );
); 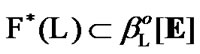 and
and
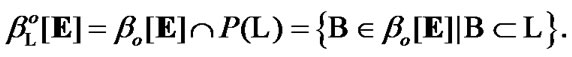
We note the obvious property: 
 In addition,
In addition,
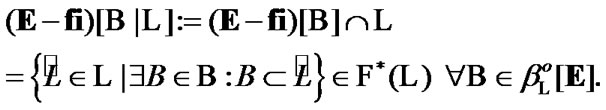
Using (5.5) and the obvious inclusion 
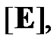 under
under  and
and 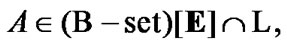 we obtain, that
we obtain, that  We note that, under
We note that, under 
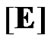 and
and 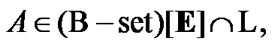 the filter
the filter
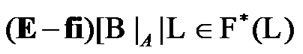
has the following properties
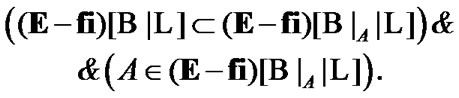 (5.8)
(5.8)
Of course, 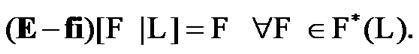 We can use this property in (5.8): for any
We can use this property in (5.8): for any  and
and 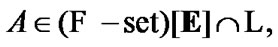 the filter
the filter 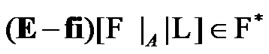
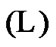 has the properties
has the properties
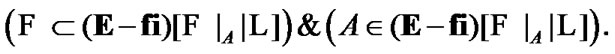 (5.9)
(5.9)
In connection with (5.9), we recall the very general property: if  and
and 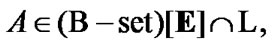 then
then 
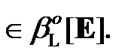 Using the maximality property, we obtain that
Using the maximality property, we obtain that
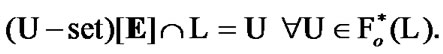
And what is more, 
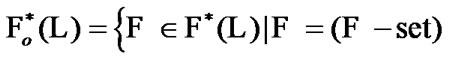
Of course, the above-mentioned properties are valid for
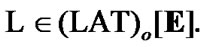 (5.10)
(5.10)
The following reasoning is similar to the construction of [13,§3.6] connected with Wallman extension; in addition, later until the end of this section, we suppose that (5.10) is valid (so, we fix a lattice with “zero” and “unit”).
So, if 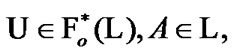 and
and 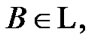 then (under condition (5.10))
then (under condition (5.10))
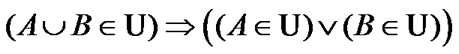 (5.11)
(5.11)
The property (5.11) is basic. As a corollary, 
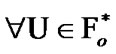
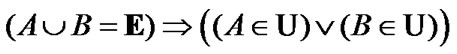 (5.12)
(5.12)
We note that by (5.11) the following property is valid:
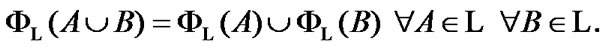
As a corollary, we obtain the property
 (5.13)
(5.13)
(so, under (5.10), the statement (5.4) is amplified). In (5.13), we have the lattice of subsets of  This important fact used below.
This important fact used below.
6. Topological Properties, 1
As in the previous section, now we fix a nonempty set 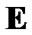 and a family
and a family  We note the following obvious property:
We note the following obvious property:

From definitions of the previous section, the following known property follows: 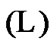
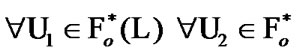
 (6.1)
(6.1)
Moreover, we note that 
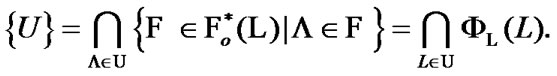 (6.2)
(6.2)
Moreover, we note that . Therefore, by (5.4)
. Therefore, by (5.4)
 (6.3)
(6.3)
As a corollary, we obtain (see Section 2) that
 (6.4)
(6.4)
We recall the very known definition of Hausdorff topology; namely, we introduce the set of such topologies: if  is a set, then
is a set, then

For any set M we suppose that
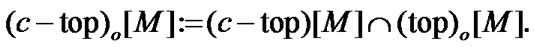
If 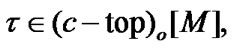 then TS
then TS 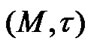 is called a compactum. Then, the obvious statement follows from the ultrafilter properties (see (5.3), (6.1)):
is called a compactum. Then, the obvious statement follows from the ultrafilter properties (see (5.3), (6.1)):
 (6.5)
(6.5)
So, by (6.5)  is a Hausdorff TS. Of course, we can use the previous statements of this section in the case of
is a Hausdorff TS. Of course, we can use the previous statements of this section in the case of  obtaining the Hausdorff topology (6.5). But, in the above-mentioned case, another construction of TS is very interesting. This construction is similar to Wallman extension (see [13,§3.6]). Moreover, in this connection, we note the fundamental investigation [14], where topological representations in the class of ideals are considered. We give the basic attention to the filter consideration in connection with construction of Section 3 concerning with the realization of AS. In this connection, we note that
obtaining the Hausdorff topology (6.5). But, in the above-mentioned case, another construction of TS is very interesting. This construction is similar to Wallman extension (see [13,§3.6]). Moreover, in this connection, we note the fundamental investigation [14], where topological representations in the class of ideals are considered. We give the basic attention to the filter consideration in connection with construction of Section 3 concerning with the realization of AS. In this connection, we note that 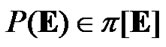 and the sets
and the sets 
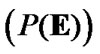 and
and  are defined. From (3.1) and definitions of Section 5, we have the equality
are defined. From (3.1) and definitions of Section 5, we have the equality 
 Moreover, from (3.2) and the above-mentioned definitions of Section 5, the equality
Moreover, from (3.2) and the above-mentioned definitions of Section 5, the equality
 (6.6)
(6.6)
follows. By these properties (see (6.6)) the constructions of Section 3 obtain interpretation in terms of filters and ultrafilters of measurable spaces.
Now, we note one simple property; in addition, we use the inclusion chain 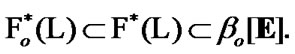 So, by (3.3)
So, by (3.3)
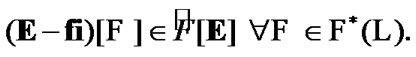
In particular, we have the following property:
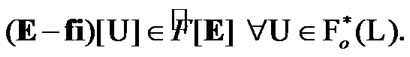 (6.7)
(6.7)
We note one general simple property; namely, in general case of 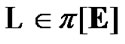
 (6.8)
(6.8)
Remark 6.1. We note that (6.8) is a variant of Proposition 2.4.1 of monograph [16]. Consider the corresponding proof. Fix  Then by (6.7)
Then by (6.7)
 (6.9)
(6.9)
From (6.9), we obtain (see Section 3) that 
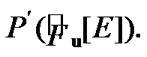 Let
Let

Then,  and
and  In addition (see Section 5),
In addition (see Section 5), 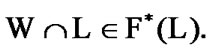 Let
Let  Then,
Then,  and, in particular,
and, in particular,  By (6.9)
By (6.9) 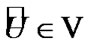 and, as a corollary,
and, as a corollary,  Then,
Then, 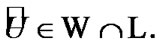 So, the inclusion
So, the inclusion 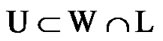 is established; we obtain that
is established; we obtain that
 (6.10)
(6.10)
From (5.1) and (6.10), we have the equality 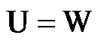
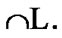 So,
So,
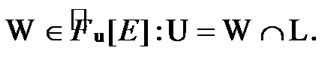
Since the choice of 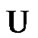 was arbitrary, the property (6.8) is established.
was arbitrary, the property (6.8) is established.
7. Topological Properties, 2
In this and following sections, we fix a nonempty set 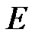 and a lattice
and a lattice  We consider the question about constructing a compact
We consider the question about constructing a compact  -space with “unit”
-space with “unit” 
 This space is similar to Wallman extension for a
This space is similar to Wallman extension for a 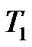 -space. But, we not use axioms of topology and operate lattice constructions (here, a natural analogy with constructions of [14] takes place). Later we use the following simple statement.
-space. But, we not use axioms of topology and operate lattice constructions (here, a natural analogy with constructions of [14] takes place). Later we use the following simple statement.
Proposition 7.1. 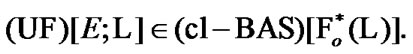
Proof. We use (5.13). In particular,  As a corollary,
As a corollary,
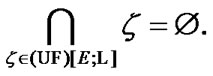 (7.1)
(7.1)
Moreover,  (see (5.4)). So,
(see (5.4)). So, 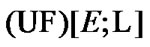 is a family with “zero” and “unit”. Moreover, by (5.13)
is a family with “zero” and “unit”. Moreover, by (5.13)
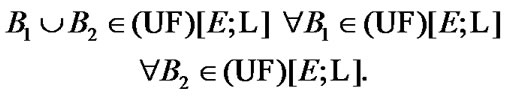
Therefore, by (2.13) the required statement is realized.
By (2.15) and Proposition 7.1 we have the following construction:
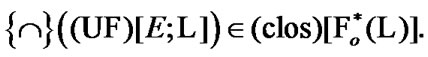 (7.2)
(7.2)
Proposition 7.2. The following compactness property is valid:
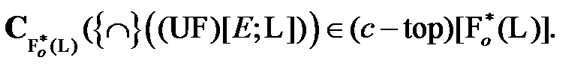 (7.3)
(7.3)
Proof. For brevity, we suppose that
 (7.4)
(7.4)
and 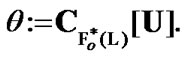 Of course, by (2.9)
Of course, by (2.9) 
 Moreover, under
Moreover, under  the family
the family

has the following obvious property
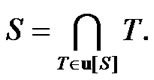 (7.5)
(7.5)
We have the equality  So,
So,  is the family of all subsets of
is the family of all subsets of  closed in the TS
closed in the TS
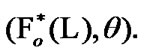 (7.6)
(7.6)
Let 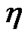 be arbitrary nonempty centered subfamily of
be arbitrary nonempty centered subfamily of  (for any
(for any  and
and 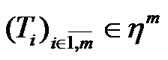 the intersection of all sets
the intersection of all sets 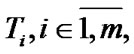 is not empty). If
is not empty). If  then the family
then the family
 (7.7)
(7.7)
has the property: 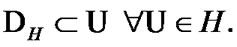 Of course,
Of course,

is centered. Indeed, choose 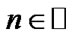 and
and 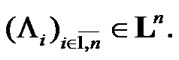 Let
Let  be a procession with the property:
be a procession with the property:
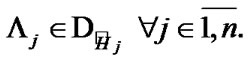
Then, in particular,  In addition, by (7.7)
In addition, by (7.7)
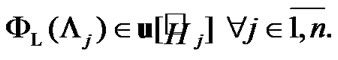 Of course,
Of course,

Since the intersection of all sets 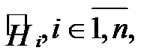 is not empty (we use the centrality of
is not empty (we use the centrality of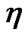 ), we choose an ultrafilter
), we choose an ultrafilter
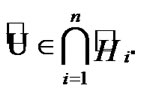
Then, 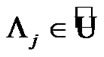 under
under 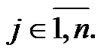 By axioms of a filter (see Section 5) we obtain that
By axioms of a filter (see Section 5) we obtain that
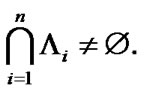
Since  is closed with respect to finite intersections, we obtain that
is closed with respect to finite intersections, we obtain that
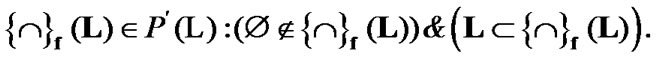 (7.8)
(7.8)
Moreover, (7.8) is supplemented by the following obvious property; namely,

From (5.7), we obtain that 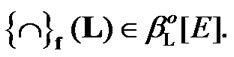 As a corollary,
As a corollary,
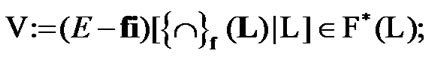
in addition, by (7.8) 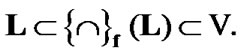 Finally, we use (5.2). Let
Finally, we use (5.2). Let 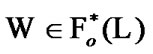 be an ultrafilter for which
be an ultrafilter for which 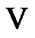
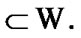 Then,
Then, 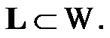 So,
So,
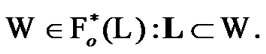 (7.9)
(7.9)
Let  Then,
Then, 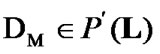 and the equality
and the equality
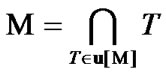 (7.10)
(7.10)
is valid (see (7.5)). Choose arbitrary 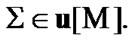 Then,
Then, 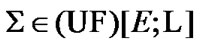 and
and  Using (5.4), we choose
Using (5.4), we choose 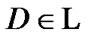 for which
for which  Then
Then
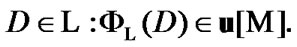
By (7.7) 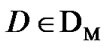 and, in particular,
and, in particular,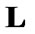
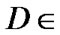 . By (7.9)
. By (7.9) 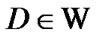 and, as a corollary,
and, as a corollary,  see (5.3). So,
see (5.3). So, 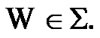 Since the choice of
Since the choice of 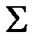 was arbitrary, we obtain that
was arbitrary, we obtain that  By (7.10)
By (7.10)  So, we have the property:
So, we have the property:
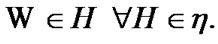
Then, the intersection of all sets of  is not empty. Since the choice of
is not empty. Since the choice of  was arbitrary, it is established that any nonempty centered family of closed (in TS (7.6)) sets has the nonempty intersection. So, TS (7.6) is compact (see [11-13]).
was arbitrary, it is established that any nonempty centered family of closed (in TS (7.6)) sets has the nonempty intersection. So, TS (7.6) is compact (see [11-13]).
Using Proposition 7.2, by  we denote the topology (7.3); so,
we denote the topology (7.3); so,
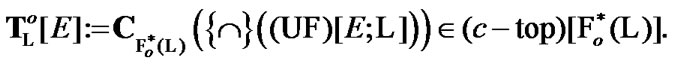
(7.11)
We have the nonempty compact TS
 (7.12)
(7.12)
Proposition 7.3. If 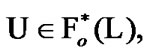 then
then

The corresponding proof follows from (6.2); of course, we use (5.4) also. From (2.18), (7.11), and Proposition 7.3, we obtain the following property:
 (7.13)
(7.13)
So, by (7.13) we obtain that (7.12) is a nonempty compact  -space.
-space.
In conclusion of the given section, we note several properties. First, we recall that
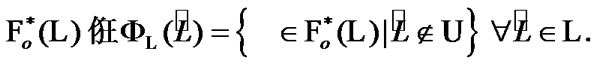 (7.14)
(7.14)
In addition, from (7.11), the obvious representation follows:
 (7.15)
(7.15)
With the employment of (7.15) the following statement is established.
Proposition 7.4. If 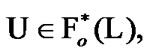 then the family
then the family

is a local base of TS (7.12) at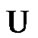 :
:

The proof is obvious. So, by (3.4) and Proposition 7.4
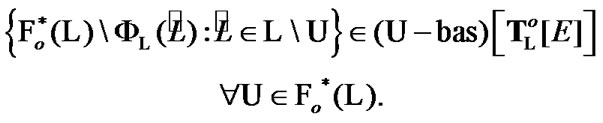
We note that, from definitions, the following property is valid:
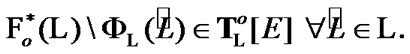 (7.16)
(7.16)
8. The Density Properties
In this section, we continue the investigation of TS (7. 12). Of course, we preserve the suppositions of Section 7 with respect to E and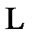 . But, in this section, we postulate that
. But, in this section, we postulate that 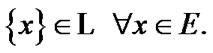 So, in this section
So, in this section
 (8.1)
(8.1)
unless otherwise stipulated. So,  and
and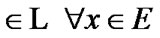
 . Therefore, with regard (3.9) and (8.1), we obtain that
. Therefore, with regard (3.9) and (8.1), we obtain that
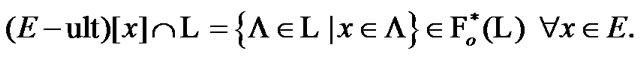 (8.2)
(8.2)
Of course, for any 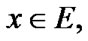 the inclusion
the inclusion 
 is valid.
is valid.
Proposition 8. 1.
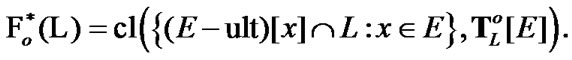
Proof. Let 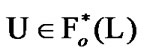 and
and  We use Propposition 7.4. Namely, we choose a set
We use Propposition 7.4. Namely, we choose a set  for which
for which
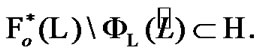 (8.3)
(8.3)
Since 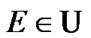 by axioms of a filter (see Section 5), we obtain that
by axioms of a filter (see Section 5), we obtain that 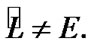 in addition,
in addition,  and by (2.4) and (8.1)
and by (2.4) and (8.1)  So,
So, 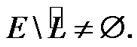 Choose arbitrary point
Choose arbitrary point  and consider the ultrafilter
and consider the ultrafilter
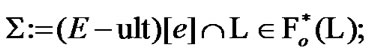 (8.4)
(8.4)
see (8.2). In addition,  As a corollary, by definitions of Section 5
As a corollary, by definitions of Section 5
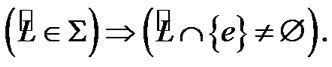 (8.5)
(8.5)
But, 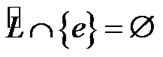 by the choice of e. Therefore, by (8. 5)
by the choice of e. Therefore, by (8. 5) 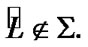 From (5.3) we have the property
From (5.3) we have the property 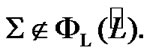 As a corollary, by (8.4)
As a corollary, by (8.4)
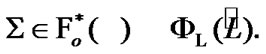 (8.6)
(8.6)
From (8.3) and (8.6), we obtain that  By (8.4)
By (8.4)
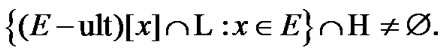 (8.7)
(8.7)
Since the choice of 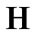 was arbitrary,
was arbitrary,

Since the choice of 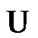 was arbitrary, the inclusion
was arbitrary, the inclusion
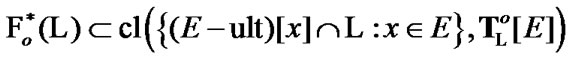
is established. The inverse inclusion is obvious (see (7. 11)).
So, we obtain that trivial ultrafilters (8.2) realize an everywhere dense set in the TS (7.12).
Returning to (7.11), we note one obvious property connected with (7.16). Namely, by (2.14) and Proposition 7.1, in general case of 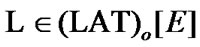

and, in particular, 
then, for 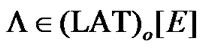

And what is more by (2.17), (7.11), and Proposition 7.1, in general case of 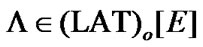
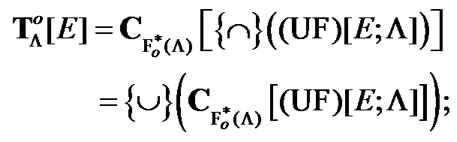 (8.8)
(8.8)
so, by (8.8)  is a base of topology (7.11). We recall that by (2.8) and (5.4), for general case of
is a base of topology (7.11). We recall that by (2.8) and (5.4), for general case of 
 (8.9)
(8.9)
Connection with Wallman extension. Let 
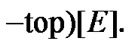 Then,
Then, 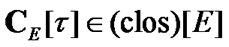 and by (2.18)
and by (2.18) 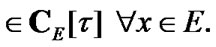
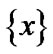 Using (2.7), we obtain that
Using (2.7), we obtain that 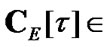
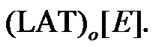 with the employment of the above-mentioned closedness of singletons, by the corresponding definition of Section 2 we obtain that
with the employment of the above-mentioned closedness of singletons, by the corresponding definition of Section 2 we obtain that
 (8.10)
(8.10)
Until the end of the present section, we suppose that
 (8.11)
(8.11)
So, in our case,  is the lattice of closed sets in T1- space. Then, (7.12) is the corresponding Wallman compact space (see [13]). On the other hand, by (8.10) and (8.11) we obtain that this variant of
is the lattice of closed sets in T1- space. Then, (7.12) is the corresponding Wallman compact space (see [13]). On the other hand, by (8.10) and (8.11) we obtain that this variant of 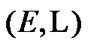 corresponds to general statements of our section (for example, see (8.2) and Proposition 8.1). In this connection, we consider the mapping
corresponds to general statements of our section (for example, see (8.2) and Proposition 8.1). In this connection, we consider the mapping

(8.12)
we denote the mapping (8.12) by . So,
. So,  and
and
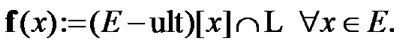
Consider some simple properties. First, we note that  is injective:
is injective: 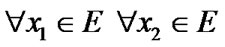
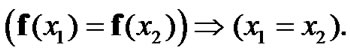 (8.13)
(8.13)
Indeed, for 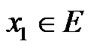 and
and 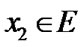 with the property
with the property 
 by (3.9) we have that
by (3.9) we have that 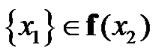 and, as a corollary,
and, as a corollary, 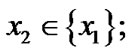 so,
so, 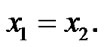
Of course, 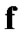 is a bijection from E onto the set
is a bijection from E onto the set
 (8.14)
(8.14)
If 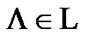 and
and 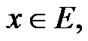 then
then  As a corollary, we obtain that
As a corollary, we obtain that
 (8.15)
(8.15)
Remark 8.1. Of course, in (8.15), we use the representation (8.12). Fix  Let
Let  Then
Then 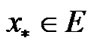 and
and  By (5.3)
By (5.3)  and, as a corollary,
and, as a corollary,  So,
So,
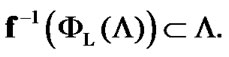 (8.16)
(8.16)
If  then
then  see (8.12). Therefore, by (5.3)
see (8.12). Therefore, by (5.3) 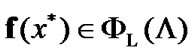 and, as a corollary,
and, as a corollary, 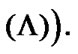
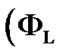
 So,
So, 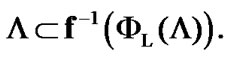 Therefore (see (8.16))
Therefore (see (8.16)) 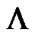 and
and  coincide.
coincide.
From (5.4) and (8.15), we obtain that
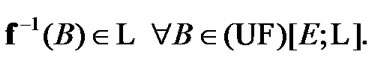 (8.17)
(8.17)
Proposition 8.2. 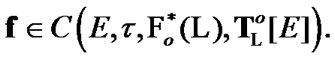
Proof. We use the construction dual with respect to (4.20). Let 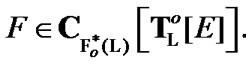 Then, by (8.8)
Then, by (8.8) 
 Therefore, for some
Therefore, for some 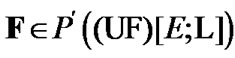

As a result, we obtain that
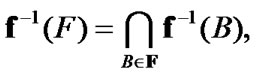 (8.18)
(8.18)
where 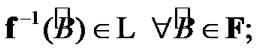 see (8.17). By (2.6), (2.9), (8.11), and (8.18) we have the property:
see (8.17). By (2.6), (2.9), (8.11), and (8.18) we have the property:
 and
and
 (8.19)
(8.19)
Since the choice of F was arbitrary, from (8.19) we obtain the required continuity property (see [16, (2.5.2)]).
Corollary 8.1. 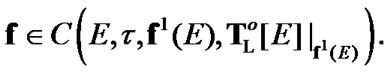
Proof. Recall that 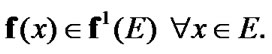 In addition, by (8.14)
In addition, by (8.14)

Let  and
and  realizes the equality
realizes the equality  By Proposition 8.2
By Proposition 8.2
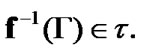 (8.20)
(8.20)
In addition, 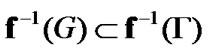 (indeed,
(indeed,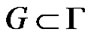 ). Let
). Let 
 Then,
Then, 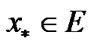 and
and 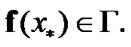 But,
But, 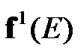
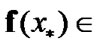 too. Then,
too. Then, 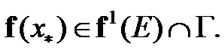 So,
So,  Therefore,
Therefore, 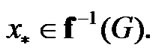 Since the choice of
Since the choice of 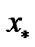 was arbitrary, the inclusion
was arbitrary, the inclusion
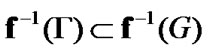
is established. So,  By (8.20)
By (8.20) 
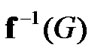 Since the choice of G was arbitrary, the inclusion
Since the choice of G was arbitrary, the inclusion
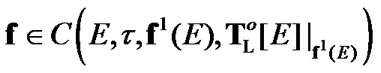 is established.
is established.
Recall that 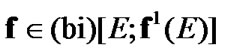 (see (4.21)).
(see (4.21)).
Proposition 8.3. 
Proof. Let 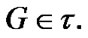 Then
Then 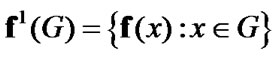 and
and 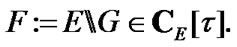 By (8.11)
By (8.11) 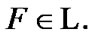 In addition, by (5.3)
In addition, by (5.3)
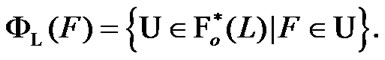 (8.21)
(8.21)
Of course, by (5.4) 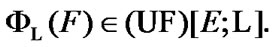 Then
Then
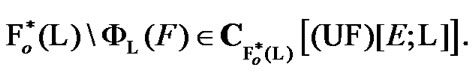
As a corollary, 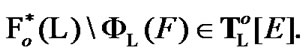 Therefore,
Therefore,
 (8.22)
(8.22)
Now, we compare 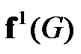 and
and  (8.22). Let
(8.22). Let 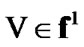
 Then, for some
Then, for some 
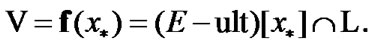 (8.23)
(8.23)
Of course, 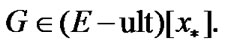 By (3.9)
By (3.9) 
 (indeed,
(indeed, ). By (8.23)
). By (8.23) 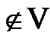
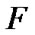 and, as a corollary,
and, as a corollary, 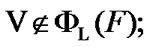 see (8.21). We obtain that
see (8.21). We obtain that
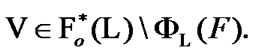 (8.24)
(8.24)
Since 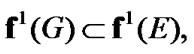 we have the inclusion
we have the inclusion 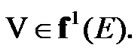 Using (8.22) and (8.24), we obtain that
Using (8.22) and (8.24), we obtain that 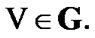 The inclusion
The inclusion
 (8.25)
(8.25)
is established. Choose arbitrary  then, by (8. 22), for some
then, by (8. 22), for some 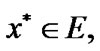 the equality
the equality 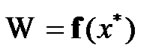 is valid. So,
is valid. So,
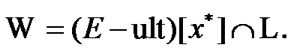 (8.26)
(8.26)
Moreover, 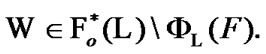 So,
So, 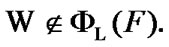 By (8.21)
By (8.21) 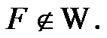 Since
Since  by (8.26)
by (8.26) 
 From (3.9), the property
From (3.9), the property  follows. Then,
follows. Then, 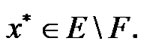 Therefore,
Therefore,  as a corollary,
as a corollary, 
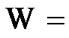 The inclusion
The inclusion 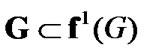 is established. Using (8.25), we obtain that
is established. Using (8.25), we obtain that 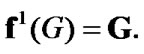 By (8.22)
By (8.22)

Since the choice of G was arbitrary, by Corollary 8.1 and (4.22) we have the inclusion
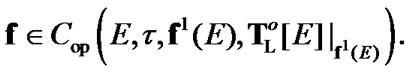
By (4.24), (8.13), and Proposition 8.3 we obtain that
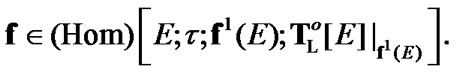 (8.27)
(8.27)
So, we construct the concrete homeomorphic inclusion of  -space in the compact
-space in the compact 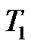 -space (in this connection, we recall that by Proposition 8.1
-space (in this connection, we recall that by Proposition 8.1

moreover, see (7.13)). So, we have the “usual” Wallman extension.
9. Ultrafilters of Measurable Space
In this section, we fix a nonempty set 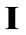 and an algebra
and an algebra  of subsets of
of subsets of  So, in this section,
So, in this section,  is a measurable space with an algebra of sets:
is a measurable space with an algebra of sets: 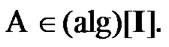 Of course, we can to use constructions of Section 5; indeed, in particular, we have the inclusion
Of course, we can to use constructions of Section 5; indeed, in particular, we have the inclusion 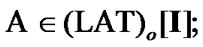 see (2.10). As a corollary, by (2.4)
see (2.10). As a corollary, by (2.4) 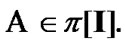 So, we use the sets
So, we use the sets 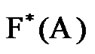 and
and 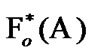 of Section 5; we use properties of these sets also. We note the known representation (see [15]):
of Section 5; we use properties of these sets also. We note the known representation (see [15]):
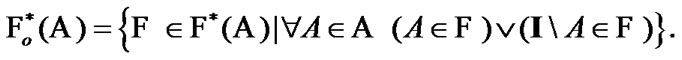 (9.1)
(9.1)
Now, we use (9.1) for investigation of TS (7.12) in the case 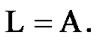 First, we note the obvious corollary of (9.1):
First, we note the obvious corollary of (9.1):
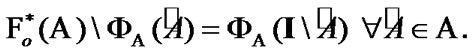 (9.2)
(9.2)
Remark 9.1. Let 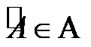 is fixed. Choose arbitrary
is fixed. Choose arbitrary  Then, by (7.14)
Then, by (7.14)  By (9.1)
By (9.1) 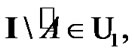 where
where 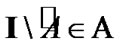 by axioms of an algebra of sets. So, by (5.3)
by axioms of an algebra of sets. So, by (5.3)  The inclusion
The inclusion
 (9.3)
(9.3)
is established. Let  Then, by (5.3)
Then, by (5.3) 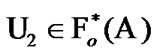 and
and  By axioms of a filter
By axioms of a filter

So, 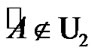 and
and 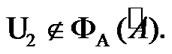 As a corollary,
As a corollary,  So, the inclusion
So, the inclusion

is established. Using (9.3), we obtain the required coincidence 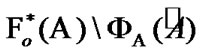 and
and 
Returning to (9.2) in general case, we note the following obvious Proposition 9.1. 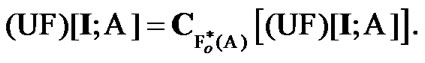
Proof. Let 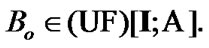 Using (5.4), we choose
Using (5.4), we choose 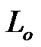
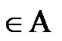 such that
such that  Then
Then 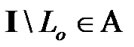 and by (9.2)
and by (9.2)
 (9.4)
(9.4)
From (5.4), we have the obvious inclusion 
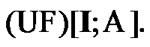 By (9.4)
By (9.4)
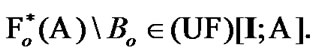
Therefore, we obtain the following property:

The inclusion 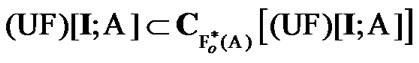 is established. Choose arbitrary
is established. Choose arbitrary
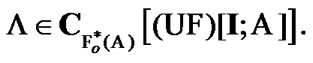 (9.5)
(9.5)
Using (2.8), we choose  such that
such that 
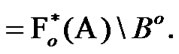 Let
Let  be the set for which
be the set for which 
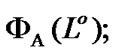 see (5.4). Then, by (9.2)
see (5.4). Then, by (9.2)
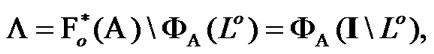 (9.6)
(9.6)
where 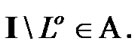 Since by (5.4)
Since by (5.4) 
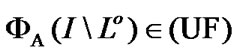 from (9.6), we obtain that
from (9.6), we obtain that

Since the choice of 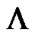 (9.5) was arbitrary, the inclusion
(9.5) was arbitrary, the inclusion

is established. So, we obtain the required equality.
From (6.4), (8.8), and Proposition 9.1, the simple (but useful) statement follows.
Proposition 9.2. 
So, for measurable spaces with algebras of sets, the topological representations of Sections 6 and 7, 8 realize the same topology. By (6.5), (7.13), and Proposition 9.2
 (9.7)
(9.7)
So, we obtain a nonempty compactum. Recall that (see (7.11), Proposition 9.2)
 (9.8)
(9.8)
is the family of all sets closed in the sense of topology (9.7). We note the following obvious property (see [15, ch.I])
 (9.9)
(9.9)
Remark 9.2. We recall (5.4). Let 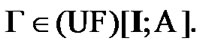 Using (5.4), we choose
Using (5.4), we choose 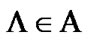 such that
such that  Then,
Then,  and by (9.2)
and by (9.2)
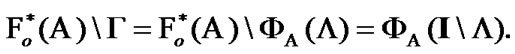 (9.10)
(9.10)
By (5.4) and (9.10) 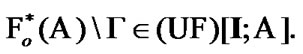 So, we establish that
So, we establish that
 (9.11)
(9.11)
From (2.10), (5.4), and (9.11), the property (9.9) follows.
Proposition 9.3. 
Proof. Recall that by statements of Section 2 and (9.8) the inclusion
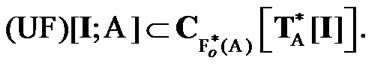 (9.12)
(9.12)
From (6.4), the inclusion 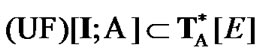 follows too. So, by (9.12)
follows too. So, by (9.12)
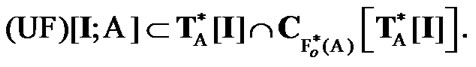 (9.13)
(9.13)
Let  Since
Since  is open, then by (6.4) we obtain that, for some family
is open, then by (6.4) we obtain that, for some family
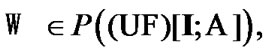 (9.14)
(9.14)
the following equality is realized:
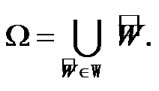 (9.15)
(9.15)
If  then by (9.15)
then by (9.15) 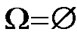 and, as a corollary,
and, as a corollary, 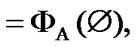
 where
where 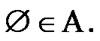 So, by (5.4) we obtain the implication
So, by (5.4) we obtain the implication
 (9.16)
(9.16)
Let  Then,
Then,  Since
Since 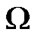 is a closed subset of a compactum, we have the compactess property of
is a closed subset of a compactum, we have the compactess property of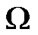 ; then, by (9.14), for some
; then, by (9.14), for some 
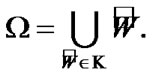 (9.17)
(9.17)
In particular, 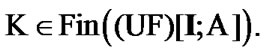 We note that
We note that 
 is closed with respect to finite unions (indeed, by (9.9)
is closed with respect to finite unions (indeed, by (9.9)  is an algebra of sets). Therefore, by (9.17)
is an algebra of sets). Therefore, by (9.17) 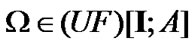 in the case
in the case 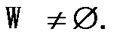 So,
So,
 (9.18)
(9.18)
Using (9.16) and (9.18), we obtain that 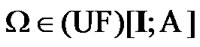 in any possible cases. Since the choice of
in any possible cases. Since the choice of  was arbitrary, the inclusion
was arbitrary, the inclusion
 (9.19)
(9.19)
in established. From (9.13) and (9.18), the required statement follows.
So,  is the family of all open-closed sets in the nonempty compactum
is the family of all open-closed sets in the nonempty compactum
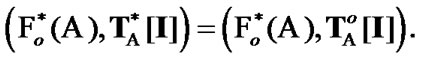 (9.20)
(9.20)
In connection with the above-mentioned property of nonempty compactum (9.20), we recall [15, ch. I]. With the employment of (9.1), the following obvious property is established: in our case of measurable space with an algebra of sets
 (9.21)
(9.21)
Remark 9.3. For a completeness, we consider the scheme of the proof of (9.21). For this, we note that by (3.9) and the corresponding definition of Section 5
 (9.22)
(9.22)
In particular, by (9.22) 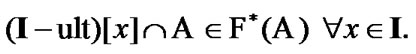 Fix
Fix 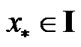 and suppose that
and suppose that

of course, 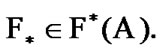 In addition,
In addition,  Then,
Then, 
 (9.23)
(9.23)
Of course, by (3.9), for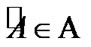 , we have the following obvious implications:
, we have the following obvious implications:
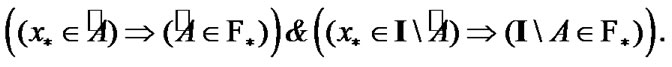
Then, by (9.23)  Since the choice of
Since the choice of  was arbitrary, by (9.1)
was arbitrary, by (9.1)  So, (9.21) is established.
So, (9.21) is established.
Using (9.21), we introduce the mapping
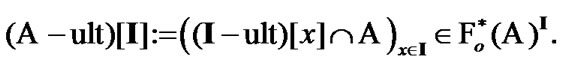 (9.24)
(9.24)
Of course, in (9.24) we have analog of the mapping 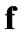 (8.12). But, in the given case, we realize the immersion of points of the initial set in the ultrafilter space under other conditions. We will use the specific character of measurable space with an algebra of sets. Now, we note the obvious property:
(8.12). But, in the given case, we realize the immersion of points of the initial set in the ultrafilter space under other conditions. We will use the specific character of measurable space with an algebra of sets. Now, we note the obvious property:
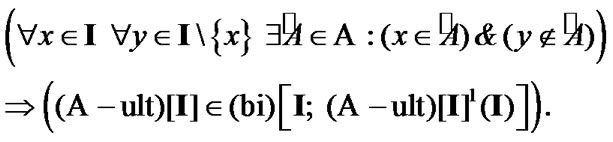 (9.25)
(9.25)
In (9.25), the statement of the premise has the following sense: algebra  is distinguishing for points of
is distinguishing for points of .
.
If 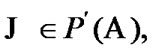 then by analogy with Section 4 we suppose that
then by analogy with Section 4 we suppose that
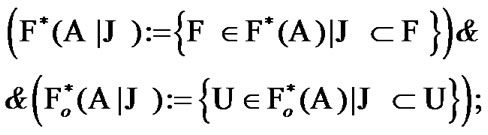 (9.26)
(9.26)
of course,  and moreover the following property is valid:
and moreover the following property is valid:
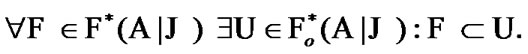 (9.27)
(9.27)
Returning to (9.25), we note that
 (9.28)
(9.28)
In (9.28), we can use  as constraints of asymptotic character. Of course,
as constraints of asymptotic character. Of course,  (see Section 5). Then, by (3.3)
(see Section 5). Then, by (3.3)
 (9.29)
(9.29)
By analogy with (9.29) we note that 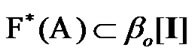 and
and 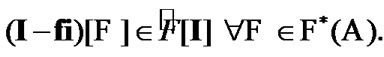 These properties permit realize an asymptotic analogs of solutions of the set (9.28). In this capacity, we can use elements of the sets
These properties permit realize an asymptotic analogs of solutions of the set (9.28). In this capacity, we can use elements of the sets 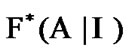 and
and  where
where 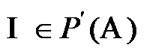 is used as “asymptotic constraints”. Of course,
is used as “asymptotic constraints”. Of course, 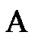 bounds our possibilities: we can use only subfamilies of
bounds our possibilities: we can use only subfamilies of .
.
Proposition 9.4. 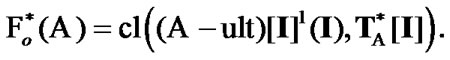
Proof. Fix  Let
Let 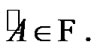 Then
Then  So,
So,  and
and 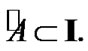 Choose arbitrary
Choose arbitrary  Then, by (9.24)
Then, by (9.24)
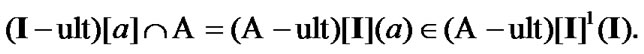 (9.30)
(9.30)
By the choice of  we have the inclusion
we have the inclusion 
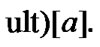 Since
Since  we obtain that
we obtain that  Then, by (9.30)
Then, by (9.30)  Since
Since 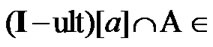
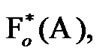 by (5.3)
by (5.3)
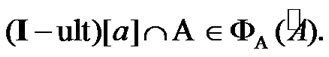 (9.31)
(9.31)
By (9.30) and (9.31) we obtain the following property
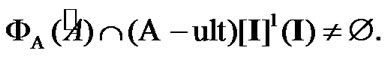
Since the choice of  was arbitrary, we have (see (8.3)) the statement
was arbitrary, we have (see (8.3)) the statement
 (9.32)
(9.32)
Choose arbitrary  Then, for some
Then, for some 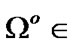
 the inclusion
the inclusion 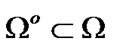 is valid. Therefore,
is valid. Therefore, 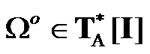 and
and 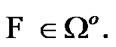 By (6.4), there exists
By (6.4), there exists 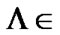
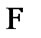 such that
such that
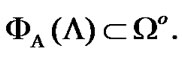 (9.33)
(9.33)
From (9.32), the property  is valid. By (9.33) we obtain that
is valid. By (9.33) we obtain that
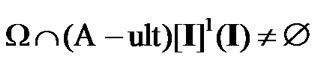
(indeed,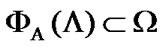 ). Since the choice of
). Since the choice of 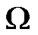 was arbitrary,
was arbitrary,

Then, 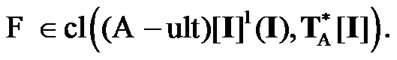 So, the inclusion
So, the inclusion
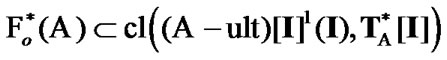
is established. The opposite inclusion is obvious.
We note that Proposition 9.4 is similar to Proposition 8.1. But, in the given section, the condition
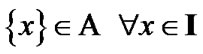 (9.34)
(9.34)
is supposed not; in Section 8 (in particular, in Proposition 8.1), the condition similar to (9.34) is essential. So, Proposition 9.4 has the independent meaning.
10. Attraction Sets Under the Restriction in the Form of Algebra of Sets
In the following, we fix a nonempty set E, a TS  where
where 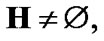 and a mapping
and a mapping  Elements
Elements 
 are considered as usual solutions and elements
are considered as usual solutions and elements 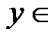
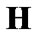 play the role of some estimates. The natural variant of an obtaining of
play the role of some estimates. The natural variant of an obtaining of  is realized in the form
is realized in the form 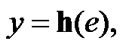 where
where 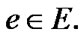 But, we admit the possibility of the limit realization of
But, we admit the possibility of the limit realization of 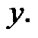 This is natural in questions of asymptotic analysis. In the last case, it is natural to use “asymptotic constraints” in the form of a nonempty subfamilies of
This is natural in questions of asymptotic analysis. In the last case, it is natural to use “asymptotic constraints” in the form of a nonempty subfamilies of 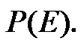 Then, we obtain constructions of Section 4 under
Then, we obtain constructions of Section 4 under  and
and 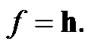 But, we admit yet one possibility: along with “usual” AS, we use the sets
But, we admit yet one possibility: along with “usual” AS, we use the sets
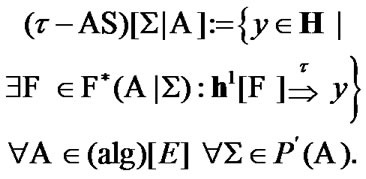 (10.1)
(10.1)
Of course, we use remarks of the conclusion of the previous section.
Proposition 10.1. If  and
and  then
then
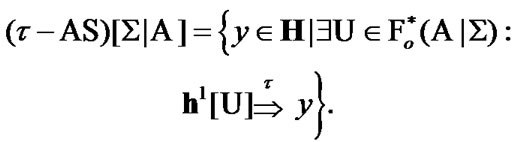 (10.2)
(10.2)
Proof. We use reasoning analogous to the proof of Proposition 4.2. We denote by  the set on the right side of (10.2). Since
the set on the right side of (10.2). Since  (see Section 9), by (10.1)
(see Section 9), by (10.1)
 (10.3)
(10.3)
Let  Then, by (10.1)
Then, by (10.1)  and, for some
and, for some 
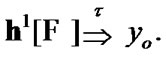 (10.4)
(10.4)
Recall that  (see Section 9). Therefore, by (4.1)
(see Section 9). Therefore, by (4.1)  Then, (10.4) denotes that
Then, (10.4) denotes that
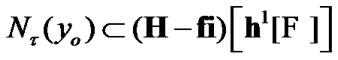 (10.5)
(10.5)
(see (3.5)). In addition, by the choice of 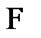 we have the inclusion
we have the inclusion  see (9.26). By (9.27), for some
see (9.26). By (9.27), for some 
 the inclusion
the inclusion 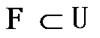 is valid. Then,
is valid. Then,

As a corollary, by(3.3) and (10.5)
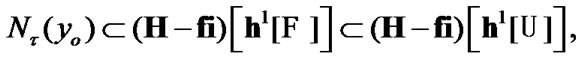
where  (see Section 9). Then, by (3.5)
(see Section 9). Then, by (3.5)
 (10.6)
(10.6)
By definition of 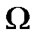 we obtain that
we obtain that 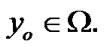 Since the choice of
Since the choice of  was arbitrary, the inclusion
was arbitrary, the inclusion
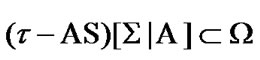 (10.7)
(10.7)
is established. Using (10.3) and (10.7), we obtain the required equality
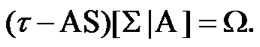 (10.8)
(10.8)
From the definition of 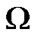 and (10.8), we obtain (10.2).
and (10.8), we obtain (10.2).
Recall that  and therefore
and therefore

By definitions of Section 3, (6.6), and (9.26) we obtain that
 (10.9)
(10.9)
From Propositions 4.2 and 10.1, we have (see (10.9)) the property:

So, our new construction is coordinated with AS of Section 4. Moreover, under  we can consider AS
we can consider AS  for
for 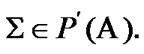
Proposition 10.2. If 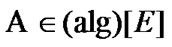 and
and  then
then
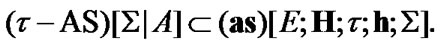 (10.10)
(10.10)
Proof. We use (6.8). Choose 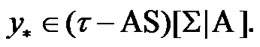 Then,
Then,  and, for some
and, for some 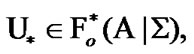 the convergence
the convergence
 (10.11)
(10.11)
is valid. Then, 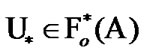 and
and  see (9.26). By (6.8) for some
see (9.26). By (6.8) for some  the equality
the equality 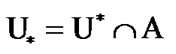 is valid. Then,
is valid. Then, 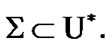 As a corollary,
As a corollary,  Now, we return to (10.11). In addition,
Now, we return to (10.11). In addition,  Therefore,
Therefore, 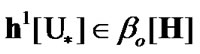 and by (3.3)
and by (3.3)
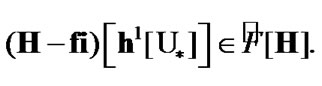
From (3.5) and (10.11), we have the obvious inclusion
 (10.12)
(10.12)
In addition, 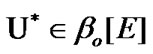 and
and  see (4. 1). Since
see (4. 1). Since  the inclusion
the inclusion 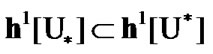 is valid. As a corollary, by (3.3)
is valid. As a corollary, by (3.3)
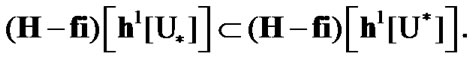
Using (10.12), we obtain the basic inclusion
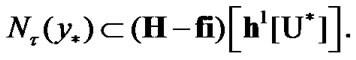 (10.13)
(10.13)
From (3.5) and (10.13), we obtain the following convergence
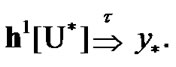 (10.14)
(10.14)
So, 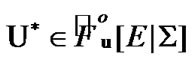 has the property (10.14). Then, by Proposition 4.2
has the property (10.14). Then, by Proposition 4.2
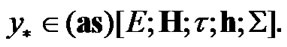
Since the choice of 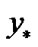 was arbitrary, the required inclusion (10.10) is established.
was arbitrary, the required inclusion (10.10) is established.
So, by (10.1) and (10.2) some “partial” AS are defined. Of course, the case for which (10.10) is converted in a equality is very interesting. For investigation of this case, we consider auxiliary constructions. In the following, in this section, we fix 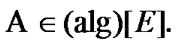 So,
So,  is a measurable space with an algebra of sets. In this case, we can supplement the property (6.8). Namely,
is a measurable space with an algebra of sets. In this case, we can supplement the property (6.8). Namely,
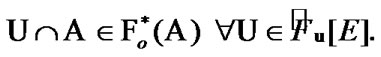 (10.15)
(10.15)
Remark 10.1. We omit the sufficiently simple proof (10.15). Now, we are restricted to brief remarks. Namely, by ultrafilter 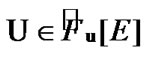 we can realize a finitely additive (0,1)-measure
we can realize a finitely additive (0,1)-measure 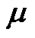 on the family
on the family  supposing that
supposing that  under
under 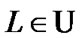 and
and 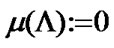 under
under 
 In connection with such possibility, we use [9,(7.6.17)] (moreover, see [9,(7.6.7)]). The natural narrowing v of
In connection with such possibility, we use [9,(7.6.17)] (moreover, see [9,(7.6.7)]). The natural narrowing v of 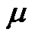 on our algebra
on our algebra 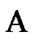 is finitely additive (0,1)-measure on
is finitely additive (0,1)-measure on 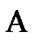 (of course,
(of course,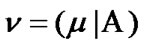 ). Therefore, for some
). Therefore, for some 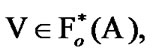 by [9,(7.6.17)]
by [9,(7.6.17)] 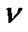 is defined by the rule
is defined by the rule
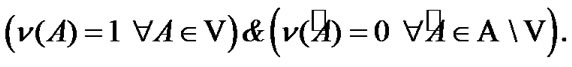 (10.16)
(10.16)
On the other hand, the family 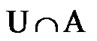 realizes
realizes 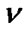 by the obvious rule:
by the obvious rule:

(10.17)
From (10.16) and (10.17), the required equality 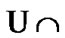
 follows. Then, by the choice of
follows. Then, by the choice of 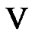 we have the inclusion
we have the inclusion 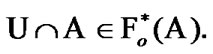
Using (6.8) and (10.15), we obtain that
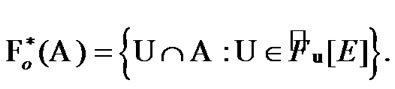 (10.18)
(10.18)
By (10.18) we establish the natural connection of  and
and  Now, we consider some other auxiliary properties.
Now, we consider some other auxiliary properties.
If  and
and  then we have the following equivalence
then we have the following equivalence
 (10.19)
(10.19)
Of course, we can use instead of  the corresponding image of a filter base in
the corresponding image of a filter base in  Indeed, by (4.1) and (10.19)
Indeed, by (4.1) and (10.19) 
 (10.20)
(10.20)
Moreover, in connection with (10.20), we note that 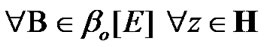
 (10.21)
(10.21)
Remark 10.2. Consider the proof of (10.21). Fix 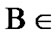
 and
and  Let
Let 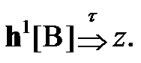 Then, by (10.20)
Then, by (10.20)

Therefore, for any , there exists
, there exists  such that
such that 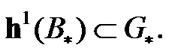 As a corollary,
As a corollary,
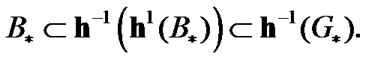
Then, 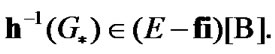 Since the choice of
Since the choice of 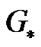 was arbitrary,
was arbitrary,

So,  Let
Let
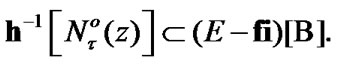 (10.22)
(10.22)
Choose arbitrary neighborhood 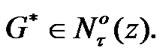 Then, by (10.22)
Then, by (10.22)  Therefore, for some
Therefore, for some 
 the inclusion
the inclusion 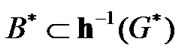 is valid. In addition,
is valid. In addition,  and
and
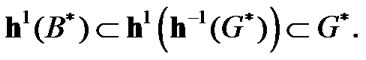
Then, 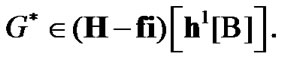 Therefore,
Therefore, 
 and by (10.20)
and by (10.20)  So,
So,

The proof of (10.21) is completed.
We note that, in (10.21), we can use instead of  arbitrary filter of
arbitrary filter of  In this connection, we recall that by constructions of Section 5, for any
In this connection, we recall that by constructions of Section 5, for any  we obtain (in particular) that
we obtain (in particular) that 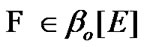 and
and
 (10.23)
(10.23)
Then, from (10.21) and (10.23), we have the following property: 
 (10.24)
(10.24)
Of course, (10.24) is the particular case of (10.21); in (10.23), we have the useful addition. We note that 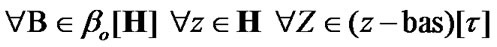

(10.25)
Remark 10.3. Fix 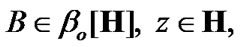 and
and 
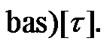 Consider the proof of (10.25). By (3.4) and (3.5) we have the following implication
Consider the proof of (10.25). By (3.4) and (3.5) we have the following implication
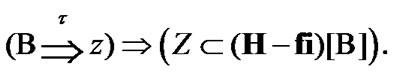 (10.26)
(10.26)
Let 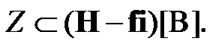 Choose arbitrary
Choose arbitrary 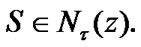 Then, by (2.18), for some
Then, by (2.18), for some 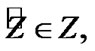 the inclusion
the inclusion 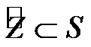 is valid. Since
is valid. Since  by filter axioms (see 3.1))
by filter axioms (see 3.1))  So, the inclusion
So, the inclusion  is established. By (3.5) we have the convergence
is established. By (3.5) we have the convergence 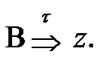 So,
So,

Now, with the employment of (10.26), we obtain (10.25).
We note the following obvious corollary of (10.25) (in this connection, we recall (10.21)): 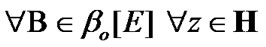
 (10.27)
(10.27)
Remark 10.4. Consider the proof of (10.27). We fix 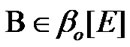 and
and 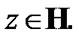 Since
Since 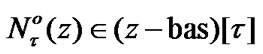 (see (3.4) and definitions of Section 3), by (10.21)
(see (3.4) and definitions of Section 3), by (10.21)
 (10.28)
(10.28)
Let the corollary of (10.28) is valid. Fix  with the property
with the property
 (10.29)
(10.29)
Let 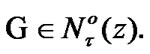 Then, by (3.4), for some
Then, by (3.4), for some 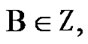 the inclusion
the inclusion 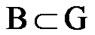 is valid, where
is valid, where 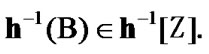 By (10.29)
By (10.29) 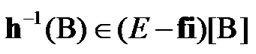 and
and  From (3.1) and (3.3), the inclusion
From (3.1) and (3.3), the inclusion  follows. Since the choice of
follows. Since the choice of 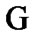 was arbitrary, the inclusion
was arbitrary, the inclusion
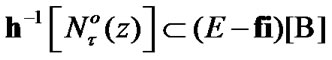
is established. By (10.21)  So, we obtain that
So, we obtain that
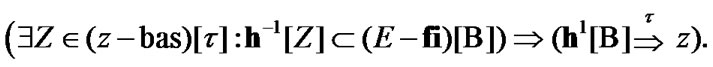
Using the last implication and (10.28), we obtain the required property (10.27).
Using (10.15), we obtain the obvious corollary of (10.27): 
 (10.30)
(10.30)
Remark 10.5. Consider the proof of (10.30), fixing  and
and  Then, by (10.15)
Then, by (10.15) 
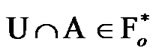 In particular (see Section 9),
In particular (see Section 9),  Now, (10.30) follows from (10.27).
Now, (10.30) follows from (10.27).
Condition 10.1. 

Remark 10.6. It is possible to consider Condition 10.1 as a weakened variant of the measurability of 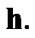 The usual measurability of
The usual measurability of 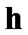 is not natural since
is not natural since  is only algebra of sets.
is only algebra of sets.
Until the end of the present section, we suppose that Condition 10.1 is valid.
Proposition 10.3. If Condition 10.1 is fulfilled, then 
Proof. Let Condition 10.1 be fulfilled. Fix 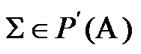 and
and  Then,
Then,  and, for some
and, for some 
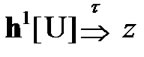 (10.31)
(10.31)
(see Proposition 4.2). Then, by (10.21) and (10.31) we have the inclusion  since
since 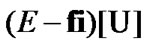
 by (3.1). As a corollary,
by (3.1). As a corollary,
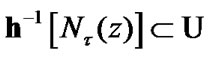
(indeed, for 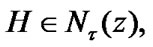 we can choose
we can choose 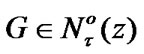 such that
such that 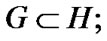 therefore, by (2.1)
therefore, by (2.1) 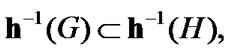
 and by (3.1)
and by (3.1)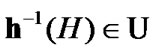 ). By Condition 10.1 there exists
). By Condition 10.1 there exists  such that
such that  In addition,
In addition,
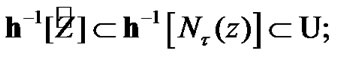 (10.32)
(10.32)
therefore, 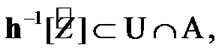 where by (10.15)
where by (10.15) 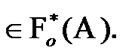
 We recall that
We recall that 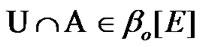 (see Section 9) and
(see Section 9) and
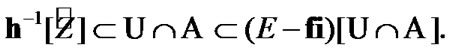 (10.33)
(10.33)
Of course, by (4.1) 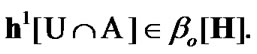 In addition, by (10.33)
In addition, by (10.33)

By (10.27)  Recall that
Recall that  Since
Since  we obtain that
we obtain that  Therefore (see (9.26)),
Therefore (see (9.26)),
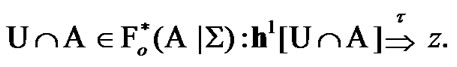
By Proposition 10.1  Since the choice of
Since the choice of 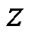 was arbitrary, we have the inclusion
was arbitrary, we have the inclusion
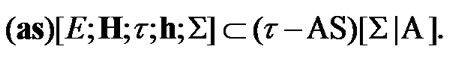 (10.34)
(10.34)
Using (10.34) and Proposition 10.2, we obtain the equality
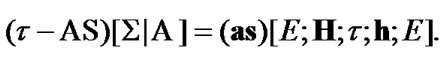
So, we can use (see Proposition 10.1 and Condition 10.1) ultrafilters of the space  as nonsequential approximate solutions in the case, when a nonempty subfamily of
as nonsequential approximate solutions in the case, when a nonempty subfamily of  is used as the constraint of asymptotic character. This property is very useful in the cases of spaces
is used as the constraint of asymptotic character. This property is very useful in the cases of spaces 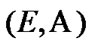 for which the set
for which the set 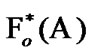 is realized effectively. In addition, for a semialgebra
is realized effectively. In addition, for a semialgebra  with the property
with the property  (see Section 2), we consider the passage
(see Section 2), we consider the passage

as an unessential transformation (see [9,§7.6] and [16,§ 2.4]; here it is appropriate to use the natural connection of ultrafilters and finitely additive (0,1)-measures). Then, after unessential transformations, the examples of [9,§ 7.6] can be used in our scheme sufficiently constructively.
11. Ultrasolutions
First, we recall some statements of [17]. In addition, we fix a nonempty set E and a TS 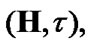 where
where  We consider the nonempty set
We consider the nonempty set 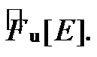 Suppose that
Suppose that  Then, we suppose that
Then, we suppose that
 (11.1)
(11.1)
So, we introduce the limit sets corresponding to ultrafilters of 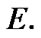 By analogy with Proposition 5.4 of [17] the following statement is established.
By analogy with Proposition 5.4 of [17] the following statement is established.
Proposition 11.1. If  then
then 
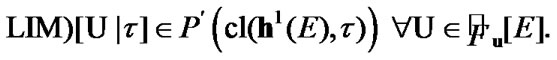
Proof. Fix  Then
Then 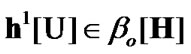 and by (4.2)
and by (4.2)
 (11.2)
(11.2)
(recall that 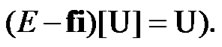 Since
Since  is a compact TS, there exists
is a compact TS, there exists 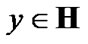 such that
such that 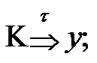 see [9, ch. I]. Then, by (3.6)
see [9, ch. I]. Then, by (3.6)  or
or
 (11.3)
(11.3)
(see (11.2)). By (3.5) and (11.3) 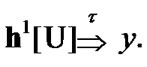 Then, by (11.1)
Then, by (11.1) 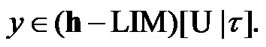 So,
So,
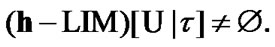 (11.4)
(11.4)
Let 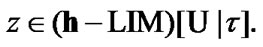 Then
Then  and
and 
 By (3.5) and (11.2)
By (3.5) and (11.2) 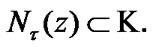 In addition, by (11.2)
In addition, by (11.2) 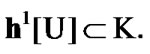 Then, by (3.1)
Then, by (3.1)

By (2.1) we obtain that

Since  and
and  for
for 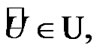 we have the property:
we have the property:
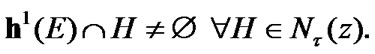
So, 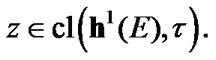 The inclusion
The inclusion
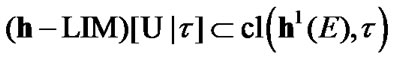
is established. Using (11.4), we obtain that 

We note the following obvious property too: if 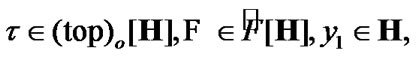 and
and 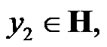 then
then
 (11.5)
(11.5)
Remark 11.1. Let the premise of (11.5) be fulfilled. Then, by (3.6)
 (11.6)
(11.6)
Then, 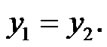 Indeed, suppose the contrary:
Indeed, suppose the contrary: 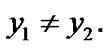 Then, by (6.1), for some
Then, by (6.1), for some 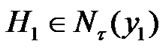 and
and 
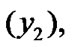 the equality
the equality  is valid. But, by (11.6)
is valid. But, by (11.6)  and
and  Then, by (3.1)
Then, by (3.1) 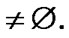
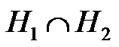 The obtained contradiction means that
The obtained contradiction means that  is impossible. So,
is impossible. So, 
Proposition 11.2. If  and
and 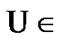
 then
then
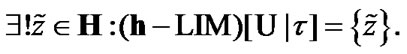
Proof. The corresponding proof is the obvious combination of (11.1), (11.5), and Proposition 11.1. Indeed, by Proposition 11.1 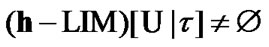 and
and 
 Let
Let 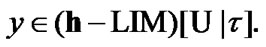 Then,
Then,  and
and
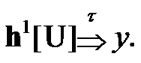 (11.7)
(11.7)
Let 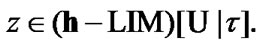 Then,
Then,  and
and
 (11.8)
(11.8)
For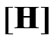

 , by (11.7) and (11.8)
, by (11.7) and (11.8)
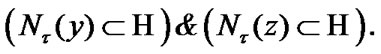
So, by (3.6)  and
and  From (11.5) the equality
From (11.5) the equality  is valid. Then,
is valid. Then, 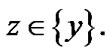 The inclusion
The inclusion
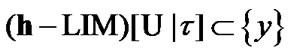 (11.9)
(11.9)
is established. But, by the choice of 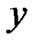 we have the inclusion
we have the inclusion  Using (11.9), we obtain that
Using (11.9), we obtain that

The uniqueness of  is obvious.
is obvious.
From Proposition 11.2 the natural corollary follows: if  then
then
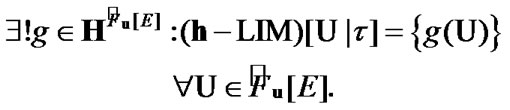 (11.10)
(11.10)
In the following, we postulate that
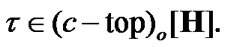 (11.11)
(11.11)
Then (see (11.10) and (11.11)), we suppose that
 (11.12)
(11.12)
is defined by the following rule: if  then
then 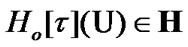 has the property:
has the property:
 (11.13)
(11.13)
We note that by (11.13) and Proposition 11.1
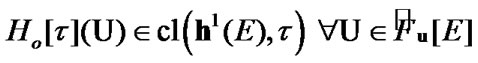 (11.14)
(11.14)
So, by (11.12) and (11.14) 
 In this connection, we note the following typical situation: under condition (11.11),
In this connection, we note the following typical situation: under condition (11.11),  and
and 
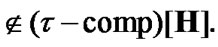 Of course, by (11.11)
Of course, by (11.11)
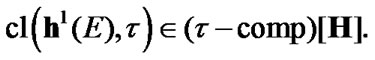
Indeed, any closed set in a compact TS is compact too. Recall that
 (11.15)
(11.15)
Returning to (11.1) and (11.13) we note that
 (11.16)
(11.16)
With the employment of (3.9), we introduce the natural immersion of E in 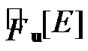 supposing that
supposing that
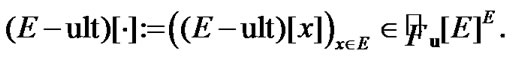 (11.17)
(11.17)
In connection with (11.17), we note the following obvious equality:
 (11.18)
(11.18)
Remark 11.2. Consider the proof of (11.18). Fix 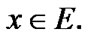 By (3.9) we obtain that
By (3.9) we obtain that
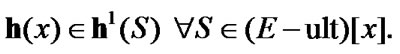 (11.19)
(11.19)
So, by (2.1) and (11.19) we obtain the following property:
 (11.20)
(11.20)
In addition, by (3.5), (3.9), and (11.16)

So,

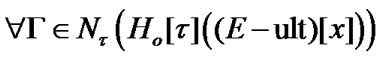 . Then, by (11.20)
. Then, by (11.20) 
 Using the separability of
Using the separability of  (11.11), we obtain the equality chain
(11.11), we obtain the equality chain

Since the choice of  was arbitrary, we obtain that (11.18) is fulfilled.
was arbitrary, we obtain that (11.18) is fulfilled.
Proposition 11.3. If  then the following equality is valid:
then the following equality is valid:
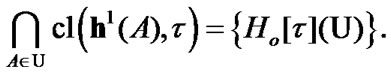
Proof. Let  Then
Then 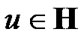 and by (11.16)
and by (11.16)
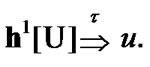
Then, by (3.5)  Therefore, for any
Therefore, for any  there exists
there exists  such that
such that 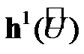
 (see (3.3) and (4.1)).
(see (3.3) and (4.1)).
Let  Then,
Then, 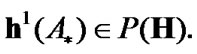 If
If  then, for some
then, for some 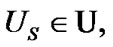 the inclusion
the inclusion  is valid; moreover,
is valid; moreover, 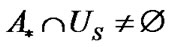 and
and
 (11.21)
(11.21)
where 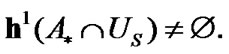 So,
So, 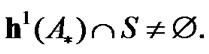 Since the choice of
Since the choice of  was arbitrary, we obtain that
was arbitrary, we obtain that
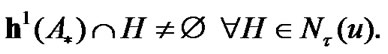
Therefore, 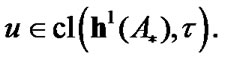 Since the choice of
Since the choice of  was arbitrary too, we have the inclusion
was arbitrary too, we have the inclusion 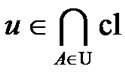
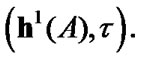 Therefore,
Therefore,

Choose arbitrary 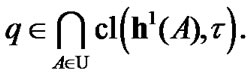 Then
Then 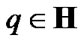 and
and
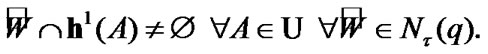 (11.22)
(11.22)
Then, for  we obtain the property
we obtain the property 
 Using (3.3), we have the following statement:
Using (3.3), we have the following statement:

Therefore, 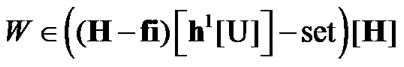 (see Section 5), where
(see Section 5), where
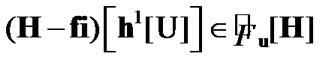 (11.23)
(11.23)
(we use (4.2)). In addition, using (6.6), (11.23), and statements of Section 5, we obtain that
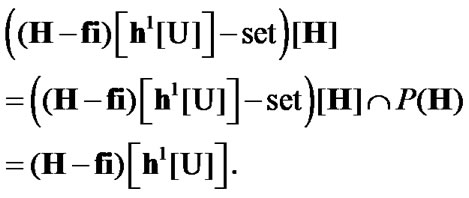
Therefore,  Since the choice of
Since the choice of  was arbitrary, we obtain that
was arbitrary, we obtain that
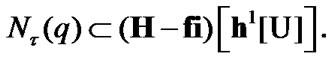
So, by (3.5)  Then, we have the following properties:
Then, we have the following properties:

By (11.5) 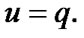 Then
Then 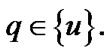 Since the choice of
Since the choice of 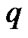 was arbitrary, we obtain that
was arbitrary, we obtain that
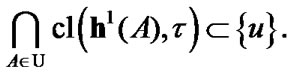
The opposite inclusion was established previously. Therefore, 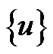 and the intersection of all sets
and the intersection of all sets 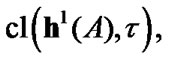
 coincide.
coincide.
From (4.15) and Proposition 11.3 we obtain that
 (11.24)
(11.24)
So, ultrafilters of 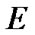 realize very perfect constraints of asymptotic character.
realize very perfect constraints of asymptotic character.
12. Ultrafilters of Measurable Space with Algebra of Sets
In this section, we fix a nonempty set E, TS 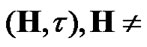
 and
and 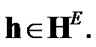 Moreover, we fix
Moreover, we fix 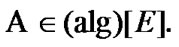 Finally, we suppose that Condition 10.1 is fullfiled. Then, we have the statement of Proposition 3 and other statements of Section 10. We suppose that (11.11) is valid also. So, we have the mapping (11.12). In addition, we have the natural uniqueness of the filter limit: (11.5) is fulfilled. Now, we supplement (11.5). Namely,
Finally, we suppose that Condition 10.1 is fullfiled. Then, we have the statement of Proposition 3 and other statements of Section 10. We suppose that (11.11) is valid also. So, we have the mapping (11.12). In addition, we have the natural uniqueness of the filter limit: (11.5) is fulfilled. Now, we supplement (11.5). Namely, 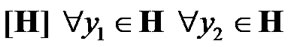

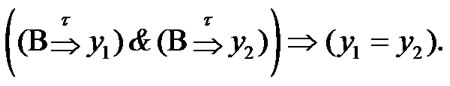 (12.1)
(12.1)
Remark 12.1. For the proof of (12.1), we fix 
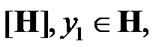 and
and 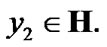 Let the premise statement of (12.1) is valid:
Let the premise statement of (12.1) is valid: 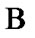 converges to
converges to  and
and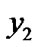 . Then, for
. Then, for 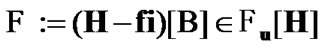 (see (3.3)), the inclusions
(see (3.3)), the inclusions

are fulfilled. Therefore, by (3.6) the following two properties are valid:
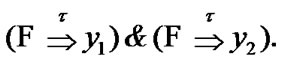
By (11.5) 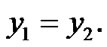 So, (12.1) is established.
So, (12.1) is established.
We recall (10.23) and (10.24): if 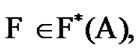 then
then 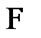
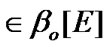 and
and  (see (4.1)). We use (10. 15).
(see (4.1)). We use (10. 15).
Proposition 12.1. 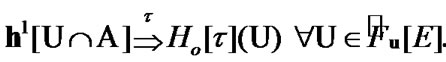
Proof. Let 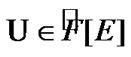 and
and  Then
Then 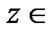
 and by Condition 10.1, for some
and by Condition 10.1, for some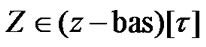 , the inclusion
, the inclusion  is fulfilled. In addition, by (11. 16)
is fulfilled. In addition, by (11. 16) 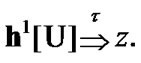 Since
Since  and
and 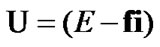
 then
then
 (12.2)
(12.2)
From (12.2) the inclusion 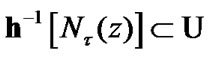 follows (namely, for any
follows (namely, for any 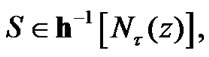 there exists
there exists 
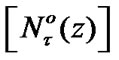 such that
such that  then,
then,  by (12.2) and
by (12.2) and 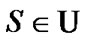 by axioms of a filter). In addition,
by axioms of a filter). In addition, 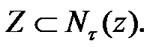 Then,
Then,
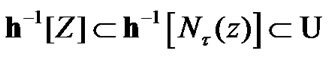
and (by the choice of 
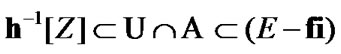
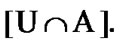 Since
Since 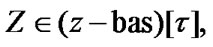 by (10.27)
by (10.27)
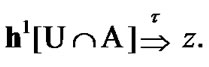
By definition of 
Proposition 12.2. 
Proof. Fix  Using (10.18), we choose
Using (10.18), we choose  such that
such that
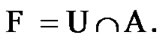 (12.3)
(12.3)
Then, by (11.12)  and by (12.3) and Proposition 12.1
and by (12.3) and Proposition 12.1
 (12.4)
(12.4)
In addition, 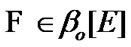 and
and  Therefore, by (12.1) and (12.4)
Therefore, by (12.1) and (12.4) 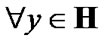

From Proposition 12.2, the obvious corollary follows; namely 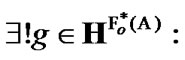
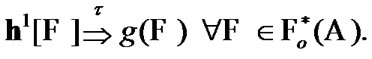
Now, we suppose that the mapping
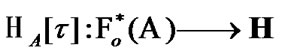 (12.5)
(12.5)
is defined by the following rule: if 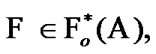 then
then
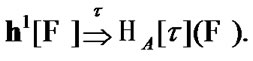 (12.6)
(12.6)
From (10.15) and (12.5), the obvious property follows; namely, 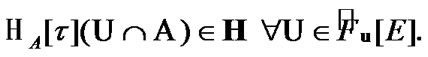
Proposition 12. 3. 
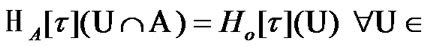
Proof. Fix  Then, by (11.12)
Then, by (11.12) 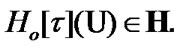 By (10.15) we obtain that
By (10.15) we obtain that 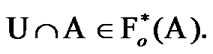 In particular,
In particular, 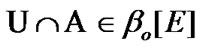 and by (4.1)
and by (4.1)  From Proposition 12.1, we have the following convergence
From Proposition 12.1, we have the following convergence
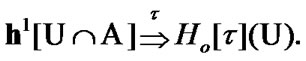 (12.7)
(12.7)
Using Proposition 12.2, (12.1), (12.6), and (12.7), we obtain that 
Proposition 12.4. If 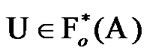 and
and 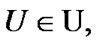 then
then 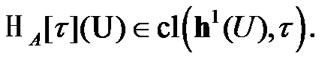
Proof. Using (10.18), we choose  such that
such that 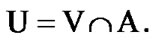 Then, by Proposition 11.3 we have the inclusion
Then, by Proposition 11.3 we have the inclusion
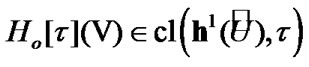 (12.8)
(12.8)
(we use the obvious inclusion 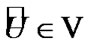 realized by the choice of
realized by the choice of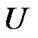 ). By Proposition 12.3
). By Proposition 12.3
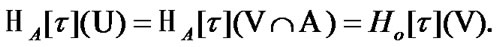
From (12.8), the inclusion 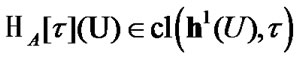 follows.
follows.
We note that (see [11,12,13]) by (11.11) the space 
 is regular: if
is regular: if  then
then
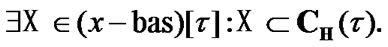 (12.9)
(12.9)
Proposition 12.5. The mapping (12.5) is continuous:
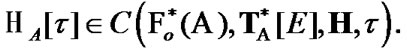 (12.10)
(12.10)
Proof. Fix  Then, by (12.5)
Then, by (12.5) 
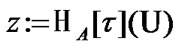 In addition, by (12.6)
In addition, by (12.6)
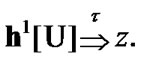 (12.11)
(12.11)
Of course, 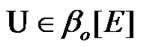 and
and 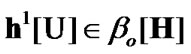 (see (4.1)). As a corollary, by (3.3)
(see (4.1)). As a corollary, by (3.3)
 (12.12)
(12.12)
From (3.5), (12.11), and (12.12), we obtain the following inclusion:
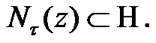 (12.13)
(12.13)
From (2.1), (3.3), and (12.13), we obtain that
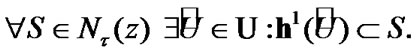 (12.14)
(12.14)
Fix  Using (12.9), we choose
Using (12.9), we choose 
 such that
such that  Then, by (3.4), for some
Then, by (3.4), for some  the inclusion
the inclusion
 (12.15)
(12.15)
is valid. Therefore, 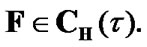 Of course,
Of course,  Therefore, by (12.14), for some
Therefore, by (12.14), for some 
 (12.16)
(12.16)
In addition,  (see (5.4)). By (6.4)
(see (5.4)). By (6.4) 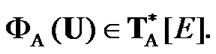 In addition, by (5.3)
In addition, by (5.3) 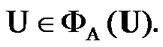 Therefore,
Therefore,
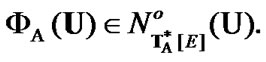 (12.17)
(12.17)
Choose arbitrary ultrafilter 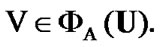 Then,
Then, 
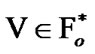 and
and  see (5.3). By Proposition 12.4
see (5.3). By Proposition 12.4
 (12.18)
(12.18)
By the closedness of  and (12.16)
and (12.16) 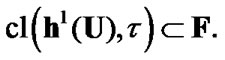 So, from (12.18), we have the inclusion
So, from (12.18), we have the inclusion

Using (12.15), we obtain that 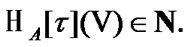 Since the choice of
Since the choice of  was arbitrary, the inclusion
was arbitrary, the inclusion
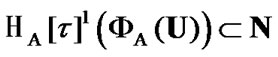 (12.19)
(12.19)
is established. Since the choice of  was arbitrary too, from (12.17), we obtain that
was arbitrary too, from (12.17), we obtain that

So, the mapping 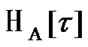 is continuous at the point
is continuous at the point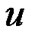 . Since the choice of
. Since the choice of  was arbitrary, the required inclusion (12.10) is established (see [16], (2.5.4)).
was arbitrary, the required inclusion (12.10) is established (see [16], (2.5.4)).
In connection with Proposition 12.5, we recall Proposition 9.2 and known statement about the possibility of an extension of continuous functions defined on the initial space; in this connection, see, for example, Theorem 3.6.21 of monograph [13]. For this approach, constructions of Section 8 are essential. Of course, under corresponding conditions, we can use the natural connection with the Wallman extension (see (8.27) and Proposition 9.2).
In this case, Proposition 12.5 can be “replaced” (in some sense) by statements similar to the above-mentioned Theorem 3.6.21 of [13] (of course, this approach requires a correction, since we consider ultrafilters of the measurable space). But, we use the “more straight” way with point of view of asymptotic analysis: we construct the required continuous mapping by the limit passage (see Proposition 12.5). We recall (9.24). Then, by (9.24) and (12.5) the mapping
 (12.20)
(12.20)
is defined; moreover, 
Proposition 12.6. The equality 
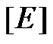 is valid.
is valid.
Proof. Fix 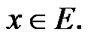 Then by (11.17)
Then by (11.17) 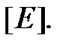
 In addition, by (11.18) the obvious equality follows:
In addition, by (11.18) the obvious equality follows:
 (12.21)
(12.21)
Moreover, by (9.24) we obtain that
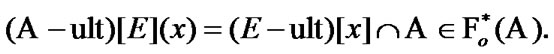 (12.22)
(12.22)
Then, by Proposition 12.3 and (12.22) we have the equality chain

So,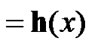
 . Since the choice of
. Since the choice of 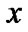 was arbitrary,
was arbitrary, 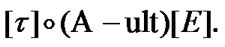

Since (9.7) is valid, from Propositions 12.5 and 12.6, we have the important corollary connected with Proposition 5.2.1 of [9]:
 (12.23)
(12.23)
is a compactificator, for which (in the considered case)
 (12.24)
(12.24)
in (12.24) we use Proposition 3.1 and Corollary 3.1 of [18]. In addition,  Therefore, by (12. 24)
Therefore, by (12. 24)
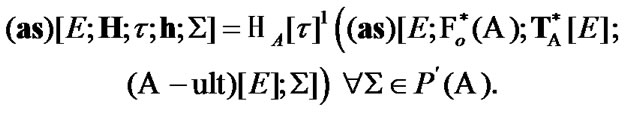 (12.25)
(12.25)
In (12.25), we have the important particular case. We consider this case in the following section.
13. Ultrafilters as Generalized Solutions
We suppose that  and
and  satisfy to the conditions of Section 12. We postulate (11.11). Finally, we postulate Condition 10.1. Therefore, we can use constructions of the previous section. In particular, (12.25) is fulfilled (the more general property (12.24) is fulfilled too). In connection with (12.25), the obtaining of more simple representations of AS
satisfy to the conditions of Section 12. We postulate (11.11). Finally, we postulate Condition 10.1. Therefore, we can use constructions of the previous section. In particular, (12.25) is fulfilled (the more general property (12.24) is fulfilled too). In connection with (12.25), the obtaining of more simple representations of AS
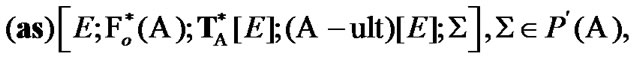
(13.1)
is important. For this goal, we use the natural construction of Theorem 8.1 in [17]. Namely, we have the following Proposition 13. 1. If  then
then 
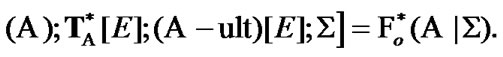
Proof. Let 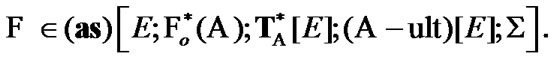 Then, by the corresponding definition of Section 4 (see (4.3))
Then, by the corresponding definition of Section 4 (see (4.3))  and, for some net
and, for some net 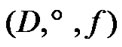 in the set E,
in the set E,
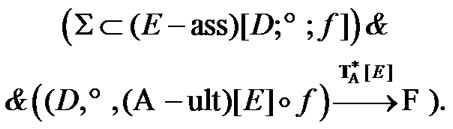 (13.2)
(13.2)
Fix 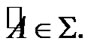 Then, by (13.2)
Then, by (13.2)  Using (3.7), we choose
Using (3.7), we choose 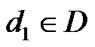 such that
such that 
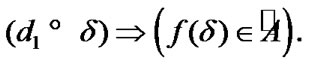 (13.3)
(13.3)
Of course, 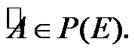 And what is more,
And what is more, 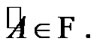 Indeed, let us assume the contrary:
Indeed, let us assume the contrary:
 (13.4)
(13.4)
Recall that  Therefore,
Therefore,  By (9.1) and (13.4) we have the inclusion
By (9.1) and (13.4) we have the inclusion  Then, by (5.4)
Then, by (5.4)  In particular (see (6.4)),
In particular (see (6.4)),
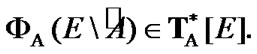 (13.5)
(13.5)
Moreover, by (5.3) 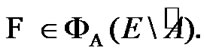 Using (13.5), we obtain that
Using (13.5), we obtain that
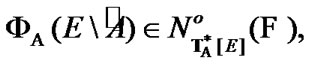 (13.6)
(13.6)
where  From (13.6) and the second statement of (13.2) we have the following property: there exists
From (13.6) and the second statement of (13.2) we have the following property: there exists  such that
such that 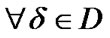
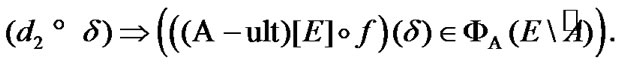 (13.7)
(13.7)
By axioms of DS there exists  for which
for which 
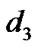 and
and 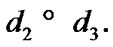 By (13.3)
By (13.3)  Moreover, by (13.7)
Moreover, by (13.7)

By (9.24)  Therefore,
Therefore,
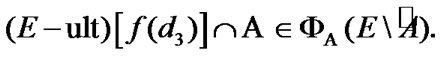
From (5.3), the inclusion 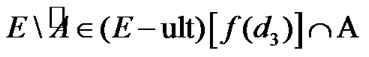 follows; in particular,
follows; in particular, 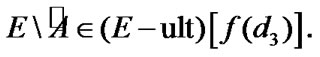 By (3.9)
By (3.9) 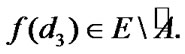 So,
So,
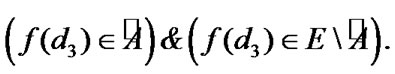
We have the obvious contradiction. This contradiction means that (13.4) is impossible. So,  Since the choice of
Since the choice of  was arbitrary, the inclusion
was arbitrary, the inclusion 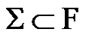 is established. Then (see (9.26)),
is established. Then (see (9.26)), 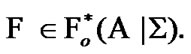 So, we obtain the inclusion
So, we obtain the inclusion
 (13.8)
(13.8)
Choose arbitrary  Then, by (9.26)
Then, by (9.26) 
 and
and  By Proposition 9.4 and [9,(3.3.7)], for some net
By Proposition 9.4 and [9,(3.3.7)], for some net  in the set
in the set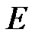 , the convergence
, the convergence
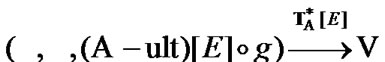 (13.9)
(13.9)
is fulfilled. Now, we use axiom of choice. Fix  Then, by the choice of
Then, by the choice of  the inclusion
the inclusion  is fulfilled. Of course, by (5.4)
is fulfilled. Of course, by (5.4)
 (13.10)
(13.10)
in addition, by (5.3) . Since by (6.4) and (13.10)
. Since by (6.4) and (13.10)  we have the inclusion
we have the inclusion
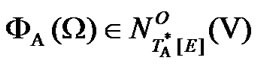 (13.11)
(13.11)
From (13.9) and (13.11), we have the property: for some  we obtain that
we obtain that .
.
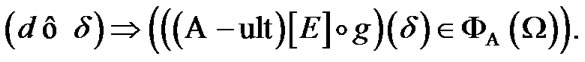 (13.12)
(13.12)
From (9.24) and (13.12), we have the following property: 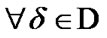
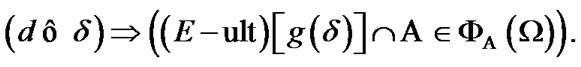 (13.13)
(13.13)
By (5.3) and (13.13) we obtain that, for 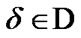 with the property
with the property 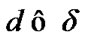 the inclusion
the inclusion 
 is valid and, as a corollary, by (3.9)
is valid and, as a corollary, by (3.9)  So,
So,  and
and

Then, by (3.7) 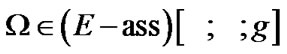 Since the choice of
Since the choice of  was arbitrary, the inclusion
was arbitrary, the inclusion
 (13.14)
(13.14)
is established. So, by (13.9) and (13.14) we obtain that the net  in the set E has the following properties:
in the set E has the following properties:

By definition of Section 4 (see (4.3)) 
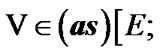 So, the inclusion
So, the inclusion

is established. Using (13.8), we have the required equality

From (12.25) and Proposition 13.1, we have the following Theorem 13.1. If  then, AS in
then, AS in 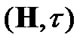 with constraints of the asymptotic character defined by
with constraints of the asymptotic character defined by  is realized by the rule
is realized by the rule
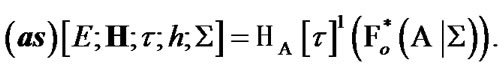
We note that, in Theorem 13.1, the set 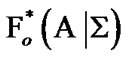 plays the role of the set of admissible generalized solutions.
plays the role of the set of admissible generalized solutions.
14. Some Remarks
In our investigation, one approach to the representation of AS and approximate solutions is considered. This very general approach requires the employment of constructions of nonsequential asymptotic analysis. This is connected both with the necessity of validity of “asymptotic constraints” and with the general type of the convergence in TS. We fix a nonempty set of usual solutions (the solution space), the estimate space, and an operator from the solution space into the estimate space. In the estimate space, a topology is given. Then, under very different constraints, we can realize in this space both usual attainable elements and AE. But, if usual attainable elements are defined comparatively simply (in the logical relation), then AE are constructed very difficult. For last goal, extensions of the initial space are used. In addition, the corresponding spaces of GE are constructed. Ultrafilters of the initial space can be used as GE. But, the realizability problems arise: free ultrafilters are “invisible”. In addition, free ultrafilters realize limit attainable elements which nonrealizable in the usual sense. In this connection, we propose to use ultrafilters of (nonstandard) measurable space; we keep in mind spaces with an algebra of sets. But, it is possible to consider the more general constructions with the employment of ultrafilters. In our investigation, ultrafilters of lattices of sets are used. On this basis, the interesting connection with the Wallman extension in general topology arises.
It is possible that the proposed approach motivated by problems of asymptotic analysis can be useful in other constructions of contemporary mathematics.
15. References
[1] J. Warga, “Optimal Control of Differential and Functional Eguations,” Academic Press, New York, 1972.
[2] R. V. Gamkrelidze, “Foundations of Optimal Control Theory,” Izdat. Tbil. Univ., Tbilissi, Russian, 1977.
[3] N. N. Krasovskii, “The Theory of the Control of Motion,” Nauka, Moscow, Russian, 1968.
[4] R. J. Duffin, “Linear Inequalites and Related Systems,” Annals of Mathematics Studies, Vol. 38, 1956, pp. 157- 170.
[5] E. G. Gol‘stein, “Duality Theory in Mathematical Programming and Its Applications,” Nauka, Moscow, Russian, 1971.
[6] N. N. Krasovskii and A. I. Subbotin, “Game-Theoretical Control Problems,” Springer Verlag, Berlin, 1988.
[7] A. G. Chentsov, “Constructing Operations of the Limit Passage with the Emploument of Ultrafilters of Measurable Spaces,” Avtomatika i telemekhanika, Vol. 6, No. 11, 2007, pp. 208-222.
[8] A. G. Chentsov and S. I. Tarasova, “Extensions of Abstract Analog of Unstable Control Problems,” Functional Differential Equations, Vol. 16, No. 2, 2009, pp. 237-261.
[9] A. G. Chentsov, “Asymptotic Attainability,” Kluwer, Dordrecht, 1997.
[10] K. Kuratowski and A. Mostowski, “Set Theory,” NorthHolland, Amsterdam, 1967.
[11] N. Bourbaki, “General Topology,” Nauka, Moskow, Russian, 1968.
[12] J. L. Kelley, “General Topology,” Van Nostrand, Prnceton, NJ, 1957.
[13] R. Engelking, “General Topology,” PWN, Warszawa, 1977.
[14] G. Crätzer, “General Lattice Theory,” Akademie-Verlag, Berlin, 1978.
[15] J. Neveu, “Bases Math Matiques Du Calcul Des Probabilit s,” Masson, Paris, 1964.
[16] A. G. Chentsov and S. I. Morina, “Extensions and Relaxations,” Kluwer Academic Publishers, Dordrecht/ Boston/London, 2002.
[17] A. G. Chentsov, “Some Constructions of Asymptotic Analisis Connected with Stone-Čech Compactification,” Contemporary Mathematics and its Applications, Vol. 26, 2004, pp. 119-150.
[18] A. G. Chentsov, “Extensions of Abstract Problems of Attainability: Nonsequential Version. Proceedings of the Steklov Institute of Mathematics,” Suppl. 2, 2007, pp. S46-S82. Pleiades Publishing, Ltd., 2007.

