Intelligent Information Management
Vol.2 No.3(2010), Article ID:1482,5 pages DOI:10.4236/iim.2012.23021
Lexicographic Constant-Weight Equidistant Codes over the Alphabet of Three, Four and Five Elements
Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Bulgaria
E-mail: todor@math.bas.bg, galina@math.bas.bg, teda_aj@yahoo.com
Received October 13, 2009; revised November 17, 2009; accepted December 21, 2009
Keywords: Lexicographic Codes, Equidistant Codes, Constant-Weight Codes, Bounds of Codes
Abstract
In this paper we consider the problem of finding bounds on the size of lexicographic constant-weight equidistant codes over the alphabet of three, four and five elements with 2 ≤ w < n ≤ 10. Computer search of lexicographic constant-weight equidistant codes is performed. Tables with bounds on the size of lexicographic constant-weight equidistant codes are presented.
1. Introduction
Consider a finite set of q elements and containing a distinguished element ?/span>zero?/span>. The choice of a set does not matter in our context and we will use the set 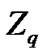 of integers modulo q. Let
of integers modulo q. Let 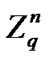 be the set of n-tuples (or vectors) over
be the set of n-tuples (or vectors) over 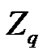 and
and  be the set of n-tuples over
be the set of n-tuples over 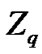 of Hamming weight w.
of Hamming weight w.
A code is called equidistant if all the Hamming distances between distinct codewords are d. A code is called constant-weight if all the codewords have the same Hamming weight w. Let  denote the maximum number of codewords in an equidistant code over
denote the maximum number of codewords in an equidistant code over 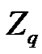 of length n and distance d (called an
of length n and distance d (called an 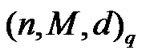 equidistant code or EC) and
equidistant code or EC) and 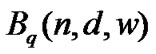 denote the maximum number of codewords in an constant-weight equidistant code over
denote the maximum number of codewords in an constant-weight equidistant code over 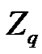 of length n, distance d, and weight w (called an
of length n, distance d, and weight w (called an 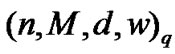 constant-weight equidistant code or ECWC). Equidistant codes have been investigated by a large number of authors, mainly as examples of designs and other combinatorial objects [1] . Some works published on this topic are [2?].
constant-weight equidistant code or ECWC). Equidistant codes have been investigated by a large number of authors, mainly as examples of designs and other combinatorial objects [1] . Some works published on this topic are [2?].
Constant-weight codes have been studied by many authors. For some references for the binary case, see Brouwer et al. [6] , Agrell [7] and for the ternary case, see Bogdanova [8] and Svanström [9] . A few papers study codes which are both equidistant and of constant weight, for example [10,11].
Let B be an ordered base 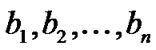 over
over 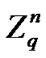 and let
and let  and
and 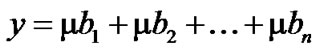 be vectors from
be vectors from .
.
Definition 1 We say that x precedes y in lexicographical order if 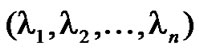 precedes
precedes  in lexicographical order, i.e.
in lexicographical order, i.e. .
.
Lexicographic codes of length n and Hamming distance d are obtained by considering all q-ary vectors with weight w in lexicographic order, and adding them to the code if they are at a distance exactly d from the words that have been added earlier. Lexicographic codes were introduced by Conway and Sloane in [12,13]. These codes may be regarded as a heuristically good 揳pproximation?to the optimal codes because of their good parameters and coding performance. Brualdi and Pless [14] have examined a similar generalization of lexicographic codes, known as greedy codes, and presented certain bounds on their parameters.
In the present paper is considered the problem of finding bounds on the size of lexicographic constant-weight equidistant codes over the alphabet of three, four and five elements. Some general bounds for equidistant and constant-weight equidistant codes are presented in Section 2. In Section 3 are described computer search methods used in our research. Section 4 presents main results in obtained in this paper. In Section 5 are described some aspects of future work in this area. In Section 6 are shown tables with bounds on the size of lexicographic constant-weight equidistant codes over the alphabet of three, four and five elements.
2. Preliminaries
Some bounds for ECWC and EC are given by the following theorems:
Theorem 1 [11]
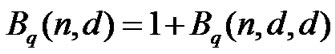
Theorem 2 (Plotkin) [4,15]

if the denominator is positive.
Theorem 3 (Delsarte) [16]
 .
.
Theorem 4
 ,
,
 ,
,
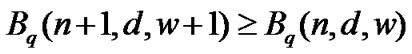 .
.
The proof of Theorem 4 is easy and we omit it here.
Theorem 5 (Trivial values)
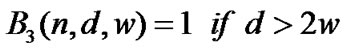 ,
,
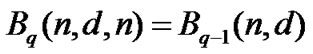 .
.
Theorem 6 (the Johnson bounds for ECWC)
The maximum number of codewords in a q-ary ECWC satisfies the inequalities:
 ,
,
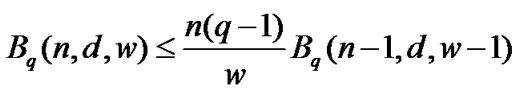 .
.
The proof of the Theorem 6 is the same as the proof of Johnson bound for constant-weight codes [9] .
Theorem 7 [11] For k=1,2,...,n, if , then
, then
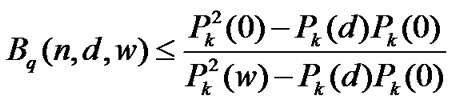
Here  is the Krawtchouk polynomial defined by
is the Krawtchouk polynomial defined by
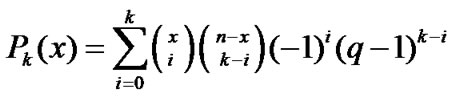
and
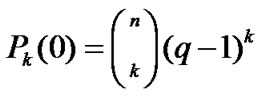
Definition 2 [5] A balanced incomplete block design with parameters (v,b,k,r,λ) (BIB design (v,b,k,r,λ) is defined as an array of v different symbols or elements in b subsets or blocks such that every block contains
Definition 3 [5] A BIB design is called resolvable (an RBIB design), if its b blocks can be separated into r groups or repetitions of q blocks in such a way that each of the v elements occurs exactly once in each repetition.
Theorem 8 [5] The optimal equidistant 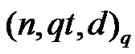 codes and RBIB designs (v=qk,b,k,r,λ) are equivalent to one another and their parameters are connected by the conditions v=M, b=nq, k=t, r=n, λ =n-d.
codes and RBIB designs (v=qk,b,k,r,λ) are equivalent to one another and their parameters are connected by the conditions v=M, b=nq, k=t, r=n, λ =n-d.
Theorem 9 If there exists an 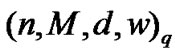 code, then there exists a
code, then there exists a  code for all integers
code for all integers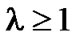 .
.
3. Computer Search of Lexicographic Constant-Weight Equidistant Codes
In the present paper is considered the problem of finding bounds on the size of lexicographic constant-weight equidistant codes using computer search methods. We apply greedy search beginning with an empty array and while looping through all possible codewords, we add one if it has weight w and is on distance d from every member of the current code. In order to restrict our search and to compare founded lexico-graphic codes with optimal constant-weight equidistant codes we use theorems from Section 2 and results from [17,18].
For improving the results we use lexicographic codes with seed. Lexicographic codes with a seed are obtained in a similar way as the standard lexicographic codes. The difference is that we use an initial set of vectors (called a seed) instead of the empty set. In order to find lexicographic codes we can start the search in the following ways:
Without seeds: As a result, we construct lexicographic code where the first codeword is the first word in the set of vectors ;
;
With seeds: In this case, it is important to choose a proper seed from one or more vectors. We apply the following methods: exhaustive search, consecutively choosing the possible seeds from restricted area of  and search with randomly selected seed.
and search with randomly selected seed.
Remark: In some cases of searching with seed with one codeword we are applying cyclic shift of the space before start searching (see Figure 1). Codewords from first to the index of the codeword included in the seed are moved at the end of the space. Thus we have two parts of lexicographically ordered spaces. Then we obtain greedy search. This search produces better results in some cases.
Example: We consider searching of 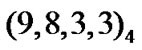 lexicographic constant-weight equidistant code.
lexicographic constant-weight equidistant code.
If we apply search without seed the best code that we can obtain is with three codewords (see Figure 2).
But if we use search with a seed we can obtain code with eight codewords (which is number of codewords of optimal code with such parameters) (see Figure 3).
4. Results
We obtain bounds for constant-weight equidistant codes using standard lexicographic codes or lexicographic codes with seeds. We use searching methods described in the previous section. These methods are included in coding theory computer package QPlus [19] . This software includes options for searching with or without a seed and seed size choosing. Also it offers searching with manually selected seed or automatically trying all possible seeds to find best code with given parameters. QPlus includes option for cyclic shift of the searching space. We perform search with all possible seeds with size one in order to find the best possible code. If the size of the space is not too large we try with seeds with bigger
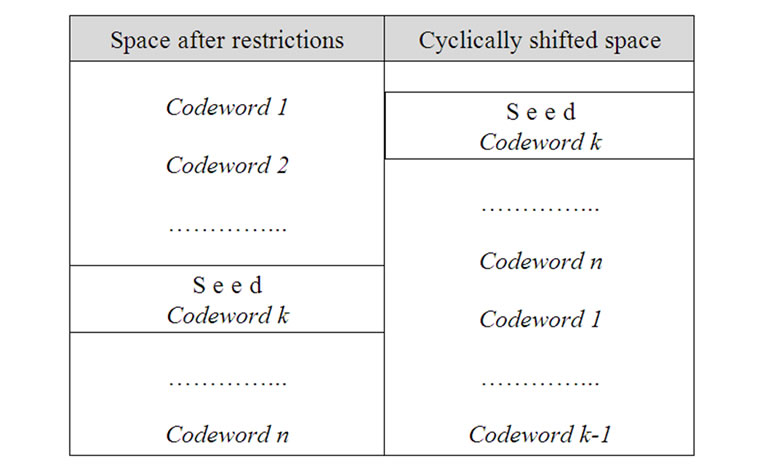
Figure 1. Cyclic shift of space.

Figure 2. 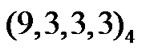 - No seed.
- No seed.

Figure 3.  - Seed 000001011.
- Seed 000001011.
size. Results shown on the next tables are obtained using lexicographic code unit of QPlus. Tables with bounds on the size of lexicographic constant-weight equidistant codes for q=3, q=4 and q=5 and for 2 ≤ w < n ≤ 10 are presented in tables, in the Appendix.
5. Conclusions
We use computer search methods in order to solve the problem of finding bounds on the size of lexicographic constant-weight equidistant codes over the alphabet of three, four and five elements with 2 ≤ w < n ≤ 10. Interesting fact that could be used for future work is that in most of the cases lexicographic codes coincide with optimal such codes [17,18].
6. Appendix
In Tables 1, 2 and 3 are shown bounds on the size of lexicographic constant-weight equidistant codes over the alphabet of three, four and five elements.

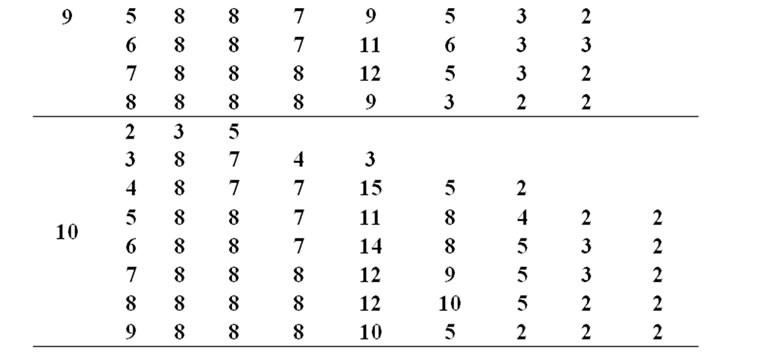
Table 1. Lexicographic bounds for .
.


Table 2. Lexicographic bounds for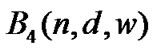 .
.


Table 3. Lexicographic bounds for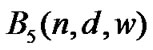 .
.
7. References
[1] C. J. Colbourn and J. H. Dinitz,"The CRC handbook of combinatorial designs"Boca Raton, CRC Press, FL, 1996.
[2] J. I. Hall, "Bounds for equidistant codes and partial projective planes"Discrete Mathematics, Vol. 17, pp. 85-94, 1977.
[3] J. I. Hall, A. J. E. M. Jansen, A.W. J. Kolen, and J. H. van Lint,"Equidistant codes with distance 12"Discrete Mathematics, Vol. 17, pp. 71-83, 1977.
[4] J. H. van Lint,"A theorem on equidistant codes"Discrete Mathematics, Vol. 67, pp. 353-358, 1973.
[5] N. V. Semakov and V. A. Zinoviev," Equidistant q-ary codes with maximal distance and resolvable balanced incomplete block designs"Problemi peredachi Informatsii, Vol. 4, No. 2, pp. 3-10, 1968.
[6] A. E. Brouwer, J. B. Shearer, N. J. A. Sloane, and W. D. Smith, "A new table of constant-weight codes,"IEEE Transactions on Information Theory, Vol. 36, pp. 1344- 1380, 1990.
[7] E. Agrell, "A. Vardy, and K. Zeger, Upper bounds for constant-weight codes,"IEEE Transactions on Information and Theory, Vol. IT-46, pp. 2373-2395, 2000.
[8] G. T. Bogdanova, "New bounds for the maximum size of ternary constant weight codes,"Serdica Mathematics Journal, Vol. 26, pp. 5-12, 2000.
[9] M. Svanström, P. R. J. Östergård, and G. T. "Bogdanova, Bounds and constructions for ternary constant-composition codes,"IEEE Transactions on Information Theory, Vol. 48, No. 1, pp. 101-111, 2002.
[10] D. R. Stinson and G. H. J. van Rees, "The equivalence of certain equidistant binary codes and symmetric BIBDs,"Combinatorica, Vol. 4, pp. 357-362, 1984.
[11] F. W. Fu, T. Klove, Y. Luo, and V. K. Wei., "On equidistant constant weight codes,"In Proceedings WCC?001 Workshop on Coding and Cryptography, Paris, France, pp. 225-232, January 2001.
[12] J. H. Conway, "Integral lexicographic codes,"Discrete Mathematics, Vol. 83, pp. 219-235, 1990.
[13] J. H. Conway and N. J. A. Sloane, "Lexicographic codes: Error-correcting codes from game theory,"IEEE Transactions on Information Theory, Vol. 32, pp. 337-348, 1986.
[14] R. A. Brualdi and V. S. Pless, "Greedy codes,"Journal of Combinatorial Theory (A), September 1993.
[15] M. Plotkin, "Binary codes with specified minimum distance,"IRE Transactions on Information Theory, Vol. 6, pp. 445-450, 1960.
[16] P. Delsarte, "Bounds for unrestricted codes, by linear programming,"Philips Research, Vol. 27, pp. 47-64, 1972.
[17] G. Bogdanova, T. Todorov, and T. Pagkou," New equidistant constant weight codes over the alphabet of three, four and five elements,"Preprint №1/2008, BAS, 2008.
[18] G. Bogdanova, T. Todorov, and V. Zinoviev," On construction of q-ary equidistant codes,"Problems of Information Transmission, Vol. 43, pp. 13-36, 2007.
[19] G. Bogdanova, T. Todorov, and V. Todorov, "Web-based application for coding theory studying,"In Proceedings of the International Congress of Mathematical Society of Southeastern Europe, Borovets, Bulgaria, pp. 94-99, September 15-21, 2003.
NOTES
This work was partly supported by Bulgarian National Science Fund (IO-03-02/2006).

