Positioning
Vol.2 No.4(2011), Article ID:8315,3 pages DOI:10.4236/pos.2011.24015
Optimization of Multi-Level Cooperative Remote Sensing Using Carriers Flying on Counter-Phase Trajectories
![]()
1National Aviation Academy, Baku, Azerbaijan; 2Research Institute of Aerospace Informatics, Baku, Azerbaijan.
Email: hasadzade2001@yahoo.com
Received July 22nd, 2011; revised August 29th, 2011; accepted September 20th, 2011.
Keywords: Remote Sensing, UAV, Optimization, Counter-Phase Trajectory, Image Forming, Calibration
ABSTRACT
The criterion for effectiveness of remote sensing system forming the image by the aim: a) further processing; b) detection of temporal changes or differences in spectral bands; accumulation and registration in GIS system is formulated. The optimal point in trajectory, where the maximum effectiveness of system’s operation of maximum information entropy at the system output is calculated. The regime limit value of parameters is calculated, upon surpassing of which the maximal effectiveness of the system may be reached.
1. Introduction
It is well-known that the registration of images is one of major operations during processing of images, obtained using different types of remote sensing devices.
It should be noted, that the images obtained using remote sensing systems are registered mainly for solving following types of tasks:
1) Processing of images;
2) Identification of temporal changes;
3) Integrating with GIS data.
The major technical challenge in image registration is accuracy of registration. As it is noted in [1], if the error of registration of the pixel is equal to one fifth of its size the error of identification of the image’s temporal changes will reach 10%.
2. Criteria for Image Registration
2.1. Existing Criteria for Image Registration
To register the images, taken from one sensor such parameters as a mean standard deviation and normalized cross-correlation are used. But if it is necessary to register and evaluate the images taken from two different RS systems one can use such parameter as mutual information 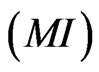 [2-5]. For registration on the basis of criteria of mutual information
[2-5]. For registration on the basis of criteria of mutual information 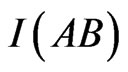 of two random variables A and B the known formula of information theory may be used
of two random variables A and B the known formula of information theory may be used
 , (1)
, (1)
where 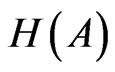 and
and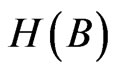 —entropies of A and B accordingly;
—entropies of A and B accordingly; —mutual entropy of A and B.
—mutual entropy of A and B.
Therefore, if we consider A and B as two different images, then in line with mutual information 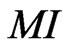 registration criterion, the registration should be carried out in such a way, that the parameter
registration criterion, the registration should be carried out in such a way, that the parameter 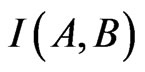 would reach its maximal value. For practical calculations of
would reach its maximal value. For practical calculations of 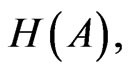
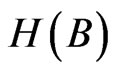 and
and  following well-known formulas may be used
following well-known formulas may be used
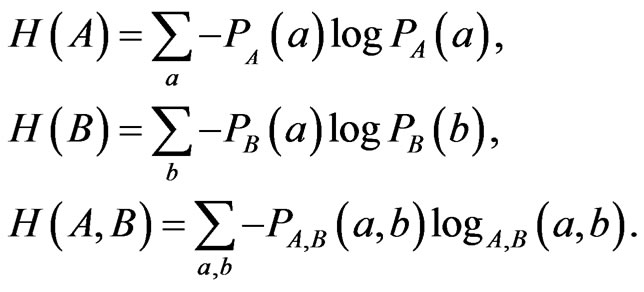
At the same time in order to evaluate the functioning of RS systems forming the images at its output the functional designation of the system should be taken into account.
So according to [6], the mutual entropy is the mean statistical indicator of information content of the signal and may be used for assessing of information contained in the image. For example, according to [6] the threemeasured mutual entropy of RS images may be calculated using well-known formula Schennon:
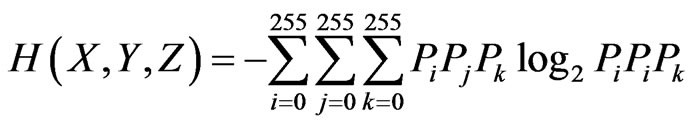 . (2)
. (2)
According to [6] the formula (2) may be used for assessing information content in three spectral channels during processing of multi-spectral images. At the same time, the formula (2) may be used for detection of temporal changes in time series of fixes scene.
2.2. The Suggested Approach to Development of Universal System of Image Registration
Thus, the criterion (1) is more relevant for assessing of implementation of such functions as images processing, collection and archiving of information in GIS. At the same time, the criterion (2) is more adjusted for assessing of similarity in spectral channels, and also in time series of images of fixed scene.
The suggested classification of RS systems designated for images forming on above mentioned criteria is shown in Figure 1.
In view of abovementioned, the following question should be considered: What criterion should be used for development of universal RS system designated for implementing all three functions described at the introduction. In order to answer to this question we can use to formula (1), rewriting it as follows
 . (3)
. (3)
According to formulas (1), (2), (3) for successful functioning of universal multi-functional RS system, i.e. to reach the condition
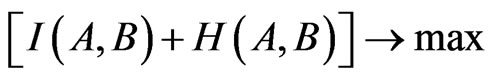
It is quite sufficient to provide for realization of following condition
 . (4)
. (4)
Thus, the formula (4) gives us the condition for effect-
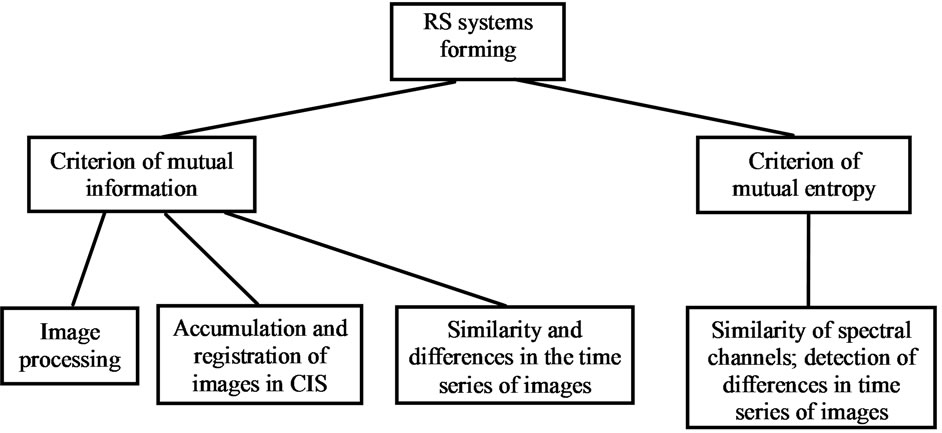
Figure 1. Classification of RS system of image forming on applied criterion.
tive functioning of universal multifunctional remote sensing image registering system. Such a multifunctionality is urgent property of sub-satellite systems forming the satellite calibration signals and images.
3. Development of Sub-Satellite Systems Forming the Satellite Calibration Signals and Images
3.1. Forming of Criterion for Calculation of Mutual Entropy in Output of Sub-Satellite System Developed on the Basis of Couple of UAV
Taking into account the aforesaid, the research task concerning remote sensing using couple of UAV may be formulated as follows.
There are two UAV moving on counter-paraphrase trajectory (Figure 2). We should determine the optimal value of total entropy formed by group of UAV-s contained of ascending and descending UAV-s. For this purposes the entropy of measuring information of UAV1 (Figure 2) at the time moment ![]() may be calculated using following formula
may be calculated using following formula
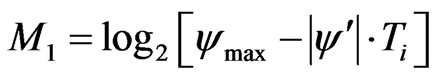 , (5)
, (5)
where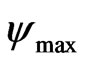 —maximal value of signal/noise ratio in the system;
—maximal value of signal/noise ratio in the system;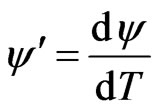 .
.
As it can be seen formula (5) increase of ![]() leads to decrease of signal/noise ratio
leads to decrease of signal/noise ratio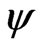 . It can be explained by turbidity of atmosphere, which is increased by increase of height of the UAV1 flight.
. It can be explained by turbidity of atmosphere, which is increased by increase of height of the UAV1 flight.
The similar formula for UAV2 may be written as
 , (6)
, (6)
where![]() —minimal value of signal/noise ratio linked with the maximal flight height.
—minimal value of signal/noise ratio linked with the maximal flight height.
The total entropy formed in the couple of UAV may be determined as
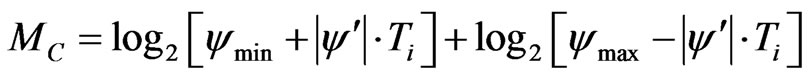 . (7)
. (7)
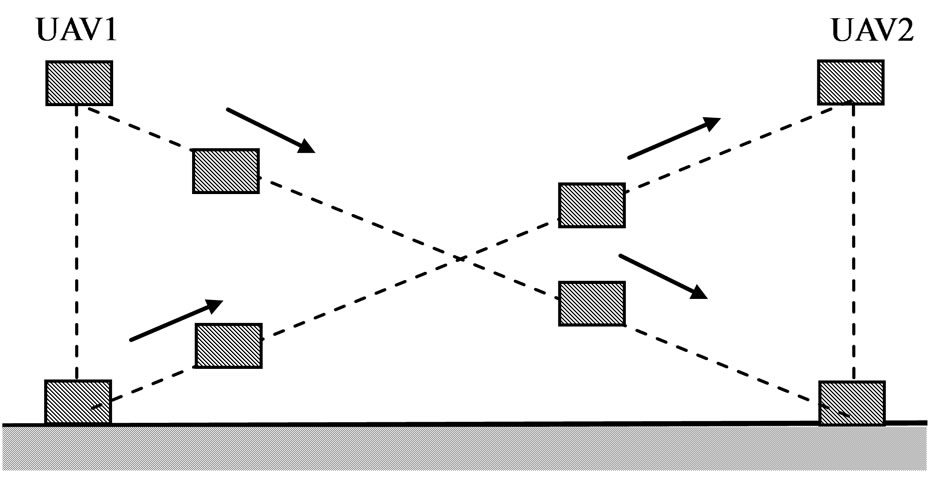
Figure 2. Counter-phrase trajectory couple UAV.
3.2. Optimization of Functioning of Sub-Satellite System, Developed on the Basis of Couple of UAV Using Total Entropy Criterion
As it is stated above, the total information entropy determined by formula (7) is used as an optimization criterion. Research of formula (7) to determine its extremum ![]() is carried out as follows. Conditionally the
is carried out as follows. Conditionally the ![]() is substituted with regular variable
is substituted with regular variable![]() . Then the first derivative on
. Then the first derivative on ![]() is taken and equaled to zero. As a result we obtained following formula for optimal value of
is taken and equaled to zero. As a result we obtained following formula for optimal value of ![]()
 .
.
In order to check up if the found point of extremum indicates minimum or maximum of criterion (7) we calculate the value of criterion (7) at following points:
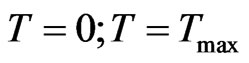 and
and .
.
As a result of calculations the following values of 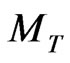 were found related with abovementioned points:
were found related with abovementioned points:
1)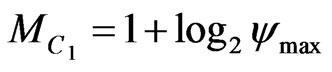 ;
;
2)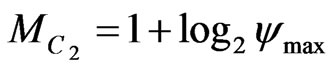 ;
;
3)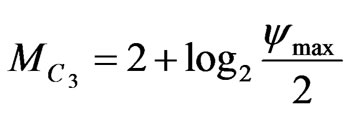 .
.
Thus, at the point of extremum we have 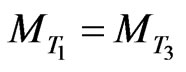 which in some conditions may exceed
which in some conditions may exceed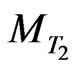 . In this case we can consider that the criterion (7) will obtain its maximal value. Therefore the condition of maximum of criterion (7) at the point
. In this case we can consider that the criterion (7) will obtain its maximal value. Therefore the condition of maximum of criterion (7) at the point 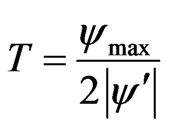 is as follows
is as follows
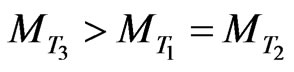
or
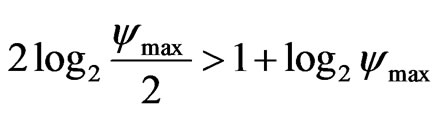 . (8)
. (8)
From unequality we find following condition
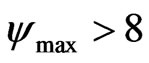 .
.
Thus, the suggested criterion of maximum entropy makes it possible to optimize the functioning of couple of UAV moving on counter-phrase trajectory.
4. Conclusions
The criterion for effectiveness of remote sensing system forming the image by the aim: a) further processing; b) detection of temporal changes of differences in spectral bands; c) accumulation and registration in GIS system is formulated.
The optimal point in trajectory, where the maximum effectiveness of system’s operation on criterion of maximum information entropy at the system output is calculated.
It is found that maximal effectiveness of the system on counter-phase trajectory can be reached if the maximal value of signal/noise ratio of measuring signal exceeds eight.
REFERENCES
- X. Dai and S. Khorram, “The effects of Image Misregistration on the Accuracy of Remotely Sensed Change Detection,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 36, No. 5, 1998, pp. 1566-1577. doi:10.1109/36.718860
- P. Viola and W. Wells, “Alignment by Maximization of Mutual Information,” Proceedings of the 5th International Conference on Computer Vision, Cambridge, 20- 23 June 1995, pp. 6-23.
- F. Maes, A. Collignon, D. Vandermeulen, G. Marchal and P. Suettens, “Multimodality Image Registration by Maximization of Mutual Information,” IEEE Transactions on Medical Imaging, Vol. 16, No. 2, 1997, pp. 187-198. doi:10.1109/42.563664
- H. Chen and P. K. Varshney, 2000, “A Pyramid Approach for Multimodality Image Registration Based on Mutual Information,” Proceedings of Fusion’ 2000, Paris, 10-13 July 2000, pp. MoD3-9-MoD3-15.
- K. Jonhson, A. C. Rhodes, I. Zavorin and J. LeMoigne, 2001, “Mutual Information as a Similarity Measure for Remote Sensing Image Registration,” Proceedings of SPIE, Orlando, 16-20 April 2001, pp. 51-61. doi:10.1117/12.428251
- X. Zhu and Y. Jia, “Solution to Joint Entropy and Its Applications in Remote Sensing.” www.isprs.org/proceedings/XXXV/congress/comm5/papers/621.pdf

