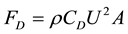Natural Science
Vol.07 No.06(2015), Article ID:56930,2 pages
10.4236/ns.2015.76034
Reaction Force on Bubbles
Kern E. Kenyon
Del Mar, California, USA
Email: kernken@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 May 2015; accepted 2 June 2015; published 5 June 2015
ABSTRACT
For large air bubbles rising steadily through still water, the upward reaction force on the spherical cap is calculated. When added to the buoyancy force on the roughly flat base of the bubble, the friction force at terminal velocity must be larger than it would be in the absence of the reaction force. Experimental data are used to estimate that the increase in the drag coefficient is expected to be about 4%.
Keywords:
Large Bubbles, Reaction Force

1. Introduction
When large air bubbles rise through still water, the main driving force is the buoyancy force, the excess hydrostatic pressure on the roughly flat bottom face, and the only retarding force is due to friction [1] . The reaction force on the smoothly spherical cap is left out of consideration in the earlier study. As water moves tangent to the cap, it accelerates away from the stagnation point at the very top of the cap. It takes a force to cause the fluid to accelerate, and it is the bubble that is producing that force. By Newton’s third law―action equals reaction, there is an equal but opposite force back on the bubble. Such a force has been called the reaction force for fluid flowing past solid bodies [2] . Here the concept is applied to an inanimate body that is capable of changing its shape as it moves through a fluid.
Significantly, for the first time it is possible to compare the magnitudes of the reaction and friction forces in the same problem. Also there is a related study of understanding the motion of flaccid bodies in fluids [3] .
In direction the reaction force on the cap has a net vertical component that attempts to pull the bubble upward; thus it points the same way as the buoyancy force and has the effect of increasing the buoyancy force. Friction must therefore be larger in order to balance both the buoyancy and reaction forces at equilibrium, or at the terminal velocity. How much bigger does friction need to be? In the calculation below the estimated increase in the drag coefficient necessary for terminal velocity when the reaction force is added to the buoyancy force turns out to be about 4%, based on the experimental data taken from [4] . A priori there is no way to guess at such a value.
It is interesting that the shape that a large bubble chooses for moving through water, a thin lens convex side up, is not what most people would consider to be “streamlined” or “aerodynamic”. However, remember that there is an actively swimming animal (without a brain even) that has evolved a similar shape: the jelly fish.
2. Calculation
Observations suggest that the cap of a large bubble is approximately spherical. That assumption will therefore be made in order to simplify the calculation. For the origin of coordinates the center of the sphere is used and the vertical axis passes through the highest point of the cap. From the origin to the tip of the cap is the radius of curvature, R, which is taken constant. The bubble has maximum thickness, h, known to be small compared to R (thin lens), constant upward speed, U, and the edge is given by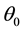 , where
, where  is measured counterclockwise from the horizontal axis (in [4] there is a good definition diagram where the angle is measured from the vertical axis, however).
is measured counterclockwise from the horizontal axis (in [4] there is a good definition diagram where the angle is measured from the vertical axis, however).
In the steady reference frame the bubble is motionless and the flow moves vertically downward toward the cap and then around it. At any point tangent to the cap the speed is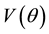 . What is of primary interest here is the acceleration tangent to the cap: dV/dt. Since near the stagnation point
. What is of primary interest here is the acceleration tangent to the cap: dV/dt. Since near the stagnation point
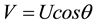 (1)
(1)
Then
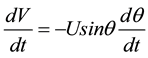 (2)
(2)
Also
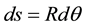 (3)
(3)
where ds is an element of arc length along the spherical cap. Therefore
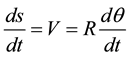 (4)
(4)
so the acceleration becomes
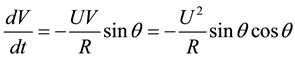 (5)
(5)
The force, F, per unit volume which causes this acceleration is
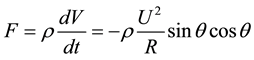 (6)
(6)
It is directed tangent to the cap sloping to the right and down, and the constant density of the water is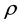 . By Newton’s third law the equal but opposite reaction force points to the left and up, and the vertical component of the reaction force,
. By Newton’s third law the equal but opposite reaction force points to the left and up, and the vertical component of the reaction force,  , is what helps drive the bubble upward together with the buoyancy force.
, is what helps drive the bubble upward together with the buoyancy force.
 (7)
(7)
Next step is to integrate the vertical force component,  , which is a force per unit volume, vertically through a layer perpendicular to the cap where fluid is also flowing approximately tangent to the cap and accelerating around it. This whole layer contributes to the reaction force per unit area of the cap. What should the thickness of this layer be?
, which is a force per unit volume, vertically through a layer perpendicular to the cap where fluid is also flowing approximately tangent to the cap and accelerating around it. This whole layer contributes to the reaction force per unit area of the cap. What should the thickness of this layer be?
Here a feature of the irrotational solution for flow past a sphere is imported: that the magnitude of the velocity component tangent to the sphere falls off with increasing distance from the origin perpendicular to the sphere, r, as the inverse cube of the distance [5] . Integrating the vertical reaction force using this function for U = U(r) produces
 (8)
(8)
Which is then averaged over the arc of the cap from 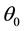 to
to 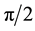 to give
to give

where the average value of 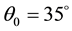
Finally, the total averaged vertical reaction force, 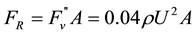
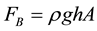
are the buoyancy and drag forces on the bubble, respectively [1] .
3. Discussion
By balancing the above buoyancy and friction forces in (10) and incorporating the empirical data from [4] , it was found in [1] that the mean drag coefficient for large bubbles is 1.0. This was considered a high value because it is known that the drag coefficient for a solid sphere is 0.4 when both the sphere and the large bubble have the same Reynolds number. If the reaction force is taken into account, the drag coefficient of the large bubble should be even higher, but in this case only by 4%. Perhaps if the bubble had a hemispheric shape, the reaction force might have been larger. That is speculation at this point.
In the above calculation, use of the inverse cube of the distance for the fall-off rate of the velocity in the irrotational solution for flow past a sphere could be questioned. For example, the analogous fall-off rate for a circular cylinder is the inverse square of the distance ([4] , p. 424), and to me physically there seems to be an inconsistency here. However, since an integration is performed over distance to obtain the reaction force per unit horizontal area, the result is not expected to be sensitive to the exact decay rate of the velocity.
References
- Kenyon, K.E. (2011) Drag of Large Bubbles. Physics Essays, 24, 1-3. http://dx.doi.org/10.4006/1.3518268
- Kenyon, K.E. (2006) Reaction Forces of Fluid Flows on Solid Boundaries. Physics Essays, 19, 507-516. http://dx.doi.org/10.4006/1.3028856
- Kenyon, K.E. (2015) Flaccid Bodies Move Faster in Fluids? International Journal of Innovation in Science and Mathematics. (In Press)
- Batchelor, G.K. (1967) An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge, 476.
- Faber, T.E. (1995) Fluid Dynamics for Physicists. Cambridge University Press, Cambridge, 135. http://dx.doi.org/10.1017/cbo9780511806735