Natural Science
Vol.07 No.01(2015), Article ID:53068,13 pages
10.4236/ns.2015.71003
Earthquake Barcode from a Single-Degree-of-Freedom System
Chein-Shan Liu1, Chih-Wen Chang2
1Department of Civil Engineering, National Taiwan University, Taipei, Taiwan
2Cloud Computing and System Integration Division, National Center for High-Performance Computing, Taichung, Taiwan
Email: liucs@ntu.edu.tw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 November 2014; revised 12 December 2014; accepted 29 December 2014
ABSTRACT
Earthquake is a violent and irregular ground motion that can severely damage structures. In this paper we subject a single-degree-of-freedom system, consisting of spring and damper, to an earthquake excitation, and meanwhile investigate the response behavior from a novel theory about the dynamical system 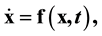 by viewing the time-varying signum function of
by viewing the time-varying signum function of 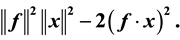 It can reflect the characteristic property of each earthquake through
It can reflect the characteristic property of each earthquake through 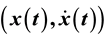 and the second component
and the second component 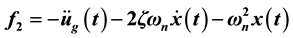 of f, where
of f, where 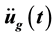 is a time-sampling record of the acceleration of a ground motion. The barcode is formed by plotting
is a time-sampling record of the acceleration of a ground motion. The barcode is formed by plotting 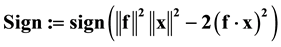 with respect to time. We analyze the complex jumping behavior in a barcode and an essential property of a high percentage occupation of the first set of dis-connec- tivity in the barcode from four strong earthquake records: 1940 El Centro earthquake, 1989 Loma earthquake, and two records of 1999 Chi-Chi earthquake. Through the comparisons of four earth- quakes, we can observe that strong earthquake leads to large percentage of the first set of dis-connectivity.
with respect to time. We analyze the complex jumping behavior in a barcode and an essential property of a high percentage occupation of the first set of dis-connec- tivity in the barcode from four strong earthquake records: 1940 El Centro earthquake, 1989 Loma earthquake, and two records of 1999 Chi-Chi earthquake. Through the comparisons of four earth- quakes, we can observe that strong earthquake leads to large percentage of the first set of dis-connectivity.
Keywords:
Earthquakes, Single-Degree-of-Freedom System, Signum Function, Barcode, Jumping Behavior, The First Set of Dis-Connectivity, Scale Invariance

1. Introduction
Earthquakes occur around the world frequently. The most are so small that they cannot be susceptible, and only a few are large enough to cause a noticeable damage of building. When a structure is subjected to an earthquake motion, its base foundation tends to move with the ground.
One of the most important applications of structural dynamics is by analyzing the response of structures to ground shaking caused by an earthquake, whose data are useful for establishing the structural response spectra. The identification and evaluation of ground motion parameters require access to the measurements of strong ground motions in an actual earthquake [1] -[3] .
The basic element of an accelerograph is a transducer element as described in [4] [5] , which in its simplest form is a single-degree-of-freedom mass-damper-spring system. Typically, the transducer has natural frequency fn = 25 Hz and damping ratio ζ = 60% for modern analog accelerographs, and fn = 50 Hz and ζ = 70% for modern digit accelerographs [4] .
A simple stationary representation of earthquake-induced ground acceleration was proposed by Kanai [6] and Tajimi [7] , based on the study of frequency content of a number of strong ground motion records. They suggested that the ground acceleration of the earth surface layer could be approximated by the absolute acceleration of a simple oscillator with a concentrated mass supported by a linear spring and a dashpot. The spectrum property of an earthquake is reflected in its interaction with the structures which have different damping ratios and natural periods. In general, one can use the response spectrum, power spectrum or the Fourier spectrum to characterize the spectrum property of an earthquake. In this paper we propose a novel method to characterize the earthquake property when it is exerted on a simple one-degree-of-freedom system:
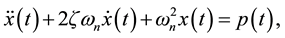 (1)
(1)
where 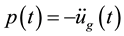 is the ground acceleration due to an earthquake; ζ is the damping ratio; and ωn is the natural frequency.
is the ground acceleration due to an earthquake; ζ is the damping ratio; and ωn is the natural frequency.
The ground motion produced by earthquake can be very complicated. The exact form of earthquakes is subjected to a high degree of uncertainty and complexity. There are several ways to estimate the ground motion parameters, which are essential for describing the important characteristics of strong ground motion in a compact quantitative form. Because of the complexity of the earthquake ground motion, the identification of a single parameter that can accurately describe all important ground motion characteristics is impossible. In this paper we try to use the barcode and the percentage of the first set of dis-connectivity in the barcode to reflect the characteristic property of an earthquake ground motion. It is known that a barcode is an optical machine-readable representation of data relating to the object to which it is attached. A main feature of the barcode is the intervened black lines and white lines with varying spacings and widths. Barcode is ubiquitously used in the identification and classification of human made products. Here we will use the barcode to identify the property of earthquake with the input 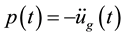 in Equation (1).
in Equation (1).
2. A System Formulation
To facilitate the formulation we write a system of first-order ordinary differential equations (ODEs):
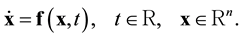 (2)
(2)
Here n = 2, 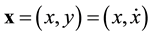 , and two components of f are
, and two components of f are 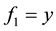 and
and 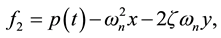 respectively.
respectively.
As that done by Liu [8] , for Equation (2) we can define a unit orientation vector:
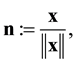 (3)
(3)
where 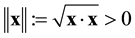 is the Euclidean norm of x, and the dot between two vectors, say
is the Euclidean norm of x, and the dot between two vectors, say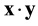 , denotes the inner product of x and y. Then we can derive [9] - [11]
, denotes the inner product of x and y. Then we can derive [9] - [11]


Equations (4) and (5) can be put together as

which is a Lie-type system endowing with the Lie-group symmetry SOo(n, 1) in the Minkowski space.
3. Two Branches Solutions
In order to develop a numerical scheme from Equation (6), we suppose that the coefficient matrix is constant with the pair

being constant in a small time stepsize.
From Equations (6) and (7) we thus need to solve a constant linear system:

Let


and Equation (8) becomes


At the same time, from the above equations we can derive the following ODEs for z, w and y:

where 


there exist two different types solutions of (z, w, y). Here, we do not give a detailed derivation of the solutions for (z, w, y) and the corresponding second generation group preserving scheme (GPS2), but the reader can refer [9] - [11] .
4. The Demonstration of Barcodes
It is significant that in Equation (14) we have derived a signum function to demand the algorithm into two branches. Without having the factor 2 before 
where θ is the intersection angle between x and f; hence, it makes no sense to define its signum function. On the contrast, by Equation (14) we have

which may be +1 or −1, depending on x and f by their intersection angle θ. When θ is in the range of 


4.1. Example 1
First we test an example with 

tion (1) in a time interval of

where 

Figure 1. Under (a) a harmonic force, showing (b) the signum function, (c) the responses, and (d) numerical error of displacement.
4.2. Example 2
Then with 


where Ri are random numbers between [−1, 1], the input, the Sign and the responses are plotted in Figure 2. It is interesting that the values of Sign are randomly jumping between +1 and −1 in some intervals of time.
4.3. Analyzing the Barcode under Earthquakes
With 



Now we analyze the Sign and the length as shown in Figure 4 within a short time interval of




Figure 2. Under (a) a random force, showing (b) the signum function, and (c) the responses.
Figure 3. Under (a) the El Centro earthquake, showing (b) the barcode, and (c) the responses.

where



We may call them the first set of dis-connectivity and the second set of dis-connectivity, respectively. Clearly, the first set of dis-connectivity is a subset of sign(c0) = +1, and the second set of dis-connectivity is a subset of sign(c0) = −1.
If Equation (2) satisfies
Figure 4. Under the El Centro earthquake, (a) showing two signum functions, and (b) the length with a small time interval.
Figure 5. A schematic plot of the area of Sign = +1, Sign = −1, sign(c0) = +1, and sign(c0) = −1 in the plane.

Under the first assumption the case in Equation (20) is impossible because it contradicts to
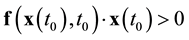


because the two sets of dis-connectivity are dis-connected, and from the first set to the second set it must go to


which means that the length grows with time. Thus, Equation (21) is proven.
For a system being excited by earthquake the value of Sign is not always +1 as that shown in Figure 1(b) for the harmonic input. As shown in Figure 3(b) the values of Sign are varying between −1 to +1 and +1 to −1 very fast, and then the Sign will return to +1 again as shown in Figure 4(a); otherwise, by Equation (21) the system will respond unstably and thus the displacement will tend to infinity. In order to compare the values of sign(c0) with the values of Sign we plot them in Figure 4(a) with solid line and dashed line, respectively, where we make a slight shift of the dashed line downward for clear. On the other hand, for a distinction the first set of dis-con- nectivity is filled by solid black points.
As shown in Figure 5, in the plane the areas of sign(c0) = +1 and sign(c0) = −1 are connected while that the sets of Sign = +1 and Sign = −1 are dis-connected as mentioned in the above. When sign(c0) changes from +1 to −1, for example from point f1 to point f2 in the figure, the Sign must jump from −1 to +1. This jumping behavior is termed a cross jumping. On the other hand, we also find the co-jumping behavior which is happened when both the Sign and sign(c0) are jumping from −1 to +1 simultaneously. The above two jumping behaviors are collected as a coupled-jumping, which renders a quite complex structure of the barcode as shown in Figure 3(b).
From Figure 4(a) we can observe the following interesting phenomena: 1) While the first set of dis-connec- tivity is a subset of sign(c0) = +1, the second set of dis-connectivity is a subset of sign(c0) = −1. 2) In a time interval of the state with Sign = −1, the state is either in the first set of dis-connectivity or in the second set of dis- connectivity. 3) From one first set of dis-connectivity to another first set of dis-connectivity there must accompany a jump from Sign = −1 to Sign = +1. This also holds for the second set of dis-connectivity. 4) From one first set of dis-connectivity to one second set of dis-connectivity, or vice-versa, there must accompany a jump from Sign = −1 to Sign = +1. For some cases this jumping only happens at one time point. 5) When sign(c0) jumps from +1 to −1 as remarked in Figure 4(a) by the symbols + and − (i.e., the length is decreased), and if the Sign is in the state of −1, then the Sign will jump from −1 to +1 as remarked in Figure 4(a) by the symbols − and +. Indeed in Figure 4(a) we can observe that there are four times to happen the cross jumping behavior in the interval of
In Figure 6 we compare the barcodes with 1)











4.4. The First Set of Dis-Connectivity under Earthquakes
In this example we let the Chi-Chi earthquake be the input to Equation (1). With 



In Figure 8 we compare the barcodes with 1)











In Figure 9(a) for the Chi-Chi earthquake with different scaling factor fr in 


Figure 6. Under the El Centro earthquake, comparing the barcodes under different scaling factor, damping ratio and natural period.
of coupled-jumping as discussed above with respect to the scaling factor fr in Figure 9(c). It can be seen that the number is either 24 or 25. In the plane as shown in Figure 5, the first set of dis-connectivity with Sign = −1 is only in one quarter. But under a strong earthquake, the high occupation of the first set of dis-connectivity is near to fifty percentage as shown in Figure 9(b).
In Figure 10, under the Chi-Chi earthquake (CHY080) as shown in (a), we plot the first set of dis-connectiv- ity which is near to forty nine percentage as shown in Figure 10(b), and the number of coupled-jumping is plotted in Figure 10(c), which is either 6 or 7.
In Figure 11(a) for the El Centro earthquake (ELC180) with different scaling factor fr in





It is surprising that the percentage of the first set of disconnectivity and the number of coupled-jumping are almost constant for each earthquake, which seems to be scale-invariant. In the plane as shown in Figure 5, the
Figure 7. Under the Chi-Chi earthquake (CHY028) in (a), (b) showing the barcode, and (c) the responses.
first set of dis-connectivity with Sign = −1 is only in one quarter. But under strong earthquakes, the high occupation of the first set of dis-connectivity is near to fifty percentage. The high percentage of occupation demonstrates the importance of the first set of dis-connectivity in the strong earthquake motion. As comparing the above four earthquakes we can also observe that stronger earthquake leads to larger percentage of the first set of dis-connectivity. Finally, under the same scaling factor fr = 0.5 in 



5. Conclusions
For a single-degree-of-freedom system subjected to an earthquake excitation, we have investigated the response
Figure 8. Under the Chi-Chi earthquake (CHY028), comparing the barcodes under different scaling factor, damping ratio and natural period.
behavior from a newly developed theory about the dynamical system of 

Figure 9. Under (a) the Chi-Chi earthquake (CHY028) with different scaling factor, showing (b) the percentage in the first set of dis-connectivity, and (c) the number of coupled-jumping.
Figure 10. Under (a) the Chi-Chi earthquake (CHY080) with different scaling factor, showing (b) the percentage in the first set of dis-connectivity, and (c) the number of coupled-jumping.
Figure 11. Under (a) the El Centro earthquake (ELC180) with different scaling factor, showing (b) the percentage in the first set of dis-connec- tivity, and (c) the number of coupled-jumping.
Figure 12. Under (a) the 1989 Loma Prieta earthquake (47379 Gilroy Array #1) with different scaling factor, showing (b) the percentage in the first set of dis-connectivity, and (c) the number of coupled-jumping.
Figure 13. Comparing the relative percentages of first set of dis-con- nectivity for the El Centro earthquake (ELC180), two records (CHY028, CHY080) of Chi-Chi earthquake, and the Loma Prieta earthquake (47379 Gilroy Array #1).
earthquakes, and its number seems scale-independence. This is just an initial study by correlating the percentage of the first set of dis-connectivity to the earthquake, and there are still many works to study the barcode and the use of it to forecast the intensity of earthquake before the rapid coming of main shock impulse. In the future, we will analyze the signal of barcode for many earthquake records, and thus we can correlate the intensity and frequency content of an earthquake to the first set of dis-connectivity.
References
- Loh, C.H., Lee, Z.K., Wu, T.C. and Peng, S.Y. (2000) Ground Motion Characteristics of the Chi-Chi Earthquake of 21 September 1999. Earthquake Engineering and Structural Dynamics, 29, 867-897. http://dx.doi.org/10.1002/(SICI)1096-9845(200006)29:6<867::AID-EQE943>3.0.CO;2-E
- Sokolov, V.Y., Loh, C.H. and Wen, K.L. (2002) Comparison of the Taiwan Chi-Chi Earthquake Strong-Motion Data and Ground-Motion Assessment Based on Spectral Model from Smaller Earthquakes in Taiwan. Bulletin of the Seismological Society of America, 92, 1855-1877. http://dx.doi.org/10.1785/0120010178
- Sokolov, V.Y., Loh, C.H. and Wen, K.L. (2003) Evaluation of Hard Rock Spectral Models for the Taiwan Region on the Basis of the 1999 Chi-Chi Earthquake Data. Soil Dynamics and Earthquake Engineering, 23, 715-735. http://dx.doi.org/10.1016/S0267-7261(03)00075-7
- Chopra, A.K. (1995) Dynamics of Structures: Theory and Applications to Earthquake Engineering. Prentice-Hall, New Jersey.
- Kramer, S.L. (1996) Geotechnical Earthquake Engineering. Prentice-Hall, New Jersey.
- Kanai, K. (1957) Semi-Empirical Formula for the Seismic Characteristics of the Ground. Bulletin of the Earthquake Research Institute, University of Tokyo, 35, 309-325.
- Tajimi, H. (1960) A Statistical Method of Determining the Maximum Responses of a Building Structure during an Earthquake. Proceeding of the 2nd World Conference on Earthquake Engineering, Japan, 781-797.
- Liu, C.-S. (2001) Cone of Non-Linear Dynamical System and Group Preserving Schemes. International Journal of Non-Linear Mechanics, 36, 1047-1068. http://dx.doi.org/10.1016/S0020-7462(00)00069-X
- Liu, C.-S. and Jhao, W.S. (2014) The Second Lie-Group SOo(n,1) Used to Solve Ordinary Differential Equations. Journal of Mathematic Research, 6, 18-37.
- Liu, C.-S. (2014) Disclosing the Complexity of Nonlinear Ship Rolling and Duffing Oscillators by a Signum Function. CMES: Computer Modeling in Engineering & Sciences, 98, 375-407.
- Liu, C.-S. (2015) A Novel Lie-Group Theory and Complexity of Nonlinear Dynamical Systems. Communications in Nonlinear Science and Numerical Simulation, 20, 39-58. http://dx.doi.org/10.1016/j.cnsns.2014.05.004

















